Bipartite Edge Correlation Clustering: Finding an Edge Biclique
Partition from a Bipartite Graph with Minimum Disagreement
Mikio Mizukami
1
, Kouich Hirata
1
and Tetsuji Kuboyama
2
1
Kyushu Institute of Technology, Kawazu 680-4, Iizuka 820-8502, Japan
2
Gakushuin University, Mejiro 1-5-1, Toshima, Tokyo 171-8588, Japan
Keywords:
Bipartite Edge Correlation Clustering, Edge Biclique Partition, Minimum Disagreement, Bipartite Correlation
Clustering, Bicluster Graph Editing, Biclustering.
Abstract:
In this paper, first we formulate the problem of a bipartite edge correlation clustering which finds an edge
biclique partition with the minimum disagreement from a bipartite graph, by extending the bipartite correlation
clustering which finds a biclique partition. Then, we design a simple randomized algorithm for bipartite edge
correlation clustering, based on the randomized algorithm of bipartite correlation clustering. Finally, we give
experimental results to evaluate the algorithms from both artificial data and real data.
1 INTRODUCTION
The notion of biclustering has first introduced by
Cheng and Chruch (Cheng and Church, 2000) in the
context of computational biology or bioinformatics
and developed by several researchers with many alter-
native formulations and different applications and ap-
proaches, see (Madeira and Oliveira, 2004; Oghabian
et al., 2014; Pio et al., 2013; Pio et al., 2015) and their
references, for example. The biclustering performs si-
multaneous row-column clustering from a matrix. In
other words, it finds a bicluster as a subset of rows
and a subset of columns, defining together a subma-
trix that shows unique, similar expression patterns ac-
cording to some sorting method.
In this paper, as combinatorial optimization rather
than computational biology, we focus on the formu-
lation of the biclustering by regarding matrices as bi-
partite graphs. In this formulation, we call the bi-
clustering the bipartite correlation clustering (Alion
et al., 2012; Asteris et al., 2016) or bicluster graph
editing (Amit, 2004), which is the problem to find
the collection of bicliques as a biclique partition from
a bipartite graph with the minimum disagreement.
Here, a biclique in a bipartite graph is a set of vertices
such that every left vertex is adjacent to every right
vertex. Also a disagreement is the number of edges
when constructs a biclique if added or when divides
two bicliques if removed.
In this context, Amit (Amit, 2004) has first
shown that the bipartite correlation clustering with
the minimum disagreement is NP-hard and provided
a polynomial-time algorithm that guarantees an ap-
proximation factor of 11. Also Alion et al. (Alion
et al., 2012) have designed both the deterministic and
the randomized algorithms of the bipartite correlation
clustering whose expected value of the disagreement
is at most 4 times of the optimum solution. Fur-
thermore, Asteris et al. (Asteris et al., 2016) have
shown a PTAS when adopting the maximum agree-
ment, not the minimum disagreement. In particu-
lar, since the randomized algorithm, called PIVOTBI-
CLUSTER (Alion et al., 2012), is simple and runs effi-
ciently, in this paper, first we focus on this algorithm.
Note that, when applying this algorithm to real
problems, it tends to construct many singletons, that
is, bicliques consisting of a single vertex adjacent to
no vertices. On the other hand, when we find some
communities in community detection from a bipartite
graph, the purpose is find subgraphs with high den-
sity of edges. Also, a biclique partition in bipartite
correlation clustering consists of biclusters such that
one vertex belongs to just one bicluster as a commu-
nity. Then, in order to achieve the purpose, we prefer
to extract bicluster with exclusive edges rather than
exclusive vertices in bipartite correlation clustering.
As more appropriate setting to achieve the pur-
pose, an edge biclique as a set of edges has been
researched from the viewpoint of combinatorial op-
timization in bipartite graphs (Chalermsook et al.,
2014; Chandran et al., 2016; Orlin, 1977). It is known
that the problem of finding an edge biclique partition
Mizukami, M., Hirata, K. and Kuboyama, T.
Bipartite Edge Correlation Clustering: Finding an Edge Biclique Partition from a Bipartite Graph with Minimum Disagreement.
DOI: 10.5220/0007471506990706
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 699-706
ISBN: 978-989-758-351-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
699

as the collection of edge bicliques with the minimum
cardinality from a bipartite graph is NP-hard (Jiang
and Raviunar, 1993) and hard to approximateas graph
coloring (Chalermsook et al., 2014).
In this paper, by extending the bipartite correlation
clustering, we formulate the bipartite edge correla-
tion clustering which finds an edge biclique partition
with the minimum disagreement from a labeled com-
plete bipartite graph. As similar as the bipartite cor-
relation clustering, we can formulate the input of the
bipartite edge correlation clustering as a (non-labeled
non-complete) bipartite graph.
Then, by improving the algorithm PIVOTBI-
CLUSTER, we design the randomized algorithm PIV-
OTBICLUSTEREDGE of the bipartite edge correlation
clustering, which outputs no singletons. Also, in this
paper, we design the deterministic versions of PIV-
OTBICLUSTER and PIVOTBICLUSTEREDGE, where
the former outputs no singletons.
Finally, we give experimental results of evaluat-
ing the algorithms in order to compare bipartite edge
correlation clustering with bipartite correlation clus-
tering and to confirm the probabilistic execution. We
use two kinds of data, one is artificial data and another
is real data of not only MovieLens datasets
1
discussed
in (Asteris et al., 2016) but also Crime (MC)
2
, Sexual
escorts (SX)
2
, arXiv cond-mat (AC)
2
, Jester 100 (J1)
2
and YouTube (YG)
2
provided from KONECT
3
.
2 BIPARTITE CORRELATION
CLUSTERING
Let G = (L, R, E) be a bipartite graph. We say that
C
i
= (L
i
, R
i
, E
i
) is a biclique in G if L
i
⊆ L, R
i
⊆ R,
E
i
⊆ E and (l, r) ∈ E
i
for every l ∈ L
i
and r ∈ R
i
. Note
that a singleton either ({l},
/
0,
/
0) or (
/
0, {r},
/
0) is al-
ways a biclique.
Definition 1. Let C = {C
1
, . . . ,C
k
} be a collection of
bicliques in G. We say that C is a biclique partition
of G if
1.
k
[
i=1
L
i
= L,
k
[
i=1
R
i
= R and
2. L
i
∩L
j
=
/
0 and R
i
∩R
j
=
/
0 for every i, j (1 ≤ i, j ≤
k, i 6= j).
Note that E is not required to coincide with
k
[
i=1
E
i
.
1
http://grouplens.org/datasets/movielens/
2
http://konect.uni-koblenz.de/networks/
{monero
crime, escorts, opshal-collaboration, jester1,
youtube-groupmemberships}
3
http://konect.uni-koblenz.de
Example 1. Let G = (L, R, E) and C
i
(1 ≤ i ≤ 4) be
the following bipartite graph and bicliques.
L = {1, 2}, R = {a, b},
E = {(1, a), (1, b), (2, b)},
C
1
= ({1}, {a, b}, {(1, a), (1, b)}),
C
2
= ({2},
/
0,
/
0),
C
3
= ({1}, {a}, {(1, a)}),
C
4
= ({2}, {b}, {(2, b)}).
Then, both {C
1
,C
2
} and {C
3
,C
4
} are biclique parti-
tions of G.
Let G = (L, R, E) be a complete bipartite graph
such that every edge e ∈ E is assigned to a label
l(e) of either 1 (positive) or −1 (negative), which
we call a labeled complete bipartite graph. Let C =
{C
1
, . . . ,C
k
} be a biclique partition of G, where C
i
=
(L
i
, R
i
, E
i
). Also let E
+
C
=
k
[
i=1
E
i
and E
−
C
= E \ E
+
C
.
Then, the disagreement da
G
(C ) of C in G is defined
as follows.
da
G
(C )
= |{e ∈ E
+
C
| l(e) = −1}| + |{e ∈ E
−
C
| l(e) = 1}|.
Definition 2 (Amit (Amit, 2004)). The problem BIC-
OCLUST of bipartite correlationclustering (or biclus-
ter graph editing) is defined as follows.
BICOCLUST
INSTANCE: A labeled complete bipartite
graph G = (L, R, E).
SOLUTION: Find a biclique partition C of G
such that da
G
(C ) is minimum.
We can formulate the problem BICOCLUST by
using a non-labelednon-complete bipartite graph G =
(L, R, E). When G is given as an instance the prob-
lem BICOCLUST, we assume that every element in E
(resp., (L× R) \ E) is assigned to 1 (resp., −1). Then,
we regard a biclique partition of a labeled complete
bipartite graph as a partition of a bipartite graph con-
taining non-bicliques, which we also call a cluster or
a bicluster.
Amit (Amit, 2004) has first shown that the prob-
lems of BICOCLUST is NP-hard. Furthermore, Alion
et al. (Alion et al., 2012) have designed both a de-
terministic and a randomized algorithms of BICO-
CLUST that output the biclique partition whose ex-
pected value of the disagreement is at most 4 times of
the optimum solution.
Algorithm 1 illustrates the randomized algorithm
PIVOTBICLUSTER (Alion et al., 2012) which guaran-
tees probabilistic 4-approximation of the problem of
BICOCLUST.
As related works to the problem BICOCLUST,
Asteris et al. (Asteris et al., 2016) have discussed the
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
700

procedure PIVOTBICLUSTER(G)
/* G = (L, R, E): bipartite graph */
Γ ←
/
0; /* Γ: set of clusters */1
while L 6=
/
0 do2
select l
1
∈ L uniform randomly;3
C ← {l
1
} ∪ N(l
1
); /* C: cluster */
L
′
← L\ {l
1
}; R
′
← R\ N(l
1
);4
foreach l
2
∈ L \ {l
1
} do5
R
1
← N(l
1
) \ N(l
2
);6
R
2
← N(l
2
) \ N(l
1
);
R
1,2
← N(l
1
) ∩ N(l
2
);
With probability min

|R
1,2
|
|R
2
|
, 1

do
7
begin8
if |R
1,2
| ≥ |R
1
| then C ← C∪ {l
2
};9
else Γ ← Γ ∪ {{l
2
}};
L
′
← L
′
\ {l
2
};10
end11
Γ ← Γ∪ {C}; L ← L
′
; R ← R
′
;12
Γ ← Γ∪ {{r} | r ∈ R};13
output Γ;14
Algorithm 1: PIVOTBICLUSTER (Alion et al., 2012).
problem of finding a biclique partition with maximiz-
ing the agreement ag
G
(C ), not minimizing the dis-
agreement, where:
ag
G
(C )
= |{e ∈ E
+
C
| l(e) = 1}| + |{e ∈ E
−
C
| l(e) = −1}|.
Then, they have shown that this problem has a
PTAS (Asteris et al., 2016). We will use the agree-
ment in Section 4.
3 BIPARTITE EDGE
CORRELATION CLUSTERING
In this paper, we focus on bipartite correlation clus-
tering based on edge bicliques as a set of edges, not
bicliques as a set of vertices, which we call bicluster
edge correlation clustering.
Definition 3. Let C = {C
1
, . . . ,C
k
} be a collection of
bicliques in G such thatC
i
= (L
i
, R
i
, E
i
). Then, we say
that C is an edge biclique partition of G if
1.
k
[
i=1
E
i
= E and
2. E
i
∩ E
j
=
/
0 for every i, j (1 ≤ i, j ≤ k, i 6= j).
It is possible that L
i
∩ L
j
6=
/
0 and R
i
∩ R
j
6=
/
0.
Example 2. Consider the bipartite graph G and the
bicliques C
i
(1 ≤ i ≤ 4) in Example 1. Also let C
5
and
C
6
be the following bicliques.
C
5
= ({2}, {b}, {(2, b)}),
C
6
= ({1}, {b}, {(1, b)}).
Then, both {C
1
,C
5
} and {C
3
,C
4
,C
6
} are edge bi-
clique partitions of G.
As the hardness results for the problem of find-
ing an edge biclique partition from a bipartite graph,
it is known that the problem of finding the edge
biclique partition whose cardinality is minimum is
NP-hard (Jiang and Raviunar, 1993) and as hard
to approximate as graph coloring (Chalermsook
et al., 2014). Furthermore, the approximation algo-
rithm (Chalermsook et al., 2014) and the FPT algo-
rithm (Chandran et al., 2016) of this problem have
discussed.
In this paper, by extending the problem BICO-
CLUST from a biclique partition to an edge biclique
partition in Definition 2, we introduce the following
problem concerned with an edge biclique partition.
Definition 4. The problem BIEGCOCLUST of bipar-
tite edge correlation clustering is defined as follows.
BIEGCOCLUST
INSTANCE: A labeled complete bipartite
graph G = (L, R, E).
SOLUTION: Find an edge biclique partition C
of G such that da
G
(C ) is minimum.
As same as the problem BICOCLUST, we can adopt
the formulation of the problem BIEGCOCLUST by
using a non-labeled bipartite graph.
By improving the algorithm PIVOTBICLUSTER
in Algorithm 1, we design the randomized algorithm
PIVOTBICLUSTEREDGE in Algorithm 2 of solving
the problem of BIEGCOCLUST.
The algorithm PIVOTBICLUSTER in Algorithm 1
finds clusters of verticeswith deleting vertices. On the
other hand, the algorithm PIVOTBICLUSTEREDGE
in Algorithm 2 finds clusters of edges with deleting
edges.
Then, the algorithm PIVOTBICLUSTEREDGE
uses the condition that E 6=
/
0 in while loop in line 2,
which is the condition that L 6=
/
0 in the algorithm PIV-
OTBICLUSTER. Also it works nothing when |R
1,2
| <
|R
1
| in line 10, and deletes l
2
from L
′
when N(l
2
) is
empty after deleting edges in E
1,2
in line 12. As same
as PIVOTBICLUSTER, PIVOTBICLUSTEREDGE al-
ways works nothing when R
1,2
=
/
0.
Example 3. Consider the bipartite graph G in Fig-
ure 1.
Then, by selecting l
1
as h1, 5, 6, 3i in this order, the
algorithm constructs a cluster C
i
and transforms to a
graph G
i
in the i-th while loop (1 ≤ i ≤ 4) in Figure 1.
In this case, the algorithm constructs every cluster
uniquely, since every probability is either 0 or 1.
Hence, algorithm outputs a set Γ
1
= {C
1
,C
2
,C
3
,C
4
}
of clusters.
Bipartite Edge Correlation Clustering: Finding an Edge Biclique Partition from a Bipartite Graph with Minimum Disagreement
701

procedure PIVOTBICLUSTEREDGE(G)
/* G = (L, R, E): bipartite graph */
Γ ←
/
0; /* Γ: set of clusters */1
while E 6=
/
0 do2
select l
1
∈ L uniform randomly;3
E
1
← {(l
1
, r) | r ∈ N(l
1
)}; C ← E
1
;4
E ← E \E
1
; /* C: cluster */
L
′
← L\ {l
1
}; R
′
← R\ N(l
1
);5
foreach l
2
∈ L \ {l
1
} do6
R
1
← N(l
1
) \ N(l
2
);7
R
2
← N(l
2
) \ N(l
1
);
R
1,2
← N(l
1
) ∩ N(l
2
);
With probability min

|R
1,2
|
|R
2
|
, 1

do
8
begin9
if |R
1,2
| ≥ |R
1
| then10
E
1,2
← {(l
2
, r) | r ∈ R
1,2
};11
C ← C ∪ E
1,2
; E ← E \E
1,2
;
if N(l
2
) =
/
0 then12
L
′
← L
′
\ {l
2
};
13
end14
Γ ← Γ∪ {C}; L ← L
′
; R ← R
′
;15
output Γ;16
Algorithm 2: PIVOTBICLUSTEREDGE.
G G
1
G
2
G
3
l
1
= 1 l
1
= 5 l
1
= 6 l
1
= 3
C
1
C
2
C
3
C
4
Figure 1: The graph G, the constructed cluster C
i
(i =
1, 2, 3, 4) and the transformed graph G
j
(j = 1, 2, 3).
On the other hand, when the selection of l
1
is
changed, the algorithm outputs different sets of clus-
ters. Figure 2 illustrates the sets Γ
1
(same as above),
Γ
2
, Γ
3
, Γ
4
and Γ
5
of clusters when the selection of
l
1
is (1) h1, 5, 6, 3i, (2) h2, 1, 4, 6i, (3) h6, 3, 1, 2i, (4)
h6, 2, 1i and (5) h6, 1, 3i in this order. In all the cases,
every probability is also either 0 or 1.
In the remainder of this section, in order to
evaluate the probabilistic effect in the randomized
algorithms PIVOTBICLUSTER and PIVOTBICLUS-
TEREDGE, we design the deterministic versions of
them.
Γ
1
Γ
2
Γ
3
Γ
4
Γ
5
h1, 5, 6, 3i h2, 1, 4, 6i h6, 3, 1, 2i h6, 2, 1i h6, 1, 3i
Figure 2: Sets Γ
i
(1 ≤ i ≤ 5) of clusters.
First, we replace the random selection of l
1
∈ L in
line 3 in Algorithm 1 and line 2 in Algorithm 2 with
the following statement.
select l
1
∈ argmax{|N(l)| | l ∈ L};
Here, when the candidates of l
1
exist more than two,
we select the minimum index of l
1
.
Next, we improve the algorithms to execute
just when |R
1,2
| ≥ |R
2
|, that is, the probability of
min{
|R
1,2
|
|R
2
|
, 1} is 1. For PIVOTBICLUSTER, we re-
place the statements from lines 7 to 11 in Algorithm 1
with the following statements.
if |R
1,2
| > 0 and |R
1,2
| ≥ max{|R
1
|, |R
2
|} then
C ← C ∪ {l
2
};
L
′
← L
′
\ {l
2
};
We denote this algorithm by DETPIVOTBICLUSTER.
Note that the algorithm DETPIVOTBICLUSTER out-
puts singletons just the last execution corresponding
to line 13 in Algorithm 1.
On the other hand, for PIVOTBICLUSTEREDGE,
we replace the statements from lines 8 to 13 in Algo-
rithm 2 with the following statements.
if |R
1,2
| > 0 and |R
1,2
| ≥ max{|R
1
|, |R
2
|} then
E
1,2
← {(l
2
, r) | r ∈ R
1,2
}; C ← C ∪ E
1,2
;
E ← E \ E
1,2
;
if N(l
2
) =
/
0 then L
′
← L
′
\ {l
2
};
We denote this algorithm by DETPIVOTBICLUS-
TEREDGE. For example, when applying the algo-
rithm DETPIVOTBICLUSTEREDGE to G in Figure 1,
we obtain just Γ
5
in Figure 2, after selecting l
1
as
h6, 1, 3i in this order.
All of the algorithms of PIVOTBICLUSTER, PIV-
OTBICLUSTEREDGE, DETPIVOTBICLUSTER and
DETPIVOTBICLUSTEREDGE run in O(nm) time,
where n = |L| and m = |R| for a bipartite graph
(L, R, E). Then, the difference between the running
time of the algorithms in Section 4 later follows from
the number of iterations.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
702

4 EXPERIMENTAL RESULTS
In this section, we give experimental results of evalu-
ating the algorithms. We use two kinds of data. One
is artificial data of 4 kinds of biclusters obtained by
selecting exclusive or overlapped and row or column.
Another is real data of not only MovieLens dataset
1
discussed in (Asteris et al., 2016) but also datasets of
Crime (MC)
2
, Sexual escorts (SX)
2
, arXiv cond-mat
(AC)
2
, Jester 100 (J1)
2
and YouTube (YG)
2
.
4.1 Artificial Data
First, we give experimental results for artificial data.
For natural numbers a, b and c (a < b), we de-
note a square enclosing four points (a, b), (a + c, b),
(a, b+ c) and (a + c, b+ c) by [a, b;c]. We regard the
square [a, b;c] as the complete bipartite graphs such
that L = {a, . . . , a + c} and R = {b, . . . , b+ c}. Then,
we prepare the following five sets D
xy
of squares as
data for clustering. Here, s,t ∈ {e, o}, e denotes “ex-
clusive” and o denotes “overlapped,” according to
(Madeira and Oliveira, 2004).
D
ee
(exclusive row and column biclusters):
[1, 1;100], [101, 101;100], [201, 201;100],
[301, 301;100] and [401, 401;100].
D
eo
(exclusive row and overlapped column
biclusters): [1, 1;100], [101, 91;100],
[201, 181;100], [301, 271;100] and
[401, 361;100].
D
oe
(overlapped row and exclusive column
biclusters): [1, 1;100], [91, 101;100],
[181, 201;100], [271, 301;100] and
[361, 401;100].
D
oo
(overlapped row and column biclusters):
[1, 1;100], [91, 91;100], [181, 181;100],
[271, 271;100] and [361, 361;100].
Furthermore, we also use data with noises by flipping
from 1% to 10% points in whole data.
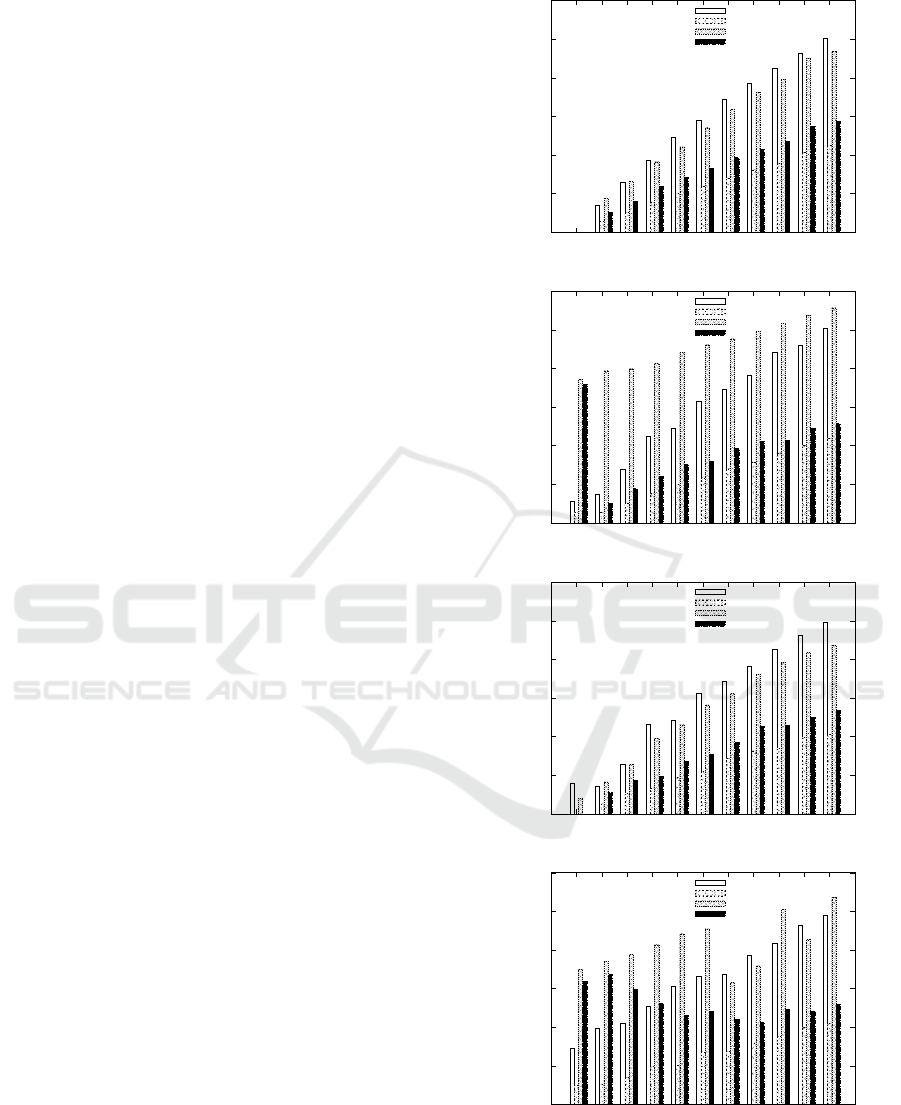
Figure 3 illustrates the average value of disagree-
ments pointed by y-axis obtained by applying the al-
gorithms to D
st
(s,t ∈ {e, o}) with k% noises pointed
by x-axis at 20 times.
Figure 3 shows that the value of disagreements
for PIVOTBICLUSTEREDGE is always smaller than
that for PIVOTBICLUSTER. Also the value of dis-
agreements for DETPIVOTBICLUSTEREDGE is al-
ways smaller than that for DETPIVOTBICLUSTER.
Then, the value of disagreements when finding an
edge biclique partition is smaller than the value of dis-
agreements when finding a biclique partition.
As the result for comparing probabilistic algo-
rithms with deterministic algorithms, the value of
0
10000
20000
30000
40000
50000
60000
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
ee
0
10000
20000
30000
40000
50000
60000
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
eo
0
10000
20000
30000
40000
50000
60000
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
oe
0
10000
20000
30000
40000
50000
60000
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
oo
Figure 3: The average value of disagreements obtained by
applying the algorithms to D
st
(s,t ∈ {e, o}) with k% noises.
Bipartite Edge Correlation Clustering: Finding an Edge Biclique Partition from a Bipartite Graph with Minimum Disagreement
703

disagreements for PIVOTBICLUSTEREDGE is always
smaller than that for DETPIVOTBICLUSTEREDGE.
On the other hand, the value of disagreements for
PIVOTBICLUSTER is smaller than that for DETPIV-
OTBICLUSTER for D
eo
and larger for D
ee
and D
oe
.
For D
oo
, the value of disagreements for PIVOTBI-
CLUSTER is larger than that for DETPIVOTBICLUS-
TER when adding with 6%, 7% and 9% noises and
smaller otherwise.
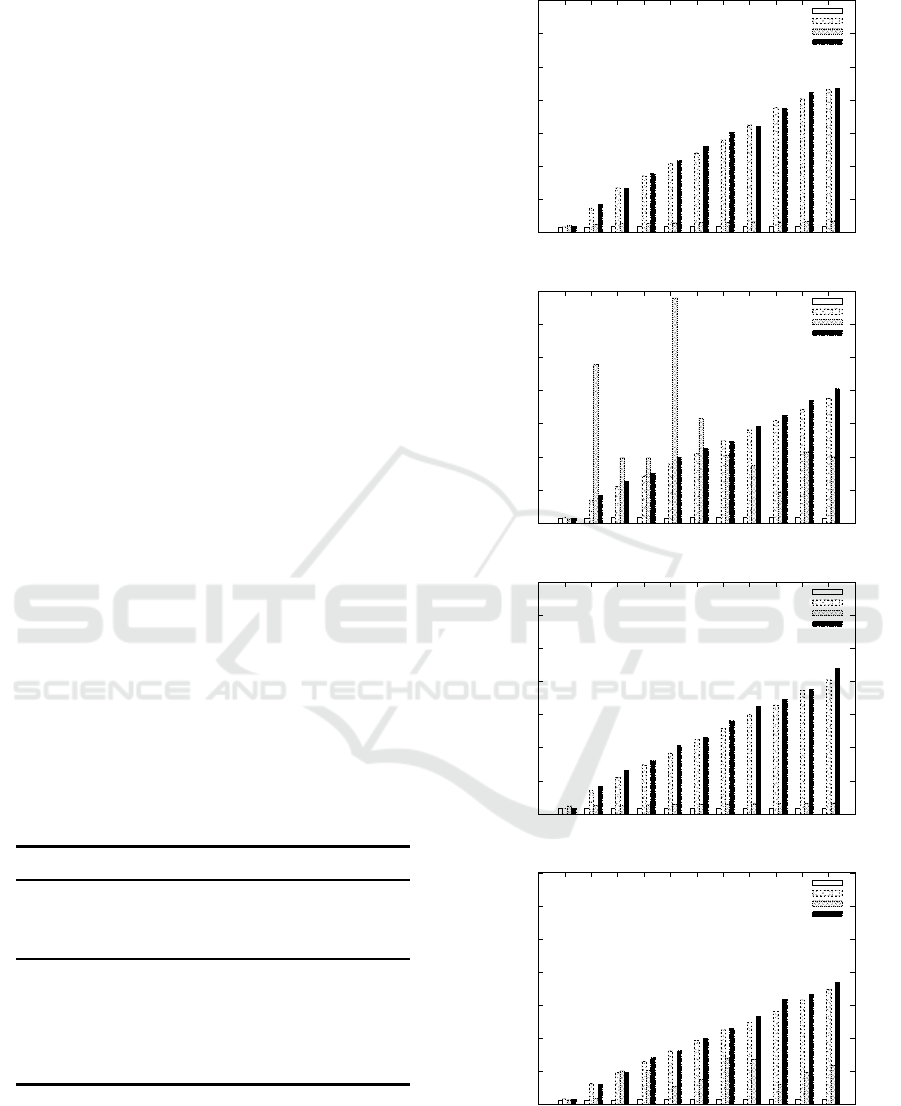
Figure 4 illustrates the average running time (sec.)
pointed by y-axis to applying the algorithms to D
st
for
s,t ∈ {e, o} with k% noises at 10 times.
Figure 4 shows that PIVOTBICLUSTER is the
fastest algorithm in four algorithms. Also, in al-
most cases, DETPIVOTBICLUSTER is the second
fastest algorithm. On the other hand, both PIVOTBI-
CLUSTEREDGE and DETPIVOTBICLUSTEREDGE
are much slower than PIVOTBICLUSTER and DET-
PIVOTBICLUSTER, except D
eo
with from 1% to 5%
noises.
By incorporating Figure 3 with Figure 4, we can
conclude that smaller value of disagreements implies
larger running time and vice versa. One of the reasons
why the algorithm is slow is that the number of itera-
tions in it is large and then the value of disagreements
decreases while iterating.
4.2 Real Data
Next, we give experimental results by using real data
such that MovieLens datasets
1
with comparing the re-
sult in (Asteris et al., 2016) and datasets of CM, SX,
AC, J1 and YG from KONECT
3
. Table 1 summarizes
such data as a bipartite graph G = (L, R, E).
Table 1: Summary of MovieLens datasets and datasets of
CM, SX, AC,J1 and YG as a bipartite graph G = (L, R, E).
dataset |L| |R| |E|
MovieLens100K 1,000 1,700 10,000
MovieLens1M 6,000 4,000 100,000
MovieLens10M 72,000 10,000 1,000,000
CM 829 551 1,476
SX 10,106 6,624 39,044
AC 16,726 22,015 58,595
J1 73,421 100 4,136,360
YG 94,238 30,087 293,360
In the following tables, we denote the algo-
rithms of PIVOTBICLUSTER implemented by (As-
teris et al., 2016), PIVOTBICLUSTER, PIVOTBI-
CLUSTEREDGE, DETPIVOTBICLUSTER and DET-
PIVOTBICLUSTEREDGE implemented by this paper
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
ee
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
eo
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
oe
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0 1 2 3 4 5 6 7 8 9 10
PivotBiCluster
PivotBiClusterEdge
DetPivotBiCluster
DetPivotBiClusterEdge
D
oo
Figure 4: The average running time (sec.) the algorithms
for D
s,t
(s,t ∈ {eo}) with k% noises.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
704

by PBC
A
, PBC, PBCE, DPBC and DPBCE, respec-
tively.
Table 2 illustrates the average value of agree-
ments, in order to compare the results in (Asteris et al.,
2016), obtained by applying the algorithms to Movie-
Lens datasets at five times and its average running
time (sec.). The first column is the average value of
agreements presented in (Asteris et al., 2016), which
implies that our implementations are correct by com-
paring with the second column. Note that the value of
disagreements is |E| minus the value of agreements.
Table 2: The average value of agreements obtained by ap-
plying the algorithms to MovieLens dataset and its average
running time.
algorithms 100K 1M 10M
PBC
A
46,134 429,277 5,008,577
PBC 46,160 429,589 5,011,629
time (sec.) 2.17 90.19 11,154
PBCE 98,497 986,577 9,780,291
time (sec.) 4.36 274.36 55,135
DPBC 45,772 427,138 4,999,434
time (sec.) 2.12 91.64 9,096
DPBCE 99,555 997,882 9,943,548
time (sec.) 2.70 156.60 18,104
Table 2 shows that the value of agreements of
PIVOTBICLUSTER (resp. DETPIVOTBICLUSTER)
is larger than that of PIVOTBICLUSTEREDGE (resp.
DETPIVOTBICLUSTEREDGE), where DETPIVOT-
BICLUSTEREDGE has the largest number. Also the
value of agreements of each of the randomized algo-
rithms is similar as that of the corresponding deter-
ministic versions.
On the other hand, the algorithm PIVOTBICLUS-
TEREDGE occupies the largest running time and
the algorithm DETPIVOTBICLUSTEREDGE does the
next largest running time.
Table 3 illustrates the average value of disagree-
ments obtained by applying the algorithms to datasets
of CM, SX, AC, J1 and YG at five times and its aver-
age running time (sec.).
Table 3 shows that the algorithm PIVOTBICLUS-
TEREDGE gives the smallest value of disagreements
for all the datasets, and the algorithm PIVOTBI-
CLUSTER gives the smallest running time. Also,
whereas the algorithm PIVOTBICLUSTEREDGE is
slowest for the MovieLens datasets in Table 2, the al-
gorithm DETPIVOTBICLUSTEREDGE is slowest for
the datasets of KONECT in Table 3.
In particular, for the J1 dataset, the value of dis-
agreements is extremely larger than other datasets.
Table 3: The average value of disagreements obtained by
applying the algorithms to CM, SX, AC, J1 and YG and its
average running time.
algorithms CM SX AC J1 YG
PBC 669 32,788 31,943 2,136,009 237,400
time (sec.) 0.15 11.17 53.48 2.48 199.96
PBCE 87 4,505 4,775 1,106,915 55,717
time (sec.) 0.19 39.13 68.62 20.25 679.02
DPBC 836 32,039 31,940 1,780,884 2,557,781
time (sec.) 0.63 171.68 167.38 7264.45 6,577.75
DPBCE 217 5,148 6,938 1,360,870 88,858
time (sec.) 0.28 65.31 84.84 67.14 1,536.84
One of the reason is that almost biclusters tend to be
stars, that is, bipartite graphs such that either L or R
is a singleton, since |R| is much smaller than |L| as
represented in Table 1.
As summary of Figures 3 and 4 and Tables 2 and
3, whereas the algorithm PIVOTBICLUSTEREDGE is
slower than the algorithm PIVOTBICLUSTER, the for-
mer gives smaller value of disagreements or larger
value of agreements than the later. In particular, ex-
cept the MovieLens datasets in Table 2, the algorithm
PIVOTBICLUSTEREDGE gives the smallest value of
disagreements and each of randomized algorithms are
faster than the corresponding deterministic version.
Finally, to analyze the extracted biclusters, Table 4
illustrates the average number (num) and the average
cardinality (crd) of extracted biclusters from the small
datasets of CM, SX and AC. Here, “w.s.” means that
“without singletons.”
Table 4: The average number and the average cardinality of
extracted biclusters from CM, SX and AC.
CM SX AC
algorithms num crd num crd num crd
PBC 519 2.67 9,513 1.76 13,803 2.81
(w.s.) 281 4.07 1,907 4.79 6,297 4.96
PBCE 441 4.30 5,769 7.60 11,588 5.44
DPBC 670 2.06 9,177 1.82 12,398 3.12
(w.s.) 162 5.37 2,141 4.53 4,315 7.10
DPBCE 419 4.49 5.756 7.68 10,816 5.85
Table 4 shows that, whereas PIVOTBICLUSTER
and DETPIVOTBICLUSTER extract larger number
of smaller biclusters, PIVOTBICLUSTEREDGE and
DETPIVOTBICLUSTEREDGE extract smaller num-
ber of larger biclusters. Also PIVOTBICLUSTER
and DETPIVOTBICLUSTER extract many singletons.
Without singletons, DETPIVOTBICLUSTER extracts
Bipartite Edge Correlation Clustering: Finding an Edge Biclique Partition from a Bipartite Graph with Minimum Disagreement
705

larger clusters for CM and AC but DETPIVOTBI-
CLUSTER does for SX.
5 CONCLUSION
In this paper, we have formulated the problem BIEG-
COCLUST of bipartite edge correlation clustering and
designed the algorithm PIVOTBICLUSTEREDGE to
solve this problem, by improving the algorithm PIV-
OTBICLUSTER (Alion et al., 2012), with designing
the deterministic versions of them. Then, we have
given experimental results to evaluate the algorithms
by using artificial data and real data such as Movie-
Lens datasets
1
and datasets from KONECT
3
.
First of all, concerned with the intractability re-
sults for BICOCLUST and BIEGCOCLUST, it is an
important work whether or not the problem BIEGCO-
CLUST is NP-hard and is non-approximable. Then, it
is a future work whether or not the algorithm PIVOT-
BICLUSTEREDGE is an approximation algorithm for
the problem BIEGCOCLUST, in particular, it guaran-
tees either approximation ratio as similar as (Amit,
2004) or probabilistic ratio as similar as (Alion et al.,
2012).
Concerned with Section 4, it is a future work to
analyze not only the value of disagreements (or agree-
ments) but also the number and the cardinality of bi-
clusters for other datasets in Table 4 and the den-
sity and the diameter of biclusters. It is also a future
work to apply the algorithm PIVOTBICLUSTEREDGE
to real data for community detection and evaluate the
algorithm.
It is a future work to extend the problem BICO-
CLUST with the maximum agreement (Asteris et al.,
2016) to the problem BIEGCOCLUST with the maxi-
mum agreement. Furthermore, since the running time
of all the algorithms is quadratic, they are not effi-
cient to large datasets, so it is a future work to design
a faster algorithm by introducing some heuristics.
In this paper, we evaluate the results of PIVOT-
BICLUSEREDGE by using the number of disagree-
ments, as same as PIVOTBICLUSER. On the other
hand, the purpose of the problem BICOCLUST is
different from that of BIEGCOCLUST. Hence, it is
an important future work to introduce a more appro-
proate new criterion to evaluate the results of PIVOT-
BICLUSTEREDGE, for example, the number of cross-
ing edges (Ahmad and Khokhar, 2007), and then in-
vestigate whether or not the problem BIEGCOCLUST
with the new criterion is intractable.
REFERENCES
Ahmad, W. and Khokhar, A. (2007). cHawk: An efficient
biclustering algorithm based on bipartite graph cross-
ing minimization. In VLDB Workshop on Data Mining
in Bioinformatics.
Alion, N., Avigdor-Elgrabli, N., Liberty, E., and van
Zuylen, A. (2012). Improved approximation algo-
rithms for bipartite correlation clustering. SIAM
J. Comput., 41:1110–1121.
Amit, N. (2004). The bicluster graph editing problem. Mas-
ter Thesis, Tel Aviv University.
Asteris, M., Kyrillidis, A., Papailiopoulos, D., and Dimakis,
A. G. (2016). Bipartite correlation clustering: Maxi-
mizing agreements. In Proc. AISTATS’16, pages 121–
129.
Chalermsook, P., Heydrich, S., Holm, E., and Karrenbauer,
A. (2014). Nearly tight approximability results for
minimum biclique cover and partitions. In Proc.
ESA’14 (LNCS 8737), pages 235–246.
Chandran, S., Issac, D., and Karrenbauer, A. (2016). On the
parameterized complexity of biclique cover and parti-
tion. In Proc. IPEC’16, pages 11:1–11:13.
Cheng, Y. and Church, G. M. (2000). Biclustering of ex-
pression data. In Proc. ISBM’00, pages 93–103.
Jiang, T. and Raviunar, B. (1993). Minimal NFA problems
are hard. SIAM J. Comput., 22:1117–1141.
Madeira, S. C. and Oliveira, A. L. (2004). Biclustering al-
gorithms for biological data analysis: A survey. IEEE
Trans. Comput. Bio. Bioinfo., 1:24–45.
Oghabian, A., S. Kilpinen, S. H., and Czeizler, E. (2014).
Biclustering methods: Biological relevance and ap-
plication in gene expression analysis. PLOS ONE,
9:e90801.
Orlin, J. (1977). Containment in graph theory: Cover-
ing graphs with cliques. Indagationes Mathematicae,
80:406–424.
Pio, G., Ceci, M., D’Elia, D., Loglisci, C., and Malerba,
D. (2013). A novel biclustering algorithm for the dis-
covery of meaningful biological correlations between
microRNAs and their target genes. BMC Bioinformat-
ics, 14:Suppl. 77.
Pio, G., Ceci, M., Malerba, D., and D’Elia, D. (2015).
CombiRNet: a web-based system for the analysis of
miRNA-gene regulatory networks. BMC Bioinformat-
ics, 16:Suppl. 9.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
706