Approximation of the Distance from a Point to an Algebraic Manifold
Alexei Yu. Uteshev and Marina V. Goncharova
Faculty of Applied Mathematics, St. Petersburg State University, 7/9 Universitetskaya nab., St. Petersburg, 199034, Russia
Keywords:
Algebraic Manifold, Distance Approximation, Discriminant, Level Set.
Abstract:
The problem of geometric distance d evaluation from a point X
0
to an algebraic curve in R
2
or manifold
G(X) = 0 in R
3
is treated in the form of comparison of exact value with two its successive approximations
d
(1)
and d
(2)
. The geometric distance is evaluated from the univariate distance equation possessing the zero
set coinciding with that of critical values of the function d
2
(X
0
), while d
(1)
(X
0
) and d
(2)
(X
0
) are obtained
via expansion of d
2
(X
0
) into the power series of the algebraic distance G(X
0
). We estimate the quality of
approximation comparing the relative positions of the level sets of d(X), d
(1)
(X) and d
(2)
(X).
1 INTRODUCTION
We treat the problem of Euclidean distance evaluation
from a point X
0
to manifold defined implicitly by the
equation
G(X) = 0 (1)
in R
n
,n ∈ {2,3}. Here G(X) is twice differentiable
real valued function and it is assumed that the equa-
tion (1) defines a nonempty set in R
n
. This prob-
lem arises in image processing, multi-object move-
ment simulation, and in the scattered data approxima-
tion problems. Being the problem of nonlinear con-
strained optimization, it can be solved with the aid
of traditional Newton-like iteration methods. How-
ever for the applications connected with the parame-
ter synthesis such as, for instance, the manifold selec-
tion best fitting to the given data set (Ahn et al., 2002;
Aigner and Jutler, 2009; Cheng and Chiu, 2014), an
analytical representation is needed for the distance as
a function of parameters of the problem (point coor-
dinates and coefficients of G(X) if the latter is a poly-
nomial).
We concern here with the following approxima-
tions for the distance d
d
(1)
= |G|/k∇Gk, (2)
d
(2)
= d
(1)

1 +
∇G
>
·H (G) ·∇G
2k∇Gk
4
G

(3)
Here ∇G stands for the gradient column vector,
>
—
for transposition, H (G) is the Hessian of G(X), k·k
is the Euclidean norm, and the right-hand sides in (2)
and (3) are calculated at X = X
0
.
Approximation (2) is known as Sampson’s dis-
tance (Sampson, 1982). We aim at comparison of
the qualities of approximations (2) and (3). We deal
mostly with the case of algebraic manifolds (1), i.e.
G(X) ∈ R[X ]. For this case, the tolerances of the ap-
proximations can be evaluated via comparison with
the true (geometric) distance value determined from
the so-called distance equation (Uteshev and Gon-
charova, 2017; Uteshev and Goncharova, 2018). In
Section 2, we outline the background of this approach
for the case of a quadric manifold, while in Section 3
we extend it to the case of manifold of an arbitrary
order. In Section 4 we discuss an applicability of the
proposed approximations to the case of non algebraic
curve (1).
2 QUADRICS
For the particular case of quadric polynomials G(X):
G(X) := X
>
AX +2 B
>
X −1 = 0 , (4)
where A = A
>
∈ R
n×n
and {X, B} ⊂ R
n
are the col-
umn vectors, formula (2) is represented as
d
(1)
=
1
2
·
|G(X
0
)|
p
(AX
0
+ B)
>
(AX
0
+ B)
. (5)
The counterpart for the formula (3) can be originated
from the following approximation
e
d
(2)
= d
(1)
s
1 +
1
2
(AX
0
+ B)
>
A(AX
0
+ B)
[(AX
0
+ B)
>
(AX
0
+ B)]
2
G(X
0
);
(6)
Uteshev, A. and Goncharova, M.
Approximation of the Distance from a Point to an Algebraic Manifold.
DOI: 10.5220/0007483007150720
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 715-720
ISBN: 978-989-758-351-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
715

suggested in (Uteshev and Goncharova, 2018). For
this particular case, both approximations d
(1)
and
e
d
(2)
can be deduced via the following consideration. First
compute the distance equation, i.e. an algebraic
equation F (z) = 0,F (z) ∈ R[z] whose roots coin-
cide with the critical values of the squared distance
function from X
0
to (4), and, generically, the small-
est positive root of this equation equals d
2
. For the
case of an ellipse G(x,y) := x
2
/a
2
+ y
2
/b
2
−1 = 0
and X
0
= (x
0
,y
0
), this equation takes the form
F (z,x
0
,y
0
) := L
2
z
4
(7)
−2L

L(a
2
+ b
2
+ x
2
0
+ y
2
0
) + a
2
y
2
0
−b
2
x
2
0

z
3
+

6L[a
4
y
2
0
+ a
2
y
4
0
−b
4
x
2
0
−b
2
x
4
0
+ L(a
2
b
2
+ x
2
0
y
2
0
)]
+[L
2
−(a
2
x
2
0
+ b
2
y
2
0
)]
2

z
2
−2a
2
b
2

a
2
b
2
MG
2
0
−

(a
2
+ b
2
)M
2
+ 3a
2
b
2
M −6 a
4
b
4
S
4

G
0
+2a
2
b
2
M
2
S
4

z + a
4
b
4
G
2
0

M
2
+ 4a
2
b
2
G
0

= 0 .
Here L := a
2
−b
2
, G
0
:= G(x
0
,y
0
),
M := x
2
0
+ y
2
0
−a
2
−b
2
, S
4
:= x
2
0
/a
4
+ y
2
0
/b
4
.
Represent the squared distance value as the formal se-
ries
d
2
(x
0
,y
0
) = `
2
G
2
0
+ `
3
G
3
0
+ .. .
in powers of the algebraic distance G
0
(which can
be treated as a small parameter in a vicinity of the
considered ellipse) and substitute it into the distance
equation. Equate to zero the coefficients of G
2
0
and
G
3
0
. This results in the approximations (5) and (6).
Further expansion of the radical in (6) in power se-
ries of G
0
, yields an analogue of approximation (3).
Similar distance equation of the degree 6 in z can be
written down for the point-to-quadric problem in R
3
.
The general expression (valid for a quadric in R
n
for
arbitrary n) can be represented via a special function
of the coefficients of a polynomial known as the dis-
criminant.
We first remind a more general notion. For
the univariate polynomials {f (x),g(x)} ⊂ R[x] their
resultant R
x
( f , g) can be defined in the form of
Sylvester’s determinant (Uspensky, 1948). For in-
stance, if
f (x) := a
0
x
4
+ ···+ a
4
, g(x) := b
0
x
3
+ ···+ b
3
,
a
0
6= 0 , b
0
6= 0, then this determinant equals













a
0
a
1
a
2
a
3
a
4
0 0
0 a
0
a
1
a
2
a
3
a
4
0
0 0 a
0
a
1
a
2
a
3
a
4
0 0 0 b
0
b
1
b
2
b
3
0 0 b
0
b
1
b
2
b
3
0
0 b
0
b
1
b
2
b
3
0 0
b
0
b
1
b
2
b
3
0 0 0













while for the general case it is composed similarly
from degg rows of coefficients of f (x) and deg f rows
of coefficients of g(x). The resultant is a polynomial
function of the coefficients of f (x) and g(x), and its
vanishment yields the necessary and sufficient con-
dition for the existence of a common zero for these
polynomials.
For the particular case g(x) ≡ f
0
(x), the expression
D
x
( f (x)) := R
x
( f , f
0
)/a
0
defines (up to a sign) the discriminant of the polyno-
mial f (x). Its vanishment yields the necessary and
sufficient condition for the existence of a multiple
zero for f (x).
Theorem 1. Let G(X
0
) 6= 0. Distance from X
0
to the
quadric (4) equals the square root from the minimal
positive zero of the distance equation
F (z) := D
µ
(Φ(µ,z)) = 0 , (8)
where
Φ(µ,z) := det

A B
B
>
−1

+ µ

−I X
0
X
>
0
z −X
>
0
X
0

provided that this zero is not a multiple one. Here
I ∈ R
n×n
is the identity matrix.
In (Uteshev and Goncharova, 2018) error esti-
mations for the approximations (5) and (6) are de-
duced in terms of maximal deviations of the mani-
folds d
(1)
= const and
e
d
(2)
= const from the quadric
(4).
Example 1. For the ellipse x
2
/18
2
+ y
2
/5
2
= 1,
approximate equidistant curves d
(1)
(x,y) = 3 and
d
(2)
(x,y) = 3 in comparison with the true equidistant
d(x,y) = 3 are presented in Fig. 1 and 2 respectively.
3 GENERAL ALGEBRAIC
MANIFOLDS
For the general case of algebraic manifold, the con-
struction of distance equation is also possible, at least,
in principle. For the planar case, this construction
is based on the following results (Uteshev and Gon-
charova, 2017):
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
716

Theorem 2. Let G(0, 0) 6= 0 and G(x,y) be an even
polynomial in y. Expand G in powers of y
2
and de-
note
e
G(x,y
2
) ≡ G(x, y). Equation G(x,y) = 0 does
not define a real curve if
(a) equation G(x,0) = 0 does not have real zeros
and
(b) equation
F (z) := D
x
(
e
G(x,z −x
2
)) = 0 (9)
does not possess positive zeros. If any of these con-
ditions fails then the distance from X
0
= (0,0) to the
curve G(x,y) = 0 equals either the minimal absolute
value of real zeros of the equation G(x,0) = 0 or
the square root from the minimal positive zero of the
equation (9) provided that this zero is not a multiple
one.
The generalization of this result to the case of an
arbitrary polynomial G(x,y), not necessarily even in
any of its variables, can be performed by reduction
to the just treated one via artificial evenization of the
problem. Unfortunately this causes the appearance of
an extraneous factor in the distance equation.
Theorem 3. Let G(0,0) 6= 0 and G(x,y) be not an
even polynomial in y. Split G into the sum of even and
odd terms in this variable:
G(x,y) ≡G
1
(x,y
2
)+yG
2
(x,y
2
), {G
1
,G
2
}⊂R[x, y
2
].
Denote
e
G(x,y
2
) := G(x,y)G(x, −y) ≡ G
2
1
(x,y
2
) −y
2
G
2
2
(x,y
2
)
and compute the polynomial F (z) via (9). The latter
is reducible over R:
F (z) ≡ F
1
(z)F
2
2
(z)
with F
2
(z) := R
x
(G
1
(x,z −x
2
),G
2
(x,z −x
2
)).
Equation G(x,y) = 0 does not define a real curve if
(a) equation G(x, 0) = 0 does not possess real ze-
ros and
(b) equation F
1
(z) = 0 does not possess positive
zeros.
If any of these conditions fails then the distance
from X
0
= (0,0) to the curve G(x,y) = 0 equals either
Figure 1: Example 1. Curve d
(1)
= 3 (green boldface) vs.
equidistant d = 3 (thin blue) to the ellipse (thin red).
the minimal absolute value of real zeros of the equa-
tion G(x, 0) = 0 or the square root from the minimal
positive zero of the equation F
1
(z) = 0 provided that
this zero is not a multiple one.
Remark 1. The conditions (a) and (b) of Theo-
rems 2 and 3 (as well as their counterparts from the
undermentioned Theorem 5) can be verified without
utilization of any numerical method. Indeed, there
exist symbolic algebraic algorithms (Sturm’s theorem
(Uspensky, 1948) or Joachimsthal’s theorem (Kalin-
ina and Uteshev, 1993)) permitting one to find the ex-
act number of real zeros of a univariate polynomial
lying within any given interval.
Example 2. For the cubic
−2x
3
+ 6xy
2
+ y
3
−13x
2
−24xy −7y
2
+3x + 9 y −6 = 0,
the polynomial F
1
(z) from Theorem 3 takes the form
234000z
9
−16231720z
8
+ 424939357z
7
−5350750701z
6
+ 34854257973z
5
−113424352224z
4
+ 148842276936z
3
−13100614064z
2
−25191108960z −7233825600.
Its minimal positive zero equals z
∗
≈ 0.737416. Dis-
tance from the origin to the cubic equals
√
z
∗
≈
0.858729. 
Application of Theorems 2 and 3 for the polyno-
mial
e
G(x,y) ≡G(x +x
0
,y + y
0
) results in the distance
equation
F
1
(z,x
0
,y
0
) = 0
for an arbitrary X
0
= (x
0
,y
0
). Unfortunately, for the
polynomial G(x,y) of a degree higher than 2, we are
not able to provide an explicit representation for the
coefficients of this equation in terms of algebraic dis-
tance G(x
0
,y
0
) similar to that from (7) for the ellipse
represented in canonical form. The only details on the
structure of this equation are contained in the follow-
ing result:
Theorem 4. If F
1
(z,x,y) is treated as a polynomial
in z then, generically, deg
z
F
1
= (degG)
2
and its free
term is divisible by G
2
(x,y).
Figure 2: Example 1. Curve d
(2)
= 3 (maroon boldface) vs.
equidistant d = 3 (thin blue) to the ellipse (thin red).
Approximation of the Distance from a Point to an Algebraic Manifold
717

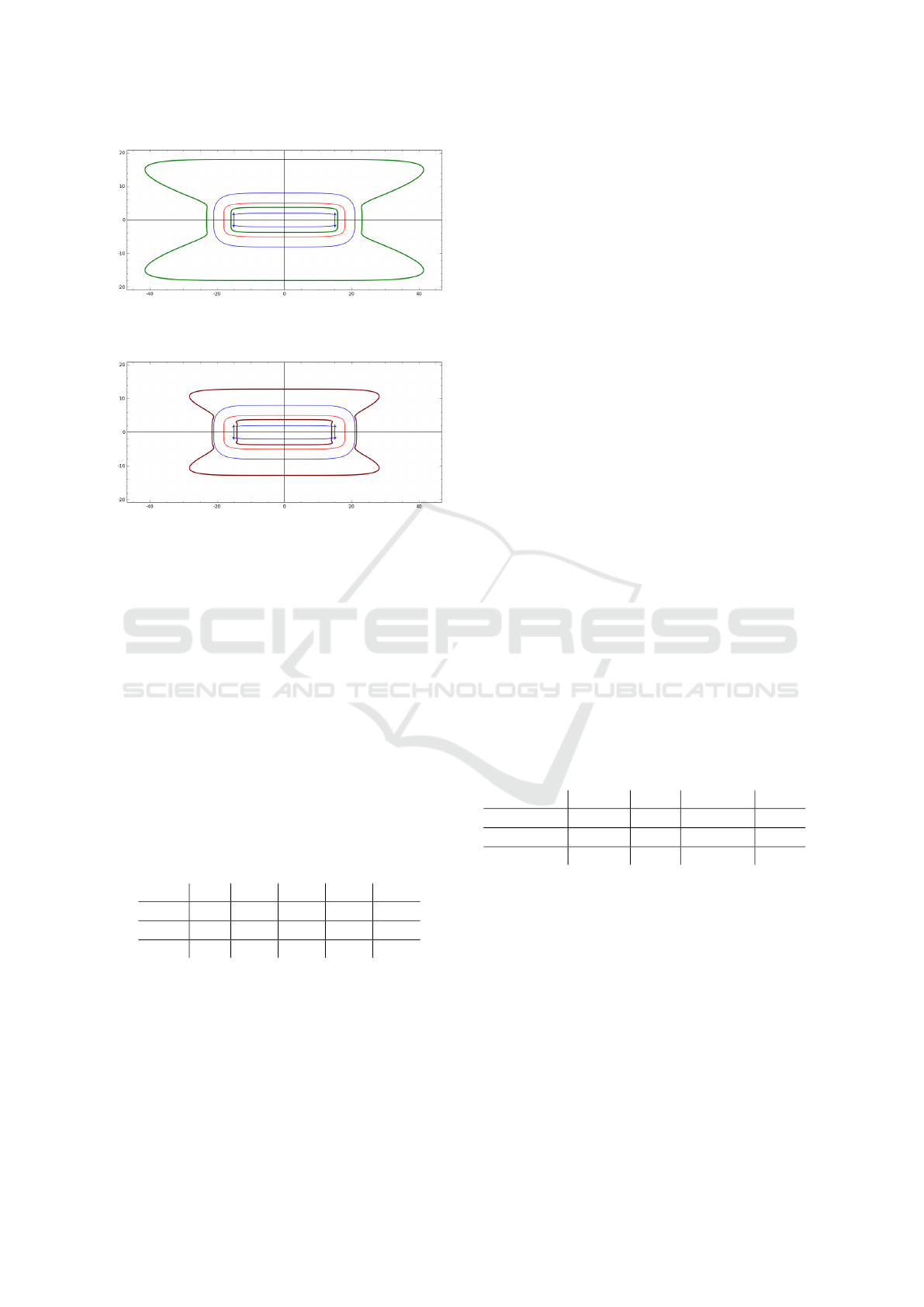
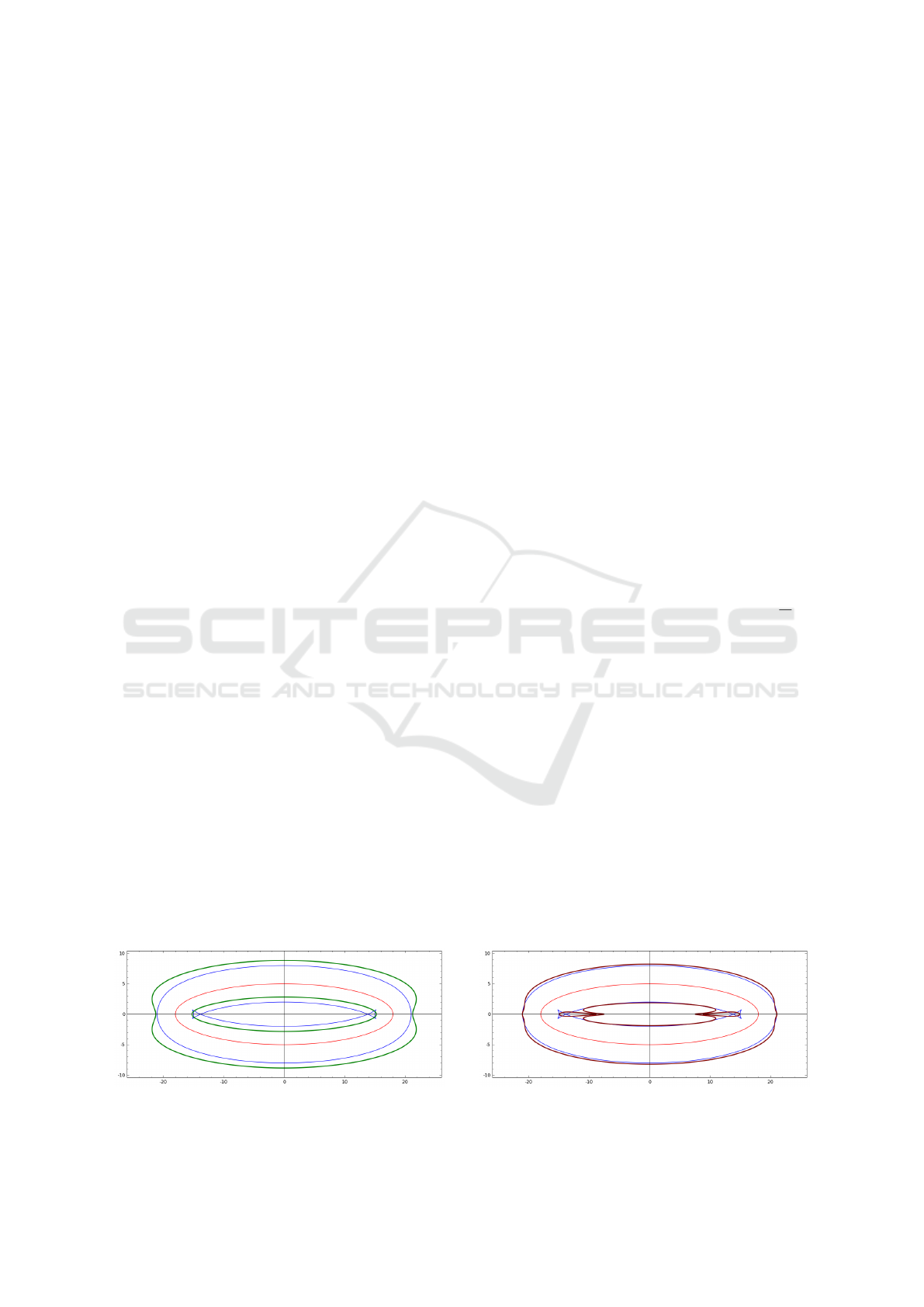
Figure 3: Example 3. Curve d
(1)
= 3 (green boldface) vs.
equidistant d = 3 (thin blue) to the superellipse (thin red).
Figure 4: Example 3. Curve d
(2)
= 3 (maroon boldface) vs.
equidistant d = 3 (thin blue) to the superellipse (thin red).
Therefore, the trick exploited in Section 2 for jus-
tification of origination of the sequence of approxi-
mations (2) and (3) can not be repeated. However,
we are still able to compare the loci of the level sets
d
(1)
(x,y) = h and d
(2)
(x,y) = h of the proposed ap-
proximations with that of the equidistant manifold
F
1
(h
2
,x,y) = 0 for (1).
Example 3. For the superellipse x
6
/18
6
+y
6
/5
6
= 1,
one has deg
z
F
1
(z,x
0
,y
0
) = 36. The leading terms of
F
1
(z,x,y) treated as a polynomial in x, y are as fol-
lows:
(x
2
+ y
2
)
30
(x
6
/18
6
+ y
6
/5
6
)
2
.
The equidistant curve F
1
(9,x,y) = 0 as well as the
curves d
(1)
(x,y) = 3 and d
(2)
(x,y) = 3 are drawn in
Fig. 3 and Fig. 4 correspondingly. Some sample val-
ues for the distance and its approximations are pre-
sented in the following table:
(x
0
,y
0
) (8,4) (19, 1) (10,6) (14,6) (20,2)
d
(1)
1.856 0.877 0.675 0.739 1.568
d
(2)
0.297 0.978 0.865 0.966 1.876
d 0.993 1.000 1.025 1.199 2.011
Remark 2. If the curve G(x,y) = 0 contains a
closed branch (oval) then the quality of distance ap-
proximations (2) and (3) for a point lying inside this
branch becomes the farther the worse than for that ly-
ing outside at the same distance. One can observe this
in the above example with the point (8,4) inside the
superellipse and the others outside.
The treatment of the 3D case is carried out simi-
larly using the notion of the discriminant of a bivariate
polynomial. We do not give here a formal definition
but restrict ourselves by presenting formula for its it-
erative computation via the univariate discriminants
D
x,y
( f (x,y)) = gcd(D
x
(D
y
( f (x,y)), D
y
(D
x
( f (x,y))) .
On computing every internal discriminant, one
should get rid of an extraneous square factor.
Theorem 5. Let G(0,0,0) 6= 0 and G(x
1
,x
2
,x
3
) be
an even polynomial in x
3
. Denote
e
G(x
1
,x
2
,x
2
3
) ≡
G(x
1
,x
2
,x
3
). Equation G(x
1
,x
2
,x
3
) = 0 does not de-
fine a real manifold if
(a) equation G(x
1
,x
2
,0) = 0 does not define a real
curve and
(b) equation
F (z) := D
x
1
,x
2
(
e
G(x
1
,x
2
,z −x
2
1
−x
2
2
) = 0 (10)
does not possess positive zeros.
If any of these conditions fails then the distance
from X
0
= (0, 0, 0) to the manifold G(x
1
,x
2
,x
3
) = 0
equals either the distance from (0,0) to the curve
G(x
1
,x
2
,0) = 0 or the square root from the minimal
positive zero of the equation (10) provided that this
zero is not a multiple one.
Extension of the result of Theorem 5 to the case
of arbitrary polynomial G is carried out in a manner
similar to that utilized in Theorem 3.
Example 4. For the cubic
−2x
3
1
+ 2x
2
1
x
2
+ 4x
1
x
2
2
+ x
3
2
−3x
2
x
2
3
−3x
1
x
2
−x
2
2
+ x
2
3
+ x
1
+ 2x
2
−x
3
−3 = 0
the distance equation is, generically, of the degree 21.
Some sample values for the distance and its approxi-
mations are presented in the following table:
(x
10
,x
20
,x
30
) (4,4,−4) (0,0,0) (−1,5, −4) (7, 2, 5)
d
(1)
0.554 1.225 1.470 2.041
d
(2)
0.611 2.143 1.666 2.592
d 0.618 1.0585 1.447 2.243
Example 5. The cross section of the torus
(x
2
1
+ x
2
2
+ x
2
3
+ 299)
2
−1296x
2
1
−1296x
2
2
= 0
and the corresponding surfaces d
(1)
= 3 and d
(2)
= 3
with the half plane x
2
= 0,x
3
≥0 are displayed in Fig.
5 and Fig. 6.
4 NON-ALGEBRAIC CURVES
For the case of implicitly defined non-algebraic
curves, distance equation cannot be obtained in the
closed form since the procedure for its construction
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
718

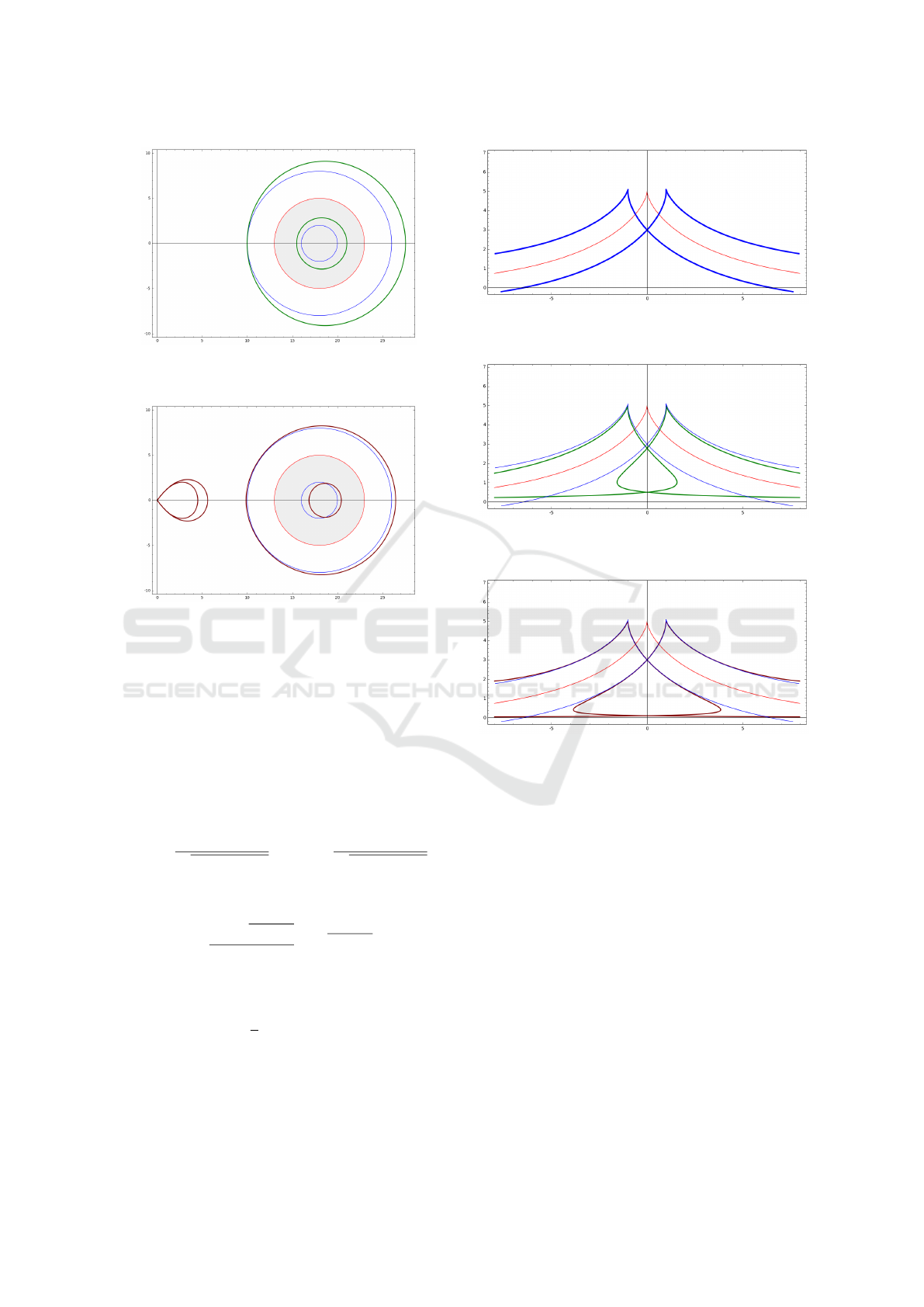
Figure 5: Example 5. Surface d
(1)
= 3 (green boldface) vs.
equidistant d = 3 (thin blue) to the torus (thin red).
Figure 6: Example 5. Surface d
(2)
= 3 (maroon boldface)
vs. equidistant d = 3 (thin blue) to the torus (thin red).
suggested in the previous section is essentially alge-
braic, i.e. it is applicable only for polynomial func-
tions. However, their equidistant curves can be found
even for this case if one is able to establish the para-
metric representation for the interested curve.
Theorem 6. If the curve is defined parametrically as
x = ζ(t), y = η(t) for t ∈ [a, b],
then its equidistant curves lying at the distance d are
defined as
x = ζ ±
d η
0
p
(ζ
0
)
2
+ (η
0
)
2
, y = η ∓
d ζ
0
p
(ζ
0
)
2
+ (η
0
)
2
.
for t ∈ [a,b].
Example 6. For the tractrix
x
2
−25

ln
5 +
p
25 −y
2
y
−
p
25 −y
2

2
= 0 ,
y ∈ (0; 5),
parametric representation is as follows
x = 5

lntan
t
2
+ cost

, y = 5 sint .
The true equidistant curves d = 1 and their com-
parison with the approximations d
(1)
(x,y) = 1 and
d
(2)
(x,y) = 1 are presented in Fig. 7, 8 and 9 respec-
tively.
Figure 7: Example 6. Equidistant d = 1 (boldface blue) to
the tractrix (thin red).
Figure 8: Example 6. Curve d
(1)
= 1 (green boldface) vs.
equidistant d = 1 (thin blue) to the tractrix (thin red).
Figure 9: Example 6. Curve d
(2)
= 1 (maroon boldface) vs.
equidistant d = 1 (thin blue) to the tractrix (thin red).
The result of Theorem 6 can evidently be extended
to the case of parametric surface in R
3
.
5 CONCLUSION
We have investigated the quality of two approxima-
tions for the distance from a point to implicitly de-
fined curve in R
2
and manifold in R
3
. Using an ana-
lytical representation of the true distance value via the
point coordinates and parameters of the manifold, it is
possible to compare the relative position of the level
sets of approximation with respect to the equidistant
manifolds. Adequacy of the suggested approxima-
tions for arbitrary manifold needs further quantitative
validation, similar to that performed in (Uteshev and
Goncharova, 2018) for the case of a quadric. How-
ever, even empirical considerations demonstrated in
Approximation of the Distance from a Point to an Algebraic Manifold
719

the present report give grounds for hope to construc-
tively resolve the best fitting manifold problem men-
tioned in Introduction.
ACKNOWLEDGEMENTS
This research was supported by the RFBR according
to the projects No 17-29-04288 (Alexei Uteshev) and
No 18-31-00413 (Marina Goncharova).
REFERENCES
Ahn, S., Rauh, W., Cho, H., and Warnecke, H. (2002). Or-
thogonal distance fitting of implicit curves and sur-
faces. In IEEE Trans. Pattern Anal. Mach. Intell., vol.
24, no. 5, pp. 620–638.
Aigner, M. and Jutler, B. (2009). Gauss–newton–type tech-
nique for robustly fitting implicit defined curves and
surfaces to unorganized data points. In in Proc. IEEE
Int. Conf. Shape Model. Appl., New York, pp. 121–
130.
Cheng, S.-W. and Chiu, M.-K. (2014). Implicit manifold re-
construction. In Proceedings of the Twenty-Fifth An-
nual ACM-SIAM Symposium on Discrete Algorithms,
pp. 161–173.
Kalinina, E. and Uteshev, A. (1993). Determination of the
number of roots of a polynominal lying in a given al-
gebraic domain. In Linear Algebra Appl. vol. 185, pp.
61–81.
Sampson, P. (1982). Fitting conic sections to very scattered
data: an iterative refinement of the bookstein algo-
rithm. In Comput. Gr. Image Process., vol. 18, pp.
97–108.
Uspensky, J. (1948). Theory of Equations. New York.
McGraw-Hill.
Uteshev, A. and Goncharova, M. (2017). Metric prob-
lems for algebraic manifolds: analytical approach. In
Constructive Nonsmooth Analysis and Related Topics
(Dedicated to the Memory of V.F. Demyanov), CNSA
2017 – Proceedings, 7974027.
Uteshev, A. and Goncharova, M. (2018). Point-to-ellipse
and point-to-ellipsoid distance equation analysis. In
J.Comput. Appl. Math., vol. 328, pp. 232–251.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
720