
Elasticity and Depth Measurement using Both Secondary Speckle and
Time Multiplexing Interference
Ariel Schwarz
1,2,
*
, Nisan Ozana
1,*
, Amir Semer
1,2
, Ran Califa
3
, Hadar Genish
3
and Zeev Zalevsky
1
1
Faculty of Engineering and the Nanotechnology Center, Bar Ilan University, Webb 1, Ramat Gan, Israel
2
Department of Electrical Engineering, Jerusalem College of Engineering, Schreiboim 26, Jerusalem, Israel
3
ContinUse Biometrics Ltd., HaBarzel 32b, Tel Aviv, Israel
Keywords: Lasers, Speckle Interferometry, Scattering, Rough Surfaces, Fourier Optics and Signal Processing.
Abstract: In this paper, we describe a technique for elasticity and depth measurement via both secondary speckle and
time multiplexing interference approach. Using external stimulation of elastic medium (in example: human
tissue) by infra-sonic vibration, photons from different depths of the elastic medium were separated. In
addition, this work uses a modulated laser that incorporates at the same scanning time, a speckle pattern
tracking method for sensing surface tilting and interferometer method for sensing z-axis movements. In this
paper, we present preliminary experiments showing the ability to separate data of light coming from different
layers in the elastic medium.
1 INTRODUCTION
Two important parameters in characterizing elastic
medium are the elasticity and depth movements of a
specific point inside or on the elastic medium. These
parameters divert in different medium types and can
indicate mechanical and physical properties of the
medium. One important medium is biological tissue
characterization. Tissue mechanical property is very
important since pathological and physiological
characteristics are related to changes in the
biomechanics of tissues. We can better understand
physiological processes of tissues, diagnose and
improve the treatment of various diseases by accurate
measurements of tissue biomechanical changes
(Greenleaf et al., 2003).
During the years, several elastography methods
were proposed for different elements size. The
elements imaging scales between big size (i.e. organ
level methods), medium size elements (i.e tissue
level methods) up to micro size elements (i.e cell
level methods). Ultrasound elastography (UE) for
organ level, that was first proposed in 1980, uses
stimulation of a elastic medium with ultrasonic
imaging (UI) technique (Dickinson et al., 1980;
Sarvazyan et al., 1998). Later on based on magnetic
*
A. Schwarz and N. Ozana contributed equally to this work
resonance imaging (MRI) technique, magnetic
resonance elastography (MRE) was presented for
organ level (Muthupillai et al., 1995). The resolution
of elasticity imaging by UE is of hundreds of
micrometers and with MRE is of several millimeters.
These two methods are limited by the spatial
resolving ability of UI and MRI techniques. Another
elastography method is based on atomic force
microscopy (AFM) for cell level. The resolution of
elasticity imaging by AFM is sub-nanometer. AFM
elastography has been mainly applied for the cells
than tissues due to the limited field of view and the
measurement procedure (Rotsch & Radmacher,
2000). Moreover, optical imaging techniques such as
multiphoton microscopy (Liang et al., 2011),
confocal Brillouin microscopy (Scarcelli & Yun,
2008), laser speckle imaging (Jacques & Kirkpatrick,
1998) and optical coherence tomography (OCT) for
tissue level were also developed for the elastography
use.
As a further of matter, OCT in the use of Optical
Coherence Elastography (OCE) is a growing field.
This field of research, which began two decades ago,
is today a breakthrough and rapidly developing study
in medical imaging in compare to traditional methods
such as cell mechanics, medical elastography, UE and
Schwarz, A., Ozana, N., Semer, A., Califa, R., Genish, H. and Zalevsky, Z.
Elasticity and Depth Measurement using Both Secondary Speckle and Time Multiplexing Interference.
DOI: 10.5220/0007521702550262
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 255-262
ISBN: 978-989-758-364-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
255

MRE. Elastography using OCT was first proposed in
1998 (Schmitt, 1998) and today it is in front of optical
elasticity imaging techniques. OCE focuses on the
micro-scale assessment in 3D that is hard to achieve
with traditional elastographic methods (Wang &
Larin, 2015). There is a wide variety of methods in
OCE techniques such as static/quasi-static or
dynamic (continuous wave or pulsed). These methods
applied to tissues either internally or externally (Sun
et al., 2011).
In this paper we present detection of high
frequencies vibrations using speckle and
conventional interferometer. Integrating both gives
the ability to detect z axes movement of a subject in
addition to the tilt movement and the ability to extract
data of the elastrographic different samples using
modulation. The tilt extraction is done by identifiying
speckle patterns trajectory using a simple correlation
calculation, which enables us to detect the mechanical
properties of the evaluated medium. For example:
compression OCE refers to detection in a bi-layer
sample; resulting in displacement versus depth due to
local strain. The strain and displacement approaches
are similar to the presented method. However, here
the presented method is using laser as a light source
with relatively high coherence length.
2 THEORETICAL
BACKGROUND
2.1 Tilting and Z-axis Detection
The speckle pattern method is based upon temporal
tracking of a secondary reflected speckle by imaging
the speckle through properly defocused optics. The
tilting changes of the object surface reflect the
movement of the speckle pattern in the x-y plane
(Garcia et al., 2008). The temporal tilting movement
of the object surface is proportional to the change in
the spatial position of the speckle pattern:
(1)
Where β is the change in the speckle pattern, α is
the time varying tilting angle of the object illuminated
surface, λ is the illumination wavelength. By
calculating the correlation, the relative movement of
patterns can be extracted. This relative movement is
obtained by allocating the time varying position of the
correlation peak.
In order to achieve a full surface vibration data, an
interferometer is used to detect the temporal changes
of the surface in the z-axis. The laser source beam
splits into two similar paths when only one is
reflected from the vibrated object. The result is phase
shifts between the two beams caused by a change in
length of one of the paths. Those phase shifts create
interference pattern (fringes) inside the visible
speckle. The number of wavelengths contained in the
path's length difference creates the fringes oscillating
frequency. Using Laser Doppler Vibrometer (LDV)
technique the velocity of the object surface vibration
in the z-axis is measured. The z-axis vibration
velocity and frequency are extracted from the
Doppler shift of the reflected laser beam due to the z-
axis motion of the surface. The operation of the
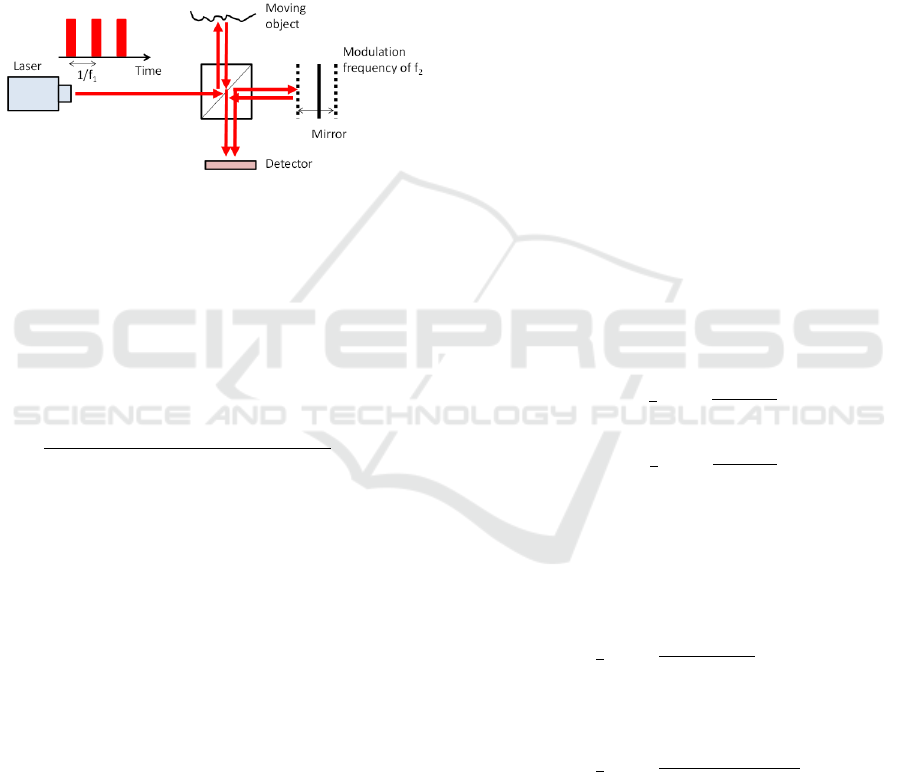
system is described as follow (Fig. 1):
Figure 1: Flow chart of the operation system.
In order to monitor the z-axis vibration, we use the
interference behaviour measurements. The
constructive and destructive interferences pattern of
the fringes imaging is according to the length
difference ΔL between the two paths. By analysing
the movement in the fringes imaging we can extract
the changes in the velocity of the object's path. The
number of the illumination wavelengths in the length
difference (the depth of the object movement),
multiple the frequency movement of the fringes
pattern imaging. For example: for object movement
of ΔL=1 mm with frequency of 1-2 Hz (like heart
beats) and laser wavelength illumination of 532 nm,
the fringes pattern movement will be with frequency
of 1880-3760 Hz.
This situation of frequency multiplication leads to
a problem due to camera limited frame rate. In order
to solve this problem a laser modulation was used.
The modulation used pulsation of the laser at
frequency f
1
and modulation of the interferometer
mirror at frequency of f
2
(Fig. 2).
In the regular case the speckle due to tilting is
flickering at frequency of µ
1
and the fringe due to
axial movement at frequency of µ
2
. In our case due to
the modulation at f
1
and at f
2
we obtain the following:
the fringe will move at µ
2
+ f
1
+ f
2
and the speckle at
µ
1
+ f
1
. The result is that we actually can use a low
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
256
sampling rate camera (and thus to use many pixels in
space and to do large field of view analysis) since the
laser will perform optical down conversion of the
spectral distribution to the low band region (because
it realizes optical sampling procedure) and the
frequency of the mirror f
2
together with the spatial
information will allow to separate between the tilting
and the axial movements. Due to the pulsation of the
laser we can down convert high temporal frequencies
to allow their sampling with the slow rate camera.
The high frequencies are folded into the low
frequency spectral band sampled by the camera.
Figure 2: Schematic description of the optical system with
Michelson interferometer (because of practical reasons in
part of our experiments Mach–Zehnder interferometer was
used).
The modulation frequency was such that the
difference between it and the object frequency
bandwidth is in the camera limited frame rate:
(2)
where k is the wave number. The difference
between the two frequencies (f
1
-f
2
) can be detected by
the slow rate camera and every change in the system
frequency due to the object changes can be detected.
2.2 The Elastographic Concept
Let us assume that we vibrate the medium at
frequency of ν
1
and that the medium has two layers.
We assume that the photons coming from the inner
layer have electrical field denoted by E
1
and the
photons coming from the outer layer have electrical
field denoted by E
2
. Since the medium is soft, the
different two layers (in our case it is two, but the
model can be expanded to larger number of layers)
are moving in a non-synchronized way: Both layers
vibrate in the same frequency but there is time
varying shift in their movement profile. This means
that photons coming from the layer 1 and layer 2 will
interfere on the camera but the interference will vary
in time such that it will contribute only low DC in
compare to patterns coming from photon reflecting
from the same layer. We also assume that the
movement amplitude is larger than the size of the
scattering points in the medium. This assumption
means that we assume the scattering points are
moving in the medium otherwise no amplitude
movement will be present. Those assumption are
needed as we wish to prove that due to the lack of
synchronization and since the integration period of
the camera is much larger than 1/ν
1
, the electrical
fields E
1
and E
2
are incoherent to each other and add
up in intensities and not in fields (i.e. they don’t
interfere with each other). This is a very important
assumption because otherwise the two fields will
interfere and create a new equivalent field that will
generate new speckle pattern while what we aim to do
is to separate between the speckle patterns generated
by E
1
and E
2
.
We will assume that the field E
1
generates speckle
patterns having averaged speckle size of d
1
and E
2
generates speckles with average size of d
2
. It is simple
to design optics in which light coming from different
depths create speckle patterns with different speckle
dimensions. To simplify the mathematics, we will
assume that the first and second speckle patterns
(coming from E
1
and E
2
respectively) are modelled as
follows:
(3)
Now assuming that both patterns are moving and
frequency of ν
1
and amplitude of d>>d
1
,d
2
yields:
(4)
Where, V
1
=dν
1
δx[0,d]. At the output plane we
interfere the two fields’ distributions with reference
field which is moving at frequency of ν
2
and add them
together in the detector:
Elasticity and Depth Measurement using Both Secondary Speckle and Time Multiplexing Interference
257

(5)
The reference field is a tilted planar wave with
angular frequency of α and it equals to:
(6)
Where V
2
is the movement velocity of the
reference beam which equals to ν
2
/α. The field in the
previous expression is captured as intensity in the
detector which also performs time integration
(according to the integration time of the camera):
(7)
The integration time is much larger than 1/ν
1
and
1/ν
2
but smaller than 1/(ν
1
-ν
2
). Thus, we obtain that:
(8)
Where c
1
and c
2
are space independent constants
and the cross correlation expression was zero because
the field distributions of the speckle patterns of s
1
and
s
2
are not correlated to each other (having different
dimensions and have non synchronized movement
due to δx(t)):
(9)
Let us now explore the expressions of
. To mathematically simplify we
will approximate the expression of s
1
and of s
2
, at
least for the case of two adjacent fringes (speckles)
to:
(10)
Thus, if we assume that our spatial observation
point is x=0 or x-coordinate falling on the peak of one
of the speckles then the expression we obtain
becomes:
(11)
Thus, the final result will be:
(12)
Since the spatial periodicity α as well as 1/d
1
are
of the same order of magnitude and the time
averaging integral coming due to the fact that the
camera samples the output intensity at lower rate
causes to the first two terms of both expression to zero
(since they change at temporal frequency of αV
2
or of
V
1
/d
1
). The third term in both expression changes
(flickers) at temporal frequencies of:
(13)
We can choose our parameters to make those two
frequencies to be low enough so that the sampling rate
of the camera will be faster than it and therefore one
over the sampling rate (proportional to the integration
time) will be smaller than 1/νF
1
and 1/νF
2
and thus
the third term in both expressions will not be averaged
to zero.
The main advantage of using the optical
interference loop in addition to the self-interference
expressed as the speckle patterns, is that it adds
another parameter of V
2
allowing on one hand to
average to zero the expression of
∫s
1
(x-V
1
t) s
2
*(x-V
1
t)dt=0 due to the integration time
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
258
of the camera and on the other hand not to average to
zero the expression of ∫cos(2πt(αV
1
-V
1
/d
1
)+φ
1
)dt or
of ∫cos(2πt(αV
1
-V
1
/d
2
)+φ
2
)dt and to allow their
detection with the camera. Since each one of those
two expressions flicker or temporally changes at
different frequency, we can separate between them
and thus to separate between s
1
and s
2
, i.e. photons
coming from different depths of the inspected
medium. As it is detailed in Eq. 10 - 13 in comparison
to OCT the depth resolution of the presented
approach is based on different temporal flickering
frequencies of the speckle pattern. The flickering
frequency is different due to different speckle size
generated by the medium elastographic properties.
The depth resolution is according to Eq. 13 due to
different flickering frequency.
3 EXPERIMENTAL RESULTS
3.1 Tilting and Z-axis Detection
In our setup we used the Mach–Zehnder
Interferometer configuration. The vibration of the
surface in the z-axis changes the path length of one of
the Mach-Zender laser paths. These changes reflect in
the interference pattern (fringes) of the two joined
beams on a detector and camera plane.
The setup includes an illumining laser (laser diode
Photop Suwtech Laser DPGL-2100F, 532 nm max
300 mW with driver Photop LDC-2500S) with a
beam splitter in order to get the two paths: the object
path and the reference path. The reference path
consists of adjustable mirrors that can change the
length of the reference path in order to calibrate the
interferometer with two similar paths and according
with its coherence length. Since the laser beam in the
reference path gets to the detector and camera
directly, while the laser beam in the object path
reaches by reflection from the object, thus the
intensities of the laser beams from the two paths on
the detector and camera planes are not the same. For
that reason, a filter was placed in the reference path
to equal the two path intensities.
In order to detect only small area of the speckle
pattern and the fringes pattern a pinhole of 200 µm
was attached to the detector. In all our experiments a
Pixelink PL-B761U camera was used as a detector.
For stabilization of the fringes pattern imaging we
need to correct the frequency multiplication caused
by the number of wavelengths contained in the in the
object path difference. The correction part of the
setup consist a feedback circuit from the detector
back to the reference path. The output signal from the
detector was passed through an op-amp differentiator
amplifier with negative feedback (Lion LE-3003D-
3). The output derived signal from the amplifier
derived the analogue amplifier driver (powered by a
DC power supply) that control a piezo actuator
(Piezomechanik SVR 1000-1) attached to a mirror in
the reference path. The controlled mirror movement
compensates the instability of the frequency
multiplication due to the number of wavelengths in
the path length changes. The object vibrations were
controlled by vibration surface controller (OSC
LS13C050, 2 1/4" Diameter, 50 ohm 0.5 Watt and
Tektronix AFG1022 signal generator).
The described configuration includes observation
of the secondary speckle pattern that is created by
illuminating the object directly for tilting information
and interferometer with phase shift measurements for
z-axis information. In order to monitor the tilting
vibration, the correlation of each of the sequential
speckles images is measured. By analysing the
changes in the correlation peak position, relative
tilting movement of the object was extracted.
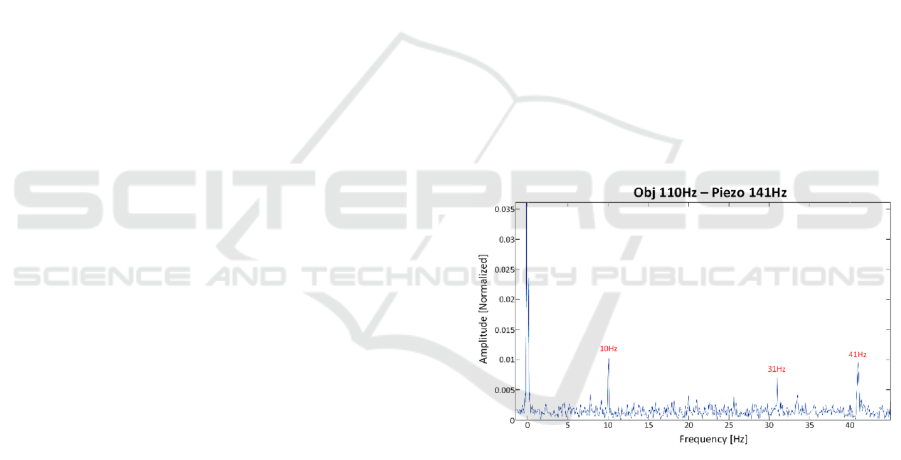
The results show that the high frequency object
signal was modulated to low frequencies within the
camera frame rate window according to the
frequencies difference (Fig. 3).
Figure 3: Piezo-mirror modulation results: the high
frequency of the object was modulated by the piezo-mirror
frequency to low frequencies. The difference frequency and
the cut frequencies (by 100Hz of the camera) of the object
and piezo-mirror.
3.2 Size of the Speckles versus Medium
Depth
The first experimental validation included
verification of the fact that indeed the size of the
speckles change versus the depth of the medium form
which they are scattered. Two experimental setups
were constructed to verify this. The first in
transmission (Fig. 4(a)) and the second in reflection
(Fig. 4(b)).
Elasticity and Depth Measurement using Both Secondary Speckle and Time Multiplexing Interference
259

(a).
(b).
Figure 4: Experimental (a) transmission and (b) reflection
setups for testing the size of speckles versus the thickness
of the scattering medium.
Proper phantoms with different thicknesses were
prepared as appearing in the lower right corner of Fig.
4(b). The obtained experimental results are seen in
Fig. 6. In Fig. 5(a) we show the change in the speckle
sizes for the transmission experiment and in Fig. 5(b)
for reflection. The speckle spot diameter for different
layer thicknesses are shown in Fig. 6.
(a).
(b).
Figure 5: Experimental results (a) transmission and (b)
reflection setups showing the dependence of the speckle
size versus the thickness of the scattering medium.
(a). (b). (c).
Figure 6: Spot diameter for different layer thicknesses: (a).
Speckle spot of 8mm layer thickness (1% concentration).
(b). Speckle spot of 4mm layer thickness (1%
concentration). (c). Spots diameter of the two different
layers thicknesses.
3.3 Coherent Temporal Elastographic
Tomography
In order to validate the full proposed concept an
experimental setup was established. The setup is seen
in Fig.7. In this experimental setup we used a
different modulation method, instead of a laser
pulsation. The modulation used a controlled vibration
of the object (medium layers) with piezo element at
frequency f
1
and modulation of the interferometer
mirror at frequency of f
2
.
Figure 7: The experimental setup of the coherent
elastographic tomography system.
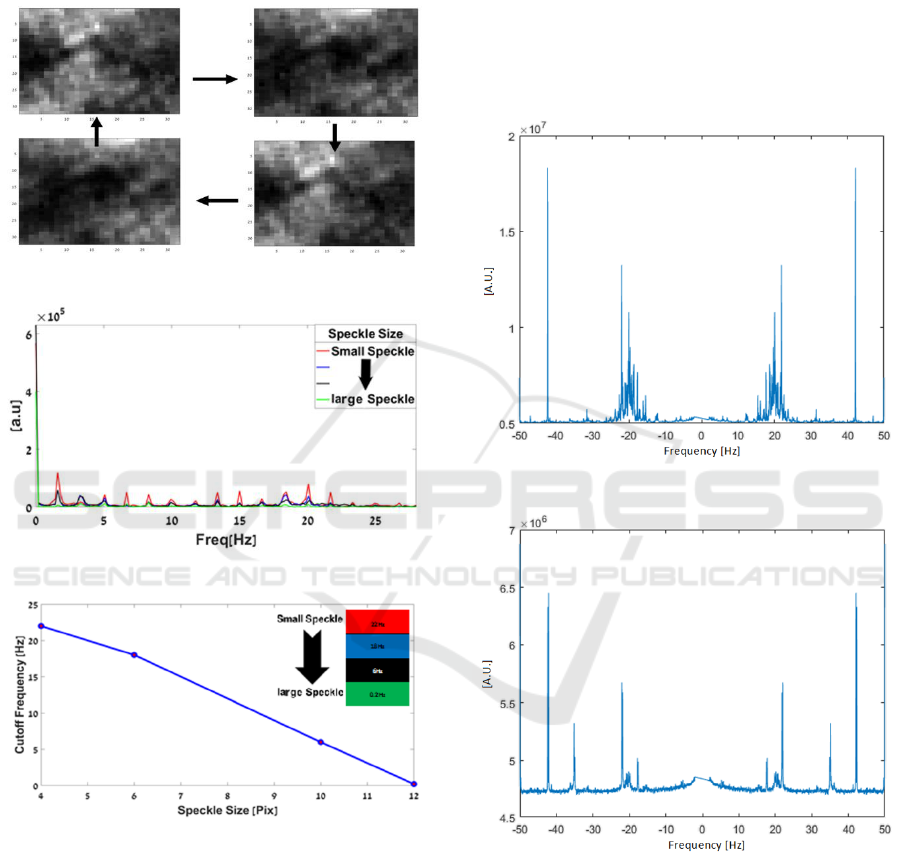
The experimental results are seen in Fig. 8-9 while
in Fig. 8(a) we show images of the flickering speckles
and in Fig. 8(b) we show the spectrum obtained for
speckles having different dimensions. In Fig. 8(c) we
present the cut off frequency obtained for speckle
having different dimensions (corresponding to
photons coming from different depths of the
inspected medium). One can see that indeed
significant change in the cut off frequency of the
flickering is obtained for different thicknesses of the
medium and thus photons coming from different
depths can be separated from each other. It is
important to note that proposed concept performs the
separation of the photons in the photonic level and not
digitally (after performing various image processing
algorithms). This separation in the photon level due
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
260
to temporal modulation and demodulation makes the
proposed concept more immune to digital and
electronic signal-to-noise ratio (SNR) restrictions that
are very dominant in the discussed type of imaging
due to the very low SNR involved.
(a).
(b).
(c).
Figure 8: Experimental results for speckles flickering at
different frequencies depending on the depth from which
they have arrived from in the inspected medium. (a).
Flickering speckles pattern. (b). Temporal spectrum of the
speckle pattern with different size. (c). Cutoff frequencies
for different speckle size.
The experimental average results of several
experiments with 20 Hz modulations of the speckles
flickering system for one and two layers and different
concentrations are showed in Fig. 9. The results
shown are the standard deviation of several
experiments. The following experiments represents
the temporal flickering of one layer, consists of 0.3%
Agarose with respect to a sample with two layers one
with 0.6% of agarose and the second with 0.3% of
agarose. Each layer length is 4mm. The different
concentrations of the agarose represent different
elastographic layers. One can see that the flickering
spectrum pattern is changed due to the combination
between the layers. The frequency change is
proportional to the elastographic value of the layer.
(a).
(b).
Figure 9: Experimental results of 20Hz modulations of the
speckles flickering system: (a). Two layers (0.6%+0.3%
concentrations, 4mm+4mm thickness). (b). One layer
(0.3% concentration, 4mm thickness).
4 CONCLUSIONS
This research showed the ability to separate data of
Elasticity and Depth Measurement using Both Secondary Speckle and Time Multiplexing Interference
261

light coming from different layers of elastic medium.
In order to achieve z-axis detection (movement of the
whole surface in the z direction) with tilting detection
(tilting angle of the surface) Mach–Zehnder or
Michelson interferometer based speckle patterns
configuration can be used. In this research we showed
several methods for setup modulation to down
convert high temporal frequencies to allow their
sampling with a slow rate camera. This research
showed that different elastographic layers (that were
represented by different concentrations of the
agarose) changes the flickering spectrum pattern and
the elastographic characters can be extracted.
REFERENCES
Greenleaf, J. F., Fatemi, M., Insana, M., 2003. Selected
methods for imaging elastic properties of biological
tissues. Annual Review of Biomedical Engineering, 5,
57-78.
Sarvazyan, A. P., Rudenko, O. V., Swanson, S. D.,
Fowlkes, J. B., Emelianov, S. Y., 1998. Shear wave
elasticity imaging: a new ultrasonic technology of
medical diagnostics. Ultrasound in Medicine &
Biology, 24, 1419-1435.
Dickinson R. J., Hill C.R., 1980. Analysis of tissue and
organ dynamics. In: Hill C. R., Alvisi C., editors.
Investigative Ultrasonology, 1, 110–114.
Muthupillai, R., Lomas, D. J., Rossman, P. J., Greenleaf, J.
F. Manduca, A., Ehman, R. L., 1995. Magnetic
resonance elastography by direct visualization of
propagating acoustic strain waves. Science, 269, 1854-
1857.
Rotsch, C., Radmacher, M., 2000. Drug-induced changes of
cytoskeletal structure and mechanics in fibroblasts: an
atomic force microscopy study. Biophysical Journal,
78, 520-535.
Liang, X., Graf, B. W., Boppart, S. A., 2011. In Vivo
Multiphoton Microscopy for Investigating
Biomechanical Properties of Human Skin. Cellular and
Molecular Bioengineering, 4, 231-238.
Scarcelli, G., Yun, S. H., 2008. Confocal Brillouin
microscopy for three-dimensional mechanical imaging.
Nature Photonics, 2, 39-43.
Jacques, S. L., Kirkpatrick, S. J., 1998. Acoustically
modulated speckle imaging of biological tissues. Optics
Letters, 23, 879-881.
Schmitt, J. M., 1998. OCT elastography: imaging
microscopic deformation and strain of tissue. Optics
Express, 3, 199-211.
Wang, S., Larin, K. V., 2015. Optical coherence
elastography for tissue characterization: a review.
Journal of Biophotonics, 8, 279-302.
Sun, C., Standish, B. A., Yang, V. X. D., 2011. Optical
coherence elastography: current status and future
applications. Journal of Biomedical Optics, 16, 043001.
Garcia, J., Zalevsky, Z., Garcia-Martinez, P., Ferreira, C.,
Teicher, M., Beiderman, Y., 2008. Three-dimensional
mapping and range measurement by means of projected
speckle patterns. Applied Optics, 47, 3032-3040.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
262
