Adversarial Media-fusion Approach to Strain Prediction for Bridges

Takaya Kawakatsu

, Kenro Aihara

, Atsuhiro Takasu

and Jun Adachi

The University of Tokyo, 2-1-2 Hitotsubashi, Chiyoda, Tokyo, Japan

National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda, Tokyo, Japan

Keywords:

Generative Adversarial Network (GAN), Civil Engineering, Structural Health Monitoring, Multimodal.

Abstract:

This paper contributes to the wide acceptance of autonomous health monitoring for real bridges. Our approach

involves dynamic simulation, whereby damage may be identiﬁed by detecting abnormal mechanical behavior

in the bridge components in response to passing vehicles. Conventionally, dynamic simulation requires expert

knowledge of mechanics, components, materials, and structures, in addition to accurate modeling. Moreover,

it requires detailed speciﬁcation of the external forces applied, such as vehicle speeds, loci, and axle weights.

This paper introduces a novel media-fusion framework to obtain a bridge dynamic model in a fully data-driven

fashion. The proposed generative model also successfully simulated strain responses for a real road bridge by

using a camera and strain sensors on the bridge. The generative network was trained by an adversarial learning

algorithm customized for media-fusion analysis.

1 INTRODUCTION

With the widespread adoption of compact devices and

drones, attention is being directed toward a fully au-

tomated approach to monitor the health of bridges us-

ing sensor fusion involving heterogeneous sensors in-

stalled on the target bridge. Our main interest in this

paper is the detection of fatal faults that may cause a

bridge to collapse, such as fractures and the corrosion

of reinforcing rods, girders, and decks. Unfortunately,

the mechanisms for damage progression on individual

real bridges are yet to be fully clariﬁed. Furthermore,

there has been no open collection of ground-truth data

for damage identiﬁcation, which would be helpful for

approaches involving data mining.

Studies of damage detection based on mechanics

can be classiﬁed according to two major approaches.

The ﬁrst uses long-term behavior of the bridge, such

as natural vibration (Bicanic and Chen, 1997), which

does not depend strongly on individual vehicles. The

second uses transient state analysis, which identiﬁes

an abnormal movement by the bridge components

in response to every passing vehicle (Huang et al.,

2016). Compared with the ﬁrst approach, the second

may provide rich information sampled under a variety

of trafﬁc conditions. To detect anomalous mechanical

responses, the dynamic system of the bridge must be

modeled in advance. One powerful solution is to use

ﬁnite element analysis (FEA) (Wu et al., 2017; Shah

et al., 2018). However, FEA requires accurate model

making by hand, which is not feasible for the majority

of existing bridges.

Our solution is to use a generative neural network

that predicts the transient responses for every passing

vehicle, which must be observed by sensors installed

upon the bridge components. The generative network

involves two networks, namely encoder and decoder.

The encoder network collects vehicle properties in a

media-fusion fashion that combines a video network

and a sensor data network. The video is recorded by

a surveillance camera above the bridge entrance and

contains rich information about every passing vehicle,

including speed, locus (left/right position in the lane),

and axle positions. The sensor data are recorded by a

strain sensor underneath the bridge deck and contain

information about axle weights. The decoder network

generates the dynamic response caused by the vehicle,

by taking the output of the encoder as its input. That

is, our neural network takes the raw sensor-data signal

as input and outputs a decoded sensor signal, thereby

modeling the transfer function between the sensors.

To realize realistic predictions, we have improved

the generative adversarial networks (GANs) (Radford

et al., 2016; Goodfellow et al., 2014). In addition, we

implemented generative networks which were trained

just by minimizing mean squared errors (MSEs). The

results in Section 4 demonstrate the effectiveness of

our approach to modeling bridge dynamics.

736

Kawakatsu, T., Aihara, K., Takasu, A. and Adachi, J.

Adversarial Media-fusion Approach to Strain Prediction for Bridges.

DOI: 10.5220/0007555007360743

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 736-743

ISBN: 978-989-758-351-3

2 RELATED WORK

It is usual for a road bridge to bend and distort as a

vehicle passes over the bridge. If we assume that all

of a vehicle’s properties could be obtained in advance,

the bridge structural response including normal strain,

shear strain and displacement would be predictable by

using a bridge model. Existing modeling techniques

can be classiﬁed according to two major approaches,

namely explicit modeling and implicit modeling. The

explicit approaches use FEA (Mohamed et al., 2017;

Mohamed and Tahar, 2017), where bridge models are

typically created manually and optimized by iterative

model updates using a test vehicle (Wu et al., 2017).

By comparing uninjured and damaged models (Shah

et al., 2018), the damage can be localized.

On the other hand, the implicit approach abandons

explicit construction of bridge structural models, not

least because accurate FEA modeling is costly. In this

approach, there are two main methods for anomalous

behavior detection. The ﬁrst method is based on using

model parameters that dominate the bridge dynamics,

such as natural frequencies (Bicanic and Chen, 1997),

damping ratios (Cao et al., 2017), and stress inﬂuence

lines (Chen et al., 2014). The second method is based

on physical observation where the anomaly is deﬁned

as a dissociation between sensor data and predictions.

The predicted data can be static (Liu and Wang, 2010;

Ma and Bi, 2011) or dynamic (Zhang et al., 2018).

Traditionally, the transient signals were explained

by using Kalman ﬁltering (Bing et al., 2011; Xiao and

Fang, 2016; Quansheng et al., 2010; Palanisamy and

Sim, 2015) for the case of quasistatic linear responses.

In a recent approach, Neves et al. (Neves et al., 2017;

Neves et al., 2018) modeled bridge vibration signals

by using a neural network that took previous 5-gram

acceleration samples, axle loads, and axle positions as

its input.

Aspects of bridge dynamics such as normal strain

and displacement can be estimated by introducing the

concept of an inﬂuence line (Chen et al., 2014; Huang

et al., 2016). The strain response by components, e.g.,

ﬂanges, girders, and deck slabs, may be explained by

a linear response model where the strain measurement

s(t) at time t is proportional to the product of axle load

w(x, t) and the value of the inﬂuence line i(x) at axle

point x:

s(t) ≈ ˆs(t) =

w(x, t)i(x)dx, (1)

where l is the bridge length. The function i(x) denotes

a proportionalityfactor for w(x, t), which is speciﬁc to

each bridge.

To predict the dynamic responses or to extract the

inﬂuence line from sensor data, the vehicle properties,

including speed, loci, axle positions, and weights, are

needed. Zaurin and Catbas (Zaurin and Catbas, 2011)

also investigated the collection of vehicle properties

via video surveillance. A problem with their approach

was that the targets were limited to test vehicles with

known axle loads. The most obvious approach to axle

weighing is to use an axle-load meter. However, it is

hard to retroﬁt an axle-load meter to existing bridges

because this meter needs paving work for installation.

Moreover, an axle-load meter is fragile and requires

frequent repair. Additionally, accurate axle weighing

may impose severe limits on vehicle traveling speed.

An alternative solution uses a bridge weigh-in-motion

(BWIM) (Lydon et al., 2015; Yu et al., 2016) system

that estimates axle weights by Eq. (1), but if the bridge

becomes damaged, the inﬂuence line may change and

lead to inaccurate axle-load estimates. The inﬂuence

line may also change its shape if the running position

in the lane changes. Accordingly, we must develop a

complex model to handle the large number and wide

variety of patterns of strain responses collected by test

runs in advance.

In a previous paper (Kawakatsu et al., 2018a), we

abandoned the collection of axle weights. Instead, we

proposed an anomaly-detection method based on the

assumption that vehicle appearances and bridge strain

responses may share common features for the passing

vehicles. As we have previously reported (Kawakatsu

et al., 2018b; Kawakatsu et al., 2019), the strain data

themselves contain rich information about the passing

vehicles. By using two convolutional neural networks

(CNNs) for video and strain signals and by comparing

the video and sensor data in a common feature space,

we could successfully identify anomalous responses.

The main problem in this work is the interpretation of

anomalous scores that are not directly associated with

physical abnormalities.

3 MEDIA-FUSION GAN

Fig. 1 illustrates the architecture of the generative net-

work. The network comprises two subnets, namely

the encoder and the decoder. The encoder extracts the

features of each vehicle, and the decoder predicts the

strain signal. Both subnets involve many preactivated

residual blocks (He et al., 2016). Note that we applied

an additional activation function to the output of each

block in addition to the two activation functions inside

the block. In this paper, we used leaky ReLU (Maas,

2013) for all activation functions except for those in

the output layers.

The encoder network shown in Fig. 1(a) is derived

from the SpiNet (Kawakatsu et al., 2018a). To obtain

Adversarial Media-fusion Approach to Strain Prediction for Bridges

737

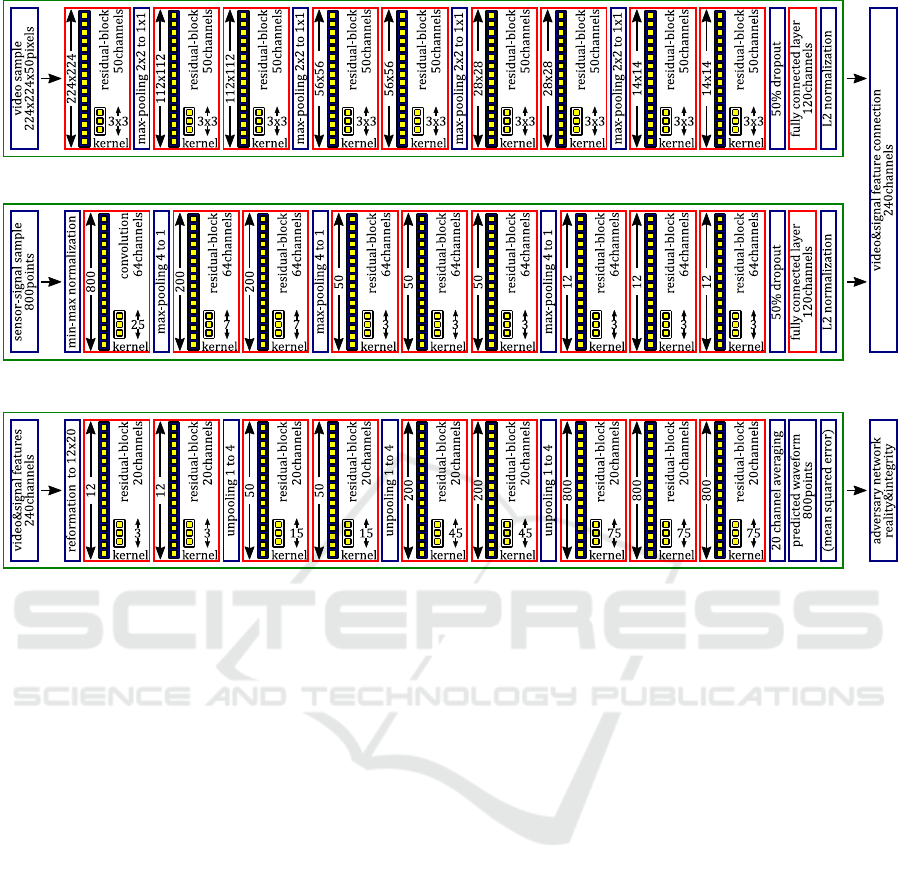
(a) Encoder network.

(b) Decoder network.

Figure 1: Media-fusion generator network architecture.

accurate predictions, the parameters of the unknown

target vehicle need to be acquired by using sensors on

the target bridge. As described in Eq. (1), the required

parameters include traveling speed, locus, axle loads,

and axle positions. These parameters are obtained by

the multimodal encoder, which combines two CNNs

for video and strain signals.

First, the video CNN receives 50 grayscale video

frames (taken over two seconds) recorded from when

the passing vehicle enters the camera’s ﬁeld of view.

Each frame is resized to 224×224 pixels in advance.

Next, the strain CNN receives four-second batches

of raw strain signals sampled at 200 Hz. We fed raw

signal sequence directly to the CNN, following Dai et

al. (Dai et al., 2017). Each sequence starts (or ends)

at the same time as the vehicle enters (LtoR) or leaves

(RtoL) the bridge. Then, each sample is scaled so that

its maximum and minimum values are normalized to

1 and 0, respectively, to enable effective learning.

Finally, the multimodal encoder outputs a feature

vector of 240 channels by combining video and signal

features of the target vehicle. To suppress overﬁtting,

we inserted a 50% dropout between the last residual

block and the following linear layer in each network.

In addition, we again normalized the video and signal

features individually to enable effective learning.

The decoder network shown in Fig. 1(b) receives

the feature vector for each target vehicle and predicts

a target waveform of 800 signal points (four seconds),

which is rescaled in the same way as the source signal.

The decoder was designed as a deep residual network,

which upsamples the feature vector by three times to

obtain target signals at 200 Hz. The upsampling was

performed just by copying each element in the source

vector into four neighboring signal points in the target

vector. A generous kernel width for each convolution

layer was set, similar to WaveGAN (Donahue et al.,

2018), to enable the layer to handle the low-frequency

signals seen in Fig. 4. The target signal was obtained

by averaging 20 channels of the feature vector into a

single channel in the ﬁnal layer.

The generator network was trained introducing the

GAN (Goodfellow et al., 2014; Radford et al., 2016)

approach. Typically, an adversary network examines

whether the generated fake data are as realistic as the

observed data (Goodfellow et al., 2014). In addition,

our adversary network examines the integrity between

the source signal and prediction, which should be high

because they were both caused by the same vehicle.

Therefore, our adversary takes a pair comprising

two signal sequences from the source sensor signal y

and target sensor signal z (or prediction ˆz), similar to

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

738

Figure 2: Media-fusion adversary network architecture.

Table 1: Classiﬁcation problem for the adversary.

Real z Fake ˆz

Consistent {y

, z

} {y

, ˆz

∼ G(x

, y

)}

Inconsistent {y

′

, z

} {y

′

, ˆz

∼ G(x

, y

)}

pix2pix (Isola et al., 2017), and classiﬁes the pair into

four classes, as shown in Table 1. These four types of

pairs are created uniformly for each n-th observation

sample {x

, y

, z

} by the sampling function s

(n) = {y

, z

}, (2)

(n) = {y

′

, z

}, (3)

(n) = {y

, G(x

, y

)}, (4)

(n) = {y

′

, G(x

, y

)}. (5)

′

was selected from the samples other than y

in the

mini batch in each training iteration. Accordingly, 4N

pairs were fed to the adversary for N samples during

the training.

Fig. 2 illustrates the architecture of the adversary

network. We modiﬁed the Model 1 CNN proposed in

a previous paper (Kawakatsu et al., 2019) to take the

source sensor signal y and target signal z as the input.

The adversary is shallower than the generator, which

may suppress overﬁtting. The target signal input may

comprise real or fake strain sequences, while the other

input is always real but is sometimes inconsistent with

the target signal. The loss function for the adversary

D is deﬁned as the cross entropy for the four classes:

∑

n=1

∑

k=1

logD(kks

(n)), (6)

where D takes a pair created by s

selected uniformly

as input and predicts the probability that the input pair

is classiﬁed to the k-th class in Table 1.

The generator G was trained so that the prediction

ˆz looks real and consistent with the observation y. To

stabilize the GAN optimization process, we added an

auxiliary MSE element to the cross entropy, following

Yang et al. (Yang et al., 2017) to obtain Eq. (7).

∑

n=1



logD(1ks

(n)) + λk ˆz − zk



, (7)

where λ was set to 1. Both networks were trained in

a mini-batch fashion that the losses L

and L

were

minimized. In each training iteration, G was updated

ﬁrst and then D was updated.

It should be noted that our generator did not take

a random noise variable as input, unlike the previous

GAN studies (Goodfellow et al., 2014; Radford et al.,

2016), because we required deterministic models and

the contribution of the random input was not obvious

in our study. In future work, we may explore a method

for handling non-deterministic behavior of the bridge

by exploiting random variables in future work.

4 EXPERIMENTAL RESULTS

Section 4 demonstrates our generative network for the

case of a 300-m prestressed concrete (PC) bridge in

Japan, denoted Bridge C, which has two lanes and

four spans. We deployed a trafﬁc surveillance camera

at the bridge entrance to capture images of vehicles in

close proximity to the vehicles. We also installed four

strain sensors beneath the bridge deck to collect strain

signals in the direction orthogonal to the bridge axis.

These sensors are shown as four red triangles denoted

as S1P4, S2P4, S3P4, and S4P4 in Fig. 3. The strain

sensor model was PKM-50S, manufactured by Tokyo

Measuring Instruments Laboratory, Co. Ltd. We also

installed an accelerometer at the center of the leftmost

span, as shown by the yellow triangle denoted A3ZP8

in Fig. 3. All of the sensors were synchronized except

for the camera, and their sampling rate was 200 Hz.

The frame rate of the camera was then set to 25 frames

per second.

Fig. 4 show two examples of the observed signals

after a large vehicle entered Bridge C from left to right

(LtoR) and from right to left (RtoL). The signal peaks

indicate the times when a wheel axle passed over the

sensor. As investigated previously (Kawakatsu et al.,

2018b; Kawakatsu et al., 2019), the response signals

contain various information about the vehicles, which

may include speed, loci, and axle numbers, although

the accuracy may be lower than that derived from the

video. However, axle weights may be better obtained

from strain data than from video data.

In preparation for the experiments, we needed to

collect times when vehicles entered or left the bridge.

For this purpose, we utilized the trafﬁc dataset DS601

prepared previously (Kawakatsu et al., 2019). DS601

was created automatically using Faster R-CNN (Ren

et al., 2015) and contains information about 996,093

vehicles which crossed over the bridge between 08:00

and 16:00 from November 2016 to April 2017. In this

work, we ignored all vehicles with two axles because

Adversarial Media-fusion Approach to Strain Prediction for Bridges

739

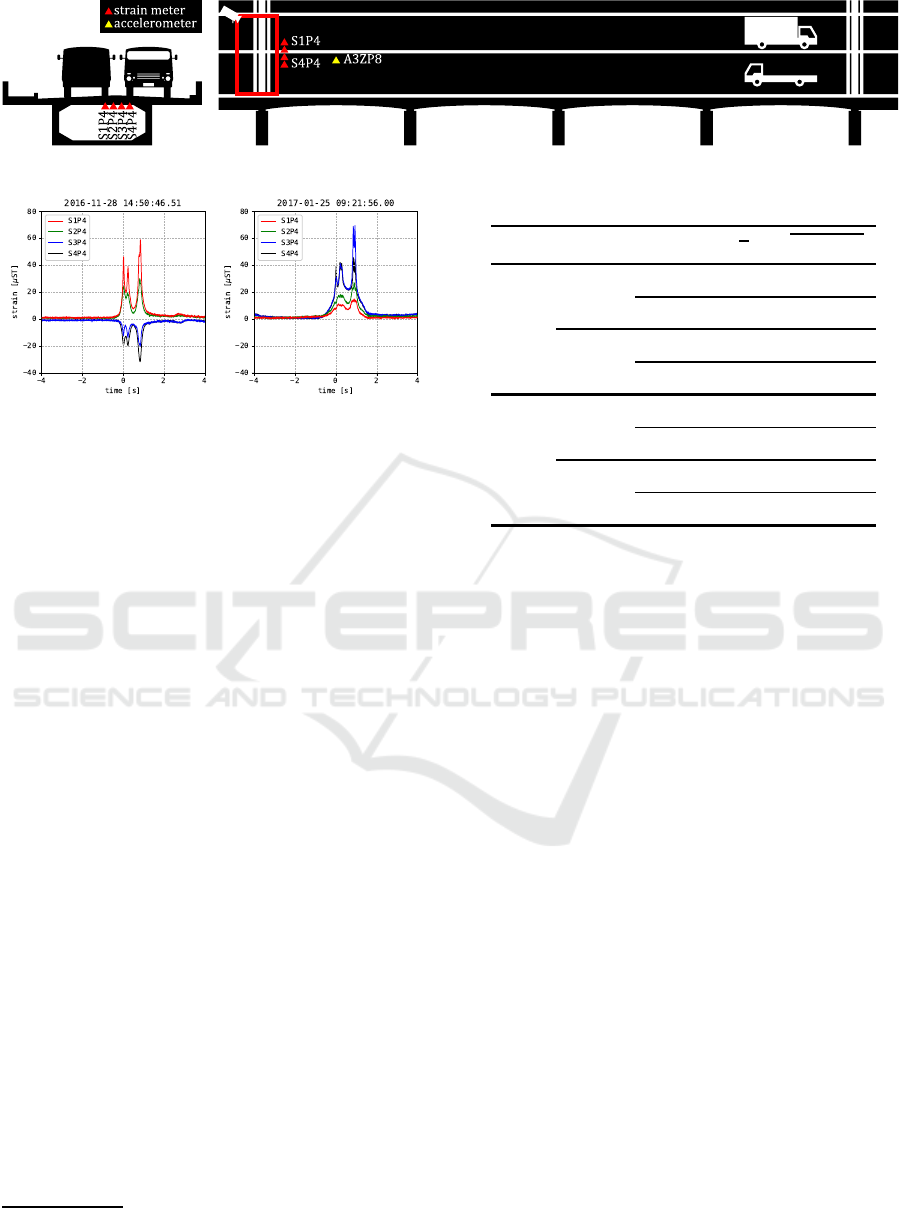
Figure 3: Installation positions of strain sensors and an accelerometer on Bridge C.

(a) An LtoR vehicle. (b) An RtoL vehicle.

Figure 4: Examples of strain responses caused by vehicles.

civil engineers are mainly interested in large vehicles.

We then collected videos of the target vehicles and

strain signals caused by the vehicles. The n-th vehicle

record is described as a triplet {x

, y

, z

} composed

of a video x, source sensor signal y, and target signal

z for the n-th vehicle. The trafﬁc dataset was divided

randomly into two subsets, namely trainval data and

evaluation data. In addition, 20% of the trainval data

were assigned as validation data, while the remaining

80% were assigned as training data. The training data

were utilized for the generator optimization, while the

validation dataset was utilized for early stopping (Yao

et al., 2007). The evaluation was performed only once

using a model that updated the minimum of the MSE

for the validation data. The trainval dataset therefore

involved 17,757 LtoR and 20,996 RtoL vehicles, and

the evaluation data involved 17,967 LtoR and 21,078

RtoL vehicles.

We implemented two derivative generator models

on Chainer

5.0.0. One was the GAN model described

in Section 3, and the other was a MSE model trained

without the GAN mechanism. They were accelerated

by a GPU (NVIDIA GeForce GTX 1080 Ti), utilizing

CUDA

9.2. We also employed the AMSGrad (Reddi

et al., 2018) for optimization, and the mini-batch size

was set to 10. The two models were trained over 200

epochs, and the evaluation processes were performed

in the manner of early stopping (Yao et al., 2007).

First, we evaluated the signal correlation between

the observationz and the prediction ˆz. Unfortunately,

there are no accepted metrics for waveform similarity

http://chainer.org

http://developer.nvidia.com/cuda

Table 2: Kendall τ coefﬁcients and MSEs for the GAN.

Lane Source Target τ k ˆz − zk

RtoL S1P4 S3P4 0.747 2.756

S4P4 0.730 3.035

S2P4 S3P4 0.756 2.645

S4P4 0.720 3.015

LtoR S3P4 S1P4 0.748 1.242

S2P4 0.687 2.018

S4P4 S1P4 0.691 1.268

S2P4 0.674 1.881

beyond squared distance and cross-correlation. In this

work, we focused on the fact that the values of signal

points could be estimated by a linear combination of

inﬂuence lines and therefore evaluated the correlation

between the signal points of the ground truth and the

prediction. It should be noted that the distributions of

the signal values were not uniform but biased strongly

toward 0 µST, as shown in Fig. 4. Therefore, we used

the rank correlation coefﬁcient τ’s (Kendall, 1938) as

metrics. Table 2 shows the average τ coefﬁcients and

the MSEs for the evaluation data. From these results,

the proposed GAN model was able to achievea strong

correlation between observation and prediction.

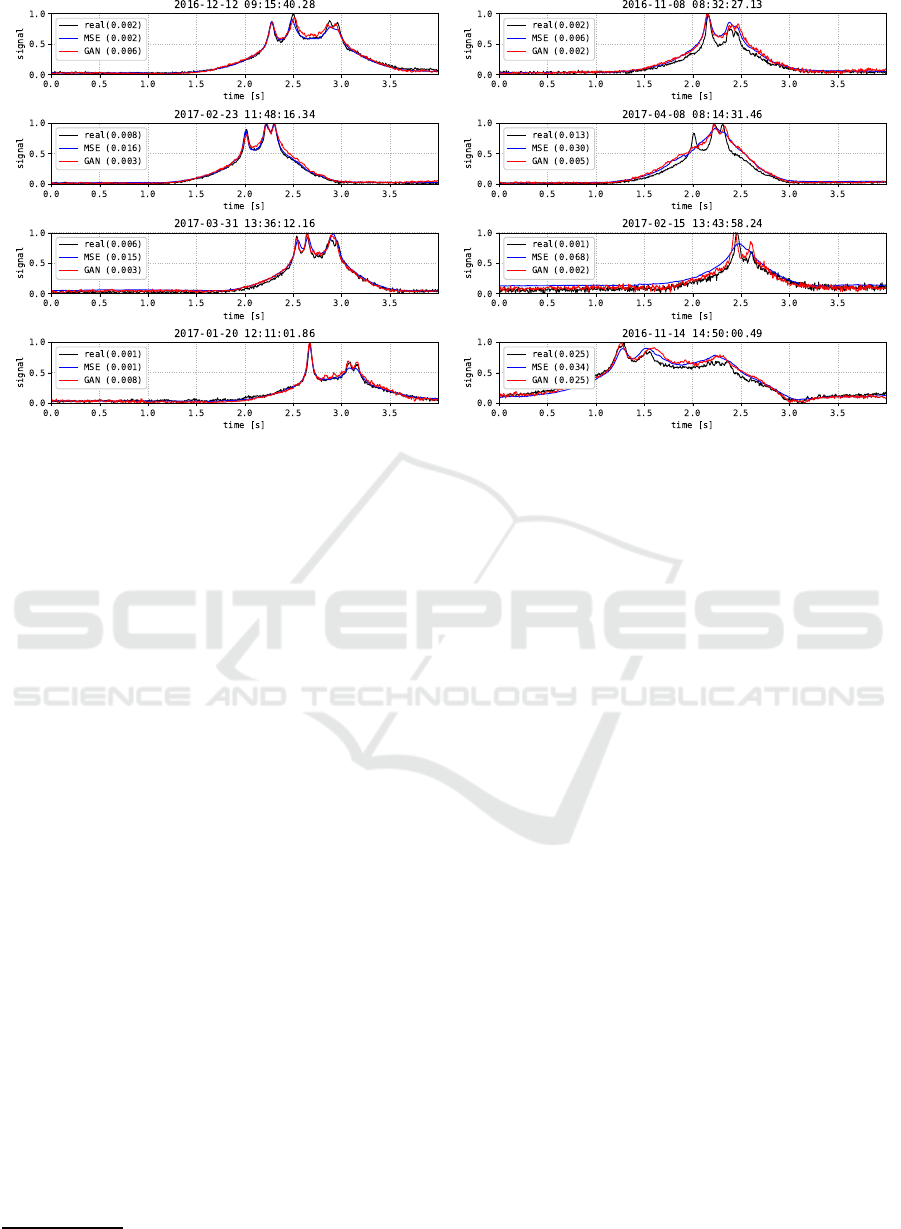
After the waveform prediction for the evaluation

dataset, we sorted the waveforms in terms of squared

error and extracted the ﬁrst and third quantiles. Fig. 5

shows examples of strain responses for LtoR vehicles

passing over strain sensor S1P4, which were predicted

using sensor S4P4. The numbers in brackets indicate

the anomaly scores (Kawakatsu et al., 2018a) for real

and fake signals. For both quantiles, the GAN model

generated realistic signals that were indistinguishable

from the real observation data. As seen in Fig. 5, the

waveforms generated by the MSE model were much

smoother than those obtained by the GAN model. The

GAN simulated not only the macroscopic signals but

also the noise components. The strain peaks indicate

the times at which axles passed over the sensors, and

the two generators successfully simulated these peaks

both in terms of peak heights and times.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

740

(a) 1st quartile. (b) 3rd quartile.

Figure 5: Strain signal prediction and anomaly scores for strain sensor S1P4 and LtoR vehicles using strain sensor S4P4.

Fig. 6 shows examples of strain signals for RtoL

vehicles crossing over strain sensor S4P4, which were

estimated using sensor S1P4. Due to the asymmetric

structure of the box girder, the shapes of the observed

signals were very different from those in Fig. 5. These

differences can be seen best in the skirts of the waves,

whose heights relative to the peaks were much greater

than those in Fig. 5. Again, our proposal successfully

simulated these gentle slopes, which start and end just

as the vehicle enters and leaves the target span on the

bridge.

5 DISCUSSION

In this work, we focused mainly on strain signals, al-

though the bridge components may produce various

kinds of mechanical responses when a vehicle crosses

the bridge. Strain responses on the deck have a strong

spatio-temporal locality, with the strain meters having

very little reaction to wheel loads at distant points and

recovering to the zero points rapidly after the vehicle

departs. In contrast, an accelerometer installed at the

center of the bridge span can react to distant vehicles,

and vibrations at the natural frequencies are likely to

be persistent. These properties make bridge vibration

analysis more difﬁcult compared with strain analysis.

Whenever abnormal strain responses are found by

comparing the predicted and observed responses, we

may locate the area of bridge damage by reference to

wheel positions on the bridge, as has been explored in

some studies (Chen et al., 2014; Huang et al., 2016).

Unfortunately, strain sensors are prone to peeling off

the surface of bridge components and thus requiring

regular inspection. This is one major motive for using

less expensive accelerometers instead of strain meters

in civil engineering applications (Sekiya et al., 2018).

Therefore, in future work, we should develop a GAN

for acceleration-response prediction as an alternative

to strain-response prediction. Note that the proposed

generator may aid in the inspection process for strain

sensors.

6 CONCLUSION

We have proposed a novel media-fusion approach to

long-term bridge health monitoring. The proposed

GAN enables direct translation between strain sensors

deployed underneath the bridge deck by consulting a

surveillance camera on the bridge. The video features

may specify vehicle properties including speed, locus,

shape, and wheel positions as explanatory variables in

the strain prediction. Even though the video may lack

informationabout axle loads, this can be compensated

for by analyzing the source sensor signals. We tested

our generative network on real observation data, with

the results demonstrating highly accurate predictions

of measured waveforms.

We expect that bridge damage (and sensor faults)

may be revealed by comparing the error distributions

of predictions collected soon after the construction of

Adversarial Media-fusion Approach to Strain Prediction for Bridges

741

(a) 1st quartile. (b) 3rd quartile.

Figure 6: Strain signal prediction and anomaly scores for strain sensor S4P4 and RtoL vehicles using strain sensor S1P4.

the bridge with the current ones. Compared with the

direct comparison of video and strain-signal data in a

common feature space, the proposed network enables

the visualization of changes in physical quantities for

individual bridge components. In future experimental

work, we will investigate the connections between the

anomaly scores and strain-signal prediction errors. In

addition, we also aim to investigate sensor types other

than strain meters for use as alternativesignal sources.

ACKNOWLEDGEMENT

This work was supported by the cross-ministerial

Strategic Innovation Promotion (SIP) program

of the

Cabinet Ofﬁce, Government of Japan.

REFERENCES

Bicanic, N. and Chen, H.-P. (1997). Damage identiﬁca-

tion in framed structures using natural frequencies.

IJNME, 40(23).

Bing, Z., Tiesheng, W., and Shanshan, L. (2011). The re-

search of monitoring model for bridge running. In IC-

SSEM.

Cao, M. S., Sha, G. G., Gao, Y. F., and Ostachowicz, W.

(2017). Structural damage identiﬁcation using damp-

ing: a compendium of uses and features. SMS, 26(4).

http://www.jst.go.jp/sip/k07.html

Chen, Z., Cai, Q., Lei, Y., and Zhu, S. (2014). Damage

detection of long-span bridges using stress inﬂuence

lines incorporated control charts. SCTS, 57(9).

Dai, W., Dai, C., Qu, S., Li, J., and Das, S. (2017). Very

deep convolutional neural networks for raw wave-

forms. In ICASSP.

Donahue, C., McAuley, J., and Puckette, M. (2018). Adver-

sarial audio synthesis. In ICLR.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In NIPS.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Identity

mapping in deep residual networks. In ECCV.

Huang, Y., Zhu, C., Ye, Y., and Xiao, Y. (2016). Damage

detection of arch structure by using deﬂection inﬂu-

ence line. In SEEIE.

Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. A. (2017).

Image-to-image translation with conditional adversar-

ial networks. In CVPR.

Kawakatsu, T., Kinoshita, A., Aihara, K., Takasu, A., and

Adachi, J. (2018a). Adversarial spiral learning ap-

proach to strain analysis for bridge damage detection.

In DaWaK.

Kawakatsu, T., Kinoshita, A., Aihara, K., Takasu, A., and

Adachi, J. (2018b). Deep sensing approach to single-

sensor bridge weighing in motion. In EWSHM.

Kawakatsu, T., Kinoshita, A., Aihara, K., Takasu, A., and

Adachi, J. (2019). Deep sensing approach to single-

sensor vehicle weighing system on bridges. IEEE Sen-

sors, 19(1):243–256.

Kendall, M. G. (1938). A new measure of rank correlation.

Biometrika, 30(1-2).

Liu, Y. and Wang, X. (2010). The application of BP neural

network in cable-stayed bridge construction monitor-

ing. In ICCIS.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

742

Lydon, M., Taylor, S., Robinson, D., Mufti, A., and OBrien,

E. (2015). Recent developmenets in bridge weigh in

motion (bwim). CSHM, 6.

Ma, Y. and Bi, H. (2011). Cable tension monitoring of sus-

pender arch bridges during cable tension adjustment

stage basis on neural network algorithm. In RSETE.

Maas, A. L. (2013). Rectiﬁer nonlinearities improve neural

network acoustic models. In ICML.

Mohamed, B. and Tahar, E. (2017). Remote sensing of dam-

age bridge structure of free vibration by using ﬁnite

element method based on subspace ﬁtting. In ICIS.

Mohamed, B., Tahar, E., and Houria, R. (2017). Remote

sensing of damage bridge structure of free vibration

by using ﬁnite element method based on jerk-energy.

In SERA.

Neves, A. C., Gonzalez, I., Leander, J., and Karoumi, R.

(2017). Structural health monitoring of bridges: a

model-free ANN-based approach to damage detec-

tion. CSHM, 7(5).

Neves, A. C., Gonzalez, I., Leander, J., and Karoumi,

R. (2018). A new approach to damage detection in

bridges using machine learning. In EVACES.

Palanisamy, R. P. and Sim, S.-H. (2015). Bridge scour mon-

itoring using extended kalman ﬁlter. In AESE.

Quansheng, S., Haiying, Y., Xiaoguang, G., Jiawei, W., and

Tong, W. (2010). Application of kalman’s ﬁltering

method in construction control for cable replacement

of the cable-stayed bridge. In ICECE.

Radford, A., Metz, L., and Chintala, S. (2016). Unsuper-

vised representation learning with deep convolutional

generative adversarial networks. In ICLR.

Reddi, S., Kale, S., and Kumar, S. (2018). On the conver-

gence of adam and beyond. In ICLR.

Ren, S., He, K., Girshick, R. B., and Sun, J. (2015). Faster

R-CNN: Towards real-time object detection with re-

gion proposal networks. In NIPS.

Sekiya, H., Kubota, K., and Miki, C. (2018). Simpli-

ﬁed portable bridge weigh-in-motion system using ac-

celerometers. JBE, 23(1).

Shah, A. A., Chowdhry, B. S., Daudpoto, J., and Ali, I.

(2018). Transient structural health monitoring of the

test bridges using ﬁnite element method. In IMTIC.

Wu, B., Lu, H., Chen, B., and Gao, Z. (2017). Study

on ﬁnite element model updating in highway bridge

static loading test using spatially-distributed optical

ﬁber sensors. Sensors, 17(7).

Xiao, C. and Fang, Z. (2016). Research on multi-sensor

information fusion algorithm with sensor fault diag-

nosis. In ICIICII.

Yang, S., Xie, L., Chen, X., Lou, X., Zhu, X., Huang, D.,

and Li, H. (2017). Statistical parametric speech syn-

thesis using generative adversarial networks under a

multi-task learning framework. In ASRU.

Yao, Y., Rosasco, L., and Caponnetto, A. (2007). On early

stopping in gradient descent learning. Constructive

Approximation, 26(2).

Yu, Y., Cai, C., and Deng, L. (2016). State-of-the-art review

on bridge weigh-in-motion technology. Advances in

Structural Engineering, 19(9).

Zaurin, R. and Catbas, F. N. (2011). Structural health mon-

itoring using video stream, inﬂuence lines, and statis-

tical analysis. SHM, 10(3).

Zhang, L., Sun, Z., Zhang, C., Dong, F., and Wei, P.

(2018). Numerical investigation of the dynamic re-

sponses of long-span bridges with consideration of

the random trafﬁc ﬂow based on the intelligent ACC-

BPNN model. IEEE Access, 6:28520–28529.

Adversarial Media-fusion Approach to Strain Prediction for Bridges

743