
Air Quality Forecast through Integrated Data Assimilation
and Machine Learning
Hai Xiang Lin
1,2
, Jianbing Jin
1
and Jaap van den Herik
2
1
Delft Institute of Applied Mathematics, Delft University of Technology, Delft, The Netherlands
2
Leiden University, Leiden, The Netherlands
Keywords:
Chemical Transport Model, Data-driven Machine Learning, Physics-based Machine Learning.
Abstract:
Numerical models of chemical transport have been used to simulate the complex processes involved in the
formation and transport of air pollutants. Although these models can predict the spatiotemporal variability of a
variety of chemical species, the accuracy of these models is often limited. Therefore, in the past two decades,
data assimilation methods have been applied to use the available measurements for improving the forecast.
Nowadays, machine learning techniques provide new opportunities for improving the air quality forecast. A
case study on PM
10
concentrations during a dust storm is performed. It is known that the PM
10
concentrations
are caused by multiple emission sources, e.g., dust from desert and anthropogenic emissions. An accurate
modeling of the PM
10
concentration levels owing to the local anthropogenic emissions is essential for an
adequate evaluation of the dust level. However, real-time measurement of local emissions is not possible,
so no direct data is available. Actually, the lack of in-time emission inventories is one of the main reasons
that current numerical chemical transport models cannot produce accurate anthropogenic PM
10
simulations.
Using machine learning techniques to generate local emissions based on real-time observations is a promising
approach. We report how it can be combined with data assimilation to improve the accuracy of air quality
forecast considerably.
1 INTRODUCTION
Air pollution is one of the most important environ-
mental issues of our time. For instance, according
to a report by the World Health Organization (WHO,
2016) the passing away of one out of every nine
persons is related to air pollution. Next to life and
death, air pollution also causes great damage to econ-
omy. A dust storm or heavy smog with low visibility
can cause a severe disruption of air traffic operations.
Over the last thirty years, large efforts have been spent
in developing numerical atmospheric models in order
to produce accurate air quality forecasts. Tradition-
ally, the so-called chemical transport model (CTM)
has been widely used to forecast the air quality index.
CTM adopts (1) physical principles and (2) statistical
methods to model the emission, advection, diffusion,
and deposition. However, the accuracy of the CTMs
is strongly affected by the model parametrization er-
rors and the emission inventories. Here we note al-
ready that a timely update of the emission inventories
is an essential prerequisite for an acceptable air qual-
ity forecast.
1.1 Data Science and Data-driven
Machine Learning
The advances in sensor technologies and the contin-
uously decreasing costs of electronic devices have
made large scale measurements feasible. A combina-
tion with the ever increasing power of computing plat-
forms has led to a new paradigm in the computational
and statistical methods for processing and analyzing
data (Hey et al., 2009). It is collectively referred to
as data science. Data-driven machine learning meth-
ods are nowadays able to deal with issues such as lo-
cal refinement. However, current knowledge is not
sufficient to formulate them into a (partial differen-
tial) equation. Therefore, data-driven machine learn-
ing techniques have been applied and they showed
us some successes in improving relevant air quality
predictions. Examples of using machine learning in
atmospheric modeling have shown remarkable per-
formances in a number of situations see (Li et al.,
2016; Fan et al., 2017; Li et al., 2017; Chen et al.,
2018). Their results demonstrate that in some cases
data-driven machine learning approaches are able to
Lin, H., Jin, J. and van den Herik, J.
Air Quality Forecast through Integrated Data Assimilation and Machine Learning.
DOI: 10.5220/0007555207870793
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 787-793
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
787

produce results with a high accuracy. However, we
have to admit that the notion of a black-box appli-
cation within data science has so far met only lim-
ited success, e.g., (Caldwell et al., 2014; Lazer et al.,
2014). Currently, we see in PM
10
(PM
10
stands for
Particulate Matter of 10 micrometers or less in diame-
ter) research that the majority of the machine learning
tools are data-driven and the knowledge about phys-
ical laws does not play any role of importance. As
our starting point we put forward that scientific prob-
lems are often under-constrained in nature as the state
space (the degree of freedom) is much larger than
the training samples (observations). For example, the
number of state variables in an atmospheric model is
outnumbering the observations by far, because for a
numerical model with millions or even billions grid
points it is impossible to perform accurate measure-
ments at every grid point and every time step.
1.2 Data Assimilation and
Theory-based Machine Learning
Data assimilation (DA) is a method which utilizes the
information of a relative small number of observa-
tions to improve the uncertain parameters and the ini-
tial conditions. Typically, DA infers the most likely
sequence of states of the dynamical systems such that
the model outputs are in agreement with the observa-
tions available at every time step. DA tries to min-
imize the difference between the outputs of the nu-
merical model and the observations. This happens un-
der the assumptions that both model and observations
contain errors and uncertainties. In fact, data assimi-
lation can be considered as one of the first methods to
integrate data with theory-based models.
Recently, several research groups have started to
study the combination of physics and theory in data-
driven machine learning models (Keller et al., 2017;
Karpatne et al., 2017; Jia et al., 2018). An example is
attempting to enforce physical consistency (e.g., con-
servation of mass and energy) through adding a regu-
larization term in the loss function. It has resulted in
more consistent output.
In this paper, we discuss a new approach, viz. to
integrate data assimilation and data-driven machine
learning so as to make them fit for air quality mod-
eling. The details of this novel approach is intro-
duced in Section.2. A case study on PM
10
concen-
tration during a dust event is performed. The re-
sults are compared to the ones from a conventional
regional chemical transport model (CTM), viz. Lotos-
Euros/air quality (AQ), in Section.3. Section 4 gives
the conclusions and also discusses the different ways
to combine physics and observations into machine
learning AQ forecast system.
2 AN INTEGRATED MACHINE
LEARNING AND DATA
ASSIMILATION SYSTEM FOR
AEROSOL FORECAST
In the following, we describe in a case study how our
system of integrating machine learning and data as-
similation works. First, we estimate the local non-
dust PM
10
concentration using data-driven machine
learning and calculate dust concentration by subtract-
ing the non-dust PM
10
value from the raw PM
10
ob-
servations. Second, the resulting dust concentrations
will be used in CTM/dust data assimilation. Third, a
full-aerosol prediction will be provided by combining
forecasts from machine learning and CTM/dust.
2.1 Data-driven Non-dust PM
10
Forecast System
The recurrent neural network, long term short mem-
ory (LSTM) is used to estimate the local non-dust
aerosol. History records for training are from a
ground-based observing network which has more
than 1000 observing stations all over China. The
simulation is expected to have an agreement with the
PM
10
concentration when there is no dust storm, and
an underestimation in case of dust storms.
The input configuration of our data-driven ma-
chine learning system is shown in Fig.1(a), while
Fig.1(b) represents the data-driven & model-based
system explained in Section.3. The Y
Y
Y
t
0
+k
represents
the output list. In this study, the output list is the non-
dust PM
10
concentration forecast t hours in advance.
W
W
W
t
0
−i
and A
A
A
t
0
−i
are vectors representing time series of
meteorological and air quality measurements in the
past m hours, respectively. W
W
W
t
0
−i
includes the local
meteorological data (temperature at 2m, dew point at
2m, wind speed v10 and u10) from European Cen-
ter for Medium-Ranged Weather Forecast (ECMWF);
while A
A
A
t
0
−i
represents a vector of stationary air qual-
ity observations (PM
2.5
, SO
2
, NO
2
, O
3
, CO) and mea-
surements from nearby sites. L represents the LSTM
non-dust PM
10
regression model based on the history
data from Jan 2013 to March 2015, observations in
the following period from April 2015 to May 2015
will be used for tests.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
788
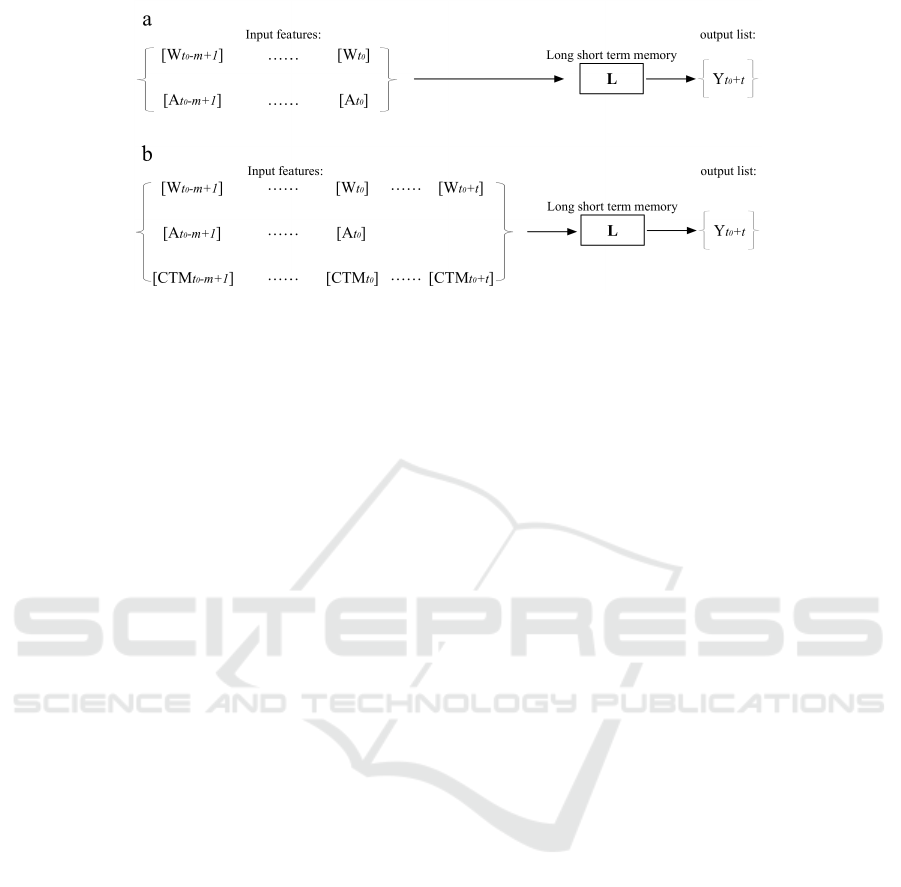
Figure 1: (a): Input configuration of the data-driven non-dust PM
10
simulation system (W
W
W
t
0
−i
, A
A
A
t
0
−i
: meteorological and air
quality records); (b): Input configuration of the data-driven & model-based non-dust PM
10
simulation system (CTM
t
0
+i
: air
quality forecast form CTMs).
2.2 Dust Storm Data Assimilation
In our previous work (Jin et al., 2018), we have
already performed dust emission data assimilation
over East Asia in which the hourly-measured PM
10
are assimilated using a reduced-tangent-linearization
4DVar. The dust emissions are estimated to best fit the
model and observation, the dust concentration fore-
cast is shown to be significantly improved using the
emission field estimated by data assimilation. Further
information can be found in (Jin et al., 2018).
2.3 A Framework of Combining Data
Assimilation and Machine Learning
The observed PM
10
cannot be fully attributed to the
dust storm, since it actually also contains a fraction
of non-dust PM
10
released in human activities. The
real dust measurement is then calculated by subtract-
ing the baseline value (in other words, non-dust PM
10
concentration) from the raw PM
10
observations. The
traditional method to model the baseline in PM
10
for
dust storm simulates non-dust PM
10
using conven-
tional CTMs. Fig.2 illustrates the three modules of
using observational data to improve forecast of PM
10
concentrations under influence of a dust storm. The
first module concerns non-dust PM
10
simulation us-
ing the data-driven machine learning without the ac-
tual emission inventories. The second module con-
cerns data assimilation which improves the estima-
tion of emission in CTM/Dust by assimilation the
baseline-removed PM
10
measurements. The third
module combines the forecasts from machine learn-
ing with observational data and CTM/Dust model to
generate the final full-aerosol prediction.
Generally, the emission inventory data by human
activities are calculated through reanalysis and are
only available after several years. So, CTM models
suffer from the absence of the actual source emission
data and subsequently their forecast accuracies are not
very high. For instance, (Timmermans et al., 2017)
showed that there is an obvious underestimation of
PM
2.5
forecast using the existing inventories. In con-
trast, we apply machine learning to generate non-dust
PM
10
fraction based on the real measurements up to
now. The non-dust PM
10
is called the PM
10
base-
line. This quality-assured PM
10
baseline would im-
prove the dust storm data assimilation. Hence, it will
generate a more accurate full-aerosol prediction.
The accuracy of machine-learning based non-dust
PM
10
model can be further improved. Another way
of integrating machine learning with the CTM model
is to include the CTM non-dust PM
10
predictions as
an extra input for the machine learning model. We
expect such an integration of physics (implemented
in the CTM model) and data science will result in a
further improvement of air quality forecast.
3 RESULTS
The result of our approach is compared to the result of
a conventional regional transport model (CTM), viz.
Lotos-Euros/air quality (AQ), which simulates the
emission, advection/diffusion, deposition of aerosols
released in anthropogenic activities.
Fig.3(a) to (c) present the scatter diagrams of fore-
cast PM
10
values against the observed PM
10
values. A
forecast value is in a good agreement with the obser-
vation when it is close to the diagonal. Fig.3(a) shows
the result of the Lotos-Euros/AQ forecasts 12 hours
in advance vs. the field PM
10
in test set (from April
2015 to May 2015). Fig.3(b) and (c) show the LSTM
forecasts of 1 hour and 12 hours in advance, respec-
Air Quality Forecast through Integrated Data Assimilation and Machine Learning
789

Figure 2: The combination of data assimilation and machine learning system. 1st module: machine learning based non-dust
PM
10
simulation; 2nd module: data assimilation to estimate the emission in CTM/dust using the baseline removed PM
10
observation; 3rd modele: full-aerosol forecast combined with dust forecast and non-dust PM
10
forecast.
tively. It is noted that the records on a severe dust
event, which lasted 2 to 3 days, are also included in
the test period. Thus parts of the Lotos-Euros/AQ and
LSTM forecasts are largely underestimated compared
to the PM
10
observations as seen in the bottom right
corners in Fig.3 (a) to (c). The CTM model Lotos-
Euros/AQ underestimates the non-dust PM
10
, which
is probably caused by the errors in the emission inven-
tories. In comparison, the two LSTM predictions are
in better agreement with the real observations. More-
over, a smaller forecast length t=1 hour gives a better
result as expected.
We also plot the variation of the non-dust aerosol
simulations and the PM
10
observations in four cities
in Fig.4, viz. Holhot(a), Beijing(b), Xingtai(c) and
Baoding(d). The orange band and blue band in the
figures show the LSTM non-dust PM
10
estimations
and the observed PM
10
, respectively. The black dot-
ted line at the bottom of each figure shows the pre-
dicted non-dust PM
10
by the Lotos-Euros/AQ. Since
all these four cities have several observing sites, we
do not only plot the averaged PM
10
observation, but
also show the spread with its maximum and minimum
measurements. Similarly, the LSTM non-dust PM
10
prediction is given together with its spread. Before the
arrival of a dust storm at these cites, the LSTM pre-
diction produces the variations as good as possible.
There is a sharp rise in the PM
10
observation values
when the dust storm arrives at a city. However, the
LSTM prediction of the non-dust fraction remains at
a low level just as was expected, because it is inde-
pendent of the dust storm. In comparison, the Lotos-
Euros/AQ is found continuously to underestimate the
non-dust PM
10
in all these cities.
4 CONCLUDING REMARKS
We have presented a new approach by integrating data
assimilation and data-driven machine learning for air
quality modeling. We distinguished three modules.
The first module uses the data-driven machine
learning to model the non-dust PM
10
with history
records of air quality and meteorological information.
The accuracy is verified to be improved compared
to the traditional chemical transport model (CTM)
which simulates the physical processes of baselines in
PM
10
concentration. In the second module, the data
assimilation is performed using the baseline-removed
observations for parameter estimations in dust mod-
eling. The third module combines the predictions
from data-driven machine learning and the CTM/dust
model to generate the final full-aerosol forecast.
Our new proposed approach is a comprehensive
framework which integrates the data-driven machine
learning and physics-based model via data assimila-
tion and data generation using a physics-based simu-
lation model. In an adjusted way we can explain this
as follows. The first module provides a solution to
cope with incomplete knowledge, the second module
uses observations to improve the physics-based (pos-
sibly partial) mode through adjustment of parameters
and initial conditions. Finally, the third module com-
bines the results of the first two modules to generate
the final prediction.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
790
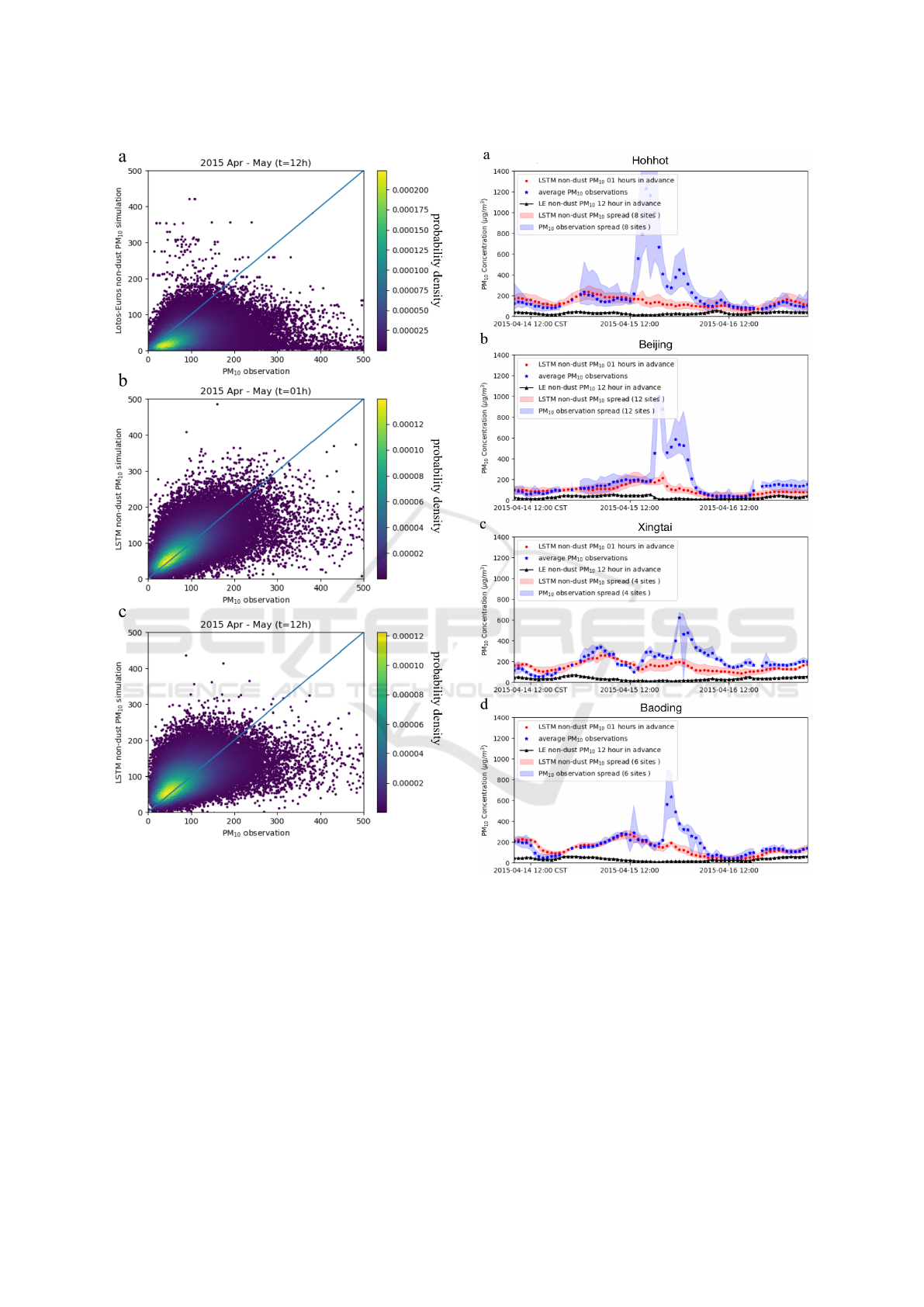
Figure 3: Lotos-Euros vs. LSTM non-dust PM
10
compari-
son.
Our first test of non-dust PM
10
simulation shows
that the machine learning outputs are better in agree-
ment with the observations when compared to the
conventional CTMs. In future experiments, we will
further explore the possibility of combining machine
learning and CTM. The effect of (1) new input fea-
tures on the baseline simulation result and (2) the dust
storm data assimilation will be explored in the near
future.
In contrast to the data-driven machine learning ap-
proach, the conventional CTM is based on the physi-
cal principles and statistic methods to model dynamic
systems. It requires thorough understanding of the
Figure 4: Time series of non-dust PM
10
simulation during
the dust storm for four cities.
underlying governing equations and well identified
parameters (e.g., the accurate emission inventories).
In practice, we often do not have complete knowl-
edge about the emission source data. What we have
now is the flexibility and generality of data-driven ma-
chine learning. It provides a powerful means to fill
this gap. In the past few years, the question how to
include physics or theory into a data-driven machine
learning system has absorbed increasingly more at-
tentions of the researchers involved. In the literature,
some researchers have used the term physics-guided
Air Quality Forecast through Integrated Data Assimilation and Machine Learning
791
or theory-based machine learning to distinguish from
the pure data-driven approaches.
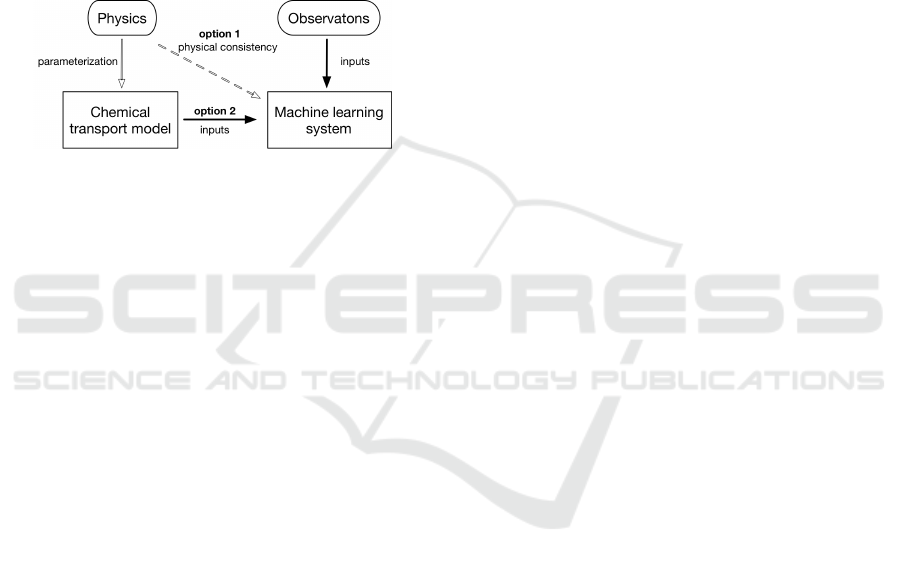
There are two options to include physical rules
into data-driven machine learning models, of which
the overview is given in Fig.5. The first option is to
enforce physical consistency through adding a regu-
larization term in the loss function. Such an approach
is based on data-driven machine learning. The second
option is to use a CTM for generating output which
is then used as input for a machine learning system.
The latter one combines knowledge of physics (for-
mulated in terms of physical parametrization) with
data-driven machine learning.
Figure 5: The combination of data assimilation and ma-
chine learning system.
Option 2 uses the mechanism depicted in Fig.1(b)
which represents the model-based & data-driven
baseline forecasts, the configuration of the extended
system. CTM
t
0
+i
gives the baseline forecasts of i
hours in advance from the CTMs. The meteorolog-
ical forecast W
W
W
t
0
+i
is also used as input.
Finally, we believe that integration of machine
learning, data assimilation and physics-based numer-
ical models can be applied to many other problems
in scientific and engineering fields. For instance, con-
sider another air quality modeling application, predic-
tions of visibility. Currently, conventional numerical
models are insufficient to produce accurate visibility
predictions, e.g., (Clark et al., 2008), due to the com-
plexity and inability to fully quantify the influence of
many factors. In (Deng et al., 2019), LSTM has been
used to learn to predict the visibility based on local
meteorological measurements such as wind and hu-
midity. A promising extension would be to combine
weather and air quality predictions with current mea-
surement data to further improve the visibility fore-
cast accuracy. Yet another auspicious application of
the integrated framework is to use machine learning
techniques to estimate errors of (physics-based) nu-
merical models. It is known that an error quantifica-
tion of the numerical model is essential for the suc-
cess of data assimilation. However, there is usually
little knowledge about these errors. Machine learn-
ing can be applied to estimate of an error model using
measurement data and twin-experiments. A quality-
assured error model can further enhance the effective-
ness of the data assimilation.
REFERENCES
Caldwell, P. M., Bretherton, C. S., Zelinka, M. D., Klein,
S. A., Santer, B. D., and Sanderson, B. M. (2014).
Statistical significance of climate sensitivity predic-
tors obtained by data mining. Geophysical Research
Letters, 41(5):1803–1808.
Chen, G., Li, S., Knibbs, L. D., Hamm, N. A. S., Cao, W.,
Li, T., Guo, J., Ren, H., Abramson, M. J., and Guo, Y.
(2018). A machine learning method to estimate PM2.5
concentrations across China with remote sensing, me-
teorological and land use information. Science of The
Total Environment, 636:52–60.
Clark, P. A., Harcourt, S. A., Macpherson, B., Mathison,
C. T., Cusack, S., and Naylor, M. (2008). Prediction
of visibility and aerosol within the operational Met
Office Unified Model. I: Model formulation and vari-
ational assimilation. Quarterly Journal of the Royal
Meteorological Society, 134(636):1801–1816.
Deng, T., Cheng, A., Han, W., and Lin, H. X. (2019). Vis-
ibility forecast for airport operations by LSTM neural
networks. Proc. ICAART.
Fan, J., Li, Q., Hou, J., Feng, X., Karimian, H., and Lin, S.
(2017). A Spatiotemporal Prediction Framework for
Air Pollution Based on Deep RNN. ISPRS Annals of
Photogrammetry, Remote Sensing and Spatial Infor-
mation Sciences, IV-4/W2:15–22.
Hey, T., Tansley, S., and Tolle, K. (2009). The Fourth
Paradigm: Data-Intensive Scientific Discovery. Mi-
crosoft Research.
Jia, X., Karpatne, A., Willard, J., Steinbach, M., Read, J.,
Hanson, P. C., Dugan, H. A., and Kumar, V. (2018).
Physics Guided Recurrent Neural Networks For Mod-
eling Dynamical Systems: Application to Monitoring
Water Temperature And Quality In Lakes.
Jin, J., Lin, H. X., Heemink, A., and Segers, A. (2018).
Spatially varying parameter estimation for dust emis-
sions using reduced-tangent-linearization 4DVar. At-
mospheric Environment, 187:358–373.
Karpatne, A., Atluri, G., Faghmous, J. H., Steinbach, M.,
Banerjee, A., Ganguly, A., Shekhar, S., Samatova, N.,
and Kumar, V. (2017). Theory-guided Data Science:
A New Paradigm for Scientific Discovery from Data.
IEEE Transactions on Knowledge and Data Engineer-
ing, 29(10):2318–2331.
Keller, C. A., Evans, M. J., Kutz, J. N., and Pawson, S.
(2017). Machine learning and air quality modeling.
2017 IEEE International Conference on Big Data (Big
Data), pages 4570–4576.
Lazer, D., Kennedy, R., King, G., and Vespignani, A.
(2014). The Parable of Google Flu: Traps in Big Data
Analysis. Science, 343(6176):1203–1205.
Li, X., Peng, L., Hu, Y., Shao, J., and Chi, T. (2016).
Deep learning architecture for air quality predic-
tions. Environmental Science and Pollution Research,
23(22):22408–22417.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
792

Li, X., Peng, L., Yao, X., Cui, S., Hu, Y., You, C., and Chi,
T. (2017). Long short-term memory neural network
for air pollutant concentration predictions: Method
development and evaluation - ScienceDirect. Environ-
mental Pollution, 231:997–1004.
Timmermans, R., Kranenburg, R., Manders, A., Hendriks,
C., Segers, A., Dammers, E., Zhang, Q., Wang, L.,
Liu, Z., Zeng, L., Denier van der Gon, H., and Schaap,
M. (2017). Source apportionment of PM2.5 across
China using LOTOS-EUROS. Atmospheric Environ-
ment.
WHO (2016). Ambient air pollution: a global assessment
of exposure and burden of disease.
Air Quality Forecast through Integrated Data Assimilation and Machine Learning
793
