
Text Recognition on Khmer Historical Documents using Glyph Class
Map Generation with Encoder-Decoder Model
Dona Valy
1,2
, Michel Verleysen
1
and Sophea Chhun
2
1
ICTEAM, Université Catholique de Louvain, Belgium
2
Department of Information and Communication Engineering, Institute of Technology of Cambodia, Cambodia
Keywords: Handwritten Text Recognition, Khmer Palm Leaf Manuscript, Glyph Class Map.
Abstract: In this paper, we propose a handwritten text recognition approach on word image patches extracted from
Khmer historical documents. The network consists of two main modules composing of deep convolutional
and multi-dimensional recurrent blocks. We utilize the annotated information of glyph components in the
word image to build a glyph class map which is to be predicted by the first module of the network call glyph
class map generator. The second module of the network encodes the generated glyph class map and
transform it into a context vector which is to be decoded to produce the final word transcription. We also
adapt an attention mechanism to the decoder to take advantage of local contexts which are also provided by
the encoder. Experiments on a publicly available dataset of digitized Khmer palm leaf manuscripts called
SleukRith set are conducted.
1 INTRODUCTION
Historical documents are very valuable since they
contain significant historical information about a
person, a place, or an event thus serve as primary
sources of important ingredients useful for
researchers in many fields of study. Preservation of
these documents are essential, and with the help of
recent technologies, they can be digitized and
centralized. However, in order to enable word search
to give the public easy and quick access to the
content of the digitized documents, a text
recognition system is needed.
Handwriting text recognition is a very
challenging task especially on old degraded
documents. Recently, the performance of such kind
of system has been improved greatly by leveraging
deep learning approaches utilizing concepts such as
convolutional neural networks (CNN) due to their
ability to extract automatically both low and more
abstract level of features from the text image. Long
short-term memory recurrent neural networks
(LSTM-RNN) are also widely used since such
network is able to store and remember information
for longer amounts of time which is suitable for
sequential problem like text recognition. While a
conventional LSTM uses its recurrence only over
one dimension (normally the x-axis of the text
image), a more robust multi-dimensional LSTM
(MDLSTM) employs sequential information from
both the vertical and horizontal axes of the image
(Graves et al., 2007) (Graves and Schmidhuber,
2009). In recent work, the combination of CNN and
RNN modules together has shown great success in
solving handwritten text recognition problems on
Latin and Chinese scripts (Voigtlaender et al., 2016)
(Ding et al., 2017) (Wu et al., 2017) (Wang et al.,
2018). To decode the final text transcription,
Connectionist Temporal Classification (CTC)
introduced by (Graves, et al., 2006) is often used
since no time-consuming annotated alignment
information is needed. This decoding technique is
one dimensional in nature and works efficiently well
for scripts with one directional writing style (for
example, left to right or top to bottom), i.e. no more
than one character is at the same horizonal or
vertical position. However, for scripts with a more
complex writing style such as Khmer, character
annotation and alignment information might still be
required to produce a more accurate recognition
result.
In this paper, we proposed a model which takes
advantage of both the convolutional module and the
multi-dimensional recurrent module to recognize
texts on a particular type of historical documents
Valy, D., Verleysen, M. and Chhun, S.
Text Recognition on Khmer Historical Documents using Glyph Class Map Generation with Encoder-Decoder Model.
DOI: 10.5220/0007555507490756
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 749-756
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
749

written in Khmer script called palm leaf
manuscripts. The proposed model also incorporates
the annotated spatial alignment information of each
character or glyph in the text image.
2 DESCRIPTION OF KHMER
HISTORICAL DOCUMENTS
2.1 Palm Leaf Manuscripts
Palm leaves were used as one of the earliest writing
mediums since centuries ago in many Southeast
Asian countries. In Cambodia, palm leaf documents
are called “Sleuk Rith” which literally means a
binding of leaves. Khmer Palm leaf manuscripts are
of important cultural value, and the content in the
manuscript themselves has been passed on from
generations to generations through scholars and
scribers. As the name implies, palm leaf manuscripts
are made from dried leaves of a specific specie of
palm tree. The dried leaves are cut and trimmed to
be long rectangular writing pages. A special kind of
sharp metal stylus is used to scribe texts onto each
page of the document, and a mixture of black ink
(normally a combination of coal and a kind of paste)
is applied afterwards to emphasize the carved letters.
All scribed pages are eventually tied and bound
together to form a complete book.
2.2 Challenges for Text Recognition
Task
Biodegradation of palm leaf pages is one of the main
issues for preservation measurement for this type of
document. The degradation influences the images of
the digitization process of the palm leaf document: it
produces noises, discoloration, and poor contrast
causing omission of texts, and other types of defects
which render pre-processing tasks including
binarization and segmentation difficult or impossible
(Kesiman et al., 2018).
Complexity of Khmer script is also a big
challenge. Khmer is recognized by the Guinness
World Records
1
to be the language with the longest
alphabet which consists of 74 distinct letters. Certain
types of letters have more than one form and/or can
be combined with other letters to create more shapes
which increase even more the number of symbols in
Khmer writing. The abundance of different symbols
in Khmer script requires a complex and
1
http://www.guinnessworldrecords.com/world-records/longest-
alphabet
sophisticated system for those letters to be
efficiently recognized and accurately classified.
On account of the large quantity of symbols,
many of those symbols are very similar and can be
distinguishable by only the appearance of some
small strokes or holes and their spatial locations. In
old handwritten form, this similarity is even more
apparent and sometimes creates an ambiguity
between symbols which requires context from
neighbouring symbols so that those ambiguous
symbols can be correctly identified.
Consonants in Khmer script are used either as
individuals or as clusters of multiple letters i.e. a
double or triple decker form which is composed of a
normal letter and one or two subscripts to merge the
sound of those consonants together. Figure 1 shows
some examples of different combinations of
consonant clusters. Vowels and diacritics can be
ascenders or descenders or can be placed at either
side (right or left) of the main consonant or the
cluster of the main consonant. Some letters even
consist of multiple parts which can be positioned at
different locations simultaneously.
Unicode encoding (U1780-U17FF) has been
adopted to represent Khmer symbols. Even though
the overall writing direction of a word is left to right,
the order of the Unicode codes in the code sequence
representing that word does not always follow the
writing order of the composing symbols. Also,
symbol to code relationship is not always one to one
i.e. some symbols can be represented by more than
one code, and some codes can represent a
combination of symbols. For instance, each
subscript of any consonant does not have its own
code but is instead represented by a sequence of two
codes: a special code “coeng” (U17D2) followed by
the code of its corresponding normal consonant.
Unlike words in Latin script whose symbols can be
identified one by one, to recognize a Khmer word,
one must look at the whole writing of the word. This
illustrates that the spatial information of each
symbol composing a word is crucial for the
recognition of that word.
Figure 1: Examples of double-decker and triple-decker
clusters of Khmer consonants.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
750

3 SLEUKRITH SET
SleukRith Set is a collection of annotated data
created from a corpus of 657 digital images of
Khmer palm leaf manuscript pages (Valy et al.,
2017). Three types of annotated data are
constructed: glyphs, words, and lines.
3.1 Isolated Glyph and Word Datasets
Annotation of SleukRith Set is done in a bottom-up
fashion. Each glyph is first manually segmented by
tracing its polygon boundary. Note that a glyph may
represent a part of a letter, a single letter, or a group
of letters. The coordinates of all vertices of the
polygon boundary are kept along with the code or
sequence of codes accordingly assigned to the glyph.
After all glyphs in a manuscript page have been
segmented and annotated, annotation at word level
can begin. To form a word, its glyph components are
grouped together. A transcription of the word is then
given. Word annotation therefore contains both the
transcription (Unicode text) and the annotated
information of its component glyphs (each glyph’s
boundary vertices and its label codes). The rectangle
patch image of each word can be generated by using
the bounding box of the union of the polygon
boundaries of all its glyph components.
3.2 Glyph Class Map
Using the annotated information of each glyph
component, a glyph class map (GCM in short)
originally called a character-class map (Valy, et al.,
2018) is built for each word patch image. Let’s
suppose a word image composing of glyphs, and
(0) represents the region bound by the
polygon boundary of the
th
glyph
. In each region
, we replace the value of each pixel by a new
value
(0
where
is the number of
glyph classes) corresponding to the class of the
glyph
(see Figure 2.b). A new image ′ with the
same dimension as is created by forming the union
of all regions
. An additional value (
0) is
used to fill in the background region of ′ where no
glyph pixels are assigned to. The new image ′ is
divided into grid of cells of
by
pixels where
and
are the height and width of each cell
respectively. Prior to this division, resizing ′ to be
of size
by
might be necessary to ensure that
all cells are of equal size i.e.
mod
0 and
mod
0. We also denote
and
to
be the number of rows and the number of columns
of the grid (
/
and
/
). Each
cell of the GCM is then assigned to one and only one
glyph class which is the pixel value contained the
most in that cell. Figure 2 shows how a GCM is
constructed.
4 TEXT RECOGNITION
We propose an end-to-end model to recognize a
handwritten text on word image patches extracted
from Khmer palm leaf manuscripts. The model
consists of two main modules: the GCM generator
and the GCM encoder-decoder. Figure 3 illustrates
the complete architecture of the proposed model.
Both modules utilize the combination of
convolutional and multi-dimensional recurrent
blocks.
4.1 GCM Generator
A GCM generator takes a grayscale word image
patch with dimension
as input and returns
a corresponding GCM of the patch as output. First,
convolutional blocks are used to extract
automatically the features of the word image patch.
Each convolutional block is composed of a
convolutional layer with a receptive field 55 at a
fixed stride 11. We increase the number of
feature maps from 64 to 128 and then to 256 to
gradually obtain from low to higher levels of
representation. To further extend the depth of the
network, we also downscale the image by a factor of
2 at the end of each convolutional block by using
maxpooling with kernel size 22 at a stride 22.
Figure 2: (a) Original word image patch , (b) New image
′, (c) GCM.
Text Recognition on Khmer Historical Documents using Glyph Class Map Generation with Encoder-Decoder Model
751

Figure 3: Overview of the architecture of proposed text
recognition model.
Convolutional blocks are activated by ReLu. To
regularize the model and to prevent overfitting,
dropout of dropped probability 0.3 is introduced
after each block. To ensure that the dimension of the
output predicted by the CGM generator is identical
to the ground truth CGM (i.e.
), the
feature map output from the convolutional blocks
needs to be divided into a grid of cells of size
which can be computed as follows:
2
(1)
2
(2)
where
is the number of convolutional blocks
which is equal to 3 in the proposed architecture. We
should also ensure that
and
are large enough
to allow the division by 2
. Therefore, we use
8 in our experiments. Each cell in the
grid is then transformed into a vector by flattening
out its dimension.
To take advantage of the importance of local
spatial context in a two-dimensional space according
to the characteristics of Khmer writing, we use
multi-directional multi-dimensional LSTM
(MDDLSTM) (Graves, et al., 2007) in our recurrent
blocks. In stead of a single hidden state from the
previous time step like in the conventional one-
dimensional LSTM, MDDLSTM makes use of two
states each from both the vertical and horizontal
axes.
To take into account all directions in the 2D
space, four grids of cells are produced from the
feature map grid. Those four grids represent four
diagonal directions: top-left to bottom-right, bottom-
left to top-right, top-right to bottom-left, and bottom-
right to top-left. The four directional grids share the
same two-layer block of MDDLSTM (each layer
with 256 hidden units) to produce four output grids
whose feature vectors in each cell are then
concatenated together to transform back into a single
grid of feature map. At each cell of the grid, we
apply a dropout (0.3) followed by a fully
connected layer (with 1024 hidden units) activated
by ReLu and another dropout (0.5). To predict
the GCM corresponding to the input word image
patch, the last layer with
1 hidden units and a
softmax activation is used to output the probabilities
of all glyph classes (including the class representing
the background) for each cell in the predicted GCM.
4.2 GCM Encoder-Decoder
An encoder-decoder model is used to convert the
GCM into final transcription of the input word
image patch. This encoder-decoder module is
separated into two sub-modules: an encoder and a
decoder. The encoder encodes the GCM generated
by the GCM generator into a representation vector
called context vector. The decoder then uses the
context vector as an initial state to predict the
Unicode transcription one letter at each time step.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
752

4.2.1 Encoder
We propose a combination of convolutional blocks
and recurrent blocks as our GCM encoder. It takes
as input the GCM and first reduces the dimension of
the vector in each cell by passing it through an
embedding layer (64 neurons) and then squash it
using Tanh activation. Since the GCM contains
information about the identity and the number of
glyphs appearing in the word image patch and also
their estimated boundary regions, two convolutional
blocks are used to capture the bottom features of the
map. Two main benefits of these convolutional
blocks are that (1) the features extracted are useful in
detecting and grouping together automatically the
neighbouring cells belonging to the same glyph
region without the need for handcrafted method such
as connected component extraction and also that (2)
the maxpooling layer down-samples the GCM
dimensionality which limits the length of the input
sequence to the recurrent block of the encoder to be
not too long. For the purpose of regularization,
dropouts are used after each convolutional block.
Due to the GCM being two-dimensional, we again
use MDDLSTM in the recurrent block of the GCM
encoder. Similar to the description of applying
MDDLSTM in the GCM generator mentioned
previously, the recurrent block output four grids
along four different diagonal directions. The four
grids are afterwards merged back together to form
the final grid with dimension ½
½
(the
GCM is down-sampled by a factor of 2 due to the
maxpooling layer in the first convolutional block)
which is used to compute the output context vector
by averaging all its cells. The final grid of the
encoder can also be referred to as the local contexts
of the GCM. Both the context vector and the local
contexts are sent to the decoder to be decoded into
word transcription.
4.2.2 Decoder with Attention Mechanism
A GCM decoder is used to predict the next letter or
character in the word transcription given the context
vector generated from the encoder and all previously
predicted characters. The characters to be predicted
are represented by integer values , 0
3 where
is the total number of Khmer
Unicode characters (which are limited between
U1780 and U17E9). We add three more character
codes to represent the start token
, the end
token
, and the unknown character
. Before
being fed to the module as input, the character
representation value is transformed into a vector
by using the one hot encoding technique. For this
module, we use a conventional one-dimensional
LSTM as the recurrent block. Figure 4 shows the
detailed architecture of the GCM decoder. Before
becoming the initial hidden state of the LSTM, the
context vector is first passed through a fully
connected layer with equal number of hidden units
(512) and is activated by Tanh function.
Since the generated GCM may contain multiple
groups of cells representing multiple regions of
glyph boundaries, each predicted character from the
decoder should be conditioned on a different region
of cells. Instead of relying only on a single encoded
context vector, the decoder should pay its attention
to particular regions in the CGM to predict
efficiently the correct character at each time step.
The local contexts provided also by the GCM
encoder are useful in this situation. We adopt the
attention mechanism proposed by (Bahdanau et al.,
2014).
Denote
a local context at position ,, 0
½
and 0½
, the attention vector
at each time step (
) is computed as a weighted
sum of the local contexts.
∗
(3)
The weight vector
of each local context
is
computed by
exp
∑∑
exp
(4)
,
(5)
where
is a small neural network with one hidden
layer of 512 units
,
;
(6)
which is used to learn the weight vector
at time
step in function of the previous hidden state of the
decoder
and each local context
. The input
to the LSTM is the concatenation of the one hot
encoding of the character and the attention vector
.
The decoder always has the start token
as its
first input at time step 0. The current hidden
state from the recurrent block is then fed into the
final output layer (after applying a dropout with
dropped probability 0.5), and a softmax
function is applied afterwards. This sotfmax
activated output is used to create the input for the
next time step. The decoder stops generating new
Text Recognition on Khmer Historical Documents using Glyph Class Map Generation with Encoder-Decoder Model
753
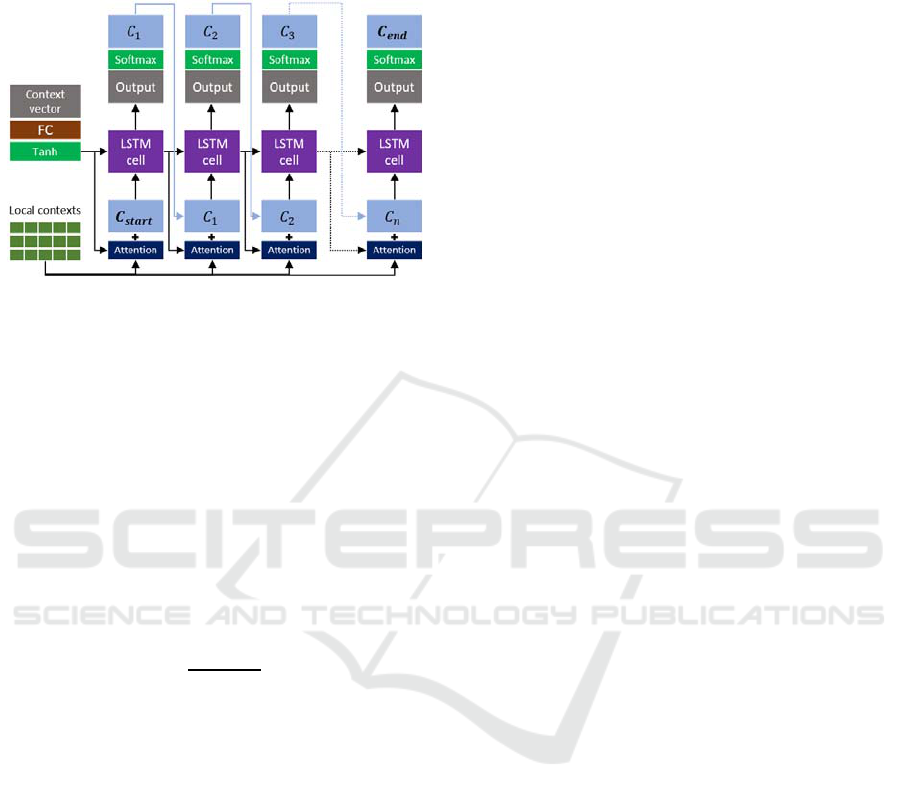
characters when the end token
is encountered
or when the output transcription reaches a maximum
length.
Figure 4: Detailed architecture of GCM decoder.
4.2.3 Beam Search
Instead of using greedy search i.e. choosing the
character with the highest probability at each time
step, we adopt the beam search with length
normalization as proposed by (Wu et al., 2016). The
beam search technique maximizes the joined
probability of all characters in the predicted word
transcription by keeping the top predictions as
hypotheses. To not let the search prefer short
transcriptions to long ones, the joined probability of
each hypothesis is normalized by being divided by
which is computed as follows:
1
(7)
where is the length of the predicted transcription in
each hypothesis. In our experiments, we select the
beam size to be 5, and the hyper parameters and
are chosen to be 5 and 0.7 respectively as
recommended by (Wu et al., 2016). The hypothesis
whose joined probability is the maximum is chosen
as the final output transcription.
5 EXPERIMENTS AND RESULTS
5.1 Training Procedure
The dataset used to train the proposed model is
generated from SleukRith set. It consists of 24,009
samples of word image patches, their corresponding
ground truth GCM, and their word transcriptions.
The dataset is divided into three parts: around 65%
for training, 5% for validating, and 30% for testing.
All word image patches are in grayscale (only one
colour channel) and are normalized by scaling so
that they are of the same height (72 pixels) but still
with variable width.
To train the complete model, two losses are
minimized. The first loss
corresponds to how well
the generator generates the CGM while the second
loss
captures the overall performance of the
model to predict the final word transcription. For
each sample image, those two losses are computed
as follows:
,
log
,
(8)
where
,
is the probability that the generator
predicts that the cell at the
th
row and the
th
column
of the predicted GCM belongs to glyph class , and
,
is equal to 1 if the cell at position , of the
ground truth GCM belongs to glyph class or
otherwise it is equal to 0. The second loss
is
computed by
,
log
,
(9)
where
,
is the predicted probability of
character of class at time step ,
,
(0
3) is the one hot encoding of the
th
character in the ground truth transcription, and
is the length of the ground truth transcription. The
total loss of the complete model is then computed by
1
(10)
where ( ∈ 0,1) is a hyper parameter to control
how generating the GCM affects the total loss.
During training the total loss of the function is
minimized using Adam optimizer (Kingma and Ba,
2014). The GCM generator and the GCM encoder-
decoder are pre-trained separately to minimize their
corresponding losses using a normal distribution
with standard deviation of 0.1 as initial weights and
constants values of 0.1 as initial biases for all layers
of the network. For the GCM encoder, the ground
truth GCM is used instead as input. We also adapt
the teacher forcing technique for the GCM decoder.
The technique feds the characters in the ground truth
word transcription to the decoder for the prediction
of later outputs instead of using the predicted output
from the previous time step of the decoder itself.
This teacher forcing behaviour forces the decoder to
stay close to the ground truth sequence resulting in
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
754

faster training. Periodically every five epochs, we
alternatively train with teacher forcing for the first
three epochs, and without it for the last two epochs.
After each module converges, the complete network
is then fine tuned by minimizing the total loss as
computed in equation (10).
The network and its modules are trained per mini
batch basis (25 samples per batch). For efficient
training, input word image patches are sorted by
their width and are then batched together so that all
image samples in the same batch have similar width.
At the start of each epoch, the order of the batch is
shuffled. To ensure that all images in the same batch
have the same dimension, they are rescaled to new
height
and width
:
1
(11)
1
,
(12)
where
,
is the minimum width of the batch,
and
and
are small values selected arbitrarily
between 0.15,0.15. This rescaling also provides
data augmentation to the training set due to the
random nature of
and
.
For every
of iterations, we evaluate the
network on the validation set and stop the training if
the evaluation result does not improve for
consecutive epochs. In our experiments we select
50 and
5.
5.2 Evaluation Protocols
We evaluate the network according to two criteria:
the generated GCM and the final word transcription.
To measure the performance of the GCM generator,
the top error rate is used. Each cell of the target
GCM is predicted by the network and is considered
to be incorrect if the target cell in the ground truth
GCM is not one of the top predictions from the
network. The error rate of one sample word image
patch is the number of incorrectly classified cells
over the total number of cells (
∗
) in that
image patch. We then obtain the final error rate of
all samples in the test set by averaging the error rate
of each sample.
To evaluate the performance of the GCM
encoder-decoder, Levenshtein distance
is used to
compute the character error rate (CER) of each word
as follows
min
,
,
|
|
(13)
where
and
are the predicted transcription
and the ground truth transcription respectively, and
|
| represents the length of the ground truth
transcription. According to this computation, the
CER of each word is always between 0,1. This
also illustrates that the error rate is higher for the
same amount of incorrectly predicted characters
when the network performs on a shorter word image
patch which makes sense since the importance of
each character is stronger in short length
transcriptions. The final CER is the average of each
word CER in the test set. Word error rate (WER),
which is the number of incorrectly predicted words
over the total number of words, is also calculated for
the evaluation.
5.3 Results
The evaluation results are shown in Table 1. We
measure the top error rate (we choose 1 and
5) of the output from the GCM generator and
also the CER and WER of the transcription
produced by the complete network. Three
experiments are conducted on the complete network
after its two modules (the GCM generator and the
GCM encoder-decoder) are pretrained separately to
minimize
and
respectively: (1) we do not do
any finetuning; (2) we finetune the complete
network on
setting the hype-parameter to
zero, i.e.
has no effect on the total loss
; and
(3) we finetune on
with 0.9 (very strong
influence of
).
By looking at the big difference between the top
1 and top 5 error rate of the generated GCM, it is
illustrated that even though the GCM generator is
sometimes not able to predict the correct glyph class
as the most probable (top 1), in most of those cases,
the probability of the correct glyph class is still high
enough to be among the top 5. Fortunately, in the
complete system, this glyph class probability
distribution of the predicted GCM is passed directly
to the GCM encoder-decoder which can be helpful
for the generation of the final word transcription.
Table 1: Evaluation results of the proposed system.
Error Rate of the
GCM Generator
(%)
Error Rate of the
Complete
Pipeline (%)
Top 1 Top 5 CER WER
(1) No finetuning 12.42 0.25 4.43 13.49
(2) Finetune on
with 0
12.81 0.24 3.88 12.11
(3) Finetune on
with 0.9
12.21 0.23 3.80 11.81
Text Recognition on Khmer Historical Documents using Glyph Class Map Generation with Encoder-Decoder Model
755

As seen in Table 1, finetuning the complete
network by minimizing
improves the overall
performance. Moreover, by enforcing the network to
produce a good GCM (i.e. set a high value to ), the
error rates of the predicted word transcription
decrease even more.
6 CONCLUSION
In this paper, we present a robust approach to
recognize handwritten texts on Khmer historical
documents. The proposed approach utilizes the
glyph class map (GCM) constructed using the glyph
annotation which contains information about the
structure, position, and identity of each glyph in the
word image to be recognized. Two main modules,
the GCM generator and the GCM encoder-decoder
are developed to generate the GCM which is to be
encoded into a context vector and also local contexts
representing the input word image before being
decoded into the final transcription. Our approach
shows promising results evaluated on data extracted
from SleukRith set, a publicly available dataset
constructed on digitized Khmer palm leaf
documents.
ACKNOWLEDGEMENTS
This research study is supported by ARES-CCD
(program AI 2014-2019) under the funding of
Belgian university cooperation.
REFERENCES
Bahdanau, D., Kyunghyun, C. & Yoshua, B., 2014. Neural
machine translation by jointly learning to align and
translate. arXiv preprint arXiv:1409.0473.
Ding, H. et al., 2017. A Compact CNN-DBLSTM Based
Character Model For Offline Handwriting Recognition
with Tucker Decomposition. The 14th IAPR
International Conference on Document Analysis and
Recognition (ICDAR), pp. 507-512.
Graves, A., Fernándex, S. & Schmidhuber, J., 2007.
Multi-Dimensional Recurrent Neural Networks. The
International Conference on Artificial Neural
Networks.
Graves, A., Fernández, S., Gomez, F. & Schmidhuber, J.,
2006. Connectionist temporal classification: labelling
unsegmented sequence data with recurrent neural
networks. The 23rd international conference on
Machine learning, pp. 369-376.
Graves, A. & Schmidhuber, J., 2009. Offline handwriting
recognition with multidimensional recurrent neural
networks. Advances in neural information processing
systems.
Kesiman, M. W. A. et al., 2018. Benchmarking of
Document Image Analysis Tasks for Palm Leaf
Manuscripts from Southeast Asia. Journal of Imaging,
4(2), p. 43.
Kingma, D. P. & Ba, J., 2014. Adam: A method for
stochastic optimization. arXiv preprint
arXiv:1412.6980.
Valy, D., Verleysen, M., Chhun, S. & Burie, J.-C., 2017.
A New Khmer Palm Leaf Manuscript Dataset for
Document Analysis and Recognition: SleukRith Set.
The 4th International Workshop on Historical
Document Imaging and Processing, pp. 1-6.
Valy, D., Verleysen, M., Chhun, S. & Burie, J.-C., 2018.
Character and Text Recognition of Khmer Historical
Palm Leaf Manuscripts. The 16th International
Conference on Frontiers in Handwritting Recognition.
Voigtlaender, P., Doetsch, P. & Ney, H., 2016.
Handwriting recognition with large multidimensional
long short-term memory recurrent neural networks.
The 15th International ConferenceIn Frontiers in
Handwriting Recognition (ICFHR), pp. 228-233.
Wang, W. et al., 2018. DenseRAN for Offline
Handwritten Chinese Character Recognition. The 16th
International Conference on Frontiers in
Handwritting Recognition, pp. 104-109.
Wu, Y. et al., 2016. Google’s Neural Machine Translation
System: Bridging the Gap between Human and
Machine Translation. arXiv preprint
arXiv:1609.08144.
Wu, Y.-C., Yin, F., Chen, Z. & Liu, C.-L., 2017.
Handwritten Chinese Text Recognition Using
Separable Multi-Dimensional Recurrent Neural
Network. The 14th IAPR International Conference on
Document Analysis and Recognition (ICDAR), pp. 79-
84.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
756
