Automatic View Selection for Distributed Dimensional Data

Leandro Ordonez-Ante, Gregory Van Seghbroeck, Tim Wauters, Bruno Volckaert and Filip De Turck

Ghent University - imec, IDLab, Department of Information Technology,

Technologiepark-Zwijnaarde 15, Gent, Belgium

Keywords:

Interactive Querying, View Selection, Clustering, Distributed Data, Dimensional Data, Data Warehouse.

Abstract:

Small-to-medium businesses are increasingly relying on big data platforms to run their analytical workloads

in a cost-effective manner, instead of using conventional and costly data warehouse systems. However, the

distributed nature of big data technologies makes it time-consuming to process typical analytical queries,

especially those involving aggregate and join operations, preventing business users from performing efﬁcient

data exploration. In this sense, a workload-driven approach for automatic view selection was devised, aimed

at speeding up analytical queries issued against distributed dimensional data. This paper presents a detailed

description of the proposed approach, along with an extensive evaluation to test its feasibility. Experimental

results shows that the conceived mechanism is able to automatically derive a limited but comprehensive set of

views able to reduce query processing time by up to 89%–98%.

1 INTRODUCTION

Existing enterprise applications often separate busi-

ness intelligence and data warehousing operations—

mostly supported by Online Analytical Process-

ing systems (OLAP)—from day-to-day transaction

processing—a.k.a. Online Transaction Processing

(OLTP) (Plattner, 2013). While OLTP systems rely

mostly on write-optimized stores and highly normal-

ized data models, OLAP technologies work on top of

read-optimized schemas known as dimensional data

models, which leverage on denormalization and data

redundancy to run computationally-intensive queries

typical from decision-support applications (e.g. re-

porting, dashboards, benchmarking, and data visual-

ization), that would result in prohibitively expensive

execution on fully-normalized databases.

Traditional data warehousing systems are expen-

sive and remain largely inaccessible for most of

the existing small-to-medium sized business (SMEs)

(Qushem et al., 2017). However, thanks to the advent

of big data, more and more cost-effective (often open-

source) tools and technologies are made available for

these organizations, enabling them to run analytical

workloads on clusters of commodity hardware instead

of costly data warehouse infrastructure. Yet in such a

distributed setting, some of the common challenges of

conventional data warehousing systems become even

more daunting to deal with: the way data is scattered

and replicated across distributed ﬁle systems such

as Hadoop’s HDFS (Shvachko et al., 2010) makes

it computationally expensive and time-consuming

to run Aggregate-Select-Project-Join (ASPJ) queries

which are one of the foundational constructs of OLAP

operations.

For typical data warehousing and related applica-

tions using materialized views is a common method-

ology for speeding up ASPJ-query execution. The

associated overhead of implementing this methodol-

ogy involves computational resources for creating and

maintaining the views, and additional storage capac-

ity for persisting them. In this sense, ﬁnding a fair

compromise between the beneﬁts and costs of this

method is regarded by the research community as the

view selection problem.

In this regard, this paper presents an automatic

view selection mechanism based on syntactic analysis

of common analytical workloads, and proves its effec-

tiveness running on top of distributed dimensionally-

modeled datasets. The paper explores the techniques

devised for abstracting feature vectors from query

statements, clustering related queries based on an es-

timation of their pairwise similarity, and deriving a

limited set of materialized views able to answer the

queries grouped under each cluster.

The remainder of this paper is organized as fol-

lows: Section 2 addresses the related work. Section

3 describes the view selection problem and presents

Ordonez-Ante, L., Van Seghbroeck, G., Wauters, T., Volckaert, B. and De Turck, F.

Automatic View Selection for Distributed Dimensional Data.

DOI: 10.5220/0007555700170028

In Proceedings of the 4th International Conference on Internet of Things, Big Data and Security (IoTBDS 2019), pages 17-28

ISBN: 978-989-758-369-8

an overview of the proposed approach for tackling

it. Section 4 elaborates on the syntactic analysis con-

ducted on analytical workloads, while Section 5 de-

scribes a proof-of-concept implementation of the de-

vised mechanism, along with the experimental setup

and performance results. Finally conclusions and fu-

ture work are addressed in Section 6.

2 RELATED WORK

Extensive research has been conducted around the

view selection problem, as evidenced in several sys-

tematic reviews on the topic such as those by (Thakur

and Gosain, 2011), (Nalini et al., 2012), (Goswami

et al., 2016), (Gosain and Sachdeva, 2017). The re-

view elaborated in (Goswami et al., 2016) groups

existing approaches in three main categories: (i)

heuristic approaches, (ii) randomized algorithmic ap-

proaches, and (iii) data mining approaches.

Heuristic and randomized algorithmic approaches

emerged as an attempt to provide approximate opti-

mal solutions to the NP-Hard problem that view se-

lection entails. Both types of approaches use mul-

tidimensional lattice representations (Serna-Encinas

and Hoyo-Montano, 2007), AND-OR graphs (Sun

and Wang, 2009; Zhang et al., 2009), or multiple

view processing plan (MVPP) graphs (Phuboon-ob

and Auepanwiriyakul, 2007; Derakhshan et al., 2008)

for selecting views for materialization. Issues re-

garding the exponential growth of the lattice structure

when the number of dimensions increases, and the

expensive process of graph generation for large and

complex query workloads, greatly impact the scala-

bility of these approaches and their actual implemen-

tation in consequence (Aouiche et al., 2006; Goswami

et al., 2016).

Unlike previously mentioned approaches, data-

mining based solutions work with much simpler in-

put data structures called representative attribute ma-

trices, which are generated out of query workloads.

These structures then conﬁgure a clustering context

out of which candidate view deﬁnitions are derived.

In (Aouiche et al., 2006; Aouiche and Darmont, 2009)

candidate views are generated by merging views ar-

ranged in a lattice structure. Since the number of

nodes in this lattice grows exponentially with the

number of views, the procedure for traversing it can

be expensive. Other data mining approaches for

view selection, including the one from (Kumar et al.,

2012), involve browsing across several intermediate

and/or historical results, which is deemed to be a very

costly and unscalable process (Goswami et al., 2016).

More recently, approaches such as (Goswami

et al., 2017) and (Camacho Rodriguez, 2018) explore

the application of materialized views on top of mas-

sive distributed data to speed up big data query pro-

cessing. While the work of Goswami et al. (Goswami

et al., 2017) addresses a solution based on a multi-

objective optimization formulation of the view selec-

tion problem, it assumes as given the set of candi-

date views from which the selection is made. On the

other hand, (Camacho Rodriguez, 2018) elaborates on

the recently enabled support for materialized views in

Apache Hive (Vohra, 2016b), however at the time of

writing there is no indication of any built-in mecha-

nism for supporting view selection with this new fea-

ture.

In view of the above, this paper elaborates on

an automatic mechanism for materialized view se-

lection on top of distributed dimensionally-modeled

data. The mechanism presented in the following sec-

tions relies on syntactic analysis of query workloads

using a representative attribute matrix as input data

structure, assembled as a collection of feature vec-

tors encoding all the clauses of each individual query

in the workload at hand. With this input, a strat-

egy for selecting a limited set of candidate material-

izable views is implemented, comprising the use of

hierarchical clustering along with a custom query dis-

tance function complying with the structure of the

feature vectors, and the estimation of a materializable

score on the resulting clustering conﬁguration, allow-

ing to unambiguously identify materializable groups

of queries.

3 MATERIALIZED VIEW

SELECTION

Before addressing an overview of the proposed ap-

proach, let’s ﬁrst deﬁne the view selection problem.

Deﬁnition 1. View Selection Problem. Based on

the deﬁnition by Chirkova et al. (Chirkova et al.,

2001): Let R be the set of base relations (compris-

ing fact(s) and dimensions tables), S the available

storage space, Q a workload on R , L the function

for estimating the cost of query processing. The view

selection problem is to ﬁnd the set of views V (view

conﬁguration) over R whose total size is at most S

and that minimizes L(R , V , Q )

In the context of the view selection approach pro-

posed herein, some assumptions are made for the sys-

tem to identify and materialize candidate views out of

the syntactic analysis of query workloads:

1. The source data collection (D

src

) complies a star

schema data model, i.e. it comprises a fact table

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

[[2,10,0,...,12,24,8],

[4,12,1,...,15,36,9],

[2,14,0,...,16,28,4],

...

[8,12,2,...,40,44,9]]

src

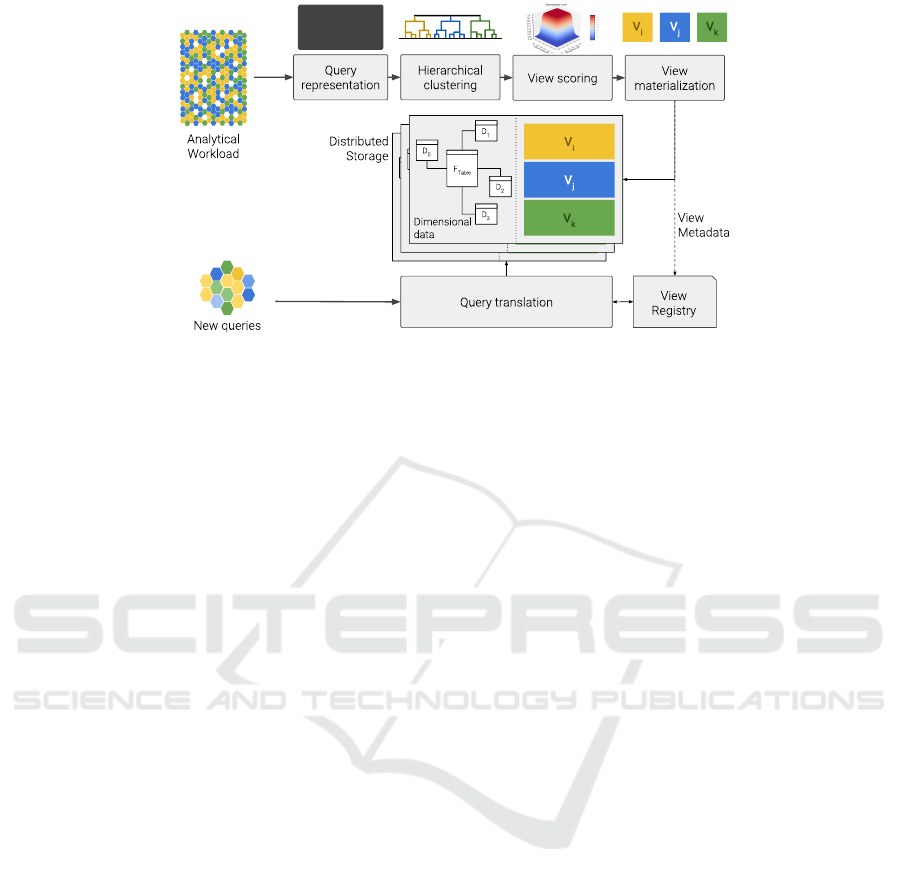
Figure 1: Materialized view selection: architecture overview.

referencing one or more dimension tables.

2. D

src

is temporary immutable. This is a com-

mon scenario in some data warehousing systems,

where analytical data is updated once in a sub-

stantial period of time —e.g. through an ETL pro-

cedure running on top of OLTP databases—, and

queried multiple times during such a period.

3. Statistical information regarding D

src

, such as the

size (row count) of each of the base tables com-

posing the dataset, as well as the cardinality of

the attributes that make up these relations is avail-

able either by querying the metadata kept by the

datastore, or by directly querying the base tables.

4. Latency is favored over view storage cost. This

means that the decision on materializing candi-

date views is driven not by storage restrictions, but

by the gain in query latency.

Figure 1 outlines the main components of the mech-

anism proposed herein to address the stated view se-

lection problem. In terms of the deﬁnition 1, given

a dimensionally modeled dataset R and a workload

Q , the view selection mechanism starts by translat-

ing the queries in Q into feature vectors represent-

ing the attributes contained in each of the clauses of

an ASPJ-query, i.e. aggregate operation, projection,

join predicates and range predicates. In contrast to

similar query representations such as the one used in

(Aouiche et al., 2006), the method proposed herein

accounts not only for query-attribute usage, but also

for query structure by deﬁning a number of region-

s/segments representative of each of the clauses of a

Select-Project-Join (SPJ) query, i.e. aggregate opera-

tion, select list, join predicates and range predicates.

This way, the devised query representation provides a

more precise speciﬁcation of the query statements in

Q .

The collection of feature vectors of Q conﬁgure

a clustering context C . This context is then fed to a

clustering algorithm able to identify groups of related

queries based on a similarity score computed via a

custom query distance function. Upon running the

clustering job, the resulting clustering conﬁguration

K comprises several groups of queries the algorithm

deemed to be similar. The idea behind building this

clustering conﬁguration is to be able to deduce view

deﬁnitions covering the queries arranged under each

cluster. The clustering algorithm might come up with

spurious clusters, i.e. groups of queries that are actu-

ally not that related. To identify those spurious clus-

ters and setting them apart from those clusters whose

corresponding candidate views are worth materializ-

ing, a materializable score is deﬁned, taking into ac-

count a measure of cluster consistency and the cluster

size. Further details on this score and the clustering

procedure are provided later in section 4.2.

Based on the results of the materializable score

computed on the clustering conﬁguration K , a subset

of the candidate views in V , V

mat

, is prescribed to

be materialized. Finally, with the views in place, the

translation of new analytical queries matching said

views is performed.

4 QUERY ANALYSIS

ASPJ-queries allow for summarization returning a

single row result based on multiple rows grouped to-

gether under certain criteria (column projection and

range predicates).

The syntactic analysis this work thrives on, starts

by mining the information contained in the select list

and search conditions clauses, encoding these values

in a feature vector representation that enables further

query processing.

Automatic View Selection for Distributed Dimensional Data

4.1 Query Representation

The procedure for obtaining a text-mining-friendly

representation of the queries takes each one of the

SELECT statements from a workload Q and extracts

the aggregate (ag

) and projection (p j

) elements,

and join ( jn

) and range (rg

) predicates, resulting

in the following tuple:

q = (ag

, p j

, jn

, rg

) (1)

The tuple above is the high-level vector represen-

tation of the queries from Q . Consider for example

the following SELECT statement:

SELECT SUM( lo _ r e ve n u e ) , d_ye ar ,

p_ c a t eg o ry

FROM lin eor der , d w date , pa r t

WHERE lo _ or d er d at e = d_ da t e k ey

AND lo _ pa rt k ey = p_ p a r tk e y

AND d_ y e a r > 2 0 10

GROUP BY d_ye a r , p_ ca t eg o r y

For the query above:

= [SUM, lo revenue]

p j

= [d year, p category]

= [d datekey, p partkey]

= [d year]

Each element of the above high-level vector represen-

tation gets mapped to a vector using a binary encoding

function, as described below.

Deﬁnition 2. Binary Mapping Function. Let R be a

relation deﬁned as a set of m attributes (a

, a

, ..., a

)

—with a

being the primary key of R—, and given

r an arbitrary set of attributes, the binary mapping

of r according to R, denoted by bm

(r), is deﬁned as

follows:

(r) =

{

}

, 1 ≤ i ≤ m

(

1, if a

∈ r

0, otherwise

(2)

Using the mapping function above, the vector rep-

resentation of each one of the query elements in Eq.1

(designated henceforth as segments), for a dimen-

sional schema comprising one fact table and N dimen-

sion tables, is deﬁned as follows:

= [aggOpCode, bm

Fact

(ag

)]

= [bm

Fact

(p j

), bm

Dim1

(p j

), ..., bm

DimN

(p j

)]

= [bm

Dim1

( jn

), ..., bm

DimN

( jn

)]

= [bm

Fact

(rg

), bm

Dim1

(rg

), ..., bm

DimN

(rg

)]

where aggOpCode designates the aggregate operation

using one-hot encoding, namely, COUNT: 00001, SUM:

00010, AVG: 00100, MAX: 01000, MIN: 10000.

A complete feature vector q representing a query

q ∈ Q is set by putting together the above-mentioned

segments, that is:

q = [ag

, pj

, jn

, rg

]

Accordingly, considering the SELECT statement in

the example above and the dimensional schema de-

scribed in (O’Neil et al., 2009) which comprises one

fact table and four dimension tables, a complete fea-

ture vector instance (its decimal equivalent for length

and clarity) is shown below:

q = [[2, 8] , [0, 0, 16, 8, 0] , [0, 1, 1, 0] , [0, 0, 16, 0, 0]]

The collection of feature vectors representing the

queries from Q are arranged as a representative at-

tribute matrix, conﬁguring a clustering context C .

4.2 Query Clustering and View

Materialization

The view selection approach documented herein re-

lies on hierarchical clustering (Friedman et al., 2009)

for deriving groupings of similar queries. In contrast

to other well-known clustering methods such as K-

Means or K-medoids, hierarchical clustering analy-

sis does not require the number of clusters upfront

as parameter. Instead, it generates a hierarchical rep-

resentation of the entire clustering context in which

observations and groups of observations are stacked

together from lower to higher levels, according to a

distance measure based on the pairwise dissimilarities

among the observations.

This way, a dissimilarity metric is required to ap-

ply hierarchical clustering analysis on a clustering

context C , along with a linkage criterion which es-

timates the dissimilarity among groups of queries as

a function of the pairwise distance computed between

queries belonging to those groups. In this sense, a

distance function, qDst, is deﬁned in which similar-

ity between two queries is determined to be propor-

tional to the number of attributes they share in a per-

segment and per-relation (fact and dimensions) basis.

Since vectors in C do not lie in an euclidean space, the

Weighted Pair Group Method with Arithmetic Mean

(WPGMA) clustering method is used as linkage cri-

terion, instead of methods such as centroid, median,

or ward (M

ullner, 2011).

Under this set-up, the clustering procedure (de-

tailed in algorithm 1) starts by assigning each query

to its own cluster (see line 1). Then, the pairwise dis-

similarity matrix between these singleton clusters, D,

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

Algorithm 1: WPGMA clustering procedure.

1: K ← C ; C = {q

, q

, . . . , q

}  Initializing clusters (singleton clusters)

2: D ← qDst(q

, q

) for all q

, q

∈ K , i 6= j  Pairwise dissimilarity matrix

3: L ← []  Output matrix

4: while |K | > 1 do

5: (a, b) ← argmin(D)  Get the nearest clusters

6: append [a, b, D [a, b]] to L

7: remove a and b from K

8: create new cluster k ← a ∪ b  Merge a and b into one cluster

9: update D: D [k, x] = D [x, k] =

qDst(a,x)+qDst(b,x)

for all x ∈ K

10: K ← K ∪ k

11: end while

12: return K , L  L: WPGMA dendrogram: ((N − 1) × 3)-matrix

is computed and an empty matrix (L) specifying the

resulting dendrogram is initialized (lines 2-3). From

D, the two most similar (nearest) clusters are merged

into one, and appended to L along with the distance

between them (lines 5-6). Then, the pairwise dissimi-

larity matrix gets updated using the WPGMA method

for computing the distance between the newly formed

cluster and the rest of the currently existing clusters

(eq. 3):

D[(a ∪ b), x] =

qDst(a, x) + qDst(b, x)

(a, b and x being clusters)

(3)

This procedure is then repeated until there is only

one cluster left. Finally, both the clustering conﬁgura-

tion (K ) and the dendrogram matrix (L) are returned

(line 12).

As mentioned earlier, spurious clusters might be

found in the derived clustering conﬁguration. To

avoid further processing of those query groups a score

was deﬁned indicating to what extent it is worth to

materialize the view derived from a particular cluster.

Deﬁnition 3. Materializable Cluster. A cluster c

from a clustering conﬁguration K is said to be ma-

terializable if the following conditions are met:

1. Queries in c are highly similar to each other.

2. Queries in c are clearly separated (highly dissim-

ilar) from queries in other clusters.

3. |c| is large enough in proportion to the size of the

workload |Q |.

A cluster meeting the ﬁrst two conditions is said to

be a consistent cluster, while the third condition pre-

vents singleton and small clusters from being further

processed. Based on the above deﬁnition, the materi-

alizable score of a cluster (mat(c) in eq. 4) is com-

puted as the product of two sigmoid functions: one

on the per-cluster silhouette score (S) (Rousseeuw,

1987)—deﬁned below in eq. 5—and the other on the

per-cluster proportions (P).

mat(c) =



1 + e

−k(S(c)−s

)



1 + e

−k(P(c)−p

)



(4)

With:

S(c) =

∑

∈c

b(q

) − a(q

)

max

{

a(q

), b(q

)

}

, P(c) =

|c|

|Q |

(5)

Where,

• k is a factor that controls the steepness of both of

the sigmoid functions,

• s

and p

are the midpoints of the silhouette and

cluster-proportion sigmoids respectively,

• a(q

) is the average distance between q

and all

queries within the same cluster,

• b(q

) lowest average distance of q

to all queries

in any other clusters.

Upon factoring out the spurious clusters, the next

step is deriving view deﬁnitions covering the queries

arranged under each of the materializable clusters

mat

⊆ K ). Algorithm 2 below details the proce-

dure conducted to derive the views V

meeting this

containment condition on each of the materializable

clusters. In this procedure, the ASPJ clauses of the

resulting views are deﬁned in terms of the union of

the corresponding attributes from each query in the

cluster (aggregate (ag

), projection (p j

), join ( jn

and range (rg

) predicates in lines 4-7).

Automatic View Selection for Distributed Dimensional Data

Algorithm 2: Procedure for deriving view deﬁnitions.

1: Let c be a cluster in K

mat

2: V ← [ag

, p j

, jn

, groupBy

]  Output view

deﬁnition

3: for each query q in c do

4: ag

← ag

∪ ag

5: p j

← p j

∪ p j

∪ rg

6: jn

← jn

∪ jn

7: groupBy

← groupBy

∪ p j

∪ rg

8: end for

9: return V

5 EVALUATION

5.1 Proof-of-concept Implementation

A bottom-up approach was adopted to test the view

selection mechanism detailed in the previous sections.

In this way, starting from a set of predeﬁned view

deﬁnitions, the effectiveness of the proposed mecha-

nism is estimated in terms of its ability for identifying

the same set of views and reconstructing their deﬁ-

nitions, upon analyzing a query workload generated

from query templates ﬁtting the original set of views

(see Figure 2).

This proof-of-concept implementation leverages

the Star Schema Benchmark (SSB) as baseline

schema and dataset, and therefore both the predeﬁned

views and query templates, as well as the query gener-

ator module were designed and built so they conform

to the data model the SSB embodies.

Thirteen ASPJ-query statements compose the full

query set of the SSB, arranged in four categories/fam-

ilies designated as Query Flights (a detailed deﬁnition

of the SSB is available at (O’Neil et al., 2009)). For

this proof-of-concept, three view deﬁnitions were de-

rived based on the original SSB query set, and from

each view deﬁnition, four query templates were pre-

pared. Additionally, one template per each one of the

13 canonical SSB queries were also composed. With

this set of 25 templates as input, a module that gener-

ates random instances of runnable queries enabled the

creation of query workloads of arbitrary size. Listings

below present the deﬁnitions of each one of the men-

tioned views.

Listing 1: Deﬁnition of View A.

SELECT sum( lo _ r e ve n u e ) , p_ bra nd1 ,

c_r egi on ,

s_r egi on , d _ ye ar

FROM lin eor der , c ust ome r , dwdate ,

par t , s u p pl ie r

WHERE lo _ cu st k ey = c_ c us tk e y

AND lo _ or d er d at e = d_ da t e k ey

AND lo _ pa rt k ey = p_ p a r tk e y

AND lo _ su pp k ey = s_ s u p pk e y

GROUP BY p_ bra n d1 , c_ reg ion ,

s_r egi on , d _ ye ar

ORDER BY p_ bra n d1 , c_ reg ion ,

s_r egi on , d _ ye ar

Listing 2: Deﬁnition of View B.

SELECT sum( lo _ o rd t ot a l p r i ce ) ,

p_ c at eg o ry , c _ city ,

s_cit y , d_ y ea r mo n th n um

FROM lin eor der , c ust ome r , dwdate ,

par t , s u p pl ie r

WHERE lo _ cu st k ey = c_ c us tk e y

AND lo _ or d er d at e = d_ da t e k ey

AND lo _ pa rt k ey = p_ p a r tk e y

AND lo _ su pp k ey = s_ s u p pk e y

GROUP BY p _ ca te g or y , c_cit y , s_ c ity ,

d_ y ea r m o n t h n u m

ORDER BY p _ ca te g or y , c_cit y , s_ c ity ,

d_ y ea r m o n t h n u m

Listing 3: Deﬁnition of View C.

SELECT sum( lo _ su p pl y co s t - l o_ ta x ) ,

c_r egi on , p_mfg r ,

s_r egi on , c_ n ati on , d _y ea r

FROM lin eor der , c ust ome r , dwdate ,

par t , s u p pl ie r

WHERE lo _ cu st k ey = c_ c us tk e y

AND lo _ or d er d at e = d_ da t e k ey

AND lo _ pa rt k ey = p_ p a r tk e y

AND lo _ su pp k ey = s_ s u p pk e y

GROUP BY c_ reg i on , p_m f gr , s_re gio n ,

c_n ati on , d _ ye ar

ORDER BY c_ reg i on , p_m f gr , s_re gio n ,

c_n ati on , d _ ye ar

5.2 Deﬁnition of the Data Serialization

Format

Since serialization formats determine the way data

structures are turned into bytes and sent over the net-

work, and how said structures are stored on disk, such

formats have a major impact on the response time of

data processing and retrieval operations performed in

a distributed fashion. This is why, prior to evaluat-

ing the performance of the proposed view selection

mechanism, the decision on which serialization for-

mat to use for encoding and storing the SSB datasets

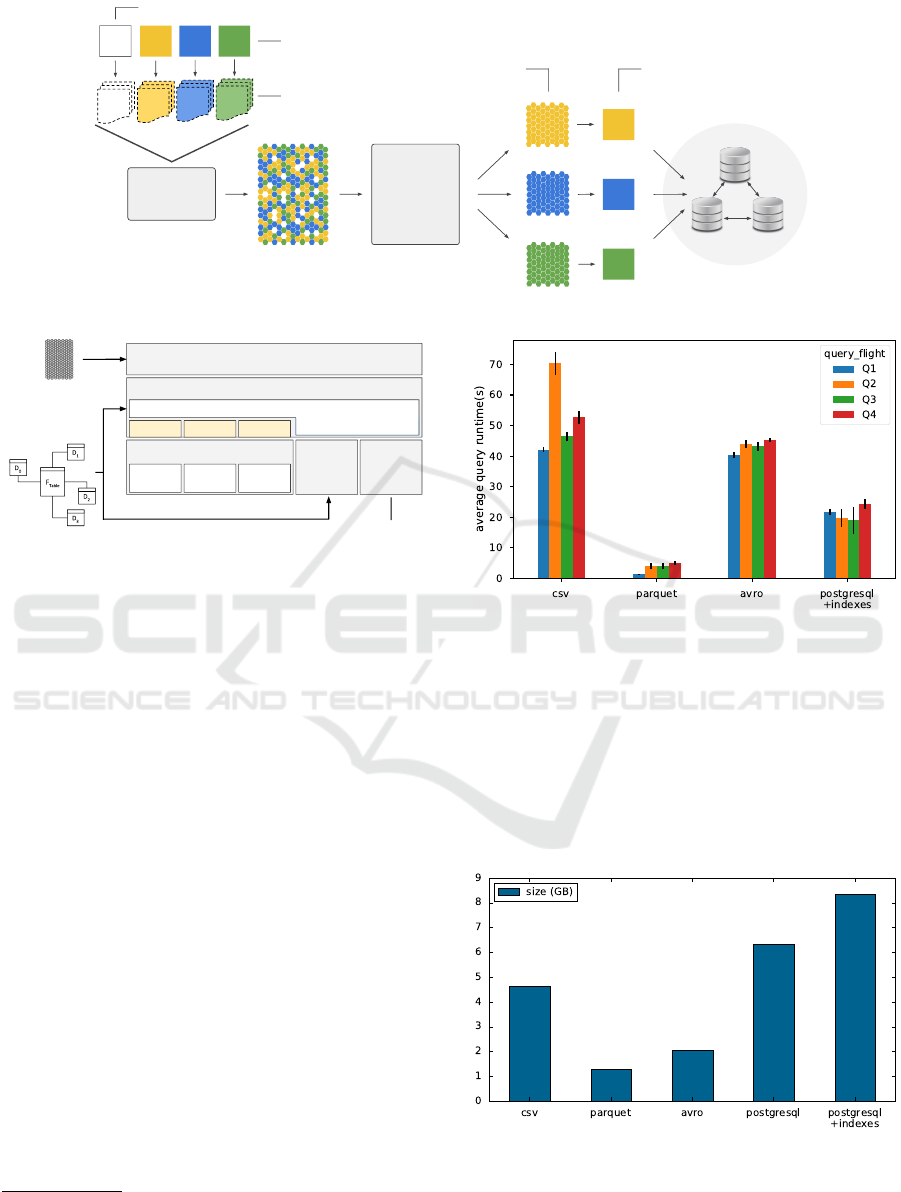
into HDFS needed to be made. Figure 3 outlines the

setup arranged to conduct a benchmark analysis on

three different data serialization formats, one being

a text-based format (CSV) and two binary schema-

driven formats (Parquet (Vohra, 2016c) and Avro

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

View

Selection

(PoC)

Predefined view

definitions

Query templates

Query

Generator

Workload

trg

Materializable

clusters

Reconstructed

views

SSB

SSB-based queries

Distributed storage

Figure 2: Proof-of-concept implementation of the proposed view selection mechanism.

Hadoop

DNode 1 DNode 3DNode 2

Spark SQL

Jupyter Notebook

SSB Workload

PostgreSQL

SSB dataset

(48 million rows)

MongoDB

View registry

CSV AVROPARQUET

SSB storage & querying

Figure 3: Set-up for deciding on the data serialization for-

mat.

(Vohra, 2016a)). By leveraging on the built-in sup-

port Spark SQL provides for these serialization for-

mats, a 48-million-row SSB dataset was encoded into

CSV, Parquet and Avro and stored in HDFS. Then,

the canonical SSB query set (consisting of 13 queries)

was run against each of the encoded datasets, as well

as against a separate dataset placed in a single-node

PostgreSQL

database serving as a reference.

Figure 4 shows the results obtained from mea-

suring the average query runtime (over 10 runs) for

each one of the serialization formats. Notice how, in

the mentioned conditions, queries running against the

Parquet-encoded dataset ran up to 10 times faster than

the reference relational database. Also, Parquet was

the only serialization format that managed to outper-

form the average query runtime of PostgreSQL.

Serialization formats also have a signiﬁcant im-

pact on the size of the encoded data structures. While

for text-based human-readable formats such as CSV

data is stored as-is, binary formats like Parquet and

Avro do apply compression on the data they encode.

Figure 5 shows a comparison between the reported

sizes (in gigabytes) of the SSB dataset for each of the

considered serialization formats. According to these

results Parquet is once again the most efﬁcient serial-

PostgreSQL 9.5.8 working with the default conﬁgura-

tion and deployed on a VMWare

 virtual machine as the

ones used for the Hadoop cluster (postgresql.org)

Figure 4: Average query-ﬂight runtime per data serializa-

tion format (SSB SF = 8).

ization format, reaching a compression ratio of 3.6:1

in relation to the uncompressed CSV-encoded dataset,

and 6.5:1 in relation to the PostgreSQL reference

database (including primary key indexes). In conse-

quence, Parquet was the chosen serialization format

for encoding the various datasets involved in the eval-

uation of the proposed view selection approach.

Figure 5: Disk space usage per data serialization format

(SSB SF = 8).

Automatic View Selection for Distributed Dimensional Data

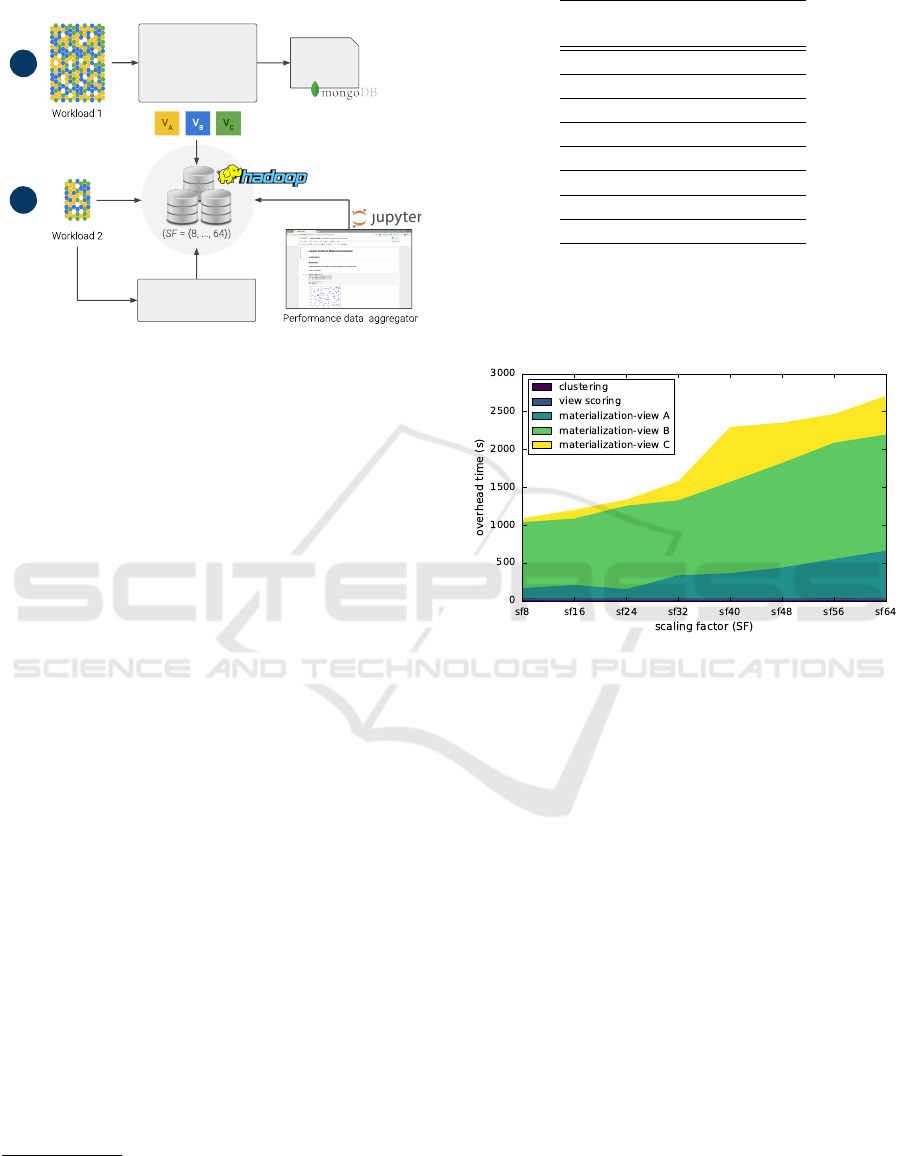
5.3 Experimental Setup

View Selection (PoC)

View

Registry

Query translator

SSB

Figure 6: View selection experiment set-up.

Figure 6 depicts the arrangement of components

and technologies used for conducting the experimen-

tal evaluation of the proposed view selection ap-

proach. This evaluation comprised two major stages:

(1) Running the view selection implementation on a

400-query workload to the point it materializes

views A, B, and C (deﬁned in section 5.1), while

keeping track of the runtime involved in the proce-

dures of query clustering, view scoring (using the

materializable score deﬁned in section 4.2), and

view creation (i.e. materialization).

(2) Once the views are materialized, run a 100-query

workload against both the base SSB dataset and

the materialized views. In doing the latter, work-

load queries ﬁrst pass through a translation com-

ponent that gathers the details of the available

materialized views from the view registry (stored

in a MongoBD

2.6.10 document database), and

adapts the incoming query statements accord-

ingly.

For all the stages, the performance information

collected from running the tests were aggregated

and visualized using Jupyter notebook

. During this

evaluation, workloads were run against eight different

sizes of the SSB dataset, as speciﬁed below in table

1. These datasets were stored into a 3-Node Hadoop

2.7.3 cluster deployed on 3 VMWare

 virtual

machines, each one with the following speciﬁcations:

Intel

 Xeon

 E5645 @2.40GHz CPU, 16GB

RAM, 250GB hard disk.

Available at mongodb.com

Available at jupyter.org

Available at hadoop.apache.org

Table 1: SSB dataset sizes.

Scaling

Factor (SF)

Dataset size

(# rows)

8 48×10

16 96×10

24 144×10

32 192×10

40 240×10

48 288×10

56 336×10

64 384×10

5.4 Results

5.4.1 View Selection Overhead

Figure 7: View selection runtime per process (|Q | = 400).

Time needed for view materialization grows as the dataset

size increases, while the overhead due to clustering and

view scoring remains invariant.

The overhead of the view selection implementa-

tion was estimated ﬁrst by running it on a 400-query

workload throughout the considered range of sizes of

the SSB dataset. Results show that, for a ﬁxed-size

workload, the runtime overhead grows nearly propor-

tional to the size of the data collection (See Figure 7),

with a major part of said overhead due to the view ma-

terialization itself. As mentioned before, the proposed

view selection mechanism involves the execution of a

sequence of steps: (1) query clustering, (2) view (or

cluster) scoring, and (3) view materialization. Out

of these only the ﬁrst two steps have to do with the

syntactical analysis of query sets described through-

out this paper, while the last one refers to the actual

materialization of the derived views in Parquet. Fig-

ure 7 shows the execution times for each one of the

three mentioned steps, including the individual ma-

terialization of each one of the three selected views.

Note how clustering and view scoring amount to only

20 seconds, and remain largely invariant as the dataset

size grows larger. Nonetheless, it is worth mentioning

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

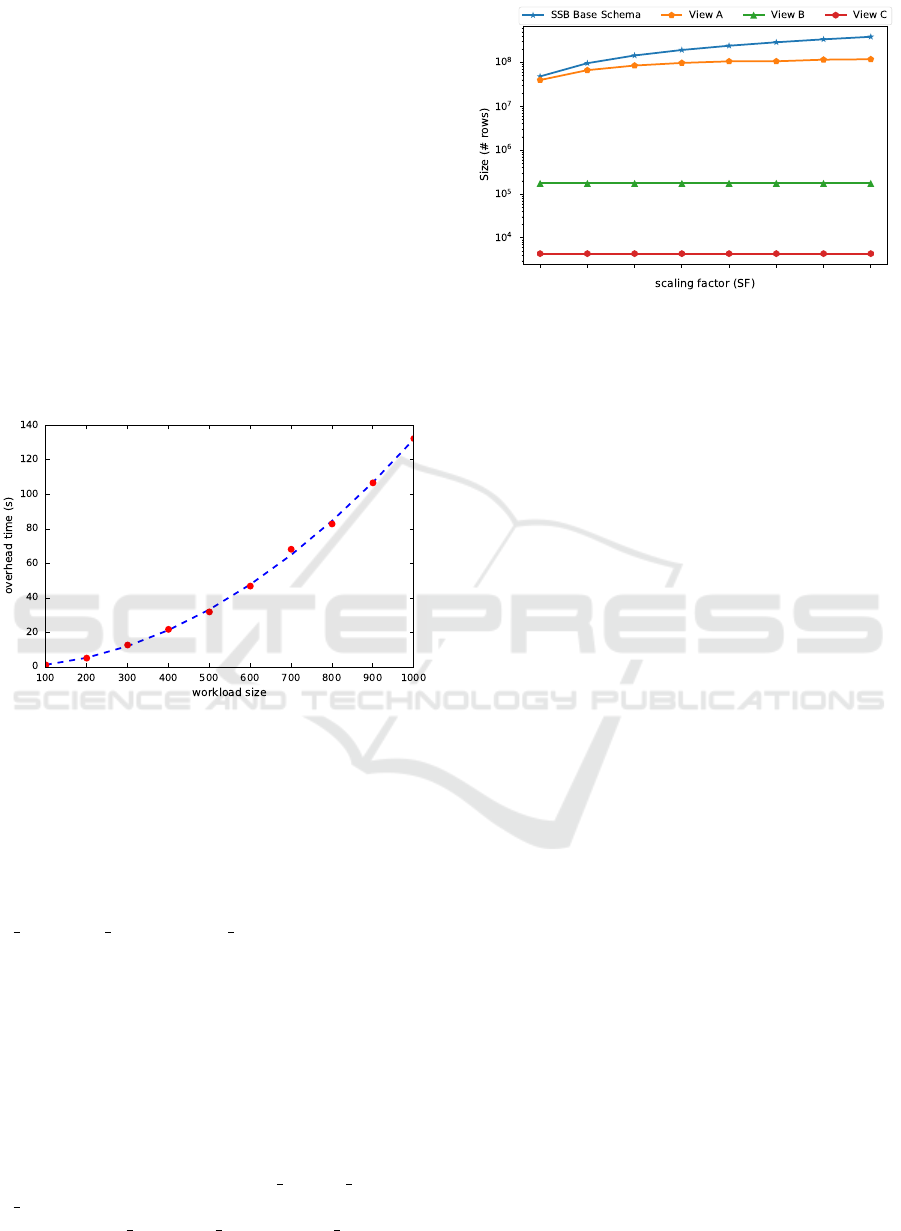
that the behaviour evidenced in Figure 7 for the ma-

terialization step cannot be assumed the same for any

arbitrary set of views, since this part of the runtime

overhead depends not only on the size of the dataset,

but also on factors such as view size, the join pred-

icates in the view deﬁnition, and —given that views

are placed in a distributed ﬁle system— also the la-

tency of the network.

On the other hand, the implementation of the

WPGMA method used in the clustering analysis re-

lies on the nearest-neighbors chain algorithm which

is known to have O(N

) time complexity (M

ullner,

2011). As Figure 8 shows, the overhead due to said

analysis features a quadratic growth as the number of

queries in the workload increases, outperforming al-

ternative approaches with exponential complexity dis-

cussed back in section 2.

Figure 8: View selection overhead vs Workload size. The

syntactical analysis features a quadratic growth w.r.t. the

size of the query set.

When it comes to storage cost, view size varies

depending on the cardinality of the ﬁelds used in the

group-by clause of their deﬁnition (Aouiche et al.,

2006), and whether or not there are hierarchical re-

lations between such attributes (e.g. the one between

c region, c nation and c city). Figure 9 shows

the size per materialized view, as well as the number

of rows in the SSB base schema for a range of values

of the scaling factor (SF). Notice that while the num-

ber of records of views A and C is fairly negligible

in comparison with the base schema, view B and the

base dataset have comparable sizes for small values of

SF. Then, the size of view B tends to stabilize around

records as the base data set gets larger. Such dif-

ference in size among the views has to do with the car-

dinality of the ﬁelds used when deﬁning said views.

For instance, view B uses ﬁelds c

city, s city and

d yearmonthnum whose cardinality is far larger than

ﬁelds such as c region, c nation and d year, used

in the remaining views.

Figure 9: View size overhead vs SSB scaling factor.

5.4.2 View Selection Performance

With the selected views already materialized, a 100-

query workload was run against each one of the eight

base SSB datasets to get a query latency baseline. Out

of those 100 queries, 75 were covered by the three

available materialized views (25 queries per view),

and the remaining ones were canonical SSB-based

queries. Once the latency baseline was built, the same

workload was issued this time with the query transla-

tion module in place, so that incoming queries match-

ing any of the deﬁnitions of the available material-

ized views get rewritten and issued against them. Fig-

ure 10 illustrates the contrast between the baseline

query runtime and the response time when queries run

against materialized views. In the light of these results

it is worth to highlight three key facts:

(i) For all the selected views the time required for

queries to run against the base dataset steadily

grows as the scaling factor (SF) increases from 8

(48 million rows) to 40 (240 million rows). This

describes an expected behaviour since the base

dataset is also growing at a uniform rate (48 mil-

lion rows per step).

(ii) From SF = 48 (288 million rows) onwards, there

is a strong though less regular increase in the av-

erage response time of queries issued against the

base datasets: queries run 5-9 times slower com-

pared to those running on the immediate smaller

dataset (SF = 40), when only a 22-27% mean in-

crease in the query runtime was expected. Such a

stark difference is consequence of Apache Spark

changing the mechanism it uses to implement join

operations. Up to SF = 40, the size of the dimen-

sion tables is small enough for Spark to broad-

cast them across the executors —collocated with

the Hadoop DataNodes— and use its most per-

formant join strategy known as Broadcast Hash

Join. However, for SF ≥ 48 some of those dimen-

Automatic View Selection for Distributed Dimensional Data

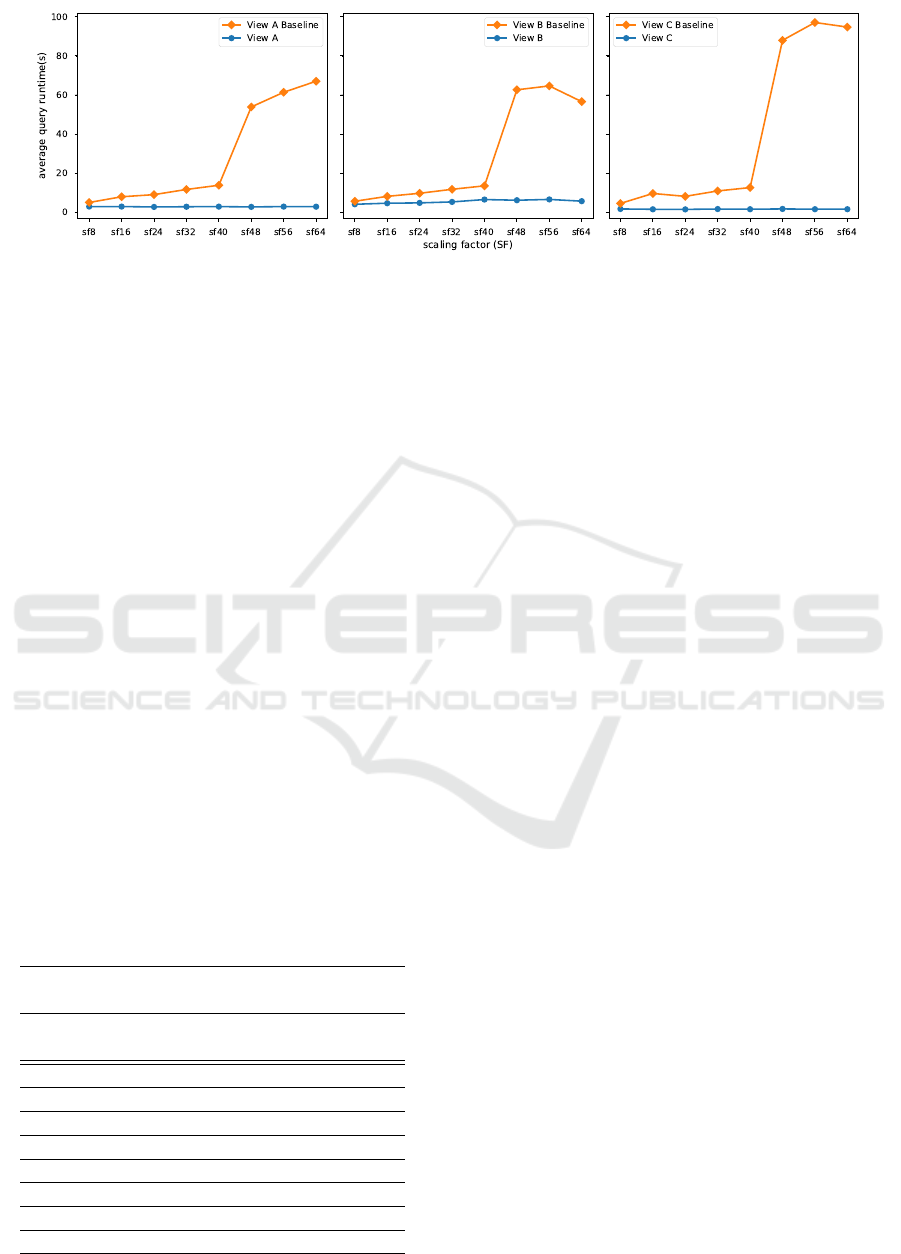
Figure 10: Query runtime per view: Baseline runtime vs. View runtime (|Q | = 100, Spark running on yarn-client mode with

3 executors and spark.executor.memory = 1Gb).

sions grows larger than the threshold set in Spark

for them to be regarded as broadcastable datasets,

compelling Spark to fall back to Sort-Merge Join,

which entails an expensive sorting step on the ta-

bles involved in the join operation, ultimately im-

pacting the query response time.

(iii) Materialized views outperform the base datasets

for any value of SF ≥ 8. Queries running on views

A and C perform 2-8 times faster than the corre-

sponding base dataset for values of SF between 8

and 40, and 22-65 times faster for larger values of

SF. Likewise, queries running against the second

view (view B) run up to 2 times faster than queries

running on the base dataset for SF ≤ 40, and up to

10 times faster for larger values of SF. The expen-

sive join operations performed for queries running

on the base dataset are bypassed for those match-

ing any of the available selected views, allowing

Spark to run those queries in a fraction of their

original query response time.

Table 2 summarizes the results obtained from running

the above test, stating the reduction in query runtime

achieved through each one of the views relative to the

average baseline query runtime.

Table 2: Query latency reduction per view (|Q | = 100).

% Reduction in

query response time

SSB Dataset

size (SF)

View A View B View C

8 40.86 26.99 61.21

16 62.66 42.64 83.36

24 69.05 50.14 80.95

32 75.16 54.48 84.06

40 78.60 51.56 87.05

48 96.02 88.96 98.00

56 96.10 89.15 98.24

64 95.36 89.82 98.46

6 DISCUSSION AND

CONCLUSIONS

The analytical workloads typical in OLAP applica-

tions feature expensive data processing operations

whose cost and complexity increases when running

on a distributed setting. By identifying recurrent op-

erations in the queries composing said workloads and

saving their resulting output on disk or memory in the

form of distributed views, it is possible to speed up the

processing time of not only known but also previously

unseen queries. That is precisely the premise behind

the mechanism detailed in this paper, which leverages

on syntactic analysis of OLAP workloads for iden-

tifying groups of related queries and deriving a lim-

ited but comprehensive set of views out of them. The

views the devised mechanism comes up with proved

an effective method for circumventing expensive dis-

tributed join operations and subsequently reducing the

query processing time by up to 89%–98% with ref-

erence to the runtime on the base distributed dimen-

sional data.

While the convenience of distributed materialized

views is more prominently perceived as the dimen-

sional data grows larger, one of the main open chal-

lenges of the proposed approach has to do with the

unbounded size of the views that the mechanism is

able to compose, which increases the associated pro-

cessing overhead and cuts down the relative beneﬁt of

using these redundant data structures. To cope with

this limitation, the view selection mechanism needs

to be aware not only of the recurrent attributes and

operations of queries but also of the cardinality of

such attributes, so that views including attributes with

high cardinality (consider for instance view B in sec-

tion 5.1) get materialized as multiple size-bounded

child views corresponding to partitions of the origi-

nal view. Additionally, by keeping track of how the

selection conditions of incoming workloads change

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

over time, it is possible to implement a continuous

view maintenance strategy that performs horizontal

partitioning on the derived views, allowing the pro-

posed mechanism to adapt to workload-speciﬁc de-

mands, using an approach similar to the one presented

in (Ordonez-Ante et al., 2017). The implementation

of the cardinality-awareness feature for the proposed

view selection mechanism, as well as the view main-

tenance strategy discussed above are the future exten-

sions of the work presented in this paper.

ACKNOWLEDGEMENTS

This work was supported by the Research Founda-

tion Flanders (FWO) under Grant number G059615N

- “Service oriented management of a virtualised fu-

ture internet” and the strategic basic research (SBO)

project DeCoMAdS under Grant number 140055.

REFERENCES

Aouiche, K. and Darmont, J. (2009). Data mining-based

materialized view and index selection in data ware-

houses. Journal of Intelligent Information Systems,

33(1):65–93.

Aouiche, K., Jouve, P.-E., and Darmont, J. (2006).

Clustering-based materialized view selection in data

warehouses. In Manolopoulos, Y., Pokorn

y, J., and

Sellis, T. K., editors, Advances in Databases and In-

formation Systems, pages 81–95, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Camacho Rodriguez, J. (2018). Materialized views in

apache hive 3.0. https://cwiki.apache.org/conﬂuen

ce/display/Hive/Materialized+views. Last accessed:

2018.10.15.

Chirkova, R., Halevy, A. Y., and Suciu, D. (2001). A formal

perspective on the view selection problem. In VLDB

2001, volume 1, pages 59–68.

Derakhshan, R., Stantic, B., Korn, O., and Dehne, F. (2008).

Parallel simulated annealing for materialized view se-

lection in data warehousing environments. In ICA3PP

2008, pages 121–132. Springer.

Friedman, J., Hastie, T., and Tibshirani, R. (2009). Clus-

tering analysis. In The elements of statistical learn-

ing: Data mining, inference and prediction, chap-

ter 14, pages 501–520. Springer series in statistics,

New York.

Gosain, A. and Sachdeva, K. (2017). A systematic review

on materialized view selection. In Satapathy, S. C.,

Bhateja, V., Udgata, S. K., and Pattnaik, P. K., editors,

FICTA 2017, pages 663–671, Singapore. Springer

Singapore.

Goswami, R., Bhattacharyya, D., and Dutta, M. (2017).

Materialized view selection using evolutionary algo-

rithm for speeding up big data query processing. Jour-

nal of Intelligent Information Systems, 49(3):407–

433.

Goswami, R., Bhattacharyya, D. K., Dutta, M., and Kalita,

J. K. (2016). Approaches and issues in view selec-

tion for materialising in data warehouse. International

Journal of Business Information Systems, 21(1):17–

47.

Kumar, T. V. V., Singh, A., and Dubey, G. (2012). Min-

ing queries for constructing materialized views in a

data warehouse. In Advances in Computer Science,

Engineering & Applications, pages 149–159, Berlin,

Heidelberg. Springer Berlin Heidelberg.

ullner, D. (2011). Modern hierarchical, agglomerative

clustering algorithms. Computing Research Reposi-

tory (CoRR), abs/1109.2378.

Nalini, T., Kumaravel, A., and Rangarajan, K. (2012).

A comparative study analysis of materialized view

for selection cost. World Applied Sciences Journal

(WASJ), 20(4):496–501.

O’Neil, P. E., O’Neil, E. J., and Chen, X. (2009). The

star schema benchmark (revision 3, june 5, 2009).

https://www.cs.umb.edu/ poneil/StarSchemaB.PDF.

Ordonez-Ante, L., Vanhove, T., Van Seghbroeck, G.,

Wauters, T., Volckaert, B., and De Turck, F. (2017).

Dynamic data transformation for low latency querying

in big data systems. In 2017 IEEE International Con-

ference on Big Data (Big Data), pages 2480–2489.

Phuboon-ob, J. and Auepanwiriyakul, R. (2007). Two-

phase optimization for selecting materialized views in

a data warehouse. International Journal of Computer,

Electrical, Automation, Control and Information En-

gineering, 1(1):119–123.

Plattner, H. (2013). A Course in In-Memory Data Manage-

ment: The Inner Mechanics of In-Memory Databases.

Springer Publishing Company, Inc.

Qushem, U. B., Zeki, A. M., Abubakar, A., and Akleylek,

S. (2017). The trend of business intelligence adoption

and maturity. In UBMK 2017, pages 532–537.

Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to

the interpretation and validation of cluster analysis.

Journal of computational and applied mathematics,

20(1):53–65.

Serna-Encinas, M. T. and Hoyo-Montano, J. A. (2007). Al-

gorithm for selection of materialized views: based on

a costs model. In Current Trends in Computer Sci-

ence, 2007. ENC 2007. Eighth Mexican International

Conference on, pages 18–24. IEEE.

Shvachko, K., Kuang, H., Radia, S., and Chansler, R.

(2010). The hadoop distributed ﬁle system. In MSST

2010, pages 1–10, Washington, DC, USA. IEEE Com-

puter Society.

Sun, X. and Wang, Z. (2009). An efﬁcient materialized

views selection algorithm based on pso. In ISA 2009,

pages 1–4. IEEE.

Thakur, G. and Gosain, A. (2011). A comprehensive analy-

sis of materialized views in a data warehouse environ-

ment. International Journal of Advanced Computer

Science and Applications, 2(5):76–82.

Vohra, D. (2016a). Apache avro. In Practical Hadoop

Ecosystem, pages 303–323. Springer.

Automatic View Selection for Distributed Dimensional Data

Vohra, D. (2016b). Apache hive. In Practical Hadoop

Ecosystem, pages 209–231. Springer.

Vohra, D. (2016c). Apache parquet. In Practical Hadoop

Ecosystem, pages 325–335. Springer.

Zhang, Q., Sun, X., and Wang, Z. (2009). An efﬁcient

ma-based materialized views selection algorithm. In

CASE 2009, pages 315–318. IEEE.

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security