A Multi-objective Approach to the Optimization of Home Care Visits

Scheduling

Filipe Alves

1,2

, Lino Costa

, Ana Maria A. C. Rocha

, Ana I. Pereira

1,2

and Paulo Leit

Research Centre in Digitalization and Intelligent Robotics (CeDRI), Instituto Polit

ecnico de Braganc¸a, Braganc¸a, Portugal

Algoritmi R&D Centre, University of Minho, Braga, Portugal

Department of Production and Systems, Algoritmi R&D Centre, University of Minho, Braga, Portugal

Keywords:

Home Health Care, Multi-objective, Scheduling, Optimization.

Abstract:

Due to the increasing of life expectancy in the developed countries, the demand for home health care services is

growing dramatically. Usually, home services are planned manually and lead to various optimization problems

in their activities. In this sense, health units are confronted with appropriate scheduling which may contain

multiple, often conﬂicting, objectives such as minimizing the costs related to the traveling distance while

minimizing the traveling time. In order to analyze and discuss different trade-offs between these objectives, it

is proposed a multi-objective approach to home health care scheduling in which the problem is solved using

the Tchebycheff method and a Genetic algorithm. Different alternative solutions are presented to the decision

maker that taking into account his/her preferences chooses the appropriate solution. A problem with real data

from a home health care service is solved. The results highlight the importance of a multi-objective approach

to optimize and support decision making in home health care services. Moreover, this approach provides

efﬁcient and good solutions in a reasonable time.

1 INTRODUCTION

Over the last decade, the increased life expectancy

resulted in increased demand for Home Health Care

(HHC) (Fikar and Hirsch, 2017). In this sense, the

number of people who needs home care services

are consequently growing worldwide (Nickel et al.,

2012). Therefore, health units that provide home care

services need to optimize their activities in order to

meet the constantly increasing demand for home care

services (Koeleman et al., 2012). This is usually due

to the manual planning of home care visits, making

it a time and effort consuming task that often leads

to inefﬁcient solutions. Thus, the operation manage-

ment within the HHC turns to be very hard because

of the high number and diversity of human and mate-

rial resources that participate in the process of home

care and the criteria to be optimized (Benzarti et al.,

2013). Regarding the literature in this ﬁeld, there

are some issues relevant to the home care visits sche-

dule. Some authors present an overview of works re-

lated to HHC (Benzarti et al., 2010). The work of

Yalc¸ındag et al. (2011) besides presenting the par-

ticular scheduling of visits also lists the well-known

routing problems in HHC. The problems that address

static multi-vehicle routing and assignment are a very

well-known and researched topic in Operations Re-

search (Baker and Ayechew, 2003; Toth and Vigo,

2014). In the context of HHC, these problems consist

in scheduling vehicles with nurses to patients (Bred-

str

om and R

onnqvist, 2008), in order to determine the

best order and time that visits should be performed. In

this subject, some works propose an approach to ﬁnd

the best schedule, minimizing the costs (Nguyen and

Montemanni, 2013). On the other hand, some prob-

lems were modeled to be solved by the “branch and

price” algorithm (Rasmussen et al., 2012). Recently,

Alves et al. (2018) proposed an approach using the ge-

netic algorithm to solve the scheduling of home visits

as a single objective optimization problem. The work

of Allaoua et al. (2013) also presents the home care

scheduling problem as a single objective by minimi-

zing the travel cost or the travel time.

In this context, it is important to mention that

new research in HHC is being targeted with multi-

objective optimization approaches (Ombuki et al.,

2006; Pasia et al., 2007). For example, Braekers et al.

(2016) presents an approach that analyzes the trade-

off between costs and client inconvenience, using a

meta-heuristic algorithm based on multi-directional

Alves, F., Costa, L., Rocha, A., Pereira, A. and Leitão, P.

A Multi-objective Approach to the Optimization of Home Care Visits Scheduling.

DOI: 10.5220/0007565704350442

In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 435-442

ISBN: 978-989-758-352-0

435

local search. Thus, multi-objective solution proce-

dures derive a set of Pareto optimal solutions that are

not yet common in HHC scheduling (Braekers et al.,

2016; Gayraud et al., 2013).

In this work, the home health care scheduling

problem is formulated as a multi-objective problem

and an instance with real data is solved. Conﬂicting

objectives, such as costs, distances or unexpected and

inconvenient events are important to be considered.

The developed approach and model try to handle the

objectives of home care services and the patient’s ob-

jectives. To achieve this goal, additional costs related

to the travelling time and the travelling distance as

well as the waiting time are minimized. The obtained

solutions assist the decision making process in terms

of these objectives. As a result of using the Tcheby-

cheff method and a Genetic algorithm, multiple alter-

natives are presented to decision makers that can in-

spect beneﬁts and trade-offs to derive daily schedules

based on individual or mutual preferences.

The paper is organized as follows. In Section 2,

the assumptions and the mathematical formulation of

the problem are presented. The multi-objective op-

timization approach is described in Section 3. Sec-

tion 4 presents the results for a case study based on

real data. In this section, the results are also analyzed

and discussed. Finally, some conclusions and future

work are drawn in Section 5.

2 PROBLEM DEFINITION

The problem arises when it is necessary to overcome

the difﬁculties that HHC services entail, such as the

vehicles delay that consequently cause bad schedules

with no viable replacement options and consequently

increase the expenses of Health Unit.

However, it is important to deﬁne the general char-

acteristics of the problem, such as the number and

characterization of health professionals, the number

of vehicles available, the number of patients and treat-

ments they need, locations that can be traveled and

their distances. This information and data allow to

create a mathematical formulation of the problem, as

an attempt to reduce the time spent on visits and con-

sequently the reduction of costs.

2.1 Assumptions

The vehicle scheduling carries out home care visits

in order to perform the necessary treatments for pa-

tients belonging to a Health Unit. This problem was

modeled, considering the number of vehicles involved

in the teams and the patients who request this type

of health care. Thus, considering a Health Unit in

Braganc¸a, with a domiciliary team that provides home

care to patients that require different types of treat-

ments, all the entities involved in the problem were

identiﬁed.

Consider the following information:

• the trips duration and distances between the dif-

ferent locations;

• the time of travel, in the same location, to visit

different patients;

• the distance, in the same location, to visit different

patients;

• the list and duration of treatments are known for

each patient (deﬁned and provided by the Health

Unit);

• the number of patients who need health care, and

who are assigned to days of home visits, are

known in advance;

• the number of vehicles available;

• all visits begin and end at the Health Unit.

The mathematical formulation considers the fol-

lowing sets:

• P is the set of np ∈ N patients that receive home

care visits, P = {p

, . . . , p

};

• V is the set of nv ∈ N vehicles that perform home

care visits, V = {v

, . . . , v

};

• L is the set of nl ∈ N locations for home care vis-

its, L = {l

, . . . , l

};

• T is the set of nt ∈ N treatments required by pa-

tients, T = {t

, . . . ,t

};

• R

, where i ∈ {1, . . . , nt}, is the set of nr

∈ N pa-

tients that receive the treatment i, R

⊂ P;

• Q

, where i ∈ {1, . . . , nl}, is the set of nl

∈ N pa-

tients that reside in location i, Q

⊂ P.

The parameters of the model are:

• D

nl×nl

is the matrix of distances between the nl

locations (the diagonal indicate the distance re-

quired to visit different patients in the same lo-

cation);

• H

nl×nl

is the matrix of time required to travel bet-

ween the nl locations (the diagonal indicate the

time required to visit different patients in the same

location);

• O

nt×1

is the vector of times required to apply each

of the nt treatments to patients.

Taking into account the information regarding

these sets and parameters, a vehicle scheduling op-

timization problem can be formulated to reduce the

time spent on visits and the costs.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

436

2.2 Mathematical Formulation

The goal is to ﬁnd the vehicle scheduling solution that

minimizes, simultaneously, the time spent on visits

and costs. A solution for this problem can be ex-

pressed by the vector x of dimension n = 2 × np with

the following structure:

x = (y, z) = (y

, ..., y

, z

, ..., z

)

where the patient y

∈ P will be visited by the vehi-

cle z

∈ V , for i = 1, . . . , np. In this vector, y

6= y

for

∀i 6= j with i = 1, . . . , np, j = 1, . . . , np. Therefore, for

a given x it is possible to deﬁne the vehicles schedu-

ling taking into account the order of the components

of x. For instance, consider a scheduling problem

with np = 5 patients to be visited by nv = 3 vehicles.

for P = {p

, p

} and V = {v

, v

}, the

vector x = (4, 3, 1, 2, 5, 2, 3, 2, 1, 1) means that patients

, p

and p

will be visited by vehicles v

, v

and v

, respectively. Thus, vehicle v

will

visit patients p

and p

; vehicle v

will visit patients

and p

; and vehicle v

will visit patient p

. For

a vehicle schedule x, the functions t

(x) and d

(x),

for l = 1, .., nv, give the total time and total distance

required to perform all visits of the vehicle l, respec-

tively. The two objective functions are deﬁned as

(x) = max

l=1,...,nv

(x) (1)

(x) = max

l=1,...,nv

(x) (2)

which represent, respectively, the maximum time and

maximum distance spent by all the vehicles to carry

out all the visits. Then, the optimization problem can

be deﬁned as:

min

x∈Ω



(x), f

(x)



(3)

where x ∈ Ω is the decision variable space and Ω =

{(y, z) : y ∈ P

, z ∈ V

and y

6= y

for all i 6= j} is

the feasible set.

3 MULTI-OBJECTIVE

APPROACH

The vehicle scheduling problem formulated previ-

ously is a multi-objective problem, since the objec-

tives conﬂict each other. The goal is to ﬁnd the set

of feasible trade-off solutions x that simultaneously

minimize f

(x) and f

(x) in order to facilitate the de-

cision maker select the solution according to his/her

preferences.

3.1 Multi-objective Optimization

When several conﬂicting objectives are optimized at

the same time, the search space becomes partially

ordered. In such scenario, solutions are compared

on the basis of the Pareto dominance. Without loss

of generality, consider a multi-objective optimization

problem where m objectives are to be minimized, for

two solutions a and b from the feasible set Ω, a so-

lution a is said to dominate a solution b (denoted by

a ≺ b) if:

∀i ∈ {1, . . . , m} : f

(a) ≤ f

(b)∧

∃ j ∈ {1, . . . , m} : f

(a) < f

(b).

(4)

Since solutions are compared against different ob-

jectives, there is no longer a single optimal solution

but a set of optimal solutions, generally known as

the Pareto optimal set. This set contains equally im-

portant solutions representing different trade-offs be-

tween the given objectives and can be deﬁned as:

P S = {x ∈ Ω |@y ∈ Ω : y ≺ x}. (5)

The images of the solutions of the Pareto optimal

set deﬁne a Pareto front in the objective space. This

Pareto front allow to identify the trade-offs between

solutions and therefore facilitate the decision making.

3.2 Tchebycheff Scalarization Method

Approximating the Pareto optimal set is the main

goal of a multi-objective optimization algorithm. The

scalarization methods can be used to obtain an ap-

proximation to the Pareto-optimal set (Miettinen,

2012) such as:

• the weighted sum method, where the weighted

linear combination of the objectives is minimized;

• the ε-constraint method, in which one of the ob-

jectives is minimized and the others are included

as constraints;

• the minimization of a weighted distance to a

reference point, e.g., the weighted Tchebycheff

method.

When using these scalarization methods, the

multi-objective problem is transformed into a sin-

gle objective optimization problem that have to be

solved using single objective optimization algorithms.

There must be some care in choosing the scalariza-

tion method since the weighted sum method does not

allow to achieve solutions belonging to non-convex

regions of the Pareto front. On the other hand, in

the ε-constraint method is difﬁcult to properly ﬁx

the limits of the constrained objectives. Since the

vehicle scheduling problem is a non-continuous and

A Multi-objective Approach to the Optimization of Home Care Visits Scheduling

437

non-convex problem, then the weighted Tchebycheff

method was adopted to solve this problem. The main

goal is to approximate the optimal Pareto solutions

that represent different trade-offs between the objec-

tives. In the weighted Tchebycheff method the L

∞

norm (i.e., minimization of the maximum difference)

is used. This distance is computed to a reference point

(or aspiration levels). The weighting coefﬁcients al-

low to obtain different trade-offs and lead with differ-

ent scaling factors of each objective. In this method,

the scalarized function is a weighted function based

on the Tchebycheff metric, to the reference point. The

weighted problem of Tchebycheff is given as follows

(Miettinen, 2012):

minmax[w

| f

(x) − z

|] (6)

where w

are the weighting coefﬁcients for objective

i, z

are the components of a reference point. An ap-

proximation to the ideal vector can be used as refer-

ence point z

= (z

, . . . , z

) = (min f

, . . . , min f

This approach can be implemented as an a pri-

ori technique in which the reference point and the

weights are deﬁned by the decision maker before the

search. There are some drawbacks in this approach

namely, the difﬁculty to deﬁne properly weights and

aspiration levels that reﬂect the decision maker pre-

ferences. Other perspective is to implement an a pos-

teriori technique in which the decision making pro-

cess takes place after the search. In this case, the re-

ference point is deﬁned as the ideal solution and the

weights are uniformly varied. In this manner, after the

search, a set of Pareto optimal solutions is presented

as alternatives and the decision maker can identify the

compromises and choose according to his/her prefer-

ences. Thus, due to its ability to solve this kind of

problems, a Genetic algorithm was assumed.

3.3 Genetic Algorithm

A Genetic algorithm (GA) (Holland, 1992) is used

to solve each single objective optimization problem

that results of the weighted Tchebycheff method.

GA is inspired by the natural biological evolution,

uses a population of individuals and new individu-

als are generated by applying the genetic operators of

crossover and mutation.

Genetic algorithm are particularly well suited to

solve vehicle scheduling problem that is non-convex

with discrete decision variable and couple with the

combinatorial nature of the search space. The ﬂe-

xibility of representation of the solutions and genetic

operators allow to handle hard constraints.

The GA used in this work is summarized in Al-

gorithm 1. Initially, a population of N

pop

individuals

is randomly generated. Each individual in the popu-

lation is a vector of decision variables x. Afterwards,

each generation, crossover and mutation operators are

applied to generate new solutions. These genetic op-

erators were designed in order to guarantee that new

solutions are feasible.

The best individuals in the population have a high

probability of being selected to generate new ones by

crossover and mutation. Therefore, the good features

of the individuals tend to be inherited by the offspring.

In this manner, population converges towards better

solutions (Ghaheri et al., 2015). The iterative proce-

dure terminates after a maximum number of iterations

(NI) or a maximum number of function evaluations

(NFE).

Algorithm 1: Genetic Algorithm.

1: P

= initialization: randomly generate a population of N

pop

individuals.

2: Set iteration counter k = 0.

3: while stopping criterion is not met do

4: P

= crossover(P

): apply crossover procedure to individuals in

population P

5: P

= mutation(P

): apply mutation procedure to individuals in pop-

ulation P

6: P

k+1

= selection(P

∪ P

): select the N

pop

best individuals of

∪ P

7: Set k = k + 1.

8: end while

3.4 Multi-objective Optimization

Framework

Figure 1 describes and illustrates the entire frame-

work of this multi-objective approach.

Genetic

Algorithm

Metric

Tchebychev

Multi-objective

Problem

Objective 1

(Time)

Objective 2

(Distance)

[ w, ref ]

Figure 1: Multi-objective optimization framework.

For the “run script”, a reference point (approxi-

mation to the ideal point) and uniformly distributed

weights are generated. “Genetic algorithm” mod-

ule solves the Tchebycheff problem deﬁned in “Met-

ric Tchebychev”. The evaluation of objective func-

tion of the vehicle scheduling optimization problem

is performed in “Multi-objective Optimization” mo-

dule that invokes time and distance objectives related

to HHC scheduling.

In this way, non-dominated solutions found by

the optimization framework for different combination

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

438

of weights allow to deﬁne an approximation to the

Pareto optimal front. The dominance relation is used

to ﬁlter the non-dominated solutions.

Based on the dominance concept, it is possible

to determine the non-dominated solution of a given

set of solutions. Among a set of solutions S, the

non-dominated set of solutions are those that are not

dominated by any members of the set S. This non-

dominated set is the best approximation to the Pareto

optimal set.

Therefore, after obtaining all the solutions, it is

necessary to create a routine, which with efﬁcient

computational procedures, allows obtaining the set

of non-dominated solutions. In the literature, there

are different procedures, such as “Naive and Slow”,

or “Continuously Updated”, which allow to compare

and identify the set of solutions (Deb, 2014). Regar-

ding the “Naive and Slow” approach, each solution i

is compared to all population solutions in order to test

the dominance by any of the other solutions. If the

solution i is dominated by any solution, it means that

there is at least one solution in the population that is

better than i in all objectives. Hence the solution i can

not belong to the non-dominated set. In this way, a

“ﬂag” is marked against the solution i to denote that it

does not belong to the non-dominated set. However,

if no solution is found to dominate the solution i, it

becomes a member of the non-dominated set. Thus,

with this procedure, any other solution in the popula-

tion can be checked for future analysis.

This approach can be presented step-by-step to

ﬁnd the set not dominated in a given set S of size N

(Deb, 2014):

• Step 1 - Deﬁne the solution counter i = 1 and cre-

ate an empty non-dominated set S

• Step 2 - For solution j ∈ S(but j 6= i), check that

solution j dominates solution i. If yes, proceed to

step 4.

• Step 3 - If more solutions are left in S, increment

j by one and proceed to step 2; Otherwise, set

= S

∪ i.

• Step 4 - Increase i by one. If i ≤ N , go to step

2; Otherwise, stop and declare S

as the set non-

dominated.

Thus, a routine similar to the previous one was im-

plemented, but with a small improvement in the clas-

siﬁcation scheme. That is, each solution is compared

to all members of the set S

, one by one. If the solu-

tion i dominates any member of S

, then this solution

is removed from S

. In this way, non-members of non-

dominated solutions are deleted from S

. Otherwise,

if solution i is dominated by any member of S

, so-

lution i is ignored. However, if the solution i is not

dominated by any member of S

, it is inserted in S

(similar to the continuously updated procedure). It is

in this way that the set S

grows with non-dominated

solutions, where the other members of S

are thus the

non-dominated set.

This approach has made possible to improve the

efﬁciency and performance of the implemented rou-

tine as it allows the dominated solutions to be re-

moved quickly.

4 NUMERICAL RESULTS

In this section, the multi-objective optimization

framework is applied to a case study.

4.1 Case Study

The case under study is related to a day of the month

of April in the year 2017. On that day the Health Unit

of Braganc¸a had ﬁve cars available (nv = 5) to per-

form the home care visits to 22 patients (np = 22).

Each patient required a certain treatment of a total of

ﬁve treatments (nt = 5). Table 1 identiﬁes which treat-

ments each patient needs (R

for i = 1, . . . , nt).

Table 1: Information about the treatments required by each

patient (R

for i = 1, . . . , nt).

Patients

Treatment 1 1, 2, 3, 6, 7, 8, 9, 17, 21, 22

Treatment 2 4, 5

Treatment 3 13, 14

Treatment 4 11, 12, 15, 16, 18, 19, 20

Treatment 5 10

The treatments needed by the patients have differ-

ent care and average times (O

for i = 1, . . . , nt), as

can be seen in the Table 2.

Table 2: Different types of care and their average times in

minutes (O

for i = 1, . . . , nt).

Average Times

Treatment 1 (Curative) 30

Treatment 2 (Surveillance and Rehabilitation) 60

Treatment 3 (Curative and Surveillance) 75

Treatment 4 (Surveillance) 60

Treatment 5 (General) 60

On the other hand, the patients are dispersed

in nine different locations (nl = 9) in the region

of Braganc¸a. Regarding the places of domiciliary

visit, Table 3 shows the locations and cities (Q

for i = 1, . . . , nl) (inserted with abbreviation for

conﬁdential data protection) of each of the patients.

A Multi-objective Approach to the Optimization of Home Care Visits Scheduling

439

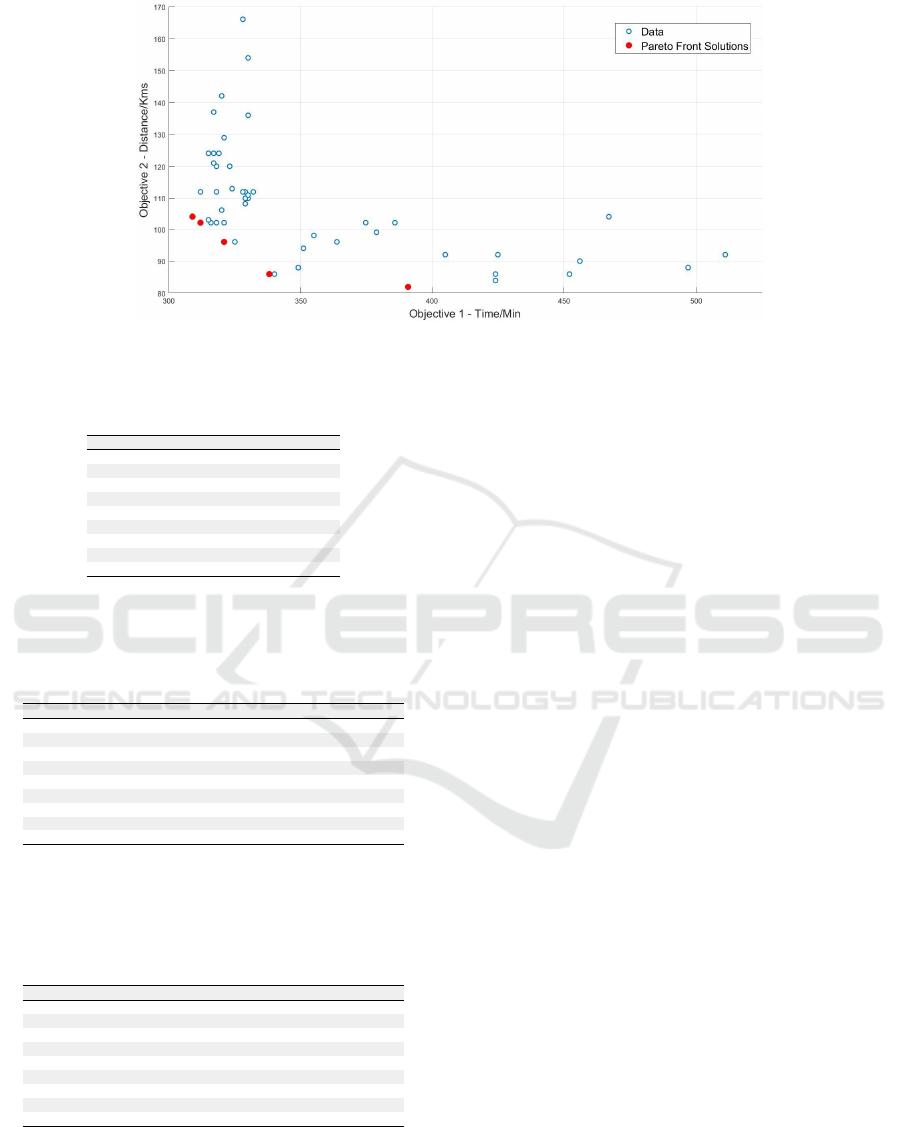
Figure 2: Pareto front and dominated solutions.

Table 3: Information of the locations of each patient (Q

for

i = 1, . . . , nl).

Locations Patients

B 1, 2, 3, 5, 6, 7, 13, 15, 16, 19, 20

P 9

A 11, 12

Sm 14

E 4

Rd 8, 10

Sd 17, 18

Mo 21

Ml 22

Table 4 shows the travel times, in minutes, be-

tween locations (H).

Table 4: Time matrix between each location in minutes (H).

A B E Ml Mo P Rd Sm Sd

A 15 16 25 21 18 29 18 15 30

B 16 15 17 18 16 29 15 15 29

E 25 17 15 34 25 37 24 25 37

Ml 21 18 34 15 23 36 27 21 36

Mo 18 16 25 23 15 15 16 15 18

P 29 29 37 36 15 15 25 36 31

Rd 18 15 24 27 16 25 15 15 25

Sm 15 15 25 21 15 36 15 15 26

Sd 30 29 37 36 18 31 25 26 15

Consequently, Table 5 is also presented, with the

distances between locations in kilometers (D).

Table 5: Distance matrix between each location in kilome-

ters (D).

A B E Ml Mo P Rd Sm Sd

A 10 14 24 21 16 28 14 11 33

B 14 10 16 21 19 31 15 11 36

E 24 16 10 35 25 36 21 20 42

Ml 21 21 35 10 30 30 28 22 47

Mo 16 19 25 30 10 12 12 12 21

P 28 31 36 30 12 10 19 24 23

Rd 14 15 21 28 12 19 10 14 25

Sm 11 11 20 22 12 24 14 10 10

Sd 33 36 42 47 21 23 25 10 10

Based on all the data presented, the main objective

is to obtain optimal vehicles scheduling solutions in

order to minimize the total time (in minutes) and the

distance (in kilometers) required to carry out the trips,

the treatments and to return to the starting point.

4.2 Discussion

For this case study, simulations were carried out on a

PC Intel(R) Core(TM) i7 CPU 2.2 GHz with 6.0GB of

RAM. The optimization framework was implemented

in MatLab



(MATLAB, 2015).

The values of the control parameters used in GA

for this problem were tuned after preliminary expe-

riments. A population size of 30 individuals (N

pop

30) and a probability rate of 50% for crossover and

mutation procedures was used. The stopping crite-

rion was based on the maximum number of iterations

deﬁned as 100 (NI = 100) or the maximum number

of function evaluations of 5000 (NFE = 5000). Since

GA is a stochastic algorithm, 10 runs were carried out

with random initial populations.

The value of the reference point was an ap-

proximation to the ideal vector and the weights

for the objectives varied in the set (w

, w

) ∈

{(1, 0), (0.75, 0.25), (0.5, 0.5), (0.25, 0.75), (0, 1)}.

For each of the weight vectors, the execution in

MatLab



(MATLAB, 2015) was performed.

The multi-objective optimization framework al-

lowed to identify a set of non-dominated solutions,

crucial to provide to the decision maker through the

visualization of solutions in the objective space.

Figure 2 shows the the set of Pareto optimal so-

lutions, i.e. the non-dominated solutions (represented

by a red circle), as well as the dominated solutions

(represented by a blue circle). The position of these

solutions express the trade-offs between the objec-

tives (time in minutes in the x axis and distance in

kilometers in the y axis). It can be seen from Figure 2

that ﬁve non-dominated solutions were found, repre-

senting the set of most interesting solutions. There-

fore, these are the solutions that must be taken into

account, because they are optimal in terms of the ob-

jectives, and each solution exhibits the trade-off that

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

440

should be explored. However, it is also important to

analyze the solution in the decision variable space.

In order to illustrate the solutions found in the de-

cision space, Gantt charts are used. Thus, the Gantt

chart aims to represent the vehicle schedule of a so-

lution. In this sense, three different vehicle sched-

ules are presented for home visits, referring to three

non-dominated solutions. The three selected non-

dominated solutions refer to the extreme points in

terms of each of the objectives and the closest solution

to the ideal vector. First, the non-dominated solution

related to the best solution in terms of minimizing the

distance traveled in kilometers (one extreme of Pareto

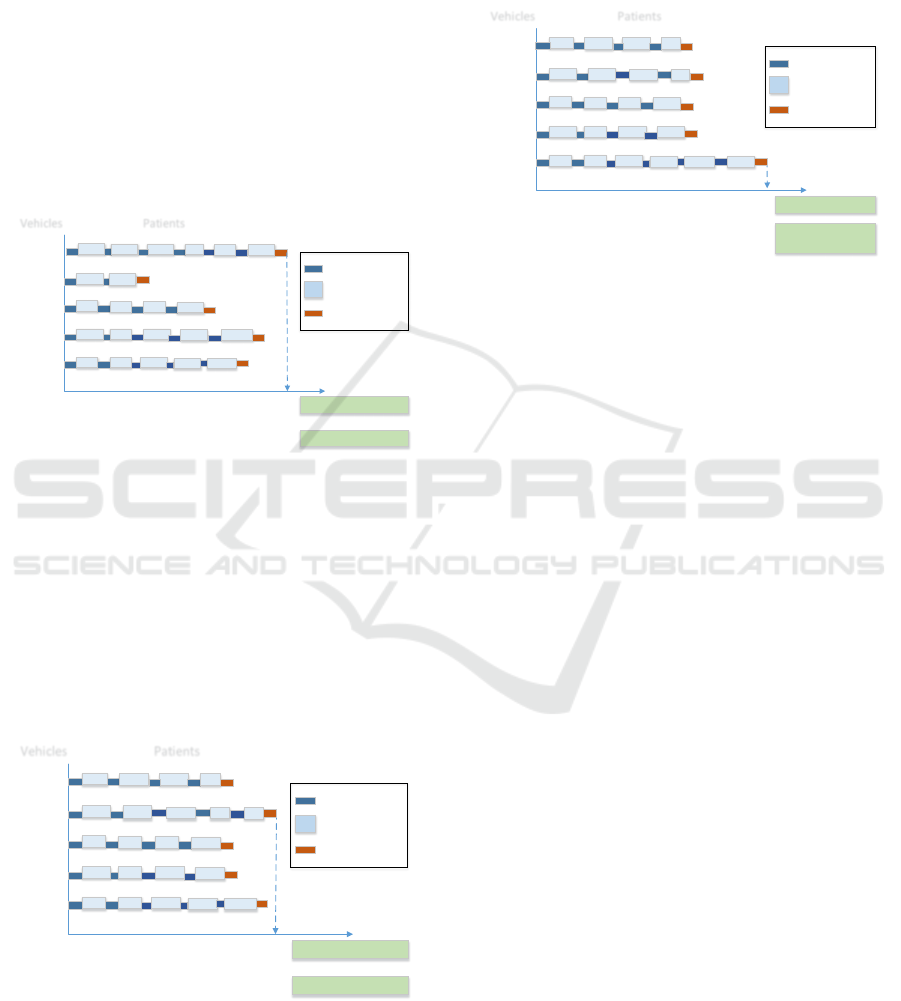
front) is presented in Figure 3.

Vehicles

Vehicle 1

Vehicle 2

Vehicle 3

Vehicle 4

Patients

1 20 15

11 12

10 9

Time traveling

Treatment time

Return to HUB

Objective 1 – Time

Objective 2 – Distance

Vehicle 5

6 19 3

22 16

391

Figure 3: Non-dominated solution that minimizes distance.

The scheduling of vehicles for home visits of this

solution shows that the goal of minimizing the dis-

tance presented the solution of 82 kilometers. In turn,

guarantees the visit to all patients but in return a max-

imum of 391 minutes is required.

A further scheduling is also presented for the best

solution in terms of minimizing the time spent in min-

utes (the opposite extreme of the Pareto front). Figure

4 shows the scheduling for this solution.

Vehicles

Vehicle 1

Vehicle 2

Vehicle 3

Vehicle 4

Patients

22 3 2

17 9

10 7

Objective 1 – Time

Objective 2 – Distance

Vehicle 5

5 19 13

11 12

309

104

Time traveling

Treatment time

Return to HUB

Figure 4: Non-dominated solution that best represents the

objective of minimizing time.

In this solution, the scheduling presents a signif-

icant improvement of time when compared with the

ﬁrst solution (309 minutes). However, the day of vis-

its ends with a maximum distance of 104 kilometers.

The scheduling of an intermediate solution to the

two extremes presented above (often referred to as the

“elbow” solution), is illustrated in Figure 5.

Vehicles

Vehicle 1

Vehicle 2

Vehicle 3

Vehicle 4

Patients

6 7 19

4 13

11 9

Objective 1 – Time

Objective 2 –

Distance

Vehicle 5

5 15 20

2 22

321

Time traveling

Treatment time

Return to HUB

Figure 5: Solution that characterizes the ”elbow” of non-

dominated solutions.

The “elbow” solution has a maximum time of 321

minutes and a maximum of 96 kilometers, since this

is the solution that is closest to the ideal solution.

In summary, a gain in the time spent is achieved

in the ”elbow” solution at the expense of an increase

in the distance traveled when compared to the 1st ex-

treme. However, this decision must be made by the

decision maker taking into account factors such as in-

dividual or mutual preferences, beneﬁts and trade-offs

to derive daily HHC schedules.

In conclusion, the analysis of viable alternatives

gives new valuable information to the decision maker.

Moreover, the multi-objective approach provides al-

ternative optimal solutions that are essential to sup-

port the decision maker to choose adequate schedules

for home visits in a Health Unit.

5 CONCLUSIONS

Home visits at the Health Unit are usually planned

manually and without any computational support,

which implies that, in addition to being a complex and

time-consuming process, the solution obtained may

not be the best. Thus, in an attempt to optimize the

process it is necessary to use strategies that allow to

minimize certain objectives, without, however, wor-

sening the quality of services provided and, always,

looking for the best optimization of the scheduling.

Thus, a multi-objective optimization model was

developed to simultaneously minimize two conﬂic-

ting objectives: the time spent and the distance trav-

eled (which consequently affects the costs). The

multi-objective optimization problem is scalarized

A Multi-objective Approach to the Optimization of Home Care Visits Scheduling

441

applying the Tchebycheff method and solved by a Ge-

netic algorithm. Different compromise solutions are

obtained. An efﬁcient and fast routine to compute the

non-dominated solutions is implemented. This deci-

sion support system was applied to a case study with

real data.

The optimal alternatives found were analyzed

both in terms of objective functions and decision vari-

ables values. For the decision maker the extreme and

“elbow” solutions can be particularly interesting and

therefore may be carefully investigated. In addition,

the approach allows the possibility of replicating the

problem with different instances, without incurring

additional costs or deﬁciencies in the service, thus

continuing to be able to serve as a support system,

which today does not yet exist.

As future work perspectives, it is intended to im-

prove the efﬁciency of the the optimization algorithm,

as well as the model by the inclusion of new objec-

tives and constraints.

ACKNOWLEDGEMENTS

This work has been supported by COMPETE:

POCI-01-0145-FEDER-007043 and FCT - Fundac¸

para a Ci

encia e Tecnologia within the project

UID/CEC/00319/2013.

REFERENCES

Allaoua, H., Borne, S., L

etocart, L., and Calvo, R. W.

(2013). A matheuristic approach for solving a home

health care problem. Electronic Notes in Discrete

Mathematics, 41:471–478.

Alves, F., Pereira, A. I., Fernandes, A., and Leit

ao, P.

(2018). Optimization of home care visits schedule

by genetic algorithm. In International Conference on

Bioinspired Methods and Their Applications, pages 1–

12. Springer.

Baker, B. M. and Ayechew, M. (2003). A genetic algorithm

for the vehicle routing problem. Computers & Opera-

tions Research, 30(5):787–800.

Benzarti, E., Sahin, E., and Dallery, Y. (2010). A literature

review on operations management based models de-

veloped for hhc services. In European Conference of

Operational Research Applied to Health Care, Gen-

ova, Italy, pages 1–21.

Benzarti, E., Sahin, E., and Dallery, Y. (2013). Operations

management applied to home care services: Analysis

of the districting problem. Decision Support Systems,

55(2):587–598.

Braekers, K., Hartl, R. F., Parragh, S. N., and Tricoire, F.

(2016). A bi-objective home care scheduling prob-

lem: Analyzing the trade-off between costs and client

inconvenience. European Journal of Operational Re-

search, 248(2):428–443.

Bredstr

om, D. and R

onnqvist, M. (2008). Combined vehi-

cle routing and scheduling with temporal precedence

and synchronization constraints. European journal of

operational research, 191(1):19–31.

Deb, K. (2014). Multi-objective optimization. In Search

methodologies, pages 403–449. Springer.

Fikar, C. and Hirsch, P. (2017). Home health care routing

and scheduling: A review. Computers & Operations

Research, 77:86–95.

Gayraud, F., Deroussi, L., Grangeon, N., and Norre, S.

(2013). A new mathematical formulation for the home

health care problem. Procedia Technology, 9:1041–

1047.

Ghaheri, A., Shoar, S., Naderan, M., and Hoseini, S. S.

(2015). The applications of genetic algorithms in

medicine. Oman medical journal, 30(6):406.

Holland, J. H. (1992). Adaptation in natural and artiﬁcial

systems: an introductory analysis with applications to

biology, control, and artiﬁcial intelligence. MIT press.

Koeleman, P. M., Bhulai, S., and van Meersbergen, M.

(2012). Optimal patient and personnel scheduling

policies for care-at-home service facilities. European

Journal of Operational Research, 219(3):557–563.

MATLAB (2015). version 8.6.0 (R2015b). The MathWorks

Inc., Natick, Massachusetts.

Miettinen, K. (2012). Nonlinear multiobjective optimiza-

tion, volume 12. Springer Science & Business Media.

Nguyen, T. V. L. and Montemanni, R. (2013). Scheduling

and routing in home health care service. In Society 40

th Anniversary Workshop–FORS40, page 52.

Nickel, S., Schr

oder, M., and Steeg, J. (2012). Mid-term

and short-term planning support for home health care

services. European Journal of Operational Research,

219(3):574–587.

Ombuki, B., Ross, B. J., and Hanshar, F. (2006). Multi-

objective genetic algorithms for vehicle routing prob-

lem with time windows. Applied Intelligence,

24(1):17–30.

Pasia, J. M., Doerner, K. F., Hartl, R. F., and Reimann, M.

(2007). A population-based local search for solving

a bi-objective vehicle routing problem. In European

conference on Evolutionary computation in combina-

torial optimization, pages 166–175. Springer.

Rasmussen, M. S., Justesen, T., Dohn, A., and Larsen, J.

(2012). The home care crew scheduling problem:

Preference-based visit clustering and temporal depen-

dencies. European Journal of Operational Research,

219(3):598–610.

Toth, P. and Vigo, D. (2014). Vehicle routing: problems,

methods, and applications. SIAM.

Yalc¸ındag, S., Matta, A., and Sahin, E. (2011). Human re-

source scheduling and routing problem in home health

care context: a literature review. ORAHS/Cardiff,

United Kingdom.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

442