
Learning of Activity Cycle Length based on Battery Limitation in
Multi-agent Continuous Cooperative Patrol Problems
Ayumi Sugiyama, Lingying Wu and Toshiharu Sugawara
Department Computer Science and Communications Engineering, Waseda University, Tokyo 1698555, Japan
Keywords:
Continuous Cooperative Patrol Problem, Cycle Learning, Multi-agent, Division of Labor, Battery Limitation.
Abstract:
We propose a learning method that decides the appropriate activity cycle length (ACL) according to environ-
mental characteristics and other agents’ behavior in the (multi-agent) continuous cooperative patrol problem.
With recent advances in computer and sensor technologies, agents, which are intelligent control programs
running on computers and robots, obtain high autonomy so that they can operate in various fields without
pre-defined knowledge. However, cooperation/coordination between agents is sophisticated and complicated
to implement. We focus on the ACL which is time length from starting patrol to returning to charging base
for cooperative patrol when agents like robots have batteries with limited capacity. Long ACL enable agent
to visit distant location, but it requires long rest. The basic idea of our method is that if agents have long-life
batteries, they can appropriately shorten the ACL by frequently recharging. Appropriate ACL depends on
many elements such as environmental size, the number of agents, and workload in an environment. Therefore,
we propose a method in which agents autonomously learn the appropriate ACL on the basis of the number
of events detected per cycle. We experimentally indicate that our agents are able to learn appropriate ACL
depending on established spatial divisional cooperation.
1 INTRODUCTION
With recent developments in technology, we can ex-
pect that agents, that are autonomous programs con-
trolling robots and computer systems, often have to
collaborate and coordinate with each other to solve
complicated and sophisticated problems. However,
creating methods for establishing cooperation among
multiple agents is challenging due to the difficulty
of realizing advanced autonomy and various com-
plex interaction patterns between agents. In partic-
ular, it is crucial to estimate others’ strategies for co-
operation between agents that have their own behav-
ioral strategies and different computational costs. In
tackling these issues, the multi-agent patrol problem
(MAPP) has attracted attention as a good case study
on many multi-agent systems because it has essen-
tial issues such as autonomy, dispersibility, commu-
nication restriction, and scalability, all of which are
required to realize intelligent autonomous distributed
systems (David and Rui, 2011).
We also extend this problem to the continuous
cooperative patrol problem (CCPP) in which multi-
ple autonomous agents with limited battery capacities
continuously move around in an environment where
events occur at a certain probability (Sugiyama and
Sugawara, 2017). In the MAPP, all nodes (locations)
are visited with the same priority/frequency because
the purpose of MAPP is to minimize idleness which
is the interval of two visits for every node. In com-
parison, agents in the CCPP are required to visit in-
dividual nodes with different visitation requirements,
which reflect that events in nodes occur with different
probabilities or reflect the importance of nodes. Thus,
high visitation requirements indicate, for example, lo-
cations that require a high-security level at which no
events must be missed in security patrolling applica-
tions. Thus, the objective of agents in the CCPP is
to minimize the duration of unawareness which is the
length of time for which agents leave occurred events
unaware without visiting the locations.
Thus, because of the importance of these prob-
lems, a number of studies have tackled MAPPs and
CCPPs in multi-agent system contexts. For example,
Cheva (Chevaleyre, 2005) classified various classes
of patrolling strategies and compared these strategies.
David and Rui (David and Rui, 2011) summarized
developments of patrolling methods and indicated is-
sues that must extensively be studied regarding the
MAPPs. We (Sugiyama et al., 2016) also proposed
62
Sugiyama, A., Wu, L. and Sugawara, T.
Learning of Activity Cycle Length based on Battery Limitation in Multi-agent Continuous Cooperative Patrol Problems.
DOI: 10.5220/0007567400620071
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 62-71
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the learning method, in which agents individually de-
cide where they should work using lightweight com-
munications and using the learning which locations
they should visit more frequently than others. They
found that the agents with their methods could ef-
fectively move around the environment by identify-
ing their responsible areas, i.e., they finally formed a
certain cooperation structure based on the division of
labors.
Although this method could be used to efficiently
patrol an environment to detect events in it, we found
that agents have to coordinate their behavior by taking
into account the interval of visits. Because we assume
that agents are (the control programs of) robots, they
often stop operation for battery charging and/or peri-
odic inspections. This interruption in operation may
negatively affect patrolling, such as security surveil-
lance. Because temporarily stopping for charging is
frequent and inevitable in actual operation, strategic
behavior is required to minimize the influence of stop-
ping by taking into account robots’ noise and the char-
acteristics of the areas in which they move around.
Although a few studies discussed the battery capac-
ity of agents (robots) (Sipahioglu et al., 2010; Jensen
et al., 2011; Bentz and Panagou, 2016), the appro-
priate timing for when to return to charge and when
to resume operation for autonomous agents was not
clarified in their methods.
A cyclic strategy, in which agents move until the
batteries become empty and then charge to make the
batteries full in different periodic phases, is one of the
simplest ways to minimize the duration of unaware-
ness in the CCPP. In this paper, a sequence of actions
from the agent leaving the charging base with a full
battery, moving around the environment, returning to
the base and completing the charge is called a round
and the time length of the moving in a round is called
activity cycle length (ACL). Performance of a cyclic
strategy depends on a battery capacity. For example,
agents with a small battery capacity cannot cover dis-
tant tasks/events, and the cumulative return cost for
recharging is high in a large environment due to fre-
quent charging. In contrast, agents with long-life bat-
teries can be expected to move more effectively and
cover distant events but they must stop operations for
a long time for recharging, resulting in a long duration
of unawareness. Therefore, because appropriate ACL
may depend on the environmental characteristics and
behaviors of other cooperative agents, agents are re-
quired to autonomously learn which ACL will lead
to better results through actual cooperative behavior
from the viewpoint of the entire performance.
In this paper, we extend the method proposed in
(Sugiyama et al., 2016) to learn appropriate ACL
in the CCPP model in order to adapt other agents’
cooperative strategies (including their ACL) and the
characteristics of the areas in which individual agents
mainly move around. In this method, we assume that
agents have long-life batteries and they can adaptively
decide their ACL by returning/restarting regardless of
their remaining battery capacities, because it is easy
to shorten ACL. Of course, they must not run out of
battery during operations. The features of our method
is that, like the method in (Sugiyama et al., 2016),
it does not require tight communication and deep in-
ference for cooperation, meaning that frequent mes-
sage exchange and the sophisticated reasoning of oth-
ers’ internal intentions are not used; this makes our
method efficient and lightweight, and thereby, our
method is applicable to dynamic environments. We
experimentally indicate that agents with our method
are able to identify appropriate ACL. Furthermore, we
found that agents established a spatial division of la-
bor, as in (Sugiyama et al., 2016); thus, agents in-
dividually identify where they should move around
as the nodes they are responsible for. This enables
agents to decide ACL differently and appropriately
for their own specific situations.
2 RELATED WORK
Various approaches, especially approaches based on
reinforcement learning for the MAPP and CCPP,
are examined so far. David and Rui (David and
Rui, 2011) summarized the development of patrolling
methods. They stated that non-adaptive solutions
such as methods based on the traveling salesman
problem often outperform other solutions in many
cases except in large or dynamic environments. To
adapt to these environments, they insisted that agents
must have high autonomy. Machado et al. (Machado
et al., 2003) evaluated reactive agents and cognitive
agents that have different depths to analyze patrol
graphs and investigated the characteristics of these
agents. In actual patrol problems, because cogni-
tive agents have greater perception, they can do more
sophisticated operations due to recent developments
in technology. Santana et al. (Santana et al., 2004)
modeled a patrolling task as a reinforcement learn-
ing problem and proposed adaptive strategies for au-
tonomous agents. Then, they showed that their strate-
gies were not always the best but were superior in
most of the experiments.
The CCPP assumes a dynamic environment in
which events occur with certain probabilities and the
duration of unawareness is considered instead of idle-
ness as in the MAPP. Ahmadi and Stone (Ahmadi and
Learning of Activity Cycle Length based on Battery Limitation in Multi-agent Continuous Cooperative Patrol Problems
63

Stone, 2006), by assuming that events to be found
were generated stochastically, proposed agents that
learn the probability of events and adjust their area of
responsibility to minimize the average required time
to detect events. Chen and Yum (Chen and Yum,
2010) modeled a patrolling environment with a non-
liner security level function in the context of a security
problem. In this model, agents have to visit each node
with a different frequency according to the values
of the function. Pasqualetti et al. (Pasqualetti et al.,
2012) studied a patrol problem in which all nodes
have different priorities, but their model was a simple
cyclic graph with a small number of nodes. Popescu
et al. (Popescu et al., 2016) proposed a patrolling
method for a wireless sensor network in which agents
collect saved data from sensors with limited storage
independently. Agents in this model decide the prior-
ities of nodes to visit on the basis of the accumulated
amount of data and data generation rate.
Sugiyama et al. (Sugiyama et al., 2016) proposed
a method called the adaptive meta-target decision
strategy with learning of dirt accumulation probabili-
ties (AMTDS/LD) by combining the learning of a tar-
get decision strategy in the planning process and the
learning of the importance of each location for clean-
ing tasks. Agents with AMTDS/LD indirectly coop-
erate with other agents by learning the importance of
nodes, which is partly taken into account reflects the
visiting frequencies of other agents. They also ex-
tended their method by introducing simple negotia-
tion to enhance the division of labor in a bottom-up
manner (Sugiyama and Sugawara, 2017). However,
they did not discuss the intervals of visits, which is an-
other key issue of the CCPP. In the CCPP, agents with
limited capacity batteries have to stop their operation
to recharge, so agents have to coordinate with each
other by adjusting timings of starting and recharging
for appropriate visiting patterns.
Other researchers also take into account battery
capacity in the multi-robot patrol problem. Jensen et
al. (Jensen et al., 2011) presented strategies for replac-
ing robots that have almost empty batteries with other
robots that have fully charged ones to keep cover-
age and minimize interruptions for sustainable patrol.
Bentz and Panagou (Bentz and Panagou, 2016) pro-
posed an energy-aware global coverage technique that
shifts distributions of effort networks according to the
degree of an agent’s energy constraints. Sipahioglu
et al. (Sipahioglu et al., 2010) proposed a path plan-
ning method that covers an environment by consider-
ing energy capacity in multi-robot applications. This
method partitions a complete coverage route into sub-
routes and assigns them to robots by considering the
energy capacities of the robots. These methods are
mainly focused on how to divide work areas for coop-
erative activities. However, they do not focus on con-
trolling the phases of ACL on the basis of the battery
capacity. Therefore, we propose a learning method
that decides the appropriate activity duration depend-
ing on the characteristics of the tasks of agents for
more effective cooperation.
3 MODEL
3.1 Environment
The environment in which agents patrol is described
by graph G = (V,E), which can be embedded into
a two-dimensional plane with a metric, where V =
{v
1
,...v
m
} is a set of nodes, so node v ∈ V has coordi-
nates v = (x
v
,y
v
). An agent, an event, and an obstacle
can exist on node v. E is a set of edges. An edge con-
necting v
i
and v
j
is expressed by e
i, j
∈ E. Agents can
move one of their neighbor nodes along an edge. An
environment may have obstacles, R
o
(⊂ V ). Agents
cannot move to and events do not occur on the nodes
in R
o
.
Node v ∈ V has the event occurrence probability
value p(v) (0 ≤ p(v) ≤ 1), and it indicates that an
event occurs on v with probability p(v). The num-
ber of unaware events without processing on v at time
t is expressed by L
t
(v), where L
t
(v) is a non-negative
integer. L
t
(v) is updated on the basis of p(v) every
tick by
L
t
(v) ←
(
L
t−1
(v) + 1 (if an event occurs)
L
t−1
(v) (otherwise).
(1)
L
t
(v) become 0 when an agent visits v. Discrete time
with units called tick is used in this model. In one tick,
events occur on nodes, agents decide their target node,
agents move to neighbor nodes, and agents process
events.
3.2 Agent
Before we describe the agent model, we explain that
one assumption which we introduce to simplify our
problem. In this study, we assume that agents always
get their own and others’ locations. An environment
with this assumption can be realized, for example,
by equipping agents with indicators, such as infrared
emission and reflection devices. We believe that this
is a reasonable assumption because technology for
sensors and positioning systems are being rapidly de-
veloped. However, we do not assume that agents can
get others’ internal information such as the adopted
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
64

strategy and the selected target node because reason-
ing by using/estimating others’ internal information
seems complicated. Because we want to focus on the
period of cyclic behavior for better cooperative work,
we do not consider this costly reasoning.
Let A = {1, . . . ,n} be a set of agents. When agents
obtain p(v) in advance, they can use p(v) for their pa-
trol. However, in actual patrol problems, p(v) is usu-
ally unknown. Moreover, the appropriate frequency
to visit depends not only on p(v) but also on the fre-
quencies of other agents’ visits.
Therefore, agents have to learn priorities to visit
nodes through their actual patrols. Agent i has the
degree of importance (simply, importance after this)
p
i
(v) for all nodes in an environment, and it reflects
both p(v) and other agents’ behavior. When i visits
node v at t and detects events L
t
(v), i updates p
i
(v),
as
p
i
(v) ← (1 − β)p
i
(v) + β
L
t
(v)
I
i
t
(v)
, (2)
where I
i
t
(v) is the elapsed time from t
v
visit
which is the
time of the last visit to v and calculated as
I
i
t
(v) = t − t
v
visit
. (3)
β (0 < β ≤ 1) is the learning rate.
3.2.1 Target Decision and Path Generation
Strategy
Agents repeatedly generate paths to move through a
planning process. The planning usually consists of
two subprocesses: target decision and path genera-
tion for patrol. Agent i first decides the next target
node v
i
tar
∈ V by using the target decision process and
then generates the appropriate path from the current
node to v
i
tar
by using the path generation process. Be-
cause our purpose is to extend the AMTDS/LD and
to compare our proposed method with AMTDS/LD,
we briefly explain it. Agent i with AMTDS/LD si-
multaneously learns the appropriate strategy s in S
plan
and p
i
(v) with Formula (2), where S
plan
is the set of
target decision strategies described below. The policy
for selecting the target decision strategy from S
plan
is
adjusted based on Q-learning with the ε-greedy learn-
ing strategy. Thus, i updates the Q-value of the se-
lecting s ∈ S
plan
on the basis of the sum of detected
events until i arrives at v
i
tar
, which is the target de-
cided by s. The details of Q-learning for this policy
and AMTDS/LD are outside the scope of this paper;
please refer to (Sugiyama et al., 2016).
We will explain the elements of S
plan
, i.e., the tar-
get decision strategies used in AMTDS/LD.
Random Selection (R).
Agent i randomly selects v
i
tar
among all nodes V .
Probabilistic Greedy Selection (PGS).
Agent i selects v
i
tar
in which i estimates the value
of unaware events EL
i
t
(v) at time t using p
i
(v) and
elapsed time from last visit I
i
t
(v) by
EL
i
t
(v) = p
i
(v) · I
i
t
(v). (4)
Then, i selects v
i
tar
randomly from the N
g
high-
est nodes in V according to the values of EL
i
t
(v),
where N
g
is a positive integer.
Prioritizing Unvisited Interval (PI).
Agent i selects v
i
tar
randomly from the N
i
highest
nodes according to the value of interval I
i
t
(v) for
v ∈ V , where N
i
is a positive integer. Agents with
this strategy are likely to prioritize nodes that have
not been visited recently.
Balanced Neighbor-Preferential Selection (BNPS).
Agent i estimates if many unaware events may
exist near nodes by using the learned threshold
value, and i selects v
i
tar
from such nodes. Other-
wise, i selects v
i
tar
by using the PGS. The details
are described elsewhere (Yoneda et al., 2013).
Note that we can also regard AMTDS, AMTDS/LD,
and our proposed method as target decision strategies.
We use the gradual path generation (GPG)
method as the path generation strategy in this re-
search (Yoneda et al., 2013). Agent i with the GPG
first calculates the shortest path from current node
to v
i
tar
and then regenerates a path to v
i
tar
by adding
nodes nearby the shortest path and whose values of
EL
i
t
(v) are identified as high. We do not explain
the GPG method in detail because it is beyond the
scope of this paper, but it is also described else-
where (Yoneda et al., 2013).
3.2.2 Battery Setting
Agent i has a battery with a limited capacity, so it
must periodically return to its charging base v
i
base
∈
V to charge its battery for continuous patrolling.
The battery specifications of agent i are denoted by
(B
i
max
,B
i
drain
,k
i
charge
), where B
i
max
(> 0) is the maxi-
mal capacity of the battery, B
i
drain
(> 0) is the amount
of battery consumption per one tick, and k
i
charge
(> 0)
is the time taken to charge one battery at charging
base v
i
base
. The remaining amount of the battery of
agent i at time t is expressed in b
i
(t)(0 ≤ b
i
(t) ≤
B
i
max
).
Agents in this model must go back to v
i
base
before
b
i
(t) becomes 0 as shown below. Agent i calculates
the potential, P (v), for all nodes in advance. P (v)
is the minimal amount of battery consumption neces-
sary to return from node v to v
i
base
and is calculated
as
P (v) = d(v, v
i
base
) × B
i
drain
, (5)
Learning of Activity Cycle Length based on Battery Limitation in Multi-agent Continuous Cooperative Patrol Problems
65

where d(v
k
,v
l
) is the shortest path length from node
v
k
to node v
l
. After agent i decides v
i
tar
on the basis
of the target decision strategy, i judges whether i can
arrive at v
i
tar
before i moves to v
i
tar
using with
b
i
t
≥ P (v
i
tar
) + d(v
i
t
,v
i
tar
) × B
i
drain
, (6)
where v
i
t
∈ V is current node of agent i at time t. If
this inequation does not hold, i changes v
i
tar
as
v
i
tar
← v
i
base
, (7)
and immediately returns to v
i
base
. Agents recharge bat-
teries at charging bases until they are full and then
restart patrol.
Our purpose is to appropriately decide ACL de-
pending on the characteristics of their working envi-
ronments, the recognition of the importances of all
locations and the behavior of other agents. Because
agents can return to the charging base earlier, it is easy
to shorten ACL if they have long-life batteries.
3.3 Performance Measure and
Requirement of CCPP
The requirement of the CCPP is to minimize The
number of unaware events, L
t
(v), by visiting impor-
tant nodes without being aware of event occurrences.
For example, in cleaning tasks, agents should vacuum
accumulated dirt as soon as possible without leaving it
and keep the amount of dirt low. Therefore, we define
a performance measure when agents adopted strategy
s ∈ S
plan
, D
t
s
,t
e
(s), for the interval from t
s
to t
e
to eval-
uate our method.
D
t
s
,t
e
(s) =
∑
v∈V
t
e
∑
t=t
s
+1
L
t
(v), (8)
where t
s
< t
e
. D
t
s
,t
e
(s) is the cumulative unaware du-
ration in (t
s
,t
e
], so a smaller D
t
s
,t
e
indicates better sys-
tem performance.
We can also consider another performance mea-
sure. For example, in security patrol applications,
agents should keep the maximal number of L
t
(v) as
low as possible, because a high value for L
t
(v) indi-
cates significant danger. This measure is defined by
U
t
s
,t
e
(s) = max
v∈V,t
s
<t≤t
e
L
t
(v). (9)
Therefore, agents in the CCPP are required to lower
one of the performance measures, D
t
s
,t
e
(s) or U
t
s
,t
e
(s),
depending on the type of application.
4 PROPOSED METHOD
In this section, we describe our method in which
agents learn the appropriate ACL to improve perfor-
mance. We named our method, which is an extension
of AMTDS/LD (Sugiyama et al., 2016), AMTDS with
cycle learning (AMTDS/CL). Agent i has ACL as s
i
c
(0 < s
i
c
≤ bB
i
max
/B
i
drain
c) (we normalize the value in
(B
i
max
,B
i
drain
) so that B
i
drain
= 1 here after). Agent
i with AMTDS/CL regards its battery capacity B
i
max
as s
i
c
and then uses the battery control algorithm in
Sec. 3.2.2. The length of ACL is a trade-off because
a longer ACL enables agents to act for a long time,
but agents also require a long charging time. In our
method, agent i selects s
i
c
from a set of possible ACLs,
S
i
c
= {s
c1
,s
c2
,...}, where max
s∈S
i
c
(s) = B
i
max
. For
simplicity, s ∈ S
i
c
is a divisor of B
i
max
.
The process of learning the appropriate ACL con-
sists of two learning subprocesses. The purpose of the
first subprocess is to decide the initial Q-values for
all possible ACLs in S
i
c
because the initial Q-values
offset the performance of Q-learning and, in general,
their appropriate values are dependent on the environ-
ment. In this subprocess, agents calculate the average
number of detected events per one tick while active
as follows. First, i selects an ACL from S
i
c
at random
and starts patrol. Then, when i returns to the base to
charge, it calculates e
i
1
by using
e
i
1
= E
i
1
/t
i
travel1
, (10)
where E
i
1
is the number of detected events in the first
round and t
i
travel1
is time length when agent i move in
the first round.
Agents repeat this subprocess and they randomly
selects an ACL in each rounds. We also denote E
i
k
and e
i
k
as the number of detected events and the aver-
age of the detected events per tick in the k-th round.
Agent i continues this process for the initial T
init
ticks,
where T
init
is a positive integer. Then, at the end of the
first subprocess, i calculates e
i
, which is the average
of the values of e
i
1
,e
i
2
,... obtained by Formula (10)
during the first subprocess. The e
i
will be set to the
initial Q-value of s
c
, Q
i
(s
c
)(∀s
c
∈ S
i
c
), in the second
subprocess.
If agent i finds that the current time t is larger than
T
init
, it enters the second learning subprocess. Before
i starts to patrol from its charging base, i decides s
c
with probability 1 − ε as
s
c
← argmax
s
0
c
∈S
c
Q
i
(s
0
c
); (11)
Otherwise, i randomly selects s
c
from S
c
. When there
is a tie break in Eq. 11, agents select one of the candi-
dates at random.
We assume that i will continuously use the se-
lected s
c
for several times without updating Q-value.
In the CCPP, it is better for agents to visit individ-
ual nodes, especially important nodes, in shorter in-
tervals when their battery levels are high. However,
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
66

Table 1: Parameters.
Model Parameter Value
PGS N
g
5
PI N
i
5
AMTDS/LD β 0.05
ε 0.05
AMTDS/LC γ 0.05
ε 0.05
T
init
100,000
when agents visit nodes so frequently, they may find
smaller number of events; therefore, the Q-values of
the short ACLs tend to be small, even if i visit the
important nodes where i must find events as many as
possible and keep the number of unaware events low.
This means that if agents update Q
i
(s
c
) every short
round, they cannot correctly evaluate the ACL. There-
fore, we introduce the parameter C
i
s
c
to make their ac-
tivity time identical regardless of the value of s
c
; this
achieves fair learning results. When agent i decides
its ACL with Formula (11), i calculates C
i
s
c
by
C
i
s
c
= B
i
max
/s
c
. (12)
After that, i selects the s
c
in C
i
s
c
rounds continuously
without updating Q-value.
After i finishes C
i
s
c
rounds patrol using the selected
s
c
, i updates Q
i
(s
c
);
Q
i
(s
c
) ← (1 − γ)Q
i
(s
c
) + γ
∑
k
0
k=k
0
−C
i
s
c
+1
E
i
k
C
i
s
c
, (13)
where k
0
indicates the number of the most recent
round. Note that the first learning subprocess is ded-
icated to calculating the initial Q-values and i never
updates Q
i
(s
c
). The calculation of initial Q-values is
mandatory for the fast convergence of Q-learning.
5 EXPERIMENTS AND
DISCUSSION
We evaluated our method in two experiments. First,
we investigated whether agents with our method learn
the appropriate ACL, by comparing the results of our
learning method with those of the AMTDS/LD with a
fixed ACL. Note that, in this experiment, all agents
had a charging base in the same location. In the
second experiment, we investigated the difference in
learned ACLs when the agents’ charging bases were
located at different locations. Therefore, they were
likely to be affected by the characteristics of the local
areas nearby the charging bases.
5.1 Experimental Setting
We constructed two simulated large environments,
called ”Office A” and ”Office B”, for agents to patrol
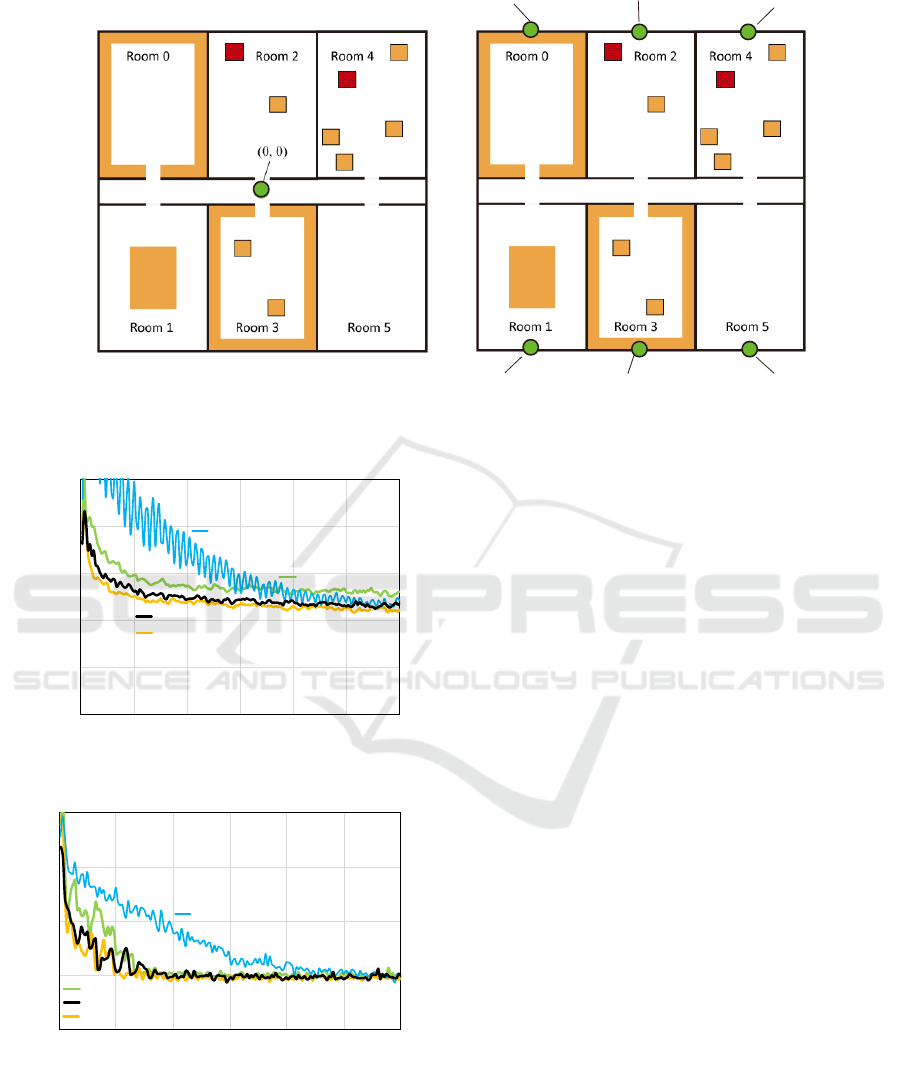
as shown in Fig. 1. These environments consisted of
six rooms (labeled Rooms 0-5), a corridor, and a num-
ber of nodes where events occurred frequently. We set
p(v) for v ∈ V as
p(v) =
10
−3
if v was in a red region,
10
−4
if v was in an orange region, and
10
−6
otherwise,
(14)
and the colored regions are shown in Fig. 1. The green
circles in these environments are charging bases. In
Office A, all agents had charging bases in the same lo-
cation. In Office B, we divided agents into six groups,
and the charging bases of each group were assigned to
one of six rooms differently. Each room had charging
bases in Office B, but agents had to return to their own
assigned charging bases. The environments are repre-
sented by a 101 × 101 2-dimensional grid graph with
several obstacles (walls). We set the length of edges
between nodes to one.
We deployed 20 agents in the environments. We
assumed that agents did not know p
i
(v) in advance,
so we initially set p
i
(v) as 0. Agents started their
patrols from the assigned v
i
base
and periodically re-
turned to v
i
base
to recharge before their batteries be-
came empty. We set the actual battery specifications
of all agents as (B
i
max
,B
i
drain
,k
i
charge
) = (2700,1,3)
and set S
c
to S
c
= {300,900,2700}. When agents
selected s
c
to be 2700, the patrol cycle length was
maximum (10,800 ticks), whose breakdown consists
of the active time (2700 ticks) and the charging time
(8100 ticks). Therefore, for the target decision strat-
egy s we measured D
t
s
,t
e
(s) and U
t
s
,t
e
(s) every 14,400
ticks, which was longer than the maximum cycle
length. In experiments below, we set AMTDS/LD or
AMTDS/CL to s. The parameter values used in the
model are listed in Table 1.
5.2 Comparison of Fixed Activity Cycle
In the first experiment, we compared the performance
results of four types of agents that used AMTDS/LD
with one of the fixed ACLs, s
c
= 300, 900, or 2700
with those by the agents with AMTDS/CL in Office A
as shown in Fig. 1(a). Hereinafter, AMTDS/LD with
fixed ACL s
c
is denoted as AMTDS/LD(s
c
). The ex-
perimental results shown below are the average values
of ten independent experimental runs. Figure 2 plots
the performance, D(s), and Fig. 3 plots the perfor-
mance of U (s) over time. Note that the smaller D(s)
Learning of Activity Cycle Length based on Battery Limitation in Multi-agent Continuous Cooperative Patrol Problems
67
(-34, -50) (0, -50) (34, -50)
(-34, 50)
(0, 50)
(34, 50)
(b) Office B(a) Office A
Figure 1: Environments.
Figure 2: Improvement in D(s) over time in Office A.
Figure 3: Improvement in U(s) over time in Office A.
and U(s) are better.
Both figures indicate that agents with
AMTDS/LD(900) were the most efficient, and
the agents with AMTDS/CL exhibited almost the
same efficiency as that with AMTDS/LD(900). The
efficiency of the agents with AMTDS/LD(2700) was
the worst and seemed unstable at first, but it gradually
improved over time. Because AMTDS/LD(2700)
requires quite a long time to recharge, the num-
ber of patrolling agents were unstably fluctuated.
However, the phases of their periodic cycles grad-
ually shifted naturally and finally disappeared. In
contrast, the converged performance of the agents
with AMTDS/LD(300) was always worse than the
others. This is because the ACL was too short to
cover the entire environment, especially areas distant
from the charging bases, and the agents in charge
of distant area had to return very frequently to the
charging bases. We can say that, in this particular
experimental environment, the ACL of 900 seemed
the best. However, this depends on the environmental
characteristics and we cannot decide the appropriate
ACL in advance. In comparison, the agents with the
proposed AMTDS/CL can adaptively select ACLs by
themselves without such a prior decision.
Figure 4 indicates the number of agents that se-
lected ∀s
c
∈ S
i
c
with AMTDS/CL over time. Note that
we plotted in this figure the values every 10,000 ticks
from 200,000 ticks; because agents started from de-
ciding the initial Q-values until 100,000 ticks and then
entered the learning of ACL from 100,000 ticks, the
learning results in the first 200,000 were unstable. We
can see from this figure that many agents selected 900
ticks for s
c
since AMTDS/LD(900) exhibited the best
performance in this environment and this was consis-
tent with the results when agents have the fixed ACL.
Additionally, we investigated the characteristics of
agents that selected 300 and 2700 as their ACL. Fig-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
68
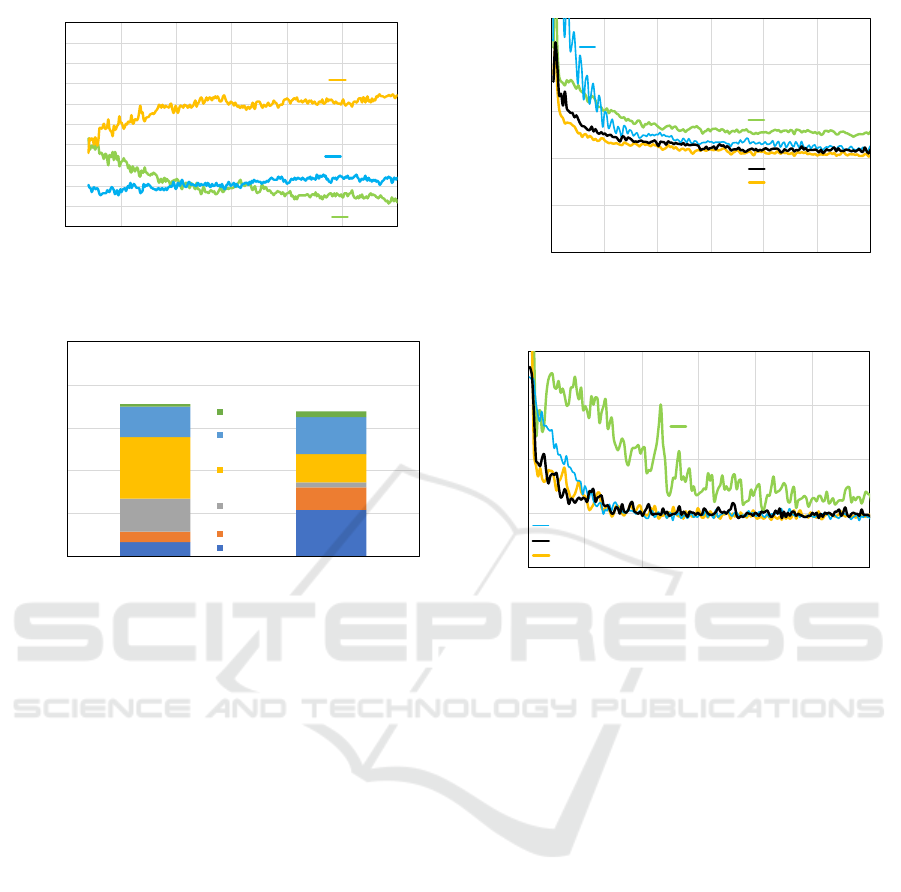
Figure 4: Number of agents selecting each s
c
over time in
Office A.
0
50000
100000
150000
200000
250000
1 (selected 300 for s
c) 7 (selected 2700 for sc)
working me in each room (cks)
Agent ID
Room 0
Room 1
Room 2
Room 3
Room 4
Room 5
Figure 5: Working time in each Room of agent 1 and agent
7 in last 1,000,000 ticks in Office A.
ure 5 shows the working time of agents whose IDs
were 1 and 7, i.e., how long they spent in each room
during the last 1,000,000 ticks. Note that Agent 1 se-
lected 300 and Agent 7 selected 2700 for their ACLs
at last, though 900 was usually the best as the ACL
in the environment. We also note that the data shown
in Fig. 5 is one result selected from the experimen-
tal trials, but we found that a similar tendency could
be observed in other trials. Agent 1 more often pa-
trolled Room 2 and Room 3 than Agent 7. Room 2
and Room 3 were near the charging base, Room 2 had
specific regions in which events frequently occurred,
and many nodes in Room 3 also had a higher p
i
(v).
Therefore, Agent 1 could find many events in Room 2
and Room 3; thus, patrolling with a short ACL was
better from the viewpoint of Agent 1 to keep the num-
ber of unaware events low.
Meanwhile, Agent 7 frequently patrolled many
rooms, some of which were distant from the charg-
ing base. We confirmed that, unlike Agent 1, Agent 7
had a high value of p
i
(v) in more and farther nodes,
so Agent 7 selected a long ACL to move around in a
large area. This analysis indicates that, from a global
viewpoint, agents with a short s
c
and long s
c
com-
plementarity covered different areas. That is because
some agents with AMTDS/CL did not select 900 for
Figure 6: Improvement in D(s) over time in Office B.
Figure 7: Improvement in U(s) over time in Office B.
s
c
and deterioration of efficiency was not occurred, al-
though AMTDS/LD(900) was best efficiency. These
results showed that agents with our method learned
the appropriate ACL s
c
without prior knowledge on
the environments, and actually, agents decided ACLs
on the basis of their learned p
i
(v) and working area.
We believe that such diversity in agent strategies also
enhances the response capabilities to environmental
changes as well as the improvement in the efficiency.
5.3 Adaptation to Environmental
Characteristics
In the second experiment, we also evaluated the four
types of agents in a slightly different environment
where there were six charging bases for each room,
named ”Office B”, as shown in Fig. 1(b). A charg-
ing base in Room n is denoted by v
base-n
. We set
Agents 0, 1, 2, and 3 to v
base-0
, Agents 4, 5, and 6
to v
base-1
, Agents 7, 8, and 9 to v
base-2
, Agents 10, 11,
12, and 13 to v
base-3
, Agents 14, 15, and 16 to v
base-4
,
and Agents 17, 18, and 19 to v
base-5
. The improve-
ment D(s) is plotted in Fig. 6, and U(s) over time in
Office B is plotted in Fig. 7.
We can confirm that the efficiency of AMTDS/CL
and AMTDS/LD(900) was almost identical from
Learning of Activity Cycle Length based on Battery Limitation in Multi-agent Continuous Cooperative Patrol Problems
69
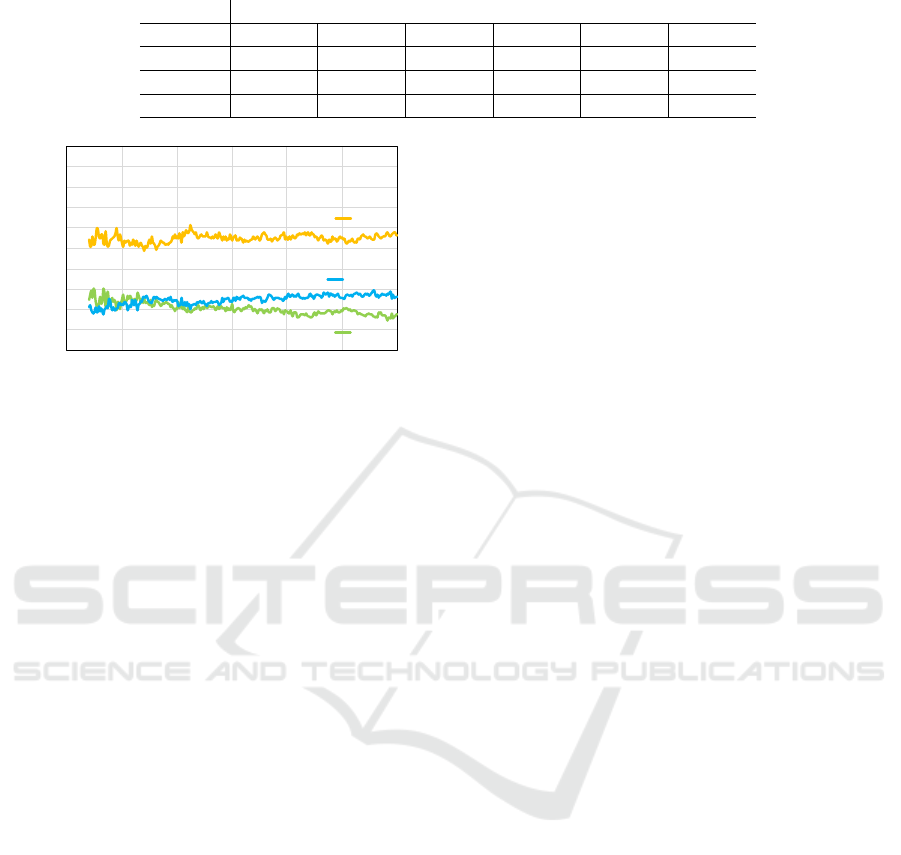
Table 2: Number of agents selecting each s
c
described by their charging bases at 3,000,000 tick in Office B.
Location of charging base
Room 0 Room 1 Room 2 Room 3 Room 4 Room 5
s
c
=300 1.2 0.3 0.2 1.7 0.0 0.0
s
c
=900 2.1 1.7 2.3 2.2 2.1 1.0
s
c
=2700 0.7 1.0 0.5 0.1 0.9 2.0
Figure 8: Number of agents selecting each s
c
over time in
Office B.
these figures. If we carefully compare Fig. 6 with
Fig. 2, the converged performances of all methods
were almost identical in both performances. How-
ever, the convergence of the AMTDS/LD(2700) in
Fig. 6 seemed faster, and the performance also
seemed stabler than those of AMTDS/LD(2700) in
Fig. 2. In Office B, the charging bases were dis-
tributed, so the patrol patterns of individual agents
differed even if agents had the same length of ACL.
Figure 7 indicates that agents with AMTDS/LD(300)
were the worst, which differed from the results of
the first experiment (see Fig. 3). This indicates that
the performance, U(s), also depended on the distance
between the charging bases and the work locations.
In the second experiment, the areas individual agents
visited were distinct, so nodes were covered by a
smaller number of agents than in Office A.
The number of agents that selected each s
c
for
AMTDS/CL as shown in Fig. 8, was similar charac-
teristic to Fig. 4. In this experiment, we were inter-
ested in the differences in ACL learned on the basis of
the locations of agents’ charging bases. Table 2 lists
the average number of agents that selected s
c
∈ S
i
c
for
AMTDS/CL for each charging base location. This ta-
ble shows that 900 was mainly selected as the value of
s
c
by many agents, but we can observe different char-
acteristics according to agents’ base locations. We
already knew that 900 was appropriate for this en-
vironment; thereby, we focused on and analyzed the
agents that selected other ACLs. Agents whose charg-
ing base was in Room 5 obviously learned that the
long ACLs were better. Because they could find only
a few events near their base (Room 5 did not have
a node with a high p(v)), they had to explore nodes
farther away to help other agents. Relatively more
agents whose bases were in Rooms 0 and 3 selected
300 as their ACL. In these rooms, there were many
nodes with a high p(v) as shown in Fig. 1. Thus,
these agents could find many events near their bases.
By selecting the shorter ACLs, they could reduce the
cost of moving to other rooms and focused on specific
nodes in the local rooms. In addition, they could visit
nearby nodes at an appropriate and shorter frequency
by improving the accuracy of the estimated p
i
(v) for
the specific nodes.
When we carefully observed the experimental
runs, we found that agents whose base was in Room 5
selected 900 as their ACL at first, but after that, they
gradually changed to 2700. We can explain this
change as follows. At first, they selected 900 since
it seemed more appropriate than others. However, af-
ter other agents whose bases were in other rooms fo-
cused on nodes near their base and improved their pa-
trol performance. In contrast, there were no nodes
with high importance values p
i
(v) in Room 5, and
agents whose base was Room 5 had to visit more of
the other rooms to find events. This suggests indi-
rect communication through learning the importance
value. Therefore, agents could perform well by learn-
ing the ACLs to improve the entire system perfor-
mance in a real-time manner, and this learning of the
length was thanks to the results of the learning of im-
portance p
i
(v).
6 CONCLUSION
We proposed an autonomous method for learning
the activity cycle length, which is how long indi-
vidual agents act to work in collaborative environ-
ments. This method reflects the activities of other
collaborative agents, which are also learning mutu-
ally to contribute to the entire performance. We ex-
perimentally showed that agents with our method,
AMTDS/CL, performed effectively comparable with
the same efficiency as the best case with a fixed ACL,
without giving any prior knowledge on the best ACL
and the environmental characteristics in advance. We
also analyzed the relationships between the selected
ACL and agents’ behaviors. Nodes were covered
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
70

with a number of agents with different frequencies,
phases, and periods; this resulted in effective cover-
ing of the environment only through lightweight com-
munication with others. We also proposed a strategy
in which agents select the appropriate activity cycle
length from among fixed possible activity cycles be-
cause we think that agents have to consider complex-
ity to estimate the environmental workload.
Our future work is to find an activity control strat-
egy in which agents estimate a workload with high
accuracy and flexibility to control their activity while
taking into account their remaining energy.
ACKNOWLEDGMENT
This work was partly supported by JSPS KAKENHI
Grant Number 17KT0044 and Grant-in-Aid for JSPS
Research Fellow (JP16J11980).
REFERENCES
Ahmadi, M. and Stone, P. (2006). A multi-robot system for
continuous area sweeping tasks. In Proceedings of the
2006 IEEE International Conference on Robotics and
Automation, pages 1724 – 1729.
Bentz, W. and Panagou, D. (2016). An energy-aware re-
distribution method for multi-agent dynamic coverage
networks. In 2016 IEEE 55th Conference on Decision
and Control (CDC), pages 2644–2651.
Chen, X. and Yum, T. P. (2010). Patrol districting and rout-
ing with security level functions. In 2010 IEEE Inter-
national Conference on Systems, Man and Cybernet-
ics, pages 3555–3562.
Chevaleyre, Y. (2005). Theoretical analysis of the multi-
agent patrolling problem. In Proceedings of Intelligent
Agent Technology, pages 302–308.
David, P. and Rui, R. (2011). A survey on multi-robot pa-
trolling algorithms. In Camarinha-Matos, L. M., edi-
tor, Technological Innovation for Sustainability: Sec-
ond IFIP WG 5.5/SOCOLNET Doctoral Conference
on Computing, Electrical and Industrial Systems, Do-
CEIS 2011, Costa de Caparica, Portugal, February
21-23, 2011. Proceedings, pages 139–146. Springer
Berlin Heidelberg.
Jensen, E., Franklin, M., Lahr, S., and Gini, M. (2011).
Sustainable multi-robot patrol of an open polyline. In
2011 IEEE International Conference on Robotics and
Automation, pages 4792–4797.
Machado, A., Ramalho, G., Zucker, J.-D., and Drogoul, A.
(2003). Multi-agent patrolling: An empirical analy-
sis of alternative architectures. In Sim
˜
ao Sichman, J.,
Bousquet, F., and Davidsson, P., editors, Multi-Agent-
Based Simulation II, pages 155–170, Berlin, Heidel-
berg. Springer Berlin Heidelberg.
Pasqualetti, F., Durham, J. W., and Bullo, F. (2012). Co-
operative patrolling via weighted tours: Performance
analysis and distributed algorithms. IEEE Transac-
tions on Robotics, 28(5):1181–1188.
Popescu, M. I., Rivano, H., and Simonin, O. (2016). Multi-
robot patrolling in wireless sensor networks using
bounded cycle coverage. In 2016 IEEE 28th Interna-
tional Conference on Tools with Artificial Intelligence
(ICTAI), pages 169–176.
Santana, H., Ramalho, G., Corruble, V., and Ratitch, B.
(2004). Multi-agent patrolling with reinforcement
learning. In Proceedings of the Third International
Joint Conference on Autonomous Agents and Multia-
gent Systems - Volume 3, AAMAS ’04, pages 1122–
1129, Washington, DC, USA. IEEE Computer Soci-
ety.
Sipahioglu, A., Kirlik, G., Parlaktuna, O., and Yazici, A.
(2010). Energy constrained multi-robot sensor-based
coverage path planning using capacitated arc routing
approach. Robot. Auton. Syst., 58(5):529–538.
Sugiyama, A., Sea, V., and Sugawara, T. (2016). Effective
task allocation by enhancing divisional cooperation in
multi-agent continuous patrolling tasks. In 2016 IEEE
28th International Conference on Tools with Artificial
Intelligence (ICTAI), pages 33–40.
Sugiyama, A. and Sugawara, T. (2017). Improvement of
robustness to environmental changes by autonomous
divisional cooperation in multi-agent cooperative pa-
trol problem. In Demazeau, Y., Davidsson, P., Bajo,
J., and Vale, Z., editors, Advances in Practical Appli-
cations of Cyber-Physical Multi-Agent Systems: The
PAAMS Collection, pages 259–271, Cham. Springer
International Publishing.
Yoneda, K., Kato, C., and Sugawara, T. (2013). Au-
tonomous learning of target decision strategies
without communications for continuous coordinated
cleaning tasks. In Web Intelligence (WI) and Intelli-
gent Agent Technologies (IAT), 2013 IEEE/WIC/ACM
International Joint Conferences on, volume 2, pages
216–223.
Learning of Activity Cycle Length based on Battery Limitation in Multi-agent Continuous Cooperative Patrol Problems
71
