Collaborative Learning of Human and Computer: Supervised
Actor-Critic based Collaboration Scheme
Ashwin Devanga
1
and Koichiro Yamauchi
2
1
Indian Institute of Technology Guwahati, Guwahati, India
2
Centre of Engineering, Chubu University, Kasugai-shi, Aichi, Japan
Keywords:
Actor-Critic Model, Kernel Machine, Learning on a Budget, Super Neural Network, Colbagging, Supervised
Learning, Reinforcement Learning, Collaborative Learning Scheme between Human and Learning Machine.
Abstract:
Recent large-scale neural networks show a high performance to complex recognition tasks but to get such
ability, it needs a huge number of learning samples and iterations to optimize it’s internal parameters. However,
under unknown environments, learning samples do not exist. In this paper, we aim to overcome this problem
and help improve the learning capability of the system by sharing data between multiple systems. To accelerate
the optimization speed, the novel system forms a collaboration with human and reinforcement learning neural
network and for data sharing between systems to develop a super neural network.
1 INTRODUCTION
During recent years, high performance computers ,
which we could never have imagined before, have
been developed. Recent large scale neural networks
and its machine learning methods rely on this compu-
tational ability.
One drawback of the machine learning methods
for neural networks is that they require a huge num-
ber of learning samples, which is usually more than
the number of internal parameters used in the learn-
ing machine. If the problem domain is unknown new
field, we cannot collect such large number of samples
in advance. Moreover, the learning method to opti-
mize these parameters usually needs a large number
of repeats to reach the optimal parameter values. One
solution to solve this problem is using the reinforce-
ment learning. However, the reinforcement learning
also wastes huge number of try-and-error testing to
get appropriate action (or label) for each situation.
Another possibility to solve this problem is us-
ing the crowd sourcing. In the crowd sourcing,
many workers in the cyberspace collaborate to solve
such open problems and yield many solution candi-
dates(e.g. (Konwar et al., 2015)). Although the crowd
sourcing techniques are able to collect many number
of solution candidates, the architecture is not designed
to get the best function for solving the problems. We
have developed a solution to this problem. In the sys-
tem, there is an online learning machine beside of
each worker (Ogiso et al., 2016). The learning ma-
chine learns corresponding worker actions to imitate
them. The learning machine’s outputs are integrated
by calculating weighted sum. The weights are deter-
mined by means of performances of workers. By us-
ing such architecture, we can extract the function of
each worker by using the online learning machines.
Note that even if each worker is absent, the learning
machine substitute the absent workers. Moreover, the
integrated solution is fed back to each worker to make
them generate better solution. By using this mecha-
nism, workers grow smarter.
The literature (Fern
`
andez Anta et al., 2015)
presents a thorough review of the research related
to this field and a mathematical analysis of mod-
ern crowd-sourcing methods. Similar to our ap-
proach, crowd-sourcing methods try to construct a ro-
bust protocol to tackle incorrect solution candidates.
The classical models answer the majority of the so-
lution candidates to realize robustness (ANTA and
LUIS LOPEZ, 2010) (Konwar et al., 2015). Al-
though these approaches are similar to ours, these
systems do not provide feedback about the integrated
solution to each worker. On the other hand, crowd-
sourcing systems based on the game theoretic ap-
proach partially provide feedback about the output of
some of the workers together with their inputs to each
crowd worker (Golle and Mironov, 2001) (Forges,
1986). These approaches provide feedback regarding
the situation of each worker and the evaluation results,
794
Devanga, A. and Yamauchi, K.
Collaborative Learning of Human and Computer: Supervised Actor-Critic based Collaboration Scheme.
DOI: 10.5220/0007568407940801
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 794-801
ISBN: 978-989-758-351-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

which is a reward, to each worker. These approaches
are similar to our new proposed method that improves
its ability by using a reinforcement learning manner.
However, these models do not provide feedback about
the integrated solution to each worker. In contrast, our
proposed new model provides feedback as to the in-
tegrated output to each worker to guide how to revise
his/her answer.
This study improves the previous study (Ogiso
et al., 2016) by replacing each learning machine
with a supervised actor-critic method (Rosenstein and
Barto, 2012). This means that each learning machine
also has the ability to explore new solutions by itself
without the help of each worker.
By using this architecture, each worker do not
need to manage the system full time because the
new model realizes semi-automatic learning. In other
words, the new method also explores better solutions
without our operations.
The learning machine suitable in this situation is a
light weight method. We found that supervised actor-
critic model using kernel method for learning is a
very light weight learning machine which can handle
one pass learning. Using this algorithm with kernel
method makes the calculations simpler for a computer
to calculate thus increasing efficiency.
Supervised Actor-Critic Model is a state of the art
algorithm which runs very light for a reinforcement
learning machine. Reinforcement Learning meth-
ods are often applied to problems involving sequen-
tial dynamics and optimization of a scalar perfor-
mance objective, with online exploration of the ef-
fects of actions. Supervised learning methods, on
the other hand, are frequently used for problems in-
volving static input-output mappings and minimiza-
tion of a vector error signal, with no explicit depen-
dence on how training examples are gathered. The
key feature distinguishing Reinforcement Learning
and supervised learning is whether training informa-
tion from the environment serves as an evaluation sig-
nal or as an error signal. In this model, both kinds of
feedback are available.
Since application of this environment for real
world problems would take huge amount of time it
was tested on a T-Rex game similar to http://www.
trex-game.skipser.com/ which was developed specifi-
cally for this project.
In the developed game, the height and width of a
part of cactus were modified to make the game player
cannot solve them easily without help. Moreover, one
another jumping option was added. But these spec-
ifications were not announced to the players before-
hand. The simulations are explained in section 4.
2 COLLABORATIVE BAGGING
SYSTEM USING SUPERVISED
ACTOR CRITIC MODEL
Bagging is an old concept of creating a super neural
network combining the intelligence of multiple neu-
ral networks working on the same problem but differ-
ent learning and testing scenarios. The idea was that
this could save a lot of computational power and time
and could also run on simpler hardware such as smart
phones or raspberry-pis.
A rough sketch of the ColBagging system is il-
lustrated in Fig 1. The system repeats two phases
alternately. The first phase is the training phase,
where each worker tries to solve a problem to be
solved. Their solutions are emitted by the correspond-
ing online incremental learning machine (MGRNN
(Tomandl and Schober, 2001)). At the same time, the
performance estimator monitors the solutions from all
workers and estimates their quality. This estimation
is usually done by the masters or by a pre-determined
evaluation function. The performance estimator out-
puts the results as the weights for the all workers.
This idea was proposed in (Ogiso et al., 2016). It
is an improved version of the bagging techniques used
before but rather a sophisticated method which calcu-
lates weighted averages of the weights of the input
neural networks which results in more accurate super
neural networks.
In this study, the previous system was improved
by introducing one variation of the reinforcement
learning method: supervised-actor critic for the learn-
ing machine (see Fig 2). By introducing super-
vised actor-critic method, the solution candidate of
each worker will be refined automatically by the ex-
ploration done by the reinforcement learning. This
means that each worker just need to help the learn-
ing machine by teaching action partly. It will not only
reduce the work of each worker but also improve the
learning speed of each learning machine.
To explain the scheme, the next section explains
the supervised actor-critic method used in this system.
3 SUPERVISED ACTOR CRITIC
MODEL
Supervised Actor Critic Model (Rosenstein and
Barto, 2012) is a variation of reinforcement learning
algorithm that introduces human input as the super-
vised signal. It is well known that the reinforcement
learning algorithm can be executed effectively by in-
troducing kernel machines, which add new kernels by
Collaborative Learning of Human and Computer: Supervised Actor-Critic based Collaboration Scheme
795

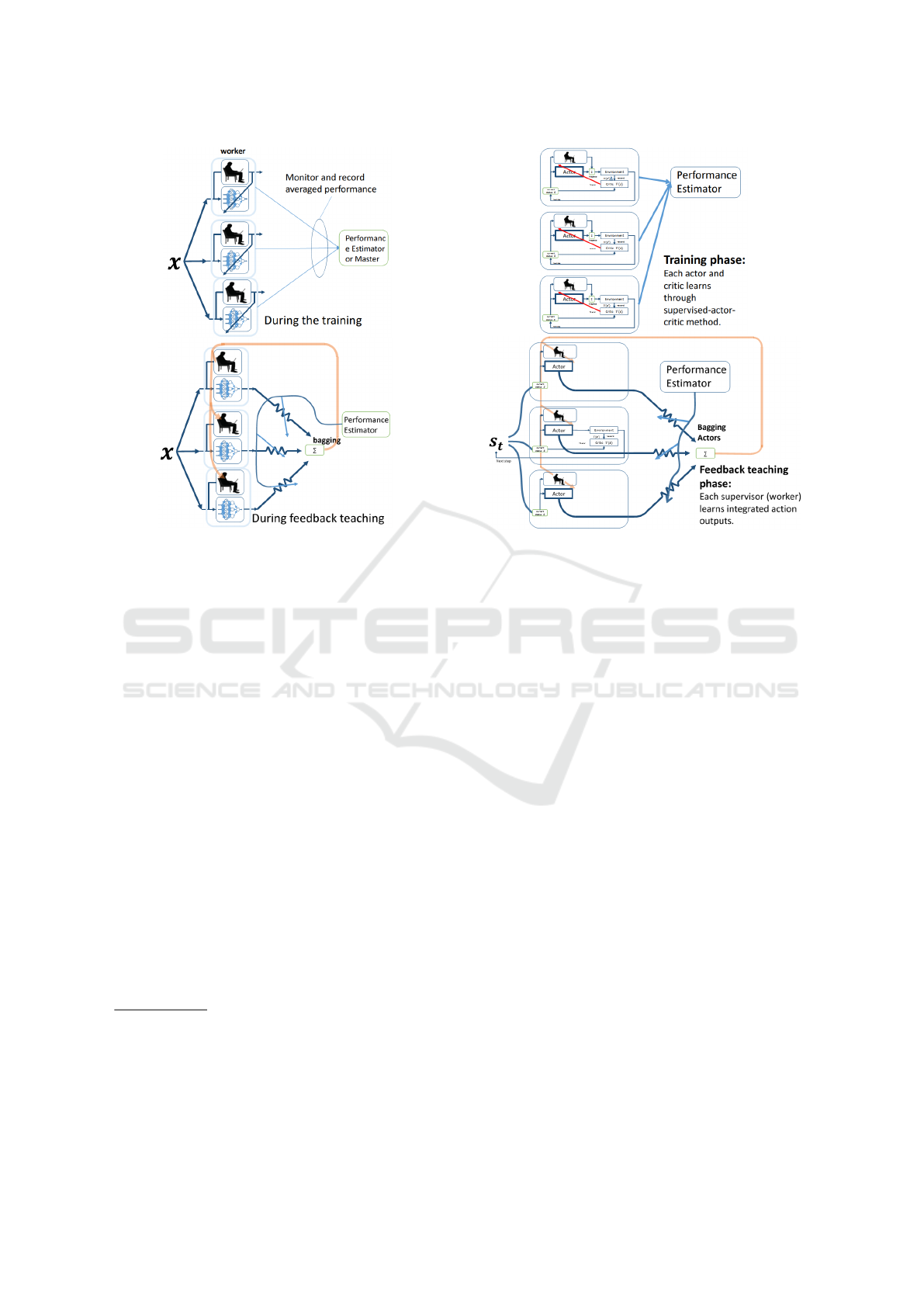
Figure 1: Collaborative Bagging system: The system re-
peats the training and feedback teaching phases alternately.
After the repeats of them several times, the reasoning is
done by integrating outputs from the learning machines.
itself (Xu et al., 2007)
1
.
We found that when this model is coupled with
Kernel Regression Neural Networks, we get a very
efficient learning machine. The supervised nature of
the algorithm handles human input and learns from
it. This reduces learning time as human input is more
filtered than raw data usually used by other reinforce-
ment learning algorithms. The algorithm also uses
two Neural Networks, one in Actor and one in Critic.
There is an evaluation of results calculated by the ac-
tor by the critic. Also since the learning works on
the reward system, we get more specific learning. In
other words we get a weighted learning system. The
added advantage is that there is more data which can
be provided to the supervisor for making a choice.
Data from both Actor and Critic Neural Network can
be supplied to the the user before he makes a call.
3.1 Calculation of TD Error
Referring to Figure 1 and Figure 2, we can under-
stand the entire model. Environment in this case is
1
We do not use the approximated linear dependency
based projection method for the kernel manipulation. In-
stead, the proposed system simply employs the least re-
cently and frequently used estimator for pruning with re-
placement of kernels as described later. This is for restrict-
ing the number of kernels to reduce the computational com-
plexity.
Figure 2: Improved collaborative Bagging system: The pre-
vious system was improved by replacing the MGRNN with
the supervised actor-critic model.
the T-Rex game in the test case scenario. The state
variables of the game are supplied to the actor model
and the critic model calculates TD error also known
as Temporal-Difference error. Refer to the following
equation:
δ = r + γ V (s
0
) −V(s) (1)
This equation is the definition of TD error. The
reward from the action is given by ’r’ and ’γ ∈ [0, 1]’
is a constant value. The function V (x) is a value func-
tion which takes in the state variables as input. In the
equation, ’δ’ is the current TD error and ’s’ and ’s
0
’ are the current state variables and the future state
variables respectively.
3.2 Actor Neural Network
The actor neural network has an output of values only
between 0 and 1. This is because the actor is supposed
to play the role of the supervisor and the supervisor
has to output only whether the T-Rex should jump or
not. The ground state is set as 0. The jump state is set
as 1. The value output by the Actor is the probability
of jump requirement at that position. The input of
the neural network is the current state variables, along
with the current jump state. The current jump state is
used to train the neural net.
The actor uses a kernel perceptron based network.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
796

Algorithm 1: Supervised Actor-Critic.
Require:
{critic value function} V (s),
{Actor policy} π
A
(s),
{Exploration size} σ,
{actor step size} α,
{critic step size} β,
{discount factor} γ ∈ [0,1],
{eligibility trace decay factor,} λ
{Ratio of supervised signal,} k ∈ {1,0}
Initialize θ, w arbitrarily
for all trials do
e = 0 (clear the eligibility trace)
s ← initialState
repeat
a
A
= π
a
(s)
a
E
= a
A
+ n, where n ∼ N (0, σ
2
)
a = ka
E
+(1 −k)a
A
, where k is determined by
the supervisor
TAKE action a, observe reward, r , and next
state s
0
.
δ = r + γV (s
0
) −V (s)
Modify Actor parameters by Algorithm 2.
Modify Critic parameters by Algorithm 3.
s = s
0
until s is terminal
end for
Therefore, the output from the actor π
a
(s) is
π
a
(s) = f


∑
j∈S
A
t−1
w
a
j
k(s, u
j
)


, (2)
where S
A
t
denotes the set of actor kernels after time
t − 1 and k(s,u
j
) denotes a Gaussian kernel function:
k(s, u
j
) ≡ exp

−
ks − u
j
k
2
2σ
2

(3)
Since the output is just a value between 0 to 1 in
(2), we use the sigmoid function: f [·] ≡ 1/(1 + e
−x
).
Actor outputs a
E
is then calculated as follows:
a
E
= π
A
(s) + n, (4)
where n denotes the normal random value n ∼
N (0,σ
2
). However, if the supervisor yield gives the
action a
S
, the actor integrates them as follows:
a
A
= ka
S
+ (1 − k)a
E
, (5)
where k denotes the ratio of introducing the super-
vised signal a
S
and we set k ∈ {0,1}. Therefore, the
parameter k is occasionally switched 1 and 0 by the
game player and the mode is changed. The final ac-
tion is a
A
.
During the learning, if there is no activated ker-
nel, the actor allocates a new kernel. Therefore, if
k(s, u
j
) < ε for all j ∈ S
A
t
, the actor allocates a new
kernel k (·, u
|S
A
t−1
|+1
), where u
|S
A
t−1
|+1
= s. Note that
the set of kernels is updated as S
A
t
= S
A
t−1
∪ {t}.
However, if such allocation process is continued
for ever, the computational complexity is also in-
creased endlessly. Under such situation, the Game
system described later slow downed and it is hard to
proceed the game. To overcome this difficulty, the ac-
tor restricts the size of the actor network. To this end,
if |S
A
t−1
| reaches an upper bound, the actor replaces
the most ineffective kernel with the new kernel.
Algorithm 2: Actor learning.
Require:
{Current Status}, s
{TDerror}, δ
t
(1).
{Set of Kernels(support set)}, S
A
t−1
{Distance threshold}, min
d
{parameter vector of π
A
(s)}, w
A
{parameter for LRFU estimation}, C
j
where j ∈
S
t−1
i
∗
= argmin
j
ks − u
j
k
2
.
MinDistance = ks − u
i
∗
k
2
Update C
j
for all j ∈ S
A
t−1
by (6).
if |S
A
t−1
| < B and MinDistance ≥ min
d
then
S
A
t
= S
A
t−1
∪ {t}, where u
|S
t
|
= s
w
a
|S
t
|
= f
−1
[a
A
]
else
if MinDistance ≥ min
d
then
j
∗
= argminC
j
{ j
∗
: Most Ineffective Ker-
nel}
u
j
∗
= s, w
A
j
∗
= f
−1
[a
A
]
else
Update w
a
by using (see (8))
end if
end if
t = t + 1.
Note that the most ineffective kernel is deter-
mined by using a least recently and frequently used
(LRFU) estimator(Lee et al., 2001), which is a page-
replacement algorithm of the virtual memory in oper-
ating systems. For the LRFU estimator, each Gaus-
sian kernel has an additional parameter C
j
, whose ini-
tial value is 1. C
j
is updated at each learning step as
follows. Therefore,
C
j
=

C
j
+ 1 j = argmin
k
ks − u
k
k
2
(1 − ε)C
j
otherwise
(6)
Then, the most ineffective kernel is determined as
j
∗
= argminC
j
(7)
Collaborative Learning of Human and Computer: Supervised Actor-Critic based Collaboration Scheme
797

Otherwise, the actor modifies existing parameter
w
A
by (8). The summarized actor learning is shown
in Algorithm 2.
w
a
= w
a
+α

kδ(a
E
− a
A
) + (1 − k)(a
S
− a
A
)

∇
w
a
π
A
(s)
(8)
3.3 Critic Neural Network
As mentioned in section 3.1, to calculate TD error i.e
’δ’ we need to calculate V (x). This value function
is being calculated by the critic neural network. It
can output a range of values so there is no need of
a sigmoid function. We sill directly use the kernel
function to calculate the value function.
Therefore, the output from the critic V (s) is
V (s) ≡
B
∑
j∈S
C
t−1
w
c
j
k(s, u
j
) (9)
The critic network also learns its output so as to
reduce the TD error. If current status s is far from the
closest kernel center of the critic, the critic allocates a
new kernel, whose parameter is w
C
|S
C
t
|
= δ. However,
if current status is closed to the nearest kernel center
of the critic, the critic modifies its parameter by the
gradient descent method. Therefore,
w
C
= w
C
+ αδ∇
w
C
V (s), (10)
where δ is calculated by (1).
Note that in the case of critic, the size of kernel set
(support set) S
C
t
is not restricted, because |S
C
t
| does not
become so large.
The summarized critic learning algorithm is
shown in Algorithm 3.
Algorithm 3: Critic learning.
Require:
{Current status}, s,
{Next status}, s
0
,
{Current Action}, a,
{TD error}, δ,
j
∗
= argmin
j∈S
C
t−1
ks − u
c
j
k
2
minDistance = kX − u
c
j
∗
k
2
if minDistance ≥ ε then
S
C
t
= S
C
t−1
∪ {t}
w
C
|S
C
t
|
= δ.
else
Update w
C
by (10).
end if
3.4 Weight Detection for ColBagging
The training of all supervised actor-critic modules are
repeated for several training sessions. Each training
session consists of several trials. Each training ses-
sion is continued until the number of trials reaches
a maximum number. After each training session, a
weighted majority of all actors is calculated and the
integrated actor output is evaluated.
The weight w
a
for the a-th actor is detected by
w
a
=
exp(γ
ˆ
S
a
)
∑
i
exp(γ
ˆ
S
i
)
, (11)
where
ˆ
S
a
denotes the score of the a-th actor of the last
training session. γ > 1 is a coefficient to determine the
sensitivity to the score. The final integrated output is
O
integrat ed
=
∑
a
w
a
π
a
(s) + n, (12)
where n denotes a noise and n ∼ N (0,σ). This noise
is added to make a condition the same as the actor-
critic learning during k = 0 in (5). In the experiment,
the score was determined by the maximum number of
cactus, which the Dino jumped over successfully. In
many cases, w
a
is nearly 1 when the a-th agent shows
the highest score, otherwise w
a
is closed to 0.
4 SIMULATIONS
The application of this learning machine is for elec-
trical bidding but for simulation purposes we had to
choose an environment where there were fast changes
and quicker data input from the environment. For this
purpose we chose the T-Rex game also known as Dino
game. It is a small, well known game found in the
Google chrome browser. We built a simpler version
of this game and used it as an environment for the
testing of our learning machine.
The entire learning machine and environment was
simulated on JAVA platform. We used Eclipse as the
IDE for development. All testing has been conducted
on Windows 10 and Ubuntu 16.04.3.
4.1 Game Environment
The learning machine was built interlinked with the
environment to handle data transfer between the two
easily. Data being transferred between the environ-
ment involved just the state variables and reward. The
game is very simple. There are just three type of cac-
tus which we must try to avoid by jumping. The speed
of the character is also exponentially increased with
the following equation:
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
798

speed = (1 + α) speed (13)
Where α is a constant which is a positive num-
ber but very small and in the order of 10
−4
which
keeps the game in a playable situation. If the value is
increased the character ends up accelerating too fast
which makes it impossible to play.
The initial speed has to be set to a certain value.
We chose this value to be 4 as it seemed to be the
most practical value for the start of the game. Also
the maximum speed of the game was set at 450 as it is
practically impossible to play the game at such a high
speed. All speeds referred to till now is the speed in
the ’X’ direction. We also have to maintain the speed
in the ’Y’ direction. This aspect of the game comes
in during jumping. There was gravity implemented
into the game as well. To increase the difficulty of the
game, we also modified a part of cactus sizes. There-
fore, the height of a part of cactus was prolonged to be
about two times higher than that of original one. Sim-
ilarly, the width of a part of cactus was also prolonged
as well.
4.2 Learning Machine
The theoretical working of the learning machine was
explained in section 3. We implemented the learning
module as a thread together with the other Game en-
vironment threads. Because we needed to run both
the learning machine and game at the same time and
for this purpose we used threads. We had two major
threads, one for the neural network and the other for
the game.
4.3 Approximated Behavior of the
Proposed System
The structure of the proposed system is similar to
the structure of the particle swarm optimization (Ven-
ter and Sobieszczanski-Sobieski, 2003). That is, if
the knowledge of the learning device of ColBagging
corresponds to the position of the particle, it can be
considered that the behavior of each particle in the
PSO corresponds to the transition of the knowledge
acquired by the learning device of Colbagging. For
this reason, first, we approximately simulate how the
knowledge of the learner changes, using PSO. Us-
ing the PSO, we can visualize the whole status of the
learning machines easily.
The PSO has an objective function to be maxi-
mized and the particle aims to move toward the posi-
tion where the objective function is maximized. Nor-
mally, each particle moves randomly, but close to its
personal best and the global best solutions. In the Col-
Bagging, each worker revises the corresponding par-
ticles moving course, according to the workers prior
knowledge. We assume that the worker can only rec-
ognize the gradient of current position and knows how
to move from the position according to the gradient
information.
Let v
i
(t) and P
i
(t) be the velocity and position
vectors of the i-th particle at time t, respectively.
These two vectors are updated at each step as follows:
P
i
(t) = P
i
(t − 1) + v
i
(t − 1). (14)
v
i
(t) = v
i
(t − 1) + c
1
r
1
(P
pbest
(i,t) − P
i
(t))
+ γc
2
r
2
(P
gbest
(t) − P
i
(t)) + γS
i
(t), (15)
where P
pbest
(i,t), P
gbest
(t) and S
i
(t) are the i-the par-
ticle’s personal-best, the global-best positions and the
supervised signal respectively. c
1
, c
2
and γ are the
fixed positive coefficients. r
1
, r
2
are the importance
weights, whose values are valid randomly at every
time step. Now, let O(position) be the objective func-
tion of this PSO. Then, the global best particle is
gbest = argmax
j
O(P
i
(t)). (16)
The supervised vector is
S
i
(t) = ∇
s
O(s)
|
s=position
i
(t)
o(s). (17)
We conducted the experiments using this PSO by
using following two objective functions. These two
functions are defined on a two dimensional space x =
[x
1
x
2
]
T
O
1
(X) =
sin(kXk)
kXk
(18)
O
2
(X) = kXk + 3 cos(kXk) + 5 (19)
In each objective function, the experiments was
done by changing the size of particles:10 and 500. In
each experiments, the parameter γ was also valid as
0.1, 0.5 and 1. Note that γ > 0 means that the PSO
is assisted by the supervised signal generated from
the gradient signals. The performances were com-
pared with that of the original PSO, where γ = 0. The
performance were measured by the averaged number
of particles reached to the optimal point over five tri-
als. In the cases of using (18), the number of reached
particles are the number of particles whose value of
the objective function is larger than 0.9. On the other
hand, in the cases of using (19) , the performance is
the averaged number of particles whose value of (19)
is less than 8. The results are shown in Figures (5)
and (6). From these figure, we can see that, in al-
most all cases, the particles converged to the optimal
solution faster than that of original one when γ > 0.
However, the convergence speed is valid depending
Collaborative Learning of Human and Computer: Supervised Actor-Critic based Collaboration Scheme
799

Figure 3: The game in action.
Figure 4: Objective functions left: Sombrero (18) and right:
Chandelier (19) ) used for PSO experiments.
Figure 5: PSO using 10 and 500 particles for the objective
function (18).
on the objective function. This is because the super-
vised signals: the gradient of the objective functions
are also valid depending on the shape of the surface
of the objective functions.
5 RESULTS
We conducted the test on 16 game players, 10 normal
game players and 6 controlled players. The 10 normal
players played with the proposed new colbagging sys-
tem, and the control played on the colbagging with-
out the feedback-teaching process. In the first ses-
sion, each person played the Dino game normally for
40 rounds. Note that each round is ended when the
Dino hits a cactus. In each session, each player can
switch between two game modes: the supervised or
Figure 6: PSO using 10 and 500 particles for the objective
function (19).
semi-automatic modes. In the supervised mode, the
Dino learns how to play by imitating the playing be-
haviors of the player. In the semi-automatic mode, the
Dino jumps according to the previous learning results.
In this mode, player’s controls were still available to
control the Dino behaviors. After the first session, the
performances of each actor were evaluated. The score
of each actor and player was determined 20× number
of jumped cactus.
Before starting the second session, the 10 normal
players watched a stream image of automatic-playing
scene of the integrated actors. The colbagging sys-
tem calculates the weighted sum of all actor’s outputs,
where the weight for each actor was determined by
(11). On the other hand, the controlled player did not
watch the integrated actor playing scene before going
to the second session. After finishing the second ses-
sion, each actor’s performance was evaluated. The
performance was measured by the maximum num-
ber of successful jumps over the cactus. The results
are plotted in Figure 7 and 8. In each figures, the
scores during the learning and test are plotted. The
test scores refers the score of actor.
We can see that the performance of each actors
were not always reflect the score during the learning.
During the training, four normal player’s scores after
the Second session were larger than those of the first
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
800

0
100
200
300
400
500
600
700
800
900
1 2
scores
sessions
0
100
200
300
400
500
600
700
800
900
1 2
scores
sessions
Figure 7: Score transition between the two sessions of 10
normal players: left:During the training, right: Test (Actor’s
score).
0
100
200
300
400
500
600
700
800
900
1 2
scores
sessions
0
100
200
300
400
500
600
700
800
900
1 2
scores
sessions
Figure 8: Score transition between the two sessions of 6
controlled players: left: During the training, right: Test (Ac-
tor’s score).
session. But, five controlled player’s scores after the
second session were larger than those of the first ses-
sion.
The performances of the controlled players after
the first and second sessions were not changed largely.
On the other hand, five normal players increased their
score. We predict that this is due to the long wait-
ing time (about two-three hours) between the first and
second sessions. Therefore, such long waiting time
makes player forget subtle operating patterns. So
far, the waiting time is needed to manually create the
streaming image of integrated actor.
Moreover, we also found that there were no guar-
antees that the actor’s performance is improved like
their players. We also predict that this is due to the
actors adjust to the later steps of the game and forgets
the early steps of the game environment. We believe
that if we reduce the waiting time and modify the hy-
per parameters for the actor to reduce the interference,
the normal-player’s performance will be superior to
the control players.
The data so far is limited, to provide reliable re-
sults. We plan to conduct more tests in future to get
enough data.
6 CONCLUSIONS
We proposed our improved collaborative learning
scheme between human and machine learning. The
system is a variation of crowd sourcing system ac-
celerated by machine learning. The system behavior
was roughly simulated by the particle swam optimiza-
tion accelerated by prior knowledge of each particle.
The results suggest that the prior knowledge accel-
erate the convergence speed. We have also conducted
the evaluation of the effectiveness of the collaboration
between real human and machine learning by using
the Dino game.
ACKNOWLEDGEMENTS
This research has been supported by Grant-in-Aid for
Scientic Research(c) 15K00321.
REFERENCES
ANTA, A. F. and LUIS LOPEZ, A. S. (2010). Reliable
internet-based master-worker computing in the pres-
ence of malicious workers. Parallel Processing Let-
ters, 22(1):1250002(17.
Fern
`
andez Anta, A., Georgiou, C., Mosteiro, M. A., and
Pareja, D. (2015). Algorithmic mechanisms for re-
liable crowdsourcing computation under collusion.
PLoS ONE, 10(3):1–22.
Forges, F. (1986). An approach to communication equilib-
ria. ECONOMETRICA, 54(6):1375–1385.
Golle, P. and Mironov, I. (2001). Uncheatable distributed
computations. In Topics in Cryptology– CT-RSA 2001
Volume 2020 of the series Lecture Notes in Computer
Science, pages 425–440. Springer-Verlag.
Konwar, K. M., Rajasekaran, S., and Shvartsman, A. A.
(2015). Robust network supercomputing with unre-
liable workers. Journal of Parallel and Distributed
Computing, 75:81–92.
Lee, D., Noh, S., Min, S., Choi, J., Kim, J., Cho, Y., and
Sang, K. C. (2001). Lrfu: A spectrum of policies
that subsumes the least recently used and least fre-
quently used policies. IEEE Transaction on Comput-
ers, 50(12):1352–1361.
Ogiso, T., Yamauchi, K., Ishii, N., and Suzuki, Y. (2016).
Co-learning system for humans and machines using a
weighted majority-based method. International Jour-
nal of Hybrid Intelligent Systems, 13(1):63–76.
Rosenstein, M. T. and Barto, A. G. (2012). Supervised
Actor-Critic Reinforcement Learning, chapter 14,
pages 359–380. Wiley-Blackwell.
Tomandl, D. and Schober, A. (2001). A modified general re-
gression neural network (mgrnn) with a new efficient
training algorithm as a robust ’black-box’-tool for data
analysis. Neural Networks, 14:1023–1034.
Venter, G. and Sobieszczanski-Sobieski, J. (2003). Particle
swam optimization. AIAA, 41(8):1583–1589.
Xu, X., Hu, D., and Lu, X. (2007). Kernel-based least
squares policy iteration for reinforcement learning.
IEEE TRANSACTIONS ON NEURAL NETWORKS,
18(4):973–992.
Collaborative Learning of Human and Computer: Supervised Actor-Critic based Collaboration Scheme
801