Experimental Implementation of Bias-free Quantum Random Number

Generator based on Vacuum Fluctuation

Ziyong Zheng

, Yichen Zhang

, Song Yu

and Hong Guo

State Key Laboratory of Information Photonics and Optical Communications,

Beijing University of Posts and Telecommunications, Beijing, 100876, China

State Key Laboratory of Advanced Optical Communication Systems and Networks,

School of Electronics Engineering and Computer Science, and Center for Quantum Information Technology,

Peking University, Beijing, 100871, China

Keywords:

Bias-free, Phase Modulation, Quantum Random Number Generation, Vacuum Fluctuation.

Abstract:

We experimentally demonstrate a bias-free optical quantum random number generator with real-time random-

ness extraction to directly output uniform distributed random numbers by measuring the vacuum ﬂuctuation

of quantum state. A phase modulator is utilized in the scheme to effectively reduce the inﬂuence of deviations

between two arms of the generator caused by the imperfect practical devices, which is an innovative solution

in the ﬁeld of quantum random number generator. In the case where the feedback modulation frequency is

much faster than the phase jitter, an unbiased result can be obtained by an additional subtraction between the

compensation signal and its average value to eliminate residual deviation. A following randomness extractor is

applied to eliminate the inﬂuence of residual side information introduced by the imperfect devices in practical

system.

1 INTRODUCTION

Random numbers are widely used in simulation (Fer-

renberg et al., 1992), lottery, cryptography (Gennaro,

2006) and other applications. The randomness of ran-

dom numbers has a signiﬁcant impact on the perfor-

mance of the whole system. Especially in cryptogra-

phy applications, random numbers with poor random-

ness will directly reduce the security of the cryptog-

raphy system (Bouda et al., 2012). The rapid devel-

opment of quantum cryptography technologies such

as quantum key distribution (Weedbrook et al., 2012;

Scarani et al., 2009; Diamanti et al., 2016; Zhang

et al., 2017; Gisin et al., 2002) which require se-

cure random number generation, unarguably acceler-

ate the researches about true random number gener-

ation. Quantum random number generator (QRNG)

exploits intrinsic probabilistic quantum processes to

directly generate true random numbers, which is re-

garded as a promising technology (Ma et al., 2016;

Bera et al., 2017; Herrero-Collantes and Garcia-

Escartin, 2017; Jennewein et al., 2000). Therefore,

many related works have been put forward in recent

years. These schemes use quantum sources includes

photon path (Jennewein et al., 2000; Stefanov et al.,

2000), photon arrival time (Wayne et al., 2009; Nie

et al., 2014; Dynes et al., 2008; Wahl et al., 2011;

Ma et al., 2005), photon number distribution(Wei and

Guo, 2009; F

urst et al., 2010; Applegate et al., 2015;

Ren et al., 2011), vacuum ﬂuctuation (Gabriel et al.,

2010; Shen et al., 2010; Symul et al., 2011; Haw

et al., 2015; Zhou et al., 2017; Raffaelli et al., 2018;

Xu et al., 2017; Zheng et al., 2018b), phase noise (Qi

et al., 2010; Guo et al., 2010; Xu et al., 2012; Abell

et al., 2014; Nie et al., 2015; Yang et al., 2016; Zhang

et al., 2016; Liu et al., 2017) and ampliﬁed spon-

taneous emission noise of quantum states (Williams

et al., 2010; Li et al., 2011; Martin et al., 2015; Liu

et al., 2013; Wei et al., 2012), etc. Typically, proto-

cols based on the measurement of vacuum ﬂuctuation

are more applied and valuable QRNG protocols, for

its convenience of state preparation, insensitivity of

detection efﬁciency and high generation speed.

The ﬁrst QRNG based on vacuum ﬂuctuation

is proposed in 2010 by measuring the quadrature

of the vacuum state, which can be expressed as

∞

−∞

ψ(x)

dx in the quadrature representation,

where

is the amplitude quadrature eigenstates and

ψ(x) is the ground-state wavefunction, which is a

Gaussian function centered around x = 0 (Gabriel

et al., 2010).

Ideally, the electrical signal output from the de-

276

Zheng, Z., Zhang, Y., Yu, S. and Guo, H.

Experimental Implementation of Bias-free Quantum Random Number Generator based on Vacuum Fluctuation.

DOI: 10.5220/0007569902760282

In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 276-282

ISBN: 978-989-758-364-3

tector should be evenly distributed near the 0 value.

While in practical system, the deviation of two signals

output from the homodyne detector caused by imper-

fect unbalanced devices, such as asymmetric beam

splitter or photodiodes (PDs) with different response

efﬁciency, will often cause the saturation of detector,

which is a great challenge for practical system. Gen-

erally, symmetrical devices will be chosen as sym-

metrical as possible so as to reduce the deviation of

the two arms. However, the practical devices can not

achieve complete symmetry. Minor deviation will be

ampliﬁed to a large voltage by the homodyne detec-

tor with a large gain, which will lead to saturation of

homodyne detector.

Protocol introduced in Ref. (Shen et al., 2010;

Symul et al., 2011; Haw et al., 2015) utilized fre-

quency shift and ﬁltering technology to obtain the sig-

nal in the required frequency band and ﬁlter out the

signal outside the band, including low frequency sig-

nals that causes signal deviation. While it is based on

the premise of unsaturated signal. When the detec-

tor is saturated, in fact, this operation can not elimi-

nate the effect of saturation basically caused by front-

end parts. An intuitive solution is to introduce an ad-

justable attenuator at both output ends of the beam

splitter so as to adjust the balance of the two arms.

However, the mechanical jitter of the practical atten-

uator will inevitably lead to imbalance and be greatly

ampliﬁed by the ampliﬁer in the detector, so that the

detector will still be saturated. Protocol introduced in

Ref. (Xu et al., 2017; Zheng et al., 2018b) proposed

an improved solution that is using AC coupling de-

tector to suppress the low-frequency components of

the signals detected by the PDs. In this way, the DC

components of the difference between the electrical

signals output from the two PDs will ﬁrstly be ﬁl-

tered out and then the signals in the remaining band

will be ampliﬁed. To some extent, the feasibility of

this scheme depends on the perfect ﬁltering of low

frequency components by transimpedance bandpass

ampliﬁer. However, in practice, the imperfection of

the ﬁlter can not eliminate the inﬂuence of low fre-

quency signals perfectly, which causes the signal still

to be affected by residual low-frequency jitter. There-

fore, how to achieve an effective and feasible devia-

tion elimination method is a meaningful and practical

problem.

We experimentally demonstrate a bias-free opti-

cal quantum random number generator with real-time

randomness extraction to directly output uniform dis-

tributed random numbers by measuring the vacuum

ﬂuctuation of quantum state. The generator utilizes

a phase modulator to effectively reduce the deviation

between two arms of the generator caused by the im-

perfect practical devices. Unbiased results can be ob-

tained by subtracting the mean value from the com-

pensated signal in every modulation period since the

feedback modulating frequency is far faster than the

phase jitter. Thus our generator can output bias-free

and real-time random numbers stably at a speed of

640 Mbps by applying a real-time randomness extrac-

tor to eliminate the inﬂuence of classical noise.

2 DEVIATION ELIMINATION

METHOD

The QRNG proposed in Ref. (Gabriel et al., 2010)

essentially exploits the quantum uncertainty of con-

tinuous observables, which is quadrature amplitude of

vacuum state to generate true random numbers. The

measurement of the quadrature amplitude collapses

the ground-state wave function, which is a Gaussian

function centered around x = 0, into quadrature eigen-

state. While the practical imperfect devices will make

the output of the two PDs different, so that there will

be a deviation after the subtraction of the two electri-

cal currents. To eliminate this deviation, a scheme

based on phase modulation is proposed with refer-

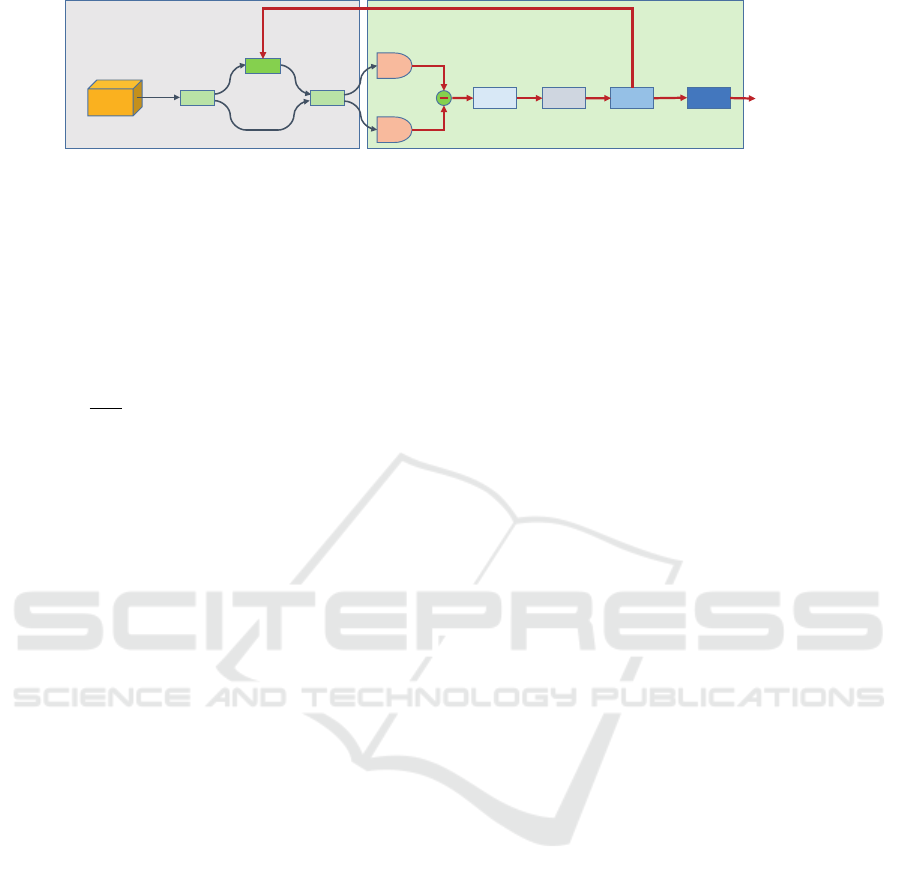
ence to laser interferometry technology. The block

diagram of the scheme is shown in Figure. 1.

The ﬁrst beam splitter (BS

) with three ports di-

vides the light beam from the CW laser into the upper

and lower arms with a transmission coefﬁcient of η

and η

. A phase modulator (PM) with insertion

loss of η

is connected to the upper arm. The two

output signals are then connected to the input ports

of the second beam splitter (BS

). Four parameters

named η

, η

are used to represent

the transmission coefﬁcients of port c

to d

, c

to d

and c

to d

. The efﬁciency of the photo-

electric conversion of the two PDs is labeled η

and

respectively.

When the vacuum noise is not considered, from

a classical point of view, it is intuitive that there is

a phase difference ∆ϕ between the upper and lower

arms. The output photocurrent of PD

can be ex-

pressed as

= |

(η

j∆φ

+ η

= η

(η

+ η

)

+ 2η

cos(∆φ).

(1)

Similarly, the photocurrent output from PD2 can be

expressed as

Experimental Implementation of Bias-free Quantum Random Number Generator based on Vacuum Fluctuation

277

)=2GYKX



9;(

'*)

)'2

+>:

)= IUTZOT[U[Y]G\K

(9  HKGSYVROZZKX

63 VNGYKSUJ[RGZUX

6* VNUZUJOUJKJKZKIZUX

9;( Y[HZXGIZUX

'36 GSVROLOKX

'*) GTGRUMZUJOMOZGRIUT\KXZKX

)'2 JGZGIGRI[RGZOUT5LLYKZKROSOTGZOUT

+>: XGTJUSTKYYK^ZXGIZUX

Balance control &

Entropy source

Electronic

circuit

'36

(9

8GTJUS

T[SHKXY

Figure 1: Scheme of the bias-free QRNG based on vacuum ﬂuctuation. The CW beams emitted by the laser diode is divided

into two beams by the ﬁrst balanced beam splitter and one arm is modulated by a phase modulator to maintain the phase

difference between the two arms as a ﬁxed value. The interference result of the second beam splitter would be a stable value.

The two input beams of the second beam splitter are treated as local oscillator (LO) separately and each LO will interfere with

the vacuum noise from the other input port of the beam splitter.

= |

(η

j∆φ

+ η

= η

(η

+ η

)

+ 2η

cos(∆φ).

(2)

So the actual current obtained by the homodyne

detector will be

i = i

− i

=η

(η

+ η

)

− η

(η

+ η

)

+ 2η

cos(∆φ)(η

− η

(3)

which indicates that i is closely related to the parame-

ters of the devices in the system. To obtain a bias-free

i, an intuitive solution is to make

(η

+ η

)−

(η

+ η

) = 0

(4)

and

−

= 0

(5)

simultaneously, which is not an easy solution to per-

fectly achieve in practical systems. A feasible alter-

native is to control the phase difference ∆ϕ between

two paths satisﬁes

cos(∆φ) = [η

(η

+ η

)

− η

(η

+ η

)]/

[2η

(η

− η

)].

(6)

In this way, the deviation can be effectively sup-

pressed, which can directly allow the increase of the

input local oscillation power. This will help to im-

prove the problem that the quantized bits of the fol-

lowing analog-to-digital converter (ADC) are wasted

caused by signals with limited amplitude.

Compared with the interference phenomenon be-

tween the classical strong light beams introduced

above, the interference between LO and vacuum state

will be different. The vacuum state is symmetrical

in the phase space, so the interference output of vac-

uum state and LO with different phases will remain

stable. In practice, the two input ports of the BS

are

connected to two light beams. Each light beams will

interfere with the other beam together with the vac-

uum ﬂuctuation introduced by the other port. Sup-

pose the vacuum ﬂuctuation obeys the Gaussian dis-

tribution N(0,σ

vac

), which means its mean value is

0 and its variance is σ

vac

. So the interference re-

sult of vacuum state from port c

and LO

from port

will follow Gaussian distribution N(µ

,σ

). Sim-

ilarly the result of vacuum state interference from

port c

and LO

from port c

will follow Gaussian

distribution N(µ

,σ

). So their difference will obey

N(µ

− µ

,σ

+ σ

). As is known, the phase jitter of

the two arms is a slow process, so in a short time inter-

val τ, the deviation between the upper and lower arms

can be treated as a constant µ

− µ

. Using this data,

we can balance the two arms through feedback con-

trolling the phase modulator. Its residual bias caused

by the limitation of the feedback control accuracy can

be eliminated by an additional subtraction operation.

The schematic diagram of feedback control is

shown in the Figure. 2. Usually, the phase difference

∆ϕ between the two arms changes at a speed slower

than KHz, which can be compensated to achieve a sta-

ble ∆ϕ when the compensation speed is much faster

PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology

278

2SWLFDOV\VWHPZLWK30

'HWHFWLRQDQGTXDQWLILFDWLRQ

1VXFFHVVLYHYDULDEOHV

 

>  O#4

9;3 > O# 4

1XQELDVHGVXFFHVVLYHGDWD

 

O O

? > 9;3  4 O# 4

'LJLWDOWRDQDORJFRQYHUWHU

JGIEJGZG# JGIEJGZG I

JGIEJGZG# JGIEJGZGI

dac_data =

JGIEJGZG# I



JGIEJGZG#I

Q



?d d' 9;3 (

?9;3 '

?!9;3 (

JGIEJGZG$  I

?JGIEJGZG"I

Figure 2: Algorithm of deviation elimination progress. We initialize the value of dac data, which represents the digital data

used to drive the DAC, to 8092. By comparing the sum of the samples collected in a time interval τ with the preset interval, the

phase difference between the two arms of the system will calculated and a feedback compensation operation will be performed

with a compensation frequency far greater than the phase jitter to make the ﬂuctuation of the interference results be stabilized

in a very small interval. And c is the step of adjusting dac data.

than the speed of phase jitter. In each compensa-

tion period τ, we sum N data sampled during the

period and compare the sum value SUM with a de-

sired value. Considering the limited sampling accu-

racy of the practical ADC and the statistical ﬂuctu-

ation caused by the limited data, we set a decision

interval [A, B] to replace the ﬁxed value introduced

above. When SUM is in the interval [A,B], the devia-

tion of the output signal is within an acceptable range

and an unbiased result can be obtained by subtracting

their mean from the N data during τ.

While in the case that the deviation makes the

SUM value out of the interval [A,B], we will adjust

the feedback voltage according to the detection re-

sults. The output voltage from digital-to-analog con-

verter (DAC) convers 2V

which means 2 times of

the half wave voltage of the PM used in the system.

When SUM is less than A, we reduce the value of

dac data by c each time, which will result to the re-

duction of the compensation voltage loaded on PM.

When the value of dac data is less than c, we can di-

rectly change the value of dac data to 2

− c due to

the two dac data value correspond to two close phase

modulation result. Conversely, when SUM is larger

than the upper bound B of the interval, we increase

the value of dac data by c each time. When the value

of dac data is greater than 2

− c, we set the value

of dac data as c. The above control process makes

the value of SUM stable in the interval [A,B], thereby

avoiding saturation of the homodyne detector.

3 EXPERIMENTAL SETUP &

RESULT

We build an all-in-ﬁber setup with off-the-shelves de-

vices according to the scheme shown in Figure. 1.

The system includes three main parts: the balance

control module, entropy source and an electronic cir-

cuit for measurement, calculation and randomness ex-

traction.

The entropy source consists of a 1550 nm dis-

tributed feedback laser (NKT Basic E15, line width

100 Hz) whose output beam is divided into two beams

by BS

(η

= 3.80dB, η

= 3.56dB). The upper

arm is modulated by a phase modulator (EOSPACE,

insertion loss η

= 3.24dB, V

= 1.240V ). The two

output signals are coupled into BS

(η

= 3.68dB,

= 3.82dB, η

= 3.76dB, η

= 3.60dB). To

suppress the deviation of the output signal by the ho-

modyne detector, a feedback control voltage will be

loaded on the PM. The following DC coupling ho-

modyne detector (Newport, 1817-FC, measurement

bandwidth 80 MHz, convertion gain of PD

5.55 ×

V /W , convertion gain of PD

5.42 × 10

V /W )

will convert the input optical signal into electrical

signal. The ADC card (ADS5463, sampling fre-

quency set as 80 MHz, sampling precision 12 bits

and input voltage range 1 VPP) samples the analog

signal and quantize it into digital value. The ﬁeld

programmable gate array (FPGA, KC705 evaluation

Experimental Implementation of Bias-free Quantum Random Number Generator based on Vacuum Fluctuation

279

board) will sum the sampled N = 1000 variables and

compare the value of sum, SUM, with the preset in-

terval [2043000,2053000]. The result of compari-

son will affect the change in dac data, which will be

converted to the phase compensation voltage through

digital-to-analog card (DAC, AD9736, sampling pre-

cision 14 bits and output voltage range 2.480 VPP)

at a speed of 80 KHz when the laser power is set

to 5 mW . In our experiment, the adjustment step of

dac data is set as 5.

The practical discontinuous phase compensation

voltage can not meet the requirement of accurate com-

pensation, which results to the compensated signal re-

main a certain bias. To solve this problem, a subtrac-

tion operation between these 1000 variables and their

mean will also be implemented on FPGA. The result

of subtraction is used to randomness estimation and

extraction.

Classical noise introduced by the imperfect de-

vices in the practical system will be controlled by the

eavesdropper, Eve, which will result to the informa-

tion leakage of random numbers, thereby damage the

security of the whole system (Bouda et al., 2012). To

eliminate the effects of the electrical noise, statistical

parameter min-entropy was proposed to quantize the

extractable randomness (Ma et al., 2013) and a the-

oretical security proved randomness extractor will be

utilized. For the random number generator based on

the measurement of the vacuum noise, the outcome

of practical measurement M and the noise data E can

be obtained when the LO is turned on and turned off

separately. M is a combination of the measurement

result of quantum noise Q and classical noise E. Q

and E are assumed to be independent and they both

obey Gaussian distribution (Haw et al., 2015). So the

min-entropy of the measurement outcome M condi-

tioned on the existing classical noise E can be given

min

(M|E) = −log



max

e∈E

max

m∈M

M|E

(m|e)



= −log



2π



− σ



−1

= log



2πσ



(7)

When the LO power is set to 5 mW , the mea-

sured voltage variance of the raw data σ

is calcu-

lated as 1.86 × 10

. The measured voltage variance

of the raw data σ

is calculated as 166.09 when the

LO power is set to 0 mW . Thus the H

min

(M|E) can

be calculated as 10.08 bits per sample or 0.84 bits per

raw data bit, which means that 84.0% random bits

can be generated from each sample. The ﬁnal ran-

dom number output rate will reach 640 Mbps after

a real-time randomness extraction based on an im-

proved Toeplitz hashing algorithm proposed in Ref.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Test item

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Propotion

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

P-value

Figure 3: Test results of 1000 × 10

random bits using

NIST standard statistical test suite. From left to right,

the 15 test items shown on the x-axis are named as Fre-

quency, Block frequency, Cumulative sums, Runs, Longest-

run, Rank, FFT, Non-periodic templates, Overlapping tem-

plates, Universal, Approximate entropy, Random excur-

sions, Random excursions variant, Serial and Linear Com-

plexity, respectively. On the y-axis, the left and right di-

agram shows the passing proportion and P-value of each

tests, separately. The dotted line shown above is the critical

boundary of 0.9805608.

(Zheng et al., 2018b). The size of Toeplitz ma-

trix is set as 1920 × 2400 to achieve a security pa-

rameter of 2

−48

. Finally, we test their randomness

through the NIST standard test suite. The NIST test

suite contains 15 statistical tests and each test will

output a statistical p-value. The signiﬁcant level α

together with β are set as 0.01. 1000 × 10

ran-

dom bits are used for testing. The sequences will

be considered to be random when the proportion of

the sequences satisﬁes p-value > β is in the range of

(1 − β − 3[(1 − β)β/N]

1/2

,1 − β + 3[(1 − β)β/N]

1/2

)

(Wang et al., 2013; Zheng et al., 2018a).The test re-

sults is shown in Figure. 3.

4 CONCLUSIONS

In this paper, a prototype of bias-free and real-time

optical quantum random number generator based on

measuring the vacuum ﬂuctuation of quantum state is

demonstrated. There are two signiﬁcant merits of our

system favorable for practical applications. First, it

can directly reduce the deviation introduced by the

unbalanced devices and achieve a bias-free output

through compensation and subtraction. Second, the

reduction of deviation makes the homodyne detector

support a greater LO power to help to achieve a higher

min-entropy. Further research can be done by explor-

ing methods to realize accurate compensation and ap-

ply the balance technology to other protocols.

PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology

280

ACKNOWLEDGEMENTS

This work was supported in part by the Key Program

of National Natural Science Foundation of China

under Grants 61531003, the National Natural Sci-

ence Foundation under Grants 61427813, the Na-

tional Basic Research Program of China under Grants

2014CB340102, China Postdoctoral Science Founda-

tion under Grant 2018M630116, and the Fund of State

Key Laboratory of Information Photonics and Optical

Communications.

REFERENCES

Abell

an, C., Amaya, W., Jofre, M., Curty, M., Ac

ın, A.,

Capmany, J., Pruneri, V., and Mitchell, M. W. (2014).

Ultra-fast quantum randomness generation by accel-

erated phase diffusion in a pulsed laser diode. Opt.

Express, 22(2):1645–1654.

Applegate, M. J., Thomas, O., Dynes, J. F., Yuan, Z. L.,

Ritchie, D. A., and Shields, A. J. (2015). Efﬁcient

and robust quantum random number generation by

photon number detection. Applied Physics Letters,

107(7):071106.

Bera, M. N., Acn, A., Ku, M., Mitchell, M. W., and Lewen-

stein, M. (2017). Randomness in quantum mechan-

ics: philosophy, physics and technology. Reports on

Progress in Physics, 80(12):124001.

Bouda, J., Pivoluska, M., Plesch, M., and Wilmott, C.

(2012). Weak randomness seriously limits the security

of quantum key distribution. Phys. Rev. A, 86:062308.

Diamanti, E., Lo, H.-K., Qi, B., and Yuan, Z. (2016). Practi-

cal challenges in quantum key distribution. Npj Quan-

tum Information, 2:16025.

Dynes, J. F., Yuan, Z. L., Sharpe, A. W., and Shields, A. J.

(2008). A high speed, postprocessing free, quantum

random number generator. Applied Physics Letters,

93(3):031109.

Ferrenberg, A. M., Landau, D. P., and Wong, Y. J. (1992).

Monte carlo simulations: Hidden errors from “good”

random number generators. Phys. Rev. Lett., 69:3382–

3384.

urst, H., Weier, H., Nauerth, S., Marangon, D. G., Kurt-

siefer, C., and Weinfurter, H. (2010). High speed op-

tical quantum random number generation. Opt. Ex-

press, 18(12):13029–13037.

Gabriel, C., Wittmann, C., Sych, D., Dong, R., Mauerer,

W., Andersen, U. L., Marquardt, C., and Leuchs, G.

(2010). A generator for unique quantum random num-

bers based on vacuum states. Opt. Lett., 4:711.

Gennaro, R. (2006). Randomness in cryptography. IEEE

Security Privacy, 4(2):64–67.

Gisin, N., Ribordy, G., Tittel, W., and Zbinden, H. (2002).

Quantum cryptography. Rev. Mod. Phys., 74:145–195.

Guo, H., Tang, W., Liu, Y., and Wei, W. (2010). Truly

random number generation based on measurement of

phase noise of a laser. Phys. Rev. E, 81:051137.

Haw, J. Y., Assad, S. M., Lance, A. M., Ng, N. H. Y.,

Sharma, V., Lam, P. K., and Symul, T. (2015).

Maximization of extractable randomness in a quan-

tum random-number generator. Phys. Rev. Applied,

3:054004.

Herrero-Collantes, M. and Garcia-Escartin, J. C. (2017).

Quantum random number generators. Rev. Mod.

Phys., 89:015004.

Jennewein, T., Achleitner, U., Weihs, G., Weinfurter, H.,

and Zeilinger, A. (2000). A fast and compact quan-

tum random number generator. Review of Scientiﬁc

Instruments, 71(4):1675–1680.

Li, X., Cohen, A. B., Murphy, T. E., and Roy, R. (2011).

Scalable parallel physical random number genera-

tor based on a superluminescent led. Opt. Lett.,

36(6):1020–1022.

Liu, J., Yang, J., Li, Z., Su, Q., Huang, W., Xu, B., and

Guo, H. (2017). 117 Gbits/s quantum random num-

ber generation with simple structure. IEEE Photonics

Technology Letters, 29(3):283–286.

Liu, Y., Zhu, M.-Y., Luo, B., Zhang, J.-W., and Guo,

H. (2013). Implementation of 1.6 Tb/s truly ran-

dom number generation based on a super-luminescent

emitting diode. Laser Physics Letters, 10(4):045001.

Ma, H.-Q., Xie, Y., and Wu, L.-A. (2005). Random num-

ber generation based on the time of arrival of single

photons. Appl. Opt., 44(36):7760–7763.

Ma, X., Xu, F., Xu, H., Tan, X., Qi, B., and Lo, H.-K.

(2013). Postprocessing for quantum random-number

generators: Entropy evaluation and randomness ex-

traction. Phys. Rev. A, 87:062327.

Ma, X., Yuan, X., Cao, Z., Qi, B., and Zhang, Z. (2016).

Quantum random number generation. Npj Quantum

Information, 2:16021.

Martin, A., Sanguinetti, B., Lim, C. C. W., Houlmann, R.,

and Zbinden, H. (2015). Quantum random number

generation for 1.25-Ghz quantum key distribution sys-

tems. J. Lightwave Technol., 33(13):2855–2859.

Nie, Y.-Q., Huang, L., Liu, Y., Payne, F., Zhang, J., and

Pan, J.-W. (2015). The generation of 68 Gbps quan-

tum random number by measuring laser phase ﬂuctua-

tions. Review of Scientiﬁc Instruments, 86(6):063105.

Nie, Y.-Q., Zhang, H.-F., Zhang, Z., Wang, J., Ma, X.,

Zhang, J., and Pan, J.-W. (2014). Practical and fast

quantum random number generation based on pho-

ton arrival time relative to external reference. Applied

Physics Letters, 104(5):051110.

Qi, B., Chi, Y.-M., Lo, H.-K., and Qian, L. (2010). High-

speed quantum random number generation by mea-

suring phase noise of a single-mode laser. Opt. Lett.,

35(3):312–314.

Raffaelli, F., Ferranti, G., Mahler, D. H., Sibson, P., Ken-

nard, J. E., Santamato, A., Sinclair, G., Bonneau, D.,

Thompson, M. G., and Matthews, J. C. F. (2018). A

homodyne detector integrated onto a photonic chip

for measuring quantum states and generating ran-

dom numbers. Quantum Science and Technology,

3(2):025003.

Ren, M., Wu, E., Liang, Y., Jian, Y., Wu, G., and Zeng,

H. (2011). Quantum random-number generator based

on a photon-number-resolving detector. Phys. Rev. A,

83:023820.

Scarani, V., Bechmann-Pasquinucci, H., Cerf, N. J., Du

sek,

M., L

utkenhaus, N., and Peev, M. (2009). The secu-

Experimental Implementation of Bias-free Quantum Random Number Generator based on Vacuum Fluctuation

281

rity of practical quantum key distribution. Rev. Mod.

Phys., 81:1301–1350.

Shen, Y., Tian, L., and Zou, H. (2010). Practical quan-

tum random number generator based on measuring the

shot noise of vacuum states. Phys. Rev. A, 81:063814.

Stefanov, A., Gisin, N., Guinnard, O., Guinnard, L., and

Zbinden, H. (2000). Optical quantum random number

generator. Journal of Modern Optics, 47(4):595–598.

Symul, T., Assad, S. M., and Lam, P. K. (2011). Real

time demonstration of high bitrate quantum random

number generation with coherent laser light. Applied

Physics Letters, 98(23):231103.

Wahl, M., Leifgen, M., Berlin, M., Rhlicke, T., Rahn, H.-J.,

and Benson, O. (2011). An ultrafast quantum random

number generator with provably bounded output bias

based on photon arrival time measurements. Applied

Physics Letters, 98(17):171105.

Wang, A., Li, P., Zhang, J., Zhang, J., Li, L., and Wang,

Y. (2013). 4.5 gbps high-speed real-time physical

random bit generator. Opt. Express, 21(17):20452–

20462.

Wayne, M. A., Jeffrey, E. R., Akselrod, G. M., and Kwiat,

P. G. (2009). Photon arrival time quantum ran-

dom number generation. Journal of Modern Optics,

56(4):516–522.

Weedbrook, C., Pirandola, S., Garc

ıa-Patr

on, R., Cerf, N. J.,

Ralph, T. C., Shapiro, J. H., and Lloyd, S. (2012).

Gaussian quantum information. Rev. Mod. Phys.,

84:621–669.

Wei, W. and Guo, H. (2009). Bias-free true random-number

generator. Opt. Lett., 34(12):1876–1878.

Wei, W., Xie, G., Dang, A., and Guo, H. (2012). High-

speed and bias-free optical random number generator.

IEEE Photonics Technology Letters, 24(6):437–439.

Williams, C. R. S., Salevan, J. C., Li, X., Roy, R., and Mur-

phy, T. E. (2010). Fast physical random number gen-

erator using ampliﬁed spontaneous emission. Opt. Ex-

press, 18(23):23584–23597.

Xu, B., Li, Z., Yang, J., Wei, S., Su, Q., Huang, W.,

Zhang, Y., and Guo, H. (2017). High speed continuous

variable source-independent quantum random number

generation. arXiv: 1709.00685.

Xu, F., Qi, B., Ma, X., Xu, H., Zheng, H., and Lo, H.-K.

(2012). Ultrafast quantum random number generation

based on quantum phase ﬂuctuations. Opt. Express,

20(11):12366–12377.

Yang, J., Liu, J., Su, Q., Li, Z., Fan, F., Xu, B., and Guo, H.

(2016). 5.4 Gbps real time quantum random number

generator with simple implementation. Opt. Express,

24(24):27475–27481.

Zhang, X.-G., Nie, Y.-Q., Zhou, H., Liang, H., Ma, X.,

Zhang, J., and Pan, J.-W. (2016). Note: Fully inte-

grated 3.2 Gbps quantum random number generator

with real-time extraction. Review of Scientiﬁc Instru-

ments, 87(7):076102.

Zhang, Y.-C., Li, Z., Chen, Z., Weedbrook, C., Zhao, Y.,

Wang, X., Xu, C., Zhang, X., Wang, Z., Li, M., Zhang,

X., Zheng, Z., Chu, B., Gao, X., Meng, N., Cai, W.,

Wang, Z., Wang, G., Yu, S., and Guo, H. (2017).

Continuous-variable qkd over 50km commercial ﬁber.

arXiv: 1709.04618.

Zheng, Z., Zhang, Y., Yu, S., and Guo, H. (2018a). Exper-

imental demonstration of gaussian distributed quan-

tum random number generator. volume 10733, pages

10733 – 10733 – 7.

Zheng, Z., Zhang, Y.-C., Huang, W., Yu, S., and Guo,

H. (2018b). 6 gbps real-time optical quantum ran-

dom number generator based on vacuum ﬂuctuation.

arXiv: 1805.08935.

Zhou, Q., Valivarthi, R., John, C., and Tittel, W. (2017).

Practical quantum random number generator based on

sampling vacuum ﬂuctuations. arXiv: 1703.00559.

PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology

282