
Using Data Mining Techniques to Forecast the Normalized Difference
Vegetation Index (NDVI) in Table Grape
Javier E. Gómez-Lagos
1
, Marcela C. González-Araya
1
, Rodrigo Ortega Blu
2
and Luis G. Acosta Espejo
2
1
Department of Industrial Engineering, Faculty of Engineering, Universidad de Talca,
Camino a Los Niches km 1, Curicó, Chile
2
Departamento de Ingeniería Comercial, Universidad Técnica Federico Santa María,
Avenida Santa María 6400, Vitacura, Santiago, Chile
Keywords: NDVI, Data Mining Techniques, Neural Networks, Fruit Crop Variability.
Abstract: The Normalized Difference Vegetation Index (NDVI) is a simple indicator that quantifies aerial biomass in
fruit crops, which is correlated with the fruit yield and quality produced by an orchard. Therefore, knowing
the NDVI values would allow predicting productive parameters above mentioned, which in turn would help
planning operational activities such as harvesting. In this study, we estimated the NDVI of a Chilean table
grape orchard based on past data using data mining techniques. For this purpose, we developed a three-step
method, obtaining NDVI predictions with high accuracy.
1 INTRODUCTION
Natural vegetation cover and agricultural crops are
frequently the subjects of remote sensing studies
(Cunha et al., 2010; Pôças et al., 2015; Font et al.,
2015; Yu and Shang, 2018). The Normalized
Difference Vegetation Index (NDVI), one of the most
common zoning tools (Pettorelli, 2013), since it is a
simple indicator that quantifies vegetation by
measuring the difference between near-infrared
(which vegetation strongly reflects) and red light
(which vegetation absorbs). It can be used to analyze
remote sensing from different platforms, including
satellite, aerial and terrestrial, and assess the amount
of biomass (Fortes Gallego et al., 2015; Sun et al.,
2017; Berger et al., 2018). In turn, the NDVI is
correlated with the quantity and quality of fruit that
an orchard would have. Therefore, knowing the
NDVI values can predict the parameters mentioned
above, which helps plan activities such as harvesting.
Spatial variability of Chilean vineyards in terms
of yield and quality is high, which fully justifies site-
specific management, particularly differential
harvesting (Ortega-Blu and Molina-Roco, 2016). In
this study, we estimate the NDVI of a Chilean table
grape orchard based on past data using data mining
techniques. The NDVI is useful for obtaining an
approximation of the amount and ripening time of the
grapes. In this regard, for plants with a high NDVI
(large above ground biomass), the fruit will mature
more slowly, while with a lower NDVI, it will mature
faster. This happens because in plants with low NDVI
the fruit will receive more solar radiation. On the
other hand, very high or very low NDVI values
usually involve low fruit production. In this manner,
all this information will support the harvest plan of
the different blocks of an orchard, making it possible
to establish the harvest days and the amount of fruit
to collect.
This study has the objective to develop and
evaluate a three-step method based on data mining
techniques to forecast NDVI based on previous NDVI
data.
This article is divided as follows: Section 2 shows
the material and methods used in this work; Section 3
shows the results, while Section 4 presents
conclusions regarding this study.
2 MATERIALS AND METHODS
The case study used in this work corresponds to a 9
ha table grape orchard located in the Region of
Valparaíso, Chile. The NDVI data was collected on
Gómez-Lagos, J., González-Araya, M., Blu, R. and Espejo, L.
Using Data Mining Techniques to Forecast the Normalized Difference Vegetation Index (NDVI) in Table Grape.
DOI: 10.5220/0007570101890194
In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 189-194
ISBN: 978-989-758-352-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
189
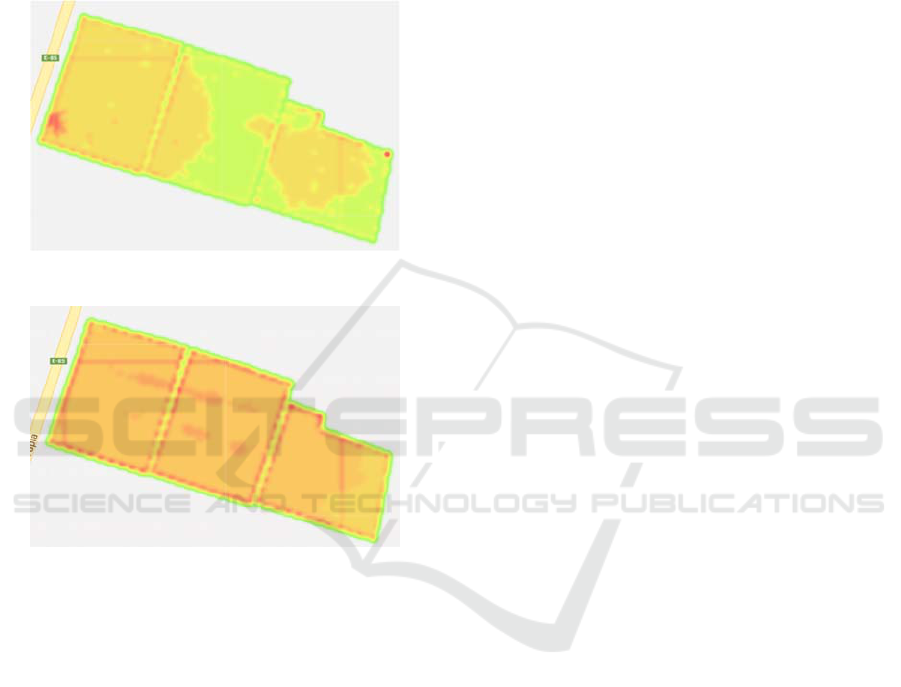
five different dates during the 2014-2015 growing
season. Dates were October 9
th
, October 30
th
,
November 11
th
, December 3
rd
of 2014, and January
12
th
of 2015. For every date, the NDVI of 3532
coordinates (points) were collected, which
correspond to every vine in the orchard. Figures 1 and
2 show the NDVI observed in two of these dates as
an example of data representation.
Figure 1: NDVI observed on October 9
th
, 2014.
Figure 2: NDVI observed on December 3
rd
, 2014.
It can be observed that when the red colour is
more intense, a greater value of the NDVI is
observed. On the other hand, when the green colour
is more intense, a lower value of the NDVI is
registered.
2.1 Proposed Method to Forecast the
NDVI
The method proposed for estimating the NDVI of the
orchard is summarized as follows:
Step 1: The NDVI data of the first four dates (each
date is a variable of the algorithm) is used in order
to perform a clustering procedure. For this
clustering, the Fuzzy c-Means Clustering
Algorithm (FCM) proposed by Bezdek et al.
(1984) was applied. This algorithm requires the
number of clusters to be formed as a parameter.
For the case study, the algorithm was run 39
times, aiming to establish the clusters, which
varied in number from 2 to 40.
Step 2: Once the clustering with different numbers
of clusters was obtained, the silhouette
representation of each cluster was used to evaluate
them. This function was developed by Rousseeuw
(1987). The number of clusters that achieves the
best value of the silhouette function was selected
and used for calculating the NDVI estimation.
This estimation is carried out in the following
step.
Step 3: The NDVI estimation for the last date
(January 12
th
, 2015) was obtained by applying
neural networks. In this way, data from the first
four days was used to train the neural network
algorithm, while the last date was used to validate
the NDVI prediction.
In the following sub-sections, we explain in more
detail each step in our methodology.
It is important to notice that every step of the
methodology was executed using R software, version
3.4.3, in a Dell 321 PowerEdge R/730 server with
Intel Xeon E5 2623-v3 and 3 Ghz.
2.1.1 Step 1: Fuzzy c-Means Clustering
Algorithm (FCM)
The FCM was proposed by Bezdek et al., (1984) for
generating fuzzy partitions and prototypes for any set
of numerical data. The clustering criterion used to
aggregate subsets is a generalized least-squares
objective function. The FCM requires the choice of
one of three norms (Euclidean, Diagonal, or
Mahalonobis), an adjustable weighting factor that
controls sensitivity to noise and the number of
clusters needs to be defined. For the case study, we
used the Euclidean distance, a weighting factor value
of 1.1 and we varied the number of clusters from 2 to
40.
It is important to mention that the value of the
weighting factor requires a calibration in order to
improve the clustering results. As mentioned
previously, we used a weighting factor equal to 1.1.
The mathematical model developed for the FCM
algorithm is:
Min
,
(1)
Subject to
1, 1,…,,
(2)
0,1,…,,1,…,.2
(3)
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
190

Where:
n is the number of points,
k is the number of clusters,
u
ij
is the degree of membership of a point i to a cluster
j,
d(x
i
, c
j
) corresponds to the distance from a point i to
the centroid of a cluster j.
The centroid c
j
is calculated iteratively during the
algorithm execution, considering the values of u
ij
. In
this way, when u
ij
converges, that is, achieves less
variation than an epsilon, the FCM algorithm stops.
The result of this algorithm is the degree of
membership of each point i to each cluster j,
represented by u
ij
.
For this case study, the distance d(x
i
, c
j
) was
calculated considering the Euclidean distance
between six coordinates. These six coordinates were
abscissa, ordinate, and the NDVI values of the first
four dates. In addition, for calculating the Euclidean
distance, it was necessary to normalize the abscissa
and ordinate. This normalization assigns to the
highest value a 1 and to the lowest value a 0.
2.1.2 Step 2: Application of Silhouettes
The silhouette function was proposed by Rousseeuw
(1987) and is based on the comparison of clusters’
tightness and separation. This silhouette shows which
objects lie well within their cluster and which ones
are merely somewhere in between clusters.
The evaluation of the 39 clusters obtained in Step
1 was carried out using the silhouette function in the
following way:
Calculate the Euclidean distance from a given
point i of a cluster j to every point of the same
cluster A. Once all these distances are obtained,
calculate the average of these distances, which is
called average dissimilarity of i to all other objects
of A, a(i).
Calculate the Euclidean distance from a given
point i of cluster A to each point of a given cluster
C (being C a different cluster from A). Then,
calculate the average of these distances. This
average is the average dissimilarity of i to all
objects of C, d(i, C).
Once the averages d(i, C) for all C A have been
computed, select the smallest of them and denote
it by b(i).
With the values of a(i) and b(i), the function of
silhouettes s(i) must be calculated according to the
following equation:
max
,
(4)
The silhouette function s(i) varies from -1 to 1. When
s(i) is closer to 1 it means that a(i) < b(i) and we can
say that i is “well-clustered”. This is explained
because if s(i) is 1, it means that a(i) = 0, that is, all
points within the cluster A are very close, and also,
the maximum value between a(i) and b(i) will be b(i).
Therefore, the formula (4) will remain b(i)/b(i) = 1.
For more details of the silhouette interpretation, see
Rousseeuw (1987).
Using silhouettes, the clusters obtained in Step 1
were evaluated in order to select the one that had the
best s(i) value (closer to 1).
2.1.3 Step 3: Neural Network for NDVI
Forecast
A neural network algorithm was developed to
estimate the NDVI of each point i for January 12
th
,
2015, using the NDVI of the previous four dates
(October 9
th
, October 30
th
, November 11
th
and
December 3
rd
of 2014). These four dates were divided
into a training sample (70% of data) and a validation
sample (30% of data); both samples were generated
randomly. Therefore, the observed NDVI on January
12
th
, 2015 was used to validate the obtained NDVI
forecast.
In the neural network algorithm, we used the
normalized data (values from 0 to 1) of the following
predictor variables: distance from a point i to the
centroid of each cluster j – d(x
i
, c
j
); the degree of
membership from point i to each cluster j (u
ij
)
multiplied by its NDVI observed in the last date
where it was collected. For the case study, it
corresponds to the NDVI observed on December 3
rd
.
In addition, the degree of membership u
ij
and the
distance d(x
i
, c
j
) were computed in Step 1 and we had
3532 coordinates (points) for each date.
For training the neuronal network, 5, 7 and 10
neurons in only one hidden layer were tested. In this
way, the number of neurons that obtains the smallest
error, that is, the smallest mean absolute percentage
error (MAPE), is selected. For our case study, 7
neurons into one hidden layer obtained the smallest
MAPE, and then this number of neurons was selected.
The computational experimentation of the neural
network algorithm was done using the nnet package
of R. This package uses the logic or sigmoid function
as the activation function for the algorithm.
3 RESULTS
The main results obtained by the proposed method are
described in this section.
Using Data Mining Techniques to Forecast the Normalized Difference Vegetation Index (NDVI) in Table Grape
191

As mentioned previously, the FCM algorithm was
run 39 times for defining the clustering with different
numbers of clusters (from 2 to 40). After performing
this procedure, the silhouette function was applied for
evaluating every clustering. Figure 3 shows the
behaviour of the silhouette values calculated for each
clustering, which varies in number from 2 to 40. In
this figure, it is possible to observe that the silhouette
value converges to 0.6 from 27 clusters. Moreover,
this is the highest value of s(i). For this reason, the
selected number of clusters for executing the neural
network algorithm was 27. In Table A.1 of the
Appendix, the obtained silhouette values are
presented.
Figure 3: Silhouette values according to the number of
clusters.
An example of three clusters obtained by the FCM
algorithm are depicted in Figures 4, 5 and 6. The red
colour represents each cluster. These clusters belong
to the selected set of 27 clusters.
Once the best clustering according to the
silhouette function was selected, the neural network
algorithm was applied for estimating the NDVI of
each point in the orchard at time “t + 1”, that is, on
January 12
th
, 2015. In this algorithm, 54 predictor
variables were used, which were: 27 d(x
i
, c
j
) and 27
u
ij
multiplied by its NDVI observed in the last date.
Figure 7 shows the observed NDVI on January 12
th
,
2015, while Figure 8 presents the estimated NDVI for
the same date by the neural network algorithm. In
these figures, similarly to Figures 1 and 2, when the
red colour is more intense, a greater value of the
NDVI is observed. On the other hand, when the green
colour is more intense, a lower value of the NDVI is
registered.
Figure 4: Cluster 1.
Figure 5: Cluster 2.
Figure 6: Cluster 3.
Figure 7: NDVI observed on January 12
th
, 2015.
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
192

Figure 8: Estimated NDVI for January 12
th
, 2015.
The NDVI forecast obtained by the neural
network algorithm presented a mean absolute
percentage error (MAPE) equal to 0.34% in the
validation sample and 1.83% in the test sample. It is
important to mention that a MAPE less or equal than
10% indicates that the accuracy (quality) of the
forecast is very good, according to the classification
proposed by Ghiani et al., (2004). In addition, we
obtained a very good NDVI prediction 40 days in
advance, being useful information for planning
agricultural activities such as harvesting.
4 CONCLUSIONS
The proposed method allowed predicting future
NDVI based on previous measurements with high
accuracy (MAPE of 1.83%).
In future researches, the following issues should
be explored:
To forecast the quality and quantity of table
grapes in a given orchard according to the
predicted or measured NDVI. In this way, it
would be possible to plan harvesting.
To model a harvesting plan according to the
grape’s quality and quantity forecast.
To study the time frequency with which data must
be collected in order to analyse its impact on the
NDVI forecast.
To analyse the possibility to reduce the number of
points to be sampled in a same cluster, since they
are homogeneous. In this way, it could be useful
to determine which points to sample, For
example, to study if the centroid of each cluster
could serve as a representative point
ACKNOWLEDGEMENTS
This work is supported by the Support Funding for
the Academic Development (FADA) of the
Departamento de Ingeniería Comercial of
Universidad Técnica Federico Santa María and by the
CYTED program through the thematic network
BigDSS-Agro, Project P515RT0123.
REFERENCES
Berger, A., Ettlin, G., Quincke, C., Rodríguez-Bocca, P.,
2018. Predicting the Normalized Difference Vegetation
Index (NDVI) by training a crop growth model with
historical data, Computers and Electronics in
Agriculture, article in press.
Bezde, J.C., Ehrlich, R., Full, W., 1984. FCM: The Fuzzy
c-Means Clustering Algorithm, Computers &
Geosciences, 10(2-3): 191-203.
Cunha, M., Marcal, A.R., Silva, L., 2010. Very early
prediction of wine yield based on satellite data from
VEGETATION, International Journal of Remote
Sensing, 31(12): 3125-3142.
Font, D., Tresanchez, M., Martínez, D., Moreno, J., Clotet,
E., Palacín, J., 2015. Vineyard yield estimation based
on the analysis of high resolution images obtained with
artificial illumination at night, Sensors, 15(4): 8284-
8301.
Fortes Gallego, R., Prieto Losada, M. D. H., García Martín,
A., Córdoba Pérez, A., Martínez, L., Campillo Torres,
C., 2015. Using NDVI and guided sampling to develop
yield prediction maps of processing tomato crop,
Spanish Journal of Agricultural Research, 13(1), e02-
004, 9 pages.
Ghiani, G., Laporte, G., Musmanno, R., 2004. Introduction
to logistics systems planning and control, John Wiley
& Sons Ltd, The Atrium, Southern Gate, Chichester,
West Sussex PO19 8SQ, England.
Ortega-Blu, R., Molina-Roco, M., 2016. Evaluation of
vegetation indices and apparent soil electrical
conductivity for site-specific vineyard management in
Chile, Precision Agriculture, 17(4): 434–450.
Pettorelli, N., 2013. The Normalized Difference Vegetation
Index, Oxford Scholarship, England.
Pôças, I., Paço, T.A., Paredes, P., Cunha, M., Pereira, L.S.,
2015. Estimation of Actual Crop Coefficients Using
Remotely Sensed Vegetation Indices and Soil Water
Balance Modelled Data, Remote Sensing, 7: 2373-2400.
Rousseeuw, P.J., 1987. Silhouettes: A Graphical Aid to the
Interpretation and Validation of Cluster Analysis,
Journal of Computational and Applied Mathematics,
20: 53-65.
Sun, L., Gao, F., Anderson, M. C., Kustas, W. P., Alsina,
M. M., Sanchez, L., Sams, B., McKee, L., Dulaney, W.,
White, W. A.,. Alfieri, J. G., Prueger, J. H., Melton, F.,
Post, K., 2017. Daily mapping of 30 m LAI and NDVI
Using Data Mining Techniques to Forecast the Normalized Difference Vegetation Index (NDVI) in Table Grape
193

for Grape Yield Prediction in California Vineyards,
Remote Sensing, 9(4): 317.
Yu, B., Shang, S., 2018. Multi-Year Mapping of Major
Crop Yields in an Irrigation District from High Spatial
and Temporal Resolution Vegetation Index, Sensors,
18(11): 3787.
APPENDIX
Table A.1: Silhouette values according to the number of
clusters.
# Clusters s(i) # Clusters s(i)
2 0.5829 22 0.4958
3 0.5363 23 0.5123
4 0.4902 24 0.5435
5 0.5027 25 0.5378
6 0.4817 26 0.5529
7 0.4812 27 0.6140
8 0.4672 28 0.6140
9 0.5104 29 0.6140
10 0.5120 30 0.6140
11 0.5138 31 0.6140
12 0.5062 32 0.6140
13 0.4965 33 0.6140
14 0.4836 34 0.6140
15 0.4935 35 0.6140
16 0.5225 36 0.6140
17 0.5213 37 0.6140
18 0.5088 38 0.6140
19 0.4947 39 0.6140
20 0.5210 40 0.6140
21 0.5023
ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems
194
