A Split-Merge Evolutionary Clustering Algorithm

Veselka Boeva

, Milena Angelova

and Elena Tsiporkova

Computer Science and Engineering Dept., Blekinge Institute of Technology, Karlskrona, Sweden

Computer Systems and Technologies Dept., Technical University of Soﬁa, Plovdiv, Bulgaria

The Collective Center for the Belgian Technological Industry, Brussels, Belgium

Keywords:

Data Mining, Evolutionary Clustering, Bipartite Clustering, PubMed Data, Unsupervised Learning.

Abstract:

In this article we propose a bipartite correlation clustering technique that can be used to adapt the existing

clustering solution to a clustering of newly collected data elements. The proposed technique is supposed to

provide the ﬂexibility to compute clusters on a new portion of data collected over a deﬁned time period and

to update the existing clustering solution by the computed new one. Such an updating clustering should better

reﬂect the current characteristics of the data by being able to examine clusters occurring in the considered

time period and eventually capture interesting trends in the area. For example, some clusters will be updated

by merging with ones from newly constructed clustering while others will be transformed by splitting their

elements among several new clusters. The proposed clustering algorithm, entitled Split-Merge Evolutionary

Clustering, is evaluated and compared to another bipartite correlation clustering technique (PivotBiCluster)

on two different case studies: expertise retrieval and patient proﬁling in healthcare.

1 INTRODUCTION

In this work, we are interested in developing evolu-

tionary clustering techniques that are suited for ap-

plications affected by concept drift phenomena. In

many practical applications such as, expertise (or doc-

ument) retrieval systems the information available in

the system database is periodically updated by col-

lecting (extracting) new data. The available data el-

ements, e.g., experts in a given domain, are usually

partitioned into a number of disjoint subject cate-

gories. It is becoming impractical to re-cluster this

large volume of available information. Proﬁling of

users with wearable applications with the purpose to

provide personalized recommendations is another ex-

ample. As more users get involved one needs to re-

cluster the initial clusters and also assign new incom-

ing users to the existing clusters. In the context of pro-

ﬁling of machines (industrial assets) for the purpose

of condition monitoring the existing original clusters

can become outdated caused by aging of the machines

and degradation of performance due to inﬂuence of

changing external factors. This outdating of models

is in fact a concept drift and requires that the cluster-

ing techniques, used for deriving the original machine

proﬁles, can deal with such a concept drift and enable

reliable and scalable model update.

Incremental clustering methods process one data

element at a time and maintain a good solution by ei-

ther adding each new element to an existing cluster or

placing it in a new singleton cluster while two existing

clusters are merged into one (Charikar et al., 1997).

Incremental algorithms also bear a resemblance to

one-pass stream clustering algorithms (O’Callaghan

et al., 2001). Although, one-pass stream clustering

methods address the scalability issues of the cluster-

ing problem, they are not sensitive to the evolution of

the data, because they assume that the clusters are to

be computed over the entire data stream.

The clustering scenario discussed herein is differ-

ent from the one treated by incremental clustering

methods. Namely, the evolutionary clustering tech-

niques considered in this work are supposed to pro-

vide the ﬂexibility to compute clusters on a new por-

tion of data collected over a deﬁned time period and

to update the existing clustering solution by the com-

puted new one. Such an updating clustering should

better reﬂect the current characteristics of the data by

being able to examine clusters occurring in the con-

sidered time period and eventually capture interesting

trends in the area. We propose and study two dif-

ferent clustering algorithms to be suited for the dis-

cussed scenario: PivotBiCluster (Ailon et al., 2011)

and Split-Merge Evolutionary Clustering. Both algo-

Boeva, V., Angelova, M. and Tsiporkova, E.

A Split-Merge Evolutionary Clustering Algorithm.

DOI: 10.5220/0007573103370346

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 337-346

ISBN: 978-989-758-350-6

337

rithms are bipartite correlation clustering algorithms

that do not need prior knowledge about the optimal

number of clusters in order to produce a good cluster-

ing solution. In the ﬁnal clustering generated by the

PivotBiCluster algorithm some clusters are obtained

by merging clusters from both side of the graph, i.e.

some of existing clusters will be updated by some of

the computed new ones. However, existing clusters

cannot be split by the PivotBiCluster algorithm even

the corresponding correlations with clusters from the

newly extracted data elements reveal that these clus-

ters are not homogeneous. This has motivated us to

develop a new Split-Merge Evolutionary Clustering

algorithm that overcomes this disadvantage. Namely,

our algorithm is able to analyze the correlations be-

tween two clustering solutions and based on the dis-

covered patterns it treats the existing clusters in dif-

ferent ways. Thus some clusters will be updated by

merging with ones from newly constructed clustering

while others will be transformed by splitting their el-

ements among several new clusters.

The rest of the paper is organized as follows. Sec-

tion 2 reviews related works. Section 3 brieﬂy dis-

cusses the PivotBiCluster algorithm and describes the

proposed Split-Merge Evolutionary Clustering tech-

nique. Section 4 introduces the two case studies used

to compare and evaluate the two algorithms. Section 5

presents the evaluation of the proposed evolutionary

clustering algorithm in expertise retrieval and patient

proﬁling in healthcare domains and discusses the ob-

tained results. Section 6 is devoted to conclusions and

future work.

2 RELATED WORK

The model of incremental algorithms for data cluster-

ing is motivated by practical applications where the

demand sequence is unknown in advance and a hier-

archical clustering is required. Incremental clustering

methods process one data element at a time and main-

tain a good solution by either adding each new ele-

ment to an existing cluster or placing it in a new sin-

gleton cluster while two existing clusters are merged

into one (Charikar et al., 1997).

To qualify the type of cluster structure present

in data, Balcan introduced the notion of clusterabil-

ity (Balcan et al., 2008). It requires that every element

be closer to data in its own cluster than to other points.

In addition, Balcan showed that the clusterings that

adhere to this requirement are readily detected ofﬂine

by classical batch algorithms. On the other hand, it

was proven by Ackerman (Ackerman and Dasgupta,

2014) that no incremental method can discover these

partitions. Thus, batch algorithms are signiﬁcantly

stronger than incremental methods in their ability to

detect cluster structure.

Incremental algorithms also bear a resemblance to

one-pass clustering algorithms for data stream prob-

lems (O’Callaghan et al., 2001). Such algorithms

need to maintain a substantial amount of informa-

tion so that important details are not lost. For ex-

ample, the algorithm in (O’Callaghan et al., 2001)

is implemented as a continuous version of k-means

algorithm which continues to maintain a number of

cluster centers which change or merge as necessary

throughout the execution of the algorithm. In ad-

dition, Lughofer proposes a dynamic clustering al-

gorithm which is equipped with dynamic split-and-

merge operations and which is also dedicated to incre-

mental clustering of data streams (Lughofer, 2012).

In (Fa and Nandi, 2012) similarly to the approach of

Lughofer a set of splitting and merging action condi-

tions are deﬁned, where optional splitting and merg-

ing actions are only triggered during the iterative pro-

cess when the conditions are met. Although, one-pass

stream clustering methods address the scalability is-

sues of the clustering problem, they are not sensitive

to the evolution of the data because they assume that

the clusters are to be computed over the entire data

stream.

The clustering scenario discussed herein is differ-

ent from the one treated by incremental clustering

methods. Namely, the evolutionary clustering tech-

nique proposed in this work is supposed to provide

the ﬂexibility to compute clusters on a new portion of

data collected over a deﬁned time period and to up-

date the existing clustering solution by the computed

new one.

Gionis et al. proposed an approach to clustering

that is based on the concept of aggregation (Gionis

et al., 2007). They are interested in a problem in

which a number of different clusterings are given on

some data set of elements. The objective is to produce

a single clustering of the elements that agrees as much

as possible with the given clusterings. Clustering ag-

gregation provides a framework for dealing with a

variety of clustering problems. For instance, it can

handle categorical or heterogeneous data by produc-

ing a clustering on each available attribute and then

aggregating the produced clusterings into a single re-

sult. Another possibility is to combine the results

of several clustering algorithms applied on the same

dataset etc. Clustering aggregation can be thought as

a more general model of multi-view clustering pro-

posed in (Bickel and Scheffer, 2004). The multi-view

approach considers clustering problems in which the

available attributes can be split into two independent

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

338

subsets. A clustering is produced on each subset and

then the two clusterings are combined into a single re-

sult. Consensus clustering algorithms deal with sim-

ilar problems to those treated by clustering aggrega-

tion techniques. Namely, such algorithms try to rec-

oncile clustering information about the same data set

coming from different sources (Boeva et al., 2014) or

from different runs of the same algorithm (Goder and

Filkov, 2008). The both clustering techniques are not

suited for our scenario, since they are used to inte-

grate a number of clustering results generated on one

and the same data set.

An interesting split-merge-evolve algorithm for

clustering data into k number of clusters is proposed

by Wang et al. (Wang et al., 2018). The algorithm

randomly divides data into k clusters initially, then re-

peatedly splits bad clusters and merges closest clus-

ters to evolve the ﬁnal clustering result. This algo-

rithm has the ability to optimize the clustering result

in scenarios where new data samples may be added in

to existing clusters. However, a k cluster output is al-

ways provided by the algorithm, i.e. it is not sensitive

to the evolution of the data, as well.

The idea for the proposed Split-Merge Evolution-

ary Clustering algorithm is inspired by the work of

Xiang et al. (Xiang et al., 2012). They have pro-

posed a split-merge framework that can be tailored

to different applications. The framework models two

clusterings as a bipartite graph which is decomposed

into connected components, and each component is

further decomposed into subcomponents. Pairs of

related subcomponents are then taken into consid-

eration in designing a clustering similarity measure

within the framework.

3 METHODS

3.1 Description of the Framework

Let us formalize the cluster updating problem we

are interested in. We assume that X is the available

set of data points and each data point is represented

by a vector of attributes (features). In addition, the

data points are partitioned into k groups, i.e. C =

, C

, . . . , C

} is an existing clustering solution of X

and each C

(i = 1, 2, . . . , k) can be considered as a dis-

joint cluster. In addition, a new set X

of recently ex-

tracted data elements (samples) is created, i.e. X ∩ X

is an empty set. Each data point in X

is again repre-

sented by a list of attributes and C

= {C

, C

, . . . , C

}

is a clustering solution of X

. The objective is to pro-

duce a single clustering of X ∪X

by combining C and

in such a way that the obtained clustering realis-

tically reﬂects the current distribution in the domain

under interest.

3.2 Pivot Bi-Clustering Algorithm

Two existing clustering techniques are suitable for

the considered context: correlation clustering (Bansal

et al., 2004) and bipartite correlation clustering (Ailon

et al., 2011). The latter algorithm seems to be better

aligned to our clustering scenario. In Bipartite Corre-

lation Clustering (BCC) a bipartite graph is given as

input, and a set of disjoint clusters covering the graph

nodes is output. Clusters may contain nodes from ei-

ther side of the graph, but they may possibly contain

nodes from only one side. A cluster is thought as a

bi-clique connecting all the objects from its left and

right counterparts. Consequently, a ﬁnal clustering is

a union of bi-cliques covering the input node set. We

compare our Split-Merge correlation clustering algo-

rithm described in the following section with PivotBi-

Cluster realization of the BCC algorithm (Ailon et al.,

2011). The PivotBiCluster algorithm is implemented

according to the original description given in (Ailon

et al., 2011).

Notice that in our considerations the input graph

nodes of the PivotBiCluster algorithm are clusters and

in the ﬁnal clustering some clusters are obtained by

merging clusters (nodes) from both sides of the graph,

i.e. some of the existing clusters will be updated by

some of the computed new ones. However, existing

clusters cannot be split by the BCC algorithm even

the corresponding correlations with clusters from the

newly extracted data elements reveal that these clus-

ters are not homogeneous.

3.3 Split-Merge Evolutionary

Clustering Algorithm

In this paper, we propose an evolutionary clustering

algorithm that overcomes the above mentioned disad-

vantage of BCC algorithm. Namely, our algorithm is

able to analyze the correlations between two cluster-

ing solutions C and C

and based on the discovered

patterns it treats the existing clusters (C) in different

ways. Thus, some clusters will be updated by merg-

ing with ones from newly constructed clustering (C

)

while others will be transformed by splitting their ele-

ments among several new clusters. One can ﬁnd some

similarity between our idea and an interactive cluster-

ing model proposed in (Awasthi et al., 2017). In this

model, the algorithm starts with some initial cluster-

ing of data and the user may request a certain cluster

to be split if it is overclustered (intersects two or more

clusters in the target clustering). The user may also

A Split-Merge Evolutionary Clustering Algorithm

339

request to merge two given clusters if they are under-

clustered (both intersect the same target cluster).

As it was already mentioned in Section 2 our evo-

lutionary clustering algorithm is inspired by a split-

merge framework proposed by Xiang et al. in (Xiang

et al., 2012). By modeling the intrinsic relation be-

tween two clusterings as a bipartite graph, they have

designed a split-merge framework that can be used

to obtain similarity measures to compare clusterings

on different data sets. The problem addressed in this

article is different from the one considered by Xiang

et al. (Xiang et al., 2012). Namely, we concern with

the development of split-merge framework that can be

used to adjust the existing clustering solution to newly

arrived data. Our framework also models two cluster-

ings (the existing and the newly constructed one) as a

bipartite graph which is decomposed into connected

components (bi-cliques) (see Fig. 1 (a), (b) and (c)).

Each component is further analysed and if it is neces-

sary it is decomposed into subcomponents (see Fig. 1

consideration in producing the ﬁnal clustering solu-

tion. For example, if an existing cluster is overclus-

tered (Fig. 1 (b)), i.e. it intersects two or more clus-

ters in the new clustering, it is split between those. If

several existing clusters intersect the same new clus-

ter, i.e. they are underclustered (Fig. 1 (a)), they are

merged with that cluster.

Let us formally describe the proposed Split-Merge

Evolutionary Clustering algorithm. The input bipar-

tite graph is G = (C, C

, E), where C and C

are sets

of clusters of left and right nodes and E is a subset of

C ×C

that represents correlations between the nodes

of two sets. The three main steps of the algorithm are

as follows:

1. Initially, all unreachable nodes from either side of

G are found. These are singleton clusters (out-

liers) in our ﬁnal clustering solution. We remove

these nodes from the graph.

2. At the second step, all bi-cliques of G are found

and considered. If a bi-clique connects a node

from the left side (C) of G with several nodes from

the elements of this node have to be split among

the corresponding nodes from C

(see Fig. 1 (b)).

In the opposite case, i.e., when we have a bi-clique

that connects a node from the right side (C

) of G

with several nodes from left those nodes have to

be merged with that node (cluster) (see Fig. 1 (a)).

All clustered nodes are removed from the graph.

3. At the ﬁnal step, the remained bi-cliques are de-

composed into split/merge subcomponents. Each

bi-clique, which is a bipartite graph, is trans-

formed into a tripartite graph constructed by two

(split and merge) bipartite graphs. Suppose G

, C

, E

) is the considered bi-clique. Then the

corresponding tripartite graph is built by the fol-

lowing two bipartite graphs: G

= (C

, E

)

and G

= (E

, C

, E

), where C

, C

and E

are

ones from G

, E

is a subset of C

× E

that repre-

sents correlations between the nodes of C

and E

is a subset of E

×C

representing correla-

tions between the nodes of E

and C

(see Fig. 1 (c)

and (d)). For example, c

∈ C

will be correlated

with all pairs (c

, c

) ∈ E

such that c

≡ c

, and

∈C

will be correlated with all pairs (c

, c

) ∈ E

such that c

≡ c

. First all overclustered nodes

of G

are split and new temporary clusters are

formed as a result. Then we perform the corre-

sponding merging for all underclustered nodes in

. For example, in Fig. 1 (d), cluster C

will

ﬁrst be split among clusters C

, C

and C

, i.e.

three new clusters, denoted by (C

, C

), (C

, C

)

and (C

, C

), will be obtained. Then at the third

step of the algorithm clusters (C

, C

) and (C

, C

)

will be merged together.

The pseudocode of the proposed Split-Merge Evo-

lutionary Clustering algorithm is given in Algo-

rithm 1. In addition, the algorithm is illustrated with

an example in Fig. 2. The clustering solution gener-

ated by the Split-Merge Clustering is compared to one

produced by the PivotBiCluster. It is interesting to no-

tice that the two algorithms will produce very differ-

ent clustering solutions on the same input graph. For

example, the Split-Merge Clustering will generate a

4-cluster solution while one obtained by the PivotBi-

Cluster will have only 2 clusters. The latter number is

quite low taking into account the number of clusters

in the two input clusterings. Moreover, as it was men-

tioned in the previous section the PivotBiCluster al-

gorithm cannot produce a clustering solution in which

existing clusters are split among new clusters.

4 CASE STUDIES

Luxburg et al. (von Luxburg et al., 2012) argue that

clustering should not be treated as an application-

independent mathematical problem, but should

always be studied in the context of its end-use. Mo-

tivated by this study we have illustrated and initially

evaluated the two studied clustering algorithms in

two different case studies. We have compared the

performance of the algorithms in expertise retrieval

domain by applying them on data extracted from

PubMed repository. In addition, a case study in proﬁl-

ing patients in healthcare domain has been conducted.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

340

Algorithm 1 : Split-Merge Evolutionary Clustering Algo-

rithm.

1: function SPLIT-MERGE(G = (C, C

, E))

2: for all nodes c ∈ C ∪C

do (*First step*)

3: if c is an unreachable node then

4: Turn c into a singleton and remove it from G

5: end if

6: end for

7: for all nodes c ∈ C ∪C

do (*Second step*)

8: Choose c

uniformly at random from C

9: if c

is the only node from C that takes part in a bi-

clique connecting it with one or several nodes from C

then

10: Split c

among the corresponding nodes from C

11: end if

12: end for

13: for all nodes c ∈ C ∪C

14: Choose c

uniformly at random from C

15: if c

is the only node from C

that takes part in a bi-

clique connecting it with one or several nodes from C then

16: Merge c

with the corresponding nodes from C

17: end if

18: end for

19: for all nodes c ∈ C do (*Third step*)

20: Choose c

uniformly at random from C

21: Split c

among its adjacent nodes from C

and form

new temporary clusters

22: end for

23: for all nodes c

∈ C

24: Choose c

uniformly at random from C

25: Merge c

with its adjacent nodes from the built set of

temporary clusters

26: Remove the clustered nodes from G

27: end for

28: return all connected components (bi-cliques) as clusters

of X ∪X

29: end function

4.1 Expertise Retrieval Domain

Currently, organizations search for new employees

not only relying on their internal information sources,

but they also use data available on the Internet to

locate the required experts. Thus the need for ser-

vices that enable ﬁnding experts grows especially

with the expansion of virtual organizations. People

are more often working together by forming task-

speciﬁc teams across geographic boundaries. The for-

mation and sustainability of such virtual organizations

greatly depends on their ability to quickly trace those

people who have the required expertise. In response

to this, research on identifying experts from on-line

data sources (Abramowicz et al., 2011), (Balog and

de Rijke, 2007), (Bozzon et al., 2013), (Hristoskova

et al., 2013), (Stankovic et al., 2011), (Singh et al.,

2013), (Tsiporkova and Tourw

e, 2011),(Boeva et al.,

2016), (Boeva et al., 2018), (Lin et al., 2017) has been

gradually gaining interest in the recent years.

4.1.1 Case Description

Let us suppose that an expertise recommender system

for ﬁnding biomedical experts based on on-line data is

under development. The system builds and maintains

Figure 1: Split-Merge Framework: a) a bi-clique that con-

tains underclustered nodes (C

and C

intersect C

); b) a

bi-clique that contains an overclustered node (C

intersects

, C

and C

); c) a bi-clique that has to be decomposed into

subcomponents d) a tripartite graph obtained by decompos-

ing the bi-clique depicted in (c) into split (left) and merge

(right) subcomponents.

a big repository of biomedical experts by extracting

the information about experts’ peer-reviewed articles

that are published and indexed in PubMed. The ex-

perts stored in such big data repositories are usually

partitioned into a number of subject categories in or-

der to facilitate the further search and identiﬁcation of

experts with the appropriate skills and knowledge. In

addition, the system database is periodically updated

by extracting new data. It is becoming impractical

to re-cluster this large volume of available informa-

tion. Therefore, the objective is to update the existing

expert partitioning by the clustering produced on the

newly extracted experts.

4.1.2 Data Sets

The data needed for our task is extracted from

PubMed, which is one of the largest repositories of

peer-reviewed biomedical articles published world-

wide. Medical Subject Headings (MeSH) is a con-

trolled vocabulary developed by the US National Li-

brary of Medicine for indexing research publications,

articles and books. Using the MeSH terms associated

A Split-Merge Evolutionary Clustering Algorithm

341

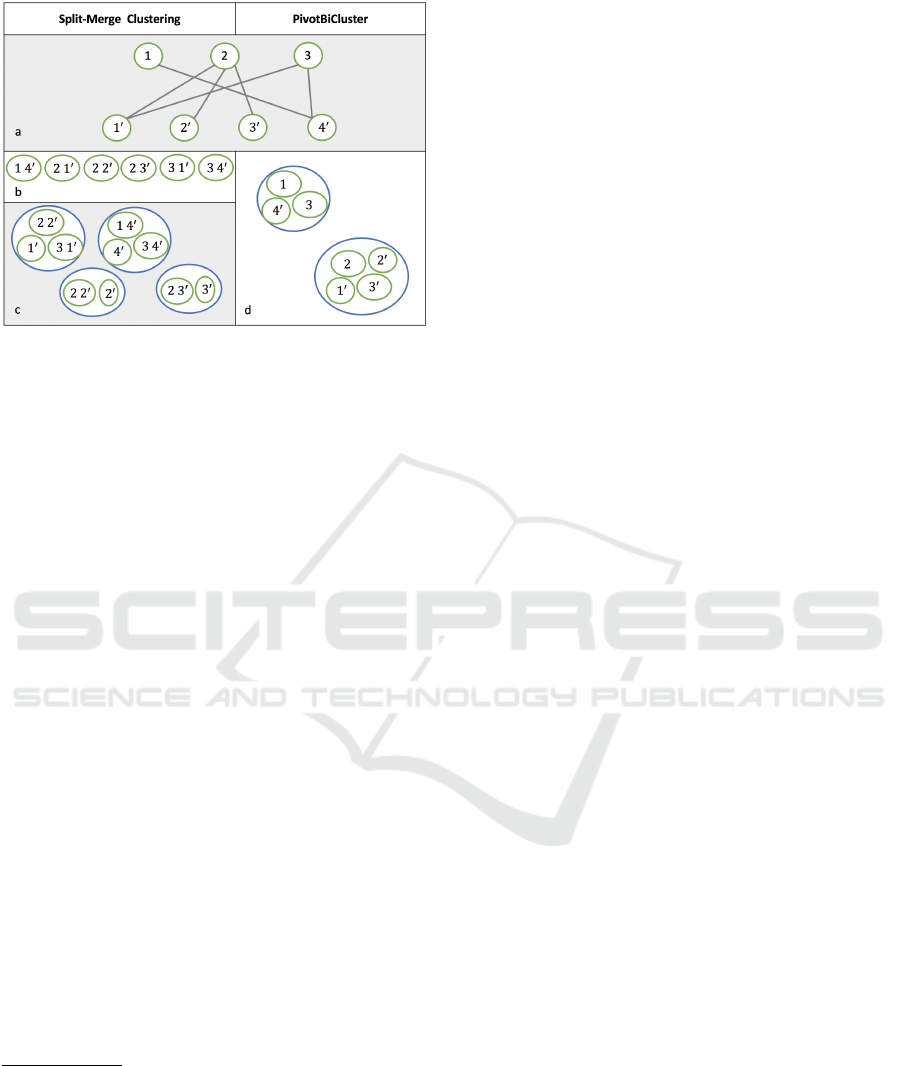
Figure 2: Clustering solutions generated by Split-Merge

Clustering (left) and PivotBiCluster (right), respectively: a)

the input bipartite graph; b) temporary clusters formed by

Split-Merge Clustering after splitting overclustered nodes

from the left (upper) set ({1, 2, 3}) of the graph among cor-

responding nodes from the right (below) set ({1

, 2

, 3

, 4

});

c) the ﬁnal clustering solution produced by Split-Merge

Clustering, d) the ﬁnal clustering solution produced by Piv-

otBiCluster.

with peer-reviewed articles published by the above

considered researchers and indexed in the PubMed,

we extract such authors and construct their expert pro-

ﬁles. An expert proﬁle is deﬁned by a list of MeSH

terms used in the PubMed articles of the author in

question to describe her/his expertise areas.

We have extracted a set of 4343 authors from the

PubMed repository. After resolving the problem with

ambiguity

the set is reduced to one containing only

3753 different researchers. Then each author is also

represented by a list of all different MeSH headings

used to describe the major topics of her/his PubMed

articles.

In addition to the above set of 3753 biomedical re-

searchers we have used a set of 102 researchers who

have taken part in a scientiﬁc conference devoted to

integrative biology

. These researchers have been

grouped into 8 clusters with respect to the confer-

ence sessions. They are considered as relevant ex-

perts, thus, used as the ground truth to benchmark the

results of the studied clustering algorithms.

A cluster is represented by a circle or an ellipse. An ellipse

with two cluster labels inside, e.g., 2 1

, means that some

elements from the ﬁrst cluster (2) are added to the second

cluster (1

This problem refers to the fact that multiple proﬁles may

represent one and the same person and therefore must be

merged into a single generalized expert proﬁle.

Integrative Biology 2017: 5th International Conference on

Integrative Biology (London, UK, June 19-21, 2017).

4.2 Patient Proﬁling in Healthcare

Domain

The volumes of current patient data as well as their

complexity make clinical decision making more chal-

lenging than ever for physicians and other care givers.

Decision Support Systems (DSS) can be used to pro-

cess data and form recommendations and/or predic-

tions to assist such decision makers (Belle et al.,

2013). Data mining techniques can be applied to iden-

tify pattern or rules about various quality problems.

For example, proﬁling together patients who share

similar clinical conditions can facilitate the diagno-

sis and initial treatment of individuals having similar

illness predisposition.

The ability of machine learning and data mining

tools to identify signiﬁcant features from complex

data sets detects their importance. A variety of such

techniques have already been proposed in healthcare

domain (Cheng et al., 2013), (Aishwarya and Anto,

2014), (Golino et al., 2014), (Menasalvas et al., 2018).

4.2.1 Case Description

Let us suppose a decision support system that can be

used to study and associate the patient anthropometric

measurements with the person increased risk for car-

diovascular disease, e.g., hypertension, is under de-

velopment. The core of the system is based on cluster-

ing techniques which provide groupings of proﬁles of

individuals with similar anthropometric features, e.g.,

such as body mass index (BMI), waist (WC) and hip

circumference (HC), and waist hip ratio (WHR). The

classiﬁcation of groups of patients who share proper-

ties in common might provide useful information for

the diagnosis and initial management of risk for hy-

pertension or other cardiovascular disease. For exam-

ple, the patients who share the same proﬁle should

probably have similar predisposition and should be

provided similar healthcare recommendations. In ad-

dition, the system must be able to update and im-

proved the produced anthropometric categories by the

clusters generated on newly arrived patients anthropo-

metric measurements.

4.2.2 Data Sets

The dataset used in this case study is publicly avail-

able and published in (Golino et al., 2014). The data

contains 400 undergraduate students aged between 16

and 63 years old, where a 56.3% are women. The fol-

lowing features describe the data: age, obesity, BMI,

WC, HC, WHR, Systolic Blood Pressure (SBP), Di-

astolic Blood Pressure (DBP), preh for women and

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

342

hyper for men, where the preh and hyper are classi-

ﬁcation labels that show what kind of blood pressure

the individual has (e.g., regular or hyper). According

to the results published in (Li et al., 2016) people can

be grouped into six clusters depending on their blood

pressure. Based on this the individuals in our test data

set have been grouped into 6 clusters. This grouping

is considered as the ground truth to benchmark the

results generated by the two studied clustering algo-

rithms.

5 EXPERIMENTS AND

DISCUSSION

5.1 Metrics

The data mining literature provides a range of differ-

ent cluster validation measures, which are broadly di-

vided into two major categories: external and inter-

nal (Jain and Dubes, 1988). External validation mea-

sures have the beneﬁt of providing an independent

assessment of clustering quality, since they validate

a clustering result by comparing it to a given exter-

nal standard. However, an external standard is rarely

available. Internal validation techniques, on the other

hand, avoid the need for using such additional knowl-

edge, but have the alternative problem to base their

validation on the same information used to derive the

clusters themselves.

In this work, we have implemented three differ-

ent validation measures for estimating the quality of

clusters, produced by the two studied clustering al-

gorithms. Since we have a benchmark clustering of

the set of 102 biomedical researchers, described in the

foregoing section, we have used the F-measure as an

external validation metric (Larsen and Aone, 1999).

The F-measure is the harmonic mean of the precision

and recall values for each cluster. For a perfect clus-

tering the maximum value of the F-measure is 1. In

addition, Silhouette Index (SI) has been applied as an

internal measure to assess compactness and separa-

tion properties of the generated clustering solutions

(Rousseeuw, 1987). The values of Silhouette Index

vary from -1 to 1.

In addition to the above two metrics, we have used

Jaccard index (Jaccard similarity coefﬁcient) (Jac-

card, 1912) to evaluate the stability of a clustering

method. The Jaccard Index ranges from 0 to 1, where

a higher value indicates a higher similarity between

clustering solutions. Jaccard Index has been used to

measure the similarity between the generated cluster-

ing solutions and the benchmark partitioning of the

data in the second case study.

5.2 Implementation and Availability

We used the Entrez Programming Utilities (E-

utilities) to download all the publications associated

with the extracted biomedical researchers (Sayers,

2010). The E-utilities are the public API to the NBCI

Entrez system and allow access to all Entrez databases

including PubMed, PMC, Gene, Nuccore and Pro-

tein. For calculation of semantic similarities between

MeSH headings, we use MeSHSim which is imple-

mented in an R package. It also supports querying

the hierarchy information of a MeSH heading and

information of a given document including title, ab-

straction and MeSH headings (Zhou and Shui, 2015).

The two studied clustering algorithms (Split-Merge

Clustering and PivotBiCluster) are implemented in

Python. The cluster validation measures (see Sec-

tion 5.1) used to validate the clustering solutions gen-

erated in our experiments are implemented in scikit-

learn library. Scikit-learn is a Python library for data

mining and data analysis. Supplementary information

is available at GitLab

5.3 Case Study 1

Initially, we use the ﬁrst built data set that con-

tains 3753 PubMed expert proﬁles of biomedical re-

searchers. Each expert proﬁle is a vector of subject

keywords describing the expert’s competence. The

researchers of this set are randomly separated in two

sets. The one set contains 2407 experts grouped into

122 clusters by using k-means and the other one has

1346 experts separated into 112 clusters again by ap-

plying k-means. The number of clusters is determined

by clustering each set applying k-means for different

k and evaluating the obtained solutions by SI. The

two clustering algorithms are then executed twice to

integrate the clustering solutions of these two data

sets. The clustering solution produced by the Pivot-

BiCluster has 95 clusters while the proposed Split-

Merge Clustering algorithm has generated a solution

with 104 clusters. The generated clustering solutions

are evaluated by SI and the average scores are -0.158

(PivotBiCluster) and 0.058 (Split-Merge Clustering),

respectively. Evidently, the Split-Merge Clustering

algorithm outperforms PivotBiCluster on this data set.

We believe this is due to the fact that it adjusts better

to data by being able not only to merge those clusters

https://gitlab.com/machine learning vm/clustering

techniques

A Split-Merge Evolutionary Clustering Algorithm

343

that are underclustered but also to split those that are

overclustered.

Next, the benchmark set of 102 different expert

proﬁles is used to generate 10 test data sets couples.

Each test couple separates the researchers randomly

in two sets. The one set (containing 70 experts) of

each couple presents the available set of experts, and

another one (32 experts) is the set of newly extracted

experts. In that way, 10 test clustering couples are

created.

We have studied two different experiment scenar-

ios. In the ﬁrst scenario the experts in each test set are

grouped into clusters of experts with similar expertise

based on the conference session information, i.e. each

set is partitioned into 8 clusters. In the second sce-

nario for each data sets the optimal number of clusters

is determined by clustering the set applying k-means

for different k and evaluating the obtained solutions

by SI. In this way, two different experiments have

been conducted on 10 test data set couples. In both

experiments, the PivotBiCluster algorithm is executed

10 times (i.e., 100 executions in total for each ex-

periment) to integrate the corresponding clusterings.

In comparison to the PivotBiCluster, the Split-Merge

Clustering is conducted only once on each test cou-

ple, since it does not start by a random cluster selec-

tion. Namely, it initially identiﬁes those bi-cliques

that have to be split and merged, respectively, i.e. the

clustering result is not dependent on the algorithm ini-

tialization.

The obtained results for SI and F-measure are

shown in Table 1 and Table 2, respectively. Observe

that the PivotBiCluster outperforms the Split-Merge

Clustering algorithm only in one case. Namely, it has

generated a higher F-measure value than the Split-

Merge Clustering algorithm in the ﬁrst experiment.

It is interesting to notice that in the second experi-

ment (see Table 2) the SI scores are not only higher

in comparison to the ones generated in the ﬁrst exper-

iment, but they are also positive. Evidently, using the

optimal number of clusters signiﬁcantly improves the

quality of the generated clustering solutions with re-

spect to compactness and separation properties. How-

ever, the corresponding F-measure scores are lower

than the ones generated in the ﬁrst experiment.

The above results support the mentioned above ar-

guments of Luxburg et al. (von Luxburg et al., 2012)

that the cluster evaluation methods can produce con-

tradictory results and often do not serve their purpose.

The main point of the authors is that clustering al-

gorithms cannot be evaluated in a problem indepen-

dent way, i.e. the known cluster validation measures

cannot be used to evaluate the usefulness of the clus-

tering. It is still not clear how we can measure the

usefulness of a newly developed clustering algorithm.

Certainly, the proposed Split-Merge Clustering algo-

rithm needs further evaluation and validation in case

studies from different application domains. Thus in

the next section we present an additional evaluation

of the two studied algorithms in a case study from

healthcare domain.

Table 1: Experiment 1: Average F-measure and SI values

generated on the clustering solutions of the 10 test data set

couples.

Experiment 1

Metrics PivotBiCluster Split-Merge Clust.

F-measure 0.618 0.582

SI -0.145 -0.129

Table 2: Experiment 2: Average F-measure and SI values

generated on the clustering solutions of the 10 test data set

couples.

Experiment 2

Metrics PivotBiCluster Split-Merge Clust.

F-measure 0.321 0.331

SI 0.137 0.157

5.4 Case Study 2

In this case study, we have used the data set explained

in Section 4.2.2. This set consists of 400 individ-

ual proﬁles and it is used to generate 10 test data

set couples by randomly separating the individuals

in two sets. The one set (280 patients) of each cou-

ple presents the available set of individual proﬁles,

and another one (120 individuals) is the set of newly

collected patients’ proﬁles. In that way similar to

the ﬁrst case study we have created 10 test data set

couples. Notice that each patient proﬁle is a vector

of the patient’s anthropometric features (BMI, WC,

HC, WHR), and the patient’s Systolic Blood Pres-

sure (SBP) and Diastolic Blood Pressure (DBP). The

patients’ proﬁles of each set have been grouped in

6 clusters according to (Li et al., 2016), see Sec-

tion 4.2.2. Namely, the individuals have been grouped

in six clusters depending on their blood pressure. The

obtained clusters are presented by their centroids.

Analogously to the ﬁrst case study, the PivotBi-

Cluster has been executed ten times for each test data

set couple (i.e., 100 executions in total). The algo-

rithm considers clusters in random order and gener-

ates a different clustering solution for each execu-

tion. As a result, the average value over these ten

executions has been calculated. The above random-

ness is not presented in the Split-Merge Clustering al-

gorithm. Therefore, it has been executed only once

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

344

over each test data set couple. Both algorithms are

explained in more detail in Section 3.

The generated clustering solutions are again eval-

uated by SI and F-measure. The obtained average SI

scores are -0.013 (PivotBiCluster) and -0.170 (Split-

Merge Clustering), respectively. Evidently, the Pivot-

BiCluster outperforms the Split-Merge Clustering al-

gorithm with respect to this evaluation criteria. The

results obtained by F-measure also support the better

performance of PivotBiCluster (0.71 against 0.46 for

Split-Merge Clustering) on this data set. However, it

is interesting to observe that the number of clusters of

the clustering solutions generated by the PivotBiClus-

ter on the test data set couples varies from 1 to 5 while

in the case of the Split-Merge Clustering the individ-

uals are grouped into 5 or 6 clusters. Notice that the

benchmark clustering (Section 4.2.2) has 6 clusters.

The above results have motivated us to use Jac-

card Index for an additional comparison of the two

studied algorithms. Namely, we have applied the Jac-

card Index to measure the similarity between the gen-

erated clustering solutions and the benchmark clus-

tering. The corresponding values are 0.081 (Pivot-

BiCluster) and 0.291 (Split-Merge Clustering), i.e.,

the Split-Merge Clustering algorithm has generated a

higher average Jaccard score than the PivotBiCluster.

In addition, we have evaluated the two clustering

algorithms with respect to the purity of the gener-

ated clustering solutions. For this purpose we con-

sider how the two main classes (regular and hyper

blood pressure) are distributed among the clusters.

The score obtained for the benchmark clustering is

0.16. The values generated for the two studied al-

gorithms are 0.025 (PivotBiCluster) and 0.17 (Split-

Merge Clustering), respectively. Evidently, the Split-

Merge Clustering performs better than PivotBiCluster

with respect to this criteria and manages to preserve

a level of purity closed to one of the benchmark clus-

tering.

6 CONCLUSION AND FUTURE

WORK

In this work, we have proposed a novel evolutionary

clustering technique, entitled Split-Merge Evolution-

ary Clustering, that can be used to adapt the existing

clustering solution to a clustering of newly collected

data elements. The proposed technique has been com-

pared to PivotBiCluster, an existing clustering algo-

rithm that is also suitable for concept drift scenarios.

The two algorithms have been evaluated and demon-

strated in two different case studies. The Split-Merge

Clustering algorithm has shown better performance

than the PivotBiCluster in most of the studied experi-

mental scenarios.

For future work, we aim to pursue further compar-

ison and evaluation of the two clustering algorithms in

different application domains and on richer data sets.

REFERENCES

Abramowicz, W., Bukowska, E., Dzikowski, J., Filipowska,

A., and Kaczmarek, M. (2011). Semantically en-

abled experts ﬁnding system - ontologies, reasoning

approach and web interface design. In ADBIS 2011,

Research Communications, Proc. II of the 15th East-

European Conference on Advances in Databases and

Information Systems, September 20-23, Vienna, Aus-

tria, pages 157–166.

Ackerman, M. and Dasgupta, S. (2014). Incremental clus-

tering: The case for extra clusters. In Proceedings of

the 27th International Conference on Neural Informa-

tion Processing Systems - Volume 1, NIPS’14, pages

307–315.

Ailon, N., Avigdor-Elgrabli, N., Liberty, E., and van

Zuylen, A. (2011). Improved approximation algo-

rithms for bipartite correlation clustering. In Algo-

rithms - ESA 2011 - 19th Annual European Sympo-

sium, Saarbr

ucken, Germany, September 5-9, 2011.

Proceedings, pages 25–36.

Aishwarya, A. and Anto, S. (2014). A medical decision

support system based on genetic algorithm and least

square support vector machine for diabetes disease di-

agnosis. International Journal of Engineering Sci-

ences & Research Technology, 3(4):4042–4046.

Awasthi, P., Balcan, M. F., and Voevodski, K. (2017). Lo-

cal algorithms for interactive clustering. Journal of

Machine Learning Research, 18(3):1–35.

Balcan, M.-F., Blum, A., and Vempala, S. (2008). A

discriminative framework for clustering via similar-

ity functions. In Proceedings of the Fortieth Annual

ACM Symposium on Theory of Computing, STOC ’08,

pages 671–680.

Balog, K. and de Rijke, M. (2007). Finding similar experts.

In Proceedings of the 30th Annual International ACM

SIGIR Conference on Research and Development in

Information Retrieval, SIGIR ’07, pages 821–822.

Bansal, N., Blum, A., and Chawla, S. (2004). Correlation

clustering. Machine Learning, 56(1-3):89–113.

Belle, A., Kon, M. A., and Najarian, K. (2013). Biomedical

informatics for computer-aided decision support sys-

tems: A survey. The Scientiﬁc World Journal, pages

1–8.

Bickel, S. and Scheffer, T. (2004). Multi-view clustering.

In Proceedings of the Fourth IEEE International Con-

ference on Data Mining, ICDM ’04, pages 19–26.

Boeva, V., Angelova, M., Boneva, L., and Tsiporkova, E.

(2016). Identifying a group of subject experts using

formal concept analysis. In 8th IEEE International

Conference on Intelligent Systems, IS 2016, Soﬁa,

Bulgaria, September 4-6, IS IEEE, pages 464–469.

A Split-Merge Evolutionary Clustering Algorithm

345

Boeva, V., Angelova, M., Lavesson, N., Rosander, O., and

Tsiporkova, E. (2018). Evolutionary clustering tech-

niques for expertise mining scenarios. In Proceedings

of the 10th International Conference on Agents and

Artiﬁcial Intelligence, ICAART, Volume 2, Funchal,

Madeira, Portugal, January 16-18, pages 523–530.

Boeva, V., Tsiporkova, E., and Kostadinova, E. (2014).

Analysis of Multiple DNA Microarray Datasets, pages

223–234. Springer Berlin Heidelberg.

Bozzon, A., Brambilla, M., Ceri, S., Silvestri, M., and

Vesci, G. (2013). Choosing the right crowd: Ex-

pert ﬁnding in social networks. In Proceedings of the

16th International Conference on Extending Database

Technology, EDBT ’13, pages 637–648. ACM.

Charikar, M., Chekuri, C., Feder, T., and Motwani, R.

(1997). Incremental clustering and dynamic informa-

tion retrieval. In Proc. of the 29th Annual ACM Sym-

posium on Theory of Computing, STOC ’97, pages

626–635.

Cheng, C. W., Chanani, N., Venugopalan, J., Maher, K., and

Wang, M. D. (2013). An icu clinical decision support

system using association rule mining. Translational

Engineering in Health and Medicine, IEEE, 1(2):8–

17.

Fa, R. and Nandi, A. K. (2012). Smart: Novel self splitting-

merging clustering algorithm. In European Signal

Processing Conference, Bucharest, Romania, August,

27-32. IEEE.

Gionis, A., Mannila, H., and Tsaparas, P. (2007). Clustering

aggregation. ACM Transaction of Knowledge Discov-

ery Data, 1(1).

Goder, A. and Filkov, V. (2008). Consensus clustering al-

gorithms: Comparison and reﬁnement. In ALENEX,

pages 109–234.

Golino, H. F., de Brito Amaral, L. S., Duarte, S. F. P., and

et al. (2014). Predicting increased blood pressure us-

ing machine learning. Journal of Obesity, 2014.

Hristoskova, A., Tsiporkova, E., Tourw

e, T., Buelens, S.,

Putman, M., and Turck, F. D. (2013). A graph-based

disambiguation approach for construction of an expert

repository from public online sources. In ICAART

2013 - Proceedings of the 5th International Confer-

ence on Agents and Artiﬁcial Intelligence, Volume 2,

Barcelona, Spain, 15-18 February, pages 24–33.

Jaccard, P. (1912). The distribution of ﬂora in the alpine

zone. New Phytologist, 11:37–50.

Jain, K. A. and Dubes, C. R. (1988). Algorithms for Clus-

tering Data. Prentice-Hall, Inc.

Larsen, B. and Aone, C. (1999). Fast and effective text min-

ing using linear-time document clustering. In Proc.

of the 5th ACM SIGKDD International Conference

on Knowledge Discovery and Data Mining, KDD’99,

pages 16–22. ACM.

Li, Y., Feng, X., Zhang, M., Zhou, M., Wang, N., and

Wangb, L. (2016). Clustering of cardiovascular be-

havioral risk factors and blood pressure among people

diagnosed with hypertension: a nationally representa-

tive survey in china. Sci Rep., 6:27627.

Lin, S., Hong, W., Wang, D., and Li, T. (2017). A survey

on expert ﬁnding techniques. Journal of Intelligent

Information Systems, 49:255–279.

Lughofer, E. (2012). A dynamic split-and-merge approach

for evolving cluster models. Evolving Systems, 3:135–

151.

Menasalvas, E. R., Tu

nas, M. J., Bermejo, G., Gonzalo,

C. M., Rodr

ıguez-Gonz

alez, A., Zanin, M., Pedro, C.

G. D., M

endez, M., Zaretskaia, O., Rey, J., Parejo,

C., Bermudez, L. J. C., and Provencio, M. (2018).

Proﬁling lung cancer patients using electronic health

records. Journal of Medical Systems, 42:1–10.

O’Callaghan, L., Mishra, N., Meyerson, A., Guha, S., and

Motwani, R. (2001). Streaming-data algorithms for

high-quality clustering. In Proceedings of IEEE In-

ternational Conference on Data Engineering, pages

685–694.

Rousseeuw, P. J. (1987). Silhouettes: A graphical aid to

the interpretation and validation of cluster analysis.

Journal of Computational and Applied Mathematics,

20:53–65.

Sayers, E. (2010). A General Introduction to the E-utilities.

In: Entrez Programming Utilities Help [Internet].

Bethesda (MD): National Center for Biotechnology

Information (US).

Singh, H. S., Singh, R., Malhotra, A., and Kaur, M. (2013).

Developing a biomedical expert ﬁnding system using

medical subject headings. In Healthcare informatics

research, 19(4): 243–249.

Stankovic, M., Jovanovic, J., and Laublet, P. (2011). Linked

data metrics for ﬂexible expert search on the open

web. In Proceedings of the 8th Extended Semantic

Web Conference on The Semantic Web: Research and

Applications - Volume Part I, ESWC’11, pages 108–

123. Springer-Verlag.

Tsiporkova, E. and Tourw

e, T. (2011). Tool support

for technology scouting using online sources. In

Advances in Conceptual Modeling. Recent Develop-

ments and New Directions, pages 371–376. Springer

Berlin Heidelberg.

von Luxburg, U., Williamson, R. C., and Guyon, I. (2012).

Clustering: Science or art? In Proceedings of ICML

Workshop on Unsupervised and Transfer Learning,

volume 27 of Proceedings of Machine Learning Re-

search, pages 65–79.

Wang, M., Huang, V., and Bosneag, A.-M. C. (2018). A

novel split-merge-evolve k clustering algorithm. In

IEEE 4th International Conference on Big Data Com-

puting Service and Applications (BigDataService),

Bamberg, Germany, March 26-29.

Xiang, Q., Mao, Q., Chai, K. M. A., Chieu, H. L., Tsang,

I. W., and Zhao, Z. (2012). A split-merge framework

for comparing clusterings. In ICML, pages 1055-

1062.

Zhou, J. and Shui, Y. (2015). MeSHSim: MeSH(Medical

Subject Headings) Semantic Similarity Measures. R

package version 1.4.0.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

346