On-the-Fly Construction of Composite Events in Scenario-Based

Modeling using Constraint Solvers

Guy Katz

, Assaf Marron

, Aviran Sadon

and Gera Weiss

The Hebrew University of Jerusalem, Jerusalem, Israel

Weizmann Institute of Science, Rehovot, Israel

Ben-Gurion University of the Negev, Be’er Sheva, Israel

Keywords:

Scenario-Based Programming, Behavioral Programming, Constraint Solvers, SMT Solvers.

Abstract:

Scenario-Based Programming is a methodology for modeling and constructing complex reactive systems from

simple, stand-alone building blocks, called scenarios. These scenarios are designed to model different traits

of the system, and can be interwoven together and executed to produce cohesive system behavior. Existing

execution frameworks for scenario-based programs allow scenarios to specify their view of what the system

must, may, or must not do only through very strict interfaces. This limits the methodology’s expressive power

and often prevents users from modeling certain complex requirements. Here, we propose to extend Scenario-

Based Programming’s execution mechanism to allow scenarios to specify how the system should behave using

rich logical constraints. We then leverage modern constraint solvers (such as SAT or SMT solvers) to resolve

these constraints at every step of running the system, towards yielding the desired overall system behavior. We

provide an implementation of our approach and demonstrate its applicability to various systems that could not

be easily modeled in an executable manner by existing Scenario-Based approaches.

1 INTRODUCTION

Modeling complex systems is a difﬁcult and error-

prone task. The emerging Scenario-Based Program-

ming approach (SBP) (Damm and Harel, 2001; Harel

and Marelly, 2003; Harel et al., 2012b) aims to miti-

gate this difﬁculty. The key notion underlying SBP is

modeling through the speciﬁcation of scenarios, each

of which represents a certain aspect of the system’s

behavior. These scenarios may describe either desir-

able behaviors that the system should strive to uphold,

or undesirable behaviors that the system should try to

avoid. The models produced in SBP are fully exe-

cutable: when composed together according to cer-

tain underlying semantics, the scenarios yield cohe-

sive system behavior.

The SBP approach has been implemented in

dedicated frameworks such as the Play-Engine and

PlayGo for the visual language of Live Sequence

Charts (LSC) language (Harel and Marelly, 2003;

Harel et al., 2010a) or ScenarioTools (Greenyer et al.,

2017) for the Scenario Modeling Langauge (SML)

textual language. Further, SBP has been implemented

on top of several standard programming languages,

such as Java (Harel et al., 2010b), C++ (Harel and

Katz, 2014), and JavsScript (Bar-Sinai et al., 2018),

and was amalgamated with the Statecharts visual for-

malism (Marron et al., 2018)

SBP has been successfully used in modeling com-

plex systems, such as web-servers (Harel and Katz,

2014), cache coherence protocols (Harel et al., 2016),

robotic controllers (Gritzner and Greenyer, 2018), and

as part of the Wise Computing effort aimed at turning

computers into proactive members of system devel-

opment teams (Harel et al., 2018).

Despite the diversiﬁed adaptations of SBP for

various programming languages and for various use

cases, a common theme remains: in all existing

frameworks, scenarios are interwoven using a very

basic mechanism. Speciﬁcally, during execution the

scenarios are synchronized at predetermined points,

and at every synchronization point each scenario de-

clares a set of events it would like to see triggered,

and a set of events it forbids from being triggered.

The execution framework then selects for triggering

one event that is requested by at least one scenario

and is not blocked by any of the scenarios. The event

is broadcast to all scenarios, and the execution con-

tinues until the next synchronization point is reached.

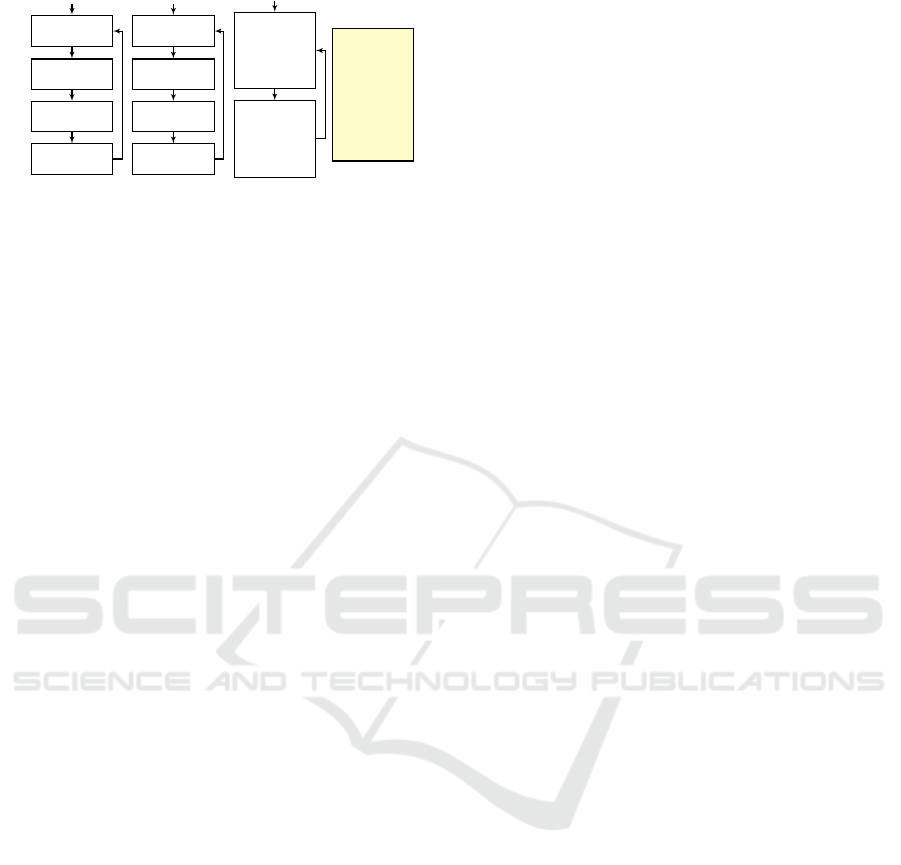
An example appears in Fig. 1.

Katz, G., Marron, A., Sadon, A. and Weiss, G.

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers.

DOI: 10.5220/0007573801410154

In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 141-154

ISBN: 978-989-758-358-2

141

wait for

WATERLOW

request

ADDHOT

request

ADDHOT

request

ADDHOT

ADDHOTWATER

wait for

WATERLOW

request

ADDCOLD

request

ADDCOLD

request

ADDCOLD

ADDCOLDWATER

wait for

ADDHOT

while

blocking

ADDCOLD

wait for

ADDCOLD

while

blocking

ADDHOT

STABILITY

···

WATERLOW

ADDHOT

ADDCOLD

ADDHOT

ADDCOLD

ADDHOT

ADDCOLD

···

EVENT LOG

Figure 1: (From (Harel et al., 2014)) A scenario-based

model of a system that controls the water level in a tank

with hot and cold water taps. Each scenario object is de-

picted as a transition system, where the nodes represent the

predetermined synchronization points. The scenario object

ADDHOTWATER repeatedly waits for WATERLOW events

and requests three times the event ADDHOT; and the sce-

nario object ADDCOLDWATER performs a symmetrical op-

eration with cold water. In a model that includes only the

objects ADDHOTWATER and ADDCOLDWATER, the three

ADDHOT events and three ADDCOLD events may be trig-

gered in any order during execution. In order to maintain

the stability of the water temperature in the tank, the sce-

nario object STABILITY enforces the interleaving of AD-

DHOT and ADDCOLD events by using event blocking. The

execution trace of the resulting model appears in the event

log.

It has been suggested that some of the beneﬁts of

SBP come from this basic event selection semantics.

In particular, the event selection mechanism is suf-

ﬁciently simple to make scenario-based models easy

to analyze automatically using formal compositional

techniques (Harel et al., 2013; Harel et al., 2015c;

Harel et al., 2016; Greenyer and Gritzner, 2018), and

even to automatically distribute, repair and synthesize

them (Harel et al., 2012a; Harel et al., 2015a; Stein-

berg et al., 2015; Greenyer et al., 2016b; Greenyer

et al., 2016a), primarily because it facilitates the au-

tomatic composition of individual scenarios that are

simple and succinct (Harel et al., 2015b). Still, the

simplicity of the event selection mechanism seems to

be a limiting factor in some cases — requiring cum-

bersome workarounds to associate complex behaviors

with simple events, and at times even preventing the

use of SBP for modeling a particular system alto-

gether.

Consider, as a toy example, a model for an au-

tonomous drone. The model contains various behav-

ioral scenarios for modeling the drone’s horizontal

and vertical movement. At every execution cycle of

the model, independent actions may be triggered for

each of the axes — climb, descend, or maintain height

for the vertical axis, and turn right, turn left or main-

tain direction for the horizontal axis. Further, climb

or descend actions are parameterized by a numeri-

cal value indicating the angular velocity of the climb

or descent; and similarly, turn right or turn left ac-

tions are parameterized by the angular velocity of the

turn. It is unclear how to express such a model in

SBP. For example, because the traditional event se-

lection mechanisms stipulates that precisely one ac-

tion be triggered in every cycle, how shall we express

the fact that multiple actions (horizontal and vertical)

may be triggered in the same cycle? And how shall

we account for the inﬁnitely-many numerical parame-

ters for ascent, decent and turning actions? Some dis-

cretization schemes may be proposed, but this seems

to go against the grain of SBP — which aims at cre-

ating simple and intuitive scenario objects.

In this paper, we propose an extension to SBP that

utilizes constraint solvers: automated tools that take

as input a set of variables and certain kinds of con-

straints on these variables, and return a variable as-

signment that satisﬁes the given constraints (or in-

dicate that no such assignment exists). Automated

solvers have become widespread and highly success-

ful in the last decades, particularly in tasks related

to program analysis and veriﬁcation (Clarke et al.,

2018). Here, we propose to use such solvers on-the-

ﬂy, as part of the execution mechanism of scenario-

based models. Speciﬁcally, we propose to augment

SBP such that in each synchronization point, each

scenario contributes to the creation of a formula that

is fed into the constraint solver — and the assignment

(of all variables) which is returned by the solver as-

sumes the role of the event selected for triggering.

Further, the very act of selecting simple events from

some set is extended into constructing, or computing

complex events based on rich speciﬁcations. This al-

lows us to specify scenarios that interact using a far

richer formalism, and can thus model more complex

systems. Compared to existing SBP approaches, this

allows for the scenarios to collaboratively construct

the events, not only choose among events that each

propose.

In particular, using constraint solvers in this fash-

ion allows us to seamlessly model the autonomous

drone system: the constraints produced in every syn-

chronization point may include multiple variables in-

dicating multiple actions; and these constraints may

include arbitrary numerical values, indicating, e.g.,

the various angular velocity parameters. We elaborate

on this example later on.

In this work we describe how a solver-based SBP

modeling framework can be implemented, focusing

mainly on the semantics but also propose a syntax,

with accompanying implementation details and ex-

amples for completeness.

The paper is organized as follows. In Section 2

we provide some necessary background on SBP and

on constraint solvers. In Section 3 we propose our

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

142

extension to SBP that allows modelers to integrate it

with constraints solvers, followed by illustrative ex-

amples. In Section 4 we describe an evaluation of our

approach, followed by a discussion of related work in

Section 5. We conclude in Section 6.

2 BACKGROUND

2.1 Scenario-Based Modeling

Before we discuss our proposed extensions to SBP,

we begin by recapping the existing, commonly used

formulation and semantics. Formally, a scenario-

based model consists of independent scenario objects

that are interwoven at run time. Each scenario re-

peatedly declares sets of events which, from its own

perspective, should, may, or must not occur. At run-

time, the scenarios are executed simultaneously and

are synchronized by a mechanism responsible for se-

lecting events that constitute the integrated system be-

havior. The scenarios never interact with each other

directly; all interactions are carried out through the

event selection mechanism.

Following the deﬁnitions in (Katz, 2013), we de-

ﬁne a scenario object O over event set E as the tuple

O = hQ,δ,q

,R,Bi, where the components are inter-

preted as follows:

• Q is a set of states, each representing one of the

predetermined synchronization points;

• q

is the initial state;

• R : Q → 2

and B : Q → 2

map states to the sets

of events requested and blocked at these states (re-

spectively); and

• δ : Q × E → 2

is a transition function, indicating

how the object reacts when an event is triggered.

Scenario objects can be composed, in the follow-

ing manner. For objects O

= hQ

,δ

i and

= hQ

,δ

i over a common event set

E, the composite scenario object O

k O

is deﬁned

by O

k O

= hQ

× Q

,δ,hq

i,R

∪ R

∪ B

where:

• h ˜q

, ˜q

i ∈ δ(hq

i,e) if and only if ˜q

∈

,e) and ˜q

∈ δ

,e); and

• The union of the labeling functions is deﬁned in

the natural way; e.g. e ∈ (R

∪ R

)(hq

i) if

and only if e ∈ R

) ∪ R

), and e ∈ (B

∪

)(hq

i) if and only if e ∈ B

) ∪ B

A behavioral model M is simply a collection of

scenario objects O

,...,O

, and the executions of

M are the executions of the composite object O = O

k ... k O

. Each such execution starts from the

initial state of O, and in each state q along the run an

enabled event is chosen for triggering, if one exists

(i.e., an event e ∈ R(q) − B(q)). Then, the execution

moves to state ˜q ∈ δ(q,e), and so on.

2.2 Constraint Solvers

As our proposed extensions to SBP rely heavily on

automated constraint solvers, we give here a very

brief introduction to some of these tools (and men-

tion sources of information for additional reading).

Broadly speaking, constraint solvers are automated

tools that take as input a set of constraints given as

a formula ϕ over a set of variables V , and either (i)

return a variable assignment that satisﬁes ϕ, or (ii) an-

swer that no such variable assignment exists. (A sat-

isfying assignment is usually called a model, but we

will refrain from using that term as to not overload it).

Different solvers differ in the kinds of constraints they

allow as part of their input, and many popular solvers

operate on constraints given in restricted forms of ﬁrst

order logic. The performance of these solvers (and the

complexity of the problems they solve) also closely

depends on the inputs they allow.

In this paper, we will focus on three kinds of au-

tomated solvers:

Boolean Satisﬁability (SAT) Solvers. These are

solvers that operate on a set V of Boolean variables,

and limit the constraint formula ϕ to be a quantiﬁer-

free propositional formula over the variables of V .

The solver then attempts to ﬁnd a Boolean assignment

that satisﬁes ϕ. For example, for V = {p,q}, the for-

mula ϕ

= (p ∨ q) ∧ (p ∨ ¬q) is satisﬁable, and one

satisfying assignment is p,¬q; whereas the formula

= (¬p ∨ ¬q) ∧ p ∧ q is unsatisﬁable. Although the

Boolean satisﬁability problem is NP-complete, there

exist many mature tools that can solve instances with

hundreds of thousands of variables (Nadel, 2009).

A particular kind of SAT solvers, called MaxSAT

solvers, attempt to ﬁnd a Boolean assignment that sat-

isﬁes as many of the input constraints as possible (and

not necessarily all of the constraints).

Linear Programming (LP) Solvers. LP solvers

operate on a set V of rational variables, and the con-

straint formula ϕ is a conjunction of linear constraints,

often referred to as a linear program. For example, for

the variables V = {x,y,z}, the constraint ϕ

= (x ≤

5) ∧ (x + y ≤ z) is satisﬁable, whereas the constraint

= (x ≤ 5) ∧ (y ≤ 2) ∧ (x + y ≥ 20) is unsatisﬁable.

LP is known to be solvable in polynomial time, al-

though many solvers use worst-case exponential al-

gorithms that turn out to be more efﬁcient in prac-

tice (Chv

atal, 1983).

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers

143

Satisﬁability Modulo Theories (SMT) Solvers.

These solvers can be regarded as generalized SAT

solvers, capable of handling formulas in rich frag-

ments of ﬁrst order logic. The satisﬁability of the for-

mulas is checked modulo background theories, which

intuitively restrict the search only to satisfying assign-

ments that “make sense” according to these certain

theories. For example, considering the theory of ar-

rays of integer elements with variable set V = {a,b},

the formula ϕ

= (a[3] ≥ b[5]) ∧ (a[4] ≤ b[0]) is sat-

isﬁable, whereas the formula ϕ

= (a = b) ∧ (a[4] 6=

b[4]) is unsatisﬁable. Modern SMT solvers support

many theories of interest, including various arithmetic

theories, the theory of uninterpreted functions, and

theories of arrays, of sets, of strings, and others (Bar-

rett and Tinelli, 2018). Further, these background the-

ories can be combined: for example, one can deﬁne

formulas that includes arrays of integers or sets of

strings, etc. The SMT problem is, in general, unde-

cidable, although certain background theories afford

efﬁcient decision procedures.

The three kinds of solvers are used for different

tasks, and all are highly successful. Many mature

tools exist, and a great deal of research is being put

into improving them further.

3 INTEGRATING SBP WITH

CONSTRAINT SOLVERS

3.1 Extending SBP

The notion underlying our proposed extension of SBP

is as follows. At each synchronization point, instead

of declaring sets of requested and blocked events,

each scenario object O

can instead declare a set

of constraint formulas Φ = {ϕ

,...,ϕ

} that are in-

tended as guiding rules for a solver-based mecha-

nisms that assembles the events. These constraint for-

mulas are labeled by a labeling function L

, which

takes a formula ϕ

and returns its labeling, i.e. a sub-

set of a ﬁnite set of predeﬁned labels L . The motiva-

tion for these labels is that they can be used to assign

different semantics to different constraint formulas.

For example, going back to the drone system de-

scribed in the introduction, one scenario can specify

that the total speeds of the rotors must be above some

threshold and another scenario can suggest to increase

one of the rotors. The labeling function is a protocol

through which the execution mechanism knows that

the ﬁrst is a “must” speciﬁcation and the latter is a

“may” condition.

At each synchronization point, the execution

mechanism collects the sets of constraint formulas

,...,Φ

produced by the individual scenario ob-

jects, and combines them into a global constraint for-

mula ϕ. This formula is then passed into a constraint

solver, and the satisfying assignment returned by the

solver is broadcast to all scenarios, which can then

change their states. If no satisfying assignment is

found, the SBP model is deadlocked, and the execu-

tion terminates. (Another possible extension in case a

deadlock is discovered is to wait for an external event,

along the lines proposed in (Harel et al., 2011), but

this is beyond our scope here).

Formally, we modify the deﬁnitions of SBP to

support integration with constraint solvers as follows.

Let V denote a set of variables, and let L denote a

ﬁnite set of labels. We deﬁne a scenario object O

over V, L as a tuple O = hQ,δ,q

,C,Li , where Q is

a set of states and q

is the initial state, as before.

The function C, which replaces the labeling func-

tions R and B in the previous deﬁnition, takes a state

q ∈ Q as input and returns a set of constraint formulas

Φ = {ϕ

,...,ϕ

} over the variables of V . The func-

tion L returns a labeling of these constraint formulas

according to the current state, i.e. L : Q × ξ → 2

where ξ represents the set of all possible formulas.

By convention, we require that L(q,ϕ) =

0 for every

ϕ such that ϕ /∈ C(q). The transition function δ is

now deﬁned as δ : Q×A(V ) → 2

, where A(V ) is the

set of all possible assignments to the variables of V .

Intuitively, given a speciﬁc state q and a variable as-

signment α ∈ A(V ), invoking δ(q,α) returns the set

of states the object may transition into.

In order to account for the new constraint for-

mulas, we modify the composition operator for

scenario objects as follows: For objects O

,δ

i and O

= hQ

,δ

i over

a common variable set V and a common label set

L , the composite scenario object O

k O

is de-

ﬁned by O

k O

= hQ

× Q

,δ,hq

i,C,Li, where

h ˜q

, ˜q

i ∈ δ(hq

i,α) if and only if ˜q

∈ δ

,α)

and ˜q

∈ δ

,α). The constraint-generating func-

tion C is deﬁned as C(hq

i) = C

) ∪ C

i.e. the constraints deﬁned by the individual objects

are combined and become the constraints deﬁned by

the composite object. We deﬁne L(hq

i,ϕ) =

,ϕ) ∪ L

,ϕ) using again the convention that

,ϕ) =

0 if ϕ /∈ C

The key difference between our extended seman-

tics and the original is in the event selection mecha-

nism. As before, a behavioral model M is a collec-

tion of scenario objects O

,...,O

, and the ex-

ecutions of M are the executions of the composite

object O = O

k O

k ... k O

. Each such execu-

tion starts from the initial state of O, and after each

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

144

state q along the run a variable assignment α is as-

sembled by invoking a constraint solver on a formula

ϕ constructed from C(q), according to the constraint

labeling L. Speciﬁcally, we assume that the modeler

also provides a constraint composition rule ψ. Given

the constraint-generating function C and the labeling

function L, ψ dictates how to construct for every state

q the constraint formula ϕ that should be passed to

the solver, and/or how to treat the various constraints

altogether (e.g., apply priorities among scenarios, or

apply various optimization goals when multiple so-

lutions exist). The execution then moves to state

˜q ∈ δ(q, α), and so on.

3.2 Illustrative Examples

The aforementioned framework is general, and can be

customized in several ways through the constraint for-

mulas, their labeling, and the constraint composition

rule ψ. We next illustrate this using a few simple ex-

amples.

Traditional SBP Semantics. The traditional se-

mantics of SBP can be obtained as follows. We al-

low only two labels L = {r,b}, where r represents re-

quest constraints and b represents block constraints.

In addition, we deﬁne the variable set V to contain

precisely one variable, V = {e}, representing the trig-

gered event. Next, we syntactically restrict the con-

straint formulas ϕ

to be of the form e = c for some

constant c; and ﬁnally, for any state q we deﬁne the

constraint composition rule to be:

ψ(q,C,L) = (

ϕ∈C(q) | r∈L(q,ϕ)

ϕ)∧(

ϕ∈C(q) | b∈L(q,ϕ)

¬ϕ)

Intuitively, at each state, each scenario object can de-

clare events it would like to see triggered (expressed

as constraints labeled r), and those it wants to prevent

from being triggered (expressed as constraints labeled

b). The constraint composition rule then translates

these individual constraints into a global formula rep-

resenting the fact that the triggered event needs to be

requested and not blocked (note that constraints la-

beled b are negated).

When using these particular restrictions, the

straightforward solver of choice is a SAT solver: since

the formula ϕ only contains propositional connectives

and the variable e can only take on a ﬁnite number of

values, we can encode these possible values using a

ﬁnite set of Boolean variables (this process is often

called bit-blasting). A modern SAT solver can then

be used for selecting the triggered event very quickly

— in a way that is likely to enable an execution that

is sufﬁciently fast for many application domains.

Autonomous Drone. The general framework we

proposed in the previous subsection can be used to

model complex interactions, which are either beyond

the reach of the traditional semantics, or at least re-

quire a great deal of effort on the modeler’s side. Let

us return to our toy aircraft example: a drone capa-

ble of simultaneous vertical and horizontal maneu-

vers. Using our extended modeling framework, we

can deﬁne our variable set V to include two variables,

V = {v, h}, where v represents the vertical angular ve-

locity and h represents the horizontal angular veloc-

ity. One scenario object can be used for setting up-

per and lower bounds on the vertical turning angular

velocities, due to the drone’s mechanical limitations

(see Fig. 2), and another can be used for limiting the

horizontal turning angular velocity (see Fig. 3). In

this case we require no labeling of the constraint, i.e.

L =

0, and the constraint composition rule ψ is a sim-

ply a conjunction of all the individual constraints.

= −5 ≤ v ≤ 5

true

Figure 2: A scenario object that puts hard limits on the ver-

tical turning angular velocity of the drone. The scenario has

a single synchronization point (indicated by a single state),

in which it contributes ϕ

= −5 ≤ v ≤ 5 to the global con-

straint set. The only transition, a self loop that does not

depend on the variable assignment returned by the solver,

indicates that the scenario continues to contribute this con-

straint, regardless of the satisfying assignment discovered

by the solver.

= −10 ≤ h ≤ 10

true

Figure 3: A scenario object that puts hard limits on the hor-

izontal turning angular velocity of the drone.

Without any additional limitations, i.e. if only

these two scenarios existed in the system, the con-

straint formula in any synchronization point would

be ϕ = ϕ

∧ ϕ

= (−5 ≤ v ≤ 5) ∧ (−10 ≤ h ≤ 10).

Because the constraint are arithmetical, linear con-

straints, we can use an LP solver to dispatch them;

and indeed, in this case an LP solver will return an

assignment such as v = 3, h = 0. Other objects in the

system, called actuators, may then process these val-

ues and adjust the drone’s engines accordingly.

Let us now consider a particular ﬂight situation.

Suppose another object is in charge of navigating the

drone to its destination, and that that object is request-

ing a right turn at an angular velocity of at least 6 de-

grees per second: ϕ

= h ≥ 6. Further suppose that

a sensor has detected an electrical wire up ahead, and

in order to circumvent it is requesting either that the

elevation be increased, or that a left turn be initiated:

= h ≤ −3 ∨ v ≥ 2. In that case, when the solver

is given the global constraint formula ϕ = ∧

i=1

, a

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers

145

possible solution is h = 8, v = 3 — which satisﬁes all

constraints, by both turning right and increasing the

drone’s altitude.

Dependency Management. So far, we have seen

two examples for constraint composition rules ψ:

when simulating the traditional SBP event selection

mechanism, we labeled individual constraints as re-

quest or block statements, and then composed them

accordingly; and in the drone example, we had no

labeling, and ψ was a simple conjunction. We now

demonstrate a situation in which yet another compo-

sition rule is useful.

Consider a system in charge of installing software

packages on a computer, similar to the standard pack-

age managers that ship with modern Linux distribu-

tions. Software packages have dependencies: for ex-

ample, installing package A might require that pack-

age B already be installed, in which case we say that

package A requires package B. Some packages may

also be incompatible with other packages: for exam-

ple, if package A is incompatible with package C, this

means that A cannot be installed alongside C. The

state of the system is the set of currently installed

software packages. Finally, the system is given a user-

supplied goal, such as “install A”. In order to achieve

the goal, the system needs to install A and any re-

quired packages, while removing the smallest number

of packages currently installed that A and its depen-

dencies are incompatible with. Of course, deciding

which packages to install and which to remove in or-

der to achieve an optimal result is a complex task.

To model this system using our extended version

of SBP, we can utilize a speciﬁc kind of SAT solver,

called a MaxSAT solver. A MaxSAT input formula

consists of subformulas labeled either hard or soft,

and the solver ﬁnds an assignment that satisﬁes the

hard constraints, and as many of the soft constraints

as possible. MaxSAT solvers play a crucial role in our

model, in the following way: for each package depen-

dency, we will introduce a scenario object that adds a

hard constraint that represents the dependency; and

we will introduce other scenario objects that express

the currently-installed packages as soft constraints.

That way, the MaxSAT solver will give us back an

assignment that indicates which packages should be

installed and which should be removed, in a way that

guarantees that the goal package is installed while the

number of previously installed packages that need to

be removed is minimized (Mancinelli et al., 2006;

Argelich and Lynce, 2008).

More speciﬁcally, our model for the package de-

pendency system is constructed as follows. The vari-

able set V consists of a Boolean variable for each

software package, e.g. {x

,...}, that signiﬁes

whether the package is installed (variable is true) or

not installed (variable is false). A change in the vari-

able’s value indicates that the package should be in-

stalled or removed. Our label set is ={h, s}, indicat-

ing whether a constraint is hard or soft, respectively.

Each dependency is represented by a dedicated ob-

ject; for example, the requirement “A requires B” is

encoded by the scenario object in Fig. 4. Other ob-

jects are used for encoding the soft constraints repre-

senting the currently installed packages—an example

appears in Fig. 5.

= (¬x

∨ x

)

true

Figure 4: A scenario object that encodes the fact the in-

stalling A requires B. Observe that the constraint is labeled

as hard, to indicate that it must never be violated.

= x

ϕ =

¬x

Figure 5: A scenario object that adds x

as a soft con-

straint if package B is currently installed (left state), and

contributes no constraints if it is not installed (right state).

Switching between the states is performed according to the

assignment discovered by the solver — speciﬁcally, it de-

pends on whether x

is assigned to true or not. We assume

the package is initially installed.

To avoid clutter, we omit the scenario object in

charge of reading the installation goal from the user,

and the scenario objects of the actuators in charge

of monitoring changes in consecutive variable assign-

ments and translating these changes into the installa-

tion or removal of packages.

4 IMPLEMENTATION AND

EVALUATION

In this section we evaluate the applicability of our ap-

proach by discussing its implementation, and by ap-

plying it to more complex problems.

4.1 Two Implementations

We developed a proof-of-concept implementation of

our approach in two platforms. The ﬁrst uses MAT-

LAB/Simulink. Scenario objects generate their con-

straints as strings. These strings are then passed into

MATLAB solve, the equation and system solver.

The solution yielded by the solver is then translated

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

146

into variable values that control classical Simulink-

driven behavior. The results of this behavior are also

fed back into the scenarios, which can then change the

constraints they present.

Below, we describe in detail a second im-

plementation, based on Python and the Z3 SMT

solver (De Moura and Bjorner, 2008). The framework

enables users to create fully-executable models using

the aforementioned approach, and then run them and

analyze the output. We plan to make the framework

available online in the near future, and also intend to

extend it; see some discussion in Section 6.

We began by implementing the basic SBP seman-

tics in our framework. For these semantics, the set

of allowed labels is L = {may,must,wait-for}: the

may label represents requested events, the must label

is used here to block the complement of the speciﬁed

event set, and the wait-for label is merely syntactic

sugar used to simplify deﬁning the transition relation.

This labeling scheme uses the composition rule

ψ(q,C,L) =

(

ϕ∈C(q) | may∈L(q,ϕ)

ϕ) ∧ (

ϕ∈C(q) | must∈L(q,ϕ)

ϕ)

For the event selection mechanism, we apply the Z3

solver for solving the formula ϕ, constructed from the

scenario objects’ may and must constraints as speci-

ﬁed above.

In our implementation, each scenario object is

modeled using a Python generator: a function that

can pause itself and yield control at any point, and

then be subsequently resumed when it is re-invoked

with the language’s next() idiom. This functionality

of Python allows us to implement the SBP idioms —

i.e., have the scenario objects pause at synchroniza-

tion points and be resumed when a satisfying assign-

ment for the variables of V has been found.

At each synchronization point, the scenario object

thus yields control, and passes to the event selection

mechanism a Python dictionary containing any sub-

set of the keys may, must, and wait-for, where each

such key is associated with a Z3 constraint.

The core of the code of the execution mechanism

appears in Fig. 6. The main function, run, takes as in-

put the set of scenario objects, and then executes the

model that is obtained by composing these objects.

Speciﬁcally, the function invokes the scenario objects,

one at a time, and waits for each of them to reach

its next synchronization point, indicated by a yield

statement. Once all scenario objects are synchro-

nized, the framework collects the constraints (in the

form of dictionaries, called tickets in the code) gen-

erated by the individual scenarios. These constraints

are then composed and passed on to Z3, which tries to

ﬁnd an assignment that satisﬁes all the must and may

constraints. If such an assignment is found, the execu-

tion framework wakes up the scenario objects whose

wait-for conditions are satisﬁed by the chosen as-

signment, and allows them to resume. They then con-

tinue to execute until they reach the next yield point,

and then the process is repeated again, possibly ad in-

ﬁnitum.

4.2 Examples

Hot-Cold Example. Using this framework, one can

specify the scenario objects from the water tank sys-

tem that appears in Fig. 1. This speciﬁcation appears

in Fig. 7. When the scenario objects deﬁned therein

are executed, the satisfying assignments obtained by

the solver during the execution alternate between as-

signing “hot” to true and “cold” to false, and vice

versa.

Consider now a situation where the customer de-

cides to change the requirements for the system. For

example, assume that the last requirement (that does

not allow to add two doses of the same type in a row)

is removed and, instead, the customer decides to add

the requirements modeled in Fig. 8. The scenarios

listed in the ﬁgure are then added instead of the last

scenario in Fig. 7.

Note that the new requirements involve a new

solver variable called “temp”, for temperature, that

the new scenarios control. Note also that this is done

without changing anything in the remaining scenarios

and that the remaining scenarios are not at all aware

of the new variable.

This example raises the following discussion:

consider, for example, the situation in Fig. 9 where,

as in the water tap example, two scenarios deal with

separate variables called x

and x

, respectively. Since

the ﬁrst scenario is not aware of the second one, it as-

sumes that the only may constraint for x

is that it is

greater than 50 — and so it does not expect the solver

to allow an assignment to x

that is smaller than 50.

According to our semantics, however, the composi-

tion rules produces the constraint ψ = x

> 50 ∨ x

50 to which the assignment {x

= 0,x

= 51} is valid.

A way to avoid this unintended behavior can be to la-

bel each proposition with the variable that it is aware

of and to solve for each set of variables separately.

Another way to avoid it can be to look for assignments

that maximize the number of satisﬁed may constraints,

e.g by using solvers that optimize the number of sat-

isﬁed clauses.

Leader Follower Benchmark Example. As a

more complex example, we used the extended SBP

modeling framework, with the composition rule de-

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers

147

def run ( scenarios):

global m # A variable where the solved model is published

tickets = [] # A list containing the tickets issued by the scenarios

# Run all scenario objects to their initial yield

for sc in scenarios :

ticket = next(sc) # Run the scenario to its first yield and collect the ticket

ticket [’sc’] = sc # Maintain a pointer to the scenario in the ticket

tickets.append ( ticket ) # Add the ticket to the list of tickets

# Main loop

while True :

# Compute a disjunction of may constraints and a conjunction of must constraints

(may , must ) = (False , True )

for ticket in tickets:

if ’may ’ in ticket:

may = Or (may , ticket [’ may’] )

if ’must ’ in ticket:

must = And(must , ticket [ ’must ’])

# Compute a satisfying assignment and break if it does not exist

sl = Solver ()

sl.add ( And(m ay , must ))

if sl. check() == sat :

m = sl. model ()

else:

break

# Reset the list of tickets before rebuilding it

oldTickets = tickets

tickets = []

# Run the scenarios to their next yield and collect new tickets

for oldTicket in oldTickets :

# Check whether the scenario waited for the computed assignment

if ’wait−for ’ in oldTicket and is tru e (m.eval( oldTicket [ ’wait−for’])):

# Run the scenario to the next yield and collect its new ticket

newTicket = next(oldTicket[’sc ’], ’ended ’)

# Add the new ticket to the list of tickets ( if the scenario didn ’t end)

if not newTicket == ’ended’:

newTicket[’sc’] = oldTicket [ ’sc ’] # Copy the pointer to the scenario

tickets.append ( newTicket )

else:

# Copy the old tickets to the new list

tickets.append ( oldTicket )

Figure 6: A python implementation of an extended SBP framework. The scenarios are assumed to be given as an array of

generators that return, using the yield command, labeled Z3 propositions expressed as dictionaries with keys that are subsets

of {may, must, wait-for}. In this code these dictionaries are called “tickets”.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

148

hot = Bool ( ’hot’)

cold = Bool(’ cold ’)

def mutual ex clusion ():

yield {’must’: Or(Not ( hot),Not( cold))}

def t hree hot ():

for i in range (3):

yield {’may ’: hot , ’wait−for’: hot}

def t hree c old ():

for j in range (3):

yield {’may ’: cold , ’w ait−for’: cold}

def n o t wo s a m e in a r o w ():

yield {’wait−for ’: true}

while True :

if is tru e (m[cold ]):

yield {’must’:Not(cold ),’wai t−for’: true}

if is tru e (m[hot]):

yield {’must’:Not(hot),’wait−for ’:true}

Figure 7: A simple example of a model that uses the solver-

based execution mechanism. The model sets the “hot” and

“cold” ﬂags, indicating that additional doses of hot and cold

water are added to a tank, according to the following ﬁve

rules: (1) do not add hot and cold doses at the same time;

(2) add three doses of hot water; (3) add three doses of cold

water; (4) never add two doses of the same type in a row.

scribed in preceding sub-section, to model a reac-

tive controller for a rover in a leader-follower sim-

ulation. In a leader-follower system, a controlled

follower rover tracks a leader rover. The follower

rover is required to follow the leader, while al-

ways staying at a safe distance from it, no mat-

ter how the leader behaves (assuming reasonable

bounds on speed and turn angles). This problem

served as a challenge problem in the MDETOOLS’18

workshop, where the organizers supplied a simula-

tion software for it. Participants of the workshop

were encouraged to demonstrate their various mod-

eling approaches by constructing software to con-

trol the follower rover (see mdetools.github.io/

mdetools18/challengeproblem.html).

The simulator provided in the MDETOOLS’18

challenge periodically emits the location of the rovers,

the distance between the rovers, and the heading angle

of the follower (compass). The follower rover can be

controlled by setting the power for the left and right

wheels in the range {−100,...,100}. For example, if

power to the left wheels is set to 40 and power to the

right wheels is set to 0, the rover will turn right.

The code for the scenarios that we created in or-

temp = Real(’ temp ’)

def h ot temp ():

yield {’must’: Implies(hot , temp > 50)}

def c old te mp ():

yield {’must’: Implies(cold , temp < 50)}

def after hot temp ():

while True :

yield {’wait−for ’: hot}

while is tru e (m[hot ]):

yield {’must’:temp>20,’wait−for’: true}

def after col d tem p ():

while True :

yield {’wait−for ’: cold}

while is tru e (m[cold ]):

yield {’must’: temp<80,’wait−for’: true}

Figure 8: New requirements for the water tap model: (1) the

temperature of a hot event must be above 50; (2) the temper-

ature of a cold event must be below 50; (3) the temperature

of an event that follows a hot event must be above 20; (4)

the temperature of an event that follows a cold event must

be below 80.

def scenario1 ():

yield {’may ’: x

> 50}

def scenario2 ():

yield {’may ’: x

> 50}

Figure 9: An example of an unintended behavior with the

may and must semantics. Since ψ = (x

<50)∨(x

>50), the

assignment {x

= 0, x

= 51} is valid despite the fact that

no scenario speciﬁed that x

may be smaller than 50. To ﬁx

this issue, we propose to change the composition rule so that

each set of variables and constraints is solved separately.

der to control the follower rover is listed in Fig.10.

The ﬁrst scenario speciﬁes the bounds for the pR and

pL variables, indicating the power to the right and left

wheels, respectively. The second scenario speciﬁes

forward and backward motion, where wheel power

is a function of the relative distance, i.e., when the

rovers get too far apart or too close, the follower grad-

ually increases or decreases power to the wheels, even

down to negative values. The third scenario speciﬁes

how the follower is steered towards the leader loca-

tion. When the relative angle (calculated from the

data emitted from the simulator) exceeds a speciﬁed

value (3 degrees), the follower will accordingly turn

left or right towards the leader. The last scenario spec-

iﬁes how to perform a turn by setting different power

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers

149

levels to the left and right wheels (note, however, that

this scenario does not trigger a turn — but rather con-

trols a turn that has been triggered by another sce-

nario). This example demonstrates the modularity of

the suggested approach and the ability to construct

complex behaviors using distinct behavioral aspects.

The ﬁnal behavior yielded in this case study is in-

deed very similar to the one yielded by the traditional

behavioral programming approach where events are

selected without a constraint solver, using direct ﬁl-

tering logic, which had been presented in (Greenyer

et al., 2018). The main difference between the tech-

niques used in these two implementations is that in the

implementation described in (Greenyer et al., 2018)

scenarios can only request ﬁnite sets of events while

here the spin() scenario, for example, speciﬁes in-

ﬁnitely many options that may happen. This allows,

as demonstrated by the turnpowers() scenario, to break

the speciﬁcation to better align with the requirements.

A Patrol Vehicle. Another example, described

brieﬂy to ﬁt space constraints, was implemented in

MATLAB/Simulink and associated solvers with the

tool described earlier in this section. It is a simula-

tion of an autonomous vehicle that moves repeatedly

in a ﬁxed route in the shape a ﬁgure eight. The main

scenarios reﬂect the following requirements: (1) The

vehicle should always attempt to accelerate to a maxi-

mum prespeciﬁed speed; (2) when the vehicle reaches

a sharp curve, it should reduce its speed below a spec-

iﬁed value until exiting the curve; and (3) after driv-

ing at a speed that is higher than a certain value, for a

length of time that is higher than some threshold, the

vehicle must reduce its allowed speed and accelera-

tion to some other values for a certain amount of time

(e.g., to avoid engine overheating).

This example illustrates and emphasizes the

power of scenarios as “stories” that progress from one

state to another and present different constraints at

different times and states. E.g., specifying the speed

constraints that hold only after detecting the arrival at

(or departure from) a sharp curve, or the passage of a

certain amount of time, appears more intuitive, and

is better aligned with the stated requirements, than

specifying ever-present constraints with conjunctions

of conditions, of, say, current speed and road curva-

ture, or, current speed and acceleration and the time

that has passed since certain events in the past.

5 RELATED WORK

The paper presents a particular approach to run-time

composition of behavior, namely, extending the ex-

isting SBP-style composition with speciﬁcation and

solving of constraints. Below we brieﬂy compare

SBP to other execution-time composition mechanism

with a special focus on the present context of con-

straint speciﬁcations (see (Harel et al., 2012b) for an

earlier, related analysis).

A key contribution of SBP over most other ap-

proaches to system speciﬁcation is its succinctness

and intuitiveness. These properties emerge from the

ability to specify forbidden behavior explicitly and di-

rectly, rather than as control-ﬂow conditions that pre-

vent certain pieces of code or speciﬁcation from ac-

tually doing the undesired action (this was accom-

plished ﬁrst with concrete lists of requested events

and ﬁlter-based blocking, and now, more generally,

with constraint solvers). For example, in SBP, one can

build, and sometimes even test, the speciﬁcation that

a vehicle is not allowed to enter a road intersection

when the trafﬁc light is red, before having coded how

vehicles behave. By comparison, other approaches,

like business-workﬂow engines, simulation engines,

and tools for test-driven development support intu-

itive speciﬁcation of executable use cases and sce-

narios, but their support for generic composition of

multiple scenarios and anti-scenarios is limited. Or-

dinary procedural and object oriented programming,

functional programming and logic programming lan-

guages provide for composition of behaviors, but the

requirements scenarios and use cases are not directly

visible in the code and are reﬂected only in emergent

properties of the actual execution.

SBP principles have been implemented in several

languages in both distributed and centralized environ-

ments. These implementations also position SBP as

a design pattern for using common constructs like

semaphores, messaging, and threads, as well as con-

cepts such as agent-orientation for incrementally and

alignment of code with requirements.

Publish-subscribe mechanisms provide for

straightforward parallel composition, but without

language support for forbidden behavior. Aspect

oriented programming (AOP) (Kiczales et al., 1997)

supports specifying and executing cross-cutting

concerns on top of a base application, but does

not support specifying forbidden behavior, state

management within an aspect, or symmetry between

aspects and base code, which SBP does.

Behavior-based models such as Brooks’s sub-

sumption architecture (Brooks, 1986) Branicky’s be-

havioral programming (Branicky, 1999), and LEGO

Mindstorms leJOS (see review in (Arkin, 1998)), also

call for constructing systems from behaviors. SBP is

a language-independent formalism with multiple im-

plementations and extends in a variety of ways each of

the coordination and arbitration mechanisms in those

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

150

def bounds ():

yield {’must’: −MAX ≤ pL ≤ MAX ∧ −MAX ≤ pR ≤ MAX}

def forward backward ():

while True :

if dist > CLOSE :

if dist < FAR :

yield {’may ’: pL = pR =

MAX(dist−CLOSE)

FAR−CLOSE

, ’wait−for ’: true}

else:

yield {’may ’: pL = pR = MAX , ’wait−for ’: true}

else:

if dist > VERY CLOSE :

yield {’may ’: pL = pR =

MAX(dist−CLOSE)

CLOSE−V ERY CLOSE

, ’wait−for ’: true}

else:

yield {’may ’: pL = pR = −MAX , ’wait−for ’: true}

def spin ():

while True :

if abs( dir er ror ) > 3:

if dir e rror > 0:

yield {’may ’: pL > pR, ’must’: pL > pR, ’wait−for ’: true}

else:

yield {’may ’: pL < pR, ’must’: pL < pR, ’wait−for ’: true}

else:

yield {’wait−for ’: true}

def turnpowers ():

yield {’must’: pL 6= pR ⇒ (pL = 0 ∧ pR = 40) ∨ (pL = 40 ∧ pR = 0)}

Figure 10: Main scenarios of the leader-follower model. The ﬁrst scenario speciﬁes the bounds for the pR and pL variables,

which represent the power for the left and right follower wheels. The second speciﬁes the follower forward and backwards

motion as a function of the distance from the leader. The third speciﬁes how the follower is steered towards the leader location

as function of dir error, which represents the relative angle (in degrees). The last scenario speciﬁes the turn powers.

architectures.

The execution semantics of behavioral program-

ming has similarities to the event-based scheduling

of SystemC (IEEE, 2006), which performs cyclical

co-routine scheduling by synchronization, evaluation,

update and notiﬁcation. SBP differs from SystemC

in its direct support for specifying scenarios and anti-

scenarios with direct relation to the original require-

ments, where SystemC provides a particular archi-

tecture for composing parallel component in certain

architectures and designs. In SBP the synchroniza-

tion is an inherent technique for continuously comply-

ing with all constraints that the requirements impose

where in SystemC synchronization is used for coordi-

nation in an otherwise parallel component execution.

This also implies differences in the details in the se-

mantics of synchronization, event selection, queuing,

and state management within a parallel component.

The BIP language (behavior, interaction, prior-

ity) and the concept of glue for assembling compo-

nents (Bliudze and Sifakis, 2008) pursue goals simi-

lar to SBPs with a focus on correctness by construc-

tion rather than on execution of intuitively speciﬁed

behaviors and constraints, with run-time resolution of

these constraints.

As mentioned earlier, SBP was recently imple-

mented in the visual formalism of Statecharts. The

Yakindu Statecharts tool extended Statecharts’ origi-

nal support for orthogonal, concurrent and hierarchi-

cal state machines (Harel, 1987), with optional speci-

ﬁcation of requested and blocked events in any state,

and a corresponding enhancement to the event selec-

tion semantics (Marron et al., 2018). These enhance-

ments also provide the formal deﬁnitions of SBP prin-

ciples, which are based on state machines and tran-

sition systems (see, e.g., (Harel et al., 2010b)), with

a direct, concrete, executable implementation that is

also readily understood by humans. This facilitates

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers

151

direct casting of inter-object behaviour, which usually

is only emergent when modeling with statecharts and

other state-machine languages, in the same language

and formalism as intra-object behaviour.

In SBP, direct execution and simulation of a model

is termed play-out. This is achieved by consulting

all constraints of the various scenarios before each

and every event selection. Thus, the complexity of

every runtime decision depends largely only on the

number of scenarios, and can ignore the number of

states in each scenario, and nondeterministic branch-

ing in future system and environment behavior. By

contrast, general program synthesis approaches for re-

active systems (see, e.g., (Bloem et al., 2012)) apply

model-checking, planning, and other techniques to-

ward resolving all speciﬁcation constraints and envi-

ronment assumptions a-priori. This produces a strat-

egy (e.g., a deterministic ﬁnite automaton) for suc-

cessfully handling all possible environment behaviors

at all reachable program states. Synthesis has been

applied on SBP speciﬁcations with request-and-block

idioms in, e.g., (Harel and Segall, 2012).

One approach for dealing with the large size of

state graphs that general synthesis has to analyze, is

via run-time planning (also termed on-the-ﬂy/online

synthesis) (see, e.g., (Blum and Furst, 1997)). In

run-time planning or synthesis, the execution mech-

anism considers a single starting state of the sys-

tem and the environment, and limits the number of

system and/or environment actions in the depth/hori-

zon of the search. This was implemented in SBP

in, e.g., smart play-out (Harel et al., 2002). An in-

teresting future research avenue is performing run-

time look-ahead or development-time total program

synthesis for SBP speciﬁcations containing rich con-

straints speciﬁcation like the ones shown in this paper.

Such research may include identifying categories of

constraint speciﬁcations that are richer than lists and

ﬁlters, but are more amenable to synthesis than arbi-

trary constraints.

Our use of constraint solvers in direct control of

executing SBP speciﬁcations, is different from other

uses of these tools in analysis and veriﬁcation of sys-

tems, including bounded model-checking (Biere et al.,

1999), symbolic execution (P

areanu and Visser,

2009), concolic testing (Sen, 2007), and others. SMT

solvers have been applied in such analysis tasks also

in the context of SBP; e.g., by enhancing SMT solvers

to deal more efﬁciently with transition systems (Katz

et al., 2015) and by using SMT solvers to efﬁciently

prove compositional properties of a collection of SBP

scenarios (Harel et al., 2013).

6 CONCLUSION

Scenario-based programming is a promising approach

for the design and modeling of complex systems, and

yet its applicability is somewhat hindered by the sim-

plistic way in which it interleaves scenario objects.

We proposed here a generalization of the approach

that lets objects interact in much more subtle and in-

tricate ways, and consequently allows SBP to faith-

fully model more complex systems. Our generaliza-

tion relies heavily on the use of automated constraint

solvers — tools that are capable of resolving the con-

straints imposed by the various scenarios and produce

a cohesive behavior. Apart from setting the theoretical

foundations for this extension, we developed a proof-

of-concept implementation and used it to demonstrate

the applicability of our approach.

In the future, we plan to continue this line of work

by developing support for model-checking, statisti-

cal analysis and synthesis algorithms for our extended

SBP. These tools exist already for traditional SBP, and

have proven useful — but extending them to our for-

mulation will entail accounting for the more ﬂexible

event selection mechanism. We also intend to apply

our extended SBP to additional, larger case-studies.

REFERENCES

Argelich, J. and Lynce, I. (2008). CNF Instances from the

Software Package Installation Problem. In Proc. 15th

RCRA Workshop on Experimental Evaluation of Algo-

rithms for Solving Problems with Combinatorial Ex-

plosion.

Arkin, R. C. (1998). Behavior-Based Robotics. MIT Press.

Bar-Sinai, M., Weiss, G., and Shmuel, R. (2018). BPjs: An

Extensible, Open Infrastructure for Behavioral Pro-

gramming Research. In Proc. 21st ACM/IEEE Int.

Conf. on Model Driven Engineering Languages and

Systems (MODELS), pages 59–60.

Barrett, C. and Tinelli, C. (2018). Satisﬁability Modulo

Theories. In Clarke, E., Henzinger, T., Veith, H.,

and Bloem, R., editors, Handbook of Model Check-

ing. Springer.

Biere, A., Cimatti, A., Clarke, E., and Zhu, Y. (1999). Sym-

bolic Model Checking without BDDs. In Proc. 5th Int.

Conf. on Tools and Algorithms for the Construction

and Analysis of Systems (TACAS), pages 193–207.

Bliudze, S. and Sifakis, J. (2008). A Notion of Glue Ex-

pressiveness for Component-Based Systems. In Proc.

19th Int. Conf. on Concurrency Theory (CONCUR),

pages 508–522.

Bloem, R., Jobstmann, B., Piterman, N., Pnueli, A., and

Saar, Y. (2012). Synthesis of Reactive(1) Designs.

Journal of Computer and System Sciences, 78(3):911–

938.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

152

Blum, A. L. and Furst, M. L. (1997). Fast Planning Through

Planning Graph Analysis. Artiﬁcial intelligence, 90(1-

2):281–300.

Branicky, M. (1999). Behavioral Programming. In Work-

ing Notes AAAI Spring Symposium on Hybrid Systems

and AI.

Brooks, R. (1986). A Robust Layered Control System for a

Mobile Robot. Robotics and Automation, 2(1):14–23.

Chv

atal, V. (1983). Linear Programming. W. H. Freeman.

Clarke, E., Henzinger, T., Veith, H., and Bloem, R. (2018).

Handbook of Model Checking. Springer.

Damm, W. and Harel, D. (2001). LSCs: Breathing Life

into Message Sequence Charts. Journal on Formal

Methods in System Design (FMSD), 19(1):45–80.

De Moura, L. and Bjorner, N. (2008). Z3: An Efﬁcient

SMT Solver. In Proc. 14th Int. Conf. on Tools and Al-

gorithms for the Construction and Analysis of Systems

(TACAS), pages 337–340.

Greenyer, J., Bar-Sinai, M., Weiss, G., Sadon, A., and

Marron, A. (2018). Modeling and Programming a

Leader-Follower Challenge Problem with Scenario-

Based Tools. In Proc. 21st ACM/IEEE Int. Conf. on

Model Driven Engineering Languages and Systems

(MODELS), pages 376–385.

Greenyer, J. and Gritzner, D. (2018). Generating Correct,

Compact, and Efﬁcient PLC Code from Scenario-

based GR(1) Speciﬁcations. In Proc. 4th Int. Conf. on

System-Integrated Intelligence: Challenges for Prod-

uct and Production Engineering (SYSINT).

Greenyer, J., Gritzner, D., Gutjahr, T., K

onig, F., Glade,

N., Marron, A., and Katz, G. (2017). ScenarioTools

— A Tool Suite for the Scenario-based Modeling and

Analysis of Reactive Systems. Journal of Science of

Computer Programming (J. SCP), 149:15–27.

Greenyer, J., Gritzner, D., Katz, G., and Marron, A.

(2016a). Scenario-Based Modeling and Synthesis for

Reactive Systems with Dynamic System Structure in

ScenarioTools. In Proc. 19th ACM/IEEE Int. Conf.

on Model Driven Engineering Languages and Systems

(MODELS), pages 16–23.

Greenyer, J., Gritzner, D., Katz, G., Marron, A., Glade, N.,

Gutjahr, T., and K

onig, F. (2016b). Distributed Execu-

tion of Scenario-Based Speciﬁcations of Structurally

Dynamic Cyber-Physical Systems. In Proc. 3rd Int.

Conf. on System-Integrated Intelligence: Challenges

for Product and Production Engineering (SYSINT),

pages 552–559.

Gritzner, D. and Greenyer, J. (2018). Synthesizing Exe-

cutable PLC Code for Robots from Scenario-Based

GR(1) Speciﬁcations. In Proc. 4th Workshop of

Model-Driven Robot Software Engineering (MORSE),

pages 247–262.

Harel, D. Kantor, A., Katz, G., Marron, A., Weiss, G., and

Wiener, G. (2015a). Towards Behavioral Program-

ming in Distributed Architectures. Journal of Science

of Computer Programming (J. SCP), 98:233–267.

Harel, D. (1987). Statecharts: A Visual Formalism for

Complex Systems. Journal of Science of Computer

Programming (J. SCP), 8(3):231–274.

Harel, D., Kantor, A., Katz, G., Marron, A., Mizrahi, L.,

and Weiss, G. (2013). On Composing and Proving the

Correctness of Reactive Behavior. In Proc. 13th Int.

Conf. on Embedded Software (EMSOFT), pages 1–10.

Harel, D. and Katz, G. (2014). Scaling-Up Behavioral Pro-

gramming: Steps from Basic Principles to Applica-

tion Architectures. In Proc. 4th Int. Workshop on Pro-

gramming based on Actors, Agents, and Decentral-

ized Control (AGERE!), pages 95–108.

Harel, D., Katz, G., Lampert, R., Marron, A., and Weiss, G.

(2015b). On the Succinctness of Idioms for Concur-

rent Programming. In Proc. 26th Int. Conf. on Con-

currency Theory (CONCUR), pages 85–99.

Harel, D., Katz, G., Marelly, R., and Marron, A. (2016).

An Initial Wise Development Environment for Behav-

ioral Models. In Proc. 4th Int. Conf. on Model-Driven

Engineering and Software Development (MODEL-

SWARD), pages 600–612.

Harel, D., Katz, G., Marelly, R., and Marron, A. (2018).

Wise Computing: Toward Endowing System Devel-

opment with Proactive Wisdom. IEEE Computer,

51(2):14–26.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2012a).

Non-Intrusive Repair of Reactive Programs. In Proc.

17th IEEE Int. Conf. on Engineering of Complex Com-

puter Systems (ICECCS), pages 3–12.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2014). Non-

Intrusive Repair of Safety and Liveness Violations in

Reactive Programs. Transactions on Computational

Collective Intelligence (TCCI), 16:1–33.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2015c). The

Effect of Concurrent Programming Idioms on Veri-

ﬁcation: A Position Paper. In Proc. 3rd Int. Conf.

on Model-Driven Engineering and Software Develop-

ment (MODELSWARD), pages 363–369.

Harel, D., Kugler, H., Marelly, R., and Pnueli, A. (2002).

Smart Play-Out of Behavioral Requirements. In Proc.

4th Int. Conf. on Formal Methods in Computer-Aided

Design (FMCAD), pages 378–398. Springer.

Harel, D., Maoz, S., Szekely, S., and Barkan, D. (2010a).

PlayGo: Towards a Comprehensive Tool for Scenario

Based Programming. In Proc. 10th Int. Conf. on Au-

tomated Software Engineering (ASE), pages 359–360.

Harel, D. and Marelly, R. (2003). Come, Let’s Play:

Scenario-Based Programming Using LSCs and the

Play-Engine. Springer.

Harel, D., Marron, A., and Weiss, G. (2010b). Pro-

gramming Coordinated Scenarios in Java. In Proc.

24th European Conf. on Object-Oriented Program-

ming (ECOOP), pages 250–274.

Harel, D., Marron, A., and Weiss, G. (2012b). Behav-

ioral Programming. Communications of the ACM,

55(7):90–100.

Harel, D., Marron, A., Weiss, G., and Wiener, G. (2011).

Behavioral Programming, Decentralized Control, and

Multiple Time Scales. In Proc. 1st SPLASH Work-

shop on Programming Systems, Languages, and Ap-

plications based on Agents, Actors, and Decentralized

Control (AGERE!), pages 171–182.

Harel, D. and Segall, I. (2012). Synthesis from live se-

quence chart speciﬁcations. Computer System Sci-

ences, 78(3):970–980.

IEEE (2006). Standard SystemC Lang. Ref. Manual. IEEE.

On-the-Fly Construction of Composite Events in Scenario-Based Modeling using Constraint Solvers

153

Katz, G. (2013). On Module-Based Abstraction and Re-

pair of Behavioral Programs. In Proc. 19th Int. Conf.

on Logic for Programming, Artiﬁcial Intelligence and

Reasoning (LPAR), pages 518–535.

Katz, G., Barrett, C., and Harel, D. (2015). Theory-Aided

Model Checking of Concurrent Transition Systems. In

Proc. 15th Int. Conf. on Formal Methods in Computer-

Aided Design (FMCAD), pages 81–88.

Kiczales, G., Lamping, J., Mendhekar, A., Maeda, C.,

Lopes, C., Loingtier, J., and Irwin, J. (1997). Aspect-

Oriented Programming. In Proc. 11th European Conf.

on Object-Oriented Programming (ECOOP), pages

220–242.

Mancinelli, F., Boender, J., Di Cosmo, R., Vouillon, J.,

Durak, B., and Leroy, R. (2006). Treinen: Manag-

ing the Complexity of Large Free and Open Source

Package Based Software Distributions. In Proc. 21st

IEEE/ACM Int. Conf. on Automated Software Engi-

neering (ASE), pages 199–208.

Marron, A., Hacohen, Y., Harel, D., M

ulder, A., and Ter-

ﬂoth, A. (2018). Embedding Scenario-based Mod-

eling in Statecharts. In Proc. 5th Int. Workshop on

Model-Driven Robot Software Engineering (MORSE).

Nadel, A. (2009). Understanding and Improving a Modern

SAT Solver. Ph.D. Thesis, Tel Aviv University.

areanu, C. and Visser, W. (2009). A Survey of New

Trends in Symbolic Execution for Software Testing

and Analysis. Int. Journal on Software Tools for Tech-

nology Transfer, 11(4):339–353.

Sen, K. (2007). Concolic Testing. In Proc. 22nd IEEE/ACM

Int. Conf. on Automated Software Engineering (ASE),

pages 571–572.

Steinberg, S., Greenyer, J., Gritzner, D., Harel, D., Katz,

G., and Marron, A. (2015). Distributing Scenario-

Based Models: A Replicate-and-Project Approach. In

Proc. 5th Int. Conf. on Model-Driven Engineering and

Software Development (MODELSWARD), pages 182–

195.

MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development

154