
Probabilistic Method for Estimation of Spinning Reserves in
Multi-connected Power Systems with Bayesian Network-based
Rescheduling Algorithm
Yerzhigit Bapin
1
and Vasileios Zarikas
1,2
1
School of Engineering, Nazarbayev University, 56 Kabanbay Batyr ave., Astana, Kazakhstan
2
Department of Engineering Informatics, University of Thessaly, Greece
Keywords: Spinning Reserve, Interconnected Power Systems, Bayesian Network, Probabilistic Reserve Estimation,
Power System Reliability.
Abstract: This study proposes a new stochastic spinning reserve estimation model applicable to multi-connected energy
systems with reserve rescheduling algorithm based on Bayesian Networks. The general structure of the model
is developed based on the probabilistic reserve estimation model that considers random generator outages as
well as load and renewable energy forecast errors. The novelty of the present work concerns the additional
Bayesian layer which is linked to the general model. It conducts reserve rescheduling based on the actual net
demand realization and other reserve requirements. The results show that the proposed model improves
estimation of reserve requirements by reducing the total cost of the system associated with reserve schedule.
1 INTRODUCTION
Reduction of the greenhouse gas emissions is
considered as one of the main issues faced by modern
society. Global warming and deteriorating ecological
situation on the planet require drastic changes to the
energy production technologies. Undoubtedly,
renewable energy and smart grid technologies have
crucial impacts in this transformation. During the last
decade, the total installed capacity of renewable
energy in the world has increased from 1.058 TW to
2.012 TW (Whiteman et al., 2017). It is expected that
the overall share of renewable energy will reach 40%
by 2040 (IEA, 2017). Nevertheless, to successfully
reach the renewable energy targets, many challenging
tasks need to be overcome in the near future. Because
of highly stochastic nature of renewable power,
accommodating large amounts of renewable
generation requires to have flexible grid from the
technical and operational perspectives.
Smooth integration of renewable energy
sources into the market and grid infrastructure will
require reconsideration of conventional operating
practices. Especially, significant attention should be
paid to the operational reliability of power systems.
Currently, there are two major reliability assessment
approaches prevailing in the electric power industry,
namely deterministic and probabilistic. Under
deterministic approach the reliability criteria are set
such that the grid system would be capable of
withstanding the loss of a single unit (N-1), or even
simultaneous loss of several power generating units
(N-k). The power system reliability evaluation based
on pure deterministic approach does not consider
stochastic processes occurring in the grid; however,
most of the present-day reliability criteria are based
on deterministic techniques. One of the reasons for
the widespread of deterministic reliability evaluation
methods is their relative simplicity and the lower
requirements applied to its input data (Billinton and
Allan, 1996). On contrary, reliability assessment
based on probabilistic techniques are more
sophisticated and require detailed information about
system characteristics such as generator outage rates,
load and renewable forecast errors, etc. The
advantage of probabilistic methods, as compared with
deterministic ones, is the ability to capture system
uncertainties and evaluate the magnitudes and effects
of these uncertainties on the operation of power
systems (Morales et al., 2014). Consequently, in
probabilistic reliability assessment methods, the
events are treated based on the likelihood of their
occurrence and the degree of their severity (Grigsby,
2013).
840
Bapin, Y. and Zarikas, V.
Probabilistic Method for Estimation of Spinning Reserves in Multi-connected Power Systems with Bayesian Network-based Rescheduling Algorithm.
DOI: 10.5220/0007577308400849
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 840-849
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
The interest in utilization of the power system
reliability assessment using probabilistic methods has
been increasing with the growth of stochastic power
generation. Various reserve estimation
methodologies considering stochastic generation
have been proposed in the last few years.
Consideration of stochastic events in most of these
methodologies is conducted in two distinct ways: one
way requires imposing an upper limit to reliability
metrics determining the loss of load or loss of energy
expectation; another way includes an economic
penalty into the objective function. Conventional
probabilistic reliability assessment methods are
generally based on analytical or Monte-Carlo (MC)
techniques. Application of Bayesian network theory
in probabilistic reliability assessment has its
advantages over conventional analytical or MC-based
probabilistic methods. Particularly, Bayesian
Networks (BNs) aim to model conditional
dependence of system components and states, which
in turn allows making inference on the events of the
interest (Zarikas and Tursynbek, 2017). The BN-
based power system reliability assessment models
provide powerful and mathematically sound
framework to analyse complex and stochastic
domains making them an effective decision-making
tool for the grid system operators.
Although, the implementation of BNs in power
system analysis is relatively new approach, several
valuable works have been published during the last
decades. In one of the earliest studies on BN-based
power system reliability assessment (Yu et al., 1999),
the authors proposed the BN model for reliability
assessment of multi-area power systems. In this
study, the BN representation of a grid system is
conducted via system components, such as, power
generating capacity, tie-line capacity, interconnected
capacity etc. The information provided by the system
components is used to determine the system state
variable – Loss of Load (LOL). Here, LOL serves as
a binary variable identifying the states when demand
exceeds available power. The overall reliability of a
power system is evaluated in terms of the Loss of
Load Probability (LOLP). The methodology was
applied to the Three-Area IEEE Reliability Test
System (RTS). The reported LOLP results show close
proximity with the analytical method. Somewhat
similar approach presented in the study by (Limin et
al., 2002). The study constructs the BN of a grid
system in two steps. First, the fault tree graph is
created for each node using bucket elimination
(Dechter, 1996). During the second step, the minimal
path set is determined by using the graph search
technique. The study by (Yongli et al, 2006) proposes
an approximate inference algorithm on BN for
reliability assessment of power systems by time-
sequence simulation. The system components are
modeled using two-state Markov model. The
methodology constructs the fault tree graph and
corresponding BN for a system of interest using the
bucket elimination method. In the study by (Ebrahimi
and Daemi, 2009) the authors present a novel BN-
based grid system reliability assessment method. The
methodology uses the MC-based data sampling
technique to generate training data. The training data
is used to construct BN representing the power
system of interest. The methodology assesses the
reliability level of a system in terms of LOLP. The
methodology has been tested on the IEEE RTS. The
reported LOLP results are very close to those
obtained using conventional probabilistic techniques.
The main contribution of this paper is to present a
hybrid method for estimation of optimal amount of
spinning reserves in multi-connected power systems
using traditional probabilistic cost-benefit analysis in
conjunction with the BN-based reserve rescheduling
algorithm.
2 METHODOLOGY
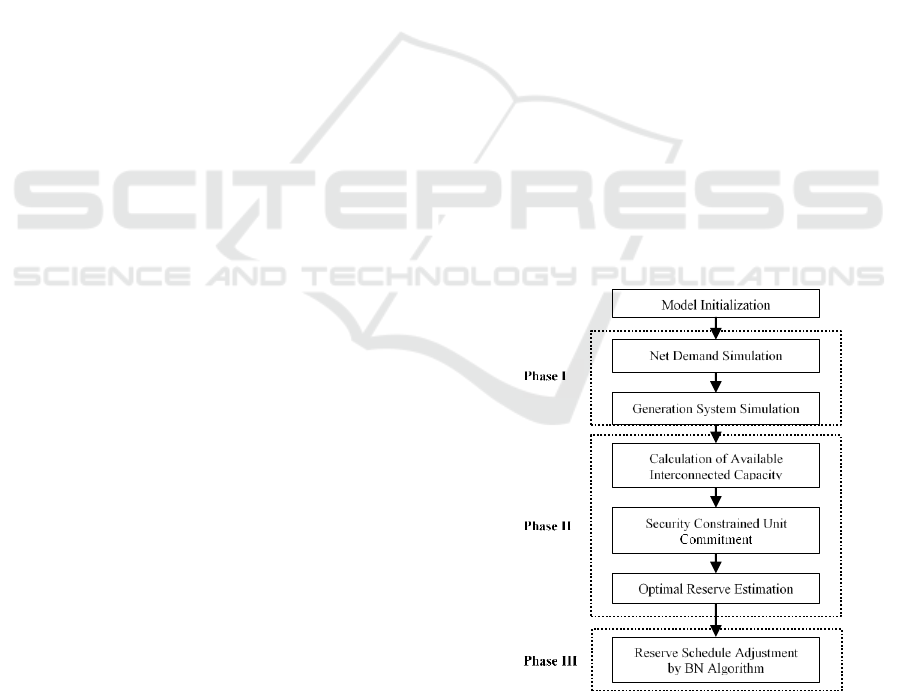
The proposed methodology is carried out in three
phases. The flowchart of the proposed methodology
is presented in figure 1.
Figure 1: Flowchart of proposed model.
During the first phase, the reliability of the power
system of interest is evaluated neglecting its
interconnection with neighbouring systems. At the
Probabilistic Method for Estimation of Spinning Reserves in Multi-connected Power Systems with Bayesian Network-based Rescheduling
Algorithm
841
second phase, the Capacity Outage Probability Tables
(COPT) of the assisting power systems are obtained
using recursive algorithm and incorporated into
COPT of the assisted system. The reliability
evaluation is performed in terms of the Expected
Energy Not Supplied (EENS), which serves as a
metric for potential shortfall in supply of electricity to
consumers. As a result, the required amount of
spinning reserves is calculated based on the level of
reliability of the system and the capacity that is
available at a given time-period. At the final phase,
the BN-based algorithm is used to adjust the reserve
schedules based on the intra-hour actual data. The
detailed description of calculations conducted during
the first, second and third phases are described below.
2.1 Phase I
2.1.1 Net Demand Model
The proposed methodology considers renewable
power as negative load, and the net demand is defined
as the difference between load and renewable power
generation given by:
t t t
D L R
(1)
where D
t
is the net demand at period t, L
t
and R
t
are
the actual load and renewable energy production at
time period t. The forecast uncertainty is taken into
consideration by implementation of parametric
assumptions. Namely, the forecast error distribution
at time period t is given by:
~ ( ; )
t
t
Y F y
(2)
where Y
t
is the forecast error at time period t, F is the
distribution function of forecast error, y and
t
is the
set of parameters characterizing F (Morales et al.,
2014).
It should be noted that throughout this paper the
superscript t denotes the time periods and subscripts
i, j, l and k denote the power generating units,
interconnected reserve units, power transmission
lines and energy system areas respectively.
In this study, we assume that the load and
renewable forecast errors follow Normal distribution
with zero mean and the standard deviation given by
the following formulas (Ortega-Vazquez and
Kirschen, 2009):
Standard deviation of load forecast error:
100
tt
k
LF
L
(3)
where
is the standard deviation of the load forecast
error distribution, k is a function depending on the
accuracy of the forecasting software and the
forecasted load at time period t.
Standard deviation of renewable forecast error:
11
5 50
tt
R F I
RR
(4)
where
is the standard deviation of renewable
power forecast error distribution at time period t,
is the forecasted renewable power at period t and
is the total installed capacity of renewable power. The
former term stays constant throughout the simulation
horizon.
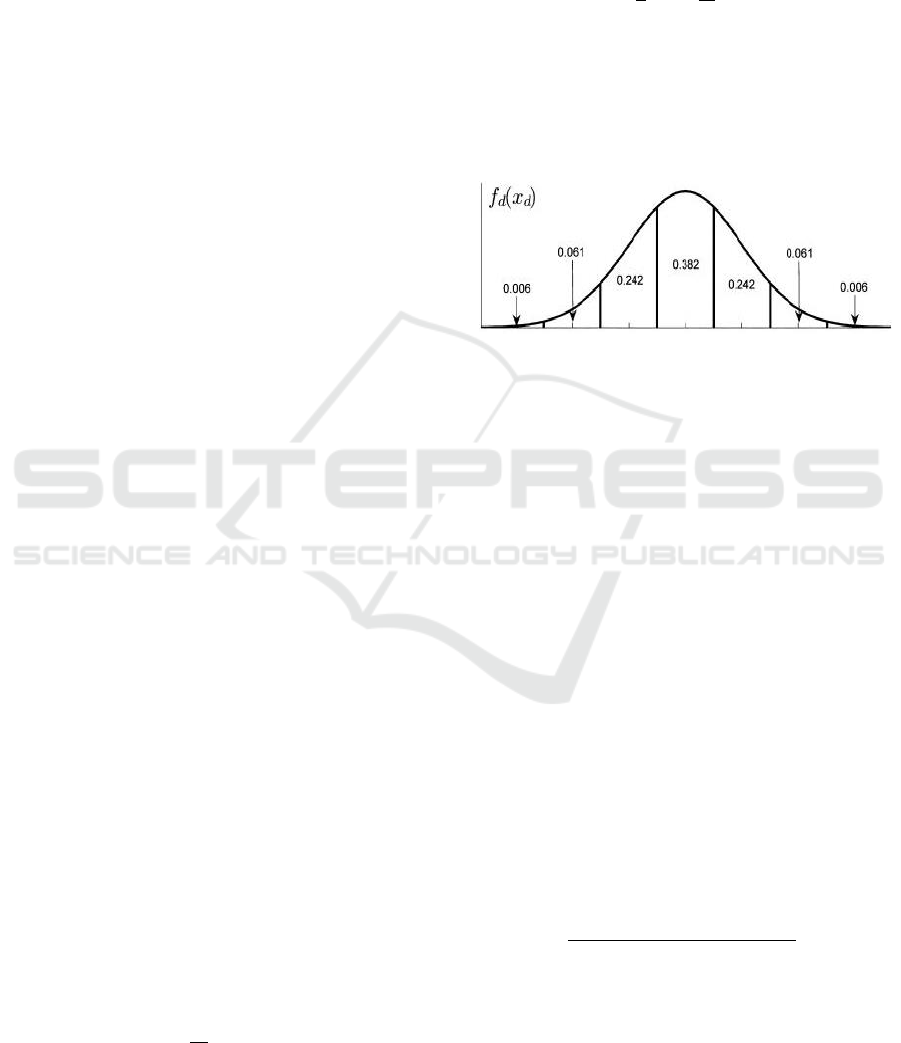
Figure 2: Seven-interval approximation of normal
distribution.
Discretization of load and renewable forecast
uncertainty can be done using seven-interval
approximation technique described in (Billinton and
Allan, 1996). Discretization is performed by dividing
the probability distribution of an error into an odd
number of equal intervals (Figure 2). These intervals
are considered as scenarios with individual
probabilities corresponding to the mid-point of each
interval. The lack of correlation between these errors
allows to calculate the net demand forecast error by
summation of the load and renewable forecast errors.
2.1.2 Generation System Model
The random outages of conventional units are
considered in the same fashion as it was done in
(Bapin et al., 2018). A random unavailability of
generating capacity can be modelled by representing
it as a Markov process. The availability and
unavailability of each generating unit in this case are
given by (5) and (6) (Billinton and Allan, 1996):
()
( ) ( )
t
i
up time
A
down time up time
(5)
1
tt
ii
UA
(6)
where
and
represent availability and
unavailability of unit i at time period t. Equations (5)
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
842

and (6) represent the probability of finding the unit
either available or on forced outage at a given period
and can be used to create the Capacity Outage
Probability Table (COPT). Creation of COPT is
carried out using the recursive algorithm described in
(Billinton and Allan, 1996) and includes information
on available capacity and corresponding probabilities
for each system state. It should be noted that
throughout this paper the units’ capacity and power
production are denoted by capital P, whereas
lowercase p denotes probability.
The Expected Energy Not Supplied (EENS) due
to a random capacity outage m at time period t is
given by (Billinton and Allan, 1996):
1
,
11
[( ) ]
M S I
t t t
smm
mi
is
s
EENS D P q q
(7)
where s is an index representing the net demand
scenario,
is the available power when generation
system is at state m during time period t, q
s
and q
m
are
the probability of scenario of the net demand and
generating system availability respectively. Finally, I,
M and S are the total number of generating units,
generation system states and net demand scenarios
respectively. It is worth noting that, although variable
highly depends on the level of capacity
forced out of service, the probability of this outage
may have even stronger impact on the loss of energy
expectation. For instance, a simultaneous failure of
two or more units may cause significant disruption of
electricity supply. However, the probability of this
event is very low, thus the overall loss of energy
expectation would be lower as compared to the single
unit outage event.
2.2 Phase II
2.2.1 Interconnected Capacity
It is very common for an electric grid to have
interconnection with neighbouring systems, as most
of the time grid interconnections improve reliability
of the system and reduce its needs in reserve capacity
(Watchorn, 1950). The cross-border electricity
trading between interconnected systems is often done
based on the contractual agreements, where the
system operators define trading time, limits, ramp
rates etc. To account for interconnected capacity, the
proposed model utilizes the equivalent assisting unit
method as described in (Billinton and Allan, 1996).
The maximum assistance level provided by
interconnected system at time period t is given by the
minimum of available interconnected capacity and
tie-line capacity (Allan et al., 1986):
max , max
, , , ,
1
min ( ),
JL
t inst t t
k j k j k j k l k
jl
IR IR IR e IR r B
(8)
Where
is the installed capacity of
interconnected unit j located in the assisting system k,
is the capacity committed for energy
generation of interconnected unit j located at assisting
system k during time period t,
is the capacity
of interconnected unit j committed for provision of
spinning reserve at assisting system k during time
period t and
is the maximum transmission
capacity of transmission line l. Finally, J and L are the
total number of interconnected reserve units and
transmission lines respectively. The maximum
capacity assistance level can be utilized to create a
capacity model in the same way as it was described in
the previous subsection. The resulting COPT is
regarded as an equivalent multi-stage generator,
which can be integrated in the existing capacity
model of an assisted system. During this phase, the
capacity assistance states are determined individually
for all assisting systems and added to the COPT of the
system of interest. It should be noted that in this paper
we assume that the interconnected capacity can only
participate in ancillary service market, thus it can only
provide up-spinning reserve service.
2.2.2 Stochastic Security Constrained Unit
Commitment
Objective Function.
In this study, the unit commitment problem is
expressed as a two-stage stochastic MILP. The first
stage involves conventional unit commitment with
stochastic reliability criteria to find the most optimal
energy production schedule. This stage is performed
for the base case scenario. The base case implies no
unit outage and results in the most economically
efficient unit commitment. The first-stage
optimization objective is to minimize the total cost of
system operation, where the total system operation
cost is given by:
Probabilistic Method for Estimation of Spinning Reserves in Multi-connected Power Systems with Bayesian Network-based Rescheduling
Algorithm
843

11
1
,,
1 1 1
()
()
TI
t t t
total i i i i
ti
I
t t t t
i i i i
i
K J M
t t t
j k j k m
k j m
up up dw dw
C C P u CS
C R C R
CIR IR SC
(9)
where
is the cost of power of generating unit i,
is the power produced by unit i during time period t,
is the binary indicator of the status of generating
unit i at time period t (0 – not operating, 1 –
operating),
is the start-up cost of unit i during
time period t,
is the cost of power of unit i,
during time period t for providing the up-spinning
reserve,
is the up-spinning reserve service
provided by unit i during time period t,
is the
cost of power of unit i, during time period t for
providing the down-spinning reserve,
is the
down-spinning reserve service provided by unit i
during time period t,
is the cost of power
provided by interconnected unit j, located at energy
system k, during time period t,
is the amount of
reserve provided by the interconnected unit j, located
at energy system k, during time period t.
is
related to the second-stage decisions and is given by:
,
11
, , ,
11
MI
t t t
m i i m
mi
JK
tt
j k j m k
jk
t
m
SC q C R
CIR IR
VOLL CE
(10)
where
is the cost of providing the spinning reserve
by intra-zonal unit i during time period t,
is the
reserve service provided by intra-zonal unit i, at
system state m, during time period t,
is the
amount of reserve provided by the interconnected unit
j, located at energy system k, at system state m, during
time period t. VOLL represents the value of lost load
– the financial loss of consumers due to interruption
in electricity supply,
is the amount of curtailed
energy when generation system is in state m, during
time period t. The objective of the second-stage is to
find the most optimal reserve schedule by comparing
different scenarios.
First-Stage Constraints.
The objective function (9) must be minimized subject
to the set of constraints specified below. Note that to
reduce the computational burden and simplify the
model, the transmission line constraints are neglected
in this study. The equality between supply and
demand of electric power is specified by the power
balance constraint, which for all time instances is
given by:
1
,,
11
()
I
t t t t t t t
i i i i i i
i
КJ
tt
j k j k
кj
up dwD P u R u R u
IR u
(11)
In addition to equation (11) the conventional units are
subject to their operating constraints, such as
minimum up and down time, ramping and capacity
limits.
Second-Stage Constraints.
The second-stage constraints specifying all capacity
outage states is presented below. For all time periods
and scenarios, the power balance equation is given
by:
,,
1
, , ,
1 1 1
()
()
I
t t t
m i i m i m
i
K J S
t t t
j k m s s m
k j s
up dwq P R R
IR D CE
(12)
Under this formulation of probabilistic reliability
criteria, the optimal spinning reserve requirement is
determined by counterweighting costs required to
operate the reserves with socioeconomic costs of
possible load curtailment. Reduction of spinning
reserves will negatively affect reliability of a system,
yet this reduction will be justified if the probability of
capacity outage is insignificant, or the social value of
curtailed load is very low.
2.3 Phase III
During recent years, rapid rise in computational
efficiency triggered the introduction of complex
machine learning algorithms into many different
areas. The scope of application of these algorithms
ranges from intellectual games, such as chess (David
et al., 2014) or go (van den Werf et al., 2003), medical
research (Eleftheriadou et al., 2009), (Deltsidou et al.,
2017), (Zarikas et al., 2015) to the power system
operation (Calabria et al., 2015) and (Steels and
Hanappe, 2008).
Aside from other machine learning algorithms,
BN-based algorithms have gained wide popularity
among power system and electrical engineers.
According to (Craciun et al., 2017) the application of
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
844
BNs by the power system engineering researchers
include, but not limited to load forecasting, power
system reliability assessment and stability analysis,
electrical networks fault analysis and power system
state estimation.
Generally speaking, BN is a probabilistic
graphical model representing variables, their mutual
dependencies and associated probabilities (Zarikas,
2007). BN models are usually expressed in terms of
causal directed acrylic graphs (Jensen and Nielsen,
2011), where each variable has one or several directed
links with other variables. The objective of BN
models is to determine posterior conditional
probability distribution of an event in question based
on new evidence (Pearl, 2005). Equation (13)
represents the Bayes’ rule serving as the foundation
for BNs.
( | ) ( )
( | )
()
p B A p A
p A B
pB
(13)
In this study, we propose a BN-based reserve
rescheduling algorithm. The main purpose of this
algorithm is to adjust the spinning reserve schedule
that was calculated during the first and second phases
of this methodology. The algorithm adjusts the
reserve requirement of the next closest time period
(t+1) based on the evidence received from the past
closest time period (t-1). Other parameters considered
by the algorithm during the adjustment procedure are
hour type (peak, non-peak) and day type (weekday,
weekend, holiday). The node specific properties, such
as, conditional probabilities or reserve
increase/decrease levels were set based on existing
practice, nevertheless, these properties can be easily
adjusted according to the user-specific preferences.
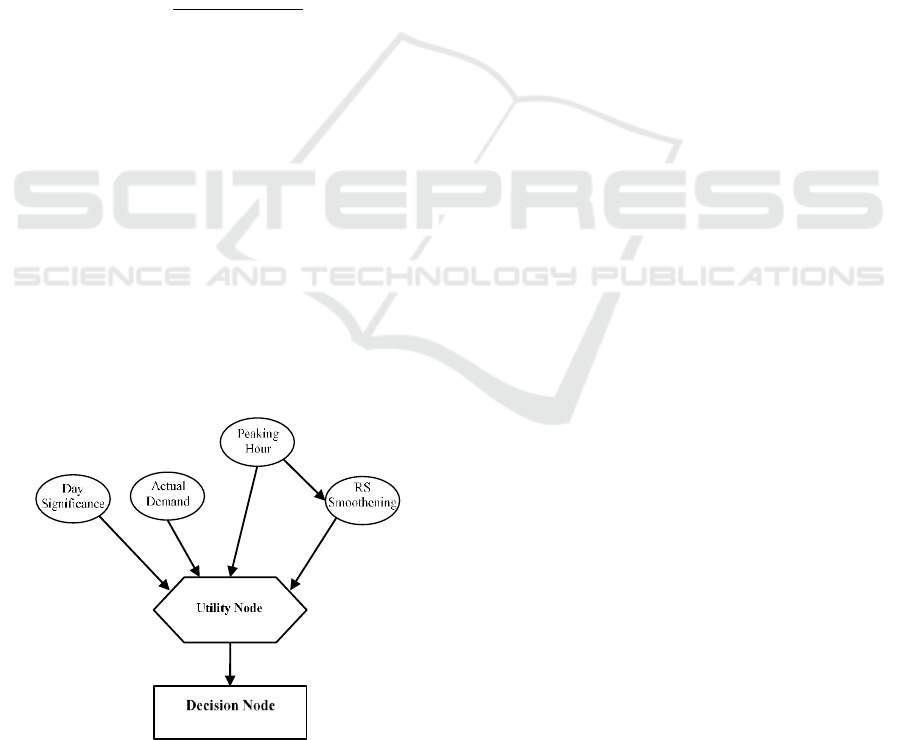
Figure 3: Part of the Influence Diagram of Proposed
Algorithm.
The algorithm was implemented in BayesiaLab 7
(Bayesia S.A.A., 2018). Figure 3 shows a simplistic
view of the decision influence diagram of the
proposed algorithm. The implemented BN consists of
2 such graphs each of every hour of one day.
The diagram consists of probabilistic, utility and
decision nodes each represented by elliptical,
hexagonal and rectangular-shaped figures
respectively. The detailed description of nodes is
provided below.
Probabilistic Nodes.
The probabilistic nodes denote variables specified
below:
Peaking Hour – denotes the variable containing
information about hour type and affects RS
Smoothening and Utility nodes. Usually, during peak-
hours energy systems pass through tremendous stress,
so the risk of electricity supply interruption is very
high. One way of reducing the level of this risk is to
increase the level of spinning reserve capacity. In
this model, the spinning reserve schedule adjustment
is set, such that, the reserve requirement is increased
by 10% for peaking time. The off-peak hours do not
affect previously calculated reserve schedule.
Day Significance – denotes the variable
containing information about day types and their
influence on spinning reserve schedule. In the
proposed algorithm, three day types were considered,
these are: weekdays, weekends and holidays.
Weekends do not have any effect on reserve schedule,
whereas weekends and holidays increase the reserve
requirement by 10% and 20% respectively.
Actual Demand – denotes the variable containing
information about the level of net demand forecast
error and its influence on spinning reserve schedule.
This node signals to adjust initial reserve schedule if
the difference between the forecasted and actual net
demand values exceed some predefined threshold. It
should be reasonable to set this threshold equal to the
expected value or the standard deviation of load/net
demand forecast error. According to (Allan et al.,
1986) it is suggested to model the load forecast
uncertainty associated with IEEE RTS using normal
distribution with a standard deviation equal to 5%.
However, since the proposed model considers not
only load, but also renewable forecast uncertainty the
average threshold was set to be equal to 10% of
forecasted value. The prior probabilities for this node
do not have big importance. For completeness we
note that there are five states in this node and the
priors are P(same actual demand with forecast
demand reserve power)=P(small positive difference
between forecast and actual value)= P(small negative
difference between forecast and actual value)=0.25.
Probabilistic Method for Estimation of Spinning Reserves in Multi-connected Power Systems with Bayesian Network-based Rescheduling
Algorithm
845

“Small” means within the 10% variance as we have
explained. The other priors P(big positive difference
between forecast and actual value)=P(big negative
difference between forecast and actual value)=0.125.
“Big” means above 10% difference.
The important thing for this node is to determine
how evidences are updated. The following
description of this subsection is devoted to this issue;
what are the conditional probabilities for updating the
node.
Mathematically, the spinning reserve adjustment
given the actual net demand of the previous hour is
expressed as follows.
Increase by 10%:
11
1 1 1
( | )
0. (
,
) 10%
0.2,
8,
t t t
UU A F
t t t
A F F
D
DD
other
p
wise
RD
D
(14)
where
is the 10% increase in reserve requirement
for time period t,
and
are the actual and
forecasted values of net demand of time period t-1.
Increase by 5%:
11
1 1 1 1
( | )
0. ,
,
( ) 10%
0
5
2
8
.,
%
t t t
U A F
t t t t
F A F F
p
D
D
DD
othe
R
rwi
D
se
D
(15)
where
is the 5% increase in reserve requirement
for time period t.
Decrease by 10%:
11
1 1 1
( | )
0.8
,
( ) 10
.2
, %
0,
t t t
DD A F
t t t
F A F
D
D D D
other
p
w se
R
i
D
(16)
where
is the 10% decrease in reserve
requirement for time period t.
Decrease by 5%:
11
1 1 1 1
( | )
0. ,
,
( ) 10%
0
5
2
8
.,
%
t t t
D A F
t t t t
F F A F
p
D
D
DD
othe
R
rwi
D
se
D
(17)
where
is the 5% decrease in reserve requirement
for time period t.
For all other cases, the probability of adjustment
the reserve requirements equal to 0.
The conditional dependencies stated above are
expanded by the example presented in table 1.
Table 1: Calculation of spinning reserve adjustment level
given actual net demand value.
Variable
Observed/
forecasted
value, MW
Difference/
adjustment,
MW
Difference/
adjustment,
%
1 467
129
10.47
1 328
268
27
10
295
The difference between the actual and forecasted
net demand, in this example, is greater than 10% of
forecasted net demand, therefore, the equation (14)
must be used in further calculation. According to
equation (14), for this particular case, the algorithm
would assign the probability of increasing previously
calculated spinning reserve by 295 MW equal to 0.8.
Note that the adjustment procedure is not finished at
this point, the final decision on the adjustment level
would be made by the Decision Node.
Reserve Schedule (RS) Smoothening – denotes the
variable containing information about spinning
reserve requirements forecasted for previous (t-1),
intra (t) and the next adjacent (t+1) time periods. As
the name suggests, the main objective of this node is
to smoothen the reserve schedule by increasing
(positive smoothening) or decreasing (negative
smoothening) reserve requirement for time period t
based on the difference between forecasted reserve
values of t-1 and t+1 time periods.
Mathematically the setting of new evidences for
the smoothening procedure concerns the definition of
the conditional probabilities. Thus, the update of of
this node is as follows.
Positive 5% smoothening:
11
11
,,
1.18 & 1.1
0.
( | )
0. ,
2,
t t t t
U F F F
t t t t
F F F F
p RR
R R R
oe
RR
R
th rwise
(18)
Negative 5% smoothening:
11
11
,,
0.98 & 0.9
0.
( | )
0. ,
2,
t t t t
D F F F
t t t t
F F F F
p RR
R R R
oe
RR
R
th rwise
(19)
Thus, in this study, the probability of applying or
not applying the smoothening given the forecasted
values of spinning reserves for t-1, t and t+1 time
periods is set to 0.8 and 0.2 respectively. For all other
cases, the probability of adjustment the reserve
requirements equal to 0.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
846
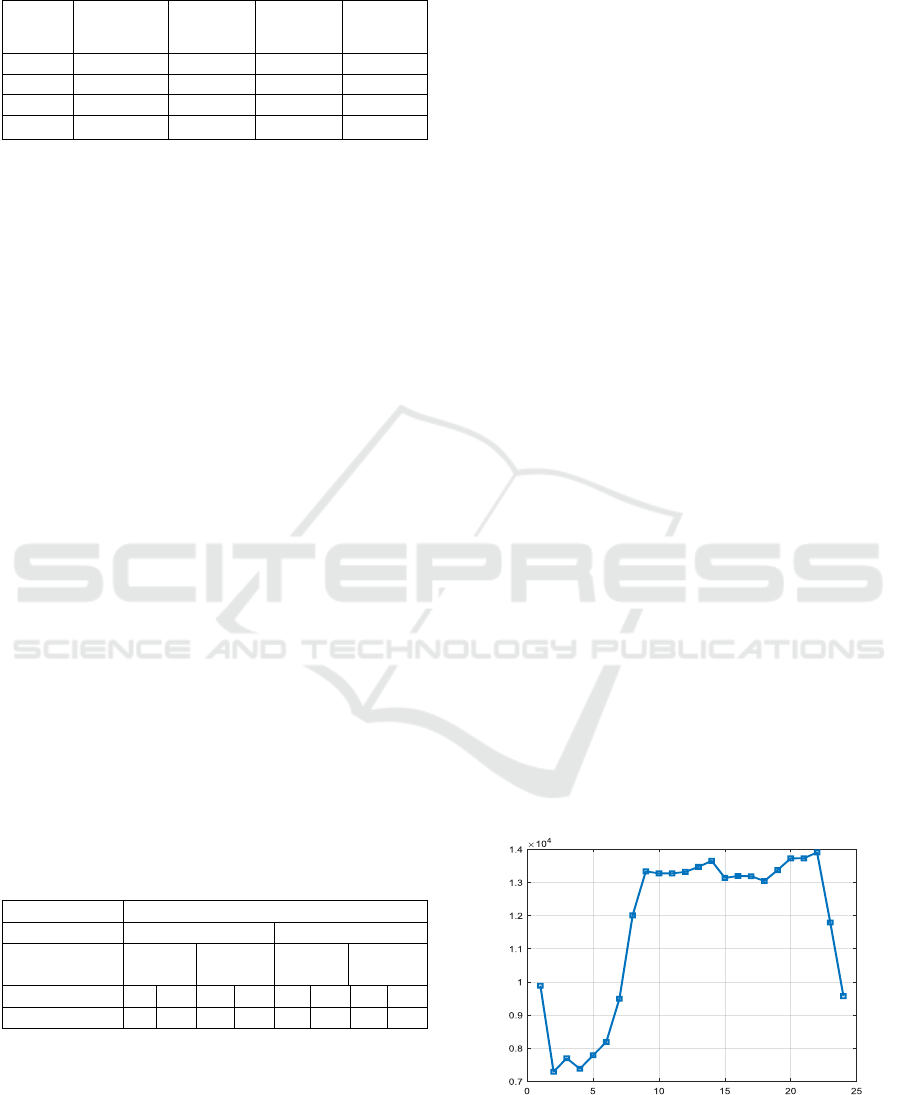
Table 2: Calculation of spinning reserve adjustment level
given forecasted reserve requirements.
Variable
Reserve
requirement,
MW
Difference,
MW
Difference,
%
Assigned
probability
232
36
13,43
-
268
-
-
-
256
8
4,48
-
0.2
The example presented in table 2 demonstrates
calculation of conditional probability of smoothening
given forecasted reserve requirements. The first step
in the smoothening procedure is to evaluate the
difference between initial reserve requirements
calculated for time periods t and t-1. The same
calculation should be conducted for time periods t and
t+1. In this particular case,
greater than
and
, thus the equation (18) must be applied.
According to the equation (18) the probability of
increasing reserve requirement by 5% would be set to
be equal to 0.2.
Utility Node.
In general, the utility node denotes a value that
contains information about the decision maker’s
goals and objectives. Usually, these types of nodes
express the decision maker’s preferences over the
outcomes over their direct predecessors.
In the proposed algorithm, the utility node
contains information about all possible combination
of relevant states of the parents, given the information
provided by probabilistic nodes. The decision
whether to adjust initial reserve schedule is made
based on the weights that are set manually. The
weights represent the strength of influence that each
combination has on the final decision. The weights
range on the scale from 0 to 10 indicating zero and
maximum influence respectively. To save the paper
space, only several combinations are presented in the
table 3.
Table 3: Utility node conditional dependence table.
Day Significance
Weekend
Actual Demand
Increase by 5%
Decrease by 10%
RS Smoothening
Positive
5%
Negative
5%
Positive
5%
Negative
5%
Peaking Hour
P
NP
P
NP
P
NP
P
NP
Value
9
7
2
4
5
4
4
7
Decision Node.
The decision node denotes a variable that is under
decision maker’s control and is used to model
decision maker’s options.
The objective of this algorithm is to find optimal
spinning reserve adjustment actions based on the set
of parameters described above. The set of decisions
available to the decision maker through this algorithm
is stated below:
1. Keep initially calculated reserve requirement;
2. Increase reserve requirement by 5%;
3. Increase reserve requirement by 10%;
4. Decrease reserve requirement by 5%;
5. Decrease reserve requirement by 10%.
3 CASE STUDY
This section presents a case study which was
conducted by applying the model on the distribution
system of Pavlodar, Kazakhstan. The main objective
of the case study is to analyze the performance of the
proposed BN-based rescheduling algorithm by
comparing it to the conventional probabilistic reserve
estimation model based on the cost-benefit analysis.
The overall performance of the model is evaluated in
terms of the total cost of reserve schedules given by
the following equation:
t t t
total
CR CR SE
(20)
Figure 4 represents the costs of the test system
presented in this case study calculated for one
particular day using equation (20).
The analysis was conducted for a 24-hour
operating horizon on 20 different days almost equally
representing weekdays, weekends and holidays. The
Value of Lost Load (VOLL) was set to 2 000 $/MWh.
The I and II Phase simulations were performed
in MATLAB R2017a. The MILP optimization was
done in IBM ILOG CPLEX Optimization Studio
12.7.1 using YALMIP. The computational efficiency
of the model is achieved by considering the system
state probabilities above 10
5
. The III Phase
calculations were conducted in BayesiaLab software.
Figure 4: Total costs of reserve schedule calculated for the
test system.
Probabilistic Method for Estimation of Spinning Reserves in Multi-connected Power Systems with Bayesian Network-based Rescheduling
Algorithm
847

Table 4 represents the results obtained by the
models. In this table CP represents conventional
probabilistic model, whereas P represents the
proposed model.
Table 4: Simulation results.
Day
CP
P
Day
CP
P
1
256
254
11
269
266
2
268
266
12
265
265
3
262
261
13
244
246
4
254
251
14
252
248
5
265
266
15
261
261
6
250
250
16
240
242
7
269
264
17
249
249
8
246
246
18
267
264
9
256
255
19
245
244
10
262
262
20
259
254
According to the simulation results, the
proposed algorithm outperformed the conventional
probabilistic reserve estimation model. The
adjustments made by the proposed model resulted in
11 reserve schedules that were on average 1.05%
cheaper than that of conventional probabilistic model.
It’s worth noting that out of 20 simulations 6 (30%)
produced totally similar results. This can be explained
by the fact that there are relatively fair number of
scenarios that end up in unchanged reserve schedule.
4 CONCLUSION
A probabilistic model to estimate the spinning
reserves in multi-connected systems with a BN-based
spinning reserve rescheduling algorithm was
discussed. The model accounts for random outages of
conventional units as well as load and renewable
forecast errors. Random unavailability of generating
capacity was modeled through a two-state Markov
process. The load and renewable forecast errors were
modeled assuming that they are normally distributed.
The model considers the interconnected capacity of
multiple energy systems through utilization of the
equivalent assisting multi-state unit approach. The
two-stage unit commitment problem was formulated
such that the mixed integer linear program could be
applied to conduct the optimization. Furthermore, to
minimize the total cost associated with spinning
reserve schedule the BN-based reserve rescheduling
algorithm was implemented. The algorithm takes into
account actual net demand, forecasted reserve
requirement of previous and next hours as well as the
day and hour types. The objective of the algorithm is
to perform reserve rescheduling if significant
deviations in actual versus predicted net demand have
occurred or there is a big difference between reserve
requirements of adjacent hours.
The proposed model was evaluated on the energy
system of Pavlodar, Kazakhstan. The goal of the case
study was to estimate the performance of the
proposed model by comparing it to the conventional
probabilistic reserve estimation model that is based
on the cost-benefit analysis. The test was conducted
for 20 different days almost equally representing
three groups (weekdays, weekends and holidays).
The results show that 11 (55%) out of 20 simulations
resulted in reserve schedules that were on average
1.05% cheaper compared to those obtained by
conventional probabilistic reserve estimation model.
ACKNOWLEDGEMENTS
This work was supported by NUIG Grant funded by
Nazarbayev University.
REFERENCES
Whiteman, J. Esparrago, and T. Rinke. 2017. Renewable
Energy Statistics 2017, Abu Dhabi, The International
Renewable Energy Agency.
International Energy Agency. 2017. World Energy Outlook
2017, Paris, France. [Online]. Available:
https://www.iea.org/weo2017/
Billinton, R., and Allan, N. R. 1996. Reliability Evaluation
of Power Systems, 2nd ed., New York: Plenum.
Morales, J. M., Conejo, A. J., Madsen, H., Pinson, P., and
Zugno, M. 2014. Integrating Renewables in Electricity
Markets: Operational Problems, vol. 205, New York:
Springer.
Grigsby, L., Power Systems. 2013. Electric Power
Engineering Handbook, 3rd ed., CRC Press.
Zarikas V., Tursynbek N., Intelligent Elevators in a Smart
Building, FTC 2017 - Future Technologies Conference
2017. 29-30 November 2017. Vancouver, BC, Canada.
Bouffard, F., and Galiana, F. 2004. An electricity market
with a probabilistic spinning reserve criterion, IEEE
Trans. Power Syst., vol. 19, no. 1, pp. 300–307.
Chattopadhyay, D., and Baldick, R. 2002. Unit commitment
with probabilistic reserve. In IEEE Power Engineering
Society Winter Meeting, New York, NY, USA.
Ortega-Vazquez M., and Kirschen, D. 2009. Estimating the
spinning reserve requirements in systems with
significant wind power generation penetration. IEEE
Trans. Power Syst., vol. 24, no. 1, pp. 114-124.
Liu, G., and Tomsovic, K., 2012. Quantifying Spinning
Reserve in Systems With Significant Wind Power
Penetration. IEEE Trans. Power Syst., vol. 27, no. 4, p.
2385–2393.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
848

Bapin, Y., Mussard, M., and Bagheri, M. 2018. Estimation
of Operating Reserve Capacity in Interconnected
Systems with Variable Renewable Energy Using
Probabilistic Approach. In 18th Conference on
Probabilistic Methods Applied to Power Systems,
Boise, ID, USA. IEEE Xplore.
Yu, D., Nguyen, T., Haddaway, P. 1999. Bayesian network
model for reliability assessment of power system. IEEE
Transaction on Power Systems, vol. 14, no. 2, pp. 426-
432.
Limin, H., Yongli, Z., Gaofeng, F. 2002. Reliability
Assessment of Power Systems by Bayesian Networks. In
Powercon’02. International Conference on Power
System Technology. IEEE Xplore.
Yongli, Z., Limin, H., Liguo, Z., Yan, W. 2008. Bayesian
Network Based Time-sequence Simulation for Power
System Reliability Assessment. In MICAI’07. 7th
Mexican International Conference on Artificial
Intelligence. IEEE Xplore.
Dechter, R., 1996. Bucket Elimination: A Unifying
Framework for Probabilistic Inference. In UAI’96.
12th Conference on Uncertainty in Artificial
Intelligence.
Ebrahimi, A., Daemi, T. 2009. A novel method for
constructing the Bayesian network for detailed
reliability assessment of power systems. In EPECS’09.
1st International Conference of Electric Power and
Energy Conversion Systems. IEEE Xplore.
C. W. Watchorn, The Determination and Allocation of the
Capacity Benefits Resulting from Interconnecting Two
or More Generating Systems, Transactions of the
American Institute of Electrical Engineers, vol. 69, no.
2, p. 1180–1186, Jan. 1950.
David, E., van den Herik, H., J., Koppel, M., Netanyahu,
N., S. 2014. Genetic Algorithms for Evolving Computer
Chess Programs. IEEE Transactions on Evolutionary
Computation, vol. 18, no. 5, pp.779–789.
Van den Werf, E., C., D., van den Herik, H., J., Uiterwijk,
J., W., H., M. 2003. Solving Go On Small Boards.
ICGA Journal, vol. 26, no. 2, pp.92–107.
Eleftheriadou A, Deftereos S, Zarikas Vasilios,
Panagopoulos G, Korres S, Sfetsos S, Karageorgiou C,
Ferekidou E, Kandiloros. 2009. Test - retest Reliability.
VEMP eliciting in normal subjects. Normative data of
Vestibular Evoked Myogenic Potential Stimulation
(VEMPS) in a large healthy population, J Otolaryngol
Head Neck Surg., vol. 38, no .4, pp. 462-473.
Deltsidou, A., Zarikas, V., Mastrogiannis, D., Kapreli, E.,
Bourdas, D., Papageorgiou, E., Raftopoulos, V., Noula,
M., Lambadiari, M. and Lykeridou, K., 2017.
Reliability analysis of Finometer and AGE-Reader
devices in a clinical research trial. International
Journal of Reliability and Safety, vol. 11, no. 1-2,
pp.78-96.
Calabria, F.A., Saraiva, J.T. and Rocha, A.P., 2015. A new
electricity market design for power systems with large
share of hydro: Improving flexibility and ensuring
efficiency and security in the Brazilian case. 2015 IEEE
Eindhoven PowerTech.
Steels, L. and Hanappe, P., 2008. Peer-to-peer transaction-
based power supply methods and systems. US
2008/0269953 A1
Craciun, M. et al., 2017. Bayesian Networks Applications
in Power System Engineering. A Review. Journal of
Sustainable Energy, vol. 8, no. 3, pp.99–105.
Zarikas, V., 2007. Modeling decisions under uncertainty in
adaptive user interfaces. Universal Access in the
Information Society, vol. 6, no. 1, pp.87-101.
Jensen, F.V. and Graven-Nielsen, T., 2011. Bayesian
networks and decision graphs, New York: Springer.
Pearl, J., 2005. Casuality: models, reasoning, and
inference, Cambridge: Cambridge University Press.
Allan, R.N., Billinton, R. and Abdel-Gawad, N.M.K., 1986.
The IEEE Reliability Test System - Extensions to and
Evaluation of the Generating System. IEEE Power
Engineering Review, PER vol. 6, no. 11, pp.24–24.
Zarikas, V., Papageorgiou, E. and Regner, P., 2015.
Bayesian network construction using a fuzzy rule based
approach for medical decision support. Expert
Systems, vol. 32, no. 3, pp.344-369.
Probabilistic Method for Estimation of Spinning Reserves in Multi-connected Power Systems with Bayesian Network-based Rescheduling
Algorithm
849
