Using Stigmergy as a Computational Memory in the Design of
Recurrent Neural Networks
Federico A. Galatolo, Mario G. C. A. Cimino and Gigliola Vaglini
Department of Information Engineering, University of Pisa, 56122 Pisa, Italy
Keywords: Artificial Neural Networks, Recurrent Neural Network, Stigmergy, Deep Learning, Supervised Learning.
Abstract: In this paper, a novel architecture of Recurrent Neural Network (RNN) is designed and experimented. The
proposed RNN adopts a computational memory based on the concept of stigmergy. The basic principle of a
Stigmergic Memory (SM) is that the activity of deposit/removal of a quantity in the SM stimulates the next
activities of deposit/removal. Accordingly, subsequent SM activities tend to reinforce/weaken each other,
generating a coherent coordination between the SM activities and the input temporal stimulus. We show that,
in a problem of supervised classification, the SM encodes the temporal input in an emergent representational
model, by coordinating the deposit, removal and classification activities. This study lays down a basic
framework for the derivation of a SM-RNN. A formal ontology of SM is discussed, and the SM-RNN
architecture is detailed. To appreciate the computational power of an SM-RNN, comparative NNs have been
selected and trained to solve the MNIST handwritten digits recognition benchmark in its two variants: spatial
(sequences of bitmap rows) and temporal (sequences of pen strokes).
1 INTRODUCTION
Recurrent Neural Networks (RNNs) are today among
the most effective solutions for modeling time series,
speech, text, audio, video, etc. (Schmidhuber, 2015).
An RNN is a special type of NN using its internal
state (memory) to process sequences of inputs. This
internal memory makes the RNN able to remember
the relevant information about the previous samples,
in order to model their dynamics.
In contrast to Feed-Forward NN (FFNN), which
does not explicitly consider the notion of sequence, in
the RNN the input information cycles through a loop.
This structure allows the simultaneous processing of
both the current and the recent samples. In the RNN,
the deep learning algorithm tweaks its weights
through gradient descent and backpropagation
through time (BPTT, Mazumdar et al., 2008). In
essence, BPTT is backpropagation (BP) applied to an
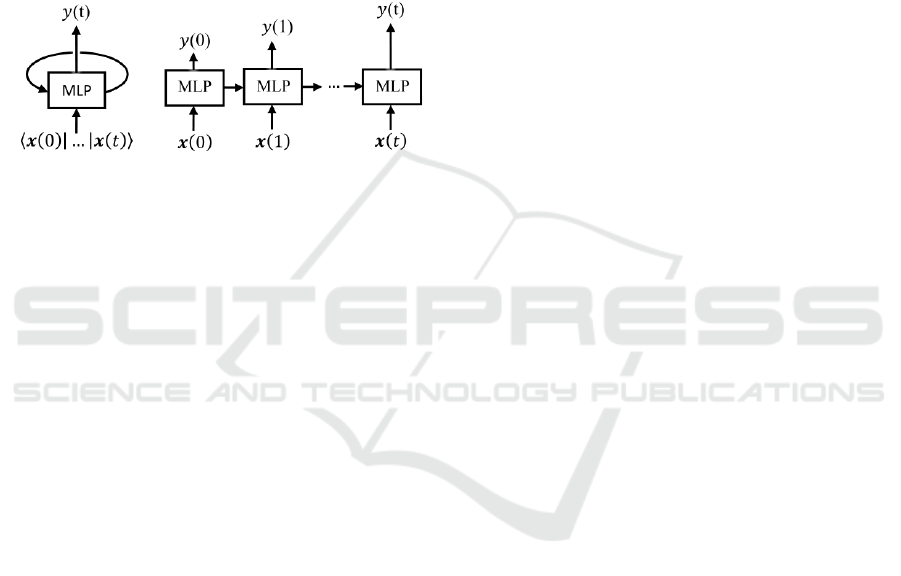
equivalent unfolded FFNN. Specifically, Figure 1a
shows a basic RNN, made by an MLP layer and a
cyclic connection from the output to the input neuron.
An RNN with finite response to finite length settles
to zero in finite time, and can be modelled as a
directed acyclic graph. This RNN can be unfolded
and transformed into an FFNN, i.e., an equivalent
static MLPs chain, with each MLP working at an
instant of time of the finite response, i.e., working
without memory (Figure 1b). Thus, within BBTT the
error is back-propagated from the last to the first time
step. The weights are updated by calculating the error
for each time step. Since the unfolded NN is static, it
can be trained by BP. However, in case of high
number of time steps, the unfolded NN is much
larger, and contains a large number of weights, which
makes BBTT computationally expensive.
A major issue with BP on large NN chains is
related to the gradient descent. In essence, BP goes
backwards through the NN to find the partial
derivatives of the error with respect to the weights, in
order to subtract the error from the weights. Such
derivatives are used by the gradient descent
algorithm, which iteratively minimizes a given
objective function. For better efficiency, the unfolded
NN can be transformed into a computational graph of
derivatives before training (Goodfellow et al., 2016).
A problem when training computational graph is to
manage the order of magnitude of gradients
throughout a large graph (Pascanu et al, 2013). The
exploding gradients problem occurs when error
gradients accumulate during an update. As a result,
very large gradients are produced and, in turn, large
updates to the network weights of long-term
830
Galatolo, F., Cimino, M. and Vaglini, G.
Using Stigmergy as a Computational Memory in the Design of Recurrent Neural Networks.
DOI: 10.5220/0007581508300836
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 830-836
ISBN: 978-989-758-351-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

components. This may cause network instability and
weights overflow. The problem can be easily solved
by clipping gradients when their norm exceeds a
given threshold (Goodfellow et al., 2016), by weight
regularization, i.e., applying a penalty to the networks
loss function for large weight values (Pascanu et al,
2013).
On the other side, the vanishing gradient problem
occurs when the values of a gradient are too small. As
a consequence, the model slows down or stops
learning. Thus, the range of contextual information
that standard RNNs can access is in practice quite
limited.
(a)
(b)
Figure 1: (a) An RNN (b) The equivalent NN unfolded in
time.
Long Short-Term Memory (LSTM, Graves et al.,
2009) is an RNN specifically designed to address the
exploding and vanishing gradient problems. An
LSTM hidden layer consists of recurrently connected
subnets, called memory blocks. Each block contains
a set of internal units, or cells, whose activation is
controlled by three multiplicative gates: the input
gate, the forget gate, and the output gate. An LSTM
network can remember arbitrary time intervals. The
cell decides whether to store (by the input gate), to
delete (by the forget gate), or to provide (output gate)
information, based on the importance assigned. The
assignment of importance happens through weights,
which are learned by the algorithm. Since the gates in
an LSTM are analog, in the form of sigmoid, the
network is differentiable, and trained by BP.
In recent years, LSTM networks have become the
state-of-the-art models for many machine learning
problems (Greff et al., 2017). This has attracted the
interest of researchers on the computational
components of LSTM variants.
This paper focuses on a novel concept of
computational memory in RNNs, based on stigmergy.
Stigmergy is defined as an emergent mechanism for
self-coordinating actions within complex systems, in
which the trace left by a unit’s action on some
medium stimulates the performance of a subsequent
unit’s action (Heylighen, 2016). To our knowledge,
this is the first study that proposes and lays down a
basic design for the derivation of Stigmergic Memory
RNN (SM-RNN). In the literature, stigmergy it is a
well-known mechanism for swarm intelligence and
multi-agent systems. Although its high potential,
demonstrated by the use of stigmergy in biological
systems at diverse scales, the use of stigmergy for
pattern recognition and data classification is still
poorly investigated (Heylighen, 2016). As an
example, in (Cimino et al.¸2015) a stigmergic
architecture has been proposed to perform adaptive
context-aware aggregation. In (Alfeo et al., 2017) a
multi-layer architectures of stigmergic receptive
fields for pattern recognition have been experimented
for human behavioral analysis. In (Galatolo et al.,
2018), the temporal dynamics of stigmergy is applied
to weights, bias and activation threshold of a classical
neural perceptron, to derive a non-recurrent
architecture called Stigmergic NN (S-NN). However,
due to the large NN produced by the unfolding
process, the S-NN scalability is limited by the
vanishing gradient problem. In contrast, the SM-RNN
proposed in this paper employs FF-NN as store and
forget cells operating on a Multi-mono-dimensional
SM, in order to reduce the network complexity.
To appreciate the computational power achieved
by SM-RNN, in this paper a conventional FF-NN, an
S-NN (Galatolo et al., 2018), an RNN and an LSTM-
NN have been trained to solve the MNIST digits
recognition benchmark (LeCun et al., 2018).
Specifically, two MNIST variants have been
considered: spatial, i.e., as sequences of bitmap rows,
and temporal, i.e., as sequences of pen strokes (De
Jong, E. D., 2018).
The remainder of the paper is organized as
follows. Section 2 discusses the architectural design
of SM-NNs. Experiments are covered in Section 3.
Finally, Section 4 summarizes conclusions and future
work.
2 ARCHITECTURAL DESIGN
Let us consider, in neuroscience, the phenomenon of
selective forgetting that characterizes memory in the
brain: information pieces that are no longer reinforced
will gradually be lost with respect to recently
reinforced ones. This behavior can be modeled by
using stigmergy. Figure 2 shows the ontology of an
SM, made by four concepts: Stimulus, Deposit,
Removal, and Mark. In essence, the Stimulus is the
input of a stigmergic memory. The past dynamics of
the Stimulus are indirectly propagated and stored in
the Mark. This propagation is mediated by Deposit
and Removal: Stimulus affects Deposit and Removal
which, respectively, reinforces and weakens Mark.
Using Stigmergy as a Computational Memory in the Design of Recurrent Neural Networks
831

Mark can be reinforced/weakened up to a
saturation/finishing level. On the other side, Mark
itself affects Deposit and Removal. This behavior can
be characterized as recurrent.
Figure 3 shows an example of dynamics of a
mono-dimensional SM, i.e., a real-valued mark
variable, generically called 𝑚(𝑡). Specifically, the
mark starts from 𝑚
(
0
)
, and for 𝑡 = 0, … ,4 it
undergoes a weakening by ∆𝑚
−
(
0
)
, … , ∆𝑚
−
(
4
)
,
respectively, up to the finishing level 𝑚. For 𝑡 =
11, … ,13 the mark variable undergoes a
reinforcement by ∆𝑚
+
(
11
)
, … , ∆𝑚
+
(
13
)
,
respectively, up to the saturation level 𝑚.
Figure 2: Ontology of a stigmergic memory.
Figure 3: Example of dynamics of a mono-dimensional
stigmergic memory.
Let us consider a mono-dimensional Stimulus,
i.e., a real-valued variable generically called 𝑠(𝑡). For
each 𝑡, ∆𝑚
+
(
𝑡
)
and ∆𝑚
−
(
𝑡
)
are determined by
Deposit and Removal, respectively, on the basis of
𝑠(𝑡). Thus, 𝑚
(
𝑡
)
is a sort of aggregated memory of
the 𝑠(𝑡) dynamics. The relationship between 𝑚(𝑡)
and 𝑠(𝑡) is not prefixed. By using 𝑚(𝑡) to feed a
subsequent classification or regression unit, this
relationship can be trained via supervised learning.
According to this concept, Figure 4 shows the
structure of an SM-RNN based classification unit.
Here, the Deposit, Removal, and Classification MLPs
are realized by spatial FF-MLPs. The SM is based on
an array of M mono-dimensional mark variables,
where M is also equal to the number of outputs of the
Deposit and Removal MLPs, as well as to the number
of inputs of the Classification MLP.
Figure 4: Structure of an SM-RNN based classification unit.
Specifically, the Linear Layer at the input of
Deposit and Removal MLP is a single layer of linear
neurons, i.e., neurons with linear activation function.
It performs a linear projection of the SM data.
The three MLPs have the same structure,
represented in Figure 5: (i) an Input Linear Layer; (ii)
a PReLU (Parametric Rectified Linear Unit)
activation function, which solves the vanishing
gradient problem; (iii) an Output Linear Layer; (iv) a
ReLU (Rectified Linear Unit) activation function, for
the Deposit and Removal MLPs, or a PReLU
activation function, for the Classification MLP,
respectively.
3 EXPERIMENTAL STUDIES
The architecture of an SM-NN has been developed
with the PyTorch framework (PyTorch, 2018) and
made publicly available on GitHub (GitHub, 2019).
The interested reader is referred to the GitHub
repository for further algorithmic details. The flow of
instructions has been modularized on different
abstraction levels, according to the best programming
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
832

practices, and it has been based on high-level
mathematical concepts. As a result, it is similar to
conventional pseudo-code, thanks to the support of
advanced machine-learning libraries, to encourage
open collaboration.
To appreciate the computational power of an SM-
RNN, different NNs have been trained to solve the
MNIST digits recognition benchmark (LeCun et al.,
2018): an SM-RNN, an FF-NN, an S-NN, an RNN
and an LSTM-NN.
Figure 5: Structure of a Deposit, Removal, or Classification
MLP.
The purpose is twofold: to measure the
computational power of SM-RNN with respect to FF-
NN, and to compare the performances of the other
existing temporal NN. For this purpose, the following
two variants of the MNIST benchmark have been
used.
In the Spatial MNIST dataset (LeCun et al., 2018),
the input image is made by 28×28 = 784 pixels, and
the output is made by 10 classes corresponding to
decimal digits. In the case of FF-NN, the handwritten
character is supplied in the form of full static bitmap.
For the other NNs, the handwritten character is
supplied row by row, in terms of 28 inputs, over 28
subsequent instants of time. In this case, once
provided the last chunk, the NN provides the
corresponding output class.
In the Temporal MNIST dataset (De Jong, E. D.,
2018), the handwritten character is supplied as a
sequence of pen strokes. In this case, at each instant
of time 𝑡, the next input is provided as a movement in
the horizontal and vertical directions (𝑑𝑥
(
𝑡
)
, 𝑑𝑦
(
𝑡
)
).
Once provided the last pen stroke, the NN provides
the corresponding output class. As an example,
Figure 6 shows the representation of a handwritten
digit in the Spatial MNIST (a) and Temporal MNIST
(b).
To adequately compare the different NNs, the
following methodology has been used. First, the FF-
NN and the SM-RNN have been dimensioned to
achieve their best classification performance.
Secondly, the S-NN, RNN and LSTM-NN have been
dimensioned to have a similar number of parameters
with respect to the SM-RNN.
Overall, the data set is made of 70,000 images. At
each run, the training set is generated by random
extraction of 60,000 images; the remaining 10,000
images makes the testing set.
(a)
(b)
Figure 6: representation of a handwritten digit in the Spatial
MNIST (a) and Temporal MNIST (b).
Table 1 shows the overall complexity of each NN.
The complexity values correspond to the total number
of parameters. Specifically, the SM is made by M =
15 mark variables. Thus, the Deposit and Removal
MLPs topology is made by 28 (temporal) + 15 (Linear
Layer) inputs, i.e. 43 inputs. The Linear Layer before
the Deposit and Removal MLPs contains 1515
weights + 15 biases = 240 parameters. The
Deposit/Removal MLPs contains the Input Linear
Layer (4320 weights + 20 biases = 880 parameters).
The PReLU contains 20 parameters. The Output
Linear Layer contains 2015 weights + 15 biases =
315 parameters. The Classification MLP contains the
Input Linear Layer (1510 weights + 10 biases = 160
parameters). The PReLU contains 10 parameters. The
Output Linear Layer contains 1010 weights + 10
biases = 110. Thus, the total number of parameter is
2402 + (880+20+315) 2 + (160+10+110) = 3,190.
For a detailed calculation of the complexity of the
other NNs, the interested reader is referred to
(Galatolo et al. 2018).
In addition, Table 1 shows the performance
evaluations, which are based on the 99% confidence
interval of the classification rate (i.e., the ratio of
correctly classified inputs to the total number of
inputs), calculated over 10 runs.
The Adaptive Moment Estimation (Adam) method
(Kingma et al., 2015) has been used to compute
adaptive learning rates for each parameter of the
gradient descent optimization algorithms, carried out
with batch method.
Using Stigmergy as a Computational Memory in the Design of Recurrent Neural Networks
833

Table 1: Performance and complexity of different NNs
solving the Spatial MNIST digits recognition benchmark.
Neural Network
Complexity
Classification rate
SM-RNN
3,190
.965 ± 0.056
FF-NN
328,810
.951 ± 0.0026
LSTM-RNN
3,360
.943 ± 0.011
S-NN
3,470
.927 ± 0.016
RNN
3,482
.766 ± 0.033
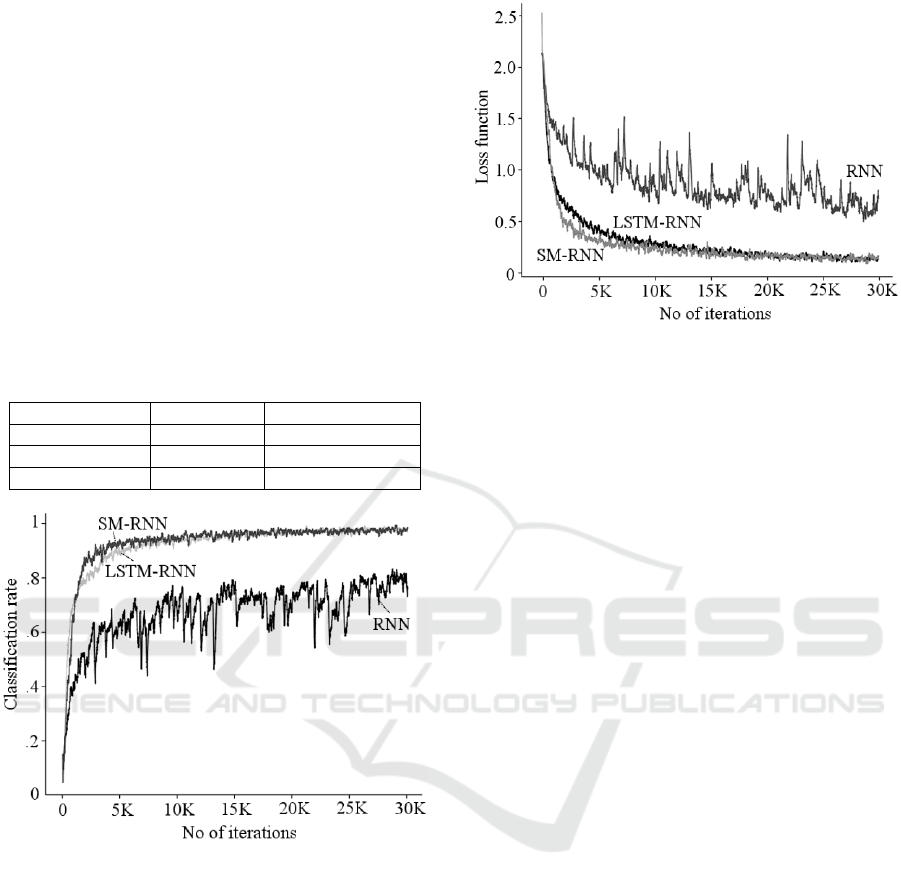
It is interesting to note in Table 1 that the SM-RNN
exhibits a classification accuracy similar to the best
NNs, i.e., LSTM-RNN and S-NN. The FF-NN,
although having a similar accuracy, employs a very
large number of parameters, about two order of
magnitude larger with respect to the others. Finally,
the RNN accuracy is sensibly lower. To assess the
quality of the training process, Figure 7 and Figure 8
show a scenario of classification rate and the function,
on the training set, against the number of iterations,
respectively. The loss function is calculated as the
Negative Log-Likelihood (NLL) using the softmax
activation function at the output layer of the NN,
which is commonly used in multi-class learning
problems.
Figure 7: Scenario of classification rate on training set
against number of iterations, for the Spatial MNIST data
set.
With regard to the Temporal MNIST data set, three
kinds of temporal NNs have been used, i.e., SM-
RNN, LSTM-RNN, and RNN.
Table 2 shows the overall complexity of each NN.
The complexity values correspond to the total number
of parameters. Specifically, the SM is made by M =
30 mark variables. Thus, the Deposit and Removal
MLPs topology is made by 4 temporal inputs (i.e., the
horizontal and vertical directions, the stroke and digit
ends) + 30 (Linear Layer) inputs, i.e. 34 inputs. The
Linear Layer before the Deposit and Removal MLPs
contains 3030 weights + 30 biases = 930 parameters.
The Deposit/Removal MLPs contains the Input
Linear Layer (3420 weights + 20 biases = 700
parameters). The PReLU contains 20 parameters. The
Output Linear Layer contains 2030 weights + 30
biases = 630 parameters. The Classification MLP
contains the Input Linear Layer (3020 weights + 20
biases = 620 parameters). The PReLU contains 20
parameters. The Output Linear Layer contains 2010
weights + 10 biases = 210. The activation ReLU
contains 10 neurons. Thus, the total number of
parameters is 9302 + (700+20+630)2 + (620+20+
210+10) = 5,420.
Figure 8: Scenario of loss function on training set against
number of iterations, for the Spatial MNIST data set.
The Recurrent NN is made by the following layers:
an Input Linear Layer (3450 weights + 50 biases =
1,750 parameters), a PReLU (50 parameters), an
Output Linear Layer (5030 weights + 30 biases =
1,530 parameters), and an activation PReLU (30
parameters). Thus, the total number of parameters is
1,750 + 50 + 1,530 + 30 = 3,360. In the Recurrent
NN, each output neuron has a backward connection
to the input and to the Classification MLP which, in
turn, is made by the following layers: the Input Linear
Layer (3050 weights + 50 biases = 1,550
parameters), the PReLU (50 parameters), the Output
Linear Layer (5010 weights + 10 biases = 510), and
the activation PReLU (10 neurons). Thus, the total
number of parameters of the Recurrent and the
Classification NNs is 3,360+1,550+50+510+10 =
5,480.
The LSTM-RNN fed by 4 inputs. For each LSTM
layer, the number of parameters is calculated
according to the well-known formula 4o(i+o+1),
where o and i is the number of outputs and inputs,
respectively. The topology is made by a 4×20 LSTM
layer, a 20×20 LSTM layer, and a 20×10 Output
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
834

Linear layer. Thus, the overall number of parameters
is 420(4+20+1) + 420(20+20+1) + 2010 + 10 =
5,490.
In addition, Table 2 shows the performance
evaluations, based on the same criteria detailed for
Table 1. It is apparent from the table that the SM-
RNN and the LSTM-RNN are equivalent in terms of
classification rate. In contrast, the RNN is not able to
gain a sufficient stability and accuracy. To assess the
quality of the training process, Figure 9 and Figure 10
show a scenario of classification rate and loss
function, on the training set, against the number of
iterations, respectively. The loss function of Figure 10
is calculated as in Figure 8.
Table 2: Performance and complexity of different NNs
solving the Temporal MNIST data set.
Neural Network
Complexity
Classification rate
SM-RNN
5,420
.9467 ± 0.0076
LSTM-RNN
5,490
.9496 ± 0.0027
RNN
5,480
.7295 ± 0.1101
Figure 9: Scenario of classification rate on training set
against number of iterations, for the Temporal MNIST data
set.
Overall, the proposed SM-RNN shows a very good
convergence with respect to the other NNs. In
consideration of the relative scientific maturity of the
other comparative NNs, the experimental results with
the novel SM-RNN looks very promising, and
encourage further investigation activities for future
work.
Figure 10: Scenario of loss function on training set against
number of iterations, for the Temporal MNIST data set.
4 CONCLUSIONS
In this paper, the concept of computational stigmergy
is used as a basis for developing a Stigmergic
Memory for Recurrent Neural Networks. Some
important issues in the research field, related to the
gradient descent, are first discussed. The novel
architectural design of the SM-RNN is then detailed.
Finally, the effectiveness of the approach is shown via
experimental studies, carried out on the spatial and
temporal MNIST data benchmarks.
Early experimental results, carried out on different
NN architectures available in the literature for spatial
or temporal data, are promising. In particular, the SM-
RNN can be appreciated for its computational power
with respect to the static FF-NN, compared on the
spatial dataset. Moreover, the SM-RNN exhibits a
classification accuracy and a computational power
similar to the best temporal NN, i.e., LSTM-RNN, on
the spatial and temporal dataset.
In order to achieve more significant results, future
work will focus on further experimentation and
investigation, as well as on a further formalization of
the approach.
ACKNOWLEDGEMENTS
This work was partially carried out in the framework
of the SCIADRO project, co-funded by the Tuscany
Region (Italy) under the Regional Implementation
Programme for Underutilized Areas Fund (PAR FAS
2007-2013) and the Research Facilitation Fund
(FAR) of the Ministry of Education, University and
Research (MIUR).
Using Stigmergy as a Computational Memory in the Design of Recurrent Neural Networks
835

This research was supported in part by the PRA
2018_81 project entitled “Wearable sensor systems:
personalized analysis and data security in healthcare”
funded by the University of Pisa
REFERENCES
Alfeo, A. L., Cimino, M. G., Vaglini, G.: Measuring
Physical Activity of Older Adults vian SMartwatch and
Stigmergic Receptive Fields. In Proceedings of the 6th
International Con-ference on Pattern Recognition
Applications and Methods (ICPRAM), 2017, pp. 724-
730, Scitepress.
Cimino, M. G., Lazzeri, A., Vaglini, G.: Improving the
analysis of context-aware information via marker-based
stigmergy and differential evolution. In International
Conference on Artificial Intelligence and Soft
Computing (ICAISC), 2015, pp. 341-352, Springer
LNAI, Cham.
De Jong, E. D., the MNIST digits stroke sequence data,
https://github.com/edwin-de-jong/mnist-digits-stroke-
sequence-data, last accessed 2018/09/03.
Galatolo, F. A., Cimino, M. G. C. A., Vaglini, G. Using
stigmergy to incorporate the time into artificial neural
networks, in Proc. of the Sixth International Conference
on Mining Intelligence and Knowledge Exploration
(MIKE), 2018, pp. 248–258, Springer Nature
Switzerland AG, LNAI 11308.
GitHub platform, https://github.com/galatolofederico/
icpram2019, last accessed 2019/01/16.
Goodfellow, I., Bengio, Y., Courville, A. and Bengio, Y.,
2016. Deep learning (Vol. 1). Cambridge: MIT press.
Graves, A., Liwicki, M., Fernández, S., Bertolami, R.,
Bunke, H. and Schmidhuber, J., 2009. A novel
connectionist system for unconstrained handwriting
recognition. IEEE transactions on pattern analysis and
machine intelligence, 31(5), pp.855-868.
Greff, K., Srivastava, R.K., Koutník, J., Steunebrink, B.R.
and Schmidhuber, J., 2017. LSTM: A search space
odyssey. IEEE transactions on neural networks and
learning systems, 28(10), pp.2222-2232.
Heylighen, F: Stigmergy as a universal coordination
mechanism I: Definition and components. Cognitive
Systems Research, 38, 4-13, (2016).
Kingma, D. P., & Ba, J. L. (2015). Adam: a Method for
Stochastic Optimization. International Conference on
Learning Representations, 1–13.
LeCun, Y., Cortes, C., Burges, C.J.C.: The MNIST
database of handwritten digits, http://yann.lecun.com/
exdb/mnist/, last accessed 2018/09/03.
Mazumdar, J. and Harley, R.G., 2008. Recurrent Neural
Networks Trained with Backpropagation Through
Time Algorithm to Estimate Nonlinear Load Harmonic
Currents. IEEE Trans. Industrial Electronics, 55(9),
pp.3484-3491.
Pascanu, R., Mikolov, T. and Bengio, Y., 2013, February.
On the difficulty of training recurrent neural networks.
In International Conference on Machine Learning (pp.
1310-1318).
PyTorch, Tensors and Dynamic neural networks in Python
with strong GPU acceleration, https://pytorch.org, last
accessed 2018/09/14
Schmidhuber, J. Deep learning in neural networks: An
overview. Neural networks 61 (2015): 85-117.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
836