Trajectory Planning for Automated Merging on Highways

Johannes Potzy

, Nadja Goerigk

, Thomas Heil

, Dennis Fassbender

and Karl-Heinz Siedersberger

Lehrstuhl f

ur Ergonomie, Technische Universit

at M

unchen, Munich, Germany

Elektronische Fahrwerksysteme GmbH, Gaimersheim, Germany

AUDI AG, Ingolstadt, Germany

dennis.fassbender@audi.de, karl-heinz.siedersberger@audi.de

Keywords:

Automated Driving, Maneuver Decision, Lane Change, Merging Maneuver, Trajectory Planing.

Abstract:

This article introduces a new approach for trajectory planning for merging on highways. The aim of the al-

gorithm, is to ﬁnd a comfortable driving strategy to merge in a gap on the target lane. Therfore, the proposed

algorithm determines a bunch of trajectories to reach surrounding gaps. The trajectory with the lowest costs

for each gap is chosen. To obtain the longitudinal component of the trajectory, a ﬁve-part section-wise deﬁned

polynomial in Frenet space is used to generate comfortable driving behaviour, with as few changes in the accel-

eration proﬁle as possible. Based on the prediction of surrounding trafﬁc, different variations of deceleration

and acceleration are combined. For each longitudinal part, a lateral component to perform a lane change into

the target gap is evaluated. The concept allows to evaluate the inﬂuence of the longitudinal driving strategy

on the dynamics required to change lanes. The algorithm is evaluated in a MATLAB simulation including a

runtime estimation.

1 INTRODUCTION

To integrate automated vehicles into disordered man-

ual trafﬁc, they have to solve complex driving tasks.

For example, when driving on highways, automated

vehicles have to change lanes in high density trafﬁc.

The wrong assessment of distances in the longitudinal

direction or wrong expectations of other trafﬁc par-

ticipants’ behaviour are the main reasons for trafﬁc

accidents (Gr

undl, 2005). Therefore, the automated

vehicle needs a distinct interpretable strategy to in-

teract with manual trafﬁc, respecting safety distances

as well as driving comfort. One popular method of

motion planning in structured environments is to gen-

erate a set of alternative trajectories to different target

positions and select the best trajectory based on a cost

function. For instance, Werling et al. (Werling et al.,

2010) use quintic polynomials for the lateral and the

longitudinal components. Based on a set of trajecto-

ries they formulate an optimization problem in order

to obtain a trajectory that satisﬁes the comfort crite-

ria of the car occupants, is collision free and mini-

mizes the deviation from to the reference path. Mc-

Naughton et al. (McNaughton et al., 2011) introduce

a lattice structure to obtain various lateral and longi-

tudinal offsets to the lane’s centre. They connect lat-

eral poses with different longitudinal positions using

cubic curvature polynomials, determining the optimal

trajectory based on a cost function. Wei et al. (Wei

et al., 2014) also use a lattice structure to generate

feasible candidate strategies. Thereafter, they are tak-

ing static and dynamic obstacles into account, due to

an interaction aware predicting of surrounding trafﬁc.

The optimal strategy is found based on a cost func-

tion. In contrast, Schwesinger et al. (Schwesinger

et al., 2013) use a closed-loop vehicle model to ob-

tain a set of feasible sample trajectories to certain

goals considering environmental constraints. To plan

the lateral trajectory Lee and Litkouhi (Lee and Litk-

ouhi, 2012) propose quintic polynomials. The algo-

rithm adapts the lateral trajectory in order to not ex-

ceed a deﬁned maximum lateral acceleration. Heil

et al. (Heil et al., 2016) use an asymmetrical lat-

eral trajectory to achieve a human-like lane change

behaviour according to Sporrer et al. (Sporrer et al.,

1998), where a human driver uses a higher lateral ac-

celeration for steering out of the initial lane than for

steering back into the target lane. Ulbrich and Mau-

rer (Ulbrich and Maurer, 2015) propose a decision al-

gorithm for tactical lane changes based on Bayesian

networks to decide if it is possible or beneﬁcial to ex-

ecute a lane change. Hansen et al. (Hansen et al.,

2016) divide driving on highways in a lane keep and a

merging maneuver. The lane keep maneuver is based

Potzy, J., Goerigk, N., Heil, T., Fassbender, D. and Siedersberger, K.

Trajectory Planning for Automated Merging on Highways.

DOI: 10.5220/0007585602830290

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 283-290

ISBN: 978-989-758-374-2

283

on a common ACC vehicle controller. If the decision

is made that a lane change is necessary or beneﬁcial

to the automated vehicle, they use two quintic poly-

nomials to synchronize to a gap. They deﬁne the op-

timum intersection of the automated vehicles with the

border of the safety area of the ﬁrst vehicle building

the gap and the entrance in the safety area of the target

vehicle on the current lane by solving an optimisation

problem minimizing the average velocity during both

parts, as well as the velocity of the automated vehi-

cles at the end of the trajectory. Based on those inter-

sections the longitudinal and lateral component of the

trajectory is deﬁned.

The aim of our planning algorithm is to achieve

comfortable driving behaviour with as few jerk min-

imal changes in the longitudinal acceleration proﬁle

as possible respecting the lateral dynamics and safety

distances to interacting trafﬁc. Therefore, we propose

a planning algorithm that generates a set of trajecto-

ries for reasonable gaps and ﬁnds the trajectory with

the lowest cost per gap. The longitudinal component

consists of a new planning approach presenting an an-

alytical solution using a piece-wise deﬁned function.

The approach allows to respect the maximum longi-

tudinal and lateral dynamics of the trajectory as well

as to check for possible collision analytically.

The structure of this article is as follows. Section

2 proposes a way to integrate the algorithm into a sys-

tem architecture. In section 3 the planning algorithm

is presented, where the sector to change lanes, the

longitudinal and lateral components of the trajectory,

cost functions and the algorithm are introduced. The

concept is evaluated using a MATLAB simulation in

section 4. A conclusion is given in section 5.

2 SYSTEM ARCHITECTURE

We propose the system architecture illustrated in ﬁg-

ure 1. To enable an automated vehicle (Ego) to merge

on highways in dense trafﬁc, we describe the free

space in the form of gaps between other cars. A pos-

sible scenario is illustrated in ﬁgure 2. The ﬁrst layer

of the system architecture is divided into the parts

perception and navigation. The second layer is the

behaviour decision and the third layer is the vehicle

controller. The perception extracts the environment

information about other road users and the road. The

navigation estimates the route and labels the lanes as

regular lanes on-ramps or off-ramps. The behaviour

decision builds the scene based on perception infor-

mation and the route. The scene comprises all in-

formation relevant to the driving task (Ulbrich et al.,

2015). Depending on the scene all reasonable gaps

PerceptionNavigation

Vehicle Control

Behaviour

Decision

Scene

Extract Reasonable Gaps

Gap Prediction

Generate Trajectories

Calculate Costs

Select Optimal

Trajectory per Gap

,...

Evaluating

Global Costs

,...

Select Optimal Trajectory

min(z

,...)

Figure 1: The ﬁgure shows a system architecture determin-

ing the best trajectory based on the surrounding gaps ex-

tracted from a scene representation. The parts of the pro-

posed planning algorithm are the blocks in grey.

GF,1

(t)s

GB,1

(t)s

GF,2

(t)

GB,2(t)

GF,0

(t)

max

Figure 2: The reference coordinate system is placed in the

middle of the Ego (red) on the left lane. The proposed plan-

ning algorithm determines the dynamics required to change

lanes for example in gap 1, built by s

GF,1

(t) and s

GB,1

(t), or

gap 2, built by s

GF,2

(t) and s

GB,2

(t), on the right lane. The

algorithm also takes the front vehicle s

GF,0

(t) and possible

lane ends s

max

into account. The black dashed area is an

area that shall be avoided by the other vehicles, including

the Ego.

are extracted. For example, due to the desired route,

gaps on the target lane are selected. The module needs

to evaluate if it is feasible to reach the gap based on

the front vehicle of the Ego, possible lane ends, the

approximated gap velocity and predicted gap sizes.

All selected gaps are given to the proposed planner.

The displacement is predicted for every gap using a

constant velocity model for the cars limiting the gap.

Based on this prediction, it is possible to calculate the

time span available to merge into the target gap. In

a second step, a number of acceleration proﬁles are

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

284

evaluated to reach this space. For each longitudinal

part a lateral planning to merge into the gap is made,

considering safety margins in Frenet space (Werling

et al., 2010). The optimal trajectory per gap accord-

ing to comfort and safety margins is considered. Par-

allel global costs evaluate criteria like the velocity of

each gap or strategic decision, for example going to

the right lane as early as possible to increase the time

reserve to reach an exit or the desired lane at an inter-

change.

The dynamic costs and the global strategic costs

are evaluated together, the optimal trajectory is trans-

formed from Frenet into global coordinates and is sent

to the vehicle controller. The transformation is given

in (Werling et al., 2010). The vehicle controller exe-

cutes the desired plan.

3 PLANNING ALGORITHM

The proposed planning approach is based on Hansen

et al. (Hansen et al., 2016). Our goal was to de-

velop an algorithm to determine the most beneﬁcial

driving strategy by ﬁnding the optimal trajectory in

a set of candidate trajectories, like in (Lee and Litk-

ouhi, 2012) or (Werling et al., 2010), for several gaps

on the target lane. The concept allows to start a lane

change at a point in the future and to combine an ac-

celerating and decelerating longitudinal driving strat-

egy to reach the gap by taking the front vehicle or

a possible lane end into account. To obtain a com-

fortable driving behaviour with as few changes in the

longitudinal acceleration proﬁle as possible, we use

a section-wise deﬁned longitudinal component with

no more than ﬁve parts. For every longitudinal com-

ponent, a lateral component is planned. Therefore, it

is possible to model the coupling of longitudinal and

lateral dynamics when changing lanes. The optimal

trajectory is found based on a cost function. Thus, the

longitudinal and lateral jerk, the deviation from the

target position to the end position of the longitudinal

trajectory and the number of parts of the section-wise

deﬁned function is taken into account. Based on the

gap prediction built by surrounding vehicles, the plan-

ning is made.

The prediction model for the extracted reasonable

gaps is introduced in section 3.1. Second, the lon-

gitudinal component in section 3.2 and thereafter the

lateral component in section 3.3 of the trajectory is

explained. Then, the cost function to determine the

optimal trajectory per gap is introduced in section 3.4.

The algorithm is given in section 3.5.

max

GF,1

GB,1

GF,0

GF,2

GB,2

Figure 3: The ﬁgure illustrates as grey dashed area the dis-

placement of the Ego gap and as blue dashed area, where a

lane change to gap two is possible.

3.1 Gap Prediction

The prediction estimates the space where following

the Ego lane or changing into a gap on the target lane

is possible. An interaction-aware prediction and un-

certainties in perception are neglected. The prediction

is not able to anticipate the reactions of other traf-

ﬁc participants to the action of the Ego and therefore

does not depict interactions between road users. Since

the planning is constantly repeated, only the ﬁrst time

step is executed until a new plan is available, the plan-

ning reacts to changing behaviour of surrounding traf-

ﬁc participants. Surrounding vehicles are predicted

with constant velocity as given in equation (1), for

each gap n:

GF,n

(t) = s

GF,n

(t = 0) + v

GF,n

(t = 0) ·t,

GB,n

(t) = s

GB,n

(t = 0) + v

GB,n

(t = 0) ·t,

(1)

where s

GF,0

(t = 0) and s

GB,n

(t = 0) are the starting

position and v

GF,n

(t = 0) and v

GB,n

(t = 0) are the

starting velocity of the gap’s front and back vehicle.

Moreover, the longitudinal distance to trafﬁc partici-

pant should not fall below a minimum. In this case

the maximum velocity of vehicle is the velocity of

its vehicle in front. Figure 3 illustrates the percep-

tion model. The grey dashed area illustrates the dis-

placement of the Ego’s front vehicle s

GF,0

(t). The

dashed blue area shows the predicted areas, where

a lane change to gap n = 2, built by the gap’s front

GF,2

(t) and back vehicle s

GB,2

(t) is possible. In addi-

tion, the concept allows to restrict the maximum dis-

placement s

max

allowed for the maneuver due to a lane

end. The prediction can be extended by interaction

aware prediction (Kesting et al., 2010), (Treiber and

Kesting, 2009) or by considering uncertainties in pre-

diction and perception (Suh and Yi, 2017).

Trajectory Planning for Automated Merging on Highways

285

(t)

Figure 4: The parts one, three and ﬁve use cubic acceler-

ation equations. The parts two and four use constant ac-

celeration equations. After part ﬁve zero acceleration is as-

sumed. The target accelerations a

t,1

and a

t,2

as well as the

time span t

are varied in the algorithm.

3.2 Longitudinal Component

The longitudinal component of the trajectory evalu-

ates different variations of acceleration and decelera-

tion to reach the target gap. To ensure collision free

driving, all acceleration proﬁles that do not reach the

blue or are outside the grey dashed area are discarded,

as illustrated in ﬁgure 3. To generate a comfortable

driving behaviour with as few changes in the acceler-

ation proﬁle as possible, a ﬁve-part section-wise de-

ﬁned function is used, as given in equation (2):

(t) =











x,1

(t), t ≤ t

x,2

(t − t

), t

< t ≤ t

= t

+ τ

x,3

(t − t

), t

< t ≤ t

= t

+ τ

x,4

(t − t

), t

< t ≤ t

= t

+ τ

x,5

(t − t

), t

< t ≤ t

= t

+ τ

(2)

The time span for each polynomial is described by τ

The section-wise deﬁned acceleration proﬁle is illus-

trated in ﬁgure 4. The algorithm varies the ﬁrst a

and

second a

target acceleration, as well as the time t

The time t

is maximum τ

. To determine the polyno-

mials of all ﬁve parts, the matrix A(t) is used, as given

in equation (3):

A(t) =







1 t t

0 1 2t 3t

0 0 2 6t 12t

20t

0 0 0 6 24t 60t

0 0 0 0 24 120t







. (3)

Cubic acceleration leads to quintic position polyno-

mials. Those can be described by the following equa-

tion (4), where i stands for the part of the section-wise

deﬁned function:

x,i



0,i

1,i

2,i

3,i

4,i

5,i



x,i

(t) =



x,i

(t), v

x,i

(t), a

x,i

(t), j

x,i

(t),

x,i

(t)



= A(t)c

x,i

(4)

At ﬁrst the time for each part of the section-wise de-

ﬁned function τ

and the constants c

2,i

, c

3,i

, c

4,i

and

ext,k

ext,i

41,i

+,i

42,i

-,i

41,k

-,k

42,k

+,k

(t)

Figure 5: In case of a jerk maximum j

ext,i

, the time span τ

+,i

before the extreme and the time span τ

-,i

after the extreme

is used. In case of a jerk minimum j

ext,k

it is vice versa. For

both cases we use the constants c

41,i

before and c

42,i

after

the extreme point.

5,i

are determined. Therefore, it is differentiated be-

tween cubic and constant acceleration equations. The

ﬁrst, third and ﬁfth part of the ﬁve-part section-wise

deﬁned solution are cubic acceleration parts. The sec-

ond and fourth part use constant acceleration equa-

tions. Thus, the time span to reach a certain target

velocity is determined for the fourth part. Thereafter,

the constants c

0,i

, c

1,i

for each part are determined by

solving the trivial solutions by using the starting posi-

tion s

s,i

and velocity v

s,i

of each part.

3.2.1 Cubic Acceleration

Solving the trivial solutions leads to c

2,i

and c

3,i

using the starting acceleration a

s,i

and jerk j

s,i

each part. The time to reach the target accelera-

tion τ

+/-,i

and the constants c

4,i

and c

5,i

are extin-

guished by solving the following boundary condi-

tions: a

x,i

(τ

) = a

t,i

, j

x,i

(τ

) = 0,

x,i

(τ

jext,i

) = 0 and

x,i

(τ

jext,i

) = j

ext,i

. At the time τ

jext,i

the jerk extreme

point j

ext,i

is reached. The time to reach the target

acceleration a

t,i

is given in equation (5):

+/-,i

3(a

t,i

− a

s,i

)

ext,i

+ j

s,i

ext,i

− j

ext,i

s,i

. (5)

The time τ

differentiates between a positive case τ

+,i

and a negative one τ

-,i

as illustrated in ﬁgure 5. In case

of a positive jerk extreme the positive case is used,

after the extreme point we use the negative one. In

case of a negative extreme point it is vice versa.

For c

4,i

between two constants is distinguished. The

constants are given in equation (6):

41,i

= −

− j

ext,i

s,i

− j

ext,i

+ 1

s,i

− j

ext,i

12τ

42,i

− j

ext,i

s,i

− j

ext,i

− 1

s,i

− j

ext,i

12τ

(6)

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

286

The constant c

41,i

is used before and the constant c

42,i

after the jerk extreme. The solution for c

5,i

is given in

the following equation (7):

5,i

12c

4,i

5( j

s,i

− j

ext,i

)

(7)

If j

s,i

is equal to j

ext,i

, the constant c

4,i

is equal to zero

and the constant c

5,i

= − j

s,i

/(60τ

We determine if the jerk proﬁle is before or after its

extreme point, based on the last plan S

x,t-1

, the cur-

rent acceleration a

and the current jerk j

. Based on

the last plan S

x,t-1

it is solved for the times where the

jerk component is equal to the current jerk j

. At the

smaller time t

and greater time t

the accelerations

e,t-1,1

and a

e,t-1,2

are evaluated based on the last plan,

respectively. Those accelerations are compared with

the current acceleration a

If the current acceleration a

is equal to the acceler-

ation a

e,t-1,1

, the current jerk is before the extreme

point. If the current acceleration a

is equal to the

acceleration a

e,t-1,2

, the current jerk is after the ex-

treme point. If the current acceleration a

is not equal

to both accelerations a

e,t-1,1

and a

e,t-1,2

the Ego stayed

not on the last plan. In such cases the jerk is always

before the extreme point.

3.2.2 Constant Acceleration

Solving the trivial solutions leads to c

2,i

and c

3,i

using the starting acceleration a

s,i

and jerk j

s,i

. While

in part two the algorithm varies the time length to hold

the target acceleration a

t,1

in part four also the time

span to reach the target velocity v

GF,n

with a certain

target acceleration a

t,2

is determined. The solution is

given in equation (8):

GF,n

− (v

+ ∆v

)

t,2

. (8)

The velocity v

is the Ego velocity at the end of the

third part of the section-wise deﬁned function and the

velocity ∆v

is caused by the acceleration of the ﬁfth

part of the section-wise deﬁned function.

3.3 Lateral Component

It is possible to start the lane change if the Ego has

reached the height of the target gap. Therefore, the in-

tersection point of the back of the Ego with the safety

area of the back vehicle t

y,s1

of the target gap is deter-

mined. Moreover, the intersection point of the front of

the Ego with the safety area of the front vehicle t

y,s2

of the target gap is evaluated. The earliest intersection

point is considered as starting time given in equation

(9):

y,s

= min(t

y,s1

y,s2

) (9)

Moreover, the lateral planning needs to be executed

if the distance to vehicle in front t

y,e1

of the Ego or

to a possible lane end t

y,e2

falls below the safety dis-

tance or the lateral planning time does exceed a max-

imum time t

y,e3

to change lane, deﬁned by Lange et

al. (Lange et al., 2013) to reach a comfortable driving

behaviour, given in equation (10):

y,e

= min(t

y,e1

y,e2

y,e3

) (10)

To determine the intersection, it is evaluated if each

part of the section-wise deﬁned longitudinal compo-

nent, considering the length of the Ego, is in front or

in back of the safety area of the considered vehicle.

If the intersection is in the constant acceleration part

of the component, it is possible to determine the time

analytically. Otherwise, to avoid a numerical solution,

the end time of a part is considered for the times t

y,s1

and t

y,s2

. Moreover, the start time of a part is consid-

ered for the times t

y,e1

and t

y,e2

. The time to change

lane t

TTLC

is given in equation (11):

TTLC

= t

y,e

−t

y,s

. (11)

To calculate the lateral component quintic polynomi-

als, introduced in (Werling et al., 2010), are used.

3.4 Cost Function

The cost function evaluates the driving comfort

caused by maximum longitudinal and lateral jerk, the

parts of the section-wise deﬁned longitudinal compo-

nent and the distance to the target point at the end of

the ﬁfth part of the longitudinal component. The tra-

jectory with the lowest costs per gap is chosen.

The cost of the longitudinal jerk j

(t) is given in equa-

tion (12), where a

tmax,1

and a

tmax,2

are the maximum

acceleration of the ﬁrst a

t,1

and second a

t,2

target ac-

celeration:







| j

(t)|dt

tmax,1

| + |a

tmax,2







(12)

The cost of the lateral jerk j

(t) is given in equation

(13), where a

ymax

is the maximum allowed lateral ac-

celeration:







| j

(t)|dt

ymax







(13)

To calculate the jerk j

(t) to evaluate the cost func-

tion the time to change lane is not constraint by t

y,e3

to reward solutions that already changed lane with a

greater time distances to the lane end or possible ve-

hicles in front of the Ego.

Trajectory Planning for Automated Merging on Highways

287

In the ﬁrst planing step of the longitudinal component

at most ﬁve section-wise deﬁned parts are possible to

reach the target velocity. With cyclical replanning,

in every time step at most ﬁve section-wise deﬁned

parts can be added to the initial plan and therefore the

possible number of parts of the section-wise deﬁned

longitudinal component with respect to the initial plan

increases. Moreover, to accelerate or decelerate to a

target acceleration in several steps implies the same

total jerk as accelerating at once to the target acceler-

ation. To keep the optimal trajectory at the initial plan

and to gain as few changes in the acceleration proﬁle

as possible, the number of parts p of the section-wise

deﬁned function, are evaluated as well, as given in

equation (14):





(14)

Furthermore, the distance at the end of the longitu-

dinal part of the trajectory s

) to the position to

the gap’s front vehicle or a possible lane end s

max(s

),s

max

) is taken into account. The cost due

to the target point are given in equation (15), where t

is the safety time for car following:



1 −

− s

)

GF,n

·t



(15)

The overall cost per trajectory is the weighted sum of

all introduced partial costs.

3.5 Algorithm

The algorithm samples the ﬁrst and the second tar-

get acceleration a

and a

, as well as the time span

to generate the set of longitudinal components.

Moreover the algorithm allows combinations of non-

negative values for a

and non-positive values for a

as target acceleration for target gaps with a smaller

target velocity than the Ego. If the target gap has a

higher velocity it is vice-versa.

At ﬁrst the algorithm samples a

. Thereafter, we de-

termine if the Ego acceleration a

is equal to the target

acceleration a

and if the Ego jerk j

is equal to zero.

In this case also τ

is equal to zero and the starting

states of the second part are equal to the Ego states.

Otherwise we determine τ

and c

using the cubic

acceleration equations. Second, the time span t

sampled by the algorithm. Since we want to obtain

one to ﬁve part-section wise deﬁned trajectories, the

time span t

starts from zero. The resulting times t

and τ

are calculated according to equation (16):



0, t

= 0

, t

> 0

= max(0,t

−t

(16)

The second part is a constant acceleration part. There-

fore, c

is determined by constant acceleration equa-

tions and τ

by sampling the time t

. Third, the second

target acceleration a

is sampled. The second target

acceleration is used to accelerate the Ego to the target

velocity of each gap. Here, the target vehicle is the

front vehicle of each gap. If t

is equal to zero we try

if the acceleration of the ﬁfth part leads directly to the

target velocity considering the end states of the sec-

ond part as the starting states. If this does not occur

the third part is similar determined as the ﬁrst part.

Next, the acceleration proﬁle for the ﬁfth part is ex-

tinguished. Therefore, the time span τ

and the con-

stants c

, c

and c

are determined using cu-

bic acceleration equations. Thereafter, it is possible

to determine the fourth part τ

and c

using constant

acceleration equations. By then, it is possible to de-

termine the missing constants c

and c

of the ﬁfth

part.

All solutions that do not reach the blue-dashed area or

are outside the grey-dashed area are neglected. There-

after, for every longitudinal planning a lateral planing

to change lane is made. All lateral plans where the

acceleration exceeds a deﬁned maximum are also ne-

glected. Then, the costs for every trajectory are cal-

culated. The algorithm returns the trajectory with the

lowest costs per gap.

4 EVALUATION

The proposed planning algorithm is evaluated in a

MATLAB simulation. Therefore, surrounding traf-

ﬁc is simulated with constant velocity and the Ego

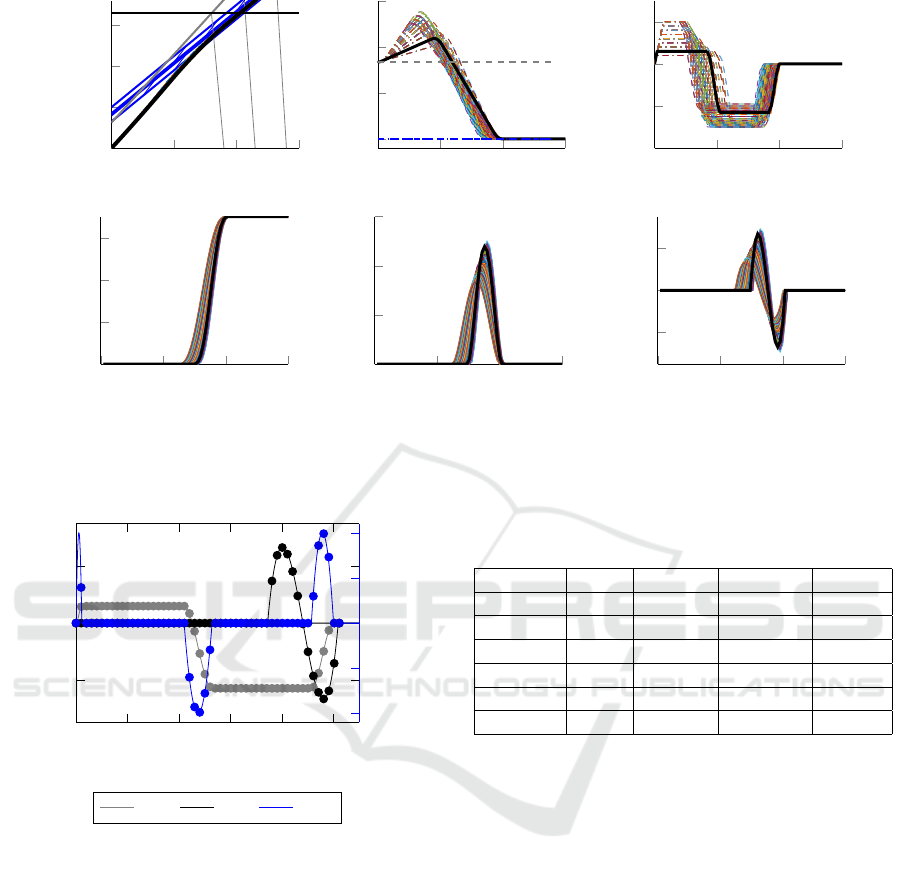
is assumed to follow the planned trajectory. Figure 6

shows the generated set of trajectories for the initial

planning, for a lane change into a gap with a smaller

velocity. Due to the vehicle in front of the Ego it is

not possible to reach gap 1. Therefore, the algorithm

only determines trajectories reaching gap 2. The thick

black trajectory is the optimal one. To solve the sit-

uation, the car ﬁrst accelerates to reach the gap and

to gain enough time to change lane with small lateral

dynamics. Second the car decelerates to target speed.

Since the number of parts of the section-wise deﬁned

longitudinal component are considered, the Ego tra-

jectory has as few changes in the acceleration proﬁle

as possible. Without the vehicle in front of the Ego

or a lane end in a greater distance the Ego would only

decelerate. To evaluate the cost function it is evalu-

ated if the Ego stays on the initial plan over the whole

maneuver. Therefore, the Ego is located cyclically on

the next time step t

step

= 0.2 s of the plan with the low-

est costs, as illustrated in ﬁgure 7. At every time step

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

288

100

200

300

−4

−2

Figure 6: Longitudinal and lateral component of the set of trajectories in Frenet coordinates: one planning step is executed

with a

t1min

= −2 m/s

, a

t1max

= 2 m/s

, a

t2min

= −3 m/s

and a

t2max

= 3 m/s

. The discretization of the target acceleration

is a

t1step

= 0.2 m/s

and a

t2step

= 0.1 m/s

. The maximum time is t

2max

= 10 s and is sampled with t

2step

= 0.2 s.

0 2 4

8 10

−2

t [s]

[m/s

]

x,opt

y,opt

x,opt

−4

−2

[m/s

]

Figure 7: The ﬁgure illustrates the devolution of the Ego

states a

x,opt

, a

y,opt

and j

x,opt

by cyclic planning of the pro-

posed algorithm. The dots visualize the Ego states at the

different planning steps. The solid lines represent the initial

planning.

the proposed algorithm is executed. The Ego stays on

the initial plan over the whole maneuver.

In addition, to evaluate the computational costs,

we evaluated different scenarios. Since, the calcula-

tion time depends not only on the discretization of the

target velocities a

, a

and the time to hold the ﬁrst

target acceleration t

, but as well on the grey and blue

dashed area. The simulation was running on an HP

Elite Book with an Intel Core i-7 v Pro CPU at 2.60

GHz with 16.0 GB RAM. The time measurement is

made over one scenario until the lane change was per-

formed and the Ego is at target speed. In all evaluated

Table 1: The sampling is executed similar as illustrated in

ﬁgure 6. The planning is performed due to one gap only.

max

[m] t

[s] max [s] mean [s] std [s]

400 1.8 0.2215 0.0805 0.0306

400 1.2 0.2143 0.0718 0.0364

400 0.6 0,1944 0.0626 0.0412

600 1.8 0.6996 0.2026 0.1783

600 1.2 0.3787 0.1071 0.0937

600 0.6 0.2463 0.0684 0.0566

scenarios, the initial distance is s

= 100m and the

initial velocity of the front vehicle of the target gap

is v

= 25 m s

−1

. The front and back vehicle of the

target gap drives with constant speed. The initial Ego

speed is v

= 33.3ms

−1

. The size of the target gap,

as well as the possible displacement on the starting

lane inﬂuences the calculation time. Thus, the time

distance from the front and the back vehicle of the

target gap t

and the distance to the lane end s

max

varied. A vehicle in front of the Ego is not taken into

account. The mean, the maximum (max) and stan-

dard deviation (std) of the computation time is listed

in table 1.

5 CONCLUSION

This article introduces a new approach for trajectory

planning of automated vehicles for merging maneu-

vers on highways. To determine the dynamics neces-

sary to reach several gaps a possible system architec-

Trajectory Planning for Automated Merging on Highways

289

ture is proposed. To evaluate those dynamics, a set

of trajectories is evaluated based on a cost function in

each time step. The longitudinal component is com-

posed of a ﬁve-part section-wise deﬁned function, to

accelerate to the target velocity of each gap. All so-

lutions outside the drivable area are discarded. The

lateral planning for potentially changing lane is exe-

cuted, dependent on the situation, at a point in the fu-

ture, considering safety distances. The cost function

evaluates the longitudinal and lateral jerk, the num-

ber of parts and the distance to the target point at the

end of the longitudinal component of the trajectory.

Evaluations in MATLAB simulations show that the

Ego stays on the same plan over the whole maneu-

ver, executing the same planning algorithm in every

time step, assuming constant behaviour of surround-

ing trafﬁc. Moreover, a ﬁrst evaluation of the compu-

tational costs of the algorithm is made.

To reach a higher discretization of one planning

step, the proposed algorithm can easily be paral-

lelised. Also, the gap prediction model can be ex-

tended to consider interactions between road users.

Moreover, for use in real trafﬁc, the model could be

extended to deal with uncertainties in prediction or

perception, to reward driving in less uncertain spaces.

REFERENCES

undl, M. (2005). Fehler und Fehlverhalten als Ur-

sache von Verkehrsunf

allen und Konsequenzen f

das Unfallvermeidungspotenzial und die Gestaltung

von Fahrerassistenzsystemen. Universit

at Regens-

burg.

Hansen, T., Schulz, M., Knoop, M., and Konigorski,

U. (2016). Trajectory planning for automated lane

changes. In ATZ worldwide, 118(7):60–65.

Heil, T., Lange, A., and Cramer, S. (2016). Adaptive and

efﬁcient lane change path planning for automated ve-

hicles. In 2016 IEEE 19th International Conference

on Intelligent Transportation Systems (ITSC), pages

479–484.

Kesting, A., Treiber, M., and Helbing, D. (2010). En-

hanced intelligent driver model to access the impact

of driving strategies on trafﬁc capacity. In Philo-

sophical Transactions of the Royal Society of London

A: Mathematical, Physical and Engineering Sciences,

368(1928):4585–4605.

Lange, A., Maas, M., Albert, M. Siedersberger, K. H., Ben-

gler, K. (2013). Automatisches Fahren - So komfort-

abel wie m

oglich, so dynamisch wie n

otig. In VDI

Wissensforum.

Lee, J. W. and Litkouhi, B. (2012). A uniﬁed framework

of the automated lane centering/changing control for

motion smoothness adaptation. In 2012 15th Interna-

tional IEEE Conference on Intelligent Transportation

Systems, pages 282–287.

McNaughton, M., Urmson, C., Dolan, J. M., and Lee, J. W.

(2011). Motion planning for autonomous driving with

a conformal spatiotemporal lattice. In 2011 IEEE In-

ternational Conference on Robotics and Automation,

pages 4889–4895.

Schwesinger, U., Ruﬂi, M., Furgale, P., and Siegwart, R.

(2013). A sampling-based partial motion planning

framework for system-compliant navigation along a

reference path. In 2013 IEEE Intelligent Vehicles Sym-

posium (IV), pages 391–396.

Sporrer, A., Prell, G., Buck, J., and Schaible, S. (1998). Re-

alsimulation von Spurwechselvorg

angen im Straßen-

verkehr. In Verkehrsunfall und Fahrzeugtechnik,

(36):69–76.

Suh, J. and Yi, K. (2017). A new adaptive uncertainty

propagation method based stochastic model predictive

control for automated driving vehicles. In 2017 Amer-

ican Control Conference (ACC), pages 5660–5665.

Treiber, M. and Kesting, A. (2009). Modeling lane-

changing decisions with mobil. In Trafﬁc and Gran-

ular Flow ’07, pages 211–221, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Ulbrich, S. and Maurer, M. Towards tactical lane change be-

havior planning for automated vehicles. In 2015 IEEE

18th International Conference on Intelligent Trans-

portation Systems, pages 989–995.

Ulbrich, S., Menzel, T., Reschka, A., Schuldt, F., and Mau-

rer, M. (2015). Deﬁning and substantiating the terms

scene, situation, and scenario for automated driving.

In 2015 IEEE 18th International Conference on Intel-

ligent Transportation Systems, pages 982–988.

Wei, J., Snider, J. M., Gu, T., Dolan, J. M., and Litkouhi,

B. (2014). A behavioral planning framework for au-

tonomous driving. In 2014 IEEE Intelligent Vehicles

Symposium Proceedings, pages 458–464.

Werling, M., Ziegler, J., Kammel, S., and Thrun, S. (2010).

Optimal trajectory generation for dynamic street sce-

narios in a frenet frame. In 2010 IEEE International

Conference on Robotics and Automation, pages 987–

993.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

290