
Balancing Exploitation and Exploration via Fully Probabilistic Design of
Decision Policies
Miroslav K
´
arn
´
y and Franti
ˇ
sek H
˚
ula
The Czech Academy of Sciences, Inst. of Inf. Theory and Automation, POB 18, 182 08 Prague 8, Czech Republic
Keywords:
Exploitation, Exploration, Bayesian Estimation, Adaptive Systems, Fully Probabilistic Design, Markov
Decision Process.
Abstract:
Adaptive decision making learns an environment model serving a design of a decision policy. The policy-
generated actions influence both the acquired reward and the future knowledge. The optimal policy properly
balances exploitation with exploration. The inherent dimensionality curse of decision making under incom-
plete knowledge prevents the realisation of the optimal design. This has stimulated repetitive attempts to
reach this balance at least approximately. Usually, either: (a) the exploitative reward is enriched by a part
reflecting the exploration quality and a feasible approximate certainty-equivalent design is made; or (b) an
explorative random noise is added to the purely exploitative actions. This paper avoids the inauspicious (a)
and improves (b) by employing the non-standard fully probabilistic design (FPD) of decision policies, which
naturally generates random actions. Monte-Carlo experiments confirm its achieved quality. The quality stems
from methodological contributions, which include: (i) an improvement of the relation between FPD and stan-
dard Markov decision processes; (ii) a design of an adaptive tuning of an FPD-parameter. The latter also suits
for the tuning of the temperature in both simulated annealing and Boltzmann’s machine.
1 INTRODUCTION
The inspected decision making is close to the tra-
ditional Markov decision process (MDP, (Puterman,
2005)). The next summary of known basic facts al-
lows us to formulate and solve the addressed prob-
lem. In order to focus on the paper’s topic, we re-
strict ourselves to a finite amount of possible agent’s
actions
1
a
t
∈ A = {1,...,k}, k ∈ N, k < ∞. They
are selected in a finite amount of epochs t ∈ T =
{1,...,l}, l ∈ N, l < ∞. The agent’s environment re-
sponds to actions by discrete-valued observable states
s
t
∈ S = {1,...,m}, m ∈ N, m < ∞. A given real re-
ward r = (r
t
( ˜s,a,s), ˜s,s ∈ S, a ∈ A)
t∈T
quantifies the
agent’s preferences. The sequence of transition prob-
abilities
p = (p
t
( ˜s|a,s), ˜s,s ∈ S,a ∈ A)
t∈T
, (1)
models the assumed Markov random environment. A
sequence of probabilities π = (π
t
(a|s), a ∈ A, s ∈
S)
t∈T
describes the agent’s optional, randomised and
*
This research has been supported by GA
ˇ
CR, grants
GA16-09848S and GA18-15970S.
1
Throughout, N denotes set of positive integers.
Markov policy. The MDP-optimal policy π
MDP
max-
imises the expected cumulative reward
π
MDP
∈ Argmax
π∈Π
Π
Π
E
π
h
∑
t∈T
r
t
(s
t
,a
t
,s
t−1
)
i
. (2)
The strategy-dependent expectation E
π
is implicitly
conditioned on a known initial state. The optimisation
runs over the set Π
Π
Π of Markov policies
Π
Π
Π =
n
π
t
(a|s) ≥ 0,
∑
a∈A
π
t
(a|s) = 1, ∀s ∈ S
t∈T
o
.
(3)
Dynamic programming (DP) provides the MDP-
optimal policy consisting of deterministic decision
rules (π
t
(a|s))
t∈T
selecting the maximisers a
MDP
t
(s) in
v
t−1
(s) = max
a∈A
E
π
[r
t
( ˜s,a,s) + v
t
( ˜s)|a,s], s ∈ S, t ∈ T.
(4)
The functional equation (4) evolves the value func-
tions v
t
(s), s ∈ S, and provides the used maximis-
ing arguments a
MDP
t
(s), s ∈ S. It is solved backwards
starting with v
|T|
(s) = 0, ∀s ∈ S. This standard solu-
tion extends to the case with the incompletely known
environment model parameterised by the transition-
probability values
p
t
( ˜s|a,s,θ) = θ( ˜s|a,s), θ ∈ Θ
Θ
Θ. (5)
Kárný, M. and H˚ula, F.
Balancing Exploitation and Exploration via Fully Probabilistic Design of Decision Policies.
DOI: 10.5220/0007587208570864
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 857-864
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
857

The set Θ
Θ
Θ is given the meaning of the parameter θ
Θ
Θ
Θ =
n
θ( ˜s|a,s) ≥ 0,
∑
˜s∈S
θ( ˜s|a,s) = 1, ∀a ∈ A, ∀s ∈ S
o
.
(6)
The parametric model (5) belongs to exponen-
tial family (Barndorff-Nielsen, 1978) and possesses
Dirichlet’s distribution D
θ
(V
0
), given by the finite-
dimensional occurrence array
V
0
= (V
0
( ˜s|a,s))
˜s,s∈S, a∈A
, V
0
( ˜s|a,s) > 0,
as its conjugate prior. With the chosen D
θ
(V
0
),
Bayesian learning (Berger, 1985) reproduces Dirich-
let’s form. It reduces to the updating of the occurrence
array
V
t
(s
t
|a
t
,s
t−1
) = V
t−1
(s
t
|a
t
,s
t−1
) + 1, initiated by V
0
,
(7)
where (s
t
,a
t
,s
t−1
) is the realised triple. This recur-
sion, together with the predictive probabilities
p( ˜s|a,s,V ) =
V ( ˜s|a,s)
∑
˜s∈S
V ( ˜s|a,s)
=
ˆ
θ( ˜s|a,s), ˜s, s ∈ S, a ∈ A,
(8)
provides the Markov transition probability of the in-
formation state (s
t
,V
t
). Thus, the MDP-optimal pol-
icy can formally be computed via DP (4) where s
is replaced by (s,V ). Such an MDP-optimal policy
(π
t
(a|s,V ))
t∈T
inevitably optimally balances the ex-
plorative effort, regarding the evolution of s
t
, and the
exploitative effort, regarding the evolution of V
t
, cf.
(Feldbaum, 1961). The number of possible informa-
tion states however, blows up exponentially. This pre-
vents the evaluation and storing of the value functions
(v
t
(s,V ))
t∈T
.
The common remedy uses of the frozen point es-
timate
ˆ
θ instead of θ in DP. This certainty-equivalent
approximation diminishes the curse of dimensional-
ity (Bellman, 1961). The approximation, however,
gives up the care about the intentional exploration.
It provably diverges from the optimal policy with a
positive probability (Kumar, 1985). This experimen-
tally well-confirmed fact has led to a range of at-
tempts to recover the intentional exploration. The
active exploration is mostly reached by introducing
a random constituent into actions (
ˇ
Crepin
ˇ
sek et al.,
2013; Duff, 2002; Wu et al., 2017). Good results are
often achieved but the proper balance between explo-
ration and exploitation is hard to find. This manifests
itself in, repeatedly admitted, sensitivity to the choice
of parameters determining the noise added to the ex-
ploitative actions.
This paper introduces the proper exploration by
employing the fully probabilistic design of deci-
sion policies (FPD, (K
´
arn
´
y and Guy, 2006; K
´
arn
´
y
and Kroupa, 2012)). FPD is closely related to the
Kullback-Leibler control (G
´
omez and Kappen, 2012;
Guan et al., 2012; Kappen, 2005). In the paper con-
text, it is important that FPD leads to the randomised,
and thus explorative policy unlike the usual MDP.
Methodologically, the paper relates MDP and
FPD in a better way than the axiomatisation (K
´
arn
´
y
and Kroupa, 2012). It also proposes the adaptation
of an optional FPD-parameter, similar to the temper-
ature in simulated annealing (Tanner, 1993) or Boltz-
mann’s machine (Witten et al., 2017). Practically, it
presents Monte Carlo experiments, which show that
the certainty-equivalent version of FPD is indeed ad-
equately explorative.
Layout: Section 2 recalls basic facts about the in-
gredients of the advocated decision policy. It for-
malises and solves the addressed problem. Section
3 summarises the results of extensive simulations re-
flecting the properties of the proposed policy. Section
4 adds concluding remarks. Appendix contains data
used in simulations so that our results can be repro-
duced.
2 FPD AND ITS RELATION TO
MDP
The environment model p (1) and any fixed policy π
in (3) determine the joint probability c
π
of states and
actions (implicitly conditioned on the initial state)
c
π
(
behaviour b ∈ B = X
t∈T
(SxA)
z }| {
s
|T|
,a
|T|
,s
|T|−1
,a
|T|−1
...,s
1
,a
1
) (9)
=
∏
t∈T
p
t
(s
t
|a
t
,s
t−1
)π
t
(a
t
|s
t−1
).
This closed-loop model c
π
(b) completely describes
(closed-loop) behaviours b ∈ B (9) consisting of ob-
served and opted variables. Thus, all design ways,
e.g. MDPs with different rewards, leading to the
same c
π
are equivalent. This observation (Ullrich,
1964) implies that decision objectives can gener-
ally be expressed via an ideal (desired) closed-loop
model c
i
(b), b ∈ B. Informally, the ideal assigns
high values to desired behaviours and small values
to undesired behaviours. With the ideal closed-loop
model chosen, the FPD-optimal policy π
FPD
makes
c
π
FPD
closest to c
i
. The FPD axiomatisation (K
´
arn
´
y
and Kroupa, 2012) specifies widely-acceptable con-
ditions under which the Kullback-Leibler divergence
D(c
π
||c
i
), (Kullback and Leibler, 1951), is the ade-
quate proximity measure. The FPD-optimal policy
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
858

π
FPD
is thus
π
FPD
∈ Arg min
π∈Π
Π
Π
D(c
π
||c
i
) (10)
= Arg min
π∈Π
Π
Π
∑
b∈B
c
π
(b)ln
c
π
(b)
c
i
(b)
.
Proposition 1 presented below describes the FPD-
optimal decision rules. The proposition is a direct
counterpart of stochastic DP (
˚
Astr
¨
om, 1970; Bert-
sekas, 2001). It uses the chain-rule factorisation of
c
i
, which delimits: (a) the ideal environment model
p
i
t
( ˜s|a,s), which is the ideal counterpart of the tran-
sition probability p
t
( ˜s|a,s), and (b) the ideal decision
rules π
i
t
(a|s) of the ideal policy.
Proof of Proposition 1 is, for instance, in (
ˇ
Sindel
´
a
ˇ
r
et al., 2008). The general FPD with the state estima-
tion, corresponding to the partially observable MDP,
is in (K
´
arn
´
y and Guy, 2006).
Proposition 1 (FPD-Optimal Policy). Decision rules
π
FPD
t
(a|s), t ∈ T, forming the FPD-optimal policy
(10) result from the following backward recursion,
t = |T|,|T|−1,...,1, initiated by w
|T|
(s) = 1, ∀s ∈ S,
π
FPD
t
(a|s) =
π
i
t
(a|s)exp[−ω
t
(a,s)]
∑
a∈A
π
i
t
(a|s)exp[−ω
t
(a,s)]
| {z }
w
t−1
(s)
, s ∈ S,
ω
t
(a,s) =
∑
˜s∈S
p
t
( ˜s|a,s)ln
p
t
( ˜s|a,s)
p
i
t
( ˜s|a,s)w
t
( ˜s)
.
(11)
The work (K
´
arn
´
y and Kroupa, 2012) contain-
ing axiomatisation of FPD also proved that: (i) any
Bayesian decision making can be arbitrarily well ap-
proximated by the FPD formulation (10); (ii) there are
FPD tasks having no standard counterpart. In other
words, FPD tasks represent the proper dense exten-
sion of Bayesian decision making. Here, we modify
the constructive way in which this result was shown.
The construction explicitly relates the standard MDP
to the less usual FPD. Importantly, it serves the pur-
pose of this paper. It shows how the MDP-optimal de-
terministic policy is arbitrarily-well approximated by
the naturally explorative, FPD-optimal, randomised
policy. The construction uses the standard notion of
entropy H
π
(Cover and Thomas, 1991) of the closed-
loop model c
π
and the given cumulative reward R
H
π
= −
∑
b∈B
c
π
(b)ln(c
π
(b)) (12)
R(b) =
∑
t∈T
r
t
(s
t
,a
t
,s
t−1
), b ∈ B.
Proposition 2 (FPD from MDP). The optimisation
(2) over policies π ∈ Π
Π
Π (3), restricted by the addi-
tional requirement, determined by an optional h > 0,
H
π
≥ h > H
π
MDP
, (13)
leads to the FPD-optimal policy (10) with respect to
the ideal closed-loop model
2
c
i
(b) ∝ exp[R(b)/λ]. (14)
The corresponding ideal environment model and the
ideal decision rules are
p
i
t
( ˜s|a,s) ∝ exp[r
t
( ˜s,a,s)/λ] (15)
π
i
t
(a|s) ∝
∑
˜s∈S
exp[r
t
( ˜s,a,s)/λ].
The optional bound h in (13) determines the scalar
parameter λ = λ(h) > 0 and
lim
h→H
π
MDP
λ(h) = 0. (16)
Proof. It can be directly verified that any policy,
which replaces some deterministic rules of the pol-
icy π
MDP
by randomised ones has a higher entropy.
Thus, when maximising the expected accumulated re-
ward (2), under the inequality constraint (13), the con-
straint becomes active. The maximisation, equivalent
to the negative-reward minimisation, reduces to the
unconstrained minimisation of the Kuhn-Tucker func-
tional (Kuhn and Tucker, 1951), given by the multi-
plier λ = λ(h) > 0,
π
FPD
∈ Arg min
π∈Π
Π
Π
∑
b∈B
c
π
(b)[−R(b) + λ ln(c
π
(b))]
= Arg min
π∈Π
Π
Π
∑
b∈B
c
π
(b)ln
c
π
(b)
exp[R(b)/λ]
= Arg min
π∈Π
Π
Π
D(c
π
||c
i
).
The additive form of the cumulative reward (12),
standard conditioning and marginalisation imply the
forms of the ideal factors (15). The limiting property
(16) corresponds with the relaxation of the constraint
(13).
Remarks
X The role of the ideal decision rule (15) differs
from the closely-related Bolzmann’s machine,
which uses the decision rules
π
t
(a|s) ∝ exp
∑
˜s∈S
r
t
( ˜s,a,s)p
t
( ˜s|a,s)/λ
, λ > 0.
(17)
2
∝ means proportionality.
Balancing Exploitation and Exploration via Fully Probabilistic Design of Decision Policies
859

X The original, less general, relation of FPD
and MDP (K
´
arn
´
y and Kroupa, 2012)
led to the ideal closed-loop model c
iorig
that exploited the environment model p =
∏
t∈T
p
t
c
iorig
(b) ∝ p(b)exp[R(b)/λ]
(14)
z}|{
= p(b)c
i
(b), b ∈ B.
(18)
Recovering the explorative nature of the certainty-
equivalent MDP-optimal policy is the main reason
for employing the constraint (13). The following ac-
counting of the influence of the incomplete knowl-
edge on resulting policy brings an additional insight
into the exploration problem. Primarily, it guides the
adaptive choice of λ = λ(h) > 0 parameterising the
ideal closed-loop model (14).
The policy π
MDP
(θ), which maximises the ex-
pected cumulative reward while using a given param-
eter θ ∈ Θ
Θ
Θ, consists of the MDP-optimal deterministic
rules
π
MDP
t
(a|s,θ) = 1 if a = a
MDP
t
(s,θ) (19)
π
MDP
t
(a|s,θ) = 0 otherwise.
There a
MDP
t
(s,θ) is the maximising argument in the
tth step of DP (4) modified by the explicit condi-
tioning on θ ∈ Θ
Θ
Θ. The decision rules
3
π
FPD
t
(a|s,V,λ)
of the constructed approximation of the FPD-optimal
policy should approximate the policy π
MDP
(θ) made
of the rules (19) exploiting also the knowledge of the
parameter θ
π
MDP
(θ) = (π
MDP
t
(a
t
|s
t−1
,θ))
t∈T
, a
t
∈ A, s
t−1
∈ S.
The approximate policy has the posterior probability
p(θ|s,V ) as the only information about θ ∈ Θ
Θ
Θ.
Works (Bernardo, 1979; K
´
arn
´
y and Guy, 2012)
imply that the expected Kullback-Leibler divergence
of π
MDP
(θ) from π
FPD
is the adequate proximity mea-
sure to be minimised by
π
FPD
= (π
FPD
t
(a
t
|s
t−1
,V
t−1
,λ
FPD
t
))
t∈T
, a
t
∈ A
via the adequately chosen λ
FPD
= λ
FPD
(s
t−1
,V
t−1
).
This dictates the selection
λ
FPD
(s
t−1
,V
t−1
) ∈ Argmin
λ>0
Z
Θ
Θ
Θ
∑
a∈A
π
MDP
t
(a|s
t−1
,θ)
(20)
×ln
π
MDP
t
(a|s
t−1
,θ)
π
FPD
t
(a|s
t−1
,V
t−1
,λ)
p(θ|s
t−1
,V
t−1
) dθ.
The optimal actions a
MDP
t
(s,θ) depend on the param-
eter θ ∈ Θ
Θ
Θ in a quite complex way. This makes us
to solve (20) for greedy (one-stage-ahead) FPD. Im-
portantly, the resulting ideal factors with the frozen
3
The dependence on λ is stressed by the condition.
λ
FPD
= λ
FPD
(s
t−1
,V
t−1
) (15) are used in the multi-step
policy design. Thus, the dynamic nature of the policy
design is not compromised unlike in the wide-spread
solutions of the exploration problem (Wu et al., 2017).
For choosing λ
FPD
(s,V ), at the observed s = s
t−1
and given V = V
t−1
, let us define, cf. (2), (6),
Θ
Θ
Θ
a
=
n
θ ∈ Θ
Θ
Θ :
∑
˜s∈S
r
t
( ˜s,a,s)θ( ˜s|a,s) (21)
≥
∑
˜s∈S
r
t
( ˜s, ˜a,s)θ( ˜s| ˜a,s), ∀ ˜a ∈ A
o
, ∀a ∈ A.
On Θ
Θ
Θ
a
, the action a = a
MDP
(θ) is optimal. For the
FPD-optimal greedy decision rule (11) and the ideal
factors (15), the optimisation (20) reads
4
λ
FPD
(s,V )
∈ Argmin
λ>0
∑
a∈A
p(Θ
Θ
Θ
a
|s,V )
"
− ¯r(a, s,V )/λ − H(a, s,V )
+ ln
∑
˜a∈A
exp
+ ¯r
t
( ˜a,s,V )/λ + H( ˜a, s,V )
#
¯r
t
(a,s,V ) =
∑
˜s∈S
r
t
( ˜s,a,s)p( ˜s|a,s,V ),
H(a,s,V ) = −
∑
˜s∈S
p
t
( ˜s|a,s,V ) ln(p
t
( ˜s|a,s,V )),
p(Θ
Θ
Θ
a
|s,V ) =
Z
Θ
Θ
Θ
a
p(θ|s,V ) dθ. (22)
Numerical solution of the scalar minimisation (22) is
simple and can be done by any off-the-shelf software.
The evaluation of probabilities p(Θ
Θ
Θ
a
|s,V ) (22) of the
sets Θ
Θ
Θ
a
, a ∈ A (21) is the only more involved step.
Even it can be made by a direct Monte Carlo integra-
tion without excessive demands on its precision.
3 EXPERIMENTS
This part provides a representative sample of made
Monte Carlo studies.
The simulated environment corresponded to MDP
with |S| = 10 possible states and |A| = 5 possible ac-
tions. These options balanced the wish to deal with a
non-trivial example and to perform extensive Monte
Carlo experiments within a reasonable time even in
the experimental Matlab implementation. Numerical
values of the time-invariant simulated environment
model p and of the time-invariant reward r are in Ap-
pendix.
4
In experiments, λ
FPD
was also optimised for the origi-
nal ideal closed-loop model (18). Then, λ
FPD
minimises an
appropriate analogy of (22).
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
860
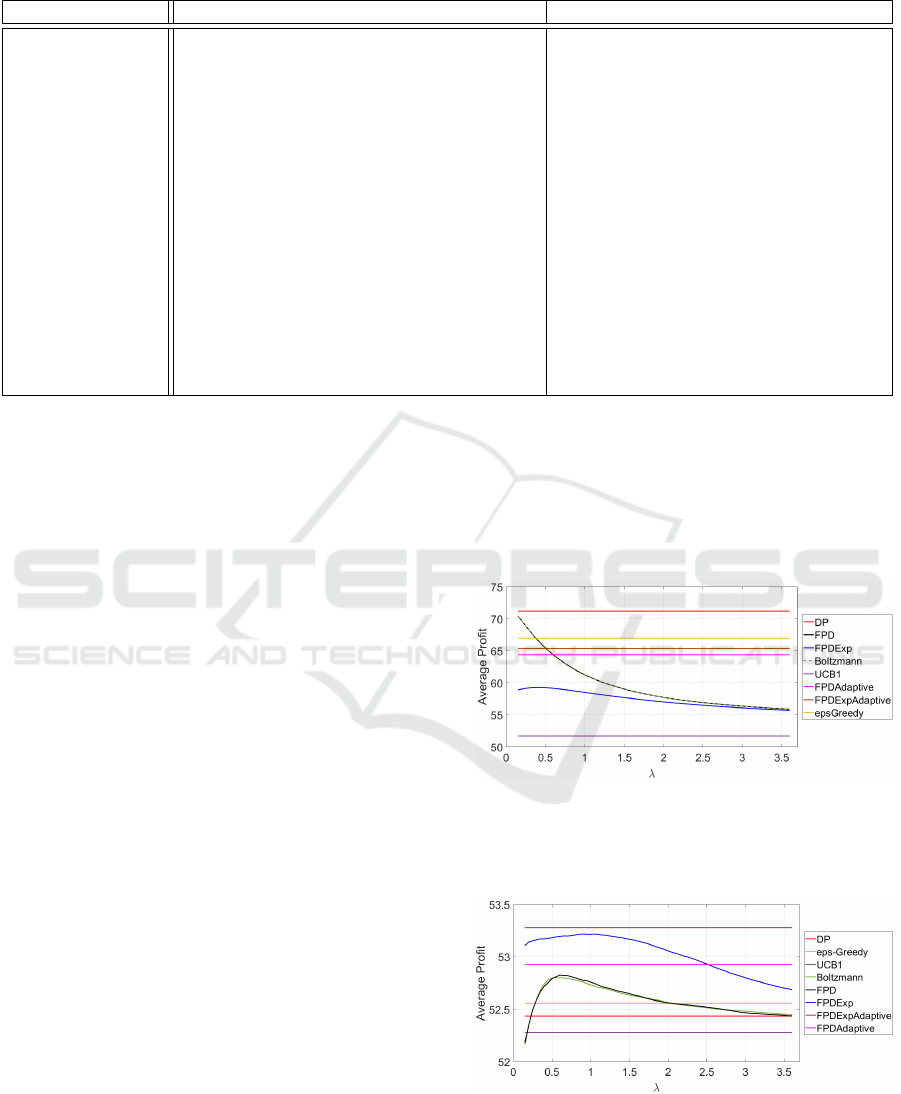
Table 1: The compared policies: CE is the certainty equivalent version of the policy and model means the environment model.
Label Characterisation Reference
DPknownPar MDP, known model (1), (2), (4)
DP MPD, learnt model, CE (2), (4), (7), (8)
FPD FPD, learnt model, CE, former ideal (18)
given λ (11), (18), (7), (8)
FPDAdaptive FPD, learnt model, CE, former ideal (18)
adapting λ (11), (18), (7), (8), (22)
FPDExp FPD, learnt model, CE, proposed ideal (14)
given λ (11), (14), (7), (8)
FPDExpAdaptive FPD, learnt model, CE, proposed ideal (14)
adapting λ (11), (14), (7), (8), (22)
Boltzmann Greedy MDP, the learnt model, CE (7), (8), (17)
Boltzmann’s machine, learnt model, given λ
eps-Greedy Greedy MDP, learnt model, CE, uniform
noise injected with probability ε = 0.3 (Vermorel and Mohri, 2005)
UCB1 Greedy MDP, learnt model, CE, noise (Auer et al., 2002; Tang and et al, 2017)
tuned according an upper confidence bound
The considered number of epochs was |T| =
10 << |Θ
Θ
Θ| ≈ |S|
2
× |A| = 500. As already said, the
proper balancing of exploration with exploitation is
vital under the conditions of this type.
The compared policies are summarised in Table 1,
which provides their labels, under which they are re-
ferred to in the figures. The table briefly characterises
them and refers to their detailed descriptions.
Policies depending on a fixed λ were judged on
the uniform grid
λ ∈ {0.15,0.20,0.25,...,3.60}. (23)
The policy quality was quantified by the sample
mean (referred to as the average profit) of sampled
cumulative rewards R (12) evaluated for 10
5
Monte
Carlo runs. Preliminary experiments verified that this
number is more than sufficient to guarantee the repre-
sentability of the results.
Results showing that the exploration is not neces-
sarily helpful are in Figure 1 with abbreviations refer-
ring to labels in Table 1. They were obtained within
the first experiment where the corresponding envi-
ronment model and the reward are described in Ta-
ble 2. The policy DPknownPar, designed under the
complete knowledge, reached the average profit of
72.11. Its variance σ = 51.72 quantifies its volatil-
ity. Straight lines correspond to policies independent
of λ varied on the considered grid (23).
The results in which exploration was significant,
were gained within the second experiment. They are
summarised in Figure 2 with abbreviations again re-
ferring to labels in Table 1. The corresponding en-
vironment model and reward are described in Table
3. The policy DPknownPar, designed under the com-
plete knowledge, reached the average profit of 62.84
and variance σ = 149.78.
Figure 1: The results of the first experiment. The average
profit is the sample mean of cumulative rewards (12) for the
compared policies, Table 1, and different λ values on the
grid (23).
Figure 2: The results of the second experiment. The average
profit is the sample mean of cumulative rewards (12) for
compared policies, Table 1, and different λ values on the
grid (23).
Balancing Exploitation and Exploration via Fully Probabilistic Design of Decision Policies
861

Discussion starts with stressing that the inspected
small number of epochs |T| respects that the
exploration-exploitation balance is vital in this case.
Otherwise, even a rare adding of random deviations
from exploitive actions, whose non-optimal character
with respect to the exploitation has negligible influ-
ence, guarantees convergence of learning and thus the
policy optimality. This distinguishes our experiments
from usual tests, e.g. (Ouyang et al., 2017), and makes
them relevant.
The experiments dealt with structurally same
static DM. The numerical choice of their parame-
ters was based on the following, qualitatively obvious
fact. The need for exploration (within the considered
short-horizon scenario) depends on the mutual rela-
tion of the prior probability p(θ|V
0
), see Table 4, and
the parameter θ
simulated
of the simulated environment
model determining transition probability, see Tables
2, 3. The influence of this relation is enhanced or at-
tenuated by the considered reward r.
The first experiment, reflected in Figure 1, in
which the DP policy is the best one warns that explo-
ration need not be always helpful. Notably, FPD and
Boltzmann’s machine with sufficiently small λ can be
arbitrarily close to its best behaviour. Due to the lack
of exploration significance no other conclusions con-
cerning the quality of the tested policies can be made.
But it calls for an improvement of λ-tuning, which
should converge to zero if the exploration is superflu-
ous.
The second experiment, reflected in Figure 2, is
more informative. The policy based on the newly
proposed relation of FPD with MDP and an adaptive
choice of λ (FPDExpAdaptive) brings the highest im-
provement (about 2%). A similar performance can be
reached for a fixed but properly chosen λ (FPDExp).
The adaptive FPD is worse (FPDAdaptive) but still
outperforms the remaining competitors. The similar-
ity of the results for the λ-dependent FPD and Boltz-
mann’s machine supports the conjecture that the per-
formance of Boltzmann’s machine can be improved
by adapting λ. This may be important in its other ap-
plications.
4 CONCLUDING REMARKS
The paper has arisen from inspecting the conjecture
that the certainty-equivalent version of non-traditional
fully probabilistic design (FPD) of decision policies
properly balances exploitation with exploration. The
achieved results support it. Moreover the paper: (a)
established a better relation of FPD to the wide-spread
Markov decision processes; (b) proposed an adaptive
tuning of the involved parameter, which can be used
in the closely-related simulated annealing and Boltz-
mann’s machine; (c) provided a sample of extensive
experiments, which confirmed that standard explo-
ration techniques are outperformed by the FPD-based
policies.
The future work will concern: (i) an algorithmic
recognition of cases in which exploration is unnec-
essary; (ii) inspection of a tuning mechanism based
on extremum-seeking control; (iii) an efficient im-
plementation of λ-tuning; (iv) application of the pro-
posed ideas to continuous-valued MDP; (v) real-life
problems, especially those in which a short, but non-
unit, decision horizon is vital as in environmental de-
cision making (Springborn, 2014).
REFERENCES
˚
Astr
¨
om, K. (1970). Introduction to Stochastic Control. Aca-
demic Press, NY.
Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-
time analysis of the multiarmed bandit problem. Ma-
chine Learning, 47(2-3):235–256.
Barndorff-Nielsen, O. (1978). Information and Exponential
Families in Statistical Theory. Wiley, NY.
Bellman, R. (1961). Adaptive Control Processes. Princeton
U. Press, NJ.
Berger, J. (1985). Statistical Decision Theory and Bayesian
Analysis. Springer, NY.
Bernardo, J. (1979). Expected information as expected util-
ity. The An. of Stat., 7(3):686–690.
Bertsekas, D. (2001). Dynamic Programming and Optimal
Control. Athena Scientific, US.
Cover, T. and Thomas, J. (1991). Elements of Information
Theory. Wiley. 2nd edition.
ˇ
Crepin
ˇ
sek, M., Liu, S., and Mernik, M. (2013). Exploration
and exploitation in evolutionary algorithms: A survey.
ACM Computing Survey, 45(3):37–44.
Duff, M. O. (2002). Optimal Learning; Computational
Procedures for Bayes-Adaptive Markov Decision Pro-
cesses. PhD thesis, University of Massachusetts
Amherst.
Feldbaum, A. (1960,61). Theory of dual control. Autom.
Remote Control, 21,22(9,2).
G
´
omez, A. G. V. and Kappen, H. (2012). Dynamic policy
programming. The J. of Machine Learning Research,
30:3207–3245.
Guan, P., Raginsky, M., and Willett, R. (2012). On-
line Markov decision processes with Kullback-Leibler
control cost. In American Control Conference, pages
1388–1393. IEEE.
Kappen, H. (2005). Linear theory for control of non-
linear stochastic systems. Physical review letters,
95(20):200201.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
862

K
´
arn
´
y, M. and Guy, T. (2012). On support of imper-
fect Bayesian participants. In Guy, T. and et al, ed-
itors, Decision Making with Imperfect Decision Mak-
ers, volume 28. Springer, Berlin. Intelligent Systems
Reference Library.
K
´
arn
´
y, M. and Guy, T. V. (2006). Fully probabilistic control
design. Systems & Control Letters, 55(4):259–265.
K
´
arn
´
y, M. and Kroupa, T. (2012). Axiomatisation of
fully probabilistic design. Information Sciences,
186(1):105–113.
Kuhn, H. and Tucker, A. (1951). Nonlinear programming.
In Proc. of 2nd Berkeley Symposium, pages 481–492.
Univ. of California Press.
Kullback, S. and Leibler, R. (1951). On information and
sufficiency. Annals of Mathematical Statistics, 22:79–
87.
Kumar, P. (1985). A survey on some results in stochastic
adaptive control. SIAM J. Control and Applications,
23:399–409.
Ouyang, Y., Gagrani, M., Nayyar, A., and Jain, R. (2017).
Learning unknown Markov decision processes: A
Thompson sampling approach. In et al, I. G., editor,
Advances in Neural Information Processing Systems
30, pages 1333–1342. Curran Associates, Inc.
Puterman, M. (2005). Markov Decision Processes: Discrete
Stochastic Dynamic Programming. Wiley.
ˇ
Sindel
´
a
ˇ
r, J., Vajda, I., and K
´
arn
´
y, M. (2008). Stochastic
control optimal in the Kullback sense. Kybernetika,
44(1):53–60.
Springborn, M. (2014). Risk aversion and adaptive man-
agement: Insights from a multi-armed bandit model of
invasive species risk. Journal of Environmental Eco-
nomics and Management, 68:226–242.
Tang, H. and et al (2017). #Exploration: A study of count-
based exploration for deep reinforcement learning. In
et al, I. G., editor, Advances in Neural Information
Processing Systems 30, pages 2753–2762. Curran As-
sociates, Inc.
Tanner, M. (1993). Tools for statistical inference. Springer
Verlag, NY.
Ullrich, M. (1964). Optimum control of some stochastic
systems. In Preprints of the VIII-th conference ETAN.
Beograd.
Vermorel, J. and Mohri, M. (2005). Multi-armed ban-
dit algorithms and empirical evaluation. In Euro-
pean conference on machine learning, pages 437–448.
Springer.
Witten, I., Frank, E., Hall, M., and Pal, C. (2017). Data
Mining: Practical machine learning tools and tech-
niques. 4th edition, Elsevier.
Wu, H., Guo, X., and Liu, X. (2017). Adaptive
exploration-exploitation trade off for opportunistic
bandits. preprint arXiv:1709.04004.
APPENDIX
This section provides considered rewards and tran-
sition probabilities used in experiments, Section 3.
Static, time-invariant cases are considered. Their
transition probabilities p( ˜s|a,s) = p(˜s|a) modelling
the environment and rewards r( ˜s,a,s) = r ( ˜s,a) de-
termining the cumulative reward (12) are the same
∀s ∈ S.
Table 2: The data used in the first experiment. Explicit values of the reward r
t
( ˜s,a,s) = r( ˜s,a), on the left-hand side and of
the transition probabilities p
t
( ˜s|a,s) = r( ˜s,a) on the right-hand side. They are constant ∀s ∈ S, t ∈ T and |S| = 10, |A| = 5.
Rows and columns correspond to states ˜s ∈ S and actions a ∈ A, respectively.
The reward r
t
The transition probability p
actions a ∈ A actions a ∈ A
states ˜s ∈ S
5 7 6 5 10 0.12 0.16 0.12 0.12 0.08
1 6 1 3 6 0.02 0.13 0.08 0.02 0.02
6 2 5 7 9 0.08 0.16 0.06 0.14 0.15
5 6 1 5 4 0.18 0.04 0.08 0.08 0.13
5 2 2 6 6 0.10 0.06 0.18 0.10 0.06
4 8 6 4 5 0.02 0.10 0.16 0.10 0.09
3 9 3 8 5 0.06 0.07 0.08 0.08 0.13
7 5 2 6 8 0.02 0.02 0.02 0.12 0.13
3 9 3 2 6 0.20 0.18 0.16 0.20 0.04
3 1 4 8 10 0.20 0.09 0.06 0.04 0.17
Balancing Exploitation and Exploration via Fully Probabilistic Design of Decision Policies
863
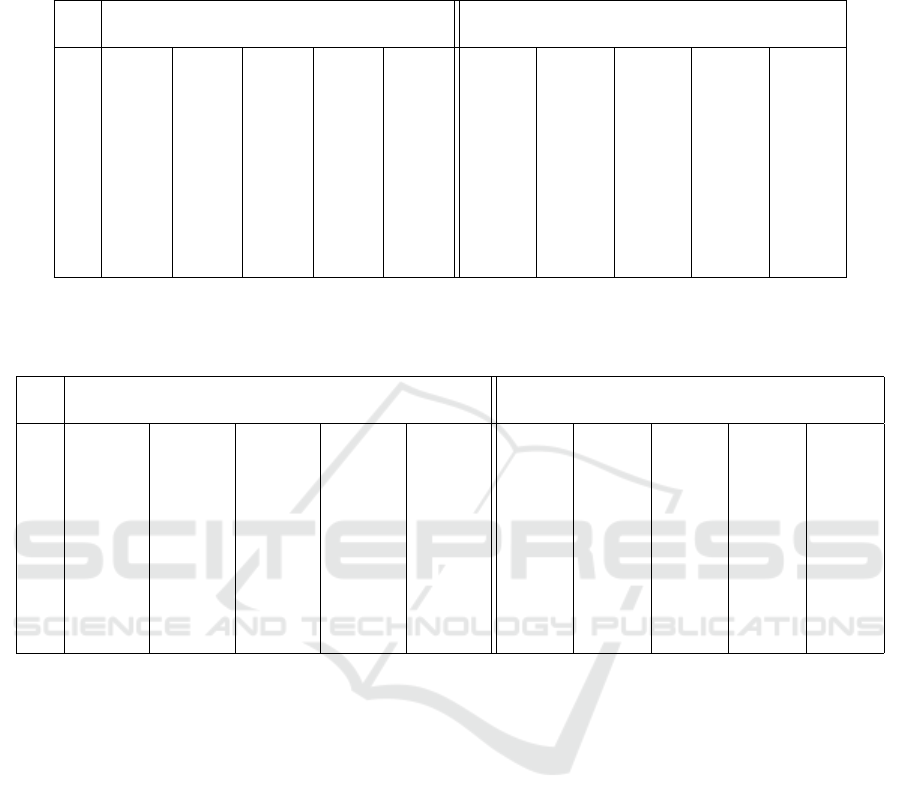
Table 3: The data used in the second experiment. Explicit values of the reward r
t
( ˜s,a,s) = r( ˜s,a), on the left-hand side and of
the transition probabilities p
t
( ˜s|a,s) = r( ˜s,a) on the right-hand side. They are constant ∀s ∈ S, t ∈ T and |S| = 10, |A| = 5.
Rows and columns correspond to states ˜s ∈ S and actions a ∈ A, respectively.
The reward r
t
The transition probability p
actions a ∈ A actions a ∈ A
states ˜s ∈ S
1 1 1 1 1 0.03 0.05 0.03 0.02 0.08
2 2 2 2 2 0.05 0.07 0.09 0.05 0.05
3 3 3 3 3 0.08 0.12 0.14 0.07 0.08
3 3 3 3 3 0.08 0.07 0.09 0.07 0.05
5 5 5 5 5 0.11 0.17 0.11 0.12 0.11
6 6 6 6 6 0.29 0.31 0.20 0.15 0.30
12 12 12 12 12 0.13 0.07 0.09 0.29 0.16
4 4 4 4 4 0.11 0.05 0.11 0.10 0.08
3 3 3 3 3 0.08 0.07 0.09 0.07 0.05
2 2 2 2 2 0.05 0.02 0.06 0.05 0.03
Table 4: The occurrence array V
0
determining the prior probability p(θ|V
0
) (7) for the first experiment on the left-hand side and
for the second experiment on the right-hand side. The occurrence arrays are constant ∀s ∈ S. Rows and columns correspond
to states ˜s ∈ S, |S| = 10, and actions a ∈ A, |A| = 5.
The first experiment The second experiment
actions a ∈ A actions a ∈ A
states ˜s ∈ S
0.1 0.1 0.1 0.1 0.1 0.03 0.04 0.02 0.06 0.08
0.1 0.1 0.1 0.1 0.1 0.05 0.06 0.05 0.09 0.05
0.1 0.1 0.1 0.1 0.1 0.08 0.11 0.07 0.09 0.08
0.1 0.1 0.1 0.1 0.1 0.08 0.06 0.07 0.09 0.05
0.1 0.1 0.1 0.1 0.1 0.11 0.15 0.10 0.11 0.11
0.1 0.1 0.1 0.1 0.1 0.29 0.19 0.36 0.26 0.30
0.1 0.1 0.1 0.1 0.1 0.13 0.06 0.12 0.14 0.16
0.1 0.1 0.1 0.1 0.1 0.11 0.11 0.10 0.06 0.08
0.1 0.1 0.1 0.1 0.1 0.08 0.09 0.07 0.06 0.05
0.1 0.1 0.1 0.1 0.1 0.05 0.13 0.05 0.06 0.03
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
864
