
Investigating the Affordances and Constraints of SimReal for
Mathematical Learning: A Case Study in Teacher Education
Said Hadjerrouit
Department of Mathematical Sciences, University of Agder, Kristiansand, Norway
Keywords: Affordances, Mathematical Learning, SimReal, Teacher Education, Visualization.
Abstract: Visualizations tools are one of the most innovative technologies that emerged the last few years in
educational settings. They provide new potentialities for mathematical learning by means of dynamic
animations and representations, interactive simulations, and live streaming of lessons. Moreover,
visualization tools have the potential to foster a visual, dynamic, distributed, and embodied mathematics
rather than individual achievements and static representations. This paper uses the visualization tool
SimReal in teacher education to explore the affordances of the tool for learning mathematics. It proposes a
framework that captures the affordances of SimReal at a technological, pedagogical, and socio-cultural
level. The aim of the article is to investigate the extent to which SimReal afford students’ mathematical
learning in teacher education. Based on the results, recommendations for future work are proposed.
1 INTRODUCTION
SimReal is a new visualization tool that is used to
teach a wide range of mathematical topics both at
the university and school level. SimReal uses a
graphic calculator, video lessons, video live
streaming, video simulations, and interactive
simulations to teach mathematics (SimReal, 2018).
In contrast to other digital tools such as GeoGebra,
SimReal has more than 5000 applications and tasks
in various areas of mathematics (Brekke and
Hogstad, 2010). The tool can be divided in small
subsets, while keeping the same structure and basic
user interface. A subset of SimReal called Sim2Bil
provides 4 windows for visualizations: simulation,
graph, formula, and menu window (Hogstad et al.,
2016),
There is a huge interest in visualization tools, but
there are few research studies that address learning
issues in authentic educational settings (Presmeg,
2014). Some research studies on SimReal focus on
teaching mathematics at the undergraduate
mathematical level (Brekke and Hogstad, 2010;
Gautestad, 2015; Hogstad, 2012). The aim of these
studies is to report on students’ attitudes using
SimReal as a supplement tool to ordinary teaching,
and its usefulness in difficult and abstract
mathematical areas. Hogstad et al. (2016) studied a
subset of SimReal called Sim2bil that aims at
exploring how engineering students use
visualizations in their mathematical communication.
Furthermore, Hadjerrouit and Gautestad (2018) used
the theory of instrumental orchestration to analyze
teachers’ use of SimReal in an engineering class.
Other studies were carried out in teacher education.
Firstly, Hadjerrouit (2015) evaluated the suitability
of the tool in teacher education using usability
criteria. Secondly, Hadjerrouit (2017) addressed the
affordances of SimReal and students’ perceptions of
the tool in teacher education. The present study is a
continuation of these two studies. Based on the
results achieved so far, the purpose of this work is to
explore the affordances of SimReal and their impact
on students’ mathematical learning in teacher
education.
The article is structured as follows. First, the
theoretical framework is described, followed by the
methodology. Then, the results are presented.
Finally, a summary of the results, future work and
recommendations conclude the article.
2 THEORETICAL FRAMEWORK
2.1 The Concept of Affordances
Among a wide range of theoretical approaches that
can be applied to explore the impact of digital tools
Hadjerrouit, S.
Investigating the Affordances and Constraints of SimReal for Mathematical Learning: A Case Study in Teacher Education.
DOI: 10.5220/0007588100270037
In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), pages 27-37
ISBN: 978-989-758-367-4
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
27

on mathematics learning (Geiger et al., 2012), the
theory of affordances provides the most appropriate
framework to address the impact of SimReal on
learning mathematics in teacher education.
The term “affordance”, originally proposed by
the perceptual psychologist James J. Gibson in his
book “The Ecological Approach to Visual
Perception” (Gibson, 1977), refers to the
relationship between an object’s physical properties
and the characteristics of a user that enables
particular interactions between user and object.
More specifically, Gibson used the term
“affordance” to describe the action possibilities
offered to an animal by the environment with
reference to the animal’s action capabilities
(Osiurak, et al., 2017)
The concept of affordances was introduced to the
Human-Computer-Interaction community by Donald
Norman in his book “The Psychology of Everyday
Things” (Norman, 1988). Accordingly, the term
“affordance” refers to the perceived and actual
properties of the thing, primarily those fundamental
properties that determine just how the thing could
possibly be used.
A number of research studies used Norman’s
ideas to implement the concept of affordances in
various educational settings. For example, Turner
and Turner (2002) specified a three-layer
articulation of affordances: Perceived affordances,
ergonomic affordances, and cultural affordances.
Likewise, Kirchner et al. (2004) described a three-
layer definition of affordance: Technological
affordances that cover usability issues, educational
affordances to facilitate teaching and learning, and,
social affordances to foster social interactions. In
mathematics education, Chiappini (2012) applied the
notions of perceived, ergonomic, and cultural
affordances to Alnuset, a digital tool for high school
algebra.
De Landa (2002) emphasized that affordances
are not intrinsic properties of the object. Rather
affordances become actualized in specific context,
e.g. the socio-cultural context of the classroom. In
other words, affordances emerge from the
relationship between the object and the particular
environment with which it is interacting. From this
perspective, the specific context of the mathematics
classroom may include several artifacts or tools that
interact with the user. Accordingly, the artifacts
being used in a mathematics classroom have
affordances and constraints. These may include
paper-pencil techniques, the blackboard, Interactive
White Board (IWB), Power Point slides, and diverse
digital tools, such as Smart phones, IPad, GeoGebra,
SimReal, and mathematics itself by means of
symbols, notations, representations, etc. Artifacts
with their affordances and constraints interact with
the user.
2.2 SimReal Affordances
Based on the research literature described above and
the specificities of mathematics education, this study
proposes three categories of affordances and
constraints at six different levels (Figure 1):
a) Technological affordances that describe the
functionalities of the tool
b) Pedagogical affordances at four levels:
Pedagogical affordances at the student level or
mathematical task level
Pedagogical affordances at the classroom level
or student-teacher interaction level
Pedagogical affordances at the subject level,
that is the area of mathematics being taught
Pedagogical affordances at the assessment
level
c) Socio-cultural affordances that cover
curricular, cultural, and ethical issues
Figure 1: Three categories of SimReal Affordances at six
different levels.
CSEDU 2019 - 11th International Conference on Computer Supported Education
28

There are two types of technological affordances:
Ergonomic and functional affordances. From the
ergonomic point of view, these are ease-of-use, ease-
of-navigation, accessibility at any time and place,
accuracy and quick completion of mathematical
activities. From the functional point of view,
SimReal helps to perform calculations, draw graphs
and functions, solve equations, construct diagrams,
and measure figures and shapes. Technological
affordances are a pre-requisite for any digital tool
and provide support for pedagogical affordances.
There are several pedagogical affordances that
can be provided at the student level, e.g., using the
tool to freely build and transform mathematical
expressions that support conceptual understanding of
mathematics, such as collecting real data and create
a mathematical model, using a slider to vary a
parameter or drag a corner of a triangle in geometry
software, moving between symbolic, numerical, and
graphical representations, simulating mathematical
concepts, or exploring regularity and change (Pierce
and Stacey, 2010). At this level, the motivational
factor is important, especially when using
visualizations to engage students in mathematical
problem solving. Furthermore, feedback in various
forms to students’ actions may foster mathematical
thinking. Programming mathematical tasks may also
be a way of using SimReal for learning and
understanding.
Likewise, several pedagogical affordances can be
provided at the classroom level (Pierce and Stacey,
2010). Firstly, affordances that result in changes of
interpersonal dimensions, such as change of
teachers’ and students’ role, less teacher-directed
and more student-oriented instruction. Secondly,
affordances that create more learner autonomy,
resulting in students taking greater control over their
own learning, and using SimReal as a “new”
authority in assessing learning. Other affordances at
this level are change of social dynamics and more
focus on collaborative learning and group work, as
well as change of the didactical contract (Brousseau,
1997). Variation in teaching and differentiation are
other affordances offered by digital tools at this level
(Hadjerrouit and Bronner, 2014). This may result in
flipping the classroom, which is another way of
using SimReal at this level.
Furthermore, three types of pedagogical
affordances can be provided at the mathematical
subject level (Pierce and Stacey, 2010). The first one
is fostering mathematical fidelity, looking at
congruence between machine mathematics and ideal
or paper-pencil mathematics, and promoting
faithfulness of machine mathematics (Zbiek et al.
2007). The second affordance is amplifying and
reorganizing the mathematical subject. The former is
accepting the goals to achieve those goals better.
Reorganizing the mathematical subject means
changing the goals by replacing some things, adding
and reordering others. For example, in calculus there
might be less focus on skills and more on
mathematical concepts (Pierce and Stacey, 2010). In
geometry, there might be emphasis on more abstract
geometry, and away from facts, more argumentation
and conjecturing (Pierce and Stacey, 2010).
Likewise, it may be useful to support tasks that
encourage metacognition, e.g., starting with real-
world applications, and using SimReal to generate
results.
Affordances at the assessment level consist of
summative and formative assessment. Summative
assessment is important for testing, scoring and
grading, and it can be provided in form of statistics
that the tool generates. Formative assessment is
equally important for the learning process. Feedback
is an essential condition for formative assessment. It
can take many forms, e.g., immediate feedback to
students’ actions, a combination of conceptual,
procedural, and corrective information to the
students, or asking question types, etc.
Finally, several socio-cultural affordances can
emerge at this level. Firstly, an important affordance
is that SimReal should provide opportunities to
concretize the mathematics subject curriculum in
teacher education. Secondly, SimReal should be tied
to teaching mathematics in schools, and support the
learning of mathematics at the primary, secondary,
and upper secondary level. In other words, SimReal
should take the requirement of adapted education
into account. Finally, other socio-cultural
affordances can also emerge at this level, in
particular those related to ethical, gender, and multi-
cultural issues.
3 THE STUDY
3.1 Participants
Fifteen teacher students (N=15) from a technology
and mathematics-based course in teacher education
participated in this work. The students were
categorized on the basis of their knowledge level in
mathematics associated with their study
programmes: Primary teacher education level 1-7,
primary teacher education level 5-10, advanced
teacher education level 8-13, and mathematics
master's programme.
Investigating the Affordances and Constraints of SimReal for Mathematical Learning: A Case Study in Teacher Education
29
The recommended pre-requisites were basic
knowledge of ICT (information and communications
technology) and experience with standard digital
tools like text processing, spreadsheets, calculators
and Internet. No prior experience with SimReal was
required.
3.2 Activities
A digital learning environment centered around
SimReal was created over two weeks, starting from
25 August to 8 September 2016. An example of
SimReal utilization is given in figure 2.
Figure 2: Example of SimReal utilization in mathematics
education.
The environment included video lectures,
visualizations, and simulations of basic, elementary,
and advanced mathematics, and diverse online
teaching material. Basic mathematics focused on
games, dices, tower of Hanoi, and prison.
Elementary mathematics consisted of multiplication,
algebra, Pythagoras and Square theorems, and
reflection. The topics of advanced mathematics were
measurement, trigonometry, conic section,
parameter, differentiation, and Fourier.
To assess experiences on specific mathematical
topics that are of considerable interest for students,
two specific mathematical tasks were chosen. The
first one was Pythagoras theorem (Pythagoras
theorem, 2018). There are many ways of
representing Pythagoras. The theorem has also been
given numerous proofs. These are very diverse,
including both geometric and algebraic proofs, e.g.,
proofs by dissection and rearrangement, Euclid's
proof, and algebraic proofs. Thus, Pythagoras is
more than just a way of calculating the lengths of a
triangle. An example of representing the theorem is
given in the following figure (Figure 3).
Figure 3: An example of representation of Pythagoras
theorem.
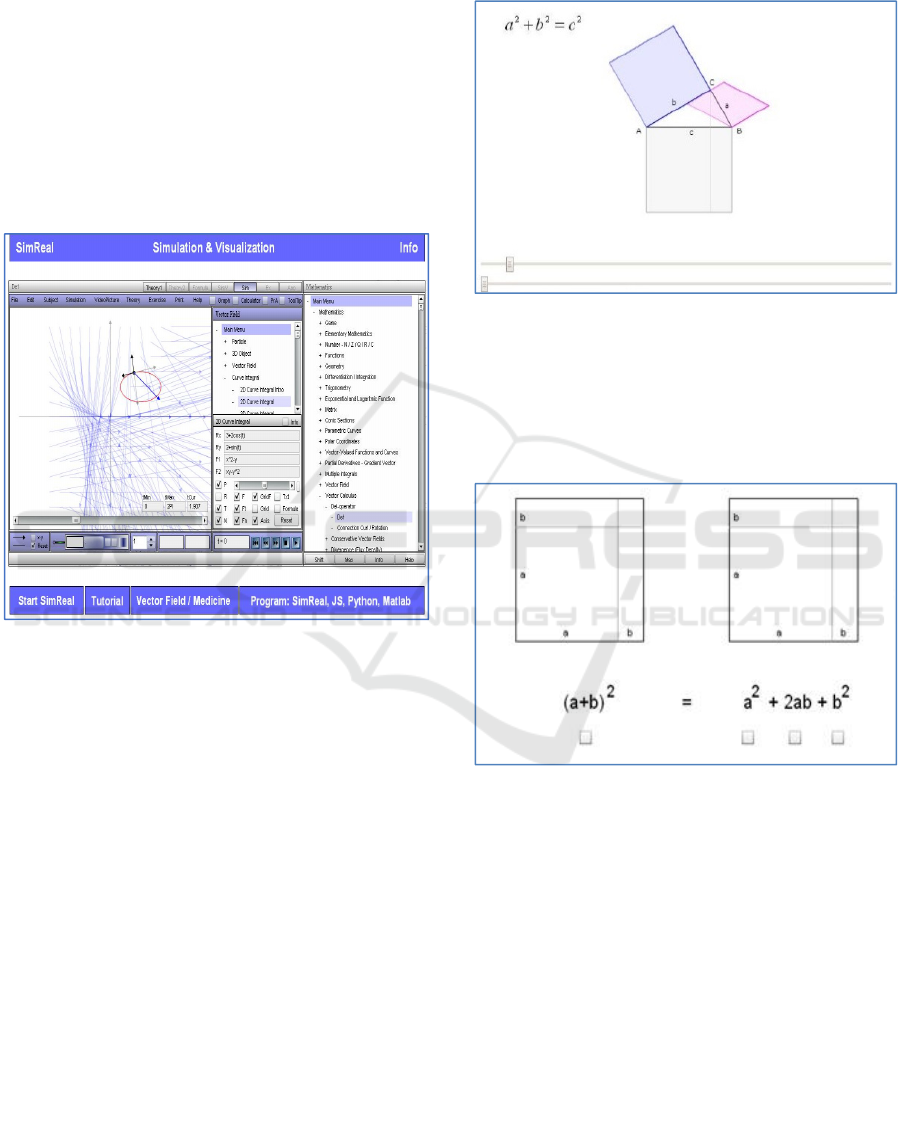
The second task was the Square theorem (Square
theorem, 2018). Like Pythagoras, there are many
ways of using and representing the theorem (Figure
4).
Figure 4: An example of representation of the Square
theorem.
3.3 Methods
This work is a single case study in teacher
education. It aims at exploring the affordances of
SimReal for mathematical learning in teacher
education. The study is exploratory in nature. Both
quantitative and qualitative methods were used to
collect and analyze students’ experiences with
SimReal. The following methods were used:
a) A survey questionnaire with a five-point
Likert scale from 1 to 5, and quantitative
analysis of the results
CSEDU 2019 - 11th International Conference on Computer Supported Education
30

b) Students’ comments in their own words to
each of the statements of the survey
questionnaire
c) Students’ written answers to open-ended
questions
d) Qualitative analysis of students’ comments on
point b and answers to open-ended questions
to point c
e) Task-based questions on Pythagoras and
Square theorem, and programming issues
The design of the survey was guided by the
theoretical framework and the research goal. To
measure the students’ perceptions of SimReal, a
survey questionnaire with a five-point Likert scale
from 1 to 5 was used, where 1 was coded as the
highest and 5 as the lowest (1 = “Strongly Agree”; 2
= “Agree”; 3 = “Neither Agree nor Disagree”; 4 =
“Disagree”; 5= “Strongly Disagree”). The average
score (MEAN) was calculated, and the responses to
open-ended questions were analyzed qualitatively.
The survey included 72 statements that were
distributed as follows: Technological affordances
(12), pedagogical affordances at the student level
(11), classroom level (19), mathematical subject
level (9), assessment level (10), and finally socio-
cultural level (11). The students were asked to
respond to the survey using the five-point Likert
scale and to comment each of the statements in their
own words. In addition, the students were asked to
provide written answers in their own words to open-
ended questions. The responses to students’
comments to the survey and open-ended questions
were analyzed qualitatively.
Of particular importance are task-based
questions on Pythagoras and Square theorems to
collect data on affordances when students engage
with these mathematical tasks. An additional
question on programming issues was given to the
students to assess the affordances of programming
languages for the learning of mathematics. Asking
task-based questions provides supplementary
information on the affordances of SimReal. This
method also provides more nuanced information
about the students’ experiences with SimReal. The
analysis of the data was guided by the specified
affordances of the theoretical framework, and open-
coding to bring to the fore information that was not
covered by the theoretical framework.
4 RESULTS
4.1 SimReal Affordances
The results achieved by means of the survey
questionnaires and open-ended questions show that
the affordances of SimReal emerge at different
educational levels. The affordances are less evident
for students from the study programme 1-7. They
become more visible at the middle level associated
with the study programme 5-10. Affordances come
to the fore at the advanced level, and for
mathematics education students.
Globally, the vast majority of the students
pointed out that SimReal still lacks an easy-friendly
interface and that it is not easy to use, to start and to
exit. For many students, the tool was accessible
anywhere and anyplace, but the navigation through
the tool is still not straightforward. On the positive
side, SimReal has a ready-made mathematical
content, and that the video lessons, simulations,
animations, and live streaming are of good quality.
This is reflected in many students’ responses.
In terms of pedagogical affordances at the
student level, many students think that SimReal
provide real-world tasks, which engage them in
mathematical problem solving, particularly when
using visualizations to simulate mathematical
concepts. Most students think that visualizations are
useful to gain mathematical knowledge that is
otherwise difficult to acquire, and they liked very
much the combination of live streaming of lessons,
video lectures, simulations, and animations. Most of
the advanced mathematical exercises (trigonometry,
differentiation, and conic section) were not difficult
for them to understand. Likewise, SimReal provided
affordances to explore variation and regularities in
the way mathematics is taught, e.g., vary a
parameter to see the effect of a graph. The students
also think that SimReal is congruent with paper and
pencil techniques. On the negative side, most
students think that SimReal is not helpful to refresh
students’ mathematical knowledge.
In terms of pedagogical affordances at the
classroom level, the majority agreed that they can
use SimReal on their own, and that the use of the
tool is not completely controlled by the teacher, and,
as a result, they do not need much help from the
teacher or textbooks to solve exercises. Likewise,
most students think that the tool can be used as an
alternative or supplement to textbooks and lectures.
The tool also facilitates various activities (problem
solving, video lectures, live streaming), and several
ways of representing mathematical knowledge
Investigating the Affordances and Constraints of SimReal for Mathematical Learning: A Case Study in Teacher Education
31

(texts, graphs, symbols, animations, visualizations).
In terms of differentiation and individualization,
many students believe that the level of difficulty of
the mathematical tasks is acceptable, but it is
relatively difficult to adjust the tool to the students’
knowledge level. Even though the degree of
autonomy is not very high, it is sufficient to allow
students work at their own pace. On the negative
side, the vast majority of the students think that
SimReal does not support much cooperation or
group work, and it does not have collaborative tools
integrated into it.
In terms of pedagogical affordances at the
mathematical subject level, most students agreed
that SimReal provides a high quality of
mathematical content. Many students also think that
SimReal provides real-world applications and tasks
that foster reflection, metacognition, and high-level
thinking. Likewise, the vast majority found that
SimReal is mathematically sound, and that the tool
can display correctly mathematical formulas,
functions, graphs, numbers, and geometrical figures.
On the negative side, the overwhelming majority
think that the software tool GeoGegra has a better
interface, and it is better to express mathematical
concepts. Finally, the combination of mathematics
and practical applications in physics is evaluated as
useful to gain mathematical understanding.
In terms of affordances at the assessment level,
most students think that SimReal provides several
assessment modes and give directly feedback in
form of dynamic animations. This is a clear
improvement compared to previous experiments.
Likewise, SimReal provides satisfying solutions
step-by-step, but not for all tasks. Still, SimReal
does not provide several types of feedback,
differentiated knowledge on student profiles, several
question types, and statistics. Finally, the degree of
interaction is evaluated as satisfying.
In terms of affordances at the socio-cultural
level, most students think that SimReal is an
appropriate tool to use in teacher education, but it
does not take sufficiently into account the
requirement for adapted education. Furthermore,
most students believed that SimReal is appropriate
to use in secondary schools, and in a lesser degree in
middle and primary schools. On the negative side,
the vast majority will not continue using video
lessons and live streaming to learn mathematics, but
some will still be using video simulations in the
future. Nevertheless, the vast majority of the
students think that the tool enables the teacher to
concretize the mathematical subject curriculum.
Summarizing, it worth noting that affordances do
not emerge in the same degree for all students.
Rather they become actualized in relationship to the
participants’ knowledge level from the 4 categories
of study programmes: Primary teacher education
level 1-7 and level 5-10, master programme, and
advanced teacher education level 8-13.
4.2 Affordances of Pythagoras
Theorem
Students were engaged in 16 different approaches to
exploring Pythagoras theorem. These were divided
in paper-based (1-9) and SimReal-based approaches
(10-16). The students were asked to report on
SimReal affordances and critically reflect on their
impact on learning Pythagoras by responding to 4
specific questions.
a) If you should choose only one of the 16 different
approaches of explaining Pythagoras, which of
them would you prefer?
The students provided a variety of solutions in order
of priority according to the perceived affordances of
the approaches. One suggestion was 2/5/7/12/15,
and 16. Some students chose a sequence of
approaches such as 2/3/5, or 2/3, or 7/14. One
student provided another set of preferences that are
worthwhile to study in details. Firstly, the student
decided to use approach 15 as a brief introduction,
and then Pythagoras 1, both as a simple
presentation of the equation of the theorem and as a
first visual proof of the theorem. Then, he suggested
to use approach 2 as a general formula and 3 as a
more specific or realistic one. The student also
suggested a combination of approach 10 (paper-
based) and 14 (SimReal-based), but without the
written explanation or mathematical formula.
Instead, one can start with a given problem such as
“find the area of the pool or the area of the baseball
field”. After having discussed suggestions to
approaching the solution, the student can then check
the explanation provided by SimReal in terms of
written text or mathematical formula. Finally, the
student would demonstrate approach 4 using a
rigorous proof through the usage of algebraic and
geometrical properties. Summarizing, several
affordances emerged in this situation: realistic task,
pen-paper formulas, SimReal visualizations with
written explanations of the theorem, rigorous
mathematical proofs of the theorem, and a
combination of paper-based and SimReal
visualizations.
CSEDU 2019 - 11th International Conference on Computer Supported Education
32

b) If you should combine one of the pen/paper
approaches and one of the digital simulations
which of them would you prefer?
The students provided a variety of approaches such
as 3/12 and 9/12. As described above, one student
combined approach 10 (pen/paper-based) with
approach 14 (SimReal-based). After the use of the
pen-and-paper solution and an attempt to calculate
the blue area of figure 14, the students could try to
calculate several areas of the figure. Example 10 and
14 have different approaches and content, but they
complement each other in terms of their affordances.
c) If you should choose the combination of the two
approaches 9 and 12, how would you in detail
explain Pythagoras?
A variety of explanations were provided to explain
Pythagoras using various elements such as the layout
and colors of the figure, the dynamic of the
simulation, and mathematical explanations. A good
combination of 9 and 12 is as follows. The student
starts with 9 (angle A=90°), and notes that the pink
and the blue area of the bottom square is equal to the
other two corresponding square areas (blue and
pink). Furthermore, the sum of the blue and pink
square areas is equal to the bottom square area,
consisting of these two rectangles. Moving on to 12,
it is worth mentioning that their area remains
unchanged. Before using the SimReal-based
simulation, some figures of rectangles on the
blackboard would be useful, revising or presenting
the formula for the area of the parallelogram. The
figures should be of various parallelograms,
including interaction with the student by considering
different bases each time and different heights. The
student concluded that a combination of moving the
scroll bar and considering cases on the blackboard
depending on the position of the parallelogram
and its height. This could be a good reasoning step
to explain why the area remains the same. The
digital simulation could be used to clarify the
question.
d) Do you think that teaching different ways of
Pythagoras by combining pen/paper and
SimReal-based simulations would help in the
understanding of this topic, or do you think it
would be confusing for the students?
The students think that the combination of pen/paper
and SimReal simulations is helpful to understand
Pythagoras depending on time and pedagogical
constraints, and students’ knowledge level as well.
They think that it would be positive to use several
approaches to teach Pythagoras considering various
students’ knowledge levels and learning styles when
solving problems. It is therefore important to present
mathematical tasks using different ways. By
showing a figure describing Pythagoras theorem, the
teacher has a good opportunity to explain the
mathematical formula in his/her own words, before
showing a SimReal simulation of the theorem. This
may motivate the students, and stimulate their
curiosity. Approach 9 or 3 combined with simulation
12 would give a good effect. In most cases, a good
combination of pen/paper and SimReal simulations
is preferable, but there may be some confusing cases
that make the understanding of the topic more
difficult. In those cases, the task should be either
pen/paper solution or SimReal simulation, but not
both approaches, even though the teaching may be
less efficient. As a result, a good way of teaching
Pythagoras is a combination of SimReal affordances
with paper-pencil solutions.
4.3 Affordances of Square Theorem
Students were engaged in 6 different approaches to
exploring the Square theorem. These are divided in
paper-based (1-3) and SimReal-based approaches (4-
6). The students were asked to study them and report
on their affordances by responding to 4 specific
questions.
a) Pen/paper proofs (1, 2, 3) versus SimReal-based
proofs (4,5,6) of the Square theorem
Most students preferred a combination of pen/paper
with SimReal proofs, but those participating in the
task should not just passively read the proofs. They
should rather take advantage of the dynamic
visualizations provided by SimReal. Regarding the
Square theorem, the pen-paper approaches 1-2-3 do
not necessarily promote students' understanding,
because these are based on a more mechanical
calculation method. SimReal simulation 4 is good
approach for visualizing the theorem. However, the
second and third approaches are somewhat tricky to
understand geometrically, but still better than just
formulas. Therefore, approaches 4-6 should be used
to create dynamic images of the Square theorem.
Another student preferred pen/paper proofs (1-3)
and think that these methods are mostly used to
describe algebraic operations and expressions.
However, these approaches are important only if the
teacher takes a more practical approach to the
theorem, and the geometrical SimReal-based
approaches could be used to enhance the
understanding of the theorem.
Investigating the Affordances and Constraints of SimReal for Mathematical Learning: A Case Study in Teacher Education
33

b) In what way do you think the use of SimReal can
provide a better understanding of the Square
theorem?
The students think that SimReal provides
affordances to improve the understanding of the
Square theorem by visualizing mathematical
concepts. More specifically, one student suggested a
quiz, and another a "fill the blanks" exercise, where
a student could get a direct result or feedback if the
answer is correct or not. Globally, the students think
that the digital visualizations are beneficial for
visually strong students, considering the fact that
upper secondary mathematics becomes more
theoretical the higher up the grade, and, as a result,
there is less focus on conceptual understanding, and
why and how to carry out calculations. Digital
simulations can have therefore a positive effect on
student learning and help them to see how
mathematical formulas work.
c) Give some comments about how you could think
to improve either by pen/paper or SimReal the
understanding of the Square theorem
Students provided many ways of improving the
understanding of the Square theorem. One solution
is giving exercises both with symbols and numbers,
but also allowing the use of expansion like (a + b) ^2
= (a + b) (a + b), until the student becomes familiar
with the theorem. The paper-and-pen exercises 1-2-3
show specific procedures on how a student can
change and calculate the Square theorem tasks, but
the procedures would have been clearer if there was
a headline for each example to show how the
theorem works. SimReal solutions 4-5-6 have digital
simulations with explanations, color coding, and
reference to formulas. These cover the Square
theorem quite well, and there is no need for
improvement. Likewise, SimReal simulations can
make it easier for students to see how the formulas
work, and this is especially true for the 1st and 2nd
approach to the Square theorem.
d) Do you prefer learning the Square theorem in
one way or do you feel a better understanding
learning it in different ways?
As already stated above, most students think that a
combination of different approaches is the most
appropriate way to provide a better understanding of
mathematics, while also being careful not to use
several approaches at the same time as this might be
counterproductive. They also argued that it is
important to see mathematics from different angles.
Using new methods to explain the solution to a
single problem will give new perspectives about the
problem and the corresponding solution, and how
these are interrelated. A good example is the figure-
based and algebraic proofs of the Square theorem.
Showing different point of views of the theorem
(like a geometrical one) and applications of the
theorem could indeed be very efficient.
Summarizing, a comparison of the results in
terms of affordances achieved by means of task-
based questions reveal that these are globally in line
those achieved by the survey questionnaire and
open-ended questions in terms of pedagogical
affordances at the student level. The issues that
correspond very well are the usefulness of
visualizations for understanding the Square and
Pythagoras theorem, the congruence of SimReal-
based visualizations with paper-pencil techniques,
and a combination of different representations and
approaches to the theorems.
4.4 Programming Affordances
Programming has rapidly grown as an innovative
approach to learning mathematics at different levels.
The topic will become compulsory in schools from
the study year 2020. As a result, it is expected to
improve SimReal by including programming tasks
using Python and other programming languages.
Given this consideration, it was worthwhile to ask
the students about the affordances of programming.
a) Would it be of interest for you to program your
own simulations in teaching mathematics?
The study reveals that SimReal can provide more
affordances in terms of programming mathematical
concepts. Basically, most students think that
teachers with experience in programming
mathematical simulations and visualizations will
open a new way of teaching mathematics. For
example, a teacher could focus on subjects and tasks
that are difficult for the students to comprehend.
Another possibility is to program tasks that are not
already covered by SimReal, but that are already
available online. Most importantly for teachers is the
use of different methods to promote understanding
and making new connections. Hence, it may be
worthwhile to take advantage of simulations and
explanations combined with some programming
examples so that the knowledge to be learned is
presented with various methods.
b) Do you think it would be of interest and help
that students program their own simulations?
The participants think that students would be
interested in programming visualizations if they
CSEDU 2019 - 11th International Conference on Computer Supported Education
34

have acquired sufficient skills in this matter. This
would contribute to enhanced motivation and
increased understanding of mathematics, because the
students will be forced to fully comprehend
mathematics before they could program
visualizations. Likewise, it could be of help for the
students if they could program their simulations by
themselves. However, it is crucial that they focus on
the mathematical part of the task rather than
programming issues alone. Programming their own
simulations could be motivating for those students
who are both interested and knowledgeable in
programming. This presupposes, however, that the
students have understood the mathematics before
getting started with programming. Students having
difficulties in mathematics should rather spend their
time on it. Hence, programming would be helpful if
it contributes to the learning of mathematics.
Likewise, advanced mathematics requires a higher
level of programming knowledge, and it may
therefore be necessary to evaluate whether students
have sufficient understanding of mathematics to be
able to program themselves. Finally, only one
student pointed out that he would not spend time on
programming, even though he sees an advantage in
it. Summarizing, programming mathematical tasks
can contribute to the understanding of mathematics,
but it is demanding in terms of efforts and time for
novice students.
5 DISCUSSION
The purpose of this work is to assess the impact of
SimReal affordances on students’ mathematical
learning in teacher education. The study provided an
important amount of empirical data on what students
perceived as affordances of SimReal and their
impact on learning mathematics at different levels.
Although this study does not aim to capture all
potential affordances, it is possible to make
reasonable interpretations of the results and draw
some recommendations for using SimReal in teacher
education.
In terms of technological affordances, there is a
need for a better and intuitive user interface and
navigation for different types of users. From a
pedagogical affordance point of view, SimReal
affords many students to do mathematics both at the
student and classroom level. It provides variation in
teaching mathematics, and visualizations are
considered as useful to gain mathematical
knowledge that is otherwise difficult to acquire. The
combination of live streaming of lessons, video
lectures, simulations, and animations is highly
valued. Students can work at their own pace, without
much interference from the teacher. SimReal also
facilitates various activities and several ways of
representing knowledge. In terms of affordances,
SimReal needs to be better adjusted to the student
knowledge levels, and it should provide a better
support for group work. Furthermore, there is a need
for feedback and review modes, more differentiation
and individualization, including the possibility of
programming their own videos and visualizations.
At the mathematics subject level, the tool has a high
quality of mathematical content. Moreover, the
mathematical notations are correct and sound.
The study shows that the affordances of SimReal
make mathematics easier to understand, because
these provide a concrete way of making
mathematical concepts more dynamic. In addition,
SimReal provides a huge variation of visualization
examples for the teacher to use in classroom, e.g.,
SimReal can support the understanding of Square
and Pythagoras theorems by visualizing the dynamic
behavior of the theorems. Nevertheless, a
combination of pen and paper, digital visualizations,
and chalk-blackboard could be more efficient to
teach mathematics than just SimReal alone.
Moreover, the students think that videos can speed
up the interest and motivation for doing
mathematics. Videos could be used as a supplement
to mathematics on the blackboard and paper-pencil,
and as an alternative way of sharing knowledge and
explaining mathematics. Videos are especially
important because these are one of the main sources
of information for young students. Most students
also think that programming mathematical tasks can
provide more affordances for the learning of
mathematics.
Moreover, many students think that the tool is
appropriate to use in teacher education and upper
secondary school level, and it enables to concretize
the curriculum. At the assessment level, works need
to be done to improve the feedback function.
Summarizing, the theoretical framework has
proven to be useful to address the affordances of
SimReal and their impact on mathematical learning
in teacher education. Nevertheless, the research
literature reveals that the concept of affordances can
be reconceptualised and extended by considering
ontological issues (Burlamaqui and Dong, 2015). As
already stated, affordances are not properties that
exist objectively. Rather affordances emerge in the
socio-cultural context of the classroom, where a
number of other artifacts and their affordances
interact with SimReal, e.g., paper-pencil, black
Investigating the Affordances and Constraints of SimReal for Mathematical Learning: A Case Study in Teacher Education
35

board, textbooks, Smart Phones, Power Point slides,
mathematical tasks and their representations, etc. A
reconceptualization of the concept of affordances
needs to take in consideration new and more
powerful theories such as Actor-Network Theory
(ANT), which does not consider technology simply
as a tool, but rather as an actor with agency that
serves to reorganize human thinking (Latour, 2005).
In this regard, Wright and Parchoma (2011)
criticized the value of affordances, and proposed
Actor-Network-Theory as an alternative framework
that may contribute to greater critical consideration
of the use of the concept “affordances”. The theory
of assemblage may also contribute to the
understanding of affordances and its relationship to
mathematical learning, which is understood as “an
indeterminate act of assembling various kinds of
agencies rather than a trajectory that ends in the
acquiring of fixed objects of knowledge” (De Freitas
and Sinclair, 2014, p. 52). Moreover, Withagen, et
al. (2017) argued that affordances are not mere
possibilities for action, but can also have the
potential to solicit actions. Hence, the concept of
agency can contribute to a better understanding of
affordances.
6 CONCLUSIONS
The purpose of this article is to assess the
affordances of SimReal for mathematical learning in
teacher education by asking students to respond to a
survey questionnaire and open-ended questions. In
addition, the students had the opportunity to
comment the items of the survey in their own words.
Task-based questions were also used to provide
more nuanced information about the students’
engagement with the Pythagoras and Square
theorem, and their views on programming
affordances as well. The data collected by means of
these methods provided an important amount of
information that gave a better sense and
interpretation of the results achieved in this study.
Even though, the results are promising, it is still
difficult to generalize the findings because of the
small sample size (N=15). In fact, amongst this
sample size there is already variance with regard to
the different primary teacher education levels.
However, it would have better for the research study
to have less variance with such a small sample size
and ensure that one or two of those groups have a
larger representation.
In future studies, students’ recommendations will
be considered to improve the teaching of
mathematics with SimReal. In terms of
technological affordances, there is a need for a better
and intuitive user interface and navigation for
different type of users. In terms of pedagogical
affordances, there is a need for better feedback and
review modes, more differentiation and
individualization, and the possibility of
programming their own videos and visualizations.
The concept of affordances will be refined by
considering other theories, such as Action-Network
Theory, agency, and assemblage theory. It is also
planned to look at students’ learning styles, for
example between visual and verbal students. Finally,
the data collection and analysis methods will be
improved to ensure more validity and reliability.
AKNOWLEGMENTS
This research was supported by MatRIC – The
Centre for Research, Innovation and Coordination
of Mathematics Teaching, project number 150401.
I would like to express my special appreciation and
thanks to Per Henrik Hogstad, and his involvement
and great support in the design and teaching of
mathematics using SimReal.
REFERENCES
Burlamaqui, L., Dong, A., 2015. The use and misuse of
the concept of affordance. In J.S. Gero, S. Hanna
(Eds.). Design Computing and Cognition. Berlin.
Springer.
Brekke, M., Hogstad, P.H., 2010. New teaching methods –
Using computer technology in physics, mathematics,
and computer science. International Journal of Digital
Society (IJDS), 1(1), 17-24.
Brousseau, G., 1997. Theory of didactical situations in
mathematics. Boston. Kluwer Academic Publishers.
Chiappini, G., 2013. Cultural affordances of digital
artifacts in the teaching and learning of mathematics.
Proceedings of ICTMT11.
De Freitas, E., Sinclair, N., 2014. Mathematics and the
body: Material entanglements in the classroom. New
York. Cambridge University Press.
DeLanda, E., 2013. Intensive science and virtual
Philosophy. New York. Bloomsbury Academic.
Gautestad, H.V., 2015. Use of SimReal+ in mathematics
at the university level. A case study of teacher’s
orchestrations in relation to the usefulness of the tool
for students [Original title (in Norwegian): SimReal+ i
matematikkundervisning på universitetsnivå: En studie
av lærerens orkestreringer i relasjon til verktøyets
nytteverdi for studentene. Master thesis. Kristiansand,
Norway. University of Agder.
CSEDU 2019 - 11th International Conference on Computer Supported Education
36

Geiger, V., Forgasz, H., Tan, H., Nigel., C., 2012.
Technology in mathematics education. In B. Perry et
al. (Eds.). Research in Mathematics Education in
Australasia 2002-2011, 111-141. Boston. Sense
Publishers.
Gibson, J. J., 1977. The ecological approach to visual
perception. Boston. Houghton Mifflin.
Hadjerrouit, S., Gautestad, H. H., 2018. Using the
visualization tool SimReal to orchestrate mathematical
teaching for engineering students. In C.S. González,
M. Castro, M.L. Nistal (2018). EDUCON 2018 -
Emerging Trends and Challenges of Engineering
Education. IEEE Global Engineering Education
Conference, 44-48.
Hadjerrouit, S., 2017. Assessing the affordances of
SimReal+ and their applicability to support the
learning of mathematics in teacher education. Issues in
Informing Science and Information Technology 14,
121-138.
Hadjerrouit, S., 2015. Evaluating the interactive learning
tool SimReal+ for visualizing and simulating
mathematical concepts. Proceedings of the 12
th
International Conference on Cognition and
Exploratory Learning in Digital Age (CELDA 2015),
101-108.
Hadjerrouit, S., Bronner, A., 2014. An instrument for
assessing the educational value of Aplusix (a+x) for
learning school algebra. In M. Searson, M. Ochoa
(Eds.). Proceedings of Society for Information
Technology and Teacher Education International
Conference 2014, 2241-2248. Chesapeake, VA:
AACE.
Hogstad, N. M., 2012. Use of SimReal+ in mathematics at
the university level. A case study of students’ attitudes
and challenges [Original title (in Norwegian): Bruk av
SimReal+ i matematiske fag på universitetsnivå. En
case-studiet av studenters holdninger og utfordringer].
Master thesis. Kristiansand, Norway. University of
Agder.
Hogstad, N. M., Ghislain, M., Vos, P., 2016. Engineering
students’ use of visualizations to communicate about
representations and applications in a technological
environment. Proceedings of INDRUM2016, 31
st
of
March, 2
nd
of April. Montpellier, France, 211-220.
Kirchner, P., Strijbos, J-W., Kreijns, K., Beers, B. J.,
2004. Designing electronic collaborative learning
environments. Educational Technology Research and
Development, 52(3), 47–66.
Latour, B., 2005. Reassembling the social: An
introduction to Actor-Network-Theory. Oxford.
Oxford University Press.
Norman, D.A., 1988. The psychology of everyday things.
New York. Basic Books.
Osiurak, F., Rossetti, Y., Badets, A., 2017. What is an
affordance? 40 years later. Neuroscience and
Behavioral Reviews 77, 403-417.
Pierce, R., Stacey, K., 2010. Mapping pedagogical
opportunities provided by mathematical analysis
software. International Journal of Mathematical
Learning 15, 1-20.
Presmeg, N., 2014. Visualization and learning in
mathematics education. In S. Lerman (Ed.).
Encyclopedia of Mathematics Education, 636-640.
Berlin. Springer.
Pythagoras theorem, 2018. Retrieved from http://grimstad.
uia.no/perhh/phh/MatRIC/SimReal/no/SimRealP/AA_
sim/Mathematics/Geometry/KeyWordIcon_Pythagora
s_Exercise.htm
SimReal, 2018. Retrieved from http://grimstad.uia.no/
perhh/phh/matric/simreal/no/sim.htm
Square theorem, 2018. Retrieved from http://grimstad.
uia.no/perhh/phh/MatRIC/SimReal/no/SimRealP/AA_
sim/Mathematics/Basic/KeyWordIcon_Square_Exerci
se.htm
Turner, P., Turner, S., 2002. An affordance-based
framework for CVE evaluation. In: People and
Computers XVII – The Proceedings of the Joint HCI-
UPA Conference, 89-104. London. Springer.
Withagen, R., Araújo, D., de Poel., H.J. (2017). Inviting
affordances and agency. New Ideas in Psychology 45,
11-18.
Wright, S., Parchoma, G., 2011. Technologies for
learning? An actor-network theory critique of
‘affordances’ in research on mobile learning. Research
in Learning Technology, 19 (3), 247–258.
Zbiek, R. M., Heid, M. K., Blume, G.W., Dick, T. P.
2007. Research on technology in mathematics
education, A perspective of constructs. In F. K. Lester
(Ed.), Second Handbook of Research on Mathematics
Teaching and Learning, 1169-1207. Charlotte, NC.
Information Age.
Investigating the Affordances and Constraints of SimReal for Mathematical Learning: A Case Study in Teacher Education
37
