Improving Students’ Performance through the Use of Simulations

and Modeling: The Case of Population Growth

Kathy Lea Malone

and Anita Schuchardt

Graduate School of Education, Nazarbayev University, Kabanbay Batyr 53, Astana, 01000, Kazakhstan

Department of Biology Education, University of Minnesota, Minneapolis, MN, 53455, U.S.A.

Keywords: Modelling Instruction, Science Modelling, Simulations, Population Growth, Scientific Reasoning.

Abstract: Internationally, students have difficulty interpreting and drawing conclusions from data. These skills are

essential components of scientific reasoning, an ability that has been shown to correlate with conceptual

change. Providing greater opportunities for students to engage in scientific practices such as modelling in

order to collect and reason with data has the potential to improve scientific reasoning skills. However, in

some subdisciplines of biology, such as population growth, data collection needs to occur over time scales

that are unfeasible in a classroom setting. Computer-based simulations of biological phenomena are one

way to overcome this limitation, but their effect on scientific reasoning has been under investigated. This

study researched the effect on scientific reasoning of computer-based simulations in a context that employed

a specific type of model-based reasoning (Modelling Instruction). Students who used computer-based

simulations in a Modelling Instruction context showed increased scientific reasoning post-instruction

compared to a comparison group. Moreover, shifts were observed in the intervention group towards more

formal reasoning whereas no such change was observed with the comparison group. This result suggests

that computer-based simulations should be further explored as a way to improve student scientific

reasoning, particularly in contexts where laboratory investigations are not feasible.

1 INTRODUCTION

Internationally, research studies and educational

policy groups have affirmed the need to have

students learn higher order thinking skills in science

classrooms (Mullis et al. 2016, p. 8; Organisation of

Economic Co-operation and Development, 2016, pp.

103-109). The results from the Programme for

International Student Assessment (PISA) have

suggested that across nations, students not only have

difficulty interpreting scientific data but also

drawing conclusions from that data (Organisation of

Economic Co-operation and Development, 2016, pp.

37-46). This deficiency might be caused by a lack of

opportunity for students to practice new skills within

the context of scientific laboratories. One contributor

might be lack of facilities. However, a more

common barrier, especially in Biology (and

particularly in topic areas such as population growth

and evolution), is likely to be difficulties in data

collection because of the time needed to see multiple

generations of data (Heaps et al. 2016, p. 221;

Oswald and Kwiatkowski, 2011, pp. 469-471). One

possible way to allow for the collection of data in

these areas that require extended time is through the

use of specially designed simulations (Huppert et al,

2002, pp. 809-812). However, there are few studies

that attempt to use simulations in population growth

within the context of secondary biology classrooms

which emphasize scientific modelling.

Interpreting and drawing conclusions from data

are essential components of scientific reasoning, a

skill that has been shown to correlate with

conceptual change (e.g., Coletta et al, 2007, p. 237;

Moore and Rubbo, 2012, pp. 4-5). Thus, it is

important to make sure that interventions improve

students’ scientific reasoning skills as these skills

can affect students’ lifelong learning. However, few

studies have focused on assessing shifts in students’

scientific reasoning when using simulations in the

context of a modelling instruction class in biology.

This paper attempts to fill this gap by describing

a quasi-experimental study in the USA that tests the

effectiveness of a simulation developed to introduce

population growth within the context of a specific

type of scientific modelling curriculum, Modelling

222

Malone, K. and Schuchardt, A.

Improving Students’ Performance through the Use of Simulations and Modeling: The Case of Population Growth.

DOI: 10.5220/0007612802220230

In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), pages 222-230

ISBN: 978-989-758-367-4

Instruction. This study was guided by the following

research goal:

1) Will Modelling Instruction students experiencing

a population growth simulation outperform a

comparison group in terms of scientific

reasoning?

2 LITERATURE REVIEW

Within this section we will investigate past

instructional interventions in population growth as

well as the use of scientific modelling simulations

and Modelling Instruction (MI) within science

classrooms. In addition, we will specifically discuss

the use of conceptual modelling and modelling

simulations within the context of population growth.

The end of this section will include a discussion of

past studies focused on scientific reasoning and

simulations.

2.1 Learning Challenges in Population

Growth

Numerous studies show that at both the

undergraduate and secondary levels, student

conceptual knowledge about population growth is

sprinkled with misconceptions. Brody and Koch

(1990, p. 23) found that high school students

consider an ecosystem’s resources to be limitless.

Munson (1994, p. 32) found that undergraduate

students think that populations exist in two constant

states: one of growth or one of decline. However,

Munson (1994, p. 32) also discovered that students

can also believe that populations increase till limits

are reached then the population crashes thus going

extinct. The effect of predator-prey relationships has

also been shown to cause student difficulties since

many think that two organisms can only affect each

other if they share this specific relationship

(Griffiths and Grant, 1985, pp. 430-431). Stammen

(2018, pp. 149-151) found that middle school

students believe that competition within an

ecosystem always involves aggressive interactions.

These alternative conceptions do not portend well

for students learning a strong correct conception of

population growth that would support learning in

other biological concepts such as evolution and

genetics.

2.2 Models, Modelling and Modelling

Instruction in Biology

Science modelling is the process by which students

are guided in the construction of science models or

empirically testing the effectiveness of science

models. A scientific model is not only a 2D or 3D

representation of a science phenomenon but can

include other representations such as graphical,

pictorial, mathematical or verbal.

Little work has been done towards incorporating

the use of models and modelling into biology either

at the secondary or the undergraduate level.

Passmore and Stewart (2002, pp. 186-194) designed

the MUSE pedagogy for secondary school students

that focused on students’ comparison of previously

determined models against empirical data. At the

college level Dauer et al (2013, pp. 240-241) had

undergraduates develop models in multiple

biological areas (one of them population growth).

While both determined that students understood

models better neither study had a control group, nor

did they test for conceptual understanding.

Modelling Instruction is a scientific modelling

pedagogy that makes use of student generated

models to develop multiple representations. See

Figure 1 for an example of model representations in

population ecology.

Figure 1: Scientific Model representations for Population

Growth Model (adapted from Dukerich, 2015, p. 1315).

Modelling Instruction makes use of a Modelling

cycle (see Figure 2) that focus on student

development of scientific models from empirical

data. The students use the data to produce a model

that consists of multiple representations. The initial

science model is used to make predictions about

behaviour which can be checked against the initial

empirical data. If predictions are not in line with the

empirical data, then revisions to the model and its

representations are produced. The revised model is

then tested in other contexts. The cycle is continuous

so that at any time predictions to not match data

Improving Students’ Performance through the Use of Simulations and Modeling: The Case of Population Growth

223

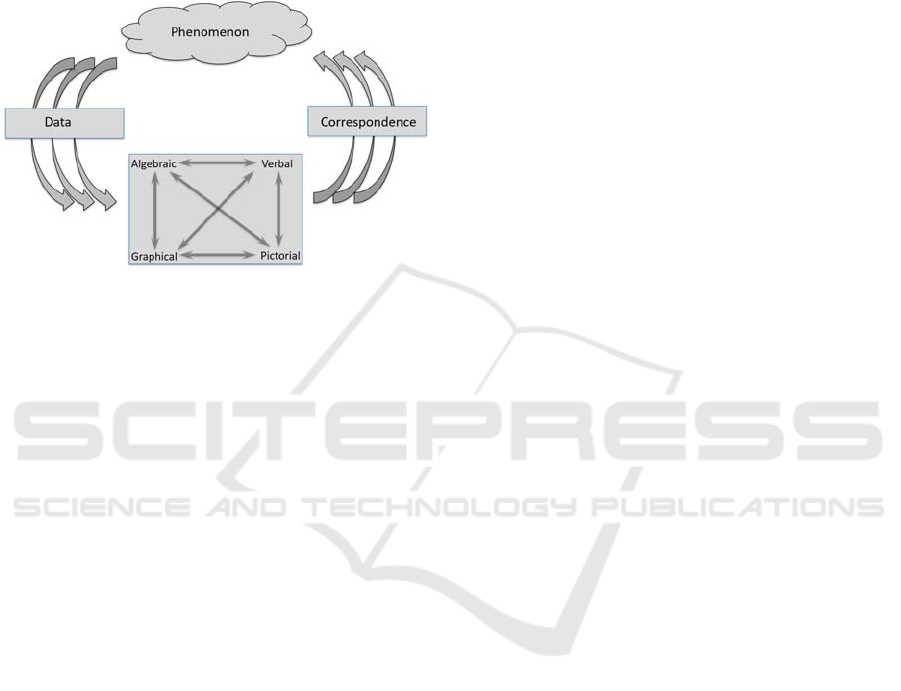
revisions of the model representations are

considered. This allows students to develop a robust

understanding of the concepts being developed.

The use of multiple representations alone has

been shown in a number of studies to produce

improved conceptual learning (e.g., Dori and

Belcher, 2005, pp. 211-212; Won et al, 2014, pp.

863-864).

Figure 2: The Modelling Cycle (adapted from Malone et

al, in press).

Modelling Instruction has been shown to be

effective at increasing student conceptual

understanding in other disciplines such as physics

(Jackson et al, 2008, pp. 15-16; Malone, 2008, pp. 4-

12, Malone and Reiland, 1995, p. 411), and

chemistry (Malone and Schuchardt, 2016, pp. 4-5).

However, only a single study has been published on

the effect of Modelling Instruction in Biology

(Malone et al, in press). Malone et al, in press)

demonstrated that the use of Modelling Instruction

and physical simulations can be effective in student

conceptual understanding in evolution. They showed

that not only did students show a decline in

alternative conceptions but also there was an

increase in their use of multiple representations to

explain evolutionary concepts over that of the

comparison group.

2.3 Simulations, and Modelling in

Population Growth

A meta-analysis showed that simulations have a

beneficial effect over that of units with no

simulations in the secondary school (D’Angelo et al.

2014, p. 42). 

In a review Smetana and Bell (2012, pp. 1362-

1364) found that the use of computer simulations

might depend upon how they are used in the

classroom. They suggested that in order to be the

most effective simulations should be used when

incorporated into pedagogy and encourage reflection

on the part of students. One study that tested the

ability of a single secondary school student to

produce a model about predation using a simulation

produced with Net Logo (Wilensky and Reisman,

2006, pp. 203-205) had mixed results. While the

student could produce a model of predation that was

predictive of observed lab outcomes in the

simulation, it was not consistent with real-life

observations. Another study used a simulation in the

seventh grade called WISE (Donnelly et al. 2016,

pp. 1344-1359). The students did show a gain in

conceptual understanding, but there was no

comparison group. However, few studies focus on

the effect of simulations which are embedded in a

modelling-based curricula unit, especially in the area

of population growth.

The use of models and modelling in the teaching

of evolution and population ecology within the

context of an engineering themed unit has been

shown to be effective at the secondary level in terms

of student conceptual understanding (Malone et al,

2018, pp. 42-44). This unit also incorporated a series

of excel based simulations that looked at not only

population growth but also natural selection. This

quasi experimental study showed that there was a

significant gain in student understanding of

population growth and natural selection over that of

a comparison group as well as an increase in student

use of multiple representations. In addition, students

demonstrated a greater fascination with science.

However, this study did not test for shifts in student

scientific reasoning skills.

The studies showing conceptual gains used

simulations that were incorporated into specific

pedagogical units. However, none focused on

scientific reasoning skills of students.

2.4 Scientific Reasoning and

Simulations

As mentioned in the introduction the link between

scientific reasoning and science has been studied.

However, fewer studies have focused on the link

between simulation use in science and scientific

reasoning.

The studies showing a link between scientific

reasoning and science have been mostly conducted

at the college level. For example, Coletta, Phillips

and Steinert (2007, p. 236) showed that when active

learning methods are used with STEM college

majors, student scientific reasoning skill as

measured by the Lawson’s Classroom Test for

Scientific Reasoning (LCTSR) was highly correlated

CSEDU 2019 - 11th International Conference on Computer Supported Education

224

to gains in physics knowledge. This study also

demonstrated a similar correlation effect in one

secondary school using Modelling Instruction.

However, pre to post gains in scientific reasoning

when using simulations in the context of a

Modelling Instruction unit have not been assessed.

Therefore, it is not known how modelling based

simulation activities affect students’ shifts in

scientific reasoning pre to post implementation.

This study attempts to fill these gaps by testing

the effects on students’ scientific reasoning skills of

a science modelling simulation embedded in a

Modelling Instruction population growth curricular

unit.

3 METHODS

This study is a quantitative evaluation study looking

at the differences in scientific reasoning skills pre to

post instruction between a treatment and a

comparison group of students.

3.1 Research Questions

The study was guided by the following research

questions.

1) Will Modelling Instruction students experiencing

population growth simulations display a greater

increase in scientific reasoning skills than

comparison students?

2) Will Modelling Instruction students demonstrate

a greater shift towards formal reasoning in terms

of Piagetian reasoning stages?

3.2 Participants and Settings

The participants in this study were high school

students located in the Midwestern region of the

United States enrolled in regular level biology

courses. All of the students attended a suburban

school district but were from a mix of high schools

within the district. The implementing cohort

consisted of 205 students and were taught by a

teacher in their first year of implementing modelling

instruction. The comparison cohort of 141 students

was taught by two different teachers. All three

teachers had similar backgrounds and total years of

teaching experience.

3.3 Population Growth Modelling

Instruction Unit

The constructed unit started with a pre-assessment

activity that asked students to consider what would

happen if all the plants in the world died. This was

used to draw out student preconceptions. No

“correct” answers were given to the question.

Students shared their initial thoughts and ideas. In

addition, the implementation teachers requested that

students supply their reasoning for any of the claims

they were making.

The students were then introduced to two species

of paramecium (P. caudatum and P. aurelia) using

microscopes. The students were asked what they

thought would happen to the size of each population

after 100 years if they were in a place with no

predators? The students were broken into groups to

develop a prediction and to develop methods to

represent or “show” their predictions to the rest of

the class. This was the first Modelling Instruction

modelling cycle for the implementation students.

Thus, most drew pictures about what would happen

over time and very few represented their predictions

in a graphical form. During group sharing, if some

students developed diagrams, storyboards and

graphical representations of their predictions these

were shared with the class during class discussion.

Thus, after the consensus depending on student

backgrounds the initial representations were quite

diverse. In this case most of the graphical

representations were in the form of bar graphs and

pie charts. As students were sharing their

representations, they were asked to describe the

biological meaning behind them.

After the prediction phase the teacher asked the

groups to consider how they might investigate this

question using paramecium. The students had to go

to the internet to find the life cycle of paramecium

and consider the number of offspring. In addition,

they were asked to consider which variables would

be independent, dependent and which would be held

constant. The students discovered that if they

actually used live paramecium the time to collect

data would be much too long to for their classes.

Consequently, the teachers introduced the use of

google sheet simulations to the students. The lab was

conducted by either dividing the class in half so that

each half worked with one or the other organism.

This allowed groups to see what happened to the

output due to the difference in growth rate between

these two organisms.

The google sheet simulation consisted of an

input sheet where students could decide upon a

Improving Students’ Performance through the Use of Simulations and Modeling: The Case of Population Growth

225

number of conditions, a graph and data sheet as well

as an equations sheet. The equations sheet was there

to show students the mathematical growth formula if

the teacher desired to do so.

The google sheet simulations were designed to

contain the variables that were requested by pilot

students for either P. caudatum or P. aurelia. The

input page asked students to select their initial

population size, whether they had limited or

unlimited resources, and the generation time. In

addition, students had to input the container size,

number of offspring produced per generation as well

as the average number of offspring that die each

generation. See Figure 3.

At this point, depending upon students’ abilities

with graphs, they either focused on just the data

charts (see Figure 4) or the simulation generated

graphs (see Figure 5). The ones that focused only on

data charts were asked to hand graph their output

data. This allowed for a comparison of graphing

techniques between groups and the ability to discuss

the reasons why a line graph was a better selection

for the output data rather than a bar graph.

Figure 3: Simulation Input Page.

Figure 4: Simulation's Data Output Page.

The output generated included the number of

“observed” as well as “predicted” paramecium

depending upon their input variables on the input

page. The students were tasked with changing their

input page in order to match the observed numbers

on the graph (see Figure 5). When they did this, they

were asked to discuss it with their teachers and

explain why and what part of their prediction they

were changing.

After the lab, students were asked to construct

large poster displays which detailed how their

predictions changed for both limited and unlimited

food supplies, large vs small containers, etc. Each

student group produced a number of representations

of their findings and then the whole class with the

guidance of the teacher developed a class consensus.

The consensus consisted of graphical representations

(see Figure 6), diagrammatic representations (see

Figure 7) as well as verbal representations. An

example of a verbal representation is as follows:

As the days go by, the number of

paramecium increase at a greater rate. The

relationship is not linear so that when you

double the days the number does not double.

Different organisms have different growth

rates.

At this point the class has not determined a

mathematical representation. The mathematical

representation was developed using the data from

the two types of paramecium.

The unit then has the students deploy or test their

new model for population growth in multiple

contexts. This allows students to refine their model

further after they discover what happens when two

paramecia are living together in the same container.

Figure 5: Simulation's Graphical Output Page - students’

predictions almost match the observed graph.

CSEDU 2019 - 11th International Conference on Computer Supported Education

226

Figure 6: Sample of Graphical Representations of the

Model.

Figure 7: Sample Diagrammatic Representation.

3.4 Research Instruments

This study made use of the 24 item two-tiered

Lawson’s Classroom Test for Scientific Reasoning

(LCTSR) as a pre and posttest (Lawson, 1978, pp.

12-15). The LCTSR has been used in multiple

studies across a number of contexts (e.g., Ding et al,

2016, p. 620; Lawson, 2000, pp. 11-12). This

assessment can be used to not only assess overall

scientific reasoning but also to look at specific

scientific sub skills. These sub-skills consist of

control of variables, correlational reasoning,

proportional reasoning and hypothetico-deductive

reasoning. In addition, the results can be used to

determine the number of students at different

Piagetian reasoning stages (i.e., Formal reasoner,

Late Transitional Reasoner, Early Transitional

Reasoner and Concrete Reasoner). Piagetian

reasoning stages are based on student abilities to

apply deductive reasoning skills to abstract

hypothetical problems. Lawson’s test allows one to

identify learners as Level 0 (Piagetian formal

operational reasoners), Level 1 and 2 (Piagetian

transitional reasoner) or Level 3 (Piagetian formal

operational reasoner). Thus, based on the student

scores obtained students can be categorized into

separate reasoning levels. Figure 8 compares the

LCTSR to the Piagetian three levels of formal

reasoning.

The pretest was given within the first 2 weeks of

the school year and the post test was given during

the last month of the school year.

Figure 8: Comparison of LCTSR with Piagetian

Reasoning Levels (from Stammen et al, 2018, p. 3).

3.5 Data Analysis and Results

Since this study is focused on population ecology

only 20 of the 24 items on the LCTSR were

analysed. The 4 items not analysed focused on

conservation of mass and volume which were not

considered pertinent to this study.

3.5.1 Single-tiered Question Analysis

In order to determine overall differences between the

two cohorts a single-tiered analysis was completed

whereby all 20 items on the LCTSR were treated as

independent from one another.

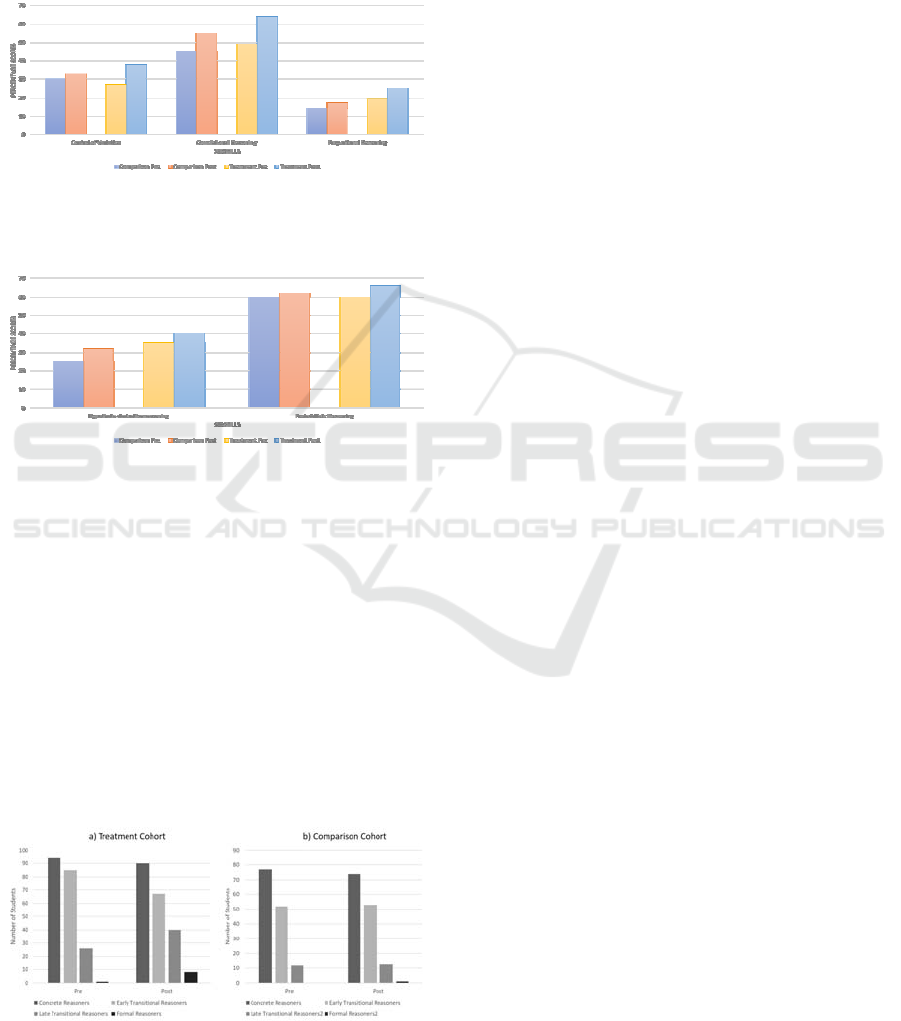
Figure 9 shows the overall average pretest and

postest scores for the two cohorts. The t-test results

for a paired pretest to posttest comparison of

scientific reasoning scores were significant for the

treatment cohort (t (410) = 3.29, p < 0.001) but not

for the comparison cohort (t (280) = 1.52, p < 0.13).

The pretests of the treatment and comparison cohorts

(M = 37.23 and 34.5, respectively) were not

significantly different from each other (t (345) = 1.2,

p < 0.23). The post test scores between the treatment

and comparison cohorts (M = 43.25 and 37.34,

respectively) were significantly different (t (345) =

2.92, p < 0.004).

Figure 9: Single-tiered LCTSR Scores by Cohort.

The distribution of scientific reasoning subskills

on the pre and posttest by cohort can be seen in

Figures 10 and 11. Across all dimensions the

posttest sub-skills developed by the treatment cohort

Improving Students’ Performance through the Use of Simulations and Modeling: The Case of Population Growth

227

were larger than that of the comparison cohort. The

proportional reasoning subskill is a bit concerning

given that it is the lowest score of all the subskills

(see Figure 10). Given the simulations focus on the

effects of one variable upon others one might expect

this score to be much higher for the treatment

cohort.

Figure 10: Scientific Reasoning Subskill Scores (Control

of Variables, and Correlational and Proportional

Reasoning) by Cohort.

Figure 11: Scientific Reasoning Subskill Scores

(Hypothetic-deductive and Probabilistic Reasoning) by

Cohort.

3.5.2 Two-tiered Question Analysis

By using the two-tiered analysis (treating paired

items as a group), the LCTSR scores can be

categorized into Piagetian reasoning stages. In this

method the largest score is 13. Therefore, students

scoring from 11-13 are categorised as Formal

Operational Reasoners whereas those scoring 0-4

would be categorized as Concrete Reasoners. Figure

12a and b show the shift in number of students in

each reasoning stage per cohort. Figure 12

demonstrates that the treatment group showed a shift

Figure 12: Pre and Post Student Reasoning Levels by

Cohort.

towards more formal reasoners. Whereas, the

comparison group only shifted one student into this

category. In both cases there was not much change

from concrete reasoners to other categories.

However, the comparison cohort did not show much

shift between any categories.

4 DISCUSSION

The single-tier item analysis demonstrated that gains

in scientific reasoning were made by the treatment

group using the population ecology simulation and

modelling instruction between assessment

administrations. However, the comparison cohort

did not make any significant gains between

administrations of the assessment. Therefore, the use

of population growth spreadsheet simulations in

conjunction with Modelling Instruction in the

context of population ecology produced a shift in

scientific reasoning skills.

The subskill scores demonstrated that the

curriculum units used by the treatment cohort

showed post assessment reasoning abilities that

exceeded that of the comparison cohort. The two

subskills showing the lowest values between cohorts

was that of proportional reasoning and control of

variables. This demonstrates that both groups need

to be exposed to activities that allow them to master

these subskills to a greater extent.

The two-tiered analysis demonstrated that the use

of a simulation in conjunction with Modelling

Instruction demonstrated the ability to assist over

6% of the students into becoming formal reasoners.

Whereas, the comparison group did not demonstrate

any major shift between reasoning levels. However,

even though the treatment cohort showed much

more positive results in terms of reasoning levels pre

to post assessment there was still very little shift in

the total number of concrete reasoners.

5 CONCLUSIONS AND FUTURE

DIRECTIONS

Overall, the study demonstrated that the use of

simulations in conjunction with Modelling

Instruction pedagogy demonstrates positive results

in terms of scientific reasoning gains versus that of

the comparison cohort. In addition, the study

demonstrated the ability of the materials to allow for

student shifts in Piagetian reasoning levels towards

more formal reasoners. Therefore, students using

CSEDU 2019 - 11th International Conference on Computer Supported Education

228

these materials should be better prepared for

advanced science study.

However, the results also demonstrated that the

materials need to be improved in order to allow for a

more authentic ability to practice control of variables

and to develop proportional reasoning skills. In

addition, differences in the simulation use between

high and low ability students should be studied in

order to develop better simulation scaffolds. Better

simulation scaffolds could allow all students show

similar gains in reasoning levels across classrooms

that contain students of varying abilities.

In addition, this study did not include cohorts

that used just the simulation or Modelling

Instruction materials without population ecology

simulations in order to tease apart the effects of the

two in terms of scientific reasoning skills. Future

studies should also include an analysis of conceptual

gains as well as that of scientific reasoning.

ACKNOWLEDGEMENTS

This research was partially funded by a grant under

the federally funded Math Science Partnership State

Grants Program, under Grant number OH160505

and OH160511. Any opinions, findings, and

conclusions or recommendations expressed in this

material are those of the authors and do not

necessarily reflect the views of the funding

organizations.

REFERENCES

Brody, M.J. and Koch, H. (1990). An assessment of 4th-,

8th-, and 11th-grade students’ knowledge related to

marine science and natural resource issues. Journal of

Environmental Education, 21(2), pp. 16–26.

Coletta, V.P., Phillips, J.A. and Steinert, J.J. (2007). Why

you should measure your students’ reasoning ability.

The Physics Teacher, 45, pp. 235-238.

D’Angelo, C., Rutstein, D., Harris, C., Bernard, R.,

Borokhovski, E. and Haertel, G. (2014). Simulations

for STEM learning: Systematic review and meta-

analysis. Menlo Park: SRI International.

Dauer, J. T., Momsen, J.L., Speth, E. B.,

MakohonMoore, S. C. and Long, T. M. (2013).

Analyzing change in students' genetoevolution

models in collegelevel introductory biology. Journal

of Research in Science Teaching, 50(6), pp. 639-659.

Ding, L., Wei, Z., and Mollohan, K. (2016). Does higher

education improve student scientific reasoning skills?

International Journal of Science and Mathematics

Education, 14, pp. 619-634.

Donnelly, D. F., Namdar, B., Vitale, J. M., Lai, K., and

Linn, M. C. (2016). Enhancing student explanations of

evolution: Comparing elaborating and competing

theory prompts. Journal of Research in Science

Teaching, 53(9), pp. 1341-1363.

Dori, Y.J., and Belcher, J. (2005). Learning

electromagnetism with visualizations and active

learning. In: J. Gilbert, ed., Visualization in Science

Education, Dordrecht, The Netherlands: Springer, pp.

198 – 216.

Dukerich, L. (2015). Applying Modeling Instruction to

high school chemistry to improve students’ conceptual

understanding. Journal of Chemical Education, 92(8),

pp. 1315-1319.

Griffiths, A. K. and Grant, B. A. C. (1985). High school

students' understanding of food webs: Identification of

learning hierarchy and related misconceptions. Journal

of Research in Science Teaching, 22(5), pp. 421-36.

Heaps, A. J., Dawson, T. D., Briggs, J. C., Hansen, M. A.

and Jensen, J. L. (2016). Deriving population growth

models by growing fruit fly colonies. The American

Biology Teacher, 78(3), pp. 221-225.

Huppert, J., Lomask, S. M. and Lazarowitz, R. (2002).

Computer simulations in the high school: Students'

cognitive stages, science process skills and academic

achievement in microbiology. International Journal of

Science Education, 24(8), pp. 803-821.

Jackson J, Dukerich L and Hestenes D (2008) Modeling

instruction: An effective model for science education.

Science Educator, 17(1), pp. 10–17.

Lawson, A.E. (1978). The development and validation of a

classroom test of formal reasoning. Journal of

Research in Science Teaching, 15, pp. 11-24.

Lawson, A.E. (2000). Classroom test of scientific

reasoning: Multiple choice version. Journal of

Research in Science Teaching, 5, pp. 11-24.

Malone KL (2008) Correlations among knowledge

structures, force concept inventory, and problem-

solving behaviors. Physics Review- Special Topics

Physics Education Research 4(2):20107.

Malone, K. and Reiland, R. (1995). Exploring Newton’s

third law. The Physics Teacher, 33(6), 410 – 411.

Malone, K.L. and Schuchardt, A.M. (2016, January). The

efficacy of modelling instruction in chemistry: A case

study. Proceedings form HICE 2016: The 14

Annual

Hawaii International Conference on Education (pp.

1513 – 1518). Honolulu, HI.

Malone, K.L., Schuchardt A.M., and Sabree, Z (in press).

Models and modeling in evolution. In U. Harms and

M. Reiss, eds., Evolution Education Re-considered,

UK: Springer.

Malone, K. L., Schunn, C. D. and Schuchardt, A. M.

(2018). Improving conceptual understanding and

representation skills through Excel-based modeling.

Journal of Science Education and Technology, 27(1),

pp. 30-44.

Munson, B. H. (1994). Ecological misconceptions. The

Journal of Environmental Education, 25(4), pp. 30-34.

Oswald, C. and Kwiatkowski, S. (2011). Population

growth in Euglena: a student-designed investigation

Improving Students’ Performance through the Use of Simulations and Modeling: The Case of Population Growth

229

combining ecology, cell biology, and quantitative

analysis. The American Biology Teacher, 73(8), pp.

469-473.

Moore, J. C. and Rubbo, L. J. (2012). Scientific reasoning

abilities of nonscience majors in physics-based

courses. Physical Review Special Topics - Physics

Education Research, 8, 1, 10106.

Mullis, I.V.S., Martin, M.O., Goh, S. and Cotter, K. (eds.)

(2016). TIMSS 2015 Encyclopaedia: Education Policy

and Curriculum in Mathematics and Science.

Retrieved from Boston College, TIMSS & PIRLS

International Study Canter website: http://

timssandpirls.bc.edu/timss2015/encyclopedia/

Organisation of Economic Co-operation and Development

(OECD, 2016). Low-Performing Students: Why they

fall behind and how to help them survive, PISA,

OECD Publishing, Paris, http://dx.doi.org/10.1787/

9789264250246-en.

Passmore, C. and Stewart, J. (2002). A modeling approach

to teaching evolutionary biology in high schools.

Journal of Research in Science Teaching, 39(3), pp.

185-204.

Smetana, L. K. and Bell, R. L. (2012). Computer

simulations to support science instruction and

learning: A critical review of the literature.

International Journal of Science Education, 34(9), pp.

1337-1370.

Stammen, A. (2018). The development and validation of

the Middle School Life Science Concept Inventory

(MS-LSCI) using Rasch analysis. (Doctoral

dissertation, Ohio State University).

Stammen, A., Malone, K.L. and Irving, K.E. (2018).

Effects of Modeling Instruction professional

development on biology teachers’ scientific reasoning

skills. Education Sciences, 8(3), https://doi.org/

10.3390/educsci8030119.

Wilensky U., and Reisman K (2006) Thinking like a wolf,

a sheep, or a firefly: Learning biology through

constructing and testing computational theories - an

embodied modeling approach. Cognition and

Instruction, 24(2), pp. 171–209.

Won, M., Yoon, H. and Treagust, D.F. (2014). Students’

learning strategies with multiple representations:

Explanations of the human breathing mechanism.

Science Education, 98 (5), pp. 840-866.

CSEDU 2019 - 11th International Conference on Computer Supported Education

230