
Thermal Analysis for Quantum Cascade Lasers using Experiments,
Simulations and Structure Function Obtained by Static Measurement
Shigeyuki Takagi
1
, Hirotaka Tanimura
1
, Tsutomu Kakuno
2
, Rei Hashimoto
2
and Shinji Saito
2
1
School of Engineering, Tokyo University of Technology, 1404-1, Katakura-cho, Hachioji city, Tokyo, Japan
2
Coporated Manufacturing Center, Toshiba Corporation, 8 Shinsugita-cho, Isogo Ward, Yokohama-city, Japan
Keywords: Quantum Cascade Lasers, QCLs, Statics Method, Dynamic Method, Heat Resistance, Three-dimensional
Simulation.
Abstract: In order to increase the output of quantum cascade lasers (QCLs), it is important to improve the heat
dissipation. For investigating the relationship between the device structure and heat dissipation properties,
three kinds of different QCL devices were prepared as follows. One is a device which has the ridge covered
with SiO
2
and thin Au, another is a device which has the ridge covered with SiO
2
embedded with Au, and the
other is a device which has the ridge covered with SiO
2
embedded with Cu. The temperature distributions
was measured with a thermos-viewer. In addition, relationship between structure and heat dissipation
properties in these structure devices are analysed with a three-dimensional model. As a result, it was clarified
from experiments and simulations to improve heat dissipation properties by embedding ridge with Au or Cu.
Furthermore, the thermal properties of the QCL device was measured by the statics method to separate the
thermal resistance of the ridge, that of substrate, and that of mount parts. It was shown that the thermal
resistance improves by more than 2 K/W from 9.3 K/W to 6.9 K/W by embedding ridge with Au or Cu.
1 INTRODUCTION
Quantum cascade lasers are n-type semiconductor
lasers in which two types of semiconductor films are
alternately stacked, and the laser light in the infrared
region can be obtained (Faist et al., 1994).
Conventional semiconductor lasers (LD) are limited
to visible wavelengths below 3 μm, and
semiconductor type lasers do not exist in the infrared
region beyond that. QCLs oscillate in this region, and
desired wavelength can be obtained just by changing
the film thickness of the multilayer film using two
kinds of materials.
In the latter half of the 2000s, commercially
available lasers have been provided, and steadily
commercialization is progressing with the detection
of trace substances and gas detection in the distance.
Particularly in the field of detection of trace
substances, since the oscillation wavelength of QCLs
is in the infrared region, it is possible to measure
many gases with high sensitivity. With such trace
substance detection and gas detection in the distance,
higher sensitivity is expected by increasing the output.
Since the amount of the laser absorption is measured
in the detection of trace substances, it is necessary to
propagate a long optical path length. Also, in far-field
gas detection, a high-power laser is required since it
detects weakly reflected light during laser light
propagation.
As a high-power laser, watt-class laser oscillation
has been reported by A. Evans et al., (2007; Bai et al.,
2008). In order to further increase the laser output, a
film structure with high oscillation efficiency and a
device structure with high heat dissipation property
are important. In this report, we focused on heat
dissipation in QCLs. As a method for evaluating the
heat dissipation property of QCLs, a method of
embedding a ridge with InP has been adopted.
Several reports on the heat distribution of QCLs
have been made. Sood et al. systematically measured
the relationship between film thickness and thermal
conductivity in super lattices of InGaAs and InAlAs
(Sood et al., 2014). Evans et al. reported the analysis
for temperature dependence of waveguide loss of
QCLs (Evans et al., 2012). G. K. Veerabathran et al.
have measured the thermal resistance by inputting
pulsed power to QCL, which is called Dynamic
method (Veerabathran et al., 2017).
On the other hand, V. Székely proposed a new
method of extracting the thermal resistance from the
Takagi, S., Tanimura, H., Kakuno, T., Hashimoto, R. and Saito, S.
Thermal Analysis for Quantum Cascade Lasers using Experiments, Simulations and Structure Function Obtained by Static Measurement.
DOI: 10.5220/0007612903030307
In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2019), pages 303-307
ISBN: 978-989-758-364-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
303
voltage-current characteristics at the time of cooling
has been introduced (Székely, 1997). This method is
called the Statics method, and is widely used for
measuring the thermal resistance of power devices. In
this method, by using the inflection point of the
thermal resistance (structure function), it is possible
to separate the thermal resistance of the ridge, that of
substrate, and that of mount parts.
In this paper, we applied this method to three
kinds of QCLs with different structures, and
separated the resistance for each constituent element
such as ridge, substrate, and mount. In addition, we
report on the thermal analysis using three-
demensionsl simulations which reproduce the
thermal characteristics of actual devices.
2 DEVICE STRUCTURE AND
CHARACTERISTICS
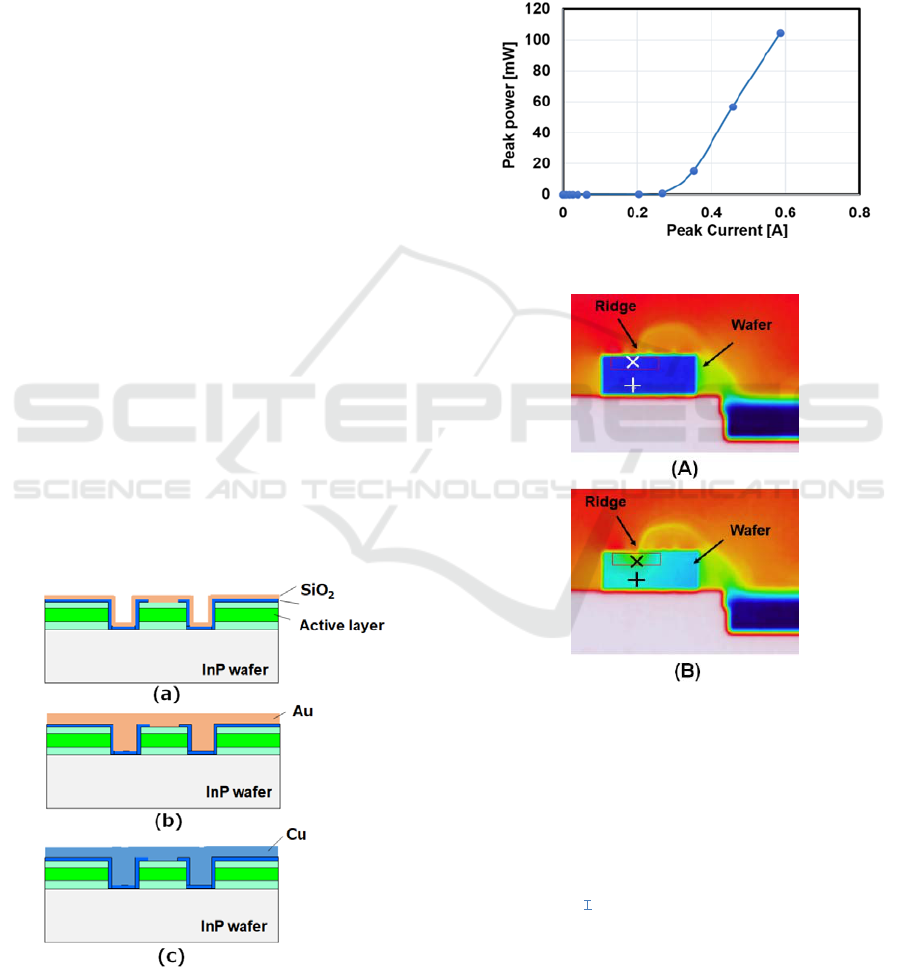
Figures 1 (a) - (c) show three kinds of device
structures comparing the temperature characteristics.
In all devices, the QCL device forms an active layer
(ridge portion) in which 22 layers of alternating layers
in the device structure (a), thin SiO
2
and Au film are
formed on the cladding layer. In the structure (b), gold
of 10µm in thickness is plated on the structure (a). In
the structure (c), Cu of 10 μm in thickness is plated
on the SiO
2
film of (a). The result of laser operation
for the device in the structure (c) is shown in Fig.2.
At an operating temperature of 0 ℃, an oscillation
wavelength of 4.41 µm and a laser peak output of
100mW have been obtained.
Figure 1: Devices structures. (a) Ridge covered with thin
SiO
2
and thin Ti/Au, (b) Ridge embedded with Au, and (c)
Ridge embedded with Cu.
In structures (a) - (c), the CuW mount was cooled
to 10℃. Power up to 4 W was applied and the device
temperature was measured with a thermos-viewer.
The thermos-viewer FSV-210L (Apiste Corp.) is
used for the measurement, and it can be measured the
temperature with a space resolution of 12.5 μm or less
with 25 μm lens and digital zoom. Fig.3 (A) shows
the measurement results without operating, and (B)
shows the result in the case of inputting 3 W of power.
Figure 2: QCL output power.
Figure 3: Temperature measurement with thermo-viewer,
(A) without power and (B) input power of 3W.
Temperatures at two points “x” and “+” in Fig. 3
(A) were measured, and the supplied electric power
was varied to obtain the temperature difference ΔT
between “x” and “+”. “x” is just under the ridge
portion, and “+” is a position 50 μm above the lower
surface of the substrate. These results are shown in
Fig.4. The measured values fluctuated by about 10%
depending on the experimental setup. The variation
ranges are shown as error with error bar. In the
structure (a), the upper surface is covered with SiO
2
with a thickness of 0.2 μm and Au with a thickness of
0.5 μm, and the heat dissipation property for releasing
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
304
heat into the atmosphere is lowered, and ΔT is large.
On the other hand, in structures (b) and (c), heat is
released to the atmosphere via Au or Cu on SiO
2
, and
ΔT decreases.
Figure 4: Temperature difference ΔT between the ridge
bottom and the bottom of the wafer (Experiment).
3 THERMAL ANALYSIS
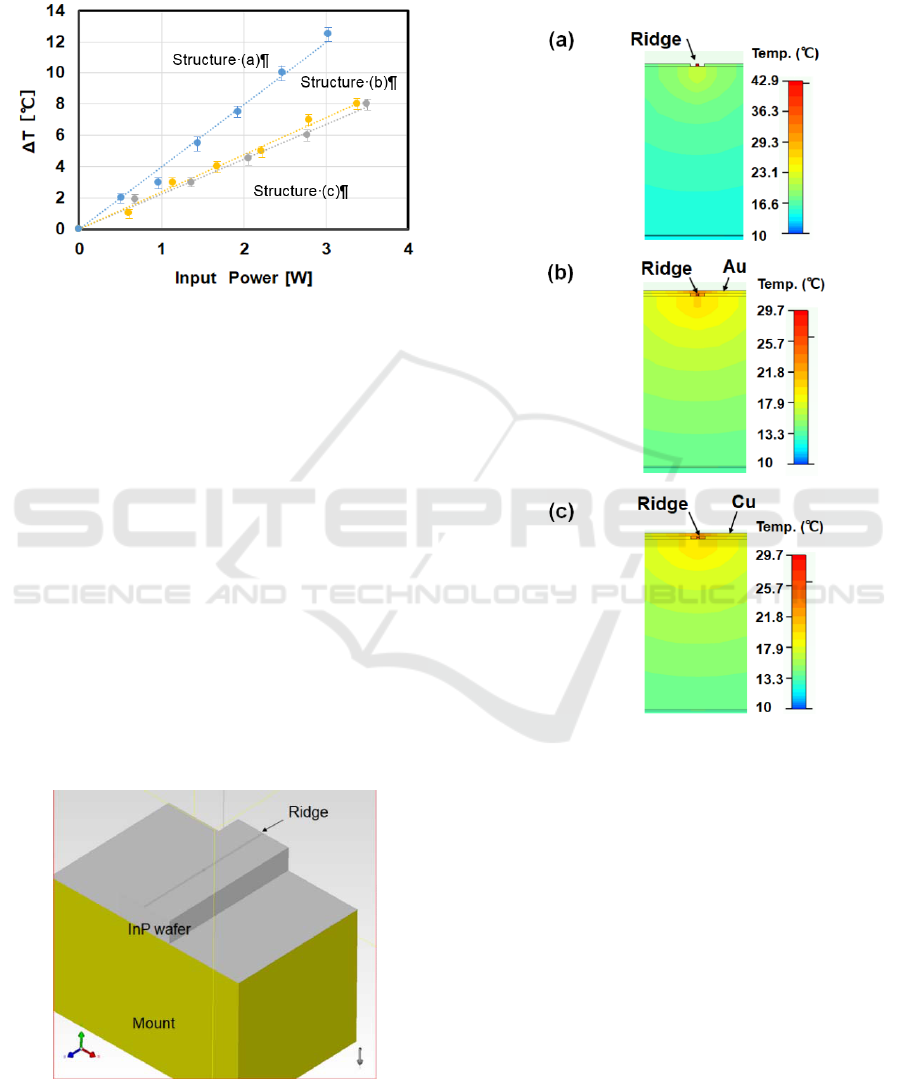
For thermal analysis inside the QCL element, a
thermal airflow analysis software FloTHERM
(Mentor Graphics Japan Co., Ltd.) was introduced to
calculate the temperature distribution in the structures
of (a), (b) and (c). 3-demensional model of the
structure (a) of is shown in Fig.5.
Assuming that the electric power applied to the
active layer in the ridge is a heating source, the
inputting powers to the active layer were changed
from 0 to 4 W. In addition, the surrounding air current
is a natural convection model in which air is heated
and rises. Because we can assume that the Cu/W
mount was cooled to 10 ℃, the temperature of Cu/W
was fixed at 10 ℃.
Figure 5: 3-Dimensional simulation model.
Figure 6 shows the calculation results. The
temperature distributions at 3 W input power are
displayed as contours. The maximum temperatures of
the ridge portion in the structures of (a), (b), and (c)
are 42.9, 29.7, and 29.7 ℃, respectively.
Figure 6: Simulation results. (A) Ridge covered with SiO
2
and thin Ti/Cu, (B) Ridge embeded with Au and (C) Ridge
embeded with Cu.
In the three-dimensional simulation, the
temperature distribution in the QCL was calculated
by changing the input to the active layer. The
temperatures in the temperature distribution were
measured at the positions of “x” and “+”
corresponding to those of Fig. 3, and the temperature
difference ΔT was obtained. Fig. 7 shows the
relationship between the input and the temperature
difference ΔT. The ΔT in the structure (a) becomes
larger than the ΔT in the structures (b) and (c). This
tendency of the ΔT coincides with that of ΔT. It is
considered that the absolute value differs because the
measurement positions of the thermos-viewer does
Thermal Analysis for Quantum Cascade Lasers using Experiments, Simulations and Structure Function Obtained by Static Measurement
305
not accurately match the measurement positions in
the calculation.
Figure 7: Temperature difference between the ridge bottom
and the bottom of the wafer (Simulation).
4 MEASUREMENT OF
THERMAL RESISTANCE AND
STRUCTURE FUNCTION BY
STATICS METHOD
Dynamic method and statics method are available for
measuring thermal resistance of semiconductor
devices. In the dynamics method, pulsed electric
power is supplied to a semiconductor device to heat
it, and the thermal resistance is measured. On the
other hand, the statics method is a method in which a
device is heated and the thermal resistance is
measured from the voltage-current characteristic
during cooling (Székely, 1997). Compared with the
dynamics method, the measurement time is short, and
it is possible to obtain highly reproducible results, and
it has been widely used as a measurement method of
thermal resistance.
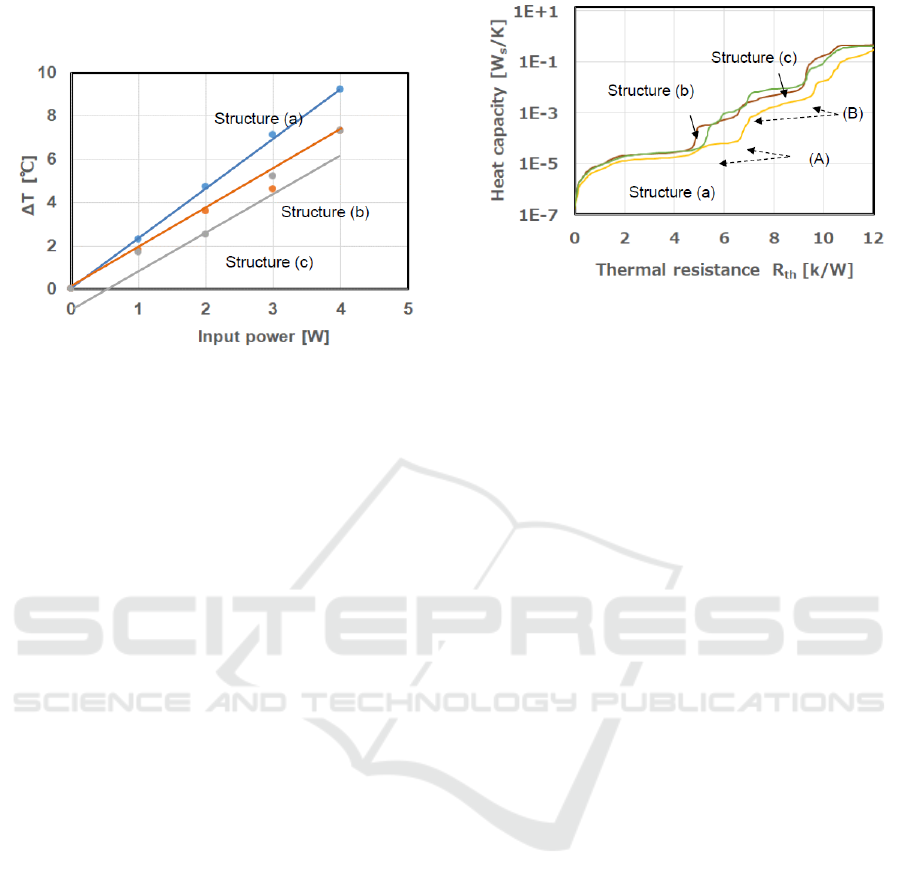
In order to measure the thermal resistance of QCL
accurately, statics method was adopted. For the
measurement, T3Ster (Siemens AG) was used. The
mounting part of the QCL device was cooled at 20 ℃
, and about 0.8 W of electric power was supplied to
the QCL device to heat it. After stopping the power
supply, the thermal resistance was calculated from the
voltage-current characteristic flowing in the device.
The measurement results are shown in Fig.8. In
the figure, the mark (A) shows the value of thermal
resistance to the periphery of the ridge. Also, the mark
(B) shows the thermal resistance value up to the InP
wafer edge. It suggests that the thermal resistance
improves by more than 2 K/W from 9.3 K/W to 6.9
K/W around the wafer edge of (B).
Figure 8: Thermal resistance vs. Heat capacity (Structure
function).
5 CONCLUSIONS
The relationship between the device structure and
heat dissipation were investigated in quantum
cascade lasers. Three types of devices were prepared
as follows. One is a device which has the ridge
covered with SiO
2
and thin Au, another is a device
which has the ridge covered with SiO
2
embedded
with Au, and the other is a device which has the ridge
covered with SiO
2
embedded with Cu.
From the results of the temperature measurement
with the thermos-viewer and the three-dimensional
thermal simulations, the effect of embedding Au and
Cu was clarified. Furthermore, the heat properties of
QCL devices were measured by the statics method
using T3Ster. As a result, the thermal resistance of the
ridge, that of InP wafer, and that of the mount were
separated from the total thermal resistance. The
improvement of thermal resistance with more than 2
K/W was attained by using Au or Cu embedding.
ACKNOWLEDGEMENTS
This work was supported by Innovative Science and
Technology Initiative for Security, ATLA, Japan.
REFERENCES
Bai, Y., Darvish, S.R., Slivken, S., Zhang, W., Evans, A.,
Nguyen, J., and Razeghi, M., 2008. Appl, Phys. Lett.,
92, 101105.
Evans, A., Darvish, S.R., Slivken, S., Nguyen, J., Bai, Y.,
and Razeghi, M., 2007. Appl. Phys. Lett., 91, 071101.
Evans, C.A., Indjin, D., Ikonic, Z., and Harrison, P., 2012,
J. Comput. Electron, 11, 137.
PHOTOPTICS 2019 - 7th International Conference on Photonics, Optics and Laser Technology
306

Faist, J., Capasso, F., Sivco, D.L., Sirtori, C., Hutchinson,
A.L., Cho, A.Y., 1994. Science, 264, 553.
Sood, A., Rowiette, J.A., Caneau, C.G., Bozorg-Graeli, E.,
Asheghi, M., and Goodeson, K.E., 2014. Appl. Phys.
Lett., 105, 051909.
Székely, V., 1997. Microelectronics Journal, 28, 277
Veerabathran, G., K., Sprengel, S., Kari, S., Andrejew, A.,
Schmelauch, H., and Amann, M., C., 2017. AIP
Advances, 7, 025208.
Thermal Analysis for Quantum Cascade Lasers using Experiments, Simulations and Structure Function Obtained by Static Measurement
307
