Securing Cargo during Transport on Roads of Different Quality

Martin Vlkovský

and Hana Vlachová

Department of Logistics, University of Defence, Kounicova 65, Brno, Czech Republic

Study Office, University of Defence, Kounicova 65, Brno, Czech Republic

Keywords: Transport Experiment, Road Safety, Cargo Securing, Shocks, Acceleration Coefficients, Statistical

Hypotheses Tests.

Abstract: The article compares the magnitude of shocks generated by the Tatra T-810 on two types of roads (high-

quality – highway and lower-quality – roads paved with granite blocks). As the primary data, sets of

acceleration coefficients in the three axes (x, y and z) were used as part of a transport experiment using a

three-axis accelerometer with a datalogger and a calibration certificate – OM-CP-ULTRASHOCK-5-CERT.

Data analysis is performed using descriptive statistics. The mean values and variations of measured

acceleration coefficients on the roads we examined are compared. The graphical comparison of the roads

studied is covered in a separate section. The results of the transport experiment show that the magnitude of

generated shocks is even higher at a lower average transport speeds on a low-quality roads. The distribution

of acceleration coefficient values also differs for both roads.

1 INTRODUCTION

Within the European Union (EU), over 76% of cargo

is transported using road transport (Fenollar-Solvay

et al., 2016). Over the last ten years (2008-2017), a

total of 147,047,868,000 tons of freight was

transported across the EU, an annual average of

14,704,787,000 tons of transported cargo

(EUROSTAT, 2018).

Due to these large volumes of cargo transported

by road, a high number of roads are overloaded.

According to the Road Transport Services Center,

established by the Ministry of Transport of the

Czech Republic, over a half of all vehicles are

overloaded during weight checks, which amount to

over 2,000 per year in the Czech Republic (CSPSD,

2014).

According to the Regional Road Administration

and Road Maintenance statistics, a single truck will

damage a road more than 10,000 passenger cars

(AKTUALNE, 2018). Cargo transport makes high

demands on road infrastructure that is more quickly

worn out (damaged). Annual maintenance is not

always able to ensure its required quality.

Quality of roadways directly affects the

magnitude of the inertial forces that affect cargo

during transport. Generally, on a damaged road,

characterized by a large amount of unevennesses

(holes, seals, etc.), higher values of acceleration

coefficients (shocks) that directly affect the

magnitude of inertial forces are assumed. On the

basis of the assumed size of inertial forces acting on

transport, it is necessary to choose appropriate

methods of securing (fastening) cargo and

evaluating the lashing capacity of the respective

fastening means.

Determining the magnitude of the inertia in the

actual transport is possible by using a suitable

measuring device (accelerometer) and the

appropriate calculation, mainly by using the

formulas from the norms, eg. EN 12195-1:2011

(UNMZ-EN 12195-1, 2011). Selected cargo

shippers and carriers use accelerometers to detect

undesirable shocks (acceleration) during shipment of

particularly fragile or otherwise sensitive goods

(dangerous goods etc.). These are, for example,

multinational companies DHL (DHL, 2018), GEIS

(GEIS, 2018) or TNT (TNT, 2018).

Exceptions do not even apply in an advanced

army, such as the United States Army, which

complements its transport and transport means

(mainly containers) with a set of measuring devices

that monitor (among others) the cargo space (SAVI

TECHNOLOGY, 2014). The temperature, relative

humidity, acceleration in individual axes, etc. are

determined in the respective transport means.

Vlkovský, M. and Vlachová, H.

Securing Cargo during Transport on Roads of Different Quality.

DOI: 10.5220/0007617900250032

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 25-32

ISBN: 978-989-758-374-2

From the point of view of inertial forces

influencing cargo, the key values of acceleration

coefficients in individual axes are primarily

influenced by the following three basic factors:

 vehicle,

 driver,

 road (Lerher, 2015 and Vlkovský et al., 2018).

In the case of a vehicle, it is also important

whether it is moving with or without cargo. The key

technical factors of the vehicle are its tires, chassis,

structure of the vehicle hull and its connection with

the chassis, including the age of the vehicle and its

individual components, etc. The driver's driving

style is a significant factor, especially the speed of

the vehicle as well as driver skills, experience and

mental condition (Vlkovský et al., 2016 and

Vlkovský and Šmerek, 2018).

The purpose of this article is to prevent problems

associated with incorrect or insufficient cargo

securing through knowledge of the transport

parameters – the roads before it starts – and thus

increase transport safety. The risks associated with

inertia forces on cargo are generally higher for

specific shipments that are carried by the military or

components of the Integrated Rescue System

(Vlkovský et al., 2018).

2 TRANSPORT EXPERIMENT

The transport experiment was carried out on two

types of roads using a Tatra T-810 6x6 (T-810) with

less than 45,000 km. The first type of highway was

the D1 highway, measured from Brno to Vyškov and

back. The second type was a lower quality transport

road (third class road); a paved road measured from

the Vyškov to Vyškov-Dědice training polygon and

back.

The transport experiment was undertaken by one

professional driver and a 3-axis accelerometer with a

datalogger and a calibration certificate – OMEGA-

OM-CP-ULTRASHOCK-5 (see the Figure 1).

A measuring range of ±5g was used to obtain the

values of the acceleration coefficients. A sampling

rate of 512 Hz was used with a record for every

second of the highest (or possibly) lowest value of

the respective acceleration coefficient in the given

axis (x, y and z) (Grzesica, 2018). The axes are

designated according the Figure 2: x – longitudinal,

y – transverse and z – vertical.

Figure 1: Mounting of the measuring device.

Figure 2: Axes designation (PRORIDICE, 2019).

The accelerometer was mounted on the steel

center frame of the vehicle body in the front of the

T-810 load compartment and the transport

experiment was carried out without any load.

Optimal climatic conditions included dry roads,

excellent visibility, absence of congestion and

rainfall. Outdoor temperature was in the range of 7-

11° C.

2.1 Methods

To accomplish a comparison of the above described

roads, as specified in section 2.2, descriptive

statistics were used and basic descriptive

characteristics were found (mean values – arithmetic

mean, modus and median, scattering, slope

coefficients and kurtosis). Comparison also includes

the detection of extreme values in individual axes

(both positive and negative). The selected values are

compared with the use of one and two-choice tests

of statistical hypotheses on the equivalence of mean

values (arithmetic mean) and variance (part 2.3).

In a separate section (2.4) a graphical

comparison of the distribution of measured values of

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

acceleration coefficients on the examined roads is

shown.

2.2 Basic Descriptive Characteristics of

Measured Data Files

The first data file (formally marked as dataset 1) was

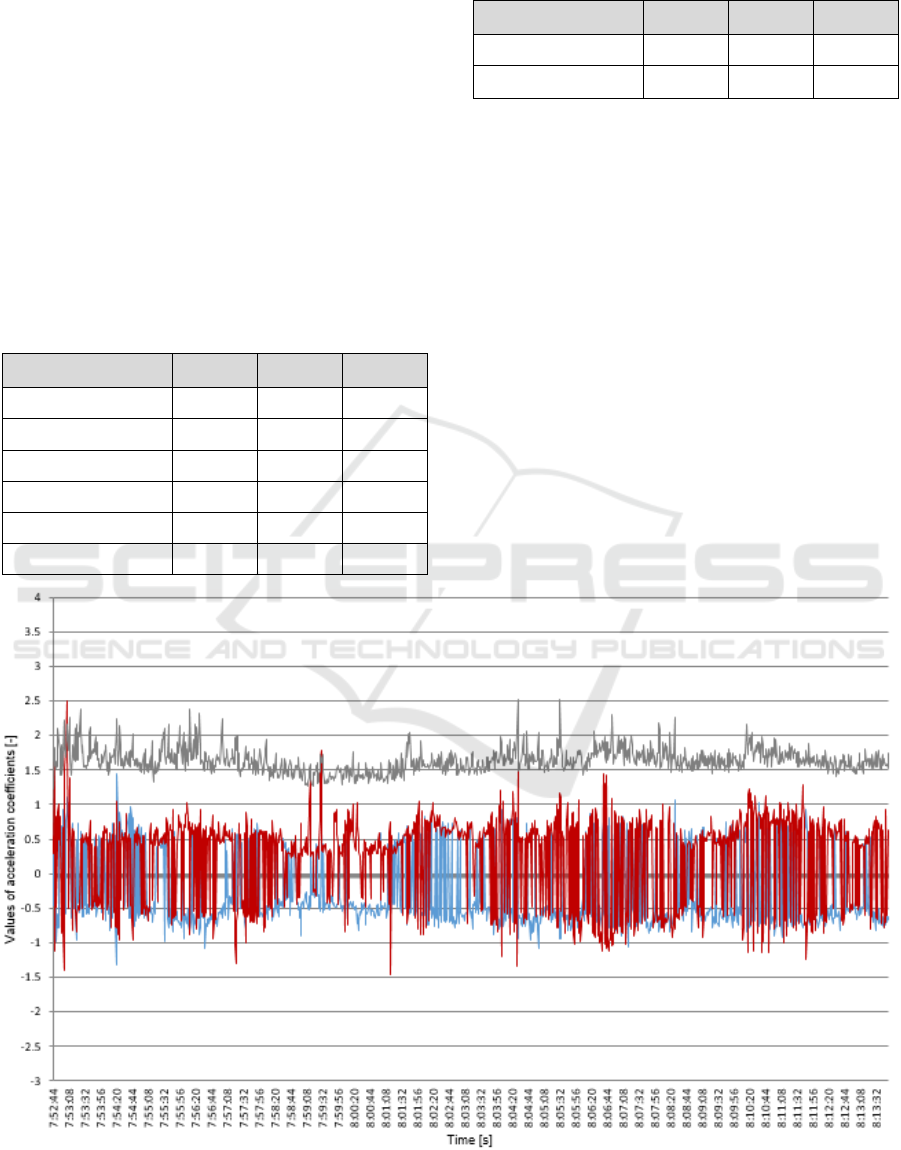
obtained on the Brno-Vyškov (highway) route (see

the Figure 3 with raw data). In a stretch of 27.0 km

long, a total of 3,804 values of acceleration

coefficients were recorded and the average vehicle

speed was 76.66 km·h

–1

. The basic descriptive

characteristics of dataset 1 as well as the extremes in

the individual axes, in both positive and negative

directions are illustrated in Tables 1 and 2.

Table 1: Dataset 1 – Basic descriptive characteristics.

Characteristics

Arithmetic Mean

–0.2953

0.2284

1.6381

Modus

–0.6100

0.5100

1.6000

Median

–0.5400

0.5000

1.6200

Variance

0.2923

0.4059

0.0304

Skewness Coeff.

1.0464

–0.5862

1.0127

Kurtosis Coeff.

–0.5327

–0.7773

2.2971

Table 2: Dataset 1 – Extremes of measured acceleration

coefficient values.

Extremes

Positive

1.4400

2.5100

1.5300

Negative

–1.3200

–1.4700

–

According to Table 1, a higher value of z-axis acuity

can be identified which is slightly elevated

(positive), while in the other two axes, the values are

less than 0. This is due, among other things, to the

displacement of the coordinate axis due to gravity

acceleration.

Z-axis scatter is also more than 13 times smaller

than the y-axis, respectively almost 10× in the x-

axis. Extremes – the highest and lowest values of the

acceleration coefficients in the individual axes are

given in Table 2.

The highest value of the acceleration coefficient

was in the y-axis where the measured value c

2.51, corresponding to 2.5 times the gravity

acceleration g.

The second data file (formally identified with

Dataset 2) was obtained on the route Vyškov – Brno

(highway). In a 27.0 km long section, a total of

4,059 values of acceleration coefficients were

recorded and the average speed of the vehicle was

Legend: blue – x axis, red – y axis, grey – z axis.

Figure 3: Dataset 1 – Raw data.

Securing Cargo during Transport on Roads of Different Quality

71.84 km·h

–1

. The basic descriptive characteristics

of Dataset 2 and the extremes in the individual axes,

in the positive and negative directions, are presented

in Tables 3 and 4.

Table 3: Dataset 2 – Basic descriptive characteristics.

Characteristics

Arithmetic Mean

–0.2530

0.2226

1.7075

Modus

–0.6500

0.6900

1.6700

Median

–0.5900

0.5700

1.6900

Variance

0.4330

0.5169

0.0291

Skewness Coeff.

0.7439

–0.5277

1.1093

Kurtosis Coeff.

–1.1524

–1.2530

5.5130

Table 4: Dataset 2 – Extremes of measured acceleration

coefficient values.

Extremes

Positive

1.6700

2.3100

1.9600

Negative

–1.3600

–1.2900

–

Table 3 shows a higher coefficient of kurtosis in

the z-axis. The highest measured value within

Dataset 2 (Table 4) was in the y-axis (c

= 2.31),

roughly equivalent to 2.3 times the gravity

acceleration g.

A third data set (formally marked with Dataset 3)

was obtained on the Vyškov – training polygon

Vyškov-Dědice (the road paved with granite blocks).

Over a 4.3 km long section, a total of 1,182

acceleration coefficient values were recorded and

the average vehicle speed was 39.29 km·h

–1

. The

basic descriptive characteristics of Dataset 3 and the

extremes in the individual axes, in the positive and

negative directions, are presented in Tables 5 and 6.

Table 5: Dataset 3 – Basic descriptive characteristics.

Characteristics

Arithmetic Mean

–0.1904

0.0730

1.9924

Modus

0.4500

0.4100

1.6000

Median

–0.5150

0.4500

1.9500

Variance

0.7927

1.0016

0.1784

Skewness Coeff.

0.1441

–0.2296

0.9992

Kurtosis Coeff.

–1.1163

–1.0862

1.9430

Table 6: Dataset 3 – Extremes of measured acceleration

coefficient values.

Extremes

Positive

1.8300

2.2800

3.1100

Negative

–3.0800

–2.4400

–

Table 5 identified higher kurtosis in the z-axis.

The highest measured value within Dataset 2 (Table

6) was in the z axis (c

= 3.11), roughly equivalent to

more than 3.1 times the gravity acceleration g.

A fourth data set (formally marked with Dataset

4) was obtained on the training polygon Vyškov-

Dědice – Vyškov (road paved with granite blocks).

Along a 4.3 km long section, a total of 1,203

acceleration coefficient values were recorded and

the average speed of the vehicle was 38.60 km·h

–1

The basic descriptive characteristics of Dataset 4 and

extremes in individual axes, positive and negative,

are given in Tables 7 and 8.

Table 7 shows the difference in variance of the z

axis, which is significantly lower than that of the

other two axes. The highest measured is in the y-axis

= 2.70), which corresponds to 2.7 times the

gravitational acceleration g.

Table 7: Dataset 4 – Basic descriptive characteristics.

Characteristics

Arithmetic Mean

–0.4425

0.0562

2.0047

Modus

–0.8000

0.8300

2.0000

Median

–0.7300

0.4500

1.9500

Variance

0.7532

1.1867

0.1742

Skewness Coeff.

0.9505

0.0755

0.8825

Kurtosis Coeff.

–0.1423

–1.1141

0.7597

Table 8: Dataset 4 – Extremes of measured acceleration

coefficient values.

Extremes

Positive

1.9700

2.7000

2.6300

Negative

–2.3000

–2.4200

–

2.3 Statistical Hypotheses Tests

For the purpose of comparing a high-quality road

(highway) with a poor quality road (paved with

granite blocks), partial zero and alternative

hypotheses were formulated to compare the

individual datasets (d

– d

) in pairs. Two single-

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

choice tests of partial statistical hypotheses were

used for testing:

 mean values compliance test,

 variances compliance test.

The zero hypothesis is assumed to be valid (resp.

partial zero hypotheses for the respective dataset

pairs) concerning the parity of the relevant dataset

parameters, for the mean values

µ = µ

, resp.

variances σ

= σ

. For an alternative hypothesis in

the double – side test applies µ ≠ µ

, resp. σ

≠ σ

Subsequently, one-sided tests are performed to

determine whether µ ˃ µ

or µ ˂ µ

, resp. σ

˃ σ

˂ σ

For test purposes, a critical value range was

constructed and a test criterion value calculated.

To test the hypothesis an appropriate statistic T =

T(x

, x

, . . . , x

) is used, the so-called test criterion

that has, when the zero hypothesis is valid, known

probability distribution (Student's or t distribution).

The area of these values of statistics is divided

into two disjoint fields:

 W

1−α

is the domain of accepting a zero

hypothesis – a set of values that testify in

favor of a zero hypothesis,

 W

is a critical domain (domain of zero

hypothesis rejection) – that testify in favor of

an alternative hypothesis.

For example, for the hypothesis test of the mean

value µ of the normal distribution zero hypothesis: µ

= µ

→ alternative hypothesis: µ > µ

will be critical

domain W

= {t,t ≥ t

1−α

(ν)}, where µ

is the expected

value of the parameter µ, t is the value of the test

criterion and t

1−α

(ν) is quantile of Student's

distribution – so-called critical value (Neubauer, et

al., 2016). Tests for variances are performed

analogously. For all tests, the level of significance

chosen was α = 0.05.

On the basis of these tests, the individual partial

zero hypotheses were verified, from which the

relevant conclusions are subsequently formulated.

A normality test was performed prior to

statistical analysis. Normality was verified

graphically using Q-Q plots (Johnson and Wichern,

2007), including the determination of skewness and

kurtosis coefficients. Minor deviations from

normality were found, especially when testing the

kurtosis of distribution. However, the graphical

analysis did not show significant deviations from

normality, theoretical quantil and the corresponding

empirical quantils were approximately on a straight

line (Vlkovský et al., 2017).

The Stat1 software tool was used to perform

statistical hypothesis tests. (Neubauer et al., 2016).

In individual partial tests (Table 9), the

hypotheses on equivalence of the mean values are

always tested (arithmetic means in absolute value)

i(abs)

for given values of acceleration coefficients in

individual axes (c

, c

and c

). Analogously,

variances in acceleration coefficients in individual

axes are tested. The aim of the tests is to find out

whether the individual data sets (d

– d

)

significantly statistically differ at the α = 0.05 level

of significance.

Table 9 shows that, using a mean value

(arithmetic averages in absolute values), there is a

statistically significant difference between individual

datasets with the exception of d

– d

. Where it

shows the similarities of both files found on the

same road in the opposite direction. A statistically

significant difference between d

and d

was shown

only in the axes x and y.

Table 9: Comparison of mean values (in absolute values)

of acceleration coefficients in all three axes.

Characteristics

i(abs)

Coef.

Dataset

–d

<µ

–d

<µ

–d

<µ

–d

<µ

–d

<µ

–d

<µ

Note: NO indicates the non-demonstration of a

statistically significant difference between the monitored

data files at the level of significance α = 0.05. Greens are

marked with statistically significant differences

demonstrated for all three axes.

From partial hypothesis tests it follows that, from

the point of view of the mean values (arithmetic

averages in absolute values), there is a statistically

significant difference at the level of significance α =

0.05 between a high-quality road (highway) and a

lower quality road (paved with granite blocks). The

conclusion is valid in both directions. Because it is

valid, it means that values are statistically

significantly lower (in all three axes) for datasets 1

and 2 compared to datasets 3 and 4.

Securing Cargo during Transport on Roads of Different Quality

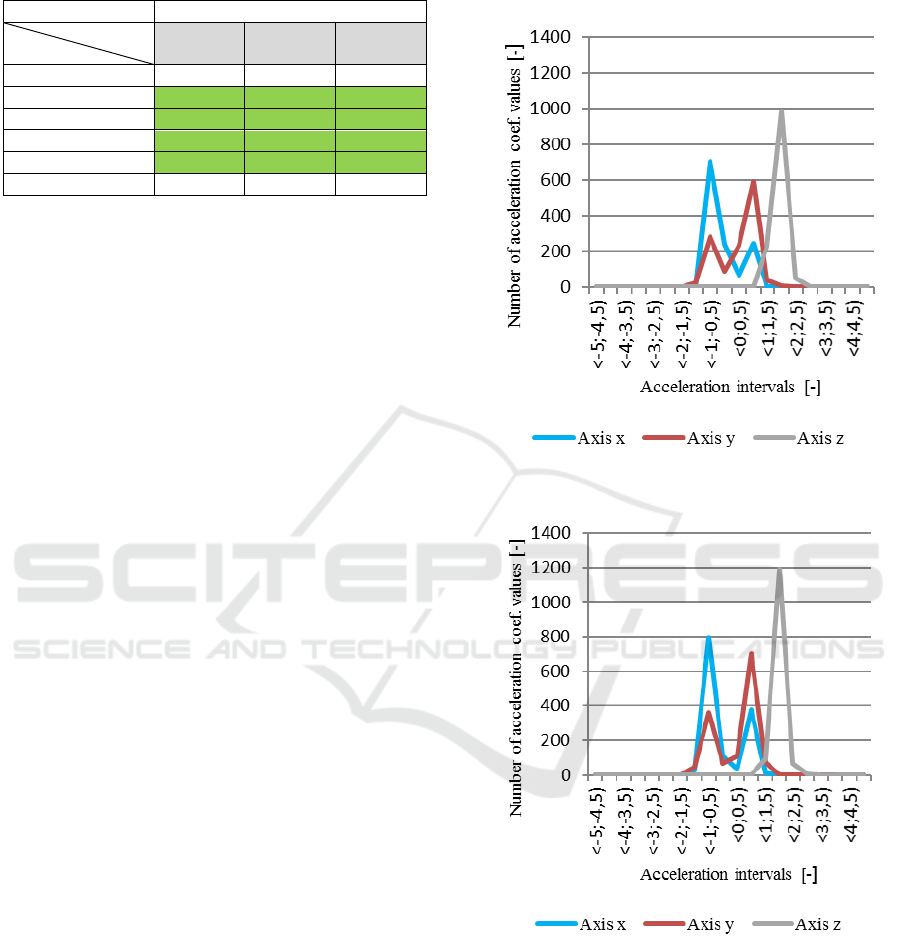
Table 10: Comparison of variances acceleration

coefficients across all three axes.

Characteristics

Coef.

Dataset

–d

<σ

–d

<σ

–d

<σ

–d

<σ

–d

<σ

–d

Note: NO indicates the non-demonstration of a

statistically significant difference between the monitored

data files at the level of significance α = 0.05. Greens are

marked with statistically significant differences

demonstrated for all three axes.

Table 10 shows that, by using variances, there is

a statistically significant difference between

individual datasets with the exception of d

and d

respectively d

and d

. Where the similarity can be

seen in both pairs of files found on the same traffic

path in the opposite direction. Statistically

significant difference d

– d

is only shown in the

axes x and y. Between the d

– d

datasets a

statistically significant difference was not

demonstrated in either of the axes

Partial hypothesis tests show that, from the point

of view of the variances, there is a statistically

significant difference in the level of significance α =

0.05 between a high-quality transport road

(highway) and a lower quality road (paved with

granite blocks). The conclusion is valid in both

directions, because the results show that variances

are statistically significantly lower (in all three axes)

for dataset 1 and 2 compared to dataset 3 and 4. For

some axes, it can be assumed that a statistically

significant difference between the pairs of the

dataset with a higher test strength (at the level of

significance α = 0.01) would be demonstrated.

2.4 Graphical Comparison of Roads

The individual datasets (d

– d

) can be viewed in

terms of the number of values of the acceleration

coefficients in the individual axes that fall within the

respective intervals. Figures 4 – 7 show the

frequencies of acceleration coefficients in individual

axes, divided into intervals of multiples of

gravitational acceleration (0.5g).

It can be seen from Figures 4 – 7 that the

character of the distribution of values at individual

intervals differs significantly between the tested

roads. Although the frequencies of the acceleration

coefficients differ, it is possible to illustrate the

different character of the high-quality road

(highway) and the lower quality road (road paved

with granite blocks).

Figure 4: Dataset 1 – Frequency of acceleration

coefficients.

Figure 5: Dataset 2 – Frequency of acceleration

coefficients.

This conclusion can be demonstrated by the

number of intervals in which the values of the

coefficients of acceleration in the individual axes

fall. While for dataset 1 it is 6 in the x-axis, 8 in the

y-axis and 4 in the z-axis, respectively 7, 8 and 4 for

dataset 2, on lower quality road it is for the dataset 3

in the x-axis 10, in the y-axis 10 and in the z-axis 7,

respectively 9, 11 and 6 for dataset 4.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

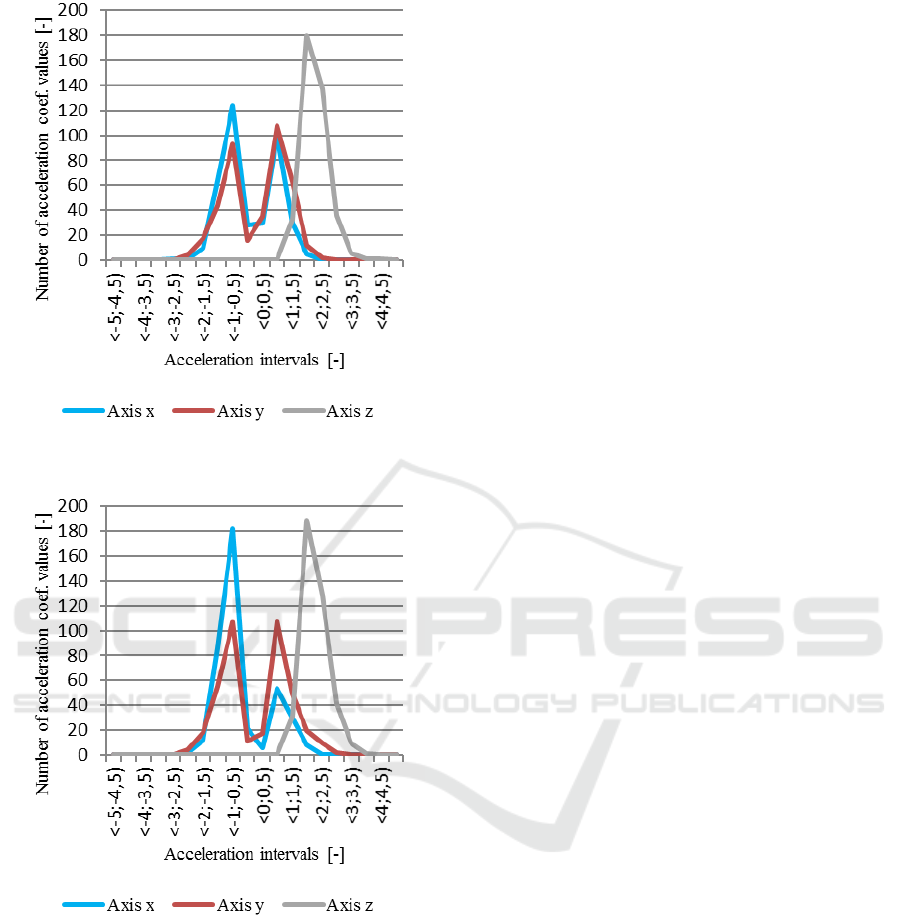
Figure 6: Dataset 3 – Frequency of acceleration

coefficients.

Figure 7: Dataset 4 – Frequency of acceleration

coefficients.

3 RESULTS AND DISCUSSION

On the basis of these comparisons, it is obvious that

even at a lower average speed (about half) there is a

statistically significant difference between the tested

roads at the significance level α = 0.05. This

conclusion applies to both tested basic descriptive

characteristics (mean values in absolute values as

well as variance of values of acceleration

coefficients in all three axes).

It can be concluded that the T-810 vehicle

generates on lower quality road (third class road) in

average greater shocks (higher values of acceleration

coefficients) even at about half the average transport

speed. At higher speeds on a lower quality road,

even greater differences in shocks can be expected.

Generated shocks can be quantified as inertial forces

that act not only on the cargo but also on the vehicle

and the driver.

The graphical comparisons show a different

distribution of values for each type of road.

Primarily the graphical view of their variance in

single intervals of 0.5g differs significantly.

Whereas for dataset 1 and 2 there is an average

variance at 6 intervals, for datasets 3 and 4 it is

almost at 9 intervals.

4 CONCLUSIONS

The shocks generated by trucks significantly

influence the life of the road and the vehicle. In the

short term, there is a key impact on the cargo, that

can be released or damaged by the effect of the

shocks (the magnitude of the acceleration

coefficients exceeding normative values according

to EN 12195-1:2011). In addition, the unfastening of

the cargo may carry secondary risks such as damage

to the vehicle, other technical means on the vehicle,

cause a traffic accident involving personal injury,

damage to the environment or other property

damage (Vlkovský et al., 2017).

The results of the analysis presented by the

article can be mainly used to optimize the fastening

of cargo by choosing a more suitable fastening

system, or fasteners with the corresponding lashing

capacity. Lashing capacity must correspond to actual

shocks (the magnitude of the acceleration

coefficients, respectively resulting inertial forces),

rather than simply theoretical assumptions of the

standards.

A specific area of transport is the shipping of

dangerous items, especially those that are directly

affected by the shocks. These primarily include

various types of explosives (Vlkovský and Rak,

2017), that are transported by the army using their

own or contracted vehicles. Transportation of

various fragile cargoes can also be considered as

problematic in this respect. Despite the use of

special packaging and vehicles for transport, types

of cargo more vulnerable to the negative effects of

shocks are mentioned.

In further research, the spectral analysis enable to

transform the data (signal) of the time series into a

Securing Cargo during Transport on Roads of Different Quality

frequency domain, which allows examination of

other aspects of transport – cargo securing (Grzesica

and Wiecek, 2016).

ACKNOWLEDGEMENTS

The paper was written with the support of the project

of long-term strategy of organization development:

ROZVOLOG: Development of Capabilities and

Sustainability of Logistics Support (DZRO

ROZVOLOG 2016–2020), funded by the Ministry

of Defense of the Czech Republic.

REFERENCES

Fenollar-Solvay, A. et al., 2016. New Intermodal Loading

Units in the European Transport Market. In

Automation, Communication and Cybernetics in

Science and Engineering. Springer. DOI: 10.1007/9

78-3-319-42620-4_52

EUROPEAN COMMISION – EUROSTAT. Ec.europa.eu.

(2018). Goods Transport by Road. [online] Available

at: http://ec.europa.eu/eurostat/tgm/table.do?tab=table

&init=1&language=en&pcode=ttr00005&plugin=1

[Accessed 12 Nov. 2018]

CENTER OF ROAD TRANSPORT SERVICES.

Cspsd.cz. (2014) [online]. Mobile Expert Units.

Available at: http://www.cspsd.cz/mobilni-expertni-

jednotky [Accessed 10 Nov. 2018]

AKTULANE – AUTO. Aktualne.cz (2018) [online]. One

Overloaded Truck Destroys the Road More than

10,000 Cars. Available at: https://zpravy.aktualne.cz/

ekonomika/auto/jeden-pretizeny-kamion-znici-silnici-

vic-nez-10tisic-osobnic/r~ed413f3a900011 e89f80ac1f

6220ee8/?redirected=1535978107 [Accessed 25 Sep.

2018]

EN 12195-1, 2011. Load Restraining on Road Vehicles –

Safety – Part 1: Calculation of Securing Forces.

UNMZ.

DHL. Dhl.com. (2018) [online]. Transportation

Managements. Available at: http://www.dh l.com/en/

logistics/industry_sector_solutions/consumer_logistics

/transportation_management.html#.WtiCQtRua70

[Accessed 05 Nov. 2018]

GEIS. Geis-group.com. (2018) [online]. Global Logistics.

[online]. Available at: https://www.geis-group.com/en

/ltl-and-ftl [Accessed 06 Nov. 2018]

TNT. Analysis.tu-auto.com. (2018) [online]. Express and

Fleet Tlematics. Available at: http://analysis.tu-

auto.com/fleet-and-asset-management/tnt-express-and-

fleet-telematics [Accessed 06 Nov. 2018]

SAVI TECHNOLOGY. Savi.com. (2018) [online]. Get

Better Asset Data Using Proven Sensor and Reader

Hardware. Available at: http://www.savi.com/wp-cont

ent/ uploads/Hardware_Overview_Final.pdf [Accessed

01 Nov. 2018]

Lerher, T., 2015. Cargo Securing in Road Transport

Using Restraining Method with Top-over Lashing.

New York: Nova. ISBN 978-1-61122-002-5.

Vlkovský, M. et al., 2018. Cargo Securing and its

Economic Consequences. In Transport Means 2018 –

Proceedings of the 22nd International Scientific

Conference Part I. Kaunas University of Technology.

ISSN 1822-296X.

Vlkovský, M. et al., 2016. The Cargo Securing based on

European Standards and its Applicability in Off-road

Transport Conditions. In ICTTE Belgrade 2016 –

Proceedings of the Third International Conference on

Traffic and Transport Engineering. Transport Means

2018 – Proceedings of the 22nd International

Scientific Conference Part I. City Net Scientific

Research Center Ltd. ISBN 978-86-916153-3-8.

Vlkovský, M., Šmerek, M., 2018. Statistical Analysis of

Driving Style and its Effect on Cargo Securing. In:

ICTTE Belgrade 2018 – Proceedings of the Fourth

International Conference on Traffic and Transport

Engineering. City Net Scientific Research Center Ltd.

ISBN 978-86-916153-X-X.

Vlkovský, M. et al., 2018. Wavelet Based Analysis of

Truck Vibrations during Off-road Transportation. In:

VETOMAC XIV – The 14th International Conference

on Vibration Engineering and Technology of

Machinery. MATEC Web of Conferences.

Grzesica, D. et al., 2018. Measurement and Analysis of

Truck Vibrations during Off-road Transportation. In:

VETOMAC XIV – The 14th International Conference

on Vibration Engineering and Technology of

Machinery. MATEC Web of Conferences.

PRORIDICE. Proridice.eu. (2019) [online]. Cargo

Securing – Basic Information. Available at:

http://soubory.proridice.eu/naklady/upevneni_nakladu

CZ.pdf [Accessed 10 Jan. 2019]

Neubauer, J. et al., 2016. Principles of Statistics:

Applications in Technical and Economic Disciplines.

Grada. Prague, 1

edition. ISBN 978-80-247-5786-5.

Johnson, R. A., Wichern, D. W., 2007. Applied

multivariate Statistical Analysis. Prentice-Hall

International. ISBN 0130418072.

Vlkovský, M., et al., 2017. Cargo Securing During

Transport Depending on the Type of a Road. In

WMCAUS 2017 IOP Conference Series: Materials

Science and Engineering. IOP Publishing Ltd. ISSN

1757-8981.

Vlkovský, M., et al., 2017. Cargo Securing During

Transportation – Using Extreme Values. In Applied

Technical Sciences and Advanced Military Tech-

nologies. Nicolae Balcescu Land Forces Academy.

ISSN 1843-682X. ISBN 978-973-153-275-2.

Vlkovský, M., Rak, L., 2017. Cargo Securing in Selected

Vehicles and Transport of Explosives. Perner's

Contacts, 2017, Vol. XII, No. 3. ISSN 1801-674X.

Grzesica, D., Wiecek, P., 2016. Advanced Forecasting

Methods Based on Spectral Analysis. In WMCAUS

2016: Procedia Engineering. Elsevier. ISSN 1877-

7058.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems