Fuzzy Estimation of Link Travel Time from a Digital Elevation Model

and Road Hierarchy Level

J. St

otzer, S. Wursthorn and S. Keller

Institute of Photogrammetry and Remote Sensing, Karlsruhe Institute of Technology, Germany

Keywords:

OpenStreetMap, Link Travel Time, Digital Elevation Model, Fuzzy Control System, Routing.

Abstract:

Link travel time is crucial for ﬁnding the fastest path in a road network which is an issue in many ﬁelds

of research. Readily available data sources like OpenStreetMap (OSM) often lack information about the

maximum speed of a road which is needed to calculate link travel time. In rural regions, the average speed

of a road depends mainly on two parameters: slope and road quality. In this paper, we develop a fuzzy

control system (FCS) which estimates link travel time based on these two input parameters. The OSM road

network and a digital elevation model (DEM) serve as free-to-use and worldwide available input data. Google

Directions API data provides a reference for the link travel time. The setup of the FCS as well as its tuning and

validation is described in detail. Furthermore, two approaches to derive slope from a DEM are presented and

compared. The FCS is applied exemplary for the BioB

ıo region in central Chile. The results of the case study

reveal the potential of this approach. Link travel times are estimated by the FCS with an R

of at least 87.8 %.

In future work, the FCS can be designed with more input parameters to achieve an even better performance.

1 INTRODUCTION

Finding the fastest path in a road network is important

for many applications such as route planning, disaster

risk management or transport of goods. To calculate

the fastest path, an associated link travel time is as-

signed to every edge in the road network. The link

travel time is the average time a vehicle spends trav-

elling an edge in the road network Stanojevic et al.

(2018). Especially in studies on critical road infras-

tructure and accessibility, link travel time often serves

as a cost factor for the road network Knoop et al.

(2012); Li et al. (2011); Scott et al. (2006).

Many of these approaches use OpenStreetMap

(OSM) data. The OSM project provides free road

network data with global coverage. OSM data is col-

lected by volunteers worldwide and can be edited by

anyone. The representation of the road network in

OSM is more than 80 % complete Barrington-Leigh

and Millard-Ball (2017). Furthermore, 40 % of coun-

tries worldwide have a fully mapped road network.

Many approaches using OSM data raised the question

of data quality which caused a number of investiga-

tions on that topic. To summarize the results, OSM

can be highly accurate and complete and in some

regions even better than commercial or administra-

tive datasets Cipeluch et al. (2010); Girres and Touya

(2010); Haklay (2010); Neis et al. (2011); Jackson

et al. (2013); Dorn et al. (2015); Demetriou (2016).

Even in some developing countries the completeness

of the road network is high at a national level Ludwig

et al. (2011); Mahabir et al. (2017).

While the quality of the OSM road network it-

self is satisfying for most approaches, routing appli-

cations need additional metadata. Although the possi-

bility to include maximum speed information in OSM

is given, most roads lack this information. Figure 1

shows the proportion of the total length of the upper

level roads (deﬁned in Table 1) with maximum speed

information per country. Worldwide, only 7.5 % of all

road elements in OSM feature a maximum speed in-

formation. However, to compute link travel time and

consequently fastest paths, speed information for ev-

ery edge in the road network is crucial.

The inﬂuencing factors on link travel time in ur-

ban and in rural areas differ a lot. While trafﬁc, turn

restrictions, one way streets and trafﬁc signals have

a huge impact on travel time in the city, other fac-

tors dominate in rural areas. Especially in developing

countries, the road quality has a considerable impact

on the link travel time. Asphalted roads allow for a

higher velocity than unsealed gravel or mud roads.

Also, the wider a road is and the more lanes it has,

the faster a vehicle can drive. Another big inﬂuenc-

Stötzer, J., Wursthorn, S. and Keller, S.

Fuzzy Estimation of Link Travel Time from a Digital Elevation Model and Road Hierarchy Level.

DOI: 10.5220/0007655800150025

In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 15-25

ISBN: 978-989-758-371-1

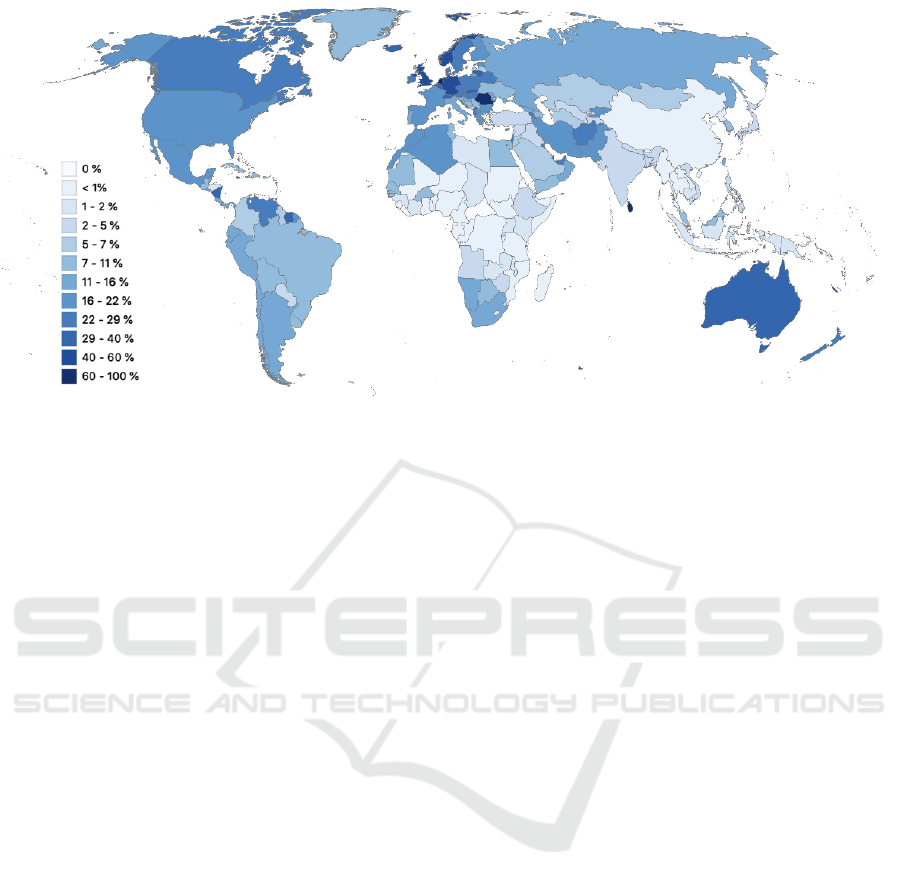
Figure 1: Proportion of the total length of all roads (road classes in Table 1) with maximum speed information in Open-

StreetMap (maxspeed tag) per country. Only 7.5 % of all road elements stored in the OSM world dataset have information on

maximum speed.

ing factor is the topography of the terrain Collischonn

and Pilar (2000). The slope of a road limits the driv-

ing speed, both by an increase in sinuosity and by the

slope itself.

Many studies and routing applications rely on

ﬁxed speed proﬁles for every road class deﬁned by

various input parameters. This leads to jumps at the

class borders. A fuzzy control system (FCS) is able

to fuzzify these input parameters and provides a more

continuous, nonlinear output. Furthermore, as it is

based on expert knowledge, it does not rely on nonex-

istent reference data to learn its behaviour.

Focusing on rural road networks, in this paper we

develop a FCS to estimate link travel time from two

input parameters: road hierarchy level and slope. The

OSM road network and SRTM (Shuttle Radar Topog-

raphy Mission) data serve as input data for the FCS.

We use the Google Directions API (GD-API) as ref-

erence data to tune and to validate the FCS. Two ap-

proaches to derive road slope from a digital elevation

model (DEM) are presented. The FCS is set up with

membership functions for the input parameters slope

and hierarchy level and for the output parameter ve-

locity. Then, it is tuned and validated with GD-API

data. A case study is performed in the BioB

ıo region

in Chile.

The main contributions of this paper are summarized

in the following:

• development of a FCS with slope and hierarchy

level as input and velocity as output parameters;

• validation of the developed concept with GD-API

data;

• enrichment of the rural OSM road network with

estimated link travel times;

• usage of open source and worldwide available

data (OSM, SRTM);

• exemplary case study for the BioB

ıo region in

Chile.

In this paper, we ﬁrst provide an overview of the

related work on link travel time in OSM in Section 2.1

and introduce the concept of Fuzzy Control in Sec-

tion 2.2. The input and reference datasets are de-

scribed in Section 3. In Section 4.1 two approaches

to calculate slope are presented. Then, the setting

up, tuning and validation of the FCS is explained in

Section 4.2. A description of the case study (Sec-

tion 5.1), the results (Section 5.2) and the discussion

(Section 5.3) are presented. Finally, a conclusion and

an outlook are given in Section 6.

2 RELATED WORK

In this section, we brieﬂy introduce the related work

on two topics. First, we investigate how link travel

time is calculated in other approaches that rely on

OSM data. Then, we introduce the concept of Fuzzy

Control, its advantages and how other studies apply

this concept.

2.1 Link Travel Time in OSM

Many routing applications exist that compute fastest

paths, and consequently link travel time, and base on

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

OSM data. Popular examples are the OpenRouteSer-

vice ORS (2018), the Open Source Routing Machine

(OSRM) Luxen and Vetter (2011), the OpenTripPlan-

ner OTP (2018) and YOURS YOURS (2018). The

latter three are open source applications and use the

maximum speed information in OSM to calculate link

travel time if available. If not, the OSM Wiki OSM

Wiki (2016) contains default speed limits for some

countries (24 countries worldwide) which are pro-

cessed and applied by these routing applications. The

applications also include other metadata like the road

type and the number of lanes (if available) to derive

ﬁxed speed proﬁles for every road class. The algo-

rithm for the OpenRouteService is not accessible by

public. But it seems more complex than the other

routing applications as it provides additional infor-

mation like the slope and type of a route. However,

like many commercial routing applications such as

Google Maps or Bing Maps the exact calculation is

not transparent.

Few studies address the issue to derive link travel

time from the OSM road network. Stanojevic et al.

(2018) present a methodology to calculate link travel

times based on origin-destination and timestamp in-

formation generated by a taxi ﬂeet and OSM data.

They estimate travel times in urban regions with 60 %

lower errors than OSRM. A lot of related work con-

centrates on urban regions and how to improve the es-

timation of travel time in trafﬁced networks. Steiger

et al. (2016) include real-time trafﬁc data into the

OpenRouteService application.

As mentioned in Section 1, the important factors

for routing in urban and rural areas differ consider-

ably. In the design standards of Asian highway routes,

the assigned maximum speed of a road in a rural re-

gion is directly dependent on the slope of the ter-

rain Behera (2008). Brabyn and Skelly (2001) model

access to public hospitals and calculate shortest and

fastest paths. To estimate the link travel time, they

consider if the road is inside or outside an urban area,

the number of lanes and the sinuosity of a road. The

sinuosity of a road is calculated with a sinuosity in-

dex. They categorize the roads by these factors and

assign ﬁxed velocities for every combination.

This study aims at ﬁlling some of the existent gaps

in the related work. Most routing applications with

OSM focus more on the city than the rural areas and

only include country wide speed limits in their travel

time calculation. Few studies focus on the calculation

of link travel time. The ones that do, rely on self-

collected or commercial datasets. To our knowledge,

a fuzzy control system has never been applied to esti-

mate link travel time with different parameters.

2.2 Fuzzy Control Systems

FCSs work on linguistic terms and partial member-

ships which are able to express fuzziness. A FCS

takes crisp input values and fuzziﬁes them with the

help of membership functions. In a second step, a rule

base provides the basis for the inference mechanism.

A defuzziﬁcation generates crisp and continuous out-

put values.

The idea of Fuzzy Control was ﬁrst introduced by

Mamdani and Assilian (1975) for a steam engine and

boiler combination. Since then, Fuzzy Control has

been applied successfully in various research areas:

in the environmental research e.g. for ﬂood simulation

Wang et al. (2011), in remote sensing e.g. for classi-

ﬁcation of multispectral data Shackelford and Davis

(2003) or in analytic chemistry Hayward and David-

son (2003). Das and Winter (2018) employ fuzzy

logic to detect the transport mode in an urban envi-

ronment.

Fuzzy Control allows for many input and many

output parameters. Such parameters can be combined

in an if-then rule Jantzen (2007). The two great-

est strengths of fuzzy control are the ability to rea-

son with uncertainty and its utilization in complex ill-

deﬁned processes without much knowledge of their

underlying dynamics Mahmoud (2018).

3 DATASETS

To create and evaluate a FCS, both input and reference

data are required. The input dataset consists of two

datasets: OSM and SRTM. The reference data for the

Fuzzy Control System is provided by the GD-API. In

the following section the input and reference data are

described.

3.1 Input Data

OpenStreetMap road data includes a hierarchic clas-

siﬁcation of the road network that is described in Ta-

ble 1. The mentioned road classes and their respec-

tive link roads (meaning roads that lead to or from

the respective road) build up the road network. Other

existing road classes, such as residential and service

roads or special road types like living streets, are not

considered.

The Shuttle Radar Topography Mission was

a joint mission by National Imagery and Mapping

Agency and the National Aeronautics and Space Ad-

ministration (NASA) to collect an open source global

elevation dataset. We use the SRTM void-ﬁlled, 1 arc-

Fuzzy Estimation of Link Travel Time from a Digital Elevation Model and Road Hierarchy Level

Table 1: Road Classes in the OSM road network.

Road Class Description

Motorway Restricted access, major divided

highway.

Trunk Most important roads in a coun-

try’s system that are not motor-

ways.

Primary Major highways, linking large

towns.

Secondary Highways, not part of a major

route, form a link in the national

route network, often link towns.

Tertiary Connect smaller settlements and

minor streets to more major

roads.

Unclassiﬁed Minor public roads, lowest level

of the network, often link vil-

lages and hamlets.

second global data NASA and USGS (2013) with a

resolution of approximately 30 m.

Due to this resolution, it has to be taken into ac-

count that one pixel of the SRTM raster may be the

average of the road itself as well as possible hills be-

side that road. Therefore, we consider the slope of the

surrounding terrain, which is, in most cases, higher

than the actual road slope.

3.2 Reference Data

The Google Directions API is a service that calcu-

lates routing directions and travel times between lo-

cations. GD-API data includes the distance in meter,

the travel time in seconds with and without trafﬁc at a

given time and the coordinates of the points on a road

closest to the input point coordinates.

The GD-API relies on Google Maps and its un-

derlying road and trafﬁc data. The quality of Google

Maps data is difﬁcult to assess, especially in develop-

ing countries. During our studies, both roads that ex-

ist in OSM and not Google Maps and vice versa have

been detected. Cipeluch et al. (2010) compare the ac-

curacy of Bing Maps, OSM data and Google Maps

data in Ireland and their results support our observa-

tions. They found that although some areas are better

served by one data source than by the others, no sin-

gle data source proves to have better overall coverage.

As for the travel time and trafﬁc data, there is no data

available to evaluate the quality of Google Maps. We

employ GD-API travel time as reference data while

keeping in mind that this might, in some cases, be un-

true.

The GD-API data is split into a dataset for tuning

the model and a dataset used to validate the model.

The tuning subset contains about 1000 roads and is

randomly selected to display a representative subset

of the complete dataset. The representative tuning

subset contains the same kilometer percentage of ev-

ery OSM road class like the entire dataset. The vali-

dation subset excludes the data used to tune the subset

and consists of 5000 representative roads.

4 METHODS

This section is divided in two parts. First, two ap-

proaches to derive road slope from a DEM are pre-

sented. Afterwards a FCS is set up, tuned and vali-

dated. The road slope value calculated in the ﬁrst part

of the sections serves as input for the FCS in the sec-

ond part.

4.1 Slope Calculation

We compare two approaches to derive the slope of the

road from the DEM. As mentioned in Section 3 both

approaches calculate a mix of road slope and terrain

slope rather than the exact road slope due to the reso-

lution of the DEM dataset. With this in mind we refer

to the results as road slope in the following.

In the ﬁrst approach, referred to as Slope Ap-

proach 1 (SA-1), a slope percentage raster is created

from the original DEM by applying the Horn algo-

Figure 2: Schema of the SA-2 to calculate road slope directly of the DEM. The numbers of the grid cell symbolize the hight

values of the terrain (in meter). In the equation length means the road segment length.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

rithm Horn (1981). Then, the OSM road network is

overlaid with the slope raster. Every road segment in-

tersects multiple pixels of the slope raster. The aver-

age of all intersecting pixels is assigned as road slope

value to the road segment.

The second approach is herein referred to as Slope

Approach 2 (SA-2) and is visualized in Figure 2.

First, the OSM road network is overlaid with the

DEM raster. Every road segment is cut in smaller

pieces by the 30 m raster pixels of the DEM. Then, the

height difference of every road segment to the road

segment before is calculated. The absolute value of

these differences along the original road segment is

summed up. Finally, the slope of the road in percent

Crisp Input

Fuzzification

(Membership functions)

Inference

mechanism

Rule

base

Defuzzification

Crisp Output

Fuzzy controller

Hierarchy level

& Slope

Velocity

Figure 4: Schema of the Fuzzy Control System.

is calculated according to the equation in the last step

of Figure 2.

4.2 Developing a Fuzzy Control System

We develop a FCS that calculates the velocity with the

two road parameters hierarchy level and road slope.

In the following section, a methodology to construct,

tune and validate a FCS is presented. A schema of the

applied FCS is presented in Figure 4.

4.2.1 Setup of the FCS

Road hierarchy level and road slope serve as input pa-

rameters to calculate the velocity by car and the travel

time, subsequently. Fuzzy logic introduces the con-

cept of partial membership. In a classical or crisp

set, members of a crisp set would only be members

if their membership was full or complete. In fuzzy

sets, however, elements can have varying degrees of

membership Mahmoud (2018). Membership func-

tions that are deﬁned on an interval of 0 (not a mem-

ber) to 1 (full member) characterize the membership

of the three parameters slope, hierarchy level and ve-

locity (see Figure 3). Linguistic terms for road hier-

archy range from very low to very high and serve as a

fuzziﬁcation of the classes in Table 1. The terms for

slope include level, rolling, mountainous and steep.

The output parameter velocity varies from very slow

to very fast. The membership functions convert crisp

input and output values into fuzzy sets (Figure 4, Step

1).

We use a Mamdani fuzzy inference system Mam-

dani and Assilian (1975) which has a rule base where

every rule contains an antecedent (IF) part and a con-

sequent (THEN) part (Figure 4, Step 2). Antecedent

Figure 3: Membership functions of the parameters (a) Slope, (b) Hierarchy level and (c) Velocity.

Fuzzy Estimation of Link Travel Time from a Digital Elevation Model and Road Hierarchy Level

and consequent variables can be aggregated using

an AND-operator. The rule base and the membership

functions for this FCS are build based on the design

standards of Asian highway routes Behera (2008).

These design standards are transferable to Chile as

they describe similar road characteristics. A slightly

lower velocity was assumed as Behera (2008) de-

scribes speed limits and not actual travel speed. 19

rules have been developed with two antecedents and

one consequent each. Two exemplary rules are:

• IF slope is level AND road hierarchy level is very

high THEN velocity is very fast.

• IF slope is mountainous AND road hierarchy level

is very low THEN velocity is slow AND very slow

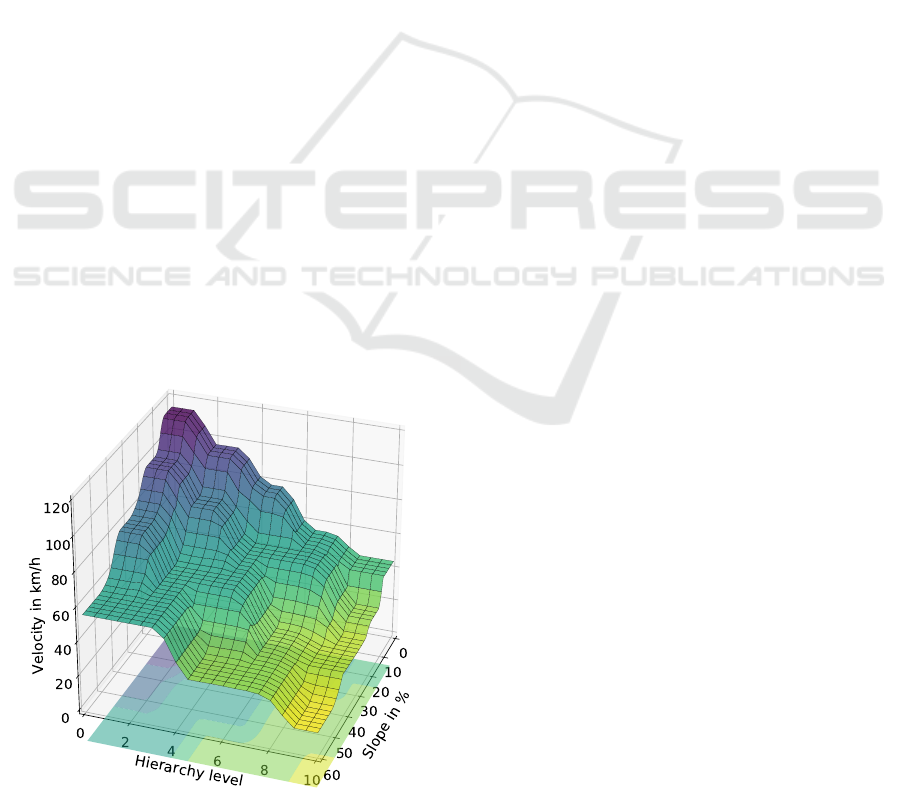
The ﬁnal step of a FCS is the defuzziﬁcation

(Figure 4, Step 4) which converts fuzzy output to

crisp output. We tested several defuzziﬁcation meth-

ods like centroid, bisector and mean-, minimum- and

maximum- of maximum. A centroid-based defuzzi-

ﬁcation (see Mahmoud (2018)) ﬁts our problem best,

as it results in a more smooth distribution. The output

of the initial FCS is illustrated in Figure 5.

4.2.2 Model Tuning

In order to adapt the initial FCS to produce better out-

puts, the output is compared to data generated by the

GD-API. As described in section 3.2, a subset of ap-

proximately 1000 roads is used to tune the FCS.

Some obstacles exist when comparing the output

of the FCS to the GD-API output. As mentioned in

Section 3, both the Google data and the OSM data

Figure 5: Fuzzy Control System.

may contain errors. Furthermore, as the GD-API al-

ways takes the shortest path, it may take a different

path between the two input coordinates than the road

from which we want to compare the velocity. Also,

the output of travel time of the GD-API is whole sec-

onds. Therefore, short road segments with a travel

time of only few seconds may be less accurate due to

rounding. An exemplary output from the GD-API of

4 s for a 100 m road segment can signify a velocity of

81 km/h (for 4.4 s) or 102 km/h (for 3.5 s).

Four types of possible errors or large inaccuracies

are captured automatically and are excluded of the

comparison:

• the distance between either the start or the end

points on the road in OSM and in Google is larger

than 50 m;

• the lengths of the road in OSM and in Google dif-

fer in more than 20 %;

• the road is shorter than 200 m;

• the request to the GD-API returns an error or an

empty result set.

The FCS is tuned with the knowledge gained by

the comparison with the GD-API. The membership

functions and the defuzziﬁcation methods are not

changed. Only the rule base is adapted to better ﬁt

the tuning subset.

4.2.3 Validation

Finally, the data is validated with the GD-API. The

validation subset with approximately 5000 roads is

used to validate the FCS (see Section 3.2). Possible

errors described above are deleted from the validation

subset and evaluated to obtain the error statistics.

5 CASE STUDY, RESULTS AND

DISCUSSION

5.1 Study Region

The model is applied exemplary for the BioB

ıo region

in central Chile. The road infrastructure of Chile is

typical of a developing country. The upper level road

network mainly consists of paved roads. But a lot of

minor roads in the category of tertiary roads or un-

classiﬁed roads are gravel or even mud roads. The

BioB

ıo region has a characteristic topography with

the coastal mountain range in the west and the An-

des in the east. Large areas of the region are rural

and not densely populated. This makes the region an

ideal candidate to apply the developed FCS. It offers

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

Figure 6: Road segment length in OSM.

a wide range of hierarchy levels and slopes. Further-

more, only 2.6 % of the roads in Chile (5.5 % of the

kilometers in the network) have corresponding speed

information in OSM, which underlines the need to

calculate velocity from another source.

The OSM data for the BioB

ıo region consists of

about 14040 km of road network. The road network

is classiﬁed as follows: 53 % tertiary roads, 18 % un-

classiﬁed roads, 12 % primary roads, 10 % secondary

roads, 6 % motorways and 1 % trunks. Figure 6 il-

lustrates the distribution of road segments of speciﬁc

lengths: once in relation to the number of roads and

once in relation to the kilometers in the road network.

This ﬁgure states clearly that there are many road seg-

ments shorter than 200 m. But their percentage in

respect to the kilometers in the road network is low

which renders them insigniﬁcant.

Before applying the FCS, the hierarchy level of

every road class in the region has to be assigned. The

fuzzy input hierarchy level ranges from 0 (very high)

to 10 (very low). Based on expert knowledge, roads

were assigned the following values: motorways 1.8,

trunks 4.3, primary roads 5, secondary roads 7, ter-

tiary roads 8.7 and unclassiﬁed roads 10. The hierar-

chy levels have to be chosen for every region while

taking into account its speciﬁc level of infrastructure

development.

5.2 Results

The initial FCS achieves an R

of 89.3 % for the SA-

1 and 87.8 % for the SA-2 (see Table 2). The FCS

performs best for motorways, followed by unclassi-

ﬁed roads. The tuned FCS reaches a slightly higher

of 89.5 % for the SA-1 and 88.3 for the SA-2. The

road classes motorway and unclassiﬁed decrease their

in the tuned FCS slightly while the others perform

better.

Figure 7 shows the deviation percentage from

GD-API seconds of the kilometer-wise largest road

classes tertiary, unclassiﬁed and primary for the initial

(left) and for the tuned (right) FCS. Negative percent-

ages signify that the FCS estimates lower travel times

than the GD-API. With the initial FCS (Figure 7, left),

the estimated travel time is generally lower than the

one of the GD-API. With the tuned FCS (Figure 7,

right), the average and median of the deviation per-

centage is around zero for all road classes and most of

the data ranges from −25 % to 25 %. The interquar-

tile range of the results of the tuned FCS is wider

than with the initial FCS. Furthermore, the interquar-

tile range and the total range is generally smaller for

the SA-2 than for the SA-1. The deviation percentage

of the SA-1 is, in most cases, slightly larger than for

SA-2.

A map of the deviation percentage with the tuned

FCS and SA-1 is illustrated in Figure 8. The deviation

percentage in the central plains of the study region is

larger than in the coastal mountain range in the west.

In the center of the region, link travel times that are

underestimated by the FCS (dark red) and link travel

times that are overestimated by the FCS (dark blue)

are often spatially close to each other. This also oc-

curs more often near urban centers. Within the urban

centers, the FCS mostly calculates lower travel times

than the GD-API.

Of the 5023 roads considered for validation, ap-

proximately 13 % were excluded due to the errors de-

scribed in section 4.2.2. The errors occurred when

the road distance between the OSM and the GD-API

data differed in more than 20 % (50 % of the errors)

and when the start or endpoints differ in more than

50 m (46 % of the errors). In 17 cases the GD-API

Table 2: R

in % for the initial and for the tuned FCS and for both slope calculation methods.

Motorway Trunk Primary Secondary Tertiary Unclassiﬁed Total

Initial

SA-1 98.0 76.0 81.1 87.1 88.1 89.5 89.3

SA-2 97.7 78.0 82.2 85.0 88.3 88.2 87.8

Tuned

SA-1 97.8 78.5 83.0 89.6 89.1 89.0 89.5

SA-2 97.5 80.1 83.7 86.3 88.6 87.4 88.3

Fuzzy Estimation of Link Travel Time from a Digital Elevation Model and Road Hierarchy Level

Figure 7: Deviation percentage of the three largest road classes in the initial (left) and in the tuned FCS (right) and respectively

for both slope calculation methods.

Figure 8: Map of deviation percentage in the tuned model with SA-1. If the percentage is negative (yellow - red), the calculated

travel time is lower than the reference travel time of the GD-API.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

responded with an error, for 5 roads it gave an empty

result.

5.3 Discussion

Two approaches to calculate road slope from a DEM,

presented in Section 4.1, are applied within the scope

of this paper. The initial expectation was that SA-

2 performs better because it approximates the actual

road slope more accurately by considering only the

pixels of the DEM that the road intersects. In contrast,

the SA-1 calculates the slope by including neighbour-

ing pixels on all sides, thus including possible hills

beside the road. When comparing both approaches,

the results are surprising: the FCS with SA-1 per-

forms slightly more accurate, both regarding the R

and regarding the deviation percentage. But, as the

interquartile range and the total range of the data is

smaller in the SA-2, the SA-2 is more precise while

less accurate than SA-1.

Regarding the R

of the initial FCS versus the

tuned FCS, the improvement is insigniﬁcant. From

the deviation percentage (see Figure 7) we gather that

the accuracy increases signiﬁcantly in the tuned FCS.

However, the precision decreases as the interquartile

range and the total range widens. When applying the

generated travel times for routing, the choice of FCS

is dependent on the requirements of the application.

The initial FCS should be chosen if an overestimation

of travel time needs to be avoided. If a more accurate

result is desired and a possible overestimation is of lit-

tle consequence, we suggest the tuned FCS. For com-

plete routes, road segments are summed up and posi-

tive and negative deviations from the GD-API nearly

cancel each other out.

For some road classes, the FCS performs better

than for others. Motorways are estimated with a very

high R

(>97.5 %). A motorway features a mostly ho-

mogeneous velocity and little slope variation and the

class contains little variety within. Both aspects facil-

itate the estimation of travel time. On the other side,

primary roads represent a very inhomogeneous class

with some roads having two lanes and others that are

only just asphalted. This poses a challenge to the FCS

which is recognizable by the lower R

and the high

interquartile range. The two largest road classes ter-

tiary and unclassiﬁed are underestimated in the initial

FCS. Probably this results from the fact that road con-

ditions of the lower road classes in Chile are worse

than expected. The road class trunk has the lowest R

value which is due to the fact that this road class is

very uncommon in Chile. Roads that are classiﬁed as

trunks in other countries are probably tagged as pri-

mary roads in Chile.

The presented fuzzy estimation of link travel time

is designed for rural application. In urban and sub-

urban regions trafﬁc, number of turns or local speed

limits play a much bigger role for the estimation of

travel time than slope and hierarchy level. Therefore,

travel times in urban centers estimated with the devel-

oped FCS should be treated with caution.

To tune and to validate the FCS, GD-API data is

applied. As mentioned in Section 3.2 some differ-

ences exist between the Google Maps data and the

OSM data. The error statistics emphasize this issue.

Some errors can not be caught and are treated as ref-

erence data which falsiﬁes the tuning and the valida-

tion. Thus, the GD-API data is only suitable to some

extend as valid reference data. However, other ref-

erence datasets that are readily available and feature

worldwide coverage do not exist.

6 CONCLUSIONS

We develop a FCS to estimate link travel time from

the two parameters road slope and road hierarchy

level. The open source and worldwide available

datasets OSM and SRTM serve as input data. The

FCS is validated with GD-API data. An exemplary

application on a case study for the BioB

ıo region in

Chile is performed successfully.

The developed FCS offers the advantages of

Fuzzy Control. It includes fuzzy input parameters and

a reasoning process of a human operator. Both enable

a relatively clean and fast design process. Especially

in comparison to the common use of ﬁxed speed pro-

ﬁles, a FCS produces a more continuous output. In

contrast to machine learning approaches, training data

is not needed as it is based on expert knowledge. For

our FCS this is a crucial beneﬁt as real training data

is unavailable. However, it has to be considered that

the ability of a FCS to perform well, highly depends

on its design. A FCS is much more susceptible to

false assumptions than for example a machine learn-

ing model would be.

The ﬁndings of this study can be used in many dif-

ferent applications. Most routing engines could ben-

eﬁt from the introduction of Fuzzy Control to com-

bine their various input parameters in order to obtain

a more continuous output. Furthermore, road slope

could also be included as one of these input parame-

ters to improve the accuracy in rural regions for these

routing engines. Many studies on critical road infras-

tructure rely on commercial travel time data as a cost

factor in the road network. They could beneﬁt very

much from estimated link travel times in rural regions.

The fuzzy estimation of link travel time has great

Fuzzy Estimation of Link Travel Time from a Digital Elevation Model and Road Hierarchy Level

potential for future development. A FCS can take

multiple input parameters so that more of the exist-

ing metadata in OSM could be included in the speed

calculation. Also, the sinuosity of a road is a big inﬂu-

encing factor on link travel time and could be an addi-

tional input parameter. In order to state which of the

presented slope calculation approaches is to be used

in which cases, further analyses in many different

study areas are needed. Another inquiring approach

could be to combine our proposed fuzzy methodol-

ogy with approaches like machine learning. A neuro-

fuzzy system could improve the estimations of the

FCS using appropriate reference data.

ACKNOWLEDGEMENTS

We thank Prof. Dr.-Ing. Stefan Hinz head of the In-

stitute of Photogrammetry and Remote Sensing at the

Karlsruhe Institute of Technology for the funding of

this work.

REFERENCES

Barrington-Leigh, C. and Millard-Ball, A. (2017). The

world’s user-generated road map is more than 80%

complete. PLOS ONE, 12(8):1–20.

Behera, S. K. (2008). Connecting India’s North East with

Bangladesh: a study of transport linkages. PhD the-

sis, Scholl of International Studies, Jawaharlal Nehru

University, India.

Brabyn, L. and Skelly, C. (2001). Geographical Access to

Services, Health (GASH): Modelling Population Ac-

cess to New Zealand Public Hospitals. In The 13

th Annual Colloquium of the Spatial Information Re-

search Centre, page 11, Dunedin, New Zealand.

Cipeluch, B., Jacob, R., Winstanley, A., and Mooney,

P. (2010). Comparison of the accuracy of Open-

StreetMap for Ireland with Google Maps and Bing

Maps. In In Proceedings of the Ninth International

Symposium on Spatial Accuracy Assessment in Natu-

ral Resuorces and Enviromental Sciences, page 4, Le-

icester, UK.

Collischonn, W. and Pilar, J. V. (2000). A direction depen-

dent least-cost-path algorithm for roads and canals.

International Journal of Geographical Information

Science, 14(4):397–406.

Das, R. D. and Winter, S. (2018). A fuzzy logic based trans-

port mode detection framework in urban environment.

Journal of Intelligent Transportation Systems, pages

1–12.

Demetriou, D. (2016). Uncertainty of OpenStreetMap data

for the road network in Cyprus. In Themistocleous,

K., Hadjimitsis, D. G., Michaelides, S., and Papa-

david, G., editors, Fourth International Conference on

Remote Sensing and Geoinformation of the Environ-

ment.

Dorn, H., T

ornros, T., and Zipf, A. (2015). Quality Evalu-

ation of VGI Using Authoritative Data – A Compari-

son with Land Use Data in Southern Germany. ISPRS

International Journal of Geo-Information, 4(3):1657–

1671.

Girres, J.-F. and Touya, G. (2010). Quality Assessment of

the French OpenStreetMap Dataset: Quality Assess-

ment of the French OpenStreetMap Dataset. Transac-

tions in GIS, 14(4):435–459.

Haklay, M. (2010). How Good is Volunteered Geo-

graphical Information? A Comparative Study of

OpenStreetMap and Ordnance Survey Datasets. En-

vironment and Planning B: Planning and Design,

37(4):682–703.

Hayward, G. and Davidson, V. (2003). Fuzzy logic applica-

tions. Analyst, 128:3.

Horn, B. (1981). Hill shading and the reﬂectance map. Pro-

ceedings of the IEEE, 69(1):14–47.

Jackson, S., Mullen, W., Agouris, P., Crooks, A., Croitoru,

A., and Stefanidis, A. (2013). Assessing Complete-

ness and Spatial Error of Features in Volunteered Ge-

ographic Information. ISPRS International Journal of

Geo-Information, 2(2):507–530.

Jantzen, J. (2007). Foundations of Fuzzy Control. John

Wiley & Sons, Ltd, Chichester, UK.

Knoop, V. L., Snelder, M., van Zuylen, H. J., and Hoogen-

doorn, S. P. (2012). Link-level vulnerability indica-

tors for real-world networks. Transportation Research

Part A: Policy and Practice, 46(5):843–854.

Li, X., Zhao, Z., Zhu, X., and Wyatt, T. (2011). Covering

models and optimization techniques for emergency re-

sponse facility location and planning: a review. Math-

ematical Methods of Operations Research, 74(3):281–

310.

Ludwig, I., Voss, A., and Krause-Traudes, M. (2011). A

Comparison of the Street Networks of Navteq and

OSM in Germany. In Advancing Geoinformation Sci-

ence for a Changing World, pages 65–84. Springer,

Berlin, Heidelberg.

Luxen, D. and Vetter, C. (2011). Real-time routing with

OpenStreetMap data. In Proceedings of the 19th ACM

SIGSPATIAL International Conference on Advances

in Geographic Information Systems - GIS ’11, page

513, Chicago, Illinois. ACM Press.

Mahabir, R., Stefanidis, A., Croitoru, A., Crooks, A., and

Agouris, P. (2017). Authoritative and Volunteered

Geographical Information in a Developing Coun-

try: A Comparative Case Study of Road Datasets in

Nairobi, Kenya. ISPRS International Journal of Geo-

Information, 6(1):24.

Mahmoud, M. S. (2018). Fuzzy Control, Estimation and

Diagnosis. Springer International Publishing, Cham.

Mamdani, E. H. and Assilian, S. (1975). An experiment in

linguistic synthesis with a fuzzy logic controller. In-

ternational Journal of Man-Machine Studies, 7(1):1–

13.

NASA and USGS (2013). Shuttle Radar To-

pography Mission. 1 Arc second void-ﬁlled.

https://earthexplorer.usgs.gov. Downloaded 25

May 2018.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

Neis, P., Zielstra, D., and Zipf, A. (2011). The Street

Network Evolution of Crowdsourced Maps: Open-

StreetMap in Germany 2007-2011. Future Internet,

4(1):1–21.

ORS (2018). OpenRouteService: The spatial services api

with plenty of features. https://openrouteservice.org/.

Accessed 30 November 2018.

OSM Wiki (2016). Using OpenStreetMap: OpenStreetMap

Wiki. http://wiki.openstreetmap.org/. Accessed 25

November 2018.

OTP (2018). OpenTripPlanner – Multimodal Trip Plan-

ning. http://www.opentripplanner.org/. Accessed 30

November 2018.

Scott, D. M., Novak, D. C., Aultman-Hall, L., and Guo, F.

(2006). Network Robustness Index: A new method

for identifying critical links and evaluating the perfor-

mance of transportation networks. Journal of Trans-

port Geography, 14(3):215–227.

Shackelford, A. and Davis, C. (2003). A combined fuzzy

pixel-based and object-based approach for classiﬁca-

tion of high-resolution multispectral data over urban

areas. IEEE Transactions on Geoscience and Remote

Sensing, 41(10):2354–2364.

Stanojevic, R., Abbar, S., and Mokbel, M. (2018). W-

edge: weighing the edges of the road network. In Pro-

ceedings of the 26th ACM SIGSPATIAL International

Conference on Advances in Geographic Information

Systems - SIGSPATIAL ’18, pages 424–427, Seattle,

Washington. ACM Press.

Steiger, E., Rylov, M., and Zipf, A. (2016).

Echtzeitverkehrslage basierend auf OSM-Daten

im OpenRouteService. AGIT Journal, 2:264–267.

Wang, X. J., Zhao, R. H., and Hao, Y. W. (2011). Flood

Control Operations Based on the Theory of Vari-

able Fuzzy Sets. Water Resources Management,

25(3):777–792.

YOURS (2018). YourNavigation - Worldwide routing on

OpenStreetMap data. http://yournavigation.org. Ac-

cessed 30 November 2018.

Fuzzy Estimation of Link Travel Time from a Digital Elevation Model and Road Hierarchy Level