
Improving Reproducibility whilst Maintaining Accuracy in Function
Point Analysis
Marcos de Freitas Jr.
1
, Marcelo Fantinato
1
, Violeta Sun
1
, Lucin
´
eia H. Thom
2
and Vanja Garaj
3
1
School of Arts, Sciences and Humanities, University of S
˜
ao Paulo, S
˜
ao Paulo – SP, Brazil
2
Institute of Informatics, Federal University of Rio Grande do Sul, Porto Alegre – RS, Brazil
3
Department of Electronic and Computer Engineering, Brunel University London, U.K.
Keywords:
Function Point Analysis, Function Points, Business Processes, Functional Size, Functional Size Measurement.
Abstract:
Existing proposals to improve the measurement reproducibility of Function Point Analysis (FPA) oversim-
plify its standard rules, threatening its measurement accuracy. We introduce a new artifact called Function
Point Tree (FPT), which allows for full data collection required to count function points, reducing the ex-
perts’ personal interpretation and thus the size variation. The new measurement method, called FPT-based
FPA (FPT-FPA), enlarges FPA standardization and systematization. Using this method allows to improve
measurement reproducibility whilst maintaining its accuracy. Preliminary results of an empirical study show
coefficients of variation for FTP-FPA lower than the maximum expected for both reproducibility and accuracy
for some scenarios.
1 INTRODUCTION
Function Point Analysis (FPA) is a standardized siz-
ing measurement method aimed at calculating a soft-
ware size measure from its functional requirements,
considering the functionality to be implemented on
user requests and replies (Albrecht, 1979). Results
obtained by FPA are widely used as a reference mea-
sure to derive other quantifiable parameters such as
effort, productivity or cost. The International Func-
tion Point Users Group (IFPUG) is the FPA regulator
agency, responsible for the improvement and devel-
opment of the rules set out in the Counting Practices
Manual (CPM) (IFPUG, 2010) in version 4.3.1. FPA
is also standardized by ISO/IEC 20926:2010.
However, a common criticism is FPA is rather sub-
jective as it requires expert judgment, restricting its
standardized use, as discussed in related work. Most
proposals to solve this subjectivity involve mapping
rules between software modeling artifacts (such as
UML) and FPA concepts to derive the functional size
(de Freitas Junior et al., 2015). However, the correct-
ness and completeness of existing artifact models are
not guaranteed as they were not built targeting FPA.
Although these approaches contribute at least par-
tially to improving the measurement reproducibility
among different measures, they overly simplify the
CPM rules. This simplification occurs because no ar-
tifact is sufficiently detailed to fully apply the stan-
dard FPA method, i.e., the IFPUG’s FPA. In the worst
cases, the FPA counting rules are not applicable be-
cause the artifact model lacks some piece of essential
information (Lavazza et al., 2008). Thus, the existing
approaches to improve reproducibility compromise
the measurement accuracy relative to the true quantity
value. Reproducibility and accuracy are interrelated
and refer to verifying consistency and concordance of
measurement results obtained from repeated measure-
ments, by different subjects, under similar or identical
conditions when compared to the true quantity value.
To overcome the issues mentioned above, we pro-
pose a new measurement method named Function
Point Tree-based Function Point Analysis (FPT-FPA).
We propose to add to the artifact model function re-
finement tree (Insfr
´
an et al., 2002) extra informa-
tion needed to count function points, arising the new
model FPT. The extra information can be collected by
a requirements analyst during the software life cycle
to keep all the information needed to IFPUG’s FPA
focused in a single artifact. This enables applying all
FPA rules based on the FPT, reducing individual in-
terpretation because of the lack of specific informa-
tion to count function points. FPT-FPA was designed
to conform to IFPUG’s FPA. Thus, we aim to improve
the reproducibility of different measured quantity val-
ues by reducing the variation among them, whilst en-
Freitas Jr., M., Fantinato, M., Sun, V., Thom, L. and Garaj, V.
Improving Reproducibility whilst Maintaining Accuracy in Function Point Analysis.
DOI: 10.5220/0007671700610072
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 61-72
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
61
suring the accuracy of the measured quantity values
relative to the true quantity value, which herein refers
to the value provided by IFPUG.
FPT-FPA was developed following the design sci-
ence research method (Hevner et al., 2004; Wieringa,
2014). Next sections present related work, the pro-
posed FPT-FPA method and experiment results.
2 RELATED WORK
We identified 15 related works with proposals simi-
lar to the new method proposed by us in this paper.
In these works, 12 base techniques or artifacts are
used, with some used more than one: UML’s class
diagram (Cantone et al., 2004; Harput et al., 2005;
Abrah
˜
ao et al., 2007; Rao et al., 2008; Lavazza et al.,
2008; Chamundeswari and Babu, 2008; Pow-Sang
et al., 2013), UML’s sequence diagram (Uemura et al.,
2001; Cantone et al., 2004; Harput et al., 2005; Rao
et al., 2008; Lavazza et al., 2008), UML’s use case di-
agram (Cantone et al., 2004; Rao et al., 2008; Lavazza
et al., 2008), Source code (Klusener, 2003; Eda-
gawa et al., 2011), Requirements engineering-based
conceptual modeling (Abrah
˜
ao and Insfr
´
an, 2008),
UML’s component diagram (Lavazza et al., 2008),
Object-oriented hypermedia’s navigation access di-
agram (Abrah
˜
ao et al., 2007), Goal and scenario
based requirements text (Choi et al., 2006), Entity-
relationship – data flow diagram (Lamma, 2004),
Entity-relationship diagram (Fraternali et al., 2006),
Vienna development method – specification language
(Miyawaki et al., 2008) and Web modeling language’s
hypertext model (Fraternali et al., 2006).
The coverage of the standard FPA steps for these
12 works ranges from about 5% (Rao et al., 2008) to
70% (Lavazza et al., 2008), with an average of 30%.
Our work proposes 100% coverage.
3 FPT-FPA OVERVIEW
The uniqueness of the new method is its compli-
ance with all steps of IFPUG’s FPA. The new method
seeks to avoid calculating an invalid number of func-
tion points when compared to the true quantity value,
which might occur by simplifying the FPA’s steps.
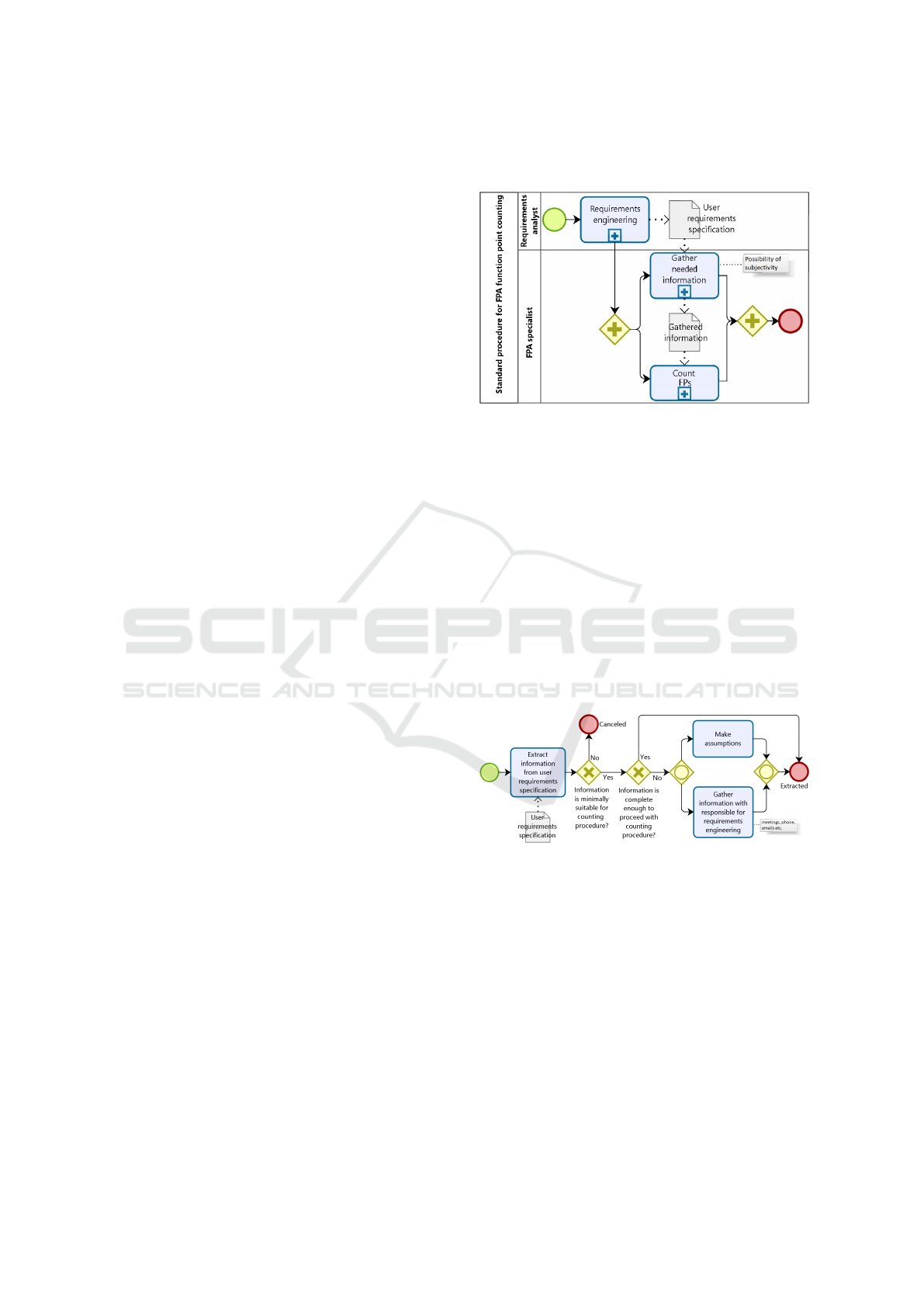
The IFPUG’s FPA counting procedure starts (cf.
Fig. 1) with a requirements engineering by the re-
quirements analyst who delivers user requirements
specification (or an equivalent artifact). No specific
format is required for this artifact, which is produced
following different approaches and techniques, in-
cluding composed ones. This subprocess is not de-
tailed herein.
Figure 1: IFPUG’s FPA procedure to count function points.
The user requirements specification is used by the
FPA expert to gather needed information. The gath-
ered information is then applied in parallel by the
same FPA expert to count FPs, which is a step also
not detailed herein. Since the user requirements spec-
ification can come in different formats, the FPA expert
should have to interpret this specification to extract
the information needed to count function points.
The first task to gather the needed information (cf.
Fig. 2) is to extract information from user require-
ments specification. Next, the FPA expert assesses
whether the elementary processes and data functions
can be identified, i.e., whether the extracted informa-
tion is minimally suitable for the counting procedure;
if not, the procedure should be canceled.
Figure 2: Subprocess gather needed information.
Following, the FPA expert assesses whether the
extra information such as DET, FTR, RET and pro-
cessing logics can be identified, i.e., whether the ex-
tracted information is full enough to proceed with the
counting procedure and whether this subprocess can
be completed with all the information extracted. If
the FPA expert identifies a lack of information, they
need to execute one or two of these tasks: (i) make as-
sumptions to complete the needed information or (ii)
informally gather information with responsible for re-
quirements engineering by meetings, e-mail, phone,
etc. Both cases can threat the reproducibility to count
function points as they may lead to important varia-
tions in the results of the function point counting.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
62
The FPT-FPA (Function Point Tree-based Func-
tion Point Analysis) method proposes to add a new
subprocess called elaborate the FPT as an extra task
to the IFPUG’s FPA counting procedure as part of the
requirements analyst duties (cf. Fig. 3). The need
for a formal FPA expert role is hence eliminated, as
the requirements analyst executes the FPA’s function
point counting with the support of the artifact FPT. A
part of the activities that should be performed by an
FPA expert is moved to the requirements analyst and
the other part is a standard procedure that can be auto-
mated. FPT-FPA improves the quality of the counting
as the requirements analyst masters the software re-
quirements. The requirements analyst does not need
knowledge in FPA as the function point counting is
automatically executed based on the FPT available.
As a potential drawback, the requirements analyst
needs to be an FPT expert, but this technique is more
related to their usual responsibilities than mastering
FPA, and then knowledge on all the FPA rules and
procedures is not required.
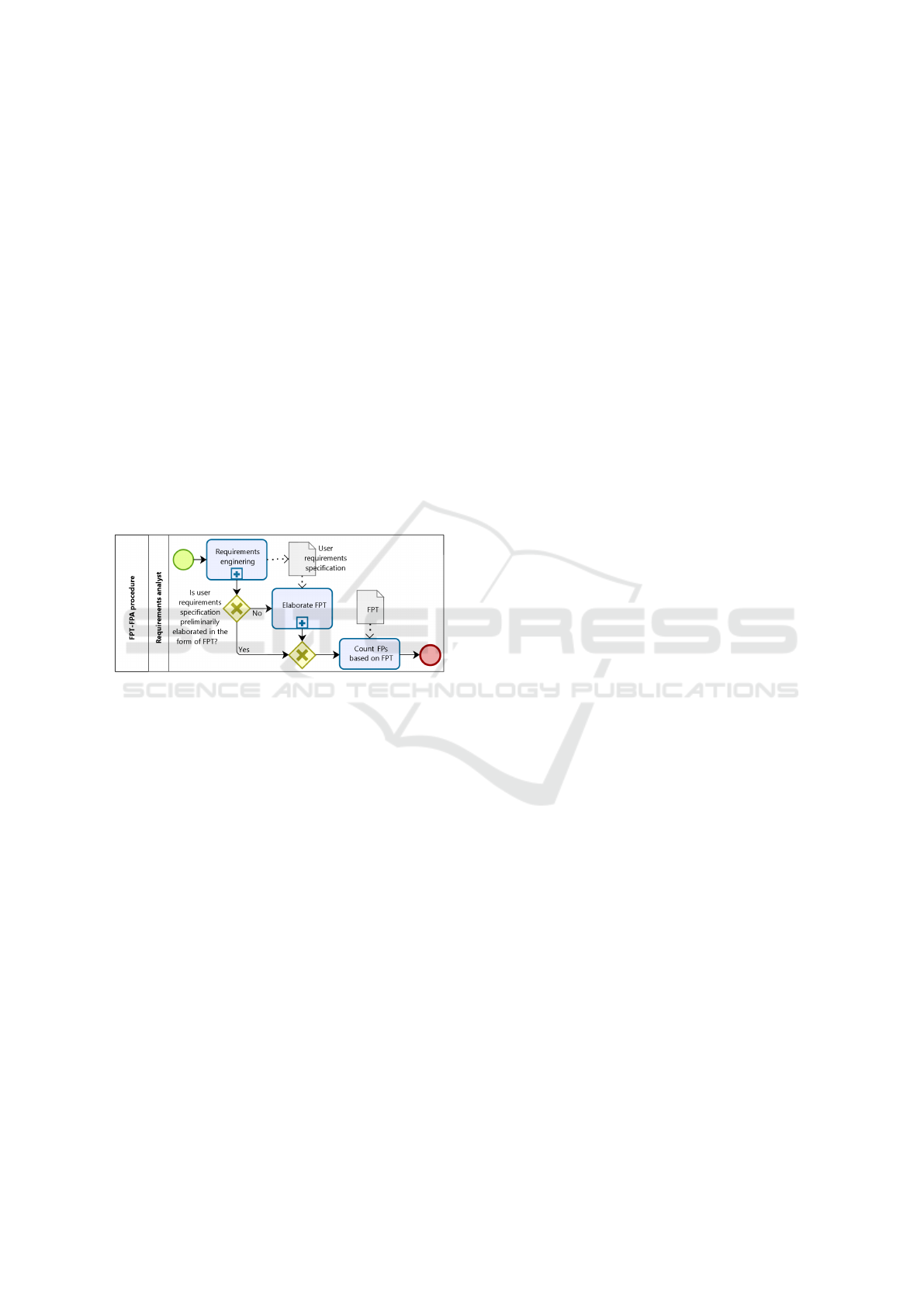
Figure 3: Procedure for the FPT-FPA’s function point count-
ing.
The FPT-FPA counting procedure also starts with
the requirements engineering, delivering the user re-
quirements specification (or a corresponding artifact)
by the requirements analyst. In this new context, the
user requirement specification, or at least a part, can
be firstly produced in an FPT, although not manda-
tory. If the user requirements specification is prelimi-
narily elaborated in the form of an FPT, it is directly
used to count FPs based on the FPT. Otherwise, the
requirements analyst needs to elaborate the FPT be-
fore proceeding with the counting. The details of the
elaborate the FPT subprocess are presented in Sec-
tion 4 whereas the details of the count FPs based on
the FPT subprocess are presented in Section 5. Be-
cause of their complexities, none of these two sub-
processes are presented visually).
4 FPT ELABORATION
An FPT is composed of three levels: root, intermedi-
ate and leaf nodes. An illustrative example of an FPT
is shown in Fig. 4. The figure represents a Human
Resources Management System (HRMS).
4.1 Level 1: Tree Root
A tree root represents the counting purpose and the
counting type. Each root must have two types of as-
sociated root markers, showing: (i) the counting pur-
pose, i.e., the purpose for which an organization needs
to count function points according to the FPA con-
cepts (cf. Fig. 5); and (ii) the counting type, referring
to what will be done with the obtained measure (cf.
Fig. 6). Exactly one root marker exists for the former
case and at least one root marker exists for the latter.
4.2 Level 2: Intermediate Nodes
No change was proposed for the intermediate level on
the function refinement tree as originally defined.
4.3 Level 3: Leaf Nodes
Leaf nodes represent the elementary functions of the
software being measured. Every leaf node must in-
clude: node markers, inclusion dependency connec-
tors (when applicable) and node attributes.
4.3.1 Node Markers
Node markers refer to the behavior of the elemen-
tary functions during software execution. Whenever a
software elementary function contains one or more of
the behavior properties represented by node markers
(cf. Figs. 5 and Fig. 6), these markers are added into
the corresponding leaf node. Fig. 7 shows node mark-
ers whose corresponding behavior is connected to at
least one processing logic. Fig. 8 shows extra node
markers for the behavior of the elementary functions
with no corresponding FPA processing logic. The
node marker PRIM represents which marker among
MAIN, BEHA and PRES is the main purpose of an
elementary function. Thus, PRIM is required for a
leaf node only when at least two of these three node
markers (MAIN, BEHA, PRES) were selected; oth-
erwise, it does not apply. For example (cf. Fig. 4),
the elementary function create employee contains the
node markers VALI, PRES, MESS, REFE, COND,
MAIN and PRIM, so the marker PRIM was added be-
cause PRES and MAIN were previously added. Thus,
PRIM is to inform whether the main purpose of this
elementary function is PRES or MAIN. Specifically,
in this example, the PRIM value is MAIN.
Improving Reproducibility whilst Maintaining Accuracy in Function Point Analysis
63

Figure 4: Example of FPT.
Figure 5: Root markers for counting purposes.
Figure 6: Root markers to represent for counting types.
4.3.2 Inclusion Dependency Connector between
Elementary Functions
An inclusion dependency connector shows an inclu-
sion dependency relationship between two elemen-
tary functions. It is used when the elementary func-
tion after the arrow does not comply with the user
functional requirements if performed alone, but only
if the elementary function contrary to the arrow is
executed first. For example, a user functional re-
quirement might require that, after registering an em-
ployee, payment details (monthly or hourly) and de-
pendents have to be registered. Both following ac-
tions do not comply with this user functional require-
ment: (i) registering an employee without sequen-
tially either registering their payment details (monthly
or hourly) or registering their dependents; and (ii) first
registering the employee’s payment details (monthly
or hourly) or first registering the employee’s depen-
dents, both without ever having previously registered
Figure 7: Node markers for the behavior of the elementary
functions for the FPA processing logics.
Figure 8: Extra node markers for elementary function be-
havior (without corresponding FPA processing logic).
this employee. Therefore, the leaf nodes create em-
ployee, create hourly paid employee, create monthly
paid employee and create dependent are connected by
an inclusion dependency connector, starting from cre-
ate employee first and heading toward the other three.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
64

4.3.3 Node Attributes
Node attributes show the information to be displayed
to or informed by a user during execution of elemen-
tary functions. For each node attribute, it should be
informed: if the information is displayed either in
screen header or footer; if the information is avail-
able for data reading or input or both; and if the infor-
mation has meaning stand-alone to business or only
when combined with another one.
4.4 Relationships Amongst Levels
All intermediate nodes are connected to the tree root
(root-intermediate connections); and all leaf nodes are
connected to an intermediate node (intermediate-leaf
connections). For the latter, these data accompanies
the connections whenever appropriate: data entity la-
bels; data entity markers; exclusion dependency con-
nectors; and data entity attributes:
4.4.1 Data Entity Label
A data entity associated with an intermediate-leaf
connection represents a software data entity main-
tained or referenced by the elementary functions rep-
resented by the corresponding leaf nodes. For exam-
ple (cf. Fig. 4), the label position represents a data
entity maintained or referenced by four elementary
functions: create, update, delete and read (position).
Each informed data entity (i.e., a data entity label) is
accompanied by these extra data: data entity markers;
exclusion dependency connectors (whenever appro-
priate); and data entity attributes – described as fol-
lows. Data entities neither maintained nor referenced
by elementary functions should not be modeled.
4.4.2 Data Entity Markers
Whenever a data entity presents one or more of the
properties related to the five markers showed in Fig.
9, the corresponding markers are added to the corre-
sponding data entity.
4.4.3 Exclusion Dependency Connector between
Data Entities
This relationship is represented by a red arrow and it
attaches two data entities together. The arrow con-
nects a data entity with other data entities that com-
pose it so that the subsequent data entities (i.e., after
the arrow) are parts of the first one (i.e., contrary to
the arrow). If the first data entity is deleted, all the
data entities connected to it by exclusion dependency
connectors are also deleted as they do not exist alone.
Figure 9: Data entity markers for data entity properties.
For example (cf. Fig. 4), if a user functional require-
ment requires that, by deleting an employee, all the
employee’s dependents and the employee data (what-
ever they are hourly or monthly paid) are also deleted;
then, the dependent data entities (dependent, hourly
paid, and monthly paid) have no meaning alone with-
out a connection to an employee. Therefore, hourly
paid, monthly paid and dependent are connected via
an exclusion dependency connector to employee.
4.4.4 Data Entity Attributes
Data entity attributes represent the information stored
in a data entity. The data entity attributes are main-
tained or referenced by the elementary functions rep-
resented by the leaf nodes. For each data entity,
all data maintained or referenced needed to execute
the corresponding elementary functions is informed.
For each data entity attribute, it is needed to inform
whether the information has meaning stand-alone to
business or only when combined with another one.
5 FPT-FPA-BASED COUNTING
Mapping rules are used so that the data modeled on
the FPT are used as input to FPA. The proposed
rules are described herein following the IFPUG’s FPA
counting steps, i.e., according to the IFPUG’s CPM
steps.
The function point counting starts by gathering the
software documentation. The only input needed is the
FPT and not all the relevant available artifacts as de-
fined by IFPUG’s FPA. The FPT is enough and hence
the only relevant and needed artifact. Therefore, the
information contained in this artifact supports the exe-
cution of the five stages of the function point counting
as follows. Only the three first stages described for IF-
PUG’s FPA are detailed here as no change is proposed
to the last two stages (calculating the functional size
and documenting the counting and report the results).
Improving Reproducibility whilst Maintaining Accuracy in Function Point Analysis
65

5.1 Boundary, Scope and Purpose
The counting boundary is represented by the tree root
as it defines – as child or grandchild nodes – all the
sets of functions and data entities to be addressed dur-
ing the counting procedure. Any other function or
data entity not added in the tree is considered out-
side of the counting border. The counting scope is
represented by all the elementary functions (i.e., leaf
nodes), and all data entities of the FPT. The full set
of elementary functions and data entities is consid-
ered belonging to the counting scope. The counting
purpose is represented by one of these root markers:
EFFO, COST, PROD or COMP. As each FPT has
only one root marker, the marker that is added in the
tree and its corresponding meaning are to define the
counting purpose. The counting type is represented in
FPT-FPA by a set of one or more of these root mark-
ers NEW, EVOL and EXIS. Since each FPT may have
one or more of these root markers, all the markers
added in the tree and their corresponding meanings
are to define the counting type.
5.2 Measuring Data Functions
This section presents the steps to measure data func-
tions.
5.2.1 Identifying the Data Functions
Each data entity is mapped to a single data function
or as part of a composed data function, unless: (i)
the data entity refers to a code data, i.e., data en-
tities whose associated elementary function (i.e., a
leaf node) has the node marker CONS are discarded;
(ii) the data entity stores only attributes unacknowl-
edged by business process users, i.e., data entities
whose information represented by its data entity at-
tributes has no meaning stand-alone to business are
discarded; (iii) the data entity describes a many-to-
many relationship between two other data entity types
and contains only foreign keys, i.e., data entities hav-
ing the data entity marker ASSO and presenting up to
two data entity attributes with meaning stand-alone to
business are discarded; and (iv) the data entity stores
only one data entity attribute, i.e., data entities pre-
senting only one data entity attribute with meaning
stand-alone to business are discarded.
All data entities complying with all previous con-
straints are mapped to a single data function or as part
of a composed data function depending on whether
they are logically dependent or independent among
them: (i) data entities logically independent of all the
other data entities, i.e., those not linked to any other
data entity by an exclusion dependency connector, are
directly mapped to a single data function each one.
Thus, only data entities having meaning to business
by their own are mapped to single data functions; and
(ii) a set of data entities logically dependent among
them, i.e., linked one to another by exclusion depen-
dency connectors, is grouped and mapped to a sin-
gle data function. Thus, data entities with meaning to
business only when combined are mapped together to
a single data function.
5.2.2 Classifying the Data Functions as Internal
Logical File (ILF) or External Interface
File (EIF)
This classification relies on the elementary functions
that manipulate the data entities components of the
data functions. These rules are followed to classify a
data function:
• ILF: data functions that comply with this con-
straint: at least one of its data entities is associated
with an elementary function (i.e., a leaf node) that
presents the node marker MAIN.
• EIF: data functions that comply with these con-
straints: (a) none of its data entities is associated
with any elementary function (i.e., a leaf node)
that presents the node marker MAIN and (b) at
least one of its data entities presents the data en-
tity marker EXTE.
5.2.3 Determining the Numbers of Data Element
Type (DET) and Record Element Type
(RET) for the Data Functions
For DETs, the number is counted of the data entity at-
tributes (associated with its data entities) with mean-
ing stand-alone to business. For RETs, it is consid-
ered the data entity properties (defined by the data en-
tity markers) of its data entities, based on two rules:
(i) each data entity marked as SUBT, ATTR or ASSO
is counted as a RET of the corresponding data func-
tion; and (ii) each data entity marked as TYPE and not
linked (by exclusion dependency connector) to any
data entity marked as SUBT is counted as a RET of
the corresponding data function.
5.2.4 Determining Complexity and Contribution
for the Data Functions
Based on the DET and RET obtained, the complex-
ity (i.e., low, medium or high) of each data function
is determined, by the direct application of the val-
ues pre-defined by IFPUG’s FPA. Finally, based on
these obtained complexities, the last step determines
the contribution on the functional size of each data
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
66

function, which is executed by the direct application
of the values pre-defined for IFPUG’s FPA.
5.3 Measuring Transactional Functions
This section presents the steps to measure transac-
tional functions.
5.3.1 Identifying the Elementary Processes
Each elementary function (i.e., a leaf node) added in
the FPT is mapped to a single elementary process or
as part of a composed elementary process, unless: (i)
the elementary function maintains or has references
to code data, i.e., elementary functions presenting the
node marker CONS are discarded according to IF-
PUG’s CPM (IFPUG, 2010); and (ii) the elementary
function does not process data or control information
retrieved from outside the boundary and does not send
data or control information to outside the border, i.e.,
elementary functions with no node attribute inform-
ing availability for user data reading or input are dis-
carded.
All the elementary functions complying with pre-
vious constraints are mapped to a single elementary
process or a part of a composed elementary process
depending on whether they are logically dependent
or independent among them: (i) elementary functions
logically independent of any other elementary func-
tion, i.e., those not linked to any other elementary
function by an inclusion dependency connector, are
each one directly mapped to a single elementary func-
tion; and (ii) a set of elementary functions logically
dependent among them, i.e., linked one to another
by inclusion dependency connectors, is grouped and
mapped to a single elementary process. According
to this classification, an elementary process maintains
software in a consistent state after its execution, i.e.,
it makes up a full transaction, is self-contained, and is
the smallest meaningful unit of activity.
5.3.2 Determining Unique Elementary Processes
Each unique elementary process is identified as a
transactional function. Two or more elementary pro-
cesses are unique elementary process if they have:
(i) the same node markers representing processing
logics (i.e., VALI, CALC, CONV, FILT, COND,
MAIN, REFE, DERI, BEHA, PRES and RETR); (ii)
the same node attributes representing Data Element
Types (DET) for the elementary process; and (iii) the
same data entities representing File Type Reference
(FTR) for the associated elementary process.
5.3.3 Classifying the Transactional Functions as
External Input (EI), External Output (EO)
or External Inquiry (EQ)
This classification relies on the primary intention (i.e.,
the node marker PRIM) of the elementary functions
that compose the transactional functions. These rules
are followed to classify a transaction function:
• EI: transactional functions that comply with this
constraint – at least one of its elementary func-
tions presents the node marker PRIM showing as
the primary intention the node markers MAIN or
BEHA.
• EO: transactional functions that comply with
these constraints – (a) none of its elementary
functions presents the node marker PRIM show-
ing as the primary intention the node markers
MAIN or BEHA, (b) at least one of its elemen-
tary functions presents the node markers CALC,
MAIN, BEHA or DERI and (c) at least one of its
elementary functions marked as CALC, MAIN,
BEHA or DERI presents at least one node at-
tribute informing availability for user data read-
ing.
• EQ: transactional functions that comply with
these constraints – (a) none of its elementary
functions presents the node marker PRIM show-
ing as the primary intention the node markers
MAIN or BEHA, (b) none of its elementary func-
tions presents the node markers CALC, MAIN,
BEHA and DERI and (c) at least one of its ele-
mentary functions presents one or more node at-
tributes informing availability for user data read-
ing.
5.3.4 Determining the Numbers of DET and
FTR for the Transactional Functions
To determine the number of DETs for a transactional
function, the number is counted of node attributes (as-
sociated with its elementary functions) with meaning
stand-alone to business. These extra rules are: (i) if
the information corresponding to a node attribute is
displayed only in the screen’s header or footer, then
this node attribute is discarded for the counting of
DETs; (ii) if one of the elementary functions presents
the node marker MESS, it is counted an extra DET
for the corresponding transactional function, consid-
ering the functional ability to display a message to the
user; and (iii) if one of the elementary functions does
not show the node marker BATC, it is counted one ex-
tra DET for the corresponding transactional function,
taking the functional ability to initiate some action.
Improving Reproducibility whilst Maintaining Accuracy in Function Point Analysis
67

Then, to determine the number of FTRs for a
transactional function, the data entities related to the
elementary functions constituents of this transaction
function is considered. Each data entity identified as a
data function (or as part of a data function) and asso-
ciated with the corresponding transactional function
is counted as an FTR for this transactional function.
5.3.5 Determining Complexity and Contribution
for the Transactional Functions
Based on the numbers of DET and FTR obtained, the
complexity (i.e., low, medium or high) of each trans-
actional function is determined, by the direct applica-
tion of the values pre-defined for IFPUG’s FPA. Fi-
nally, based on these obtained complexities, the last
step determines the contribution on the functional size
of each transactional function, which is executed by
the direct application of the values pre-defined for IF-
PUG’s FPA.
6 EVALUATION OF FPT-FPA
An empirical study was conducted to evaluate FPT-
FPA regarding its measurement reproducibility and
accuracy. A quasi-experiment was run to test the
hypothesis that FPT-FPA enables a higher repro-
ducibility and accuracy than IFPUG’s FPA. A quasi-
experiment was applied since it would be impractical
to randomly select the subjects because of the com-
plexity of this study (Easterbrook et al., 2008; Kamp-
enesa et al., 2009).
6.1 Support Tool
A tool was prototyped to support the function point
counting based on the FPT-FPA method. The proto-
type was aimed at demonstrating the automation fea-
sibility of FPT-FPA and helping verify and validate
the proposed method as a proof of concept. The eval-
uation also considered the method execution manu-
ally to ensure its correctness regardless of whether the
tool is used or whether the tool is correctly imple-
mented. A full tool for commercial purposes was not
the primary goal and hence non-functional require-
ments such as usability, performance and others were
not addressed. The FPT was simplified on the graphic
representation of the elements root markers, nodes
and data entity labels (cf. Fig. 4).
The prototype tool was developed on the .NET
4.5 framework, using the programming language C#
according to the object-oriented paradigm. For data
storage, XML format was used with a set of properties
called LINQ (Language Integrated Query), which en-
ables the development of queries using the C# syntax.
The prototype tool architecture is organized based on
the MVC (Model View Controller) software architec-
tural pattern [38]. In addition to the three standard
MVC layers, an extra layer – called persistence – was
created, dedicated specifically to the communication
between software and database, to maximize the ben-
efits of the logical separation provided by the MVC
layers.
Fig. 10 shows a use case diagram representing
the prototype functional requirements. The diagram
brings five main use cases to be used by the only ac-
tor to whom the system is designed – the requirements
analyst. Thus, with the proposed method, an FPA ex-
pert would be no longer needed and the requirement
analyst would receive some extra tasks.
Fig. 11 shows a screenshot of the prototype. The
figure shows a part of the FPT previously shown in
Fig. 4, with limitations of the prototype because of the
scenario mentioned at the beginning of this section.
The full FPT is not shown in this figure because of
readability.
6.2 Experiment Design
This section presents the planning of the experiment
that was carried out. The experiment was designed
based on a framework for experimental software engi-
neering (Wohlin et al., 2012). The experiment aimed
to investigate whether the proposed method shows
better reproducibility and accuracy levels when com-
pared to reference values obtained by IFPUG’s FPA.
Based on the GQM (Goal/Question/Metric) template
(Basili and Rombach, 1998), the goal pursued in this
experiment was: to analyze the proposed method for
the purpose of evaluating it in comparison with IF-
PUG’s FPA regarding reproducibility and accuracy,
from the point of view of the researcher, in the context
of M.Sc. students and practitioners measuring func-
tion points.
The analysis of the results considered:
• Reproducibility as the agreement between the
measurement results of different subjects. Repro-
ducibility was examined as calculated by different
subjects by FPT-FPA, by comparing the obtained
calculation results among subjects. We expected
to get a coefficient of variation for the results with
FPT-FPA lower than 17.67%, as this is the aver-
age of the coefficients of variation found in re-
lated work on reproducibility (Connolley, 1990;
Low and Jeffery, 1990; Kemerer, 1993). Although
the only found sources are out-of-date, they can
be used as a reference value as FPA can be kept
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
68

Figure 10: Use case diagram for the support prototype.
Figure 11: Screenshot of the developed prototype.
without substantial changes along these years.
• Accuracy as the agreement between the measure-
ment results and the true quantity value. Accuracy
was examined as calculated by different subjects
by FPT-FPA, by comparing the results with the
official reference value as reported by IFPUG. We
expected to get a coefficient of variation between
the results with FPT-FPA and the IFPUG’s official
value lower than 10.71% as this is the average of
the coefficients of variation found in related work
on accuracy (Uemura et al., 2001; Lamma, 2004;
Fraternali et al., 2006; Miyawaki et al., 2008;
Abrah
˜
ao and Insfr
´
an, 2008; Adem and Kasirun,
2010; Edagawa et al., 2011).
For the analysis of these two criteria, the total
numbers of measured function points were consid-
ered, i.e., the sum of all Base Functional Compo-
nents (BFC), from both data functions (ILF and EIF)
and transactional functions (EI, EO and EQ). Thus,
the reproducibility and accuracy analyses were per-
formed by evaluating the method as a whole and not
focusing on specific components. Regardless, some
breakdown values are also presented relating to BFCs
to help identify where reproducibility and accuracy
problems may be located specifically.
The other parameters of the designed experiment
are presented as follows:
• Subjects: a group of 17 participants with an ed-
ucation background in information systems (or
similar) was selected. Most of the subjects had the
experience of working in the industry for between
1 and 20 years. The subjects were selected by
convenience, with the majority being from orga-
nizations related to software and systems develop-
ment. The remaining subjects were selected from
an academic stricto sensu graduate program. As
the proposal assumes that the FPA expert would
be no longer needed, as the elaboration of the
FPT can be done directly by other roles, the se-
lected subjects were mainly requirements or sys-
Improving Reproducibility whilst Maintaining Accuracy in Function Point Analysis
69

tems analysts (or related roles), who are the tar-
get users of the proposed method. The only con-
straint was that they should not have previously
known FPA to avoid the application of the previ-
ous experience and personal techniques in manag-
ing the provided information instead of using the
FPT-FPA method.
• Variables:
– Independent Variables: the primary indepen-
dent variable refers to the methods being com-
pared – FTP-FPA and FPA. The secondary in-
dependent variable was the type of execution
of the FTP-FPA method, i.e., manual or auto-
mated.
– Dependent Variables: the two dependents
variables are – reproducibility and accuracy.
• Treatment: the higher-level treatment refers to
the primary independent variable – FPT-FPA ver-
sus IFPUG’s FPA. All the subjects carried out
only the FPT-FPA method, contributing to an ob-
servation from each subject. The IFPUG’s FPA
method was not carried out during the experiment
execution as the values for reproducibility and ac-
curacy found in the literature were used as a refer-
ence for comparison with FPT-FPA. As the lower-
level treatment, to address the secondary goal, the
subjects were randomly assigned to two groups to
compare the performance for: manual execution
– eight subjects executed FPT-FPA manually; and
automated execution – nine subjects executed
PPT-FPA supported by the prototype.
• Instrumentation:
– Training: the subjects were provided with
the description of the proposed method, an
overview of the experiment and no example.
– Object: a software specification previously
measured by IFPUG’s was used with 125 func-
tion points (IFPUG, 2010); all the subjects
elaborated an FPT for the object; subsequently,
they counted the function points for this sys-
tem, based on the elaborated tree.
– Prototype or Results Form: the prototype was
provided to those subjects who should use it
during the experiment and a form was provided
to the other ones.
– Characterization Form: each subject reported
basic personal information and the total time
spent.
• Hypotheses:
– Hypothesis A: refers to the primary indepen-
dent variable and the dependent variable of re-
producibility: the hypothesis is that FPT-FPA
has a reproducibility coefficient of variation
equal to or greater than 17.67%, i.e., FPT-FPA
has an equivalent or higher reproducibility than
IFPUG’s FPA.
– Hypothesis B: refers to the primary indepen-
dent variable and the dependent variable of ac-
curacy: the hypothesis is that FPT-FPA has
an accuracy coefficient of variation equal or
greater than 10.71%, i.e., FPT-FPA has an
equivalent or higher accuracy than IFPUG’s
FPA.
6.3 Subjects Profile
Fig. 12 shows the profile of the subjects, includ-
ing their education background, current position and
work experience. All the 17 subjects held at least a
graduate degree in information systems or related ar-
eas and seven of them also held a lato sensu post-
graduate degree. From them, 13 were working in the
industry, with the majority acting as a system or re-
quirements analyst, and also one developer and one
manager. Some of these 13 subjects working in the in-
dustry were also enrolled in a Master of Science Grad-
uate Program in Information Systems. The remaining
four subjects to complete 17 were fully enrolled in the
same master program; with some previous experience
in the industry. The length of work experience for the
sample ranges from 1 to 20 years.
6.4 Results Achieved
Table 1 shows a results breakdown per subject. These
results include the number of function points mea-
sured, the time spent and the type of execution – Man-
ual (M) or Automated (A). Table 2 shows the mean
values for the function points measured by FPT-FPA
and other derived values needed to evaluate repro-
ducibility and accuracy, for both automated and man-
ual executions.
As for time spent by the subjects applying FPT-
FPA, the following mean values were obtained (in
hours): 2.45 for execution via support prototype and
4.48 for manual execution. The relationship between
the two groups was 55% automated/manual.
For reproducibility, the coefficient of variation,
relative to the mean (to measure reproducibility), cal-
culated as 9.99%, when observing the measurement
results for all subjects is nearly half the maximum de-
fined as the study goal compared to the related work
(i.e., 17.67%). This value shows that, on reproducibil-
ity, the proposed method is on average substantially
better than other approaches present in literature.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
70
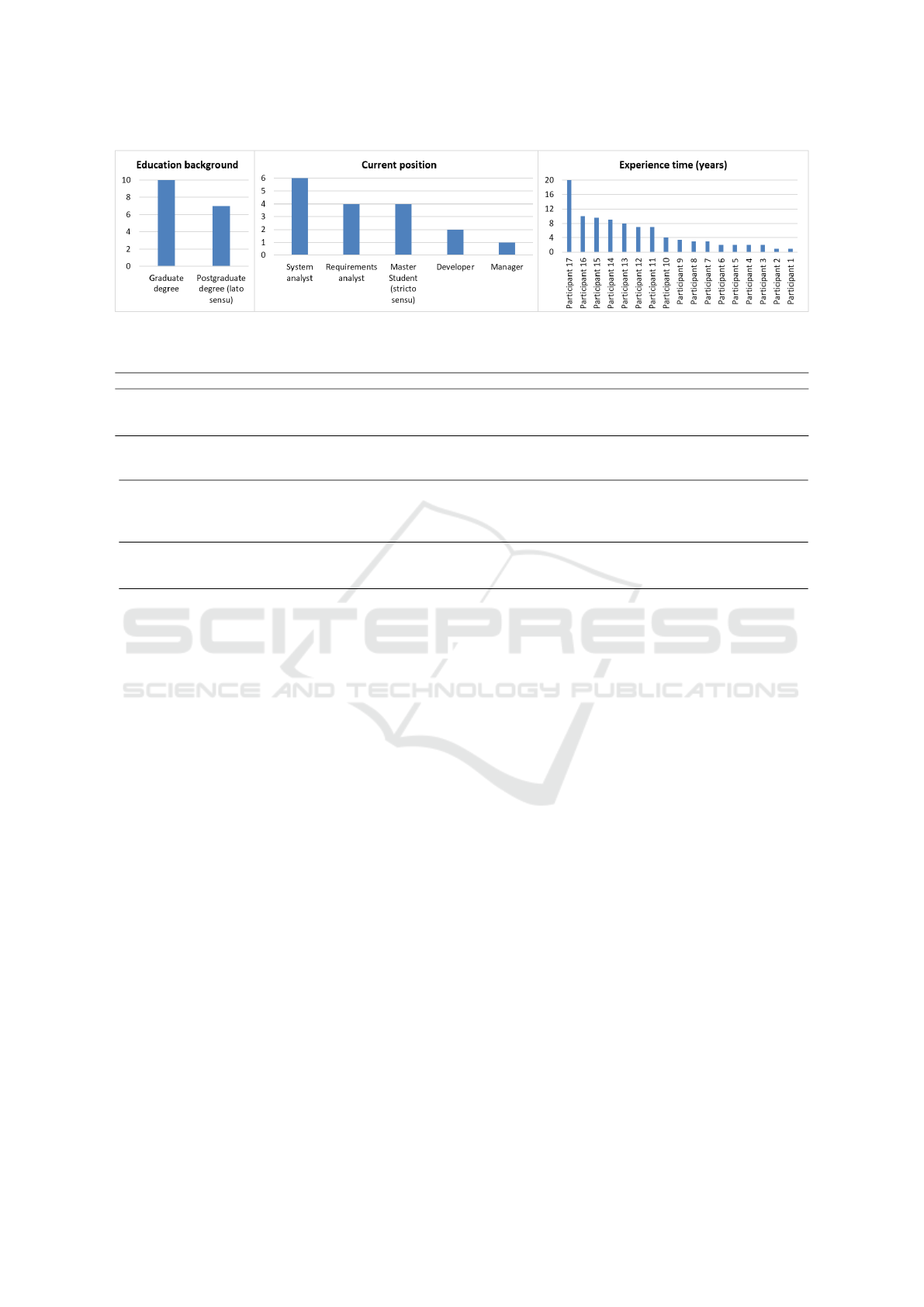
Figure 12: Selected subjects profile.
Table 1: Measurement results – totalized data and transactional functions (Reference value = IFPUG’s official value).
Ref. value P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12 P13 P14 P15 P16 P17 Mean
# of FPs (total) 125 104 109 88 110 111 102 101 124 124 122 124 118 124 128 128 122 130 115.82
Execut. time (h) N/A 1.7 2.5 2.6 1.1 2.3 2.1 4.5 2.8 3.5 4.2 3.8 3.2 3.0 5.0 8.0 7.5 2.1 3.52
Execut. type N/A A A A A A A A A M M M M M M M M M –
Table 2: Consolidated results on reproducibility and accuracy (totalized data and transactional functions).
Relative to the mean Relative to the true quantity value –
(reproducibility) IFPUG’s official value (Accuracy)
Perspective of analysis Mean of the
measured values
Standard
deviation
Coefficient
of variation
Standard
deviation
Coefficient
of variation
All subjects (M+A) 115.82 11.57 9.99% 14.76 11.81%
Only manually (M) 124.44 3.50 2.81% 3.54 2.83%
Only automated (A) 106.13 9.64 9.08% 21.19 16.95%
For accuracy, the coefficient of variation relative
to the IFPUG’s official value, calculated as 11.81%
based on the measurement results for all subjects, is
slightly higher than the maximum defined as the study
goal compared to the related work (i.e., 10.71%). This
value shows that, on accuracy, the proposed method is
less accurate than those found in related work. How-
ever, when considering different perspectives, better
results are also found. For example, when the re-
sults are evaluated taking into account only the sub-
jects who executed the method manually, it is also
observed a better coefficient of variation calculated as
2.83%, which is much lower than the maximum value
defined as the study goal (i.e., 10.71%).
7 CONCLUSION
FPA has played a key role in private and public
organizations. It is imperative to get reliable and
valid results with the application of this measure-
ment method. However, several issues exist regard-
ing the reproducibility and accuracy of the function
point counting executed using IFPUG’s FPA. This
work aimed to define a measurement method called
Function Point Tree-based Function Point Analysis
(FPT-FPA), aiming to provide a better standardiza-
tion to count function points. This standardization is
achieved by a new artifact model that includes all in-
formation needed for the counting, called FPT. The
FPT enables counting with improved reproducibility
among different measures whilst maintaining the ac-
curacy with IFPUG’s FPA.
The evaluation showed that the proposed method
presented positive values when the proposed method
was manually executed, on both reproducibility and
accuracy; showing that the proposed method has con-
ceptual soundness. However, the results were not so
good when the proposed method was executed sup-
ported by the prototype, mainly on accuracy; show-
ing that the prototype solution still requires adjusts to
present a more important contribution.
Future works may include finding the better ad-
justments to the method conceptual rules and the pro-
totype to ensure that all the functional requirements
are completely and correctly added by the technical
users in the FPT. These actions are needed to deliver
results with a higher reproducibility and accuracy, re-
gardless of external factors.
REFERENCES
Abrah
˜
ao, S. and Insfr
´
an, E. (2008). A metamodeling ap-
proach to estimate software size from requirements
specifications. In Proceedings of the 34th Euromicro
Conference Software Engineering and Advanced Ap-
plications, pages 465–475.
Improving Reproducibility whilst Maintaining Accuracy in Function Point Analysis
71

Abrah
˜
ao, S., Mendes, E., Gomez, J., and Insfr
´
an, E. (2007).
A model-driven measurement procedure for sizing
web applications: Design, automation and validation.
In Proceedings of the 10th International Conference
on Model Driven Engineering Languages and Sytems,
pages 467–481.
Adem, N. A. Z. and Kasirun, Z. M. (2010). Automating
function points analysis based on functional and non
functional requirements text. In Proceedings of the
2nd International Conference on Computer and Au-
tomation Engineering, pages 664–669.
Albrecht, A. J. (1979). Measuring application develop-
ment productivity. In Proceedings of the Joint SHARE,
GUIDE, and IBM Application Development Sympo-
sium, pages 83–92.
Basili, V. R. and Rombach, H. D. (1998). The TAME
project: towards improvement-oriented software envi-
ronments. IEEE Transactions on Software Engineer-
ing, 14(6):758–773.
Cantone, G., Pace, D., and Calavaro, G. (2004). Applying
function point to unified modeling language: Conver-
sion model and pilot study. In Proceedings of the 10th
International Symposium on Software Metrics, pages
280–291.
Chamundeswari, A. and Babu, C. (2008). An extended
function point approach for size estimation of object-
oriented software. pages 139–145.
Choi, S., Park, S., and Sugumaran, V. (2006). Function
point extraction method from goal and scenario based
requirements text. In Proceedings of the 11th Inter-
national Conference on Applications of Natural Lan-
guage to Information Sytems, pages 12–24.
Connolley, M. J. (1990). An Empirical Study of Function
Point Analysis Reliability. MIT, USA.
de Freitas Junior, M., Fantinato, M., and Sun, V. (2015).
Improvements to the function point analysis method:
A systematic literature review. IEEE Transactions on
Engineering Management, 62(4):495–506.
Easterbrook, S., Singer, J., Storey, M.-A., and Damian, D.
(2008). Selecting empirical methods for software En-
gineeringeering research, pages 285–311.
Edagawa, T., Akaike, T., Higo, Y., Kusumoto, S., Hanabusa,
S., and Shibamoto, T. (2011). Function point mea-
surement from web application source code based on
screen transitions and database accesses. Journal of
Sytems and Software, 84(6):976–984.
Fraternali, P., Tisi, M., and Bongio, A. (2006). Automat-
ing function point analysis with model driven devel-
opment. In Proceedings of the 16th Conference of
the Center for Advanced Studies on Collaborative Re-
search, page 18.
Harput, V., Kaindl, H., and Kramer, S. (2005). Extend-
ing function point analysis of object-oriented require-
ments specifications. In Proceedings of the 11th Inter-
national Software Metrics Symposium, pages 39–39.
Hevner, A. R., March, S. T., Park, J., and Ram, S. (2004).
Design science in information system research. MIS
Quarterly, 28(1):75–105.
IFPUG (2010). Function Point Counting Practices Man-
ual, release 4.3.1. International Function Point Users
Group, Westerville, Ohio.
Insfr
´
an, E., Pastor, O., and Wieringa, R. (2002). Require-
ments engineeringeering-based conceptual modelling.
Requirements Engineering, 7(2):61–72.
Kampenesa, V. B., Dyb
˚
aa, T., Hannaya, J. E., and Sjøberga,
D. I. K. (2009). A systematic review of quasi-
experiments in software engineeringeering. Informa-
tion and Software Technology, 51(1):71–82.
Kemerer, C. F. (1993). Reliability of function points mea-
surement: A field experiment. Communications of the
ACM, 36(2):85–97.
Klusener, S. (2003). Source code based function point anal-
ysis for enhancement projects. In Proceedings of the
29th International Conference on Software Mainte-
nance, pages 373–376.
Lamma, E. (2004). A system for measuring function points
from an ER-DFD specification. The Computer Jour-
nal, 47(3):358–372.
Lavazza, L. A., del Bianco, V., and Garavaglia, C. (2008).
Model-based functional size measurement. In Pro-
ceedings of the 2nd International Symposium on
Empirical Software Engineering and Measurement,
pages 100–109.
Low, G. C. and Jeffery, D. R. (1990). Function points
in the estimation and evaluation of the software pro-
cess. IEEE Transactions on Software Engineering,
16(1):64–71.
Miyawaki, T., Iijima, J., and Ho, S. (2008). Measuring func-
tion points from VDM-SL specifications. In Proceed-
ings of the 5th International Conference on Service
Sytems and Service Manag., pages 1–6.
Pow-Sang, J. A., Villanueva, D., Flores, L., and Rusu, C.
(2013). A conversion model and a tool to identify
function point logic files using UML analysis class di-
agrams. In Proceedings of the Joint Conference of the
23rd International Workshop on Software Measure-
ment and the 8th International Conference on Soft-
ware Process and Product Measurement, pages 126–
134.
Rao, K. K., Nagaraj, S., Ahuja, J., Apparao, G., Kumar,
J. R., and Raju, G. S. V. P. (2008). Measuring the func-
tion points from the points of relationships of UML.
In Proceedings of the 1st International Conference
on Computer and Electrical Engineering, pages 748–
752.
Uemura, T., Kusumoto, S., and Inoue, K. (2001). Function-
point analysis using design specifications based on the
Unified Modelling Language. Journal of Software
Maintenance: Research and Practice, 13(4):223–243.
Wieringa, R. J. (2014). Design science methodology for
information systems and software Engineeringeering.
Springer.
Wohlin, C., Runeson, P., H
¨
ost, M., Ohlsson, M. C., Reg-
nell, B., and Wessl
´
en, A. (2012). Experimentation in
Software Engineeringeering. Springer, 1 edition.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
72
