Recursive Pedagogy: Automatic Question Generation using Real-time

Learning Analytics

Fatima Abu Deeb

and Timothy Hickey

King Saud bin AbdulAziz University for Health Sciences, Al Ahsa, Saudi Arabia

Brandeis University, Waltham, MA, U.S.A.

Keywords:

Problem Solving Learning Environment, Peer Review, Educational Technology, Collaborative Learning,

Computer-supported Pedagogy.

Abstract:

In this paper we introduce the notion of Recursive Pedagogy, which is a computer-supported approach to

teaching and learning in which students solve problems assigned by an instructor using a Problem Solving

Learning Environment, and their attempts to solve that problem are then used by the system to create new

kinds of problems to help them build high level cognitive skills. The Recursive Pedagogy approach generalizes

an approach we introduced earlier: the Solve-Then-Debug (STD) pedagogy to teach coding. In STD, students

write a program given its description and, when their code passes all of the unit tests, they debug a sequence of

incorrect programs submitted by their peers, starting with those with the most common errors. In this paper,

we discuss two new Recursive Pedagogies that we have implemented in the Spinoza Python Tutor: Solve-

Then-Critique-Correct-Solutions shows students correct programs from their peers and asks them to critique

the code relative to a rubric; Solve-Then-Analyze-Unit-Tests shows students results of a set of unit tests and

asks them to describe the probable error based on the unit test results. After students submit their Recursive

Pedagogy analysis of a peer’s attempt, they are shown other students’ analyses of that attempt and are asked to

select the best one. Recursive Pedagogies are designed to build skills in problem-solving, debugging, testing,

and composing high quality solutions. Moreover, they can be used in a ﬂipped class and they keep all students

engaged in either problem solving or one of the other skills.

1 INTRODUCTION

There is a growing body of evidence demonstrating

that active learning in STEM classes can improve

learning outcomes (Freeman et al., 2014), increase

retention (Rath et al., 2007) and increase diversity

(Haak et al., 2011). One approach to incorporating

active learning in a class is to use a Problem Solv-

ing Learning Environment (PSLE) which allows the

instructor to pose problems in class for the students

to solve. Two mathematics PSLEs are WebWork

(Gage et al., 2002) and CalcTutor (Kime et al., 2015).

There are many PSLEs for coding including Spinoza

(Abu Deeb and Hickey, 2015), Codingbat (Parlante,

2007), CloudCoder (Andrei Papancea, 2013), and

many others.

Most PSLEs allow the students to submit multi-

ple attempts and provide immediate feedback about

the correctness of these attempts. They store student

interaction with the system to allow the instructor to

use these data to gauge a student’s understanding and

mastery of speciﬁc activities and concepts.

In a typical class using a PSLE the instructor

would use a Solve-Then-Debrief (STDB) pedagogy

in which they introduce new content in lecture format

and then test student understanding of the content by

assigning a problem in the PSLE, then stopping the

activity at the appropriate time, and moving into a de-

brief state where they discuss the most common errors

and compare and contrast the variety of possible so-

lutions.

If the PSLE is designed for classroom orchestra-

tion (e.g. Spinoza (Abu Deeb and Hickey, 2017) or

PCRS (Zingaro et al., 2013)), the instructor would be

able to monitor the progress of the students in real-

time and decide when to end the problem solving ac-

tivity based on actionable real-time learning analytics.

One major issue that arises when using a PSLE as

an in-class activity is that the students have different

skill levels. Some students will complete the problem

solving process very quickly and then have nothing to

do, while others will struggle and never complete the

204

Deeb, F. and Hickey, T.

Recursive Pedagogy: Automatic Question Generation using Real-time Learning Analytics.

DOI: 10.5220/0007673502040211

In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), pages 204-211

ISBN: 978-989-758-367-4

problem, even if given the entire class time.

Partly motivated by this weakness of the Solve-

Then-Debrief pedagogy using traditional PSLEs,

we developed the Solve-Then-Debug Pedagogy

(Abu Deeb et al., 2018). After students correctly

solved a problem using the PSLE they were shown se-

lected incorrect attempts from their classmates which

represented the most common errors their class had

made, and they were led through a seven step process

to analyze the attempt and contrast their analyses with

that of their peers.

The Solve-Then-Debug process can keep all stu-

dents actively engaged and moreover can help them

build valuable analytic skills. It does require that the

PSLE maintain an equivalence relation on incorrect

attempts so that it can ﬁnd the most common mistakes

and select actual student attempts from the largest of

those equivalence classes.

After using Solve-Then-Debug in a large Python

Programming class, we realized that this same ap-

proach could be used to help students develop a much

wider range of important programming skills, includ-

ing the ability to

• critique correct solutions for clarity, simplicity, ef-

ﬁciency, and programming style

• effectively analyze unit-test results,

• write and analyze program speciﬁcations

• create effective unit-tests specifying important

corner cases

and many others. In this paper we formalize these ob-

servations and present a generalization of the Solve-

Then-Debug approach which we call Recursive Ped-

agogy (RP) which can be applied to any Problem

Solving Learning Environment which supports what

we call Constructionist Problems. The fundamental

idea is that whenever a student solves the original

problem, the system analyzes all previous attempts

made by their classmates, groups them into equiva-

lence classes, and formulates a new kind of problem

by selecting representatives from those equivalence

classes.

For coding PSLEs in Computer Science courses,

the original problem typically involves writing a pro-

gram to solve a problem. This corresponds to the

”Create” activity at the top of Bloom’s taxonomy of

Cognitive Processes (Krathwohl, 2002). The addi-

tional Recursive Pedagogy problems usually involve

additional high level activities such as the Analyze

or Evaluate cognitive processes. They help students

build their ability to analyze other students’ attempts

along a number of dimensions. We will focus mostly

on Problem Solving Learning Environments for Cod-

ing and we will describe in detail the Recursive Ped-

agogies available in Spinoza, but as we will see this

approach is applicable in a wide-variety of ﬁelds.

The notion of Recursive Pedagogy can also be

used in a collaborative learning context such as Pair

Programming or POGIL, since group problem solving

still is subject to the problem of some groups complet-

ing the work more quickly than others, especially in

large classes.

2 RELATED WORK

Recursive Pedagogy is most similar to Contributing

Student Pedagogy (CSP) (Herman, 2012; Falkner

and Falkner, 2012) in which students are encouraged

to contribute in a valuable way to the work of their

peers. Peer Review is the best known example of CSP

(Søndergaard and Mulder, 2012; Clarke et al., 2014).

In Peer Review, students are asked to apply a rubric

to grade the submissions of their peers. Research on

Calibrated Peer Review (Walvoord et al., 2008) has

provided evidence that if this is done carefully, the

reviews can be nearly as accurate as those obtained

using Teaching Assistants. Calibrated Peer Review

requires all of the students to grade the same three

sample assignments representing poor, average, and

excellent work, and then it uses each student’s perfor-

mance on these grading tasks to calibrate their skill as

a grader. The calibration is then used to weight their

grading of other students work and to select graders

with at least one highly skilled grader for each group.

In recursive pedagogy, students analyze the work

of their peers just as in Peer Review and their work

helps other students learn the skills and concepts be-

ing taught as in Peer Review and CSP.

There are some fundamental differences though.

The goal of Recursive Pedagogy is not to grade stu-

dents work, especially since in this context students

are typically making multiple attempts, getting feed-

back, and eventually getting the correct answer. In-

deed, as originally conceived most students engaging

in RP will not have their work directly analyzed by

others, and those that do will usually not see the com-

ments that others have made. Moreover, RP works

best if the attempts can be automatically analyzed for

correctness and automatically put into a natural equiv-

alence class. Neither of these are features of tradi-

tional Peer Review or CSP. Finally, the RP approach

provides a multi-step online process where students

alternately perform their own analysis and then see

and evaluate the analyses of their peers so they can

learn from each other both to solve problems effec-

tively and to critique attempted solutions.

Thus the main difference between our approach

Recursive Pedagogy: Automatic Question Generation using Real-time Learning Analytics

205

and Peer Review is that Peer Review engages students

in a reviewing dialog where the reviews directly con-

tribute to improving that particular document being

reviewed and every student has their work reviewed

in this way. In our approach, the purpose of the re-

views is for the reviewer to learn how to analyze at-

tempted solutions and the person whose work is being

analyzed won’t necessarily see those comments and

hence couldn’t use them to improve their work.

3 RECURSIVE PEDAGOGIES

FOR GENERAL PSLES

In this section we introduce the notion of Recursive

Pedagogies for PSLEs in general. We present the

properties that a PSLE must have to effectively sup-

port Recursive Pedagogies and we provide algorithms

for picking the Recursive Pedagogy problems effec-

tively and efﬁciently.

3.1 Constructionist Problems

Recursive pedagogies are applicable for any problems

in which an attempted solution can be algorithmically

analyzed for correctness and which can also be ef-

fectively critiqued by the teacher or a fellow student.

Therefore, the optimal kind of problem for recursive

pedagogy is one where the attempted solutions belong

to a large space of solutions, ideally where the user

constructs an answer using some formal language,

e.g. coding, or mathematics. The PSLE tests these

attempted solutions for correctness automatically us-

ing unit testing or some other uniform rubric.

Another important property for Recursive Pedago-

gies is that the domain must support a natural equiv-

alence relation on the space of possible attempts, so

that the system can identify the ”most common mis-

takes.” These kinds of problems are often assigned

in STEM courses in Mathematics, Computer Science,

Physics, and Chemistry.

In CS1 classes, a programming problem that asks

students to write code to satisfy speciﬁed constraints

belongs to this type of problem as the students could

have many ways to construct attempted solutions. The

correctness of these attempts can be tested against

an instructor-designed suite of unit tests. The at-

tempted solutions can be grouped together in equiv-

alence classes in many different ways (e.g. by the re-

sults of the unit tests).

In a Mathematics class, the instructor could ask

the student to calculate the derivative of some func-

tion, and expect the student to write the result, not

choose it from a multiple choice answer. The student

could submit the attempt they made and get immedi-

ate feedback about correctness. Similar solutions pro-

duced by all the students are grouped together in the

same category of attempts. In this case different cat-

egories of attempts will correspond to different errors

that could signal common misconceptions in forming

the derivative. The teacher or students could analyze

or critique an attempted solution by trying to point

out possible misconceptions that would have resulted

in that error. They could also suggest ways of simpli-

fying the answer to make it more clear.

In a problem where a STEM course is taught us-

ing programming, we can assume that students will

be writing programs with relatively simple algorithms

and that they have enough knowledge about coding to

do so easily. So we expect most errors would be due

to not having full mastery of the domain knowledge

of the problem. Student could critique each other’s

attempted solutions by pointing out these mistakes in

the domain knowledge.

There are many PSLEs that support this kind of

problem, for example for Mathematics classes we

have WebWork (Gage et al., 2002), CalcTutor (Kime

et al., 2015), and ProveIt (Ferraro, 2010). In pro-

gramming, we have Spinoza (Abu Deeb and Hickey,

2015), codingbat (Parlante, ), cloudcoder (Andrei Pa-

pancea, 2013) and many others.

3.2 Problem Solving Markov Models

for RP

In any PSLE which supports constructionist problems

a Problem Solving Markov Model (PSMM) can be

created (Abu Deeb et al., 2016). A PSMM is a graph

where each node represents an equivalent class of at-

tempted solutions and each edge represents consecu-

tive attempts from a member of one class to a member

of the second class. The size of the node represents

the frequency of the attempt and the color represents

its correctness. The edges are labelled with the prob-

ability that a student will make that transition. The

PSMM is used in Recursive Pedagogy to select the

most common attempts of some particular type (e.g.

logic errors, syntax errors, correct solutions). We will

provide examples in the next section.

3.3 A Strategy for Choosing the

Attempts in Recursive Pedagogy

Some Recursive Pedagogies rely on choosing at-

tempts from the most common PSMM nodes. This is

a little subtle though, because the ranking of the sizes

of the PSMM nodes changes as time progresses. The

precise algorithm we have implemented in Spinoza is

CSEDU 2019 - 11th International Conference on Computer Supported Education

206

described in detail in (Abu Deeb and Hickey, 2017)

and it proceeds by taking the chronologically ﬁrst at-

tempt in the largest equivalence class that the student

has not yet seen. Typically the Recursive Pedagogy

will restrict the nodes of interest (e.g. only incor-

rect attempts, or only attempts made by at least 5%

of the class, etc.), and students will do 2-10 of these

RP problems for each problem they solve.

3.4 Scalability for Recursive Pedagogy

Since all students comment on the same Recursive

Pedagogy problems, often in the same order, the ini-

tial problems will get comments from large numbers

of students. A student who is in the second phase

may not be able to read through all of those com-

ments to select the best one, especially in a class of

over 100 students. Thus, there is a need to algorith-

mically limit the number of comments to be shown to

the students. One possible approach is to only keep

some of the most popular and some of the most re-

cent comments. Another approach is to only show the

ﬁrst 20 comments or so, as the ﬁrst ones are coming

from the fastest students who most likely know how

to solve the problem and are more likely to provide

better comments.

Another use of Recursive Pedagogy is to generate

hints for students who are still working on the initial

problem. If their most recent attempt is in the equiv-

alence class of a problem that has been selected as an

RP problem, then the instructor can choose to allow

them to see the critiques of that problem by other stu-

dents in the RP phase. The same issue of information

overload arises with hint generation as with RP com-

ments. One needs to decide which of the RP com-

ments to show the still strugging student. One pos-

sible solution is to ask the Teaching Assistants (TAs)

to provide hints and only show hints from those TAs.

We could also show just the most popular comments

as hints.

4 RECURSIVE PEDAGOGIES IN

SPINOZA

In this section we present the Recursive Pedagogies

that are currently implemented in Spinoza, describe

the pedagogy for each of these problems, and provide

some justiﬁcation for the choices made in designing

these pedagogies.

4.1 Solve-Then-Debug

Any PSLE that supports a Constructionist problem

solving activity, can be extended to include the Solve-

Then-Debug (STD) pedagogy which adds another

layer to the Solve-Then-Debrief (STDB) activity. It

helps engage the fastest students in the learning pro-

cess and can also provide additional hint generation

for the slower students. It was ﬁrst introduced in

(Abu Deeb et al., 2018).

The Solve-Then-Debug activity begins with the

instructor asking the students to solve a problem in a

PSLE. The students solve the problem all at the same

time, and they are allowed to submit multiple attempts

until they get the correct result.

After a student solves a problem correctly, they

can move to the next phase which we call the de-

bug phase; this guarantees that the debugger knows

at least one way to solve the problem, which could

make the debugging more accurate.

In the debug phase, the PSLE creates a problem

solving Markov Model for this problem, and the stu-

dent is given a problem from the largest incorrect

node in the Markov Model that they have not yet de-

bugged. We choose the largest node to allow students

to recognize the most common mistakes, and also to

increase the possibility that other students, who are

still in the solve phase, could be helped by these de-

bugging comments.

The student will see the ﬁrst attempt that belongs

to that category of error, and then is asked to classify

that error (syntax, logic, incomplete) and give a com-

ment describing why that attempt is incorrect. All stu-

dents who debug that node, will see the same attempt

and hence that attempt will acquire very many com-

ments. This was designed to insure that students are

beneﬁting from each other’s comments, but as men-

tioned above, this can create a problem if hundreds of

students are commenting on the same problem. We

discussed some remedies to this over-commenting is-

sue in the previous section.

The student in the debug phase can press the ”run”

button and see the results of the unit tests on the de-

bug problem code, but our system doesn’t allow them

to edit the buggy code. We make this restriction, be-

cause we do not want the students to write their solu-

tion to the problem; we want them to think critically

about the error and imagine the feedback they will get

using their ﬁx.

After the student submits their comment, they can

then see other students’ comments on the same incor-

rect attempt, and the restriction on editing the attempt

is removed, but we also add a restriction to prevent

the student from editing their original comment. Stu-

Recursive Pedagogy: Automatic Question Generation using Real-time Learning Analytics

207

Figure 1: This view of the student debugging comments from the Solve-Then-Debug activity has been annotated with X’s for

incorrect comments and checkmarks for correct comments, with a letter indicating which of the two main errors the comment

is referring to: (a) a logic error where all centuries are incorrectly counted as leap years and (b) a style issue since the code

can be written in one line, e.g. return y%4==0 and y%100!=0 or y%400==0.

dents are not allowed to change their comments since

otherwise they might be tempted to just copy other

students’ comments blindly in the next step without

trying ﬁrst, and not engage in critical thinking. At this

point, the student can then edit the buggy code and

get feedback of correctness or can use other students’

comments to try to ﬁx the buggy attempt. This step al-

lows the student to test their hypothesis, either by the

Spinoza unit-test feedback on their edited attempt, or

from looking at the other students’ comments.

The student must then pick the comment which

they think is most accurate, this is to encourage them

to read all the comments as it might help them gain in-

sights that they missed in their own debugging anal-

ysis, and also help develop their skills in critiquing

other students analyses. After choosing the most ac-

curate comment they can then move to the next debug

problem with the second highest number of attempts

and the cycle repeats until the instructor stops the ac-

tivity.

In a large class, it is rarely the case that the fastest

students will end up solving all the generated debug

practice problems before the instructor stops the ac-

tivity. However, in case a student does ﬁnish all the

major common misconceptions, Spinoza allows the

student to view all the subsequent versions in each

node, until all the versions are commented by this stu-

dent. Lastly if the student ﬁnishes all the debug prac-

tice problems, they can view their previous comments

and other students comments to all the debug practice

problems they have completed.

If the instructor chooses to enable hints in this ac-

tivity, then a struggling student who is still in the solve

phase, and gets an error that is in the same equivalence

class of a debug problem already solved by other stu-

dents, will be able to choose to see the comments on

that related attempt. This will allow slower students to

engage in critical thinking, as they would need to ex-

amine the different suggestions their peers provided

and pick the best one to try. Since these hints were

written by fellow students, they may contain both in-

sights and misleading suggestions.

Below is an incorrect attempt at writing a python

program to return true if the argument y is a leap year

and false otherwise. Fig. 1 shows an ”other students

comments” pane for this attempt where we have an-

notated the comments to show our analysis of their

comments.

def is_leap_year(y):

if y%400==0:

return True

elif y%4==0:

return True

elif y%100!=0:

return True

else:

return False

This problem was debugged by 10 students and 7

out of 10 gave correct comments. Two students indi-

cated that they do not know how to debug the prob-

lem. The last student just gave a completely wrong

comment on the coding style.

4.2 Solve-Then-Analyze-Unit-Tests

”Solve-Then-Analyze-Unit-Tests” is a variant of

Solve-Then-Debug. In this RP the students as before

CSEDU 2019 - 11th International Conference on Computer Supported Education

208

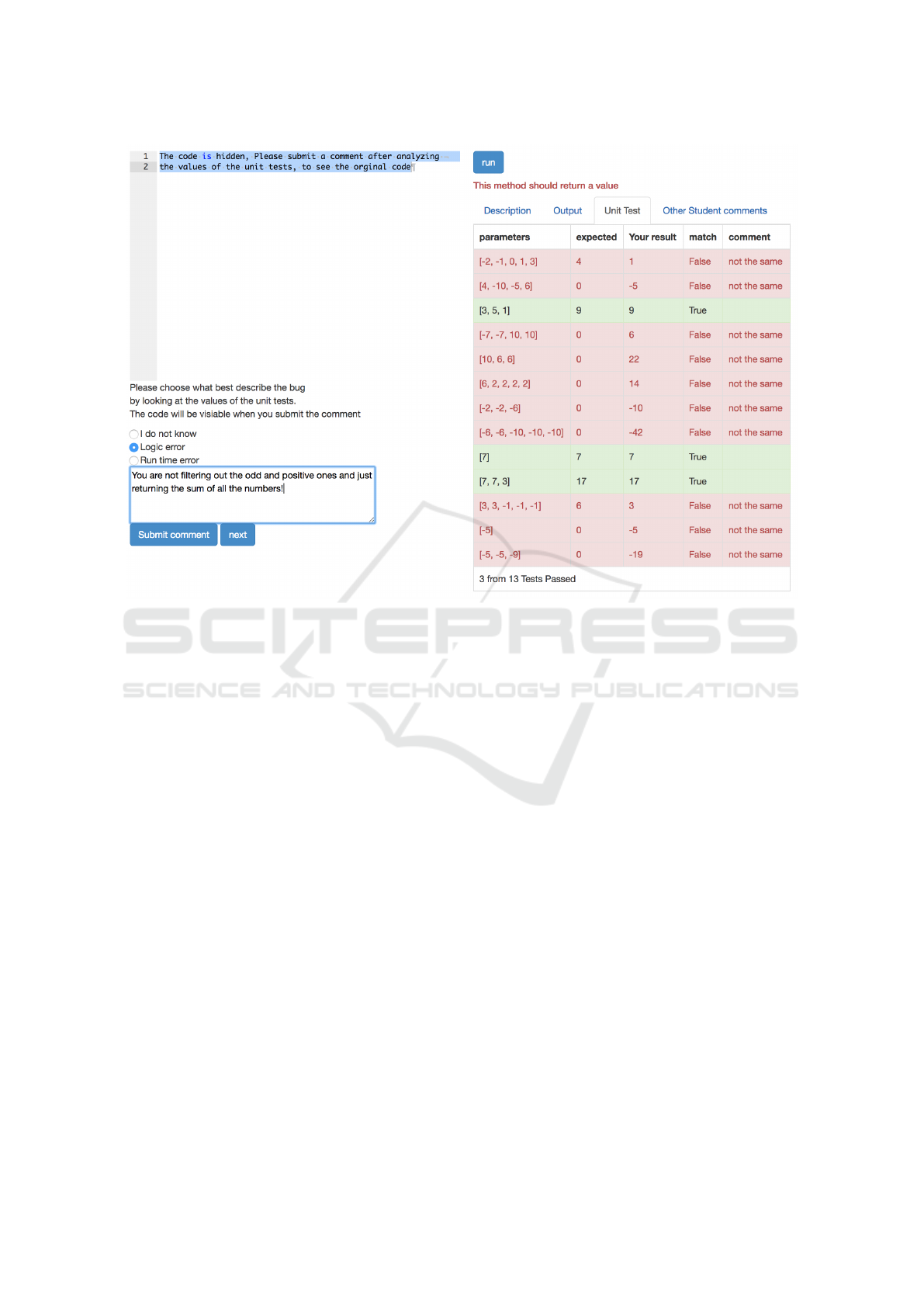
Figure 2: Solve-Then-Analyze-Unit-Tests.

will need to solve an instructor speciﬁed problem and

after they solve the problem correctly, they can ad-

vance to ”Analyze-Unit-Tests” phase. The ”Analyze-

Unit-Test” phase is different from the debug phase of

STD in that the student will only see the result of the

unit tests. The code that generates these unit tests will

be hidden as in Figure 2. After the student submits a

comment describing how to ﬁx the program to meet

the description of the problem, the code will be shown

to them along with other students’ comments for the

same version of the program. The student can edit

the code at this point to conﬁrm their analysis or con-

sider other students’ comments. To advance to the

next ”Analyze-Unit-Tests” problem, the student must

select the best comment that describes the bug based

on the unit tests.

We speculate that ”Solve-Then-Analyze-Unit-

Tests” (STAUC) would be better for providing a gen-

eral hint for the students who are still in the Solve

phase, as the students in the analyze phase will not be

presented with the code at that point so they will not

give too speciﬁc comment that suits only one version

of that class of attempt. For example, with hints gen-

erated by the Solve-Then-Debug pedagogy, students

often refer to some speciﬁc variable by name or to an

error on a particular line number. A problem in the

same equivalence class is unlikely to have a variable

with the same name or an error on that same line num-

ber, though they may well have the same error.

4.3 Solve-Then-Critique-Correct-

Solution

Another recursive pedagogical activity that we have

implemented in Spinoza is Solve-Then-Critique-

Correct-Solution. In this activity, all students are ﬁrst

asked to solve a problem using a PSLE, as usual. Af-

ter a student solves the problem correctly, the student

moves to the critique phase. In the critique phase

the PSLE selects a correct problem for all students

to critique. Ideally it would follow the same Markov

Model approach and use some ﬁner equivalence rela-

tion on the space of correct solutions to group them

into nodes and pick the most common nodes ﬁrst.

This categorization could be based on the style or

the simplicity of the solutions. Our current version

in Spinoza does not do any ﬁner analysis and simply

moves through the solutions in chronological order.

Our current implementation for Solve-Then-

Critique-Correct-Solution has two main steps. Af-

ter the student solves the problem, they are presented

with a correct solution by one of their classmates and

a rubric. After they submit their critique they can

see other students’ evaluations of the same attempt

Recursive Pedagogy: Automatic Question Generation using Real-time Learning Analytics

209

Figure 3: Solve-Then-Critique-Correct-Solution view of other students’ critiques of the ”movieCost” problem with selection

checkboxes for the best critique. Several students made no comments at all, but three made quite insightful comments, which

were then seen by all later students.

and they must select the best critique before they can

move on to the next problem. For example, Fig. 3

shows the critiques of the student attempt shown be-

low, which is a correct solution to a particular prob-

lem to calculate the cost of a movie ticket based on

the patron’s age.

def movieCost(age):

if age <18:

return 6

if age >=65:

return 6

else:

return 10

This step can help the student evaluate the quality

of their own critique by comparing it to the critiques

of their peers.

4.4 Preliminary Results

Spinoza was tested in a small Introduction to Python

Programming class with 19 students in Fall 2018.

Students were asked to solve Python programming

problems both in class and as homework. They were

also asked to complete six Recursive Pedagogy prob-

lems for each Spinoza programming problem they

completed. At the end of the semester students were

asked to complete a short survey about their impres-

sions of using Spinoza with Recursive Pedagogy, 15

out of 19 completed the survey.

When asked which type of Recursive Pedagogy

they liked the most, 53% selected the Solve-Then-

Debug (STD), 33% chose Solve-Then-Analyze-Unit-

Tests (STAUT), and 13% chose Solve-Then-Critique-

Correct-Solution (STCCS). When asked which was

most challenging, the results were 47% for STAUT,

33% for STCCS, and 20% for STD. A majority pre-

ferred having a mixture of different kinds of Re-

cursive Pedagogies (67%) rather than just one type

(33%). A plurality (40%) preferred to use Spinoza as

an in-class activity only, while (33%) preferred to use

it both as an in-class and a homework activity. Only

13% wanted to use it as homework only, and another

13% didn’t want to use Recursive Pedagogy at all.

5 CONCLUSIONS AND FINAL

REMARKS

This paper presented the idea of Recursive Pedagogy

which is a computer supported pedagogy designed

speciﬁcally for a class of students with varying skills

and speeds that are using a problem solving learning

environment to support active learning. It provides

some initial evidence that students found this peda-

gogy useful and interesting, but larger trial are needed

to determine its efﬁcacy.

In the future we intend to implement more exam-

ples of RP in Spinoza and to explore adding Recursive

Pedagogy to other PSLEs such as CalcTutor. We also

CSEDU 2019 - 11th International Conference on Computer Supported Education

210

plan to explore the use of different equivalence rela-

tions that look into the structure of the programs and

not just the behavior under unit tests.

REFERENCES

Abu Deeb, F., DiLillo, A., and Hickey, T. J. (2018). Using

ﬁne grained programming error data to enhance cs1

pedagogy. In International Conference on Computer

Supported Education.

Abu Deeb, F. and Hickey, T. (2015). Spinoza: The code

tutor. In Proceedings of the International Conference

on Computer and Information Science and Technol-

ogy, Ottawa, Canada.

Abu Deeb, F. and Hickey, T. (2017). Flipping introductory

programming classes using spinoza and agile peda-

gogy. In 2017 IEEE Frontiers in Education Confer-

ence (FIE), pages 1–9. IEEE.

Abu Deeb, F., Kime, K., Torrey, R., and Hickey, T. (2016).

Measuring and visualizing learning with markov mod-

els. In Frontiers in Education Conference (FIE), 2016

IEEE, pages 1–9. IEEE.

Andrei Papancea, Jaime Spacco, D. H. (2013). An open

platform for managing short programming exercises.

Proceedings of the ninth annual international ACM

conference on International computing education re-

search, pages 47–52.

Clarke, D., Clear, T., Fisler, K., Hauswirth, M., Krishna-

murthi, S., Politz, J. G., Tirronen, V., and Wrigstad,

T. (2014). In-ﬂow peer review. In Proceedings of the

Working Group Reports of the 2014 on Innovation &

Technology in Computer Science Education Confer-

ence, pages 59–79. ACM.

Falkner, K. and Falkner, N. J. (2012). Supporting and

structuring “contributing student pedagogy” in com-

puter science curricula. Computer Science Education,

22(4):413–443.

Ferraro, M. (2010). ProveIt math and proof practice.

Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K.,

Okoroafor, N., Jordt, H., and Wenderoth, M. P. (2014).

Active learning increases student performance in sci-

ence, engineering, and mathematics. Proceedings

of the National Academy of Sciences, 111(23):8410–

8415.

Gage, M., Pizer, A., and Roth, V. (2002). Webwork: Gen-

erating, delivering, and checking math homework via

the internet.

Haak, D. C., HilleRisLambers, J., Pitre, E., and Freeman, S.

(2011). Increased structure and active learning reduce

the achievement gap in introductory biology. Science,

332(6034):1213–1216.

Herman, G. L. (2012). Designing contributing student ped-

agogies to promote students’ intrinsic motivation to

learn. Computer Science Education, 22(4):369–388.

Kime, K., Torrey, R., and Hickey, T. (2015). Calctutor:

Applying the teachers dilemma methodology to cal-

culus pedagogy. In Frontiers in Education Conference

(FIE), 2015 IEEE, pages 1–8. IEEE.

Krathwohl, D. R. (2002). A revision of bloom’s taxonomy:

An overview. Theory into practice, 41(4):212–218.

Parlante, N. Codingbat code practice.

Parlante, N. (2007). Nifty reﬂections. ACM SIGCSE Bul-

letin, 39(2):25–26.

Rath, K. A., Peterfreund, A. R., Xenos, S. P., Bayliss, F.,

and Carnal, N. (2007). Supplemental instruction in in-

troductory biology i: enhancing the performance and

retention of underrepresented minority students. CBE-

Life Sciences Education, 6(3):203–216.

Søndergaard, H. and Mulder, R. A. (2012). Collaborative

learning through formative peer review: pedagogy,

programs and potential. Computer Science Education,

22(4):343–367.

Walvoord, M. E., Hoefnagels, M. H., Gafﬁn, D. D., Chum-

chal, M. M., and Long, D. A. (2008). An analysis of

calibrated peer review (cpr) in a science lecture class-

room. Journal of College Science Teaching, 37(4):66.

Zingaro, D., Cherenkova, Y., Karpova, O., and Petersen,

A. (2013). Facilitating code-writing in pi classes. In

Proceeding of the 44th ACM Technical Symposium

on Computer Science Education, SIGCSE ’13, pages

585–590, New York, NY, USA. ACM.

Recursive Pedagogy: Automatic Question Generation using Real-time Learning Analytics

211