
Efficient Task Scheduling in Cloud Computing using an Improved
Particle Swarm Optimization Algorithm
Guang Peng and Katinka Wolter
Department of Mathematics and Computer Science, Free University of Berlin, Takustr. 9, Berlin, Germany
Keywords:
Task Scheduling, Cloud Computing, Scientific Workflow, Particle Swarm Optimization, Multi-objective
Optimization, Gaussian Mutation.
Abstract:
An improved multi-objective discrete particle swarm optimization (IMODPSO) algorithm is proposed to solve
the task scheduling and resource allocation problem for scientific workflows in cloud computing. First, we
use a strategy to limit the velocity of particles and adopt a discrete position updating equation to solve the
multi-objective time and cost optimization model. Second, we adopt a Gaussian mutation operation to update
the personal best position and the external archive, which can retain the diversity and convergence accuracy
of Pareto optimal solutions. Finally, the computational complexity of IMODPSO is compared with three
other state-of-the-art algorithms. We validate the computational speed, the number of solutions found and the
generational distance of IMODPSO and find that the new algorithm outperforms the three other algorithms
with respect to all three metrics.
1 INTRODUCTION
Task scheduling and resource allocation is one ac-
tive research area in cloud computing. Cloud service
providers offer three different categories of service
Infrastructure as a Service (IaaS), platform as a Ser-
vice (PaaS), and Software as a Service (SaaS) (Mas-
dari et al., 2017). Since clients want to best utilize
the computing and memory resources offered by IaaS,
more and more complicated applications are applying
full or partial offloading to the Cloud. The users are
charged based on a pay per use model.
Workflow descriptions have been frequently used
to model scientific problems in areas such as as-
tronomy, biochemistry and physics (Rodriguez and
Buyya, 2014). These scientific workflows usually
have high computational complexity. So, cloud com-
puting provides a high-performance computing envi-
ronment for executing scientific workflows. Differ-
ent cloud resources are located in different regions
and have different capabilities for executing applica-
tions. According to the workflow and quality of ser-
vice (QoS) requirements, the task scheduling and re-
source allocation for scientific workflow needs to as-
sign different tasks to different cloud resources.
It is known that the task scheduling and resource
allocation problem is a NP-hard combination opti-
mization problem (Zhan et al., 2015). Rezvani (Rez-
vani et al., 2014) and Ergu (Ergu et al., 2013) used
a traditional integer linear programming (ILP) al-
gorithm and an analytic hierarchy process (AHP)
method to solve the resource allocation problems,
respectively. Traditional mathematical methods are
often used to solve simple models and they have
low efficiency for solving complex models. Due
to their strong heuristic search ability, different evo-
lutionary algorithms have been commonly used to
solve the different task scheduling and resource allo-
cation problems. Verma (Verma and Kaushal, 2014)
adopted the heuristic genetic algorithm (HGA) which
uses a chromosome to represent a schedule to solve
the task scheduling and resource allocation problem
with a deadline constraint. Singh (Singh and Kalra,
2014) and Hamad (Hamad and Omara, 2016) pro-
vided an improved genetic algorithm (GA) with a
Max-Min and tournament selection approach to solve
the task scheduling problems in cloud computing, re-
spectively. A GA often has slower convergence speed
and relatively needs more time to search for the opti-
mal solution.
Huang (Huang et al., 2013) presented a work-
flow scheduling model based on the weight aggrega-
tion of cost and makespan and used a heuristic parti-
cle swarm optimization (PSO) algorithm to obtain a
schedule satisfying various QoS requirements. Cao
(Cao et al., 2014) modelled security threats by means
58
Peng, G. and Wolter, K.
Efficient Task Scheduling in Cloud Computing using an Improved Particle Swarm Optimization Algorithm.
DOI: 10.5220/0007674400580067
In Proceedings of the 9th International Conference on Cloud Computing and Services Science (CLOSER 2019), pages 58-67
ISBN: 978-989-758-365-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of a workflow scheduling model and used a discrete
PSO based on the feasible solution adjustment strate-
gies to solve the model. PSO has a faster search but
is also easily caught in local optima. Liu (Liu et al.,
2011) used an ant colony optimization (ACO) algo-
rithm to solve the service flow scheduling with var-
ious QoS requirements in cloud computing. Li (Li
et al., 2011) used a load balancing ant colony opti-
mization (LBACO) algorithm to solve the cloud task
scheduling problem. The single ACO has low ef-
ficiency and is easily trapped in a local minimum.
Some researchers combined these algorithms to im-
prove performance. Gan (Gan et al., 2010) proposed
a hybrid genetic simulated annealing algorithm for
task scheduling in cloud computing. Liu (Liu et al.,
2014) used an integrated ACO with a GA to solve
a task scheduling model with multi QoS constraints
in cloud computing. Ju (Ju et al., 2014) presented a
hybrid task scheduling algorithm based on PSO and
ACO for cloud computing. These hybrid algorithms
can improve the search ability to a certain extent, but
increase the complexity of the algorithm at the sane
time.
The different evolutionary algorithms above are
mainly used to solve the task scheduling and re-
source allocation problems with only one objective
function. However, the task scheduling and resource
allocation problems in cloud computing are nor-
mally multi-objective optimization problems which
need to satisfy different QoS requirements. Sofia
(Sofia and GaneshKumar, 2018) adopted a nondom-
inated sorting genetic algorithm (NSGA-II) to solve
a multi-objective task scheduling model minimizing
energy consumption and makespan. NSGA-II may
need more time to sort the nondominated solutions.
Ramezani (Ramezani et al., 2013) designed a multi-
objective PSO (MOPSO) algorithm for optimizing
task scheduling to minimize task execution time, task
transfer time and task execution cost. MOPSO sorts
the archive members based on the QoS function with
weight aggregation for time and cost, where it is dif-
ficult to set the weight. Tsai (Tsai et al., 2013) used
an improved differential evolutionary algorithm to op-
timize a multi-objective time and cost model of task
scheduling and resource allocation in a cloud comput-
ing environment, but the model did not consider data
interdependency between the cloud customer tasks.
In this paper, considering the multi-objective op-
timization properties of workflow scheduling, we
present a multi-objective cost and time model con-
sidering data interdependency for a workflow appli-
cation in cloud computing. Since Durillo (Durillo
et al., 2009) and Nebro (Nebro et al., 2009) analyzed
the performance of six representative MOPSO algo-
rithms and concluded that all of them were unable to
solve some multi-modal problems satisfactorily. Ad-
ditionally, they studied the issue and found that the ve-
locity of the algorithms can become too high, which
can result the swarm explosion. Here, our motiva-
tion is twofold. First, we use a velocity constriction
mechanism to improve the search ability as well as
the convergence speed. Also, the Gaussian mutation
operation is applied to enhance the diversity. Then we
can obtain an efficient IMODPSO algorithm to solve
the proposed multi-objective cost and time model.
Our second goal is to compare the performance of
IMODPSO with three state-of-the-art multi-objective
optimization algorithms, i.e. NSGA-II (Deb et al.,
2002), MOEA/D (Zhang and Li, 2007) and MOEAD-
DE (Li and Zhang, 2009), which are the representa-
tive algorithms based on the Pareto ranking method
and decomposition approach. Especially, the decom-
position approach is a potential method in the current
multi-objective optimization research. The main con-
tribution of this paper is that the proposed IMODPSO
algorithm can achieve better accuracy and diversity
schedules satisfying different QoS requirements at a
lower cost than the competitors.
The rest of this paper is organized as follows: Sec-
tion 2 gives a brief introduction of multi-objective op-
timization. Section 3 presents the structure of the sci-
entific workflow application and the multi-objective
time and cost optimization model. The proposed
IMODPSO algorithm is illustrated in Section 4. Sec-
tion 5 discusses the simulations and results. Conclu-
sions and future directions will be highlighted in Sec-
tion 6.
2 MULTI-OBJECTIVE
OPTIMIZATION
Many real-world engineering optimization problems
often involve the simultaneous satisfaction of multiple
functions which are usually in conflict, that means the
improvement of one objective value can result in the
degradation of other objectives. Instead of finding a
single best one solution in single-objective optimiza-
tion, multi-objective optimization problems have a set
of trade-off solutions to satisfy all conflicting objec-
tives. A multi-objective optimization problem can be
defined as follows (Reyes-Sierra et al., 2006):
min y = F (x) = [ f
1
(x), f
2
(x), ··· , f
m
(x)]
s.t. g
i
(x) ≤ 0, i = 1, 2, ··· , p
h
j
(x) = 0, j = 1, 2, · · · , q
(1)
Where x = (x
1
, x
2
, ··· , x
n
) ∈ D is a n-dimension
decision vector in a decision space D; y =
Efficient Task Scheduling in Cloud Computing using an Improved Particle Swarm Optimization Algorithm
59

( f
1
, f
2
, ··· , f
m
) ∈ Y is a m-dimension objective vec-
tor in an objective space Y . g
i
(x) ≤ 0 (i = 1, 2, ··· , p)
refers to i-th inequality constraint and h
j
(x) ≤
0 ( j = 1, 2, ··· , q) refers to j-th equality constraint. In
the following, four important definitions for the multi-
objective optimization problems are given.
Definition 1 (Pareto Dominance).
A decision vector x
0
=
x
0
1
, x
0
2
, ··· , x
0
n
∈ D is said
to dominate a decision vector x
1
=
x
1
1
, x
1
2
, ··· , x
1
n
∈
D, denoted by x
0
≺ x
1
, if and only if
f
i
x
0
≤ f
i
x
1
, ∀i ∈
{
1, 2, ··· , m
}
f
j
x
0
< f
j
x
1
, ∃ j ∈
{
1, 2, ··· , m
}
(2)
Definition 2 (Pareto Optimal Solution).
A solution vector x
0
=
x
0
1
, x
0
2
, ··· , x
0
n
is called a
Pareto optimal solution, if and only if ¬∃x
1
: x
1
≺ x
0
.
Definition 3 (Pareto Optimal Solutions Set).
The set of Pareto optimal solutions is defined as
P
s
=
x
0
¬∃x
1
≺ x
0
.
Definition 4 (Pareto Front).
The Pareto optimal solutions set in the objec-
tive space is called Pareto front, denoted by PF =
{
F (x) = ( f
1
(x), f
2
(x), ··· , f
m
(x))
|
x ∈ P
s
}
.
3 PROBLEM DESCRIPTION
In this section we first present an example for the type
of problems we address in this paper. Then we intro-
duce our formally defined time and cost model.
3.1 Application and Schedule
Generation
We illustrate how the applications we consider can be
mapped onto resources by discussing an example.
The workflow application can be represented as a
directed acyclic graph G = (T, E), where the set of
vertices T = (T 1, T 2, ··· , T N) denotes N application
tasks and an edge E(Ti, T j) denotes the data depen-
dency between task Ti and T j. Ti is said to be the par-
ent task of T j if T j needs to receive the results from
Ti. Thus, T j cannot be executed until all of its par-
ent tasks are finished. Fig. 1 shows a directed acyclic
graph of a workflow application with nine tasks.
Task 1
Task 2
Task 3
Task 4
Task 5
Task 6
Task 7
Task 8 Task 9
In
Out
_
12
Out_13
Out
_
14
Out_25
Out_36
Out_47
Out
_
58
Out_68
Out
_
78
Out_89 Out
Figure 1: Graph workflow application with nine tasks.
In a cloud computing environment, resources are
located in different regions and have different pro-
cessing capacity for the workflow application tasks.
Assuming that the processing capacity in terms of
floating point operations per second (FLOPS) (Ro-
driguez and Buyya, 2014) is known we can calcu-
late the execution time of each application task. The
different resources need some time to receive and
preprocess each application task. The time needed
to transmit data for further processing from a par-
ent task to a child task, where the next processing
step takes place, is associated as data transfer time
to the child task. So, the total time of each task in-
cludes the receive time, the execution time and the
transfer time. The receive time and the transfer time
are proportional to the data size and inversely propor-
tional to the bandwidth of the network. The schedul-
ing of the workflow application tasks means to prop-
erly assign the different tasks to different resources.
One of the goals when computing a good schedule
of the tasks is to minimize the total time (Makespan)
needed to complete the workflow application. Assum-
ing that there are three different resources, an example
of a schedule generated for a workflow application is
shown in Fig. 2.
R1
R2
R3
T1_Totoal
T2_Total
T3_Total
T4_Total
T5_Total
T6_Total
T7_Total
T8_Total T9_Total
Makespan
Time
Resource
Figure 2: Example of a schedule generated for a workflow.
3.2 Multi-objective Time and Cost
Model
To generalize the discussion, let us assume that
there are M tasks of one workflow application and N
different resources. Let T
Rece
, T
Exe
, T
Trans
, and T
wait
be the receive time, execution time, transfer time
and waiting time, respectively. T (i)
Rece
is computed
by the data size of task i divided by the network
bandwidth. T(i)
Exe
is computed by the data size of
task i divided by the processing ability of assigned
resource. T (i)
Trans
is computed by the transmission
data size produced by parent tasks of task i divided by
the network bandwidth. Let T (i) Total represent the
completion time of task i. T
Res j
denotes the total time
to execute all the tasks in resource j. And Makespan
is the maximum time to complete the whole work-
flow application. T (i) Total, T
Res j
and Makespan
CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science
60

are shown as follows:
T (i) Total = T (i)
Rece
+ T (i)
Exe
+ T (i)
Trans
(3)
T
Res j
=
∑
T (i) Total +
∑
T
wait j
(4)
Makespan = Max (T
Res 1
, ···T
Res j
, ··· , T
Res N
) (5)
Let C
Rent
be the cost per unit time while us-
ing a cloud resource. C
Rent Rece
(i), C
Rent Exe
(i), and
C
Rent Trans
(i) represent the receive cost, execution
cost and transfer cost of task i, respectively. C
Total
is the overall cost of completing the workflow appli-
cation, which is defined as follows:
C
Total
=
M
∑
i=1
C
Rent Exe
(i) +
M
∑
i=1
C
Rent Rece
(i)
+
M
∑
i=1
C
Rent Trans
(i)
(6)
C
Rent Rece
(i) = T (i)
Rece
×C
Rent
C
Rent Exe
(i) = T (i)
Exe
×C
Rent
C
Rent Trans
(i) = T (i)
Trans
×C
Rent
(7)
Based on the above two objective functions, the
multi-objective optimization model of scheduling the
workflow application is constructed. It aims to find
a schedule to minimize the total cost and makespan
simultaneously.
4 PROPOSED IMODPSO
APPROACH
4.1 Particle Position Encoding
The scheduling of an workflow application is a NP
complete problem. When using a particle swarm op-
timization algorithm to solve the model we first adopt
an integer encoding. Each particle position represents
one schedule, and each position variable represents
the task assigned to the corresponding resource. So,
the length of encoding is equal to the number of tasks
of the workflow application. Considering the work-
flow application with nine tasks and three different
resources, Table 1 shows an example of an encoded
schedule [3, 1, 2, 2, 1, 2, 1, 2, 3], which means that task
1 is assigned to resource 3, task 2 is assigned to re-
source 1 etc.
Table 1: Particle position encoding.
Dimension 1 2 3 4 5 6 7 8 9
Encoding 3 1 2 2 1 2 1 2 3
4.2 Updating the Velocity and Position
In PSO, each particle position represents a po-
tential solution of the model (Kennedy and
Eberhart, 1995). Each particle has a position
X
i
(t) = [X
i,1
(t), X
i,2
(t), ··· , X
i,D
(t)] and a velocity
V
i
(t) = [V
i,1
(t),V
i,2
(t), ··· ,V
i,D
(t)] in a D-dimensional
search space. According to the personal best
position Pbest
i
(t) = [P
i,1
(t), P
i,2
(t), ··· , P
i,D
(t)]
and global best particle position Gbest (t) =
[G
1
(t), G
2
(t), ··· , G
D
(t)], the particle can move
to a better position while finally approaching the
optimal solution. The velocity and position updating
equations are calculated as follows:
V
i j
(t + 1) = wV
i j
(t) +C
1
r
1
(Pbest
i j
(t) − X
i j
(t))
+C
2
r
2
(Gbest
j
(t) − X
i j
(t))
(8)
X
i j
(t + 1) = X
i j
(t) +V
i j
(t + 1) (9)
Where i and j represent the j-th dimension of the
i-th particle, t is the index of the current iteration, w is
the inertia weight, C
1
and C
2
are the acceleration co-
efficients, r
1
and r
2
are uniformly distributed in [0, 1].
In order to control the particle’s velocity, we
applied a speed constriction coefficient χ obtained
from the constriction factor developed from Clerc and
Kennedy (Clerc and Kennedy, 2002), which can im-
prove the convergence ability of the algorithm.
χ=
2
2−ϕ−
p
ϕ
2
−4ϕ
(10)
ϕ=
C
1
+C
2
i f C
1
+C
2
> 4
0 i f C
1
+C
2
≤ 4
(11)
The new velocity constrained updating equation
and the velocity boundary constraint equation are re-
vised as follows:
V
i j
(t + 1) = χ •V
i j
(t + 1) (12)
V
i j
(t + 1) =
delta
j
i f V
i j
(t + 1) > delta
j
−delta
j
i f V
i j
(t + 1) ≤ −delta
j
V
i j
(t + 1) otherwise
(13)
delta
j
=
U pper limit
j
− Lower limit
j
2
(14)
Where U pper limit
j
and Lower limit
j
are the up-
per and lower boundaries of the j-th variable in each
particle.
To make the PSO suitable for solving a discrete
scheduling model, the position updating equation is
revised as follows:
X
i j
(t + 1) =
X
i j
(t) +V
i j
(t + 1)
(15)
The sign
bc
indicates that if the new position is be-
yond the lower or upper boundary of the position, then
Efficient Task Scheduling in Cloud Computing using an Improved Particle Swarm Optimization Algorithm
61

the new position should be the lower or upper bound-
ary. Otherwise, the updating position needs to adopt
the round operation to guarantee that positions are al-
ways integer numbers. With regard to the discrete
scheduling optimization problem, the global best par-
ticle can be selected from the nondominated solutions
stored in external archive randomly for each particle
during each iteration.
4.3 The Gaussian Mutation
Different from only one solution in the single opti-
mization problem, there exist some nondominated so-
lutions which are called Pareto optimal solutions in
multi-objective optimization problems. During the
iterations of the multi-objective particle swarm op-
timization algorithm, an external archive is used to
store the nondominated solutions. Furthermore, the
personal best position is updated by comparing the
Pareto dominance relationship with the current parti-
cle. To retain the diversity of solutions, a Gaussian
mutation operation is utilized for updating the per-
sonal best position. This can improve convergence
properties of the algorithm as it avoids that the algo-
rithm is stuck in a local optimum from which a Gaus-
sian mutation can direct it away. Moreover, the muta-
tion can enhance the diversity of the solutions.
The main idea of the Gaussian mutation operation
is to use the Pareto dominance relationship to com-
pare the current particle and Pbest. If Pbest is dom-
inated by the current particle, then Pbest is updated;
otherwise, the Gaussian mutation is adopted to disturb
the current particle to obtain a new particle which is
used to re-compare the Pareto dominance relationship
with Pbest. If the new particle dominates Pbest, then
it is used to replace Pbest; otherwise, Pbest is pre-
served. However, if they are nondominated, one of
them is selected randomly.
The Gaussian mutation operation is defined as fol-
lows. The mutation rate P
b
is changed by the itera-
tions.
X
i j
=
X
i j
+ delta
j
× randn
, i f rand <= P
b
X
i j
, i f rand > P
b
(16)
P
b
= 1 −
r
t
MaxIt
(17)
Where delta
j
is calculated according to Eq. 14.
rand is a random uniformly distributed value in [0, 1],
randn is a random Gaussian distributed value. t is the
index of the current iteration, MaxIt is the maximum
number of iterations. The operation (
bc
) guarantees
the position of particles to be integer encoded.
4.4 Updating the External Archive
After using the Gaussian mutation operation to up-
date the personal best solution, the obtained new par-
ticles are applied to update the external archive. The
Pareto dominance relationship is used to compare the
new particle and each solution in the external archive.
Then the new nondominated particles are added to the
external archive and the dominated solutions are elim-
inated from the external archive. Due to the diversity
of new particles created by Gaussian mutation, the
nondominated solutions in the external archive can be
updated with better convergence and diversity during
the iterations. The algorithm of updating the external
archive is shown as Algorithm 1.
Algorithm 1: Updating external archive.
Input: L solutions in archive, new N particles created by mutation
Out: The updated external archive
1. for i=1 to N do
2. for j=1 to L do
3. Compare dominance between particle i and solution j;
4. if Particle i is dominated by solution j then
5. Ignore the particle i;
6. elseif Solution j is dominated by particle i then
7. Delete solution j and add particle i into the external archive;
8. else
9. Add the particle i into the external archive;
10. endif
11. endfor
12. endfor
Based on the above improved operations, the pro-
cedure of the IMODPSO algorithm is shown as Algo-
rithm 2.
Algorithm 2: IMODPSO.
Input: T application tasks, R resources, initialize N particles
Out: The Pareto front
1. for t=1 to MaxIt do
2. for j=1 to N do
3. Select leader for each particle;
4. Update velocity (Eq. 12);
5. Update position (Eq. 15);
6. Evaluate the particle;
7. Update Pbest by Gaussian mutation operation;
8. Update the external archive according to Algorithm 1;
9. endfor
10. if archive size > max archive then
11. Maintain the external archive by crowding distance method;
12. endif
13. endfor
4.5 Comparison of Computational
Complexity with other
State-of-the-Art Algorithms
To analyze the computational complexity of the
proposed IMODPSO algorithm, we compare the
computational complexity of IMODPSO with three
CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science
62

other state-of-the-art algorithms, i.e. NSGA-II (Deb
et al., 2002), MOEA/D (Zhang and Li, 2007), and
MOEA/D-DE (Li and Zhang, 2009). NSGA-II is
known to be well-suited for fast nondominated sort-
ing. MOEA/D and MOEA/D-DE adopt a decomposi-
tion method using different evolutionary mechanisms.
The population size in all experiments is N, the
number of objectives of the multi-objective optimiza-
tion model is M. The archive size is set to be L.
The number of weight vectors in the neighborhood
of MOEA/D and MOEA/D-DE is T . The compu-
tational complexity for updating the external archive
is O(MNL), so the overall complexity of IMODPSO
is O(MNL). The computational complexity for up-
dating the neighbor population is O(MNT ), so the
overall complexity of MOEA/D and MOEA/D-DE
is O(MNT ). The computational complexity for fast
nondominated sorting is O(MN
2
), so the overall com-
plexity of NSGA-II is O(MN
2
). Normally, when
optimizing a multi-objective discrete problem, L is
smaller than N and close to T . Therefore, the pro-
posed IMODPSO algorithm has generally a lower
computational complexity for solving discrete opti-
mization problem.
5 SIMULATIONS AND RESULTS
In this section we first describe the experiment setup
and then discuss the results obtained from running the
experiments.
5.1 The Experiment Scenario
To test the performance of the different algorithms
for solving the multi-objective optimization model,
an experiment scenario based on the workflow appli-
cation in Section 2 is created (Rodriguez and Buyya,
2014). The matrix of receive time, execution time and
transfer time are set to (a), (b) and (c), respectively.
The unit of time is one hour. The rental cost on the
available three resources is as shown in Table 2. The
above parameters are an example, but the experiments
demonstrate what we theoretically showed above.
T
R
=
0.6 0.3 0.5
1 0.4 0.3
1.2 0.8 1.4
0.7 0.5 1.3
0.9 0.6 0.9
0.4 0.2 1
1.2 0.7 3
0.8 0.5 4
1.5 1.1 2.6
(a)
T
E
=
1.4 0.7 3.5
3 2.6 5.7
8.8 5.2 13.6
6.3 3.5 10.7
7.1 3.4 9.1
2.6 1.8 6
10.8 6.3 15
8.2 4.5 16
10.5 6.9 16.4
(b)
T
T
=
0 9 9 9 0 0 0 0 0
0 0 0 0 5 0 0 0 0
0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 7 0 0
0 0 0 0 0 0 0 2 0
0 0 0 0 0 0 0 3 0
0 0 0 0 0 0 0 2 0
0 0 0 0 0 0 0 0 10
0 0 0 0 0 0 0 0 0
(c)
Table 2: Rental cost on available resource.
Resource no. Rent cost (USD/per hour)
R1 6.2
R2 11.0
R3 2.5
5.2 Experiment Results
To prove the efficiency and effectiveness of the pro-
posed IMODPSO algorithm, we have used NSGA-
II, MOEA/D, and MOEA/D-DE to perform the same
experiments for comparison. IMODPSO, NSGA-II,
MOEA/D, and MOEA/D-DE have been implemented
in Matlab and are run on Intel Core i5-6300U 2.4GHz
CPU with 4GB RAM. The parameter settings in our
experiments are as follows.
The population size in IMODPSO, NSGA-II,
MOEA/D, and MOEA/D-DE is set to be 100. All
the algorithms run for 200 generations. The external
archive size is 100. NSGA-II and MOEA/D adopted
the simulated binary crossover (SBX) operator and
polynomial mutation for reproducing an offspring.
The crossover probability is set to be 1 and muta-
tion probability is set to be reciprocal of the number
of decision variables. MOEA/D-DE adopted the DE
operator and polynomial mutation for updating the
neighbor population. The mutation and crossover pa-
rameters of DE operator are set to be 0.5 and 1, re-
spectively. The polynomial mutation probability of
MOEA/D-DE is set to be reciprocal of the number of
decision variables. Both the neighborhood sizes of
MOEA/D and MOEA/D-DE are set to be 20.
The Pareto fronts produced by all four algorithms
are shown in Fig. 3. It can be seen that the results
Efficient Task Scheduling in Cloud Computing using an Improved Particle Swarm Optimization Algorithm
63

obtained by IMODPSO are better than the other three
algorithms. Not only the convergence of IMODPSO
is the best, but also the diversity of the Pareto so-
lutions. MOEA/D-DE and NSGA-II can get better
Pareto solutions than MOEA/D. Both MOEA/D-DE
and NSGA-II have their own advantages. MOEA/D-
DE may converge better, and NSGA-II can have more
diversity in the solutions. The specific objective func-
tions of the Pareto solutions are listed in Table 3,
Makespan is denoted by M
S
, and C
Total
is denoted by
C
T
. From Table 3, IMODPSO seems to have stronger
search ability and get the most number of Pareto opti-
mal solutions. MOEA/D and MOEA/D-DE can only
search for fewer quantities of Pareto optimal solu-
tions.
30 40 50 60 70 80 90 100 110 120
Makespan
250
300
350
400
450
500
550
C
Total
IMODPSO
MOEA/D-DE
MOEA/D
NSGA-II
Figure 3: The comparing Pareto fronts.
Table 3: The different Pareto optimal solutions obtained by
four algorithms.
IMODPSO MOEA/D-DE MOEA/D NSGA-II
M
S
C
T
M
S
C
T
M
S
C
T
M
S
C
T
37 515.2 38 455.5 48 499 38 455.5
38 455.5 40 440 56 493.7 40 440
40 440 61 424.5 58 466.3 55 438.5
55 438.5 65 403.3 73 454.2 61 424.5
58 422.1 67 400.5 79 450.8 65 403.3
62 421.9 68 391 81 405.6 67 400.5
65 403.3 75 383 85 374.9 68 391
67 400.5 82 382.5 90 368.8 75 383
68 391 86 381 99 360.3 86 381
75 383 89 374 89 374
76 377 91 371.5 91 371.5
85 374.9 97 355.3 98 363.5
89 374 107 292.3 102 362.5
90 368.8 111 277.5 103 356.5
91 348.5 107 300.5
103 338.1 111 277.5
107 292.3
111 277.5
In order to verify the efficiency and reliability of
the proposed algorithm, we executed each algorithm
30 times independently and used three performance
metrics to evaluate the different algorithms. The Gen-
erational Distance (GD) (Van Veldhuizen, 1999) has
been used to evaluate convergence, the Number of
Pareto Solutions (NPS) is our metric for diversity and
the Computation Time (CT) for computation speed.
All are calculated to compare the performance of
these four algorithms. GD and CT are the smaller the
better, and NPS is the opposite. The unit of CT is one
second.
The box diagrams of different performance met-
rics obtained by four algorithms are shown in Fig. 4,
Fig. 5, and Fig. 6. From Fig. 4, we can see that
GD obtained by IMODPSO is lower than the gen-
erational distance of the other three algorithms. In
addition, IMODPSO can find the Pareto optimal solu-
tions which represent the true Pareto front in nearly
half of the cases. The convergence of MOEA/D-
DE algorithm is relatively better than that of NSGA-
II for solving the discrete scheduling problem. The
worst convergence is MOEA/D. The NPS perfor-
mance metric in Fig. 5 demonstrates that the diversity
of IMODPSO is the best among the four algorithms.
Besides, the stability of Pareto solutions obtained by
IMODPSO is very high. Compared with MOEA/D-
DE, NSGA-II has higher diversity in the solutions.
Moreover, MOEA/D has a large fluctuation in the di-
versity of the solution.
As for the computation time in Fig. 6, IMODPSO
has the shortest search time and is hence much bet-
ter than the other three algorithms. This can be ex-
plained by the fact that MOEA/D-DE and MOEA/D
need more time to update the neighbor population,
and NSGA-II needs more time to perform the fast
nondominated sorting approach. Furthermore, the
different computational complexity also verifies the
computational speed of these four algorithms.
IMODPSO MOEA/D-DE MOEA/D NSGA-II
-2
0
2
4
6
8
10
12
14
16
GD
Figure 4: The boxplot of Generational Distance (small bet-
ter).
CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science
64
IMODPSO MOEA/D-DE MOEA/D NSGA-II
8
10
12
14
16
18
NPS
Figure 5: The boxplot of Number of Pareto Solutions (large
better).
IMODPSO MOEA/D-DE MOEA/D NSGA-II
2
4
6
8
10
12
14
CT
Figure 6: The boxplot of Computation Time (small better).
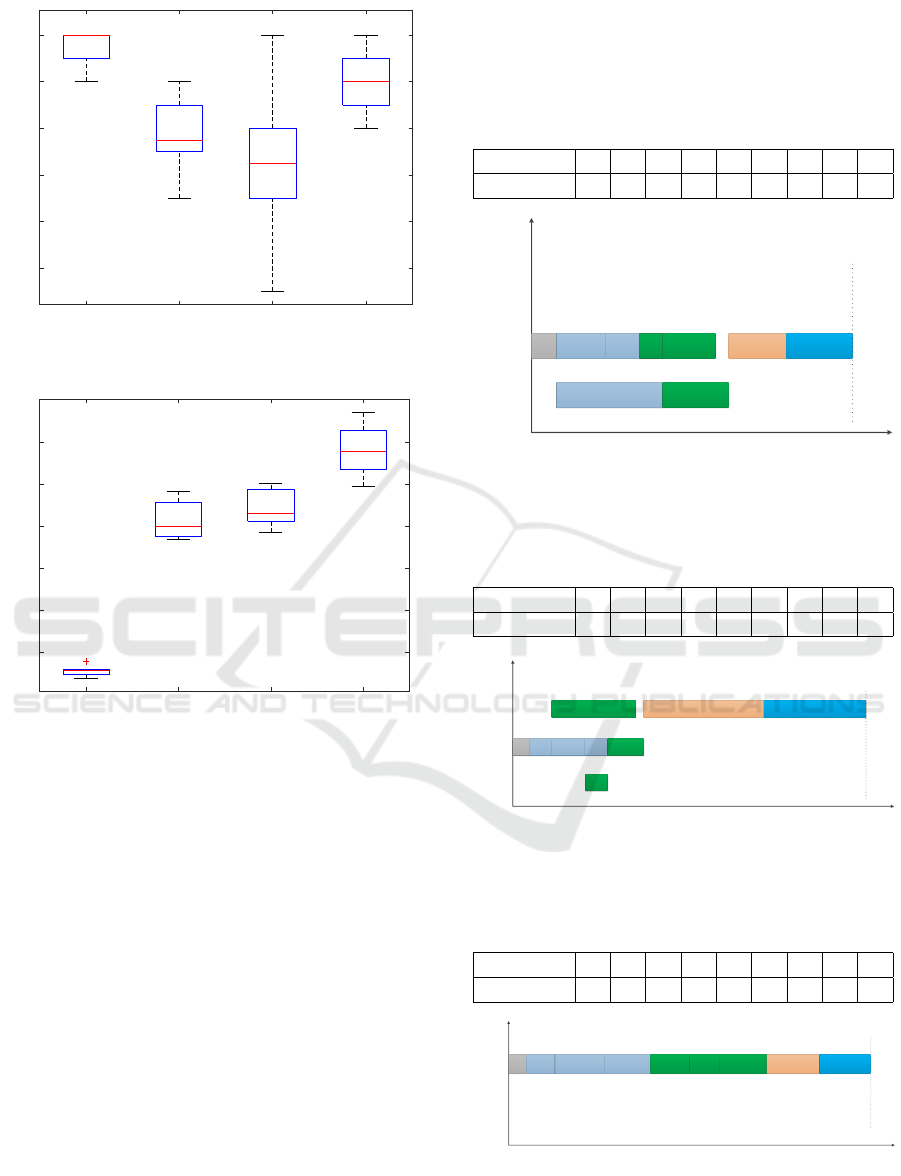
5.3 Analysis of Specific Schedules
In a specific scenario, the sum of the receive time and
execution time for each task on each of the available
resource is fixed. The transfer time is an important
factor, that needs to be taken into consideration se-
riously. The best schedule will minimize the total
cost and the Makespan. IMODPSO can obtain differ-
ent nondominated solutions which represent different
optimal schedules at a time. We choose three typi-
cal nondominated solutions from IMODPSO and an-
alyze them specifically. The Makespan of the differ-
ent schedules are one minimal, an intermediate and a
maximal one, respectively. Table 4, Table 5 and Ta-
ble 6 show the three different specific schedules and
Fig. 7, Fig. 8 and Fig. 9 show the three different Gantt
Charts. The first schedule does not assign any task to
resource 3 because the execution time in resource 3 is
relatively big compared with others. The third sched-
ule assigns all tasks to resource 3 because the rental
cost of resource 3 is the cheapest and the transfer time
can be ignored. Due to the different nondominated
solutions representing the different Makespan and to-
tal cost, the decision maker can decide for a suitable
schedule according to the specific requirements.
Table 4: The first schedule (Makespan=37, C
Total
=515.2).
Task 1 2 3 4 5 6 7 8 9
Resource 2 1 2 2 1 2 2 2 2
R1
R2
R3
T1
1
T3
6
T2
9+4
T4
4
T6
2
T5
8
T7
7
T8
2+5
T9
8
Makespan
Time
Resource
Figure 7: The first Gantt Chart (Makespan=37,
C
Total
=515.2).
Table 5: The second schedule (Makespan=65,
C
Total
=403.3).
Task 1 2 3 4 5 6 7 8 9
Resource 2 2 2 2 3 1 2 3 3
R1
R2
R3
T1
1
T3
6
T2
5+10
T4
4
T6
T5
1+3
T7
7
T8
3+2+20
T9
19
Makespan
Time
Resource
3
Figure 8: The second Gantt Chart (Makespan=65,
C
Total
=403.3).
Table 6: The third schedule (Makespan=111,
C
Total
=277.5).
Task 1 2 3 4 5 6 7 8 9
Resource 3 3 3 3 3 3 3 3 3
R1
R2
R3
T1
4
T2
Makespan
T3
6
15
T4
12
T5
10
T6
7
T7
18
T8
20
T9
19
Time
Resource
Figure 9: The third Gantt Chart (Makespan=111,
C
Total
=277.5).
Efficient Task Scheduling in Cloud Computing using an Improved Particle Swarm Optimization Algorithm
65

6 CONCLUSIONS
This paper has presented an improved multi-objective
discrete particle swarm optimization algorithm to
solve the task scheduling and resource allocation
problem for the scientific workflows in cloud com-
puting. It makes the three main contributions: a) the
velocity constriction strategy is applied to improve the
search ability of the algorithm in the discrete space; b)
the Gaussian mutation operation is adopted to boost
the diversity of the nondominated solutions in the ex-
ternal archive; c) the different performance metrics
of IMODPSO are compared with three other state-
of-the-art algorithms to validate the efficiency of pro-
posed algorithm. Experiments have shown that the
IMODPSO algorithm can obtain the Pareto optimal
solutions with good convergence and diversity using
less computation time. It is proved to be a stable
and efficient algorithm for solving the multi-objective
discrete task scheduling and resource allocation prob-
lem.
Future research will focus on optimizing large-
scale task scheduling and resource allocation problem
in the more practical engineering environment.
REFERENCES
Cao, J. F., Chen, J. J., and Zhao, Q. S. (2014). An opti-
mized scheduling algorithm on a cloud workflow us-
ing a discrete particle swarm. Cybernetics and infor-
mation technologies, 14(1):25–39.
Clerc, M. and Kennedy, J. (2002). The particle swarm-
explosion, stability, and convergence in a multidimen-
sional complex space. IEEE transactions on Evolu-
tionary Computation, 6(1):58–73.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
NSGA-II. IEEE transactions on evolutionary com-
putation, 6(2):182–197.
Durillo, J. J., Garc
´
ıa-Nieto, J., Nebro, A. J., Coello,
C. A. C., Luna, F., and Alba, E. (2009). Multi-
objective particle swarm optimizers: An experimen-
tal comparison. In International conference on evolu-
tionary multi-criterion optimization, pages 495–509.
Springer.
Ergu, D., Kou, G., Peng, Y., Shi, Y., and Shi, Y. (2013).
The analytic hierarchy process: task scheduling and
resource allocation in cloud computing environment.
The Journal of Supercomputing, 64(3):835–848.
Gan, G. N., Huang, T. L., and Gao, S. (2010). Genetic sim-
ulated annealing algorithm for task scheduling based
on cloud computing environment. In Intelligent Com-
puting and Integrated Systems (ICISS), 2010 Interna-
tional Conference on, pages 60–63. IEEE.
Hamad, S. A. and Omara, F. A. (2016). Genetic-based
task scheduling algorithm in cloud computing envi-
ronment. International Journal of Advanced computer
Science and Applications, 7(4):550–556.
Huang, J., Wu, K., Leong, L. K., Ma, S., and Moh, M.
(2013). A tunable workflow scheduling algorithm
based on particle swarm optimization for cloud com-
puting. The International Journal of Soft Computing
and Software Engineering, 3(3):351–358.
Ju, J. H., Bao, W. Z., Wang, Z. Y., Wang, Y., and Li, W. J.
(2014). Research for the task scheduling algorithm
optimization based on hybrid PSO and ACO for cloud
computing. International Journal of Grid and Dis-
tributed Computing, 7(5):87–96.
Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-
mization. In Proceedings of ICNN’95 - International
Conference on Neural Networks, volume 4, pages
1942–1948 vol.4.
Li, H. and Zhang, Q. (2009). Multiobjective optimization
problems with complicated pareto sets, MOEA/D and
NSGA-II. IEEE Transactions on evolutionary compu-
tation, 13(2):284–302.
Li, K., Xu, G. C., Zhao, G. Y., Dong, Y. S., and Wang,
D. (2011). Cloud task scheduling based on load bal-
ancing ant colony optimization. In 2011 Sixth Annual
ChinaGrid Conference, pages 3–9. IEEE.
Liu, C. Y., Zou, C. M., and Wu, P. (2014). A task scheduling
algorithm based on genetic algorithm and ant colony
optimization in cloud computing. In Distributed Com-
puting and Applications to Business, Engineering and
Science (DCABES), 2014 13th International Sympo-
sium on, pages 68–72. IEEE.
Liu, H., Xu, D., and Miao, H. K. (2011). Ant colony op-
timization based service flow scheduling with various
QoS requirements in cloud computing. In 2011 First
ACIS International Symposium on Software and Net-
work Engineering, pages 53–58. IEEE.
Masdari, M., Salehi, F., Jalali, M., and Bidaki, M. (2017).
A survey of pso-based scheduling algorithms in cloud
computing. Journal of Network and Systems Manage-
ment, 25(1):122–158.
Nebro, A. J., Durillo, J. J., Garcia-Nieto, J., Coello, C. C.,
Luna, F., and Alba, E. (2009). Smpso: A new
pso-based metaheuristic for multi-objective optimiza-
tion. In Computational intelligence in miulti-criteria
decision-making, 2009. mcdm’09. ieee symposium on,
pages 66–73. IEEE.
Ramezani, F., Lu, J., and Hussain, F. (2013). Task
scheduling optimization in cloud computing applying
multi-objective particle swarm optimization. In Inter-
national Conference on Service-oriented computing,
pages 237–251. Springer.
Reyes-Sierra, M., Coello, C. C., et al. (2006). Multi-
objective particle swarm optimizers: A survey of the
state-of-the-art. International journal of computa-
tional intelligence research, 2(3):287–308.
Rezvani, M., Akbari, M. K., and Javadi, B. (2014). Re-
source allocation in cloud computing environments
based on integer linear programming. The Computer
Journal, 58(2):300–314.
Rodriguez, M. A. and Buyya, R. (2014). Deadline based re-
source provisioningand scheduling algorithm for sci-
CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science
66

entific workflows on clouds. IEEE transactions on
Cloud Computing, 2(2):222–235.
Singh, S. and Kalra, M. (2014). Scheduling of independent
tasks in cloud computing using modified genetic algo-
rithm. In Computational Intelligence and Communi-
cation Networks (CICN), 2014 International Confer-
ence on, pages 565–569. IEEE.
Sofia, A. S. and GaneshKumar, P. (2018). Multi-objective
task scheduling to minimize energy consumption and
makespan of cloud computing using NSGA-II. Jour-
nal of Network and Systems Management, 26(2):463–
485.
Tsai, J. T., Fang, J. C., and Chou, J. H. (2013). Optimized
task scheduling and resource allocation on cloud com-
puting environment using improved differential evo-
lution algorithm. Computers & Operations Research,
40(12):3045–3055.
Van Veldhuizen, D. A. (1999). Multiobjective Evolutionary
Algorithms: Classifications, Analyses, and New Inno-
vations. PhD thesis, Air Force Institute of Technology,
Wright Patterson AFB, OH, USA. AAI9928483.
Verma, A. and Kaushal, S. (2014). Deadline con-
straint heuristic-based genetic algorithm for workflow
scheduling in cloud. International Journal of Grid and
Utility Computing, 5(2):96–106.
Zhan, Z. H., Liu, X. F., Gong, Y. J., Zhang, J., Chung,
H. S. H., and Li, Y. (2015). Cloud computing
resource scheduling and a survey of its evolution-
ary approaches. ACM Computing Surveys (CSUR),
47(4):63:1–63:33.
Zhang, Q. and Li, H. (2007). MOEA/D: A multiob-
jective evolutionary algorithm based on decomposi-
tion. IEEE Transactions on evolutionary computation,
11(6):712–731.
Efficient Task Scheduling in Cloud Computing using an Improved Particle Swarm Optimization Algorithm
67
