Efficient Computing of the Bellman Equation in a POMDP-based
Intelligent Tutoring System
Fangju Wang
University of Guelph, 50 Stone Road East, Guelph, Ontario, Canada
Keywords:
Intelligent Tutoring System, Computer Supported Education, Partially Observable Markov Decision Process,
Computational Complexity,
Abstract:
The Bellman equation is a core component in the POMDP model, which is an effective tool for handling
uncertainty in computer supported teaching. The equation is also a cost bottleneck in implementing a POMDP.
The cost to compute it is typically exponential. To build a POMDP-based intelligent tutoring system (ITS)
for practical tutoring, we must develop efficient techniques for computing the equation. In this paper, we first
analyze the cost in computing the equation, identifying the major factors that contribute to the complexity. We
then report our techniques for efficient computing of the Bellman equation. The techniques were developed
on the basis of close examination of features of tutoring processes. They are especially suitable for building
POMDP-based tutoring systems.
1 INTRODUCTION
In a tutoring process, a teacher may often be uncertain
about student knowledge states, and therefore uncer-
tain about choices of the most beneficial teaching ac-
tions (Woolf, 2009). In computer supported adaptive
tutoring, uncertainty exists in observing student states
and in choosing tutoring actions. An intelligent tu-
toring system (ITS) should be able to choose optimal
teaching actions under uncertainty. Handling uncer-
tainty has been a challenging task. The partially ob-
servable Markov decision process (POMDP) model is
an effective tool to deal with uncertainty. It may en-
able a tutoring system to take optimal actions when
states are not completely observable.
In a system with a POMDP for modeling tutor-
ing processes, the agent solves the POMDP to choose
optimal teaching actions. POMDP-solving is typi-
cally of exponential complexity (Carlin and Zilber-
stein, 2008; Rafferty et al., 2011). In recent years,
researchers have conducted extensive research to de-
velop tractable techniques for POMDP-solving, and
have achieved good progresses. However, most of
the techniques are still expensive when applied to real
world problems. Computational complexity has been
a major obstacle to applying POMDPs in building
practical systems.
Our research is aimed at developing efficient tech-
niques for POMDP-solving, which are especially
suitable for building adaptive tutoring systems. In
the previous stages, we developed new techniques of
policy trees. Using the techniques, we could signifi-
cantly reduce the costs in making a decision, and build
space efficient ITSs for platforms with limited storage
spaces (Wang, 2016; Wang, 2017).
In the research reported in this paper, we develop
techniques to further improve efficiency in comput-
ing trees. The techniques achieve better efficiency by
localizing computing within smaller state spaces. In
this paper, we focus on cost reduction in evaluating
the Bellman equation, which is one of the core equa-
tions in the POMDP model, and has been a cost bot-
tleneck in building POMDP-based systems.
This paper is organized as follows. In sec-
tion 2, we describe the structure and computing in
a POMDP-based ITS to provide a technical back-
ground, and also review some work related with
POMDP-based ITSs. In section 3, we survey the ex-
isting work for improving efficiency in POMDP solv-
ing, in both general POMDP systems and POMDP-
based ITSs. In section 4, we analyze computing costs
in a POMDP-based intelligent tutoring systems, and
identify the major factors that contribute to the great
computational complexity. In section 5, we describe
our techniques to reduce costs for POMDP solving,
with emphasis on evaluating the Bellman equation. In
section 6, we present and analyze some experimental
results.
Wang, F.
Efficient Computing of the Bellman Equation in a POMDP-based Intelligent Tutoring System.
DOI: 10.5220/0007676000150023
In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), pages 15-23
ISBN: 978-989-758-367-4
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

2 POMDP-BASED INTELLIGENT
TUTORING SYSTEMS
Intelligent tutoring systems have been developed as
useful teaching aids in areas including mathematics
(Woolf, 2009), physics (VanLehn et al., 2010), medi-
cal science (Woolf, 2009), and many others (Cheung
et al., 2003). Numerous students have benefited from
one-to-one, adaptive tutoring offered by ITSs.
Adaptive tutoring is the teaching in which a
teacher chooses optimal teaching actions based on in-
formation about student knowledge states. It is impor-
tant for an ITS to store and trace the state information.
The major components in an ITS include a student
model, a teaching model, and a domain model. The
student model is for storing and tracing information
of student states. In each tutoring step, the tutoring
agent accesses this model for information of the stu-
dent’s current state, then consults the tutoring model
with the state information for a tutoring strategy, and
then based on the strategy retrieves the domain model
to get the knowledge to teach.
When states are completely observable to the tu-
toring agent, we can use a Markov decision process
(MDP) to model adaptive tutoring. An MDP may
model a decision-making process in which the agent
knows exactly what the current states are, and can
choose actions available in different states to maxi-
mize rewards. However, in adaptive tutoring, student
states are not always completely observable. Thus the
MDP model has limitations when applied in building
ITSs. The partially observable Markov decision pro-
cess (POMDP) model, an extension of MDP, may be
more suitable.
Major parts of an POMDP includes a set of states,
a set of actions, a set of observations, a reward func-
tion, and a policy. In a decision step, the agent is in a
state. The decision is to choose an action that is avail-
able in the state and maximizes the reward. Such an
action is referred to as the optimal action. When the
agent does not know exactly what the current state
is, it infers information of states from the current ob-
servation, and represents the information as a belief,
which is a set of probabilities that the agent is in dif-
ferent states. Based on the belief, the agent uses the
optimal policy to choose the optimal action. As men-
tioned, the calculation to find the optimal policy is
referred to as POMDP-solving.
We can build an ITS by casting its components
onto a POMDP: The student model is mapped to the
state space, with each POMDP state representing a
student knowledge state; The tutoring model is im-
plemented as the policy, which is a function of beliefs,
returning actions.
At a point in a tutoring process, the agent is in a
state, which represents the current knowledge state of
the student. The agent does not have exact informa-
tion about the state, but has a belief about the states.
Based on the belief, the agent chooses and takes a tu-
toring action. The action causes the agent to enter
a new state, where the agent has a new observation.
Then the agent updates its belief based on the previ-
ous belief, the immediate action, and the new obser-
vation. And then it starts the next step of tutoring.
Since 1980’s, researchers have applied the
POMDP model to handle uncertainty in intelligent tu-
toring, and developed POMDP-based ITSs to teach
in different areas (Cassandra, 1998; Williams et al.,
2005; Williams and Young, 2007; Theocharous
et al., 2009; Rafferty et al., 2011; Chinaei et al.,
2012; Folsom-Kovarik et al., 2013). In the systems,
POMDPs were used to model student states, and to
customize and optimize teaching. In a commonly
used structure, student states had a boolean attribute
for each of the subject contents, actions available to
a tutoring agent were various types of teaching tech-
niques, and observations were results of tests given
periodically. Researchers agreed that computational
complexity of POMDP-solving in ITSs was a major
difficulty in developing practical systems (Cassandra,
1998; Rafferty et al., 2011; Folsom-Kovarik et al.,
2013).
3 RELATED WORK
Since the early years of POMDP research, it has
been a major topic to develop efficient algorithms for
POMDP-solving (Braziunas, 2003). In the follow-
ing, we first review the work to develop efficient algo-
rithms for “general” POMDP problems, then the work
in building POMDP-based ITSs.
The method of policy trees is a practical one for
POMDP-solving (Kaelbling et al., 1998). In this
method, solving a POMDP is to evaluate a set of pol-
icy trees and choose the optimal. In a policy tree,
nodes are labeled with actions, and edges are labeled
with observations. After an action, the possible ac-
tions at the next decision step are those connected by
the edges of observations from it. Each policy tree
is associated with a value function. In choosing an
optimal tree, the value functions of a set of trees are
evaluated. Policy tree value functions and their evalu-
ation will be discussed in more details in the next sec-
tion. As will be seen that the number of policy trees
and the costs for evaluating individual trees grow ex-
ponentially. To achieve better efficiency, researchers
have developed algorithms, some were related to the
CSEDU 2019 - 11th International Conference on Computer Supported Education
16

method of policy trees.
Sondik’s one-pass and two-pass algorithms are
exact algorithms for POMDP-solving (Cassandra,
1988). The one-pass algorithm starts with an arbi-
trary belief, generates sets of vectors and then sweeps
through the belief space where the vectors are use-
ful. The two-pass algorithm has an additional pass in
which the sets are merged. The linear support algo-
rithm by Cheng is inspired by Sondik’s idea, but has
less strict constraints (Cheng, 1988). The algorithm
starts with a belief, generates the vector for that belief
and then checks the region in the belief space to see if
the vector is correct at all vertices.
The witness algorithm developed by Littman et al
(Littman, 1994) uses the same basic structure in the
algorithms by Sondik and Cheng. In each decision
step, it finds the best value function for each action.
After it finds the best value functions, it combines
them into the final value function.
In the field of POMDP-based ITSs, researchers
developed POMDP-solving techniques by taking into
consideration the special features of intelligent tu-
toring. Rafferty and co-workers created a POMDP-
based system for teaching concepts (Rafferty et al.,
2011). A core component of the system was a tech-
nique of fast teaching by POMDP planning. The tech-
nique was for computing approximate POMDP poli-
cies, which selected actions to minimize the expected
time for the learner to understand concepts.
Rafferty et al. developed a method of forward
trees, for solving the POMDP. The forward trees were
variations of policy trees. A forward tree was built by
interleaving branching on actions and observations.
For the current belief, a forward trees was constructed
to estimate the value of each pedagogical action, and
the best action was chosen. The learner’s response,
plus the action chosen, was used to update the belief,
and then a new forward search tree was constructed
for selecting a new action for the updated belief. The
cost of searching the full tree is exponential in the
task horizon, and requires an O(|S|
2
) operations at
each node. To reduce the number of nodes to search
through, the researchers restricted the tree by sam-
pling actions, and limited the horizon to control the
depth of the tree.
In the work reported in (Wang, 2016), an exper-
imental ITS was developed for teaching concepts in
computer science. A POMDP was used in the system
to model processes of intelligent tutoring. A method
of policy trees was proposed for POMDP-solving. In
the method, policy trees were grouped. To choose
an optimal action for responding to a given student
query, the agent dynamically created a group of pol-
icy trees related with the query, evaluated the trees,
and chose the optimal. For reducing the costs in mak-
ing a decision, techniques were developed to mini-
mize sizes of the tree and decrease the number of trees
to evaluate.
The research for improving POMDP-solving
have made good progress towards building practical
POMDP-based ITSs. Various techniques have been
developed. However, they were still very costly. For
example, as the authors of (Rafferty et al., 2011)
concluded, computational challenges existed in their
technique of forward trees, despite sampling only a
fraction of possible actions and using short horizons.
Also, how to sample actions and how to shorten a
horizon are challenging problems. Computational
complexity has been a barrier to applying the POMDP
model to intelligent tutoring.
4 THE BELLMAN EQUATION
FOR VALUE FUNCTIONS
4.1 The Bellman Equation in a POMDP
As discussed, the method of policy trees is a practical
technique for POMDP-solving. In the method, each
policy tree is associated with a value function, which
is used to evaluate the tree. The value function of
policy tree τ is denoted as V
τ
. Eqn (1) is the Bellman
equation for V
τ
:
V
τ
(s) = R (s,a)+γ
∑
s
0
∈S
P(s
0
|s,a)
∑
o∈O
P(o|a,s
0
)V
τ(o)
(s
0
)
(1)
The Bellman equation is a core equation in the
POMDP model. It is evaluated in every decision step.
In applying the POMDP model to intelligent tutoring,
the Bellman equation is a cost bottleneck. Before an-
alyzing the costs for POMDP-solving, we explain the
symbols in the equation.
S is the set of states of the POMDP. s ∈ S is the
state that the agent is currently in, i.e. the current
state. V
τ
(s) evaluates the long term return of taking
the tree (policy) τ in state s. a is the root action of τ,
i.e. the action that the root of τ is labeled with. R (s, a)
is the expected immediate reward that the agent re-
ceives after it takes a in s, calculated in Eqn (2). s
0
is
the next state, i.e. the state that the agent enters into
after taking a in s. P(s
0
|s,a) is the transition proba-
bility that the agent’s state changes from s into s
0
after
the agent takes a. O is the set of observations. o ∈O is
the observation that the agent perceives after taking a
and enters s
0
. P(o|a, s
0
) is the observation probability
that the agent observes o after it takes a and enters s
0
.
τ(o) is the subtree in τ which is connected to the root
Efficient Computing of the Bellman Equation in a POMDP-based Intelligent Tutoring System
17

by the edge labeled with o. γ is a reward discount-
ing factor (0 ≤ γ ≤ 1), which assigns weights to the
rewards in the future.
The R (s,a) in Eqn (1) is calculated as
R (s,a) =
∑
s
0
∈S
P(s
0
|s,a)R (s,a,s
0
) (2)
where R (s, a, s
0
) is the expected immediate reward af-
ter the agent takes a in s and enters s
0
.
In Eqn (1), the first term on the right hand side is
the expected immediate reward and the second term
is the discounted expected reward in the future. The
function evaluates the long term return when the agent
takes policy tree τ in state s.
As discussed before, in a POMDP, states are not
completely observable, the agent infers state informa-
tion, represents the information as beliefs, and makes
decisions based on beliefs. When a method of pol-
icy trees is used, a tree value function is a function of
belief. In the following, we describe how the value
function of belief is defined in terms of the Bellman
equation, and how the policy is defined in terms of the
value function of belief.
Belief b is a distribution over the states, defined as
b = [b(s
1
),b(s
2
),...,b(s
|S|
)] (3)
where s
i
∈ S (1 ≤ i ≤|S|) is the ith state in S, b(s
i
) is
the probability that the agent is in s
i
, and
∑
|S|
i=1
b(s
i
) =
1.
From Eqns (1) and (3), we have the value function
of belief b given τ:
V
τ
(b) =
∑
s∈S
b(s)V
τ
(s). (4)
Then we have policy π(b) returning the optimal policy
tree
ˆ
τ based on b:
π(b) =
ˆ
τ = argmax
τ∈T
V
τ
(b), (5)
where T is the set of trees to evaluate in making the
decision. In a decision step, π(b) guides the agent
to choose an action based on the current belief b to
maximize the long term return.
4.2 Analysis of Costs for Choosing
Optimal Actions
Figure 1 illustrates the general structure of a policy
tree, in which a
r
is the root action, a is an action, and
|O| is the number of possible observations. In every
subtree, the root node has |O| children, connected by
edges labeled with all the possible observations. Ex-
pect the root action a
r
, every node may be labeled
with all the possible actions in A. Therefore, the num-
ber of policy trees with root action a
r
is exponential,
as will be discussed shortly.
a aa
...
a
r
o
|O|
o
1
aa a
...
o
2
o
1
o
2
o
|O|
...
...
...
... ...
Figure 1: The general structure of a policy tree.
When a technique of policy trees is used for
POMDP-solving, finding the optimal policy is to eval-
uate all the policy trees and identify the optimal tree.
In each decision step, the agent finds the optimal pol-
icy tree based on the current belief (see Eqn (5)). It
then takes the root action of the tree.
From Eqn (5), we can see that to find the optimal
policy tree
ˆ
τ, we need to calculate V
τ
(b) for every
τ ∈T . The cost is O(|T |), where |T |is the number of
trees in T . From Eqn (4) we can see that to calculate
V
τ
(b), the number of times to calculate V
τ
(s) is |S|,
the number of states in S. The cost is O(|S|).
In the following, we examine the costs for calcu-
lating the Bellman Equation for V
τ
(s) in (1). The cost
for calculating the first term on the right hand side is
O(|S|) (see Eqn (2)), and the cost for the second term
is O(|S||O|) because of the double nested sums. For
each node in τ, we calculated both terms.
The size of a policy tree (i.e. the number of nodes)
depends on the number of possible observations and
the horizon. When the horizon is H, the number of
nodes in a tree is
H−1
∑
t=0
|O|
t
=
|O|
H
−1
|O|−1
. (6)
Therefore the cost for calculating an individual tree
could be O(|S||O|
H
)
Now we estimate the total number of trees. At
each node, the number of possible actions is |A|. Thus
the number of all possible H-horizon policy trees is
|A|
|O|
H
−1
|O|−1
. (7)
Therefore |T | can be approximately O|A
|O|
H
|.
From the above analysis, the cost related to eval-
uating the Bellman equation could be approximated
as
O(|S||S||O|
H
|A|
|O|
H
), (8)
where the first |S| is for s ∈ S in Eqn (4), the second
|S| is for the s
0
∈S in Eqn (1), the third factor approx-
imates the tree size, and the last factor approximates
the number of trees.
CSEDU 2019 - 11th International Conference on Computer Supported Education
18

Based on the analysis, we developed a set of tech-
niques to improve the efficiency in POMDP-solving.
The techniques reduce the sizes of state space, obser-
vation set, and tree set, and shortens horizons, in cal-
culating the Bellman equation in choosing a tutoring
action. Before presenting the techniques, we define
states, actions, observations, etc. in a POMDP-based
ITS.
5 DEFINITIONS IN A
POMDP-BASED ITS
We built a POMDP-based ITS for experimenting the
techniques we develop, including those to improve
computing efficiency. It is a system teaching concepts
in software basics. It teaches a student at a time, on a
one-to-one base.
We define the states in terms of concepts in the
instructional subject. In software basics, concepts in-
clude program, instruction, algorithm, and many oth-
ers. We associate each state with a state formula,
which is of the form:
(C
1
C
2
C
3
...C
N
), (9)
where C
i
is the boolean variable for the ith concept
C
i
, taking a value
√
C
i
or ¬C
i
(1 ≤ i ≤ N), and N is
the number of concepts in the instructional subject.
√
C
i
represents that the student understands C
i
, and
¬C
i
represents that the student does not. A formula is
a representation of a student knowledge state. For ex-
ample, formula (
√
C
1
√
C
2
¬C
3
...) is a representation
of the state in which the student understands C
1
and
C
2
, but not C
3
, ... States thus defined have Markov
property. This is a commonly used method for defin-
ing states in POMDP-based ITSs (Cassandra, 1998;
Rafferty et al., 2011).
In most subjects of science and mathematics, con-
cepts have prerequisite relationships with each other.
To study a concept well, a student should understand
its prerequisites first. The prerequisite relationships
can be represented by a directed acyclic graph (DAG),
with a vertex representing a concept and an edge rep-
resenting a prerequisite relationship. The concepts in
formula (9) are topologically sorted from the DAG of
the concepts in the instructional subject. In a state
formula, all the prerequisites of concept C
i
are in
C
1
,...,C
i−1
.
Asking and answering questions are the primary
actions of the student and system in a tutoring pro-
cess. Other actions are those for greeting, confirma-
tion, etc.
In an ITS for teaching concepts, student actions
are mainly asking questions about concepts. Asking
“what is a query language?” is such an action. We
assume that a student action concerns only one con-
cept. In this paper, we denote a student action of ask-
ing about concept C by (?C), and use (Θ) to denote
an acceptance action, which indicates that the student
is satisfied by a system answer, like “I see”, “Yes”,
“please continue” or “I am done”.
The system actions are mainly answering ques-
tions about concepts, like “A query language is a high-
level language for querying.” We use (!C) to denote a
system action of teaching C, and use (Φ) to denote a
system action that does not teach a concept, for exam-
ple a greeting.
In the experimental ITS, we represent system ac-
tions by POMDP actions, and treat student actions as
POMDP observations.
Since many concepts have prerequisites, When
the student asks about a concept, the system should
decide, based on its information about the student’s
state, whether it would start with teaching a prerequi-
site for the student to make up some required knowl-
edge, and, if so, which one to teach. The optimal ac-
tion is to teach the concept that the student needs to
make up in order to understand the originally asked
concept, and that the student can understand it with-
out making up other concepts.
6 SHORTENING HORIZONS AND
DECREASING OBSERVATIONS
In this section, we present our techniques for shorten-
ing horizons and decreasing the number of observa-
tions, to reduce sizes of individual trees. In the fol-
lowing two sections, we present our techniques for
decreasing the number of trees to evaluate in making
a decision, and the techniques for reducing the state
space.
The cost for evaluating a policy tree is dependent
on the size of the tree. As calculated in Eqn (6), the
size of a tree is exponential in H, the horizon of the
POMDP. To reduce the tree size, we must decrease
exponent H, and also the base |O|. For discussing our
techniques, we first define tutoring session, as well as
the original question and current question in a ses-
sion.
In our research, we observed that in a window of a
tutoring process between human student and teacher,
student questions likely concern concepts that have
prerequisite relationships with each other. Based on
this, we split a tutoring process into tutoring sessions.
A tutoring session is a sequence of interleaved student
and system actions, starting with a question about a
concept, possibly followed by answers and questions
Efficient Computing of the Bellman Equation in a POMDP-based Intelligent Tutoring System
19

concerning the concept and its prerequisites, and end-
ing with a student action accepting the answer to the
original question. If, before the acceptance action, the
student asks a concept that has no prerequisite rela-
tionship with the concept originally asked, we con-
sider that a new tutoring session starts.
We classify questions in a session into the original
question and current questions. The original question
starts the session, concerning the concept the student
originally wants to learn. We denote the original ques-
tion by (?C
o
), where C
o
is the concept concerned in
the question and superscipt o stands for “original”. A
current question is the question to be answered by the
agent at a point in the session, usually for the student
to make up some prerequisite knowledge. We denote
a current question by (?C
c
), where C
c
is the concept
concerned in the question, and superscipt c stands for
“current”. Concept C
c
is in (℘
C
o
∪C
o
), where ℘
C
o
is the set of all the direct and indirect prerequisites of
C
o
.
Take concepts derivative and function in calcu-
lus as an example. Function is a prerequisite of
derivative. At a point in a tutoring process, the stu-
dent asks question “What is a derivative?” If deriva-
tive has no prerequisite relationship with the concepts
asked/taught right before the question, we consider
the question starts a new tutoring session, and it is
the original question of the session. If the agent be-
lieves that the student already understands all the pre-
requisites of derivative, and answers the question di-
rectly, the question is also the current question when
the agent answers it. If the agent teaches derivative in
terms of function, and then the student asks question
“What is a function?”, the system action of teaching
derivative is not an optimal because the student needs
to make up a prerequisite. At this point the question
about function is the current question.
A policy tree is a stochastic model of a tutoring
process. In a policy tree, the root action is a system
action available in the current state, the root actions of
subtrees are possible system actions in the future, and
the edges are possible student questions. Based on the
above observation and analysis, in a tutoring session
we limit the A and O in a tree to (℘
C
o
∪C
o
), where C
o
is the concept in the original question of the tutoring
session. In the worst case, the students asks about all
the prerequisites of C
o
, and the system teaches all of
them. In such a case, the maximum length of a path
from the root to a leaf is the number of prerequisites of
C
o
, i.e. |℘
C
o
|. In this way, both H and |O| are |℘
C
o
|.
Typically, ℘
C
o
is a small subset of the concepts in an
instructional subject. It can be seen from Eqn (6) that
the sizes of trees can be significantly reduced.
7 CREATING OPTIMAL POLICY
TREES
To decrease the number of trees to evaluate in mark-
ing a decision, i.e. the T in Eqn (5), we create opti-
mal policy trees, instead of all the possible trees. The
value function of optimal policy tree
ˆ
τ is defined as
V
ˆ
τ
(s) = R (s,a) + γ
∑
s
0
∈S
P(s
0
|s,a)
∑
o∈O
P(o|a,s
0
)V
ˆ
τ(o)
(s
0
)
(10)
where
ˆ
τ is the optimal policy tree in s, and
ˆ
τ(o) is the
optimal subtree in
ˆ
τ that is connected to the root of
ˆ
τ
by the edge labeled with o.
...
...
... ...
o
1
o
2
o
|O|
b
′
o
1
b
′
o
2
b
b
′
o
|O|
o
1
o
2
o
|O|
b
′′
o
1
b
′′
o
2
ˆa
′
o
1
ˆa
′
o
2
ˆa
′
o
|O|
ˆa
′′
o
1
ˆa
′′
o
2
ˆa
′′
o
|O|
a
r
b
′′
o
|O|
......
...
Figure 2: An optimal policy tree with predicted beliefs.
We use Figure 2 to illustrate the structure of an op-
timal policy tree and the process of creating it. The b
beside the root node is the actual current belief while
the bs beside other nodes are predicted beliefs. An ˆa
in a node is the optimal action chosen based on the
predicted belief beside the node. For example, b
0
o
1
is
the predicted belief if the agent takes a
r
and the ob-
serves o
1
, and ˆa
0
o
1
is the optimal action based on b
0
o
1
.
A belief is a set of probabilities (see Eqn (3)).
To predict a belief, we predict each of the probabili-
ties. The following is the formula to calculate element
b
0
(s
0
) in predicted belief b
0
:
b
0
(s
0
) = [P(o|a,s
0
)
∑
s∈S
b(s)P(s
0
|s,a)]/P(o|a) (11)
where P(s
0
|s,a) and P(o|a,s
0
) are transition proba-
bility and observation probability, P(o|a) is the total
probability for the agent to observe o after a is taken,
calculated as
P(o|a) =
∑
s∈S
b(s)
∑
s
0
∈S
P(s
0
|s,a)P(o|a,s
0
). (12)
P(o|a) is used in Eqn (11) as a normalization. Using
Eqn (11) we can calculate b
0
from b, a
r
, and o
i
. In the
same way, we can use it to calculate b
00
from b
0
, and
so on.
CSEDU 2019 - 11th International Conference on Computer Supported Education
20

In the following, we use b
0
o
i
as an example, to
show how to choose the optimal action (1 ≤i ≤ |O|).
Let b
0
o
i
be
b
0
o
i
= [b
0
o
i
(s
1
),b
0
o
i
(s
2
),...,b
0
o
i
(s
|S|
)]. (13)
In b
0
o
i
we can find the j such that b
0
o
i
(s
j
) ≥ b
0
o
i
(s
k
) for
all the k 6= j (1 ≤ j,k ≤|S|). Assume the state formula
of s
j
is
(
√
C
1
√
C
2
...
√
C
l−1
¬C
l
...¬C
N
0
). (14)
The belief and state formula indicate that most prob-
ably the student does not understand C
l
, but under-
stands all of its prerequisites. Therefore, R (s
j
,(!C
l
))
would return the highest reward value. Considering a
single step, we choose (!C
l
) as the optimal action ˆa
0
o
1
on the basis of b
0
o
i
, and connect the edge with o
i
to it.
By applying a dynamic tree creation technique
with the actual current belief and predicted future be-
liefs, for each a ∈A we create one optimal policy tree
with a as its root action, instead of an exponential
number of trees. Experimental results showed that
the optimal tree has been a good approximation in
choosing optimal teaching actions, while computing
efficiency has been dramatically improved.
8 REDUCING STATE SPACE
In the cost formula (8) of calculating the Bellman
equation, a |S| appears to be a linear factor. Actually,
|S| itself is exponential. When there are N concepts in
an instructional subject, the number of state formulae
defined in (9) is 2
N
. This implies that the number of
possible states could be 2
N
. As can be seen in Eqn (1),
the cost for evaluating a value function is proportional
to the size of state space. To improve efficiency, we
partition the state space into smaller subspaces. The
partitioning technique is also based on prerequisite re-
lationships between concepts in the instructional sub-
ject.
In our partitioning technique, we first subdivide
concepts such that concepts having prerequisite rela-
tionships are in the same group, with some very “ba-
sic” concepts being in two or more groups. As men-
tioned before, the concepts in an instructional sub-
ject and their prerequisite relationships can be repre-
sented by a directed acyclic graph (DAG). The DAG
can be implemented as an adjacency matrix M, with
each column in M containing the direct prerequisites
of a concept. From M, we can calculate M
0
in which
each column contains the direct and indirect prereq-
uisites of a concept. By merging the M
0
columns
having common prerequisites, we can group concepts
that have prerequisite relationships with each other.
For details of the grouping method, please see (Wang,
2015).
For each group of concepts, we create a state sub-
space. States are defined on the basis of the concepts
in the group, in the way discussed in a previous sec-
tion. In the subspace, we associate each state with a
state formula, as defined in (9). Considering the pre-
requisite relationships, we found that the majority of
state formulas are invalid. Formula (...¬C
i
...
√
C
j
...)
is invalid if C
i
is a prerequisite of C
j
(i < j) because
in real situation there does not exist such a state that
a student understands C
j
but does not understand its
prerequisite C
i
. We consider a state with an invalid
formula an invalid state. In the subspace, we include
valid states only. The space partitioning and invalid
state elimination allow us to deal with very small |S|
in calculating the Bellman equation.
Furthermore, we discovered that in a belief (see
(3)), quite often only a small number of states have
large enough probabilities. In computing Eqn (1) for
evaluating trees, most states contribute little to V
τ
(b),
because of small b(s) values. This suggests that we
would not lose much information if we do not evalu-
ate V
τ
(s) for the s that have small probabilities in the
current belief. In this way, we significantly further
reduce the first |S| in the cost formula (8).
In an ITS, State transition between two states is
in one direction. That is, for states s
i
and s
j
, if there
is a transition from s
i
to s
j
, then there is no transi-
tion from s
j
to s
i
(i 6= j). As described, a POMDP
state represents a student knowledge state. A teach-
ing action may enable a student to understand some
new knowledge, and thus change the student’s knowl-
edge state. Normally, no system action may reverse
the state change. Therefore, for teaching action a, if
we have transition probability P(s
j
|s
i
,a) > 0, we will
have P(s
i
|s
j
,a
0
) = 0 for any a
0
.
In an ITS teaching concepts, a system action
teaches one concepts. For the current state, a system
action may cause transitions into a small number of
destination states. Therefore, the transition probabil-
ities from the current state to other states are all 0.
In calculating Eqn (1), by summing over only those
s
0
such that P(s
0
|s,a) > 0, the second |S| in the cost
formula (8) can be drastically reduced.
9 EXPERIMENTS AND ANALYSIS
In our experiments, we tested the system performance
in adaptive teaching and its computing efficiency. The
data set used in the experiments included 90 concepts
in software basics, in which each concept had zero to
five prerequisites.
Efficient Computing of the Bellman Equation in a POMDP-based Intelligent Tutoring System
21

9.1 Adaptive Teaching
In the evaluation of performance in adaptive teach-
ing, 30 students participated in the experiment, who
were adults without formal training in computing.
They had different levels of knowledge in the sub-
ject. The students were randomly divided into two
equal size groups. Group 1 studied with the ITS with
the POMDP turned off, and Group 2 studied with the
POMDP turned on. Each student studied with the
ITS for about 45 minutes. The student asked ques-
tions about concepts in the subject, and the ITS taught
the concepts. When the POMDP was on, the ITS
chooses tutoring actions based on its beliefs about the
students’ knowledge states. When the POMDP was
off, the ITS directly taught the concepts asked, or ran-
domly taught prerequisites of the concepts asked.
The performance parameter was rejection rate,
which was the ratio of the number of system actions
rejected by a student to the total number of system
actions for teaching the student. After a system ac-
tion teaching a concept, if the student said ”I already
know it”, or asked about a prerequisite of the concept,
we consider that the system action was rejected. A
rejected system action was not an optimal action. A
lower rejection rate indicated better performance in
adaptive teaching.
we used an independent-samples t-test method to
analyze the experimental data. For each student, we
calculated a rejection rate. For the two groups, we cal-
culated mean rejection rates
¯
X
1
and
¯
X
2
. The two sam-
ple means were used to represent population means
µ
1
and µ
2
. The alternative and null hypotheses are:
H
a
: µ
1
−µ
2
6= 0, H
0
: µ
1
−µ
2
= 0
We calculated two sample means: 0.5966 and
0.2284, and two variances 0.0158 and 0.0113, for the
twe groups. The group studying with the POMDP
turned on had much lower rejection rate. In the ex-
periment, n
1
=15 and n
2
=15, thus the degree of free-
dom was (15 − 1) + (15 − 1) = 28. With alpha at
0.05, the two-tailed t
crit
was 2.0484 and we calculated
t
obt
= +8.6690. Since the t
obt
was far beyond the non-
reject region defined by t
crit
= 2.0484, we could reject
H
0
and accept H
a
. The analysis suggested that the
POMDP could reduce the rejection rate. This implies
that the POMDP helped the system improve adaptive
teaching.
9.2 Computing Efficiency
We tested our techniques for improving computing
efficiency in calculating the Bellman equation, on a
desktop computer with an Intel Core i7-4790 3.2 GHz
64 bit processor and 24GB RAM. The operating sys-
tem was Ubuntu Linux, and the experimental ITS was
coded in C. The same data set of software basics was
used for testing computing efficiency.
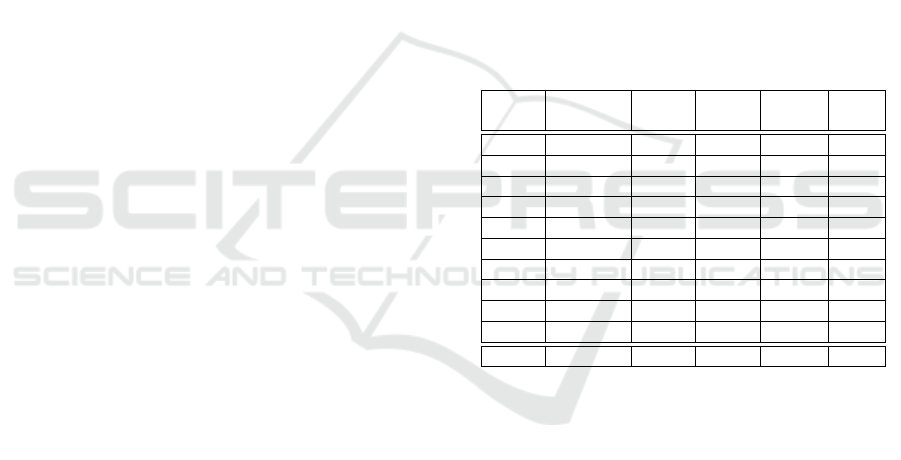
In Table 1, we list the results of partitioning the
state space, creating policy trees in subspaces, and
the time for creating the biggest trees in milliseconds.
Column 2 lists the numbers of concepts in the sub-
spaces. Based on the definitions of actions and ob-
servations, they were the numbers of possible actions
and observations in the subspaces. The values in col-
umn 3 are the numbers of valid states, and the val-
ues in column 6 are the time for creating the largest
trees, in the subspaces. We subdivided the 90 con-
cepts into 10 groups, based on concept prerequisite
relationships. Subspace 3 had the largest number of
valid states, and subspace 10 had the largest number
of trees. Subspace 10 also had the largest tree. The
tree height was 25, and size was 32,275 nodes.
Table 1: Numbers of concepts, valid states, trees, and max-
imum tree heights in subspaces.
Sub- # of # of # of Max Max
space concepts states trees height time
1 11 72 86 16 1
2 12 45 168 16 2
3 21 1,501 190 14 1
4 17 129 271 24 12
5 20 403 257 22 3
6 21 1,201 275 22 2
7 22 503 321 25 8
8 19 281 328 20 2
9 20 327 363 22 3
10 22 682 438 25 47
Total 5,144 2,697
It can be seen in the table, that the subspaces had
very small numbers of valid states. For example, in
the largest subspace, i.e. subspace 3 of 21 concepts,
the number of valid states was 1,501, which was much
smaller than 2
21
. The total number of valid states in
all the subspaces was 5,144, much smaller than 2
90
.
The number of trees in a subspace was very small,
compared with a number that is exponential in the
horizon. Also, tree sizes were manageable by using
the current computers.
Our techniques allow us to localize calculation of
the Bellman equation. To choose a tutoring action, the
agent can calculate the equation within a subspace.
As the test results showed, the calculation could be
conducted with relatively small numbers of states and
trees, and limited sets of actions and observations.
The localized calculation has improved the comput-
ing efficiency in choosing tutoring actions. The worst
case response time was 1.56 seconds, including the
CSEDU 2019 - 11th International Conference on Computer Supported Education
22

time for updating a belief, creating trees, and evalu-
ating the trees to find the optimal. In the worst case,
the largest tree was evaluated. For a tutoring system,
such response time could be considered acceptable.
10 CONCLUDING REMARKS
Without efficient techniques for calculating the Bell-
man equation, we are not able to build a POMDP-
based ITS for practical tutoring. The work reported in
this paper is a part in our continuing research for ef-
ficient POMDP-solving in ITSs. We developed tech-
niques for reducing the state space, tree set, and obser-
vation set involved in calculating the Bellman equa-
tion. Integrated use of the techniques has generated
encouraging initial results.
REFERENCES
Braziunas, D. (2003). POMDP solution methods: a sur-
vey. Technical report, Department of Computer Sci-
ence, University of Toronto.
Carlin, A. and Zilberstein, S. (2008). Observation compres-
sion in DEC-POMDP policy trees. In Proceedings of
the 7th International Joint Conference on Autonomous
Agents and Multi-agent Systems, pages 31–45.
Cassandra, A. (1988). Exact and approximate algorithms
for partially observable Markov decision problems.
PhD thesis, Department of Computer Science, Brown
University, USA.
Cassandra, A. (1998). A survey of pomdp applications. In
Working Notes of AAAI 1998 Fall Symposium on Plan-
ning with Partially Observable Markov Decision Pro-
cess, pages 17–24.
Cheng, H. T. (1988). Algorithms for partially observable
Markov decision process. PhD thesis, Department of
Computer Science, University of British Columbia,
Canada.
Cheung, B., Hui, L., Zhang, J., and Yiu, S. M. (2003).
Smarttutor: an intelligent tutoring system in web-
based adult education. Elsevier The journal of Systems
and software, 68:11–25.
Chinaei, H. R., Chaib-draa, B., and Lamontagne, L. (2012).
Learning observation models for dialogue POMDPs.
In Canadian AI’12 Proceedings of the 25th Cana-
dian conference on Advances in Artificial Intelligence,
pages 280–286.
Folsom-Kovarik, J. T., Sukthankar, G., and Schatz, S.
(2013). Tractable POMDP representations for intel-
ligent tutoring systems. ACM Transactions on In-
telligent Systems and Technology (TIST) - Special
section on agent communication, trust in multiagent
systems, intelligent tutoring and coaching systems
archive, 4(2):29.
Kaelbling, L. P., Littman, M., and Cassandra, A. R. (1998).
Planning and acting in partially observable stochastic
domains. Artificial Intelligence, 101(1-2):99–134.
Littman, M. (1994). The witness algorithm: solving par-
tiallu observable markov decision processes. Techni-
cal report, Department of Computer Science, Brown
University.
Rafferty, A. N., Brunskill, E., Thomas, L., Griffiths, T. J.,
and Shafto, P. (2011). Faster teaching by POMDP
planning. In Proceesings of Artificial Intelligence in
Education (AIED 2011), pages 280–287.
Theocharous, G., Beckwith, R., Butko, N., and Philipose,
M. (2009). Tractable POMDP planning algorithms for
optimal teaching in spais. In IJCAI PAIR Workshop
2009.
VanLehn, K., van de Sande, B., Shelby, R., and Gershman,
S. (2010). The andes physics tutoring system: an ex-
periment in freedom. In et al, N., editor, Advances in
Intelligent Tutoring Systems, pages 421–443.
Wang, F. (2015). Handling exponential state space in a
POMDP-based intelligent tutoring system. In Pro-
ceedings of 6th International Conference on E-Service
and Knowledge Management (IIAI ESKM 2015),
pages 67–72.
Wang, F. (2016). A new technique of policy trees for
building a POMDP based intelligent tutoring system.
In Proceedings of The 8th International Conference
on Computer Supported Education (CSEDU 2016),
pages 85–93.
Wang, F. (2017). Developing space efficient techniques for
building POMDP based intelligent tutoring systems.
In Proceedings of The 6th International Conference
on Intelligent Systems and Applications (Intelli 2017),
pages 44–50.
Williams, J. D., Poupart, P., and Young, S. (2005). Fac-
tored partially observable Markov decision processes
for dialogue management. In Proceedings of Knowl-
edge and Reasoning in Practical Dialogue Systems.
Williams, J. D. and Young, S. (2007). Partially observable
Markov decision processes for spoken dialog systems.
Elsevier Computer Speech and Language, 21:393–
422.
Woolf, B. P. (2009). Building Intelligent Interactive Tutors.
Morgan Kaufmann Publishers, Burlington, MA, USA.
Efficient Computing of the Bellman Equation in a POMDP-based Intelligent Tutoring System
23