An Efficient Heuristic Method for Repairing Event Logs Independent

of Process Models

Li Kong

, Chuanyi Li

, Jidong Ge

, Zhongjin Li

1,2

, Feifei Zhang

and Bin Luo

State Key Laboratory for Novel Software Technology, Software Institute, Nanjing University, Nanjing 210093, China

School of Computer, Hangzhou Dianzi University, Hangzhou 310018, China

Keywords: Log Repair, Process Mining, Event Log, Edit Distance.

Abstract: Due to the big volume of data and complex execution, event logs of business processes inevitably contain

various errors. In the field of process mining, if we derive process models from the event data without

repairing, it is very likely that the resulting process is extremely different from what we expect. Current

methods of repairing logs generally compare the log with an existing reference model to seek an optimal

alignment, which requires that there should be a reliable reference model. Therefore, this paper presents an

approach which only refers to the log itself to repair mistaken traces. We identify loop structures and frequent

event sequences (sound conditions) between certain events. For each trace, basic trace and loop events are

separated in advance. The basic trace is split into several parts to get repaired one by one according to sound

conditions. Then loop events are added back and checked according to corresponding loop structure we

discover. The repaired log should be as clean as possible and as similar to the original log as possible so that

correctness and integrity of the original log are guaranteed. Experimental results based on different logs prove

that our approach is effective and efficient.

1 INTRODUCTION

Process mining is a young and emerging research

discipline which sits between data mining and

machine learning. It establishes links between their

actual executing processes and their data on the one

hand and process models on the other hand. Process

mining includes three main aspects, namely process

discovery (learning process models from raw event

data), conformance checking (monitoring deviations

by comparing model and log) and process

enhancement (extend or improve an existing process

model) (Aalst et al., 2011; Polyvyanyy et al., 2016).

Among them, process discovery targets at extracting

information from event logs, which store execution

data logged by information systems, to discover real

process models which are mainly presented by Petri

net (Murata et al., 1989), YAWL (Aalst et al., 2005)

or high level Petri net (Jensen et al., 1991) without

any prior information (Aalst et al., 2004). Lots of

algorithms have been put forward to efficiently

achieve the goal. Event log is the starting point of this

research. In enterprises, hospitals, government and

other agencies, execution data logged by information

systems are often stored in system or application logs

which can be converted into event logs. Ideally, an

event log reflects the dominant behavior accurately of

a business process as it occurs in an organization at a

particular time. That is, the log is complete and clean.

Based on this, discovery algorithms are performed to

build process models that we expect.

However, due to the large quantity of data and

complex execution, real-life process event logs often

contain multiple kinds of errors. Events may get

missed, redundant, dislocated or misspelled. If we

ignore this problem and extract information from logs

without cleaning, the aforesaid applications and

mining over event data will be far from reliable.

Failing to effectively detect and repair mistaken

behaviors in log has a bad effect on the quality of the

discovered model. In spite of a degree of noise-

tolerance, many state of the art discovery algorithms

still strongly rely on the correctness of source log,

such as the α-algorithm (Aalst et al., 2004) and its

extensions (Medeiros et al., 2004; Aalst et al., 2007;

Wen et al., 2009), Heuristic algorithm (Weijters et al.,

2006) methods based on regions of languages

(Bergenthum et al., 2007) and methods based on

regions of states (Solé et al., 2010). Most of the

existing methods for log repair (Wang et al., 2013;

Kong, L., Li, C., Ge, J., Li, Z., Zhang, F. and Luo, B.

An Efﬁcient Heuristic Method for Repairing Event Logs Independent of Process Models.

DOI: 10.5220/0007676400830093

In Proceedings of the 4th International Conference on Internet of Things, Big Data and Security (IoTBDS 2019), pages 83-93

ISBN: 978-989-758-369-8

Original

Log

Repaired

Log

Loop Structure is null?Traces

yes

Repaired

Traces

Repair Basic

Trace

Remove Loop

Events

Loop Structure is null?

Add back

Repair Loop

Events

Basic

Traces

Loop

Events

yes

Figure 1: The overall framework of log repair process.

Song et al., 2016; Song et al., 2015) are based on

alignment between event logs and given process

models or process specifications, which is used

extensively in conformance checking (Leoni et al.,

2013; Adriansyah et al., 2011; Leoni et al., 2015),

another important aspect of process mining.

Conformance checking techniques compare event

logs with process models so that deviations can be

diagnosed and quantified. According to this, it is

convenient to find out what is wrong with the logs and

how to repair to accord with the models. The optimal

alignment should be that the trace in the log and the

occurrence sequence in the model have the shortest

edit distance. However, this way is unworkable when

we do not have the reference models or specifications.

In this paper, we deal with the challenge of fixing

event logs that may contain various errors by

discovering rules the logs should follow. Since there

is no process model as a reference, we have to rely on

the event log itself. Our method identifies loop

structure(s) and divides a complete log into several

subsections without loop events where there are more

than one frequent event sequences (sound conditions)

in each subsection. Such subsections and sound

conditions are recorded in a subsection list. Accepting

one condition as sound or not depends on its total

occurrences in the log. To make the subsection list

complete, sequential events are also recorded and

frequency of each event sequence is set to an

extremely large number. When repairing, event

sequence belonging to subsection is modified to a

sound condition which is most similar to it. Figure 1

shows the process of log repair introduced in this

paper. To the best of our knowledge, there does not

exist a method of repairing an event log by adding and

deleting certain events without the availability of a

reference model.

Main contributions in this paper are summarized

as follows:

 We develop a general framework to transform

a mistaken trace into a most similar one

conforming to the log;

 We present an effective approach based on

heuristic to filter sound rules the logs should

follow, namely loop structures, choice

relationship, concurrency relationship and

sequential relationship;

 We report the experimental evaluation on

synthetic data.

The rest of paper is structured as follows. Section

2 reviews related work with a focus on alignment

between logs and models. Section 3 defines the

proposed technique while section 4 presents a

detailed solution to log repair. Section 5 reports on the

experimental results and shows that our method is

feasible and efficient. The last part of this paper is the

summary and prospect on this field.

2 RELATED WORK

Current methods for log repair largely rely on

alignment between event logs and given process

models or process specifications. This is actually an

important method in conformance checking (Rozinat

et al., 2008). Fitness (Aalst et al., 2012), precision

(Adriansyah et al., 2013), generalization and

simplicity are used to describe how good a model

represents reality. There has been lots of research on

this topic. The conflicts in alignment show something

wrong, point out where deviations take place and how

severe they are. Reference (Bezerra et al., 2013)

discusses four algorithms for detecting anomalies in

logs of process aware systems. Reference (Leoni et

al., 2012a) aligns event logs and declarative models.

Sometimes it is required to take not only control flow,

but also data and resources into account (Leoni et al.,

2012b).

Existing conformance checking can be used to

align the runs of the given process model to the traces

in the log. If there is a move in the log, but it does not

execute in the model, we call it a log move; if the

model contains a move, but it is not recorded in the

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

log, we call it a model move. In our view, if a log

move or model move appears, there is a problem. If

this problem is very infrequent, the log rather than the

model should be repaired (Fahland et al., 2015).

As stated before, where infrequent problems are

in alignment are where outliers occur in event log and

research has been conducted on log recovery based on

alignment. Missing events can be recovered by

referring to process specifications and heuristics

(Song et al., 2015). Reference (Leoni et al., 2013)

repairs logs with missing events by repairing the

control flow and the timestamps. Reference (Song et

al., 2016) presents an approach which handles not

only missing, but also redundant and dislocated

events. Repairs above all require the availability of

both event log and perfect reference model.

Reference (Conforti et al., 2017) presents an

automated technique to the removal of infrequent

behavior from event logs by conducting an automaton

from the log. In addition, two traces also can be

aligned (Bose et al., 2012).

3 PROBLEM STATEMENT

First, we introduce definitions of Petri net and event

log, and then we describe the problem to be solved.

3.1 Preliminaries

In this paper, we use Petri nets to represent process

models. A Petri net is a directed graph, where places

are represented by circles, transitions are represented

by rectangles and flow relations are represented by

directed arcs.

Definition 1 (Petri Net). A Petri net is a triple PN=

(P, T, F) where P is a finite set of places, T is a finite

set of transitions, P ∩ T = Ø and F ⊆ (TⅩP) ∪ (PⅩT)

is a set of flow relations.

A Petri net starts with a place and also ends with

a place. Places are presented as circles and transitions

are presented as rectangles. More details are

presented in (Murata et al., 1989).

An event log consists of tremendous event traces,

each of which records the footprint of a process

instance. A trace is a succession of events according

to the time sequence and these ordered events can

fulfil one execution of the process. We also call a

trace case and each case has a unique case identifier.

Different cases may own the same succession of

events. An event can also have many other attributes

such as the resource(s) involved, the transaction type,

costs, etc. These factors are beyond the discussion of

the paper.

Definition 2 (Event Log). A log W over a set of tasks

T and time domain TD is defined as W= (E, C, α, β,

γ, <) where E is a set of events; C is a set of case

identifiers; α: E→T is a function linking each event

to a task; β: E→C is a function linking each event to

a case; γ: E→TD is a function linking each event to a

timestamp; <∈ E×E is a total ordering over the events

in E. A trace σ in a log is represented by a sequence

of events belonging to E.

3.2 Problem Definition

Traces may have missing, redundant or dislocated

events. Dislocation can also be treated as the mixture

of the first two cases. Our objective is to repair

nonconforming event sequences according to the

rules the log should follow (including loop structures,

concurrency relationship, choice relationship and

sequential relationship). The rules are identified

based on heuristic and recorded in a list. Each

repaired trace should conform to the rules and be as

similar to the original trace as possible. In our work,

we try to minimize the edit distance between the

original one and repaired one.

Definition 3 (Edit Distance). If there are two event

sequences σ

and σ

, the edit distance ED(σ

, σ

)

between them is minimal number of edit operations

required to transform σ

to σ

or from σ

to σ

Definition 4 (Sound Condition). All sound

conditions within a subsection is defined as a set of

tuples including each complete event sequence and its

occurrence in the log: sc = {(sequence, frequency) |

frequency> threshold}.

For an event sequence σ, its repaired sequence σ’

is also an event sequence such that 1) σ’ ∈ sc; 2) for

any other sequence σ’’ ∈ sc, ED(σ, σ’’) >= ED(σ, σ’).

A repaired trace is the combination of different

repaired sub-sequences.

4 HEURISTIC LOG REPAIR

In this section, we present our detailed technique for

log repair. The method is named Heuristic log repair.

Before the actual repair work, we need some

preparations. If there exist loop structures, remove

loop events from traces to get basic traces. For logs

produced by process models without loops, traces are

already basic traces. Then sound conditions within

each subsection are discovered using basic traces and

filtered by certain thresholds. When repairing, firstly

we split each basic trace into several parts and

transform each part into a sound condition belonging

to that part which is most similar to it. Repaired parts

An Efﬁcient Heuristic Method for Repairing Event Logs Independent of Process Models

Figure 2: Loop with Same Start and End (up) and Loop with

Different Start and End (down).

are combined into a repaired basic trace. Loop events

are added back and loop events of each loop are

checked and repaired according to corresponding

loop structure.

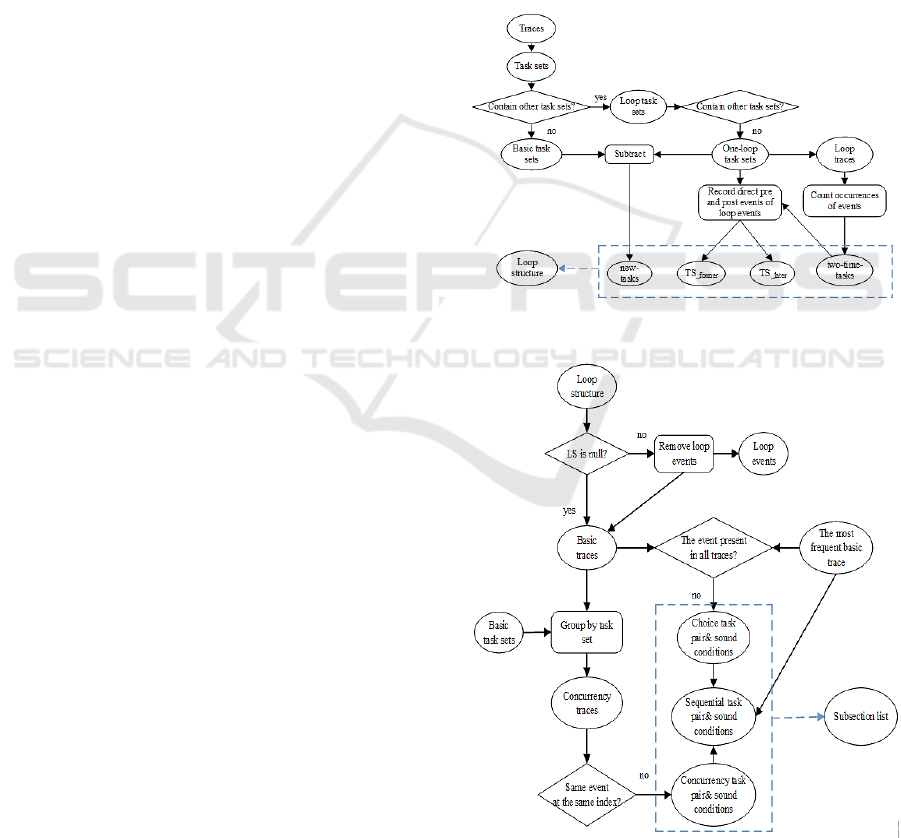
4.1 Loop Structure Identification

In this section, we introduce how to get loop

structures by comparing “task sets” of traces.

Definition 5 (Task Set). Given an event sequence σ,

task set τ(σ) is the set of tasks producing the events.

Example 1. If there is a trace σ= ABCDECDF, τ(σ)

= {A, B, C, D, E, F}. A task set TS of a log W = {τ(σ)

| σ



W}.

There are two kinds of loop structures, as is shown

in Figure 2. If in a trace with a loop structure

executing once, each task only produces one event,

this loop belongs to the first type, Loop with Same

Start and End. Otherwise it belongs to the other type,

Loop with Different Start and End.

As we can see, in Figure 2, If s executes once,

there is only one s in the trace. If t executes once, e

appears twice in the trace. s and t only appear in traces

with loops. Ordered task sequence generating events

like them is referred to as new-task (nt). If in a trace,

a loop executes once and there are tasks producing

more than one event, this ordered task sequence is

referred to as two-time-task (mt). Events in a trace

generated by nt and mt (except the first occurrence of

events from mt) are collectively called loop events

(le). For each loop structure, the task set directly

before the first occurrence of nt and not after the last

mt (or nt if mt does not exist) is called TS

_former

, the

task set directly after the last occurrence of mt (or nt

if mt does not exist) but not before the first nt is called

_later

For simplicity, we only consider traces with one

loop structure and get one kind of loop structure once.

If there are two traces σ

and σ

, τ(σ

) is a proper

subset of τ(σ

), τ(σ

) is not superset of any other task

set, then in σ

no loop executes and in σ

tasks execute

in the same route except that a loop executes. So we

need to find all task sets of traces without iteration

and with one type of iteration.

Definition 6 (Basic Task Set). A task set ts is

regarded as a basic task set if: 1)





TS, ts ⫋ ts

;





TS, ts



ts.

Definition 7 (One-loop Task Set). A task set ts is

regarded as a one-loop task set if: 1)





TS, ts

⫋ ts 2) ∀ ts



TS, ts

≠ts

, ts

⊄ ts.

For each loop structure, given the task sets, nt can

be got by subtracting a subset from a superset, and mt

can be got by counting the number of events

generated by the same tasks. Every time the loop

executes for one more time, the sequence of events

newly generated is the sequence of events produced

once by nt and mt belonging to the current loop.

Obviously, if the loop starts with the same start and

end, in other words, mt is null. TS

_former

can be got by

subtracting tasks producing events directly after the

last occurrence of the last task in mt from tasks

directly before the first occurrence of the first task in

nt. Similarly, we can get TS

_later

Definition 8 (Loop Structure). The set of loop

structure(s) a log contains is defined as LS = {ls | ls =

(TS

_former

, TS

_later

, nt, mt)} where ls is one of loop

structure. If the log is generated by a model without

any loop, LS is null.

Example 2. The event log contains traces:

case1: ABCDEFHJ, case2: ABDCEFHJ, case3:

ADBCEFHJ (their task set is ABCDEFHJ, ts

);

case4: ABCDEGHJ, case5: ABDCEGHJ, case6:

ADBCEGHJ (their task set is ABCDEGHJ, ts

);

case7: ABTUCDEFHJ, case8: ABDTUCEFHJ,

case9: ABTUDCEFHJ (their task set is

ABCDEFHJTU, ts

);

case10: ABTUCDEGHJ, case11: ABDTUCEGHJ,

case12: ABTUDCEGHJ, case13:

ADBTUTUCEGHJ (their task set is

ABCDEGHJTU, ts

);

case14: ABCDS

DEFHJ, case15:

ABDCS

DEFHJ, case16: ADBS

DCEFHJ,

case17: ADS

DBCEFHJ (their task set is

ABCDEFHJS

);

case18: ABCDS

DEGHJ, case19:

ABDCS

DEGHJ, case20:

ADBS1S2DS

DCEGHJ (their task set is

ABCDEGHJS

, ts

Comparing ts

and ts

, we get nt: TU; choose

ABTUCDEFHJ, clearly there are no events from the

same task, so this loop structure has no mt; Events

before the first occurrence of T are B and D, event(s)

after the last occurrence of U are C and D, so TS

1_former

is {B}, TS

1_later

is {C}. ls

= (B, C, TU,);

Comparing ts

and ts

, we get nt: S

; choose

ADS

BCDEFHJ, and we get mt: D; Event only

before the first occurrence of S

is D, event only

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

after the last occurrence of D is E, so TS

2_former

is {D},

2_lster

is {E}. ls

= (D, E, S

, D);

Loop structures got by comparing s

and s

and by

comparing s

and s

are the same as above.

Having identified each loop structure, if LS is not

empty, it is time to remove les of every trace in W.

Each remaining event sequence is referred to as a

basic trace and the new log is referred to as W_

basic

Also, we record a sequence of all les of a trace in

basic

. Besides, to add le back to a position as close

to its original position as possible, we keep a record

of its previous event sequence. If W is produced by a

model without any loop structure, itself is equal to

basic

Definition 9 (Loop Events Set). We define the set of

loop events of W as LE = {le | le = (CID, id, former,

later, e, fe)}, where CID is the case identifier, id is the

identifier of this loop event in the trace, former and

later are TS

_former

and TS

_later

of the ls that le is in, e is

and the name of this event and fe is the sequence of

events before this event in the original trace.

Example 3 (Example 2 continued). For case3, since

it contains no nt, its basic trace is itself and it has no

le; for case7, its basic trace is ABDCE, its loop events

include (7, 1, {B}, {C}, T, ADB), (7, 2, {B}, {C}, U,

ADBT), (7, 3, {B}, {C}, T, ADBTU) and (7, 4, {B},

{C}, U, ADBTUT).

The process of identifying loop structures in a log

is represented in Figure 3.

4.2 Subsection List Discovery

Besides discovering loop structures, we also need

discover concurrency and choice relationship

(collectively called non-sequential relationship since

loops have been ruled out) in original process model

and event sequences related. Such rules will be

concluded in a list. For the sake of convenience in

repairing, tasks of sequential relationship are also

included in the list. The process is shown in Figure 4.

To each non-sequential relationship, we wish to

get the task set after which different executions begin

(referred to as T

_before

) and the task set before which

different executions end (referred to as T

_after

_before

, T

_after

) is regarded as a boundary task pair. If

a boundary task pair covers another pair in time

scope, we will omit the covered pair. Task set of all

events occurring within a subsection is recorded as

t_set. One possible events sequence within a

boundary task pair is referred to one condition and its

total occurring time is recorded as frequency. In order

not to omit any event, we add T

_after

to the end of each

condition. If .the frequency of a condition is above or

equal to the threshold, it is accepted as a sound

condition and therefore recorded.

When deciding sequential relationship, T

_before

an artificial mark “start” when before a choice or

concurrency interval tasks are all in sequential

relationship or the task before which different

executions end, T

_after

is an artificial mark “end” when

it gets to the end of the model or task after which

different executions begin. But “end” will not be

added to the end of sound condition. Each boundary

task pair has only one sound condition and frequency

is set to an extremely large number, like 99999999.

Definition 10 (Subsection List). A Subsection List

of a log is defined as LIST = {list | list = (T

_before

, T

_after

t_set, sc)}.

Figure 3: Loop structure identification.

Figure 4: Subsection list discovery.

An Efﬁcient Heuristic Method for Repairing Event Logs Independent of Process Models

Concurrency relationship can be identified by

checking traces sharing the same basic task set. Since

there is no loop event, these traces also should have

the same length. For each basic task set, its

corresponding traces are called concurrency traces.

We define the occurrence number of the most

frequent concurrency trace σ

as max_fre. If in a

position, events in all traces are not from the same

task, tasks producing them must be in a concurrency

interval. When considering whether to accept a

position in σ

, number of traces that have an event

produced by a different task in this position should be

above Threshold_

= max_fre / λ

. To each part of

continues positions, tasks producing events directly

before the first position and after the last position

forms a boundary task pair. Each condition is

accepted as a sound condition if the frequency is

above Threshold_

concurrency

= max_fre_condition / μ

where max_fre_condition refers to the biggest

occurrence number of a condition within the

boundary task pair.

Then we choose the basic trace σ

with highest

frequency and check if each task producing an event

in σ

executes in all other traces. If not, this task is in

a choice interval. We accept this task in a position if

the number that the task dose not execute in a trace in

the whole log is above Threshold_

= N / λ

where N

is the total number of traces in the log. To each part

of continues positions, tasks producing events

directly before the first position and after the last

position forms a boundary task pair. Each event

sequence within the pair is accepted as a sound

condition if the frequency is above Threshold_

choice

max_fre_condition / μ*x where if part of this event

sequence is in concurrency relationship, x is the

number of types of conditions within sharing the

same part, else x is 1.

Tasks in sequential relationship and sound

conditions are identified using the most frequent basic

trace.

Example 4 (Example 3 continued). Basic traces are

ABCDEFHJ, ABDCEFHJ, ADBCEFHJ (task set:

ABCDEFHJ, ts

); ABCDEGHJ, ABDCEGHJ,

ADBCEGHJ (task set: ABCDEGHJ, ts

). Comparing

three basic traces of ts

, we find that from the second

to the fourth index, events are produced by different

tasks. As a result, (A, E) is a concurrency interval.

Choosing ABCDEFHJ, F is absent in half of the

traces. So (E, H) must be a choice interval. If we

subtract BCDE and FH from ABCDEFHJ, we get the

sequential intervals: (“start”, A) and (H, “end”).

Considering frequency, LIST= {(“start”, A, {A}, {(A,

99999999)}), (A, E, {B, C, D, E}, {(BCDE, 6),

(BDCE, 8), (DBCE, 6)}), (E, H, {F, G, H}, {(FH, 10),

(GH, 10)}), (H, “end”, {J}, {(J, 99999999)})}.

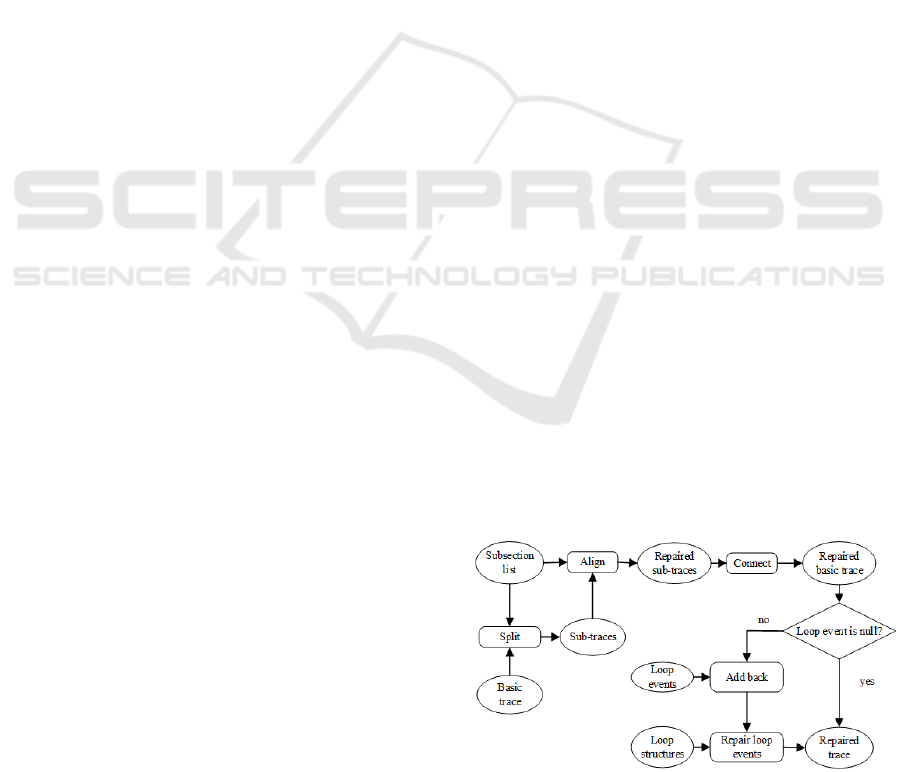
4.3 The Three-step Repair Process

Having discovered rules the log should follow, we

can take a three-step repair approach. For each trace,

its basic trace is split, repaired and combined first. If

the log contains loop structure(s), loop events of the

trace are added back. After that, loop event sequences

belonging to each loop structure are checked

according to the structure. The repair process is

shown in Figure 5.

When repairing the basic trace, we firstly split it

into several event sequences belonging to each

subsection. Then we compare each sequence with

sound conditions in the corresponding subsection and

choose the one with shortest edit distance between the

original sequence and with highest frequency. If there

is no event in this subsection, choose the shortest and

most frequent sound condition. Connecting each

chosen condition, we get a repaired basic trace which

takes the fewest steps to transform from the original

basic trace.

Example 5 (Example 4 continued). The subsection

list and loop structures are as above. Suppose there is

a basic trace ACBDEGHJ with case id = 21. Its loop

events are: le

= (21, 1, {D}, {E}, S

, ACBD) and le

= (21, 2, {D}, {E}, S

, ACBDS

). We divide the basic

trace into four sub-traces: A, CBDE, GH and J. Then

we compare each sub-trace with the sound conditions.

Both ED(CBDE, BCDE) and ED(CBDE, BDCE) are

2. Since frequency of BDCE is higher, we transform

CBDE into BDCE. Connecting repaired sub-traces,

we get ABDCEGHJ.

After repairing basic traces, add each loop event

le back to a position p where the event sequence seq

before p has the shortest edit distance with its fe. Then

it can return to its original place as close as possible.

For each le = (CID, id, former, later, e, fe):

Set tag

= 1, tag

= 1 (two integers);

Figure 5: The repair process.

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

 If



e’



seq, e’



former





e’’



seq, e’’



later, then add le after seq;

 If



e’



seq, e’



former





e’’



seq,

e’’



later, then add le to tag

position(s) before

e’’’ such that σ(e’’’) = later, tag

+1;

 If



e’



seq, e’



former, then add le to

tag

position(s) after e’’ such that σ (e’’) =

former, tag

+1.

Example 6 (Example 5 continued). For le

= (21, 1,

{D}, {E}, S

, ACBD), the event sequence ABD has

the shortest distance with ACBD. D in ABD



{D}

and no event in ABD belongs to {E}. So we add S

after ABD in ABDCEGHJ and get ABDS

CEGHJ.

The operation on le

is similar.

To repair the loop events, we need to classify them

according to nt and mt belonging to each loop

structure. Then for each loop structure, compare loop

events in the trace with the sequence (nt+mt). Here

similarity of two sequences is based on Longest

Common Subsequence (LCS).

Definition 11 (Longest Common Subsequence). If

there are two event sequences σ

and σ

, the longest

common subsequence LCS(σ

, σ

) between them is

the longest subsequence common to σ

and σ

Since execution times of each loop are unlimited,

we in turn compare loop events in the trace belonging

to the current loop with correct loop events generated

once, twice, et al. Every time we record LCS and the

comparison stops when LCS stabilizes. Shortest loop

event sequence with a maximal LCS is referred to as

chosen loop sequence (CLS).

Definition 12 (Chosen Loop Sequence). If there is

an event sequence, its chosen loop sequence (CLS) is

an event sequence σ_

= (nt+mt)*i(i>=0), if LCS (σ,

) = LCS(σ, σ

_i+1

) and when i >0, LCS(σ, σ

) >

LCS(σ, σ

_i-1

For each loop, corresponding loop events in the

trace minus LCS is the events to be deleted and CLS

minus LCS is the events to be added. We can modify

them directly in the traces since loop events have been

added back.

Example 7 (Example 6 continued). Trace

ABDS

CEGHJ does not have loop events

belonging to ls

. Its loop event sequence of ls

is S

Length of LCS(S

, ) is 0, length of LCS(S

D) is 2, length of LCS(S

, S

D) is also

2 and we can stop comparing. So we choose S

D as

CLS and LCS(S

, S

D)= S

. S

minus LCS is

null. CLS minus LCS is D, indicating that D need to

be added after S

. Doing this, we get the repaired

trace ABDS

DCEGHJ.

The whole process of log repair introduced in this

paper is described in Algorithm 1.

5 EVALUATION

Algorithm 1: HeuristicLogRepair.

Input: Event log W

Output: Filtered Log W_

1 Basic Task Set BTS, One-loop Task Set LTS ←

GetTaskSet (W);

2 If (LTS != NULL) {

3 Loop structure LS ← GetLoopStructure

(BTS, LTS, W);

4 Basic Log W_

basic

, Loop Events LE ←

RemoveLoopEvents (W, LS);

5 } else W_

basic

← W;

6 Subsection List LIST ← GetSubsectionList

(W_

basic

, BTS);

7 Filtered Basic Log W_

basic

← RepairBaicTrace

(W_

basic

, LIST);

8 If (LS != NULL) {

9 W_

temp

← AddBack (W_

basic

, LE);

10 Longest common subsection LCS ← GetLCS

(LE, LS);

11 Filtered Log W_

← RepairLog(LCS, W_

temp

);

12 } else W_

← W_

basic

;

13 Return W_

In this section we present the results of our approach

compared with two plugins in proM (Dongen, 2015).

The first is called Filter Log using Simple Heuristics

(SH) and it removes traces not starting or ending with

a specified event as well as undesirable events in

traces. The other one is called Filter out low-

frequency Traces (FL) and it removes traces whose

occurrence number is below the threshold you set.

Different process models are used to generate

correct logs and we artificially add mistakes to the

logs. We deal with mistaken logs using SH, FL and

our approach and do conformance checking between

every repaired log and the corresponding process

model. We define two criteria to express accuracy of

each method:

||||

move modelmove log

fitness Event





where |E|

refers to the total number of events of the repaired log,

|log move| and |model move| respectively refer to the

total number of log moves and model moves in the

alignment.

correct|

fitness Trace *



where |correct| refers to

the number of traces conforming to the model, n

refers to number of traces in the repaired log, M refers

to total number of types of traces in the original log

and |m| refers to number of types of traces accepted

by the model in the repaired log.

Both Event fitness and Trace fitness reflect how

the repaired log conforms to the process model.

An Efﬁcient Heuristic Method for Repairing Event Logs Independent of Process Models

Table 1: Data of logs used in the evaluation.

Logs with redundant events

Log of

Error

rate

Events

Log

of M4

Error

rate

Events

L1_

10%

42405

L4_

10%

42394

L1_

20%

42705

L4_

20%

42794

L1_

30%

43065

L4_

30%

43066

L1_

40%

43423

L4_

40%

43404

L1_

50%

43756

L4_

50%

43712

L1_

60%

44100

L4_

60%

44068

L1_

70%

44398

L4_

70%

44388

L1_

80%

44773

L4_

80%

44735

L1_

90%

45012

L4_

90%

45060

Logs with missing events

Log of

Error

rate

Events

Log

of M5

Error

rate

Events

L2_

10%

40652

L5_

10%

44041

L2_

20%

40272

L5_

20%

43716

L2_

30%

39881

L5_

30%

43377

L2_

40%

39500

L5_

40%

43060

L1_

50%

39144

L5_

50%

42757

L2_

60%

38770

L5_

60%

42431

L2_

70%

38379

L5_

70%

42105

L2_

80%

38012

L5_

80%

41801

L2_

90%

37636

L5_

90%

41462

Logs with redundant and missing events

Log of

Error

rate

Events

Log

of M6

Error

rate

Events

L3_

10%

40086

L6_

10%

39702

L3_

20%

40111

L6_

20%

39697

L3_

30%

40121

L6_

30%

39713

L3_

40%

40133

L6_

40%

39708

L3_

50%

40165

L6_

50%

39758

L3_

60%

40181

L6_

60%

39751

L3_

70%

40195

L6_

70%

39776

L3_

80%

40216

L6_

80%

39784

L3_

90%

40221

L6_

90%

39796

Logs of different sizes

Log

L10

L11

Labels

Events

13333

30042

44016

53596

61133

However, only Trace fitness expresses the integrity

and better reflects how the repaired log conforms to

the original log and how a method restores the

mistaken log.

5.1 Experimental Setup

The programs are implemented in Java and all the

experiments were performed on a computer with

AMD A10-7300 Radeon R6, 10 Compute Cores

4C+6G, 1.90GHz CPU and 8 GB memory.

We set λ

to 10, λ

to 40 and μ to 2 in our

experiments. In the first experiment, we deal with

logs generated by 3 models without loop structures.

We use models M1, M2 and M3, each of which

has 30 transitions, to automatically generated 2000

traces. For the log from M

, we only add events to

traces at random places and the mistaken traces

account for 10% - 90% of the whole, each time 10%

is increased. For the log from M

, we delete events

and for the log from M

, we both add and delete

events.

In the second experiment, loops are taken into

consideration and model M

, M

and M

with 30

transitions and loop structures are used. Other settings

are as above.

To handle mistaken logs of different sizes, five

models, M

, M

, are used to generate

original logs. There are 10, 20, 30, 40 and 50

transitions in each model and mistaken logs are got

by both adding and deleting events. Mistaken traces

account for 60% of the whole log.

Table 1 reports the characteristics of logs used in

the experiments, including error rates, sizes and

number of events.

5.2 Accuracy

For processes without loops, we can skip identifying

loop structures and dealing with loop events. Types

of traces in original logs generated by M

, M

and M

are 12, 323 and 24 respectively. Figure 6a and 6b, 6c

and 6d, 6e and 6f show Event fitness and Trace fitness

of three approaches dealing with logs with only

redundant events, with only missing events and with

both redundant and missing events respectively. From

Fig. 6, Event fitness of FL and our approach is close

to 1 and is relatively stable, while SH performs much

worse as the error rate increases. Besides, Trace

fitness of ours is obviously superior to FL and SH,

because FL simply removes all low-frequency

mistaken traces, losing many types of correct traces.

Note that in Fig. 6d, when 90% of traces have missing

events, Trace fitness of our approach is not high

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

(a) Event fitness with redundant events

(b) Trace fitness with redundant events

(d) Trace fitness with missing events

(e) Event fitness with mixed errors

(f) Trace fitness with mixed errors

Figure 6: Event fitness and Trace fitness on logs without loops.

(a) Event fitness with redundant events

(b) Trace fitness with redundant events

(d) Trace fitness with missing events

(e) Event fitness with mixed errors

(f) Trace fitness with mixed errors

Figure 7: Event fitness and Trace fitness on logs with loops.

0.334. That is because this log has too many different

execution sequences and it is very easy to fail to

discover all correct types. However, performances of

other methods are even poorer, 0.052 and 0.146

respectively.

In the second experiment, traces of original logs

generated by M

, M

and M

have 36, 394 and 72

types respectively. Figure 7a and 7b, 7c and 7d, 7e

and 7f record event fitness and trace fitness using

three approaches to repair logs with only redundant

events, with only missing events and with both

redundant and missing events respectively. Figure 7

shows the same regularity that Event fitness of FL and

our method is almost the same and Trace fitness of

our approach is better. SH has the worst performance

anyway. Figure 8 shows the average value of Trace

fitness on logs above and our approach performs the

best.

Types of traces in original logs generated by M

, M

and M

are 8, 48, 356, 246 and 857 in the

third experiment. Event fitness and Trace fitness are

demonstrated in Figure 9a and 9b. FL and our

approach perform better than SH no matter what the

model size is. When the log becomes more complex,

our approach can still get higher Trace fitness than

FL.

5.3 Efficiency

In the experiment with different logs that all contain

2000 traces, Figure 10a, 10b and 10c individually

show average time consumed to repair the log gener-

An Efﬁcient Heuristic Method for Repairing Event Logs Independent of Process Models

Table 2: Discovering time on logs.

Log

Discovering time (secs)

Inductive

ILP-based

Alpha

ILP-based

Heuristics

0.93

3.47

3.24

_filter

0.58

3.26

3.13

1.27

4.74

11.12

_filter

0.85

3.41

3.25

1.80

21.87

90.84

_filter

1.07

4.27

4.72

L10

2.74

85.20

392.68

L10

_filter

1.13

4.35

4.96

L11

3.70

335.22

1162.45

L11

_filter

1.24

5.76

6.02

Figure 8: Average Trace fitness.

ated by models without loops, with loops and of

different sizes. When the log contains no loop and 30

different tasks, time needed varies from 0.97 second

to 2.66 seconds. When loops exist, it takes 3.56 to

5.04 seconds. When the process size increases from

10 to 50, runtime increases from 2.07 seconds to 6.95

seconds. Time performance is acceptable.

We are also interested in time spent on

discovering models by different mining algorithms.

Table 2 shows time performance for logs L7, L8, L9,

L10 and L11, with and without using our repair

method. After repairing, discovering time is markedly

reduced, especially when the log contains many tasks.

6 CONCLUSIONS

In this paper we present a technique for log repair

when a sound reference model is unavailable. The

core idea is to discover rules the log should follow

and repair traces according to the rules. Since

situations containing loops are unlimited, loop

structures, if there are, are identified in advance.

Sound condition in each subsection are discovered

using basic traces and filtered by specific thresholds.

The experimental results from a variety of logs of

different error rates and different sizes to show that

our method can effectively transform most of the

mistaken traces into correct ones and guarantee the

integrity of the log. Time performance is also within

acceptance.

(a) Event fitness

(b) Trace fitness

Figure 9: Event fitness and Trace fitness on logs of different

model sizes.

(a)

(b)

(c)

Figure 10: Runtime of our method on different logs.

IoTBDS 2019 - 4th International Conference on Internet of Things, Big Data and Security

It will be interesting to explore potential behaviors

not contained in the current log and improve the

accuracy when the log is complex as future work.

Also, we would like to implement our approach as a

plugin in proM.

ACKNOWLEDGMENTS

This work was supported by the Key Program of

Research and Development of China

(2016YFC0800803), the National Natural Science

Foundation, China (No.61802095, 61802167,

61572162, 61572251), the Fundamental Research

Funds for the Central Universities. Chuanyi Li is the

corresponding author (lcynju@126.com).

REFERENCES

Aalst, W., 2011. Process Mining: Discovery, Conformance

and Enhancement of Business Processes. Springer.

Berlin, Germany.

Polyvyanyy, A., Aalst, W. and Hofstede, A., 2016. Impact-

Driven Process Model Repair, ACM Trans. Softw. Eng.

Methodol, vol. 25, no. 4.

Murata, T., 1989. Petri nets: Properties, analysis and

applications, In Proc. IEEE, vol. 77, no. 4.

Aalst, W. and Aalst, W., 2005. YAWL: yet another

workflow language. In Inf. Syst, vol. 30.

Jensen, K., 1991. High-Level Petri Nets: Applications and

Theory of Petri Nets. Informatik-Fachberichte,

Springer. Berlin, Germany.

Aalst, W., Weijters, T and Maruster, L., 2004. Workflow

Mining: Discovering Process Models from Event Logs,

In IEEE Trans. Knowl. Data Eng., vol. 16, no.

Medeiros, A., Dongen, B. and Aalst, W., 2004. Process

Mining: Extending the α-algorithm to Mine Short

Loops. In Technical report, WP113 Beta Paper Series,

Eindhoven University of Technology.

Wen, L., Aalst, W. and Wang, J., 2007. Mining: Process

Models with Non-Free-Choice Constructs. In Data

Mining and Knowledge Discovery, vol. 15, no. 2.

Wen, L., Wang, J. and Aalst, W., 2009. A Novel Approach

for Process Mining Based on Event Types. In Journal

of Intelligent Information Systems, vol. 32, no. 2.

Weijters, A., Aalst, W. and Medeiros, A., 2006. Process

Mining with the HeuristicsMiner Algorithm. In

Technical report, WP113 Beta Paper Series, Eindhoven

University of Technology.

Bergenthum, R., Desel, J., and Lorenz, R., 2007. Process

Mining Based on Regions of Languages. In Proc. 5th

Int. Cof. Business Process Manage.

Solé, M. and Carmona, J., 2010. Process Mining from a

Basis of State Regions, Springer. Berlin, Germany.

Wang, J., Song, S. and Zhu, X., 2013. Efficient Recovery

of Missing Events. In Proc. VLDB Endowment, vol. 6,

no. 10.

Song, W., Xia, X., and Jacobsen, H., 2016. Efficient

Alignment between Event Logs and Process Models, In

IEEE Trans. Service Computing, vol. 10, no. 1.

Song, W., Xia, X., and Jacobsen, H., 2015. Heuristic

Recovery of Missing Events in Process Logs. In Proc.

IEEE Int. Conf. Web Services.

Leoni, M. and Aalst, W., 2013. Aligning Event Logs and

Process Models for Multi-Perspective Conformance

Checking: An Approach Based on Integer Linear

Programming. In Proc. 11th Int. Conf. Business

Manage.

Adriansyah, A., Dongen, B. and Aalst, W., 2011.

Conformance Checking using Cost-Based Fitness

Analysis. In Proc. 15th IEEE Int. Enterprise Distrib.

Object Comput. Conf.

Leoni, M., Maggi, F., and Aalst, W., 2015. An alignment-

based framework to check the conformance of

declarative process models and to preprocess event-log

data. In Inf. Syst.

Rozinat, A. andAalst, W., 2008. Conformance checking of

processes based on monitoring real behavior. In Inf.

Syst., vol. 33, no. 1.

Aalst, W., Adriansyah, A. and Dongen, B., 2012.

Replaying History on Process Models for Conformance

Checking and Performance Analysis. In Wiley

Interdisciplinary Rev.: Data Mining Knowl. Discovery,

vol.2, no. 2.

Adriansyah, A., Munoz-Gama, J. and Carmona, J., 2013.

Alignment Based Precision Checking, Springer. Berlin,

Germany.

Bezerra, F. and Wainer, J., 2013. Algorithms for anomaly

detection of traces in logs of process aware information

systems. In Inf. Syst., vol. 38, no. 1.

Leoni, M., Maggi, F. and Aalst, W., 2012a. Aligning Event

Logs and Declarative Process Models for Conformance

Checking, Springer. Berlin, Germany.

Leoni, M., Aalst, W. and Dongen, B., 2012b. Data- and

Resource-Aware Conformance Checking of Business

Processes, Springer. Berlin, Germany.

Fahland, D. and Aalst, W., 2015. Model repair-aligning

process models to reality. In Inf. Syst., vol. 47.

Conforti, R., Rosa, M. and Hofstede, A., 2017. Filtering Out

Infrequent Behavior from Business Process Event

Logs. In IEEE Trans. Knowl. Data Eng., vol. 29, no. 2.

Bose, R. and Aalst, W., 2012. Process Diagnostics Using

Trace Alignment: Opportunities, Issues, and

Challenges. In Inf. Syst., vol. 37, no. 2.

Dongen, B., Medeiros, A. and Verbeek, H., 2015. The

ProM Framework: A New Era in Process Mining Tool

Support, Springer. Berlin, Germany.

An Efﬁcient Heuristic Method for Repairing Event Logs Independent of Process Models