SQL for Stored and Inherited Relations

Witold Litwin*

Université Paris-Dauphine PSL Pl. de Mal. de Lattre, Paris, France

Keywords: SQL Databases, Information Systems, Non-procedural Data Definition and Manipulation, Logical

Navigation

Abstract: A stored and inherited relation (SIR) is a stored relation (SR) extended with inherited attributes (IAs)

calculated as in a view. Without affecting the normal form of the SR, IAs can make queries free of logical

navigation or of value expressions. A view of the SR can do the same. The virtual (dynamic, computed…)

attributes (VAs) possibly extending SRs at major DBSs, can do as well for value expressions defining them.

VAs are less procedural to declare than any alternate view. Likewise, altering any attribute of an SR with

VAs leading to view altering otherwise is less procedural. We propose extensions to SQL generalizing the

latter two properties to SIRs. In particular, one may define IAs through value expressions not supported as

VAs at present. Also, to define an IA instead of a VA is at most as procedural. We motivate our proposals

through the "biblical" Supplier-Part DB. We postulate SIRs standard on SQL DBSs.

1 INTRODUCTION

Universally applied Codd’s (relational) model for a

Database (Management) System (DBS), (Codd,

1969) & (Codd, 1970), proposed two constructs: a

stored relation (SR) and a view. An SR, often called

also base table, has stored attributes, (SAs), only,

often called columns. Clients or applications provide

the stored tuples. The SR definition (scheme) does

not allow calculating any of these. A view has only

the inherited attributes (IRs). These are basically

only calculated on-the-fly from SRs or from other

views through relational or value expressions in the

view scheme. In 1992, we proposed an additional

construct. It was an SR with IAs added to, (Litwin,

1992). Examples showed it attractive. No further

work followed however.

We now refine our proposal for SQL DBs. We

call our construct Stored and Inherited Relation,

(SIR). For every SIR R, we define every SA as usual

for an SR. We calculate IAs as in a view. We refer

to the calculus scheme within SIR scheme as to

Inheritance Expression (IE). For every SIR R, a

single Create Table R defines both the SAs and the

IE. As we will show, the IAs of a SIR may then

model properties inconvenient to declare as SAs.

Supposing indeed the SR formed by all the SAs of a

https://www.lamsade.dauphine.fr/~litwin/witold.html

SIR normalized, declaring an SA instead of an IA

could adversely impact the normal form or could

imply impractically frequent updates.

It will appear next that an SQL query addressing

SAs and IAs in a SIR, may avoid the logical

navigation. That one is otherwise necessary for

every equivalent query to the DB scheme with

normalized SRs only. We recall that such navigation

occurs whenever a query refers to several relations,

usually through a relational expression with joins

over foreign keys, defined in the query. Also, IAs in

a SIR may avoid selected value expressions to

queries. Altogether, it will appear that an SQL query

to a DB with SIRs should end up usually less

procedural (simpler, more usable…) than the

equivalent to a DB with normalized SRs only, by the

basic measure of fewer characters per query, without

all unnecessary spaces. We recall that clients usually

prefer less procedural statements and find joins

dreadful, the outer ones especially, (Date, 1991),

(Jajodia, 1990).

On the other hand, it will appear also that for

every SIR R, there is always at least one specific

view R that we call equivalent to SIR R. Every such

view R defines mathematically the same SQL

relation as SIR R. Also, for every SA in SIR R with

unambiguous proper name, view R has an IA

bearing the same proper name at least. We recall that

"mathematically the same” means abstraction of the

implementation. Whether a value is stored in SIR R

Litwin, W.

SQL for Stored and Inherited Relations.

DOI: 10.5220/0007676700370048

In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 37-48

ISBN: 978-989-758-372-8

or calculated in view R becomes irrelevant. For SQL

relations, it also means that for the attributes of view

R the same order as in SIR R, unlike perhaps for

equal mathematical relations, (Date, 2004) . At least

for every SQL query to SIR R where the

unambiguous proper names above are not prefixed,

every equivalent view R provides for the same

outcome as SIR R. Actually, one knows such

prefixing useless in SQL queries, i.e., the outcome is

independent of.

Every equivalent view R provides then in

particular also for every query to SIR R free of the

logical navigation or of selected value expressions.

That property, de facto independent of SIRs, makes

equivalent views, without being called so, the basic

“escape routes” since decades for clients tired by the

navigation or value expressions within the

equivalent queries to normalized SRs only, i.e.,

intended for the same outcome. An equivalent view

may in particular be universal, providing all the

attributes and, possibly, all the values of the DB in

one relation, (Maier, 1984).

We propose extensions to Create Table

accommodating SIRs. Likewise, we propose

extensions to Alter Table. We show that for every

SIR R, IE in Create Table R can be less procedural

than Create View R of any equivalent view R. SIR R

expanding with IAs some SR, say R_, provides in

this way for the simpler queries to R_ at lower

procedural data definition cost. Likewise, it will

appear that for every SIR R and every view R,

altering SIR R can be less procedural. We show also

how to implement SIRs on popular DBSs, with

negligible storage and processing overhead.

In particular, we show that some popular DBSs

provide unknowingly already for limited SIRs for

decades. These are SRs possibly carrying also so-

called virtual attributes (VAs) or computed,

generated… columns. We recall that one declares a

VA as a named value expression in Create Table.

Queries avoid the expression by simply referencing

the name. The advantage is that for any number of

VAs in Create Table, their declarations are

altogether always less procedural than any Create

View of an equivalent view. The advantage extends

to all the other SQL DDL statements concerning

VAs.

Our clauses for SQL aim at the same goal. But

the declarations generalize the gain to every SIR.

More specifically, we gain also for value

expressions defining IAs that cannot be VAs.

Finally, we gain for every SIR with, in addition or

instead, IAs avoiding the logical navigation, as

already discussed.

Next section defines SIRs for SQL DBs. We

illustrate our proposals with the "biblical" Supplier-

Parts DB. Section 3 discusses the implementation of

SIRs over a popular DBS. We show the storage and

processing overhead negligible. Section 4 discusses

the related work. Section 5 concludes that SIRs

should be standard on SQL DBSs and proposes

future work.

2 STORED AND INHERITED

RELATIONS

2.1 The Concept

We qualify the SR expanded with IAs of base of

SIR R. Each IA extends every base tuple with a

calculated value or is null. The latter occurs when

the calculus through IE does not provide a value. As

said already, we suppose IA values basically

immaterial. Finally, an easy to see property of every

SIR R is that the primary key of the base is also a

key of (entire) R. For practical reasons we consider

the former as the primary key of R as well.

For every SIR R, its base has its proper default

proper name that is simply R_ below. As every

relation name, every default name should be unique

in the DB. Next, every SIR considered below is an

SQL relation. Hence, the order of attributes matters

and DBA may intentionally inter-mix IAs and SAs.

Furthermore, we suppose every SQL naming rule

applying to SIRs. For every SIR R in particular, one

may qualify every SA or IA A as R.A. One may

qualify further every SA A of every SIR R as R_.A.

That is the default we motivate soon and more in

(Litwin, 2016a).

Below, we may refer to any SQL dialect, DB or

DBS providing for SIRs as SIR SQL, SIR DB or

SIR DBS. In practice, we mean by SIR SQL a

backward compatibility with some popular SQL

dialect, e.g., MySQL dialect. We refer to the latter as

to the kernel (SQL or dialect). Every SIR SQL

should preserve the SQL syntax and every capability

of the kernel. Especially, every kernel's statement

should continue to apply to any SR or view in a SIR

DB.

2.2 Creating a SIR

We create every SIR through kernel's Create Table

SQL DDL statement expanded with the IE. We base

the design of that statement on a specific SQL view.

Given some SR R, we call that view conceptually

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

expanded view (of) R and denote as C-view R or

view R simply. As the name suggests, every C-view

R presents every tuple of SR R expanded with some

or all attributes and values that conceptually should

be in SR R. Typical reason for not being there

nonetheless for some, is that each would create some

notorious normalization anomaly. As known, every

such attribute may then be within another relation.

Alternatively, one may define it only in a query

through a named value expression over SAs in SR R

or over other IAs referred to or defined in the query.

It is well known that for every relation, say F,

with attributes of C-view R missing in SR R because

of the normalization, a key of F in R represents

conceptually all the attributes of F. We recall that

such keys, perhaps composed, are usually qualified

of foreign. C-view R inherits first every attribute and

tuple of R, including thus every foreign key. Next,

every C-view R tuple has in principle every IA value

that every foreign key represents, except for the

referenced key. In practice, DBA can restrict the

inherited set, e.g., because of security concerns.

Each IA represented through foreign key in C-view

R inherits every value through some relational

expression over F. Every foreign key in C-view R

inherits in contrast all its values from SR R only. A

foreign key may thus have a value in C-view R that

is not in F. Every IA otherwise inherited from F is

null in every tuple with such a value.

As already hinted to, C-view R may also or even

only, have IAs with values inherited through value

expressions from SR R itself or may have IAs

inheriting through a value expression from such IAs

and so on. Finally, C-view R may have conceptual

attributes inherited through value expressions and

out of SR R not because of anomalies, but since they

would require impractically frequent updates or

would eat storage relatively uselessly.

Technically, to declare C-view R, one has to first

rename SR R. No relations may share a name indeed

in an SQL DB. We suppose R_ as default new name

for SR R. Create View R for C-view R has then to

be so that for every tuple t' of SR R_, there is exactly

one tuple t of view R with t' as sub-tuple. For every

t, Create View R should furthermore value or make

null every other IA as above discussed. Next, view R

should not have other tuples.

The known practical result is that query Q to C-

view R may avoid the logical navigation or value

expressions necessary for an equivalent query Q' to

SR R and to any of attributes in some F or requiring

a value expression in Q' over some attributes of SR

R. The known result is that Q ends up less

procedural than Q'. We will illustrate it with

examples soon. Actually, also it is also known that

lesser procedurality characterizes in this way most of

practical queries. That is why, without being named

so, C-views are in fact already among those already

discussed views that simplify queries for decades.

We intend SIR R as a single construct merging

C-view R and SR R. More precisely, we aim on SIR

equivalent to C-view R with the only difference that

SIR R has R_ as the base, i.e., that every attribute

R_.A of view R is materialized back in SIR R into

SA A of SR R. Accordingly, we define SIR R

through Create Table R of SR R, expanded with the

scheme of every IA A in C-view R, with full source

name other than R_.A. The order of SAs and of IAs

in SIR R is that of all the IAs in C-view R. The

whole Create Table R consists accordingly of the R_

scheme and of the IE. It may appear as designed

through the following steps.

Start with: 'Create Table R As ('. Continue with

the intended C-view R scheme, i.e., the SQL

expression that would follow Select keyword in

Create View R. If the scheme includes R_.* term,

expand it to every attribute of R_, referred to by its

proper name. Also, when relevant, refine the

remaining part of C-view R in Create Table R to its

implicit form we discuss in next section. Next,

expand every R_.A with its data type etc. intended

for Create Table R for SR R. Finally, append every

table option, declaring thus optional multi-attribute

primary key, indexing, partitioning…

Observe that the result conforms to our generic

requirement on the primary key of every SIR R.

Also, observe that our rule for default source naming

of SAs in SIR R, keeps all the clauses From…

within view R referring there to R_, valid for SIR R

as well. Instead of referring to stand-alone SR R_,

i.e., defined by dedicated Create Table R, they

simply refer to the base of SIR R, equal to the

former as an SQL relation and with respect to the

full attribute naming.

For every SIR R, it follows from all the above

that IE is C-view R scheme with Select list restricted

to only and every IA A not with full source name

R_.A in view R. If not refined as we spoke about, IE

contains that sub-list (without Select keyword) and

the From… clauses of C-view. If C-view R names

every IA that is an SA in SIR R or declares all these

as R_.*, then IE is a strict sub-list of the Select list in

view R, followed by the From… clauses of the view.

Recall also that for every SIR R, the scheme of its

base R_ has the procedurality of that of SR R. As we

already hinted to and will illustrate with examples, it

follows that every IE of SIR R, has strictly lower

procedurality than Create View R for C-view R.

SQL for Stored and Inherited Relations

SIR R becomes consequently more advantageous

than SR R and C-view R for the avoidance of the

logical navigation or of selected value expressions.

In what follows, we qualify of explicit, every IE

with the above sub-list. We denote it as E or E

for

SIR R. Observe that while these IAs are always

contiguous in E

, they may be separated by SAs in

Create Table R, we recall.

Ex. 1. Recall the ‘biblical’ Supplier-Part DB,

often named S-P in short, modelling some suppliers,

parts and supplies. Every supply contains some

quantity of a part shipped by some supplier. A

supplier may supply nothing for the time being.

Likewise, a part may be not supplied. S-P motivated

the original proposal of the relational model, [C69],

[C70]. Variants settled the relational (conceptual

schema) design rules of SRV-model, based on NFs

as known. Through these rules, S-P molded about

every practical DB. The variant we pick up below

seems best known, (Date, 2004) . We refer to it as S-

P1. We restate S-P1 into variants with different

SIRs. We call S-P2 the variant that follows.

S-P1 has three well-known relations: S (S#,

SNAME, STATUS, CITY), P (P#, PNAME,

COLOR, WEIGHT, CITY), SP (S#, P#, QTY).

Figure 1 shows the original sample data type for

every attribute. Actually, the figure shows S-P2 DB.

S-P1.S and P are the same SRs as in S-P2. For S-

P1.SP, data types are these of S-P2.SP at the figure.

The latter is however SIR SP that we present it in

detail soon. All the SA definitions at the figure skip

some practical details, e.g., the data length. We

underline the primary key, as usual.

Figure 2 shows the original sample data values

for S-P1. For S-P1.SP, these are among those of SIR

SP there, according to the attribute names. For the

relational algebra, considered by the original S-P1

proposal, the order of attributes in a relation, hence

the left-to-right one at the figures does not matter.

As known, it does for SQL, e.g., for Select * From

SP. The S-P1 scheme is the optimal one, in the sense

of having the minimal number of SRs free of

normalization anomalies, (Date, 2012) .

The notorious drawback of S-P1 is that practical

Select queries to SP usually need values from S or P

as well. E.g., most actual clients searching for a

supply need the supplier or part name(s). These are

evidently conceptual attributes of every supply.

However they are not in SP, since the notorious

normalization anomaly would make SP losing its

BCNF form (in fact, SP is in 5

form even). Every

related query has then to logically navigate over SP

and S or P or both through inter-relational joins

SP.S# = S.S# or SP.P# = P.P#. One knows well that

clients usually hate the logical navigation, feeling it

making the queries more procedural than they

should be, (Maier, 1984). The well-know “escape

route” for S-P1 is adding the (universal) view,

named view SP, providing the image of SP with

every tuple preserved bijectively and expanded with

every matching value of every attribute of S and of P

or with nulls otherwise. Such a view avoids the

logical navigation to more queries than any other

view of SP with fewer attributes or values. To create

view SP, one has to rename first SR SP, to, say, SP_,

since every relation in an SQL DB must have a

different name. Then, likely the least procedural

view SP declaration in SQL is as follows, provided

the removal of all the spaces added for easier

readability only, e.g., after each comma:

(1) Create View SP As (Select SP_.*,

SNAME, STATUS, S.CITY, PNAME, COLOR,

WEIGHT, P.CITY From (SP_ Left Join S On

SP_.S# = S.S#) Left Join P On SP_.P# =

P.P#);

Unlike for the original SR SP, the SQL

formulation of a typical query to SP, such as name

of the supplier, quantity supplied and name of the

part for every supply with supplier Id ‘S1’, does not

need the logical navigation. The query becomes

notably less procedural, as one may easily verify.

To have a DB, say S-P2, with S, P and SIR SP,

instead of S-P1 with S, P and SP renamed to SP_,

and view SP defined by (1), one should figure out

first whether the view qualifies as C-view SP. This

is the case. First, view SP inherits bijectively every

tuple of SP_ as exactly one sub-tuple and has no

other tuples. In particular, (SP_.S#, SP_.P#) is the

primary key of SP_ and (SP.S#, SP.P#) is the one of

view SP. The rationale for all these properties is that

S.S# and P.P# are also the keys for S and P,

respectively. Accordingly, for the first tuple of SP_

at Figure 2 for instance, i.e., with SAs S# = S1 and

P# = P1, the join clauses match only one source

tuple in S and only one in P. Only a single tuple in

view SP results from that is the first one at the

figure. Similarly for SAs S# = S1 and P# = P2 etc.

View SP qualifying thus as C-view SP, we can

define SIR SP as above discussed through the

following Create Table SP:

(2) Create Table SP (S# Char, P# Char,

Qty Int, SNAME, STATUS, S.CITY, PNAME,

COLOR, WEIGHT, P.CITY From (SP_ Left

Join S On SP_.S# = S.S#) Left Join P On

SP_.P# = P.P#), Primary Key (S#, P#));

Figure 1 shows S-P2 scheme. Figure 2 shows the

content of SIR SP that would result for the sample

data of S-P1. Every SA is in plain text and every IA

in Italics. We suppose the SAs schemes in S-P2.SP

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

these of S-P1.SP, hence of SP_ for C-view SP.

These SAs and their tuples form also the base SP_ of

S-P2.SP. These SRs are equal, hence SP_ preserves

the normal form of S-P2.SP. The (underlined) key of

S-P2.SP is also that of S-P1.SP. Its definition in

Create Table SP in (2) above follows entire E

, as

required for every Create Table R for SIR R. E

the string: ‘SNAME…P.P#’ that happens to be

contiguous one. This string is also a (strict) substring

in (1) hence in C-view SP, as well as is defining the

SQL projection there on the enumerated IAs. These

are also all and only IAs in (2). As only a substring,

it is strictly less procedural than (1).

More precisely, assuming all spacing

unnecessary for SQL syntax in (1) removed, its

procedurality, say p

, is p

= 144 (characters). E

saves then the string ‘Create View SP As (Select

SP_.*,’. This reduces the procedurality to p

= 112.

Likely the simplest measure of procedurality gain

(reduction) is p

. E

appears then 1.29 times less

procedural than (1). Alternate measures are also

possible, (Litwin, 2016a.).

The remaining part of (2) is simply Create Table

SP for S-P1.SP that (2) replaces in S-P2. Thus, there

is neither procedurality loss nor gain on SA schemes

in (2), with respect to SAs schemes for (1).

In both statements (1) and (2) above, the already

reminded SQL ordering makes all the SAs preceding

all the IAs. It is our subjective choice. The rationale

is that keeping the IAs inheriting from SP_ together,

minimizes, in SQL, the procedurality of view SP,

through SP_.*. Note nevertheless that many consider

‘*’ less safe for Create View than the list of

attributes '*' represents. The latter choice would

make E

reducing procedurality even more, 1.44

times in fact. The same would occur if an IA

dispersed the SAs of SP within Create Table SP and

in C-view SP thus. The list of IAs (contiguous) in

would still consist of the same IAs, but now non-

contiguous in Create Table SP. The same From

clause of (2) would follow both lists. Finally, for S-

P2, the query Select * From SP; would output the

attribute order at Figure 1 for the tuples of Figure 2.

Observe also that in (1), every prefix SP_ in joins

refers to SR SP_ that is one of the source relations of

view SP. In (2) in contrast, it refers to SIR SP base

SP_, hence to a part of SIR SP itself. We qualify

below every join in some SIR R referring similarly

to a part of R, of recursive. Actually, a recursive join

may be a

-join, as one may easily find out.

Recursive joins are basically not permitted in SQL

views, we recall. The example suggests them in

contrast typical for IEs.

The graphic at Figure 1 schematizes the

proposed evolution of the "biblical" SR SP in S-P1

into SIR SP in S-P2. At the left, we have S-P1

scheme. Next, we have S-P1 with SP renamed to the

default name of SP_ and the C-view SP, as defined

by (1). This is what DBA could do best at present to

avoid the logical navigation within queries to SP.

The view contains the sub-view that is a virtual copy

of SP_, with every SA of SP_ becoming an IA.

Finally, at the right, SP_ replaced its copy, becoming

the base SP_ of our SIR SP.

In all rectangles, the grey color symbolizes SAs

and green IAs. The green rectangle of S-P1 with

view SP is as large as SIR SP. It is larger than the

green one of SIR SP by its left sub-part. That one is

fully redundant with SP_, as just discussed. The

redundancy costs view SP the clause S_.* in (1),

with respect to the IE in SIR SP, as defined by (2).

This is the core of the higher procedurality of Create

View SP with respect to the IE in Create Table SP

for SIR SP. By the same token, it is the cause of

lower procedurality of Create Table SP as in (2) than

of Create Table SP_ followed by Create View SP as

in (1).

2.3 Implicit IEs

As said above, the IE ‘SNAME…P.P#’ for SIR SP

is an explicit one that we denoted thus ESP. One

defines an explicit ER as a view could be. For some

SIR, the IE can also be a furthermore a specific

expression that we call implicit and denote as I or

IR. An IR can contain a generic character '#' or

brackets () around an SA or several consecutive

SAs, forming a foreign key. Alternatively, IR may

define only IAs being named value expressions not

followed in Create Table by any From… clause(s).

Every IR is intended to be less procedural than an

ER could ever be. We define three following rules

for an IR definition. Rules 1 define and Rule 2

defines each preprocessing of IR to a specific ER

denoted EIR. Rule 1 concerns '#', Rule 2 deals with

(…). Rule 3 preprocesses every IR with value

expressions.

Rule 1. Create Table R may contain, after the last

SA scheme, IR in the form: ‘# From R1…R2… ;',

with (necessarily) some Ri = R_ or Ri = R ; i ≥ 1.

Let also R'1, R'2… be, successively, all the other

relations. Then, EIR is:

EIR = R'1.*,R'2.*… From R1…R2…;

The terms R'1.*,R'2.*… that precede Ri in From

clause, insert into Create Table R before the first SA

scheme. All the others replace #.@

Rule 2. IR contains brackets (). In Create Table

R, these form term(s): (A1,A2...)…. Each A is an

SQL for Stored and Inherited Relations

SA scheme. A1,A2… names also a foreign key of

some relation F. DBA may designate F through the

usual Foreign Key clause. This one is mandatory if

the term does not designate the referenced key of F

uniquely. Alternatively, F is designated by the

equality of all the (proper) name(s) A1,A2… with all

the (proper) name(s) of key attribute(s) of F. DBS

preprocesses Create Table R with the discussed IR

towards EIR as follows.

Rule 3. The IE defines every its IA A as: V As

A. Also, the IE has no From… clauses. Finally the

kernel supports VAs. Then, every term V As A is

preprocessed into the VA-term of the kernel so that

Create Table R statement becomes the kernel's one.

The final result for every such statement is SR R

with VAs that kernel SQL would create.@

Ex. 2. To illustrate Rule1, suppose for S-P1 that

only selected clients should be able to match the

supplies of any supplier or part. All the others may

still access every relation, nevertheless. The DBA

may therefore use a secret function Enc, encrypting

SP.S# and SP.P# of every supply. The DBA may

furthermore provide the selected clients with the

following universal view SP, after renaming SR SP

to SP_, as already discussed. The right join replaces

the left one in (1) for the sake of the example.

(3) Create View SP As (Select * From (S

Right Join SP_ On SP_.S# = Enc (S.S#))

Left Join P On SP_.P# = Enc (P.P#));

View SP defined so may clearly be C-view SP

for SIR SP with base SP_. Given Rule 1, DBA may

define ISP simply as:

(4) I

= # From (S Right Join SP_ On

SP_.S# = Enc (S.S#)) Left Join P On

SP_.P# = Enc (P.P#));

Clause From is the same for (3) and (4). Hence,

ISP remains less procedural than View SP. Actually,

(4) is 1.4 times less procedural than (3). When one

declares Create Table SP, DBS applies Rule 1 and

pre-processes it using (4) to:

Create Table SP (S.*, S# Char, P# Char,

Qty Int, SNAME, STATUS, S.CITY, PNAME,

COLOR, WEIGHT, P.CITY, P.* From (S

Right Join SP_ On SP_.S# = Enc (S.S#))

Left Join P On SP_.P# = Enc (P.P#)),

Primary Key (S#, P#));

EISP is then equal to:

(5) E

= S.*, P.* From (S Right Join

SP_ On SP_.S# = Enc (S.S#)) Left Join P

On SP_.P# = Enc (P.P#));

In Create Table SP, S.* term of EISP precedes

all the SAs, since S precedes SP_ in the right join

within From clause. P.* replaces #. The list S.*,

SP_.*, P.* would be simply a more procedural

expression of '*' in (3) that we spoke about in

general terms.

As in general for every ER and C-view R, EISP

in (5) is also less procedural than Create View SP of

C-view SP defining it as E

, i.e., Create View SP

As (Select S*, S_P.*, P* From (S Right

Join SP_…);

. In fact, one may easily see that (5)

remains also less procedural than (3). ISP as in (4) is

not thus really necessary here for our goal. However,

visibly, it could not be so if relations S and P had

instead longer names, e.g., SUPPLIERS and

PARTS_IN_STOCK. This would prove our point

that without Rule 1, we could not attain our goal of

an IE being always less procedural than the C-view

it may replace.

Ex. 3. To illustrate Rule 2, suppose, just for the

sake of the example, that S is atypical, namely is

S (SNAME, S#, STATUS, CITY). Suppose also the

referential integrity between SP, S and P. DBA of S-

P2 can then declare the following SIR, instead of

(2), with the advantage of visibly less procedural

Create Table:

(6) Create Table SP ((S# Char), (P#

Char), Qty Int From S, P, SP_ Where

SP_.S# = S.S# And SP_.P# = P.P#,

Primary Key (S#, P#));

Clause Where of (6) is visibly less procedural

than the one with outer joins in (2). It is however

obviously possible only for the referential integrity.

The IE for scheme (6) contains two terms conform

to Rule 2. Hence ISP is:

(7)I

= (), () From S, P, SP_ Where

SP_.S# = S.S# And SP_.P# = P.P# ;

Given (6), first () indicates presence of the

foreign key of S to expand to all the attributes of S

except for S.S#. SP should furthermore preserve the

total order in S, with however, in SP, the foreign key

SP.S# instead of the referenced one S.S#. Likewise,

2nd () does for P. The order of all non-added

attributes in SP should finally remain unaffected.

ISP (7) should thus be preprocessed to EISP as

follows:

(8) EISP = SNAME, STATUS, S.CITY,

PNAME, COLOR, WEIGHT, P.CITY, QTY From

S, P, SP_ Where SP_.S# = S.S# And

SP_.P# = P.P#);

Finally, the resulting Create Table SP should be:

(9) Create Table SP (SNAME, S# Char,

STATUS, S.CITY, P# Char, P#, PNAME,

PNAME, COLOR, WEIGHT, P.CITY, Qty Int

From S, P, SP_ Where SP_.S# = S.S# And

SP_.P# = P.P#, Primary Key (S#, P#));

If DBA considered C-view SP instead, the least

procedural one would be:

(10) Create View SP As (SNAME, SP_.S#,

STATUS, S.CITY, SP_.P#, PNAME, COLOR,

WEIGHT, P.CITY, QTY, From S, P, SP_

Where SP_.S# = S.S# And SP_.P# = P.P#);

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

(10) is clearly more procedural than (8), hence is

not a practical alternative. However, DBA can be

interested only in the freedom from the logical

navigation for practical queries, i.e., those where no

unique proper attribute name is (uselessly) prefixed

with source name. E.g., for (10) a query Select S#

From SP Where SNAME = 'Smith' would be a

practical one, while Select SP_.S# From SP… would

not. The following view can make then more sense

for the DBA than (10):

(11) Create View SP (Select S.*, P.*,

QTY From S, P, SP_ Where SP_.S# =

S.S# And SP_.P# = P.P#);

Indeed, view SP defined by (11) is visibly less

procedural than (10), taking advantage of '*'. It is

however not a C-view SP. The full source names of

attributes S# and P# are indeed S.S# and P.P#,

unlike in (10) and unlike it should be for any C-view

SP. The DBA can nevertheless realize that (11) is

still an equivalent view. At least for every SQL

query to SIR SP where the unambiguous proper

names above are not prefixed, it provides for the

same outcome as SIR SP. We call every such view

query equivalent or Q-view. SIR SP here illustrates

thus the case where only I is less procedural than an

equivalent view. More precisely, with respect to ISP

(9), Create View SP (11) is 1.2 times more

procedural. It would be so, also for any equivalent

variant of (11). See (Litwin, 2016a.) for more on Q-

views. Likewise, see there easy examples illustrating

Rule 3. Example in next section also illustrates that

rule.

2.4 Other DDL Statements for SIR

Model

We now focus on SIR SQL DDL statements other

than Create Table. We continue supposing every

such statement backward compatible with some

kernel (dialect). E.g., for MySQL SQL as the kernel,

we suppose Create View of SIR SQL, being simply

the MySQL Create View, except that among source

relations could be SIRs. We suppose similarly for

SQL Server as the kernel etc.

The other SQL DDL statements we suppose for

SIRs are all the popular ones, i.e., Alter Table, Drop

Table, Alter View, Drop View and Create Index. For

Alter Table R for some SR R or SIR R, we suppose

for the former the semantics of Alter Table R of the

kernel SQL. E.g., for MySQL kernel thus, Add may

create an SA or IA intended as VA or may be

followed by optional First and After keywords

specifying how the added SA mixes with the

existing SA and VAs. Also, one Alter Table may

alter several attributes, unlike for SQL standard. On

the other hand, for every kernel, Alter Table R for R

that is an SR may expand R with an IE. This is done

only through the clause specific to Alter Table for

SIRs, we named IE as well, and refer to as IE-clause.

Every IE-clause defines new IE replacing an existing

one, if any. It acts thus similarly to every Select

expression in any Alter View at present, replacing

the existing view scheme. IE-clause is finally

mutually exclusive with the existence of IAs defined

as VAs.

The IE-clause defines the IE and, necessarily, the

placement of each IA among all the SAs. The latter

are defined by Create Table and, perhaps, successive

Alter Table statements, including the one with the

IE-clause. The IE-clause for SIR R may define all

this in the terms of C-view R after the Select

keyword. As for IR, the IE-clause may alternatively

contain instead of some or even all such terms the

generic character '#' or terms in brackets (). As for

an IE, the rationale is to have IE-clause less

procedural even when C-view or Q-view definition

takes advantages of '*' we have discussed. Every IE-

clause with '#' is preprocessed to as IR with would

be, with however the additional insert(s) by name or

as R_.*, of every SA into the list of the attributes

resulting from the preprocessing. Thus, for sole '#',

there is the additional insert of R_.* at the position

determined by R_ or R in From clause. The

additional inserts for every term Ri.# are the

(unique) names of every SA with the proper name of

some Aj in Ri. The position of each insert is

determined by that of Aj among the attributes of Ri,

as we discussed for Rule 2.

Next, for every SIR R, we allow Alter Table R to

drop the IE through simple Drop_IE verb. This

obviously alters SIR R into SR R. Then, if Alter

Table drops, adds or renames any SAs, new IE

clause is optional. Like would be optional the Alter

View R statement for C-view R resulting from Alter

Table R_ with the same alterations of SAs. Next, for

any SIR R, we prohibit to drop all SAs, as usual for

every alteration of every SR R, besides. In

particular, we prohibit thus for every SIR R, any

alterations into a view instead. If such need occurs,

one should use Drop Table R followed by Create

View R. Likewise, if view R should evolve to SIR

R, we presume Drop View R followed by Create

Table R. These procedures are obviously the

simplest to put into practice.

We discuss in (Litwin, 2016a) Drop Table R and

all the others remaining SQL DDL commands.

Ex. 4. DBA adds to S-P2.P the IA WEIGHT_KG

defined as Round (WEIGHT * 0.454). S/he also

SQL for Stored and Inherited Relations

adds WEIGHT_T in tons. For application dependent

reasons, WEIGHT_T should precede WEIGHT_KG.

1. MySQL is the SQL kernel dialect for SIRs:

(12) Alter Table P Add WEIGHT_KG / 1000

As WEIGHT_T After WEIGHT, Round (WEIGHT

* 0.454) As WEIGHT_KG After WEIGHT_T;

Both IA schemes are so since these IAs could be

VAs. As the result, Alter modifies SR P into SIR P

that, e.g., on MySql, could be S-P1.P with two VAs

added. By not needing parentheses around the value

expressions, (12) is (slightly but still) less procedural

than the similar altering adding VAs WEIGHT_T

and WEIGHT_KG directly under MySQL.

2. The SQL dialect for SIRs does not have VAs,

e.g., MS Access.

(13) Alter Table P IE (P#, PNAME,

COLOR, WEIGHT, WEIGHT_KG / 1000 As

WEIGHT_T, Round (WEIGHT * 0.454) As

WEIGHT_KG, CITY From P_) ;

3. The DBA from (2) above decides to drop

WEIGHT_T.

(14) Alter Table P IE (P#, PNAME,

COLOR, WEIGHT, Round (WEIGHT * 0.454)

As WEIGHT_KG, CITY From P_) ;

For view P, if the SQL dialect provides Alter

View, then the DBA could use:

(15) Alter View P As (Select P#, PNAME,

COLOR, WEIGHT, Round (WEIGHT * 0.454)

As WEIGHT_KG, CITY From P_) ;

If the kernel does not provide Alter View, DBA

would need Drop View P followed (atomically) by

Create View P.

4. DBA of S-P2 has created SP initially as S-

P1.SP SR. Then, s/he decided to alter SP to SIR SP

at Figure 1. Thus all the IAs should follow the base

SP_. Regardless of the kernel dialect, the following

statement should do:

(16) Alter Table SP IE (S.#, P.# From

(SP_ Left Join S On SP_.S# = S.S#) Left

Join P On SP_.P# = P.P#);

Suppose now that DBA rather prefers to create SIR

SP as in Ex. 2. IE-clause would be then ISP (4). The

preprocessing would rewrite it to:

IE (S.*, S#, P#, Qty, SNAME, STATUS,

S.CITY, PNAME, COLOR, WEIGHT, P.CITY,

P.* From (S Right Join SP_ On SP_.S# =

Enc (S.S#)) Left Join P On SP_.P# = Enc

(P.P#)), Primary Key (S#, P#));

Likewise, for the alteration to SP from Ex. 3, IE-

clause would be defined as in (7). The preprocessing

would insert SA names, making IE-clause like in (9)

without the data type declarations.@

Altering SR P to SIR P as in (13) is (slightly, but

still) less procedural than Create View P for any

equivalent view P, C-view P, in particular (why?).

Likewise, the alteration (14) is visibly less

procedural than (15). The difference increases if one

uses Drop View P followed by Create View P

instead of (15), e.g., for MsAccess kernel. Likewise,

altering SR SP to SIR SP as in (16), is visibly less

procedural than Create View SP for any equivalent

view SP or C-view SP. In fact, the actual view

creation should be typically even more procedural

by far. The reason is that since the view should be

named as the existing SR, SQL requires first to

rename the SR. This needs one more statement with

its procedurality adding on. Furthermore, to avoid

any run-time error for a client, both statements

should typically be again an atomic transaction. That

one requires additional SQL statements. An atomic

transaction is likewise needed for Drop View

followed by Create View above discussed.

Ex. 5 Consider again S-P1.SP becoming either

SIR S-P2.SP or C-view SP. For the former, the

single Alter SP statement (16) suffices. To create the

C-view SP in contrast, one has to first rename SP

into SP_. This costs one Alter SP Rename To SP_P

statement. Then, one has to formulate the already

mentioned Create View SP as in (1). For the

atomicity, SQL Begin Transaction and Commit

brackets are necessary. Likewise, SQL Error Code

tests for Commit or Rollback should follow every

DDL statement. All this leads to several SQL

statements (how many?). The result is clearly

several times more procedural than (16).@

Similar savings occur for any equivalent view

SP. It is also so for SIR SP variant (6) and Q-view

SP (7).

Finally, SA name change, SA addition or

deletion leads to similar advantages of SIRs. E.g.,

work out the shortening of SP_.QTY to Q, (i) for S-

P2.SP and C-view SP and (ii) for SP variant (6) and

its Q-view SP.

Our examples obviously generalize to every SIR.

It should be clear thus that to alter any SR R to SIR

R, should be always several times less procedural

than renaming every SR R to R_ and creating C-

view R or Q-view R. Next, for every SIR R, altering

an IA A through IE-clause, should be always less

procedural than altering A in C-view R or Q-view R.

In the same time, that altering an SA of SIR R

should be always several times simpler than altering

R_.A and C-view R or dropping and recreating view

R instead. Finally, every altering of SIR R with IAs

preprocessed to VAs, by adding, modifying or

dropping such IAs, is equally or less procedural that

the same operation on SR R with these VAs today.

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

2.5 DML Statements for SIRs

SQL DML statements manipulate relations

regardless of their implementation. We presume

therefore operationally for every SIR DB, that the

syntax of every DML statement (query) is that of the

kernel SQL dialect. The semantical difference is that

a name in the statement may refer to a SIR or its

base. Then, for every query Q referring to any SIR

R the outcome of Q should be as if it addressed C-

view R instead. If Q refers to R_ in contrast, the

outcome should be that of R_ supposed stand-alone

SR R_. Every update query Q addressing SIR R is

accordingly valid (executable) only if C-view R is

updatable by Q. In practice, the updatability will

depend on the kernel DBS, [D4]. The constraint may

impair even Q addressing R, but updating SAs of R

only. Q should refer then to R_.

Ex. 6, Suppose SQL Server kernel. Every

statement Update SP…. would fail, even if it

addressed an SA only. C-view SP is indeed a view

with joins, while such views are not updatable at that

kernel. One should formulate every such update as

Update SP_.... In contrast, every Update SP…

addressing SAs only would be OK for, e.g., MS

Access or MySQL kernel. Both are indeed free of

that restriction. But, every Delete From SP… in S-

P2 would fail even under MS Access because of

these joins (it would succeed however in QBE of

MS Access, perhaps surprisingly). Again, it would

succeed with this dialect only if formulated as a

Delete From SP_... .

3 IMPLEMENTING SIRS

3.1 Basic Processing Scheme

As already said, the most practical way towards a

SIR DB seems the reuse of a popular SQL DBS as

the kernel DBS with its SQL as the kernel dialect.

One way is to create the SIR-layer, managing SIR

SQL DDL and DML statements through the calls for

the kernel services, Figure 3. For the kernel DBS,

SIR-layer appears then as any clients.

In particular, for the Create Table R statement

received, SIR-layer determines first the relation to

create. If R is an SR, SIR-layer forwards the

statement as is. In turn, the processing must be more

involved for every SIR R. Except for R with VAs,

the simplest seems to represent every SIR R in the

kernel as stand-alone SR R_ and C-view R. SIR-

layer simply forwards then every query Q as is to the

kernel. This one processes Q either towards view R

or towards R_ only. Only for every SIR R with VAs,

hence for the kernel with VAs as well, the simplest

design, implied actually by Rule 3, appears that SIR-

layer simply forwards the preprocessed Create Table

R. The kernel creates SR R with VAs accordingly.

We qualify of basic (processing) scheme, (BPS),

the processing as above sketched. Thus, for Create

Table R for SIR R in every case other than applying

Rule 3, BPS always starts with the preprocessing of

, if there is any into E

. Next, BPS passes Create

Table R_ statement to kernel DBS, using for that all

and only SAs of Create Table R. Then BPS creates

the C-view simply as follows. Let A1,…,Am be the

list of the names of every SA and of every IA in

attribute list of E

, in the order resulting from that in

Create Table R. Then, BPS simply issues to the

kernel the following statement, with From, Where

etc. clauses of E

Create View R As (Select A1,…,Am

From…Where…)

Ex. 7. (1) We submit to SIR-layer S-P2 scheme

at Figure 1. BPS finds no IEs in Create Table S and

Create Table P. It passes each statement to the

kernel that creates each SR. BPS determines that

Create Table SP in contrast defines ESP we

discussed. If BPS found any of ISP we discussed, it

would eventually pre-process it to EISP. For ESP,

BPS issues the following two statements to the

kernel DBS. We systematically omit below the

statements making an atomic transaction from the

presented ones, obviously necessary.

Create Table SP_… ;/* With all and only

stored attributes of SP at Figure 1.

Create View SP As (… ;/* Statement (1).

We leave as exercise the variants for each ISP

already discussed.

(2) Suppose now the kernel dialect backward

compatible with MySQL, hence supporting VAs.

Suppose also that DBA creates SIR P with IAs

WEIGHT_KG and WEIGHT_T defined as in (12).

BPS forwards Create Table P from SIR-layer as is to

the kernel DBS. The result is SR P with VAs.

(3) Suppose that the kernel dialect does not

support VAs. Create Table P for SIR P may only

define both IAs as for a view, i.e., again as in (12)

for each. BPS generates two statements for the

kernel:

Create Table P_… /* With attributes of

P at Figure 1.

Create View P As Select P#, PNAME,

COLOR, WEIGHT, WEIGHT_KG/1000 As

WEIGHT_T, WEIGHT_KG As Round (WEIGHT *

0.454), CITY From P_; @

SQL for Stored and Inherited Relations

Figure 3 illustrates BPS outcome for S and SP as

in S-P2 and P as in Ex. 7. We call the result S-P3

DB. SIR-layer shows SIRs as rectangles. Each size

reflects the number of tuples and tuple width

appearing to the client. The lower part displays SRs

and C-views within the kernel DBS similarly.

3.2 BPS of Other DDL & of DML

Statements

Alter Table R and Drop Table R for SIR-layer also

require from BPS more processing than calling their

kernel counterparts only. For every SIR R, each

statement requires in fact the atomic transaction that

DBA should formulate to R_ and C-view R instead.

We recall from Section 2.3 that the latter is always

more procedural than the former, usually several

times. See (Litwin 2016a) for more details, as well

as for BPS for the other DDL statements. As

motivating example, spell out BPS outcome for

Alter Table SP for Ex. 5 and its follow up in

Section 2.3.

BPS implementation is a future work. In the

meantime, (Litwin, 2016) simulates BPS for S-P2 on

MS Access as the kernel. As detailed also in

(Litwin, 2016), one may experiment with every

manipulation of SP or P we have discussed.

3.3 Operational Overhead of

SIR-Layer

The kernel storage for every SIR data is in practice

the one for the base data only. C-view storage

should be obviously always negligible. The storage

for the SIR-layer meta-tables should be clearly

larger. But, it should remain still typically negligible

with respect to the data storage. Altogether, the

storage for a SIR DB should be only negligibly

greater than that required by the DB with the SIR

bases as stand-alone SRs only or with C-views or Q-

views in addition.

For DDL statements, the processing cost of each

by BPS is clearly negligible. Same for DML, since

the SIR-layer passes every query as is to the kernel.

Hence, the SIR-layer overhead through BPS has no

incidence on the query evaluation in practice.

4 RELATED WORK

We have shown that SIRs may make a relational DB

less-procedural. As shown, the views would be more

procedural to maintain. As already mentioned, same

rationale already motivated VAs, decades ago. As

discussed also, every SR with VAs is a specific SIR

R. SIRs generalize thus the old rationale for VAs to

SRs with IAs too complex to be VAs at present, e.g.,

T_QTY, or to those helping with the logical

navigation. The rationale for VAs proved

appreciated. We may thus reasonably hope SIRs

becoming popular as well.

Besides, the current capabilities of every popular

DBS with VAs are not all that the research has

proposed. E.g., some forms of VAs, hence of IAs,

could be updatable, (Litwin, 1986).

As mentioned, our example SIR S-P2.SP is a

new type of a universal relation that one may call

thus a universal SIR. There were various proposals

for universal relations, (Mendelzon, 2004), (Vardi,

2011). If a universal view R is a C-view R, the

universal SIR R should be always less procedural to

define and maintain.

We leave for future research the relational design

of a DB with SIRs, e.g., porting the decomposition

theorems, (Heath, 1971), (Fagin, 1977), (Jajodia,

1990) and others in (Date, 1991). Next, one knows

that S-P1 DB was the mold for the practical ones.

One may thus expect the benefits of SIRs extending

to most of practical DBs as well.

Finally, the inheritance model for IEs is the

original one of the relational model. We discuss

alternate proposals in (Litwin 2016a), e.g.,

(Stonebraker, 1996) and (Postgres SQL).

5 CONCLUSIONS

SIRs provide for queries free of logical navigation or

of selected value expressions. SIRs may be in

addition always less procedural to define or alter

than any equivalent view. The procedurality is

furthermore always the same or lesser than for VAs

when the kernel DBS provides those. The

implementation of SIRs on a popular DBS appears

finally simple and with negligible operational

overhead. We can therefore expect the practical

interest in SIRs even wider than in VAs.

Consequently, we postulate SIRs as we proposed

them standard on SQL DBSs.

Future work should start with prototype

implementation. MySQL seems the best kernel for.

It is open-source and provides all the useful

abundantly discussed features. The relational design

rules for SIRs we have mentioned appear also a

promising goal. Next, BPS could perhaps optionally

create materialized C-views. MySQL and SQL

Server provide statements for. Those could speed-up

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

query processing for IEs with complex value

expressions, (Goldstein, 2001), (Halevy, 2001),

(Larson, 2007), (Valduriez, 1987) . Finally, most of

major DBSs are now interoperable, (Litwin, 1986) .

Multidatabase SIRs, inheriting from several DBs,

appear attractive as well.

ACKNOWLEDGMENTS

We thank Prof. Emeritus Peter Scheuermann for

helpful discussions.

REFERENCES

Codd, E., F., 1969. Derivability, Redundancy and

Consistency of Relations Stored in Large Data Banks.

IBM Res. Rep. RJ 599 #12343.

Codd, E., F., 1970. A Relational Model of Data for Large

Shared Data Banks. CACM, 13,6.

Date, C.J. 2004. An Introduction to Database Systems.

Pearson Education Inc. ISBN 0-321-18956-6.

Date, C. J., & Darwen, H., 1991. Watch out for outer join.

Date and Darwen Relational Database Writings.

Date, C. J.,, 2012. Database Design and Relational

Theory, Normal Forms and All That Jazz. O'Reilly.

Fagin, R. 1977. Multivalued Dependencies and a New

Normal Form for Relational Databases, ACM TODS.

2,3, 262-278.

Goldstein, J. Larson, P., 2001. Optimizing Queries Using

Materialized Views: A Practical, Scalable Solution.

ACM SIGMOD.

Halevy, A.,Y., 2001. Answering queries using views: A

survey. VLDB Journal 10: 270–294.

Heath, I., J., 1971. Unacceptable file operations in a

relational data base. ACM SIGFIDET '71 Workshop

on Data Description, Access and Control, 19-33.

Jajodia, S., Springsteel, F., N., 1990. Lossless outer joins

with incomplete information. BIT, 30, 1, 34-41.

Larson, P., Zhou J., 2007. Efficient Maintenance of

Materialized Outer-Join Views. ICDE.

Litwin, W., Abdellatif, A. 1986. Multidatabase

Interoperability. IEEE COMPUTER, Dec.

Litwin, W. Vigier, Ph., 1986. Dynamic attributes in the

multidatabase system MRDSM, IEEE-ICDE.

Litwin, W. Ketabchi, M., Risch, T., 1992. Relations with

Inherited Attributes. HPL. Palo Alto, CA. Tech. Rep.

HPL-DTD-92-45, 30.

Litwin, W., 2016. Supplier-Part Databases with Stored and

Inherited Relations Simulated on MS Access.

Lamsade Tech. E-Note. pdf

Litwin, W., 2016a. SQL for Stored and Inherited

Relations. Lamsade E-Report, updated: Mars, 2019.

https://www.lamsade.dauphine.fr/~litwin/Relations%2

0with%20Inherited%20Attributes%20Revisited.pdf

Mendelzon, A. 2004. Who won the Universal Relation

wars? Stanford InfoLab, http://infolab.stanford.

edu/jdu-symposium/talks/mendelzon.pdf .

Maier, D, Ullman, J. D., Vardi, M., Y., 1984. On the

foundations of the universal relation model. ACM-

TODS, 9, 2, 283-308.

Postgres SQL. https://www.postgresql.org/ .

Stonebraker, M. Moore, 1996. D. Object-Relational

DBMSs: The next Great Wave. Morgan Kaufmann. 2

Ed. 1998.

Vardi, M., Y., 2011. The rise, fall, and rise of dependency

theory: Part 1, the rise and fall. Sigmod/Pods.

Valduriez P., 1987. Join indices. ACM TODS, 12(2), 218–

246.

APPENDIX

S-P2 Scheme

Table S Table P Table SP

S# Char, P# Char, S# Char,

SNAME Char, PNAME Char, P# Char,

STATUS Int, COLOR Char, QTY Int

CITY Char; WEIGHT Char, SNAME, STATUS, S.CITY, PNAME, COLOR, WEIGHT, P.CITY

CITY Char; From (SP_ Left Join S On SP_.S#=S.S#) Left Join P On SP_.P#=P.P#), Primary Key (S#, P#));

Figure 1: S-P1 and S-P2 schemes.

SIR SP

SP_

C-view SP

S-P1

S-P2

S-P1 with C-view SP

P P

SQL for Stored and Inherited Relations

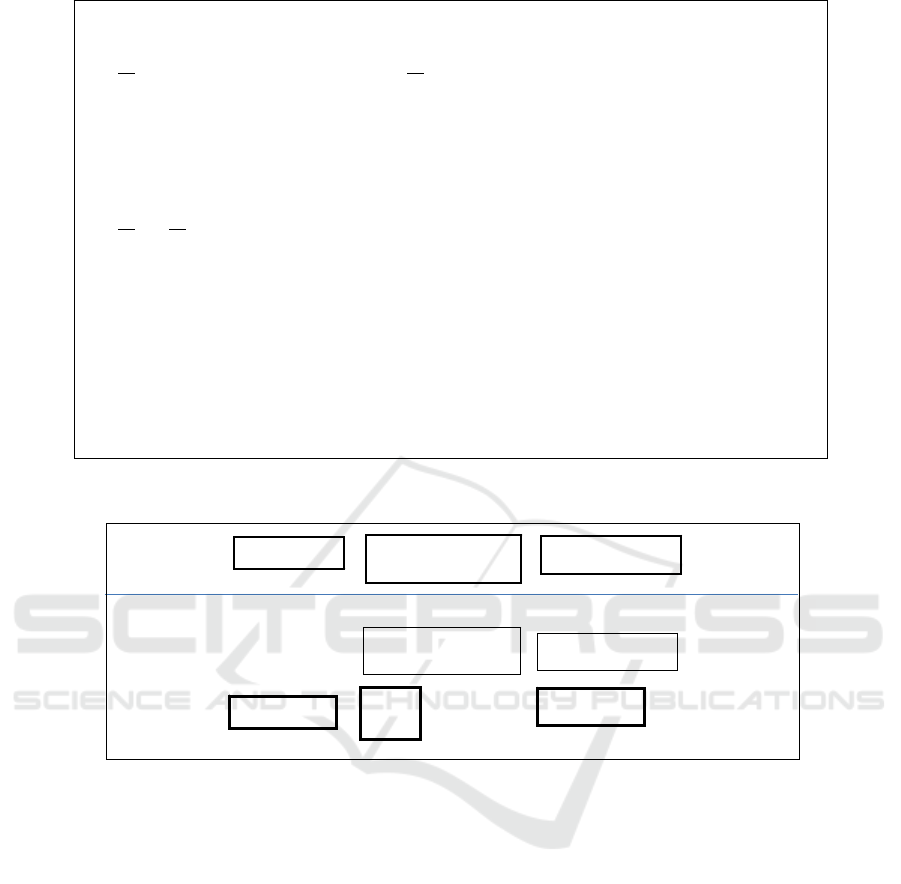
Figure 2: S-P2 content. IA (proper) names and values are in Italics.

Figure 3: S-P3 DB. Above: SIRs. Below: C-views and SRs within the kernel DBS.

S-P2 Content

Table S Table P

S# SNAME STATUS CITY P# PNAME COLOR WEIGHT CITY

S1 Smith 20 London P1 Nut Red 12 London

S2 Jones 10 Paris P2 Bolt Green 17 Paris

S3 Blake 30 Paris P3 Screw Blue 17 Oslo

S4 Clark 20 London P4 Screw Red 14 London

S5 Adams 30 Athens P5 Cam Blue 12 Paris

P6 Cog Red 19 London

Table SP

S# P# QTY SNAME STATUS S.CITY PNAME COLOR WEIGHT P.CITY

S1 P1 300 Smith 20 London Nut Red 12 London

S1 P2 200 Smith 20 London Bolt Green 17 Paris

S1 P3 400 Smith 20 London Screw Blue 17 Oslo

S1 P4 200 Smith 20 London Screw Red 14 London

S1 P5 100 Smith 20 London Cam Blue 12 Paris

S1 P6 100 Smith 20 London Cog Red 19 London

S2 P1 300 Jones 10 Paris Nut Red 12 London

S2 P2 400 Jones 10 Paris Bolt Green 17 Paris

S3 P2 200 Blake 30 Paris Bolt Green 17 Paris

S4 P2 200 Clark 20 London Bolt Green 17 Paris

S4 P4 300 Clark 20 London Screw Red 14 London

S4 P5 400 Clark 20

ondon Cam

lue 12 Paris

SIR Layer

Kernel DBS

SP_

C-views

SRs

S-P3 DB

(CS)

S-P3 DB

(IS)

ICEIS 2019 - 21st International Conference on Enterprise Information Systems