
Multi-Label Network Classification via Weighted Personalized
Factorizations
Ahmed Rashed, Josif Grabocka and Lars Schmidt-Thieme
Information Systems and Machine Learning Lab, University of Hildesheim, Hildesheim, Germany
Keywords:
Multi-relational Learning, Network Representations, Multi-Label Classification, Recommender Systems,
Document Classification.
Abstract:
Multi-label network classification is a well-known task that is being used in a wide variety of web-based and
non-web-based domains. It can be formalized as a multi-relational learning task for predicting nodes labels
based on their relations within the network. In sparse networks, this prediction task can be very challenging
when only implicit feedback information is available such as in predicting user interests in social networks.
Current approaches rely on learning per-node latent representations by utilizing the network structure, howe-
ver, implicit feedback relations are naturally sparse and contain only positive observed feedbacks which mean
that these approaches will treat all observed relations as equally important. This is not necessarily the case
in real-world scenarios as implicit relations might have semantic weights which reflect the strength of those
relations. If those weights can be approximated, the models can be trained to differentiate between strong and
weak relations. In this paper, we propose a weighted personalized two-stage multi-relational matrix factori-
zation model with Bayesian personalized ranking loss for network classification that utilizes basic transitive
node similarity function for weighting implicit feedback relations. Experiments show that the proposed mo-
del significantly outperforms the state-of-art models on three different real-world web-based datasets and a
biology-based dataset.
1 INTRODUCTION
The classification of multi-label networks is one of
the widely used tasks in network analysis such as
in predicting or ranking user interests in social net-
works (Grover and Leskovec, 2016; Perozzi et al.,
2014; Krohn-Grimberghe et al., 2012), classifying
documents (Tang et al., 2015) in citation networks,
predicting web-page categories in large network of
websites and also in some biological domains such as
predicting protein labels in protein-protein interaction
networks (Grover and Leskovec, 2016).
The typical approach to predict node labels is by
extracting a set of informative features from each
node and train a classification model on them. This
typical way of feature processing has two main sig-
nificant drawbacks. First, to extract such informative
features, one needs a prior expert domain knowledge
to develop the features engineering process required
to preprocess the raw data. Second, to extract useful
features, a decent amount of raw information should
be embedded with each node such as user profile de-
tails in social networks or document contents in cita-
tion networks. This kind of node embedded informa-
tion might not always be available or accessible due
to privacy settings.
Alternatively, current approaches rely on learning
latent features for each node by analyzing the net-
work structure and optimizing an objective function
that will increase the accuracy of predicting node la-
bels (Cai et al., 2018). Multi-relation matrix facto-
rization (Krohn-Grimberghe et al., 2012; Jamali and
Ester, 2010; Singh and Gordon, 2008) is one famous
example that follows this approach. This model re-
presents network relations as matrices, and it factori-
zes the target relation matrix into two smaller matri-
ces that represent the latent features of the interacting
nodes. The main advantage of these alternative ap-
proaches is that they can be better generalized to al-
most all network classification tasks without any need
for feature engineering or expert domain knowledge.
However, they face significant challenges with very
sparse networks and especially if these networks have
implicit feedback relations. These implicit relations
are dominantly very sparse, and relation edges are
either observed or unobserved without explicit weig-
Rashed, A., Grabocka, J. and Schmidt-Thieme, L.
Multi-Label Network Classification via Weighted Personalized Factorizations.
DOI: 10.5220/0007681203570366
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 357-366
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
357

hts. In various real-world scenarios, those implicit
relations have hidden semantic weights (Lerche and
Jannach, 2014) which are not directly quantifiable but
can be approximated using different weighting functi-
ons such as similarity measures. Current approaches
that utilize the network structure to learn latent node
representations fail to realize these hidden weights of
implicit relations. A famous example of such relati-
ons is the friendship relation in social networks. This
relation is a type of implicit feedback relations that
models the interaction between nodes that have same
types, and it is expressed as sparsely observed edges
connecting those nodes. This kind of friendship rela-
tions frequently occurs in multi-relational settings and
it is not only for representing a relation between users,
but it can also represent a relation between any same
type nodes. In networks data, all of the friendship ob-
served edges would have the same importance weight
while in real-life, some friendship relations are stron-
ger than others. The real-life weights of such relati-
ons can be approximated by measuring the similarity
between each two interacting nodes. The main ad-
vantage of using similarity is that it can be calculated
using simple information from network structure such
as nodes degrees without any need of complex auxili-
ary information which might not be available such as
frequency interaction or timestamps.
In this work, we introduce a similarity based per-
sonalized two-stage multi-relation matrix factoriza-
tion model(Two-Stage-MR-BPR) for multi-label net-
work classification and ranking. It utilizes the ba-
sic transitive node similarity for weighting implicit
friendship relations and a two-stage training protocol
to optimize the Bayesian personalized ranking loss.
By optimizing the BPR loss, the model will output a
ranked list of labels instead of only one label for any
target node which means it will be suitable for recom-
mender system problems and node classification pro-
blems if we just assume the top label as the predicted
class.
The weighted Two-Stage-MR-BPR overcomes the
drawbacks of MR-BPR and outperforms it in all of
our experiments as it can distinguish between obser-
ved and unobserved relations along with learning the
different strength weights of the observed relations.
Our contributions can be summarized as follows :
• We utilize the transitive node similarity to approxi-
mate the semantic weights of all implicit relations
that have interacting nodes of the same type to al-
low the Two-Stage-MR-BPR model to learn the
strength weights of relations.
• We propose a generalized two-stage learning algo-
rithm that utilizes all available implicit and weig-
hted relations for training the MR-BPR model.
• We conduct multiple experiments on four real-
world datasets. The results show that the pro-
posed weighted Two-Stage-MR-BPR outperform
the MR-BPR and current state-of-art models in
multi-label and single-label classification pro-
blems.
The rest of the paper is organized as follows. In
Section 2, we summarize the related work. We dis-
cuss the problem formulation of the multi-label clas-
sification task in section 3. In section 4, we present
and discuss the technical details of the Two-Stage-
MR-BPR model. We present the experiential results
in section 5. Finally, we conclude with discussing
possible future work in section 6.
2 RELATED WORK
Current approaches for multi-label node classification
automate the process of features extraction and engi-
neering by directly learning latent features for each
node. These latent features are mainly generated ba-
sed on the global network structure and the connecti-
vity layout of each node. In earlier approaches such
as (Tang and Liu, 2009a; Tang and Liu, 2009b), they
produce k latent features for each node by utilizing
either the first k eigenvectors of a generated modula-
rity matrix for the friendship relation (Tang and Liu,
2009a) or a sparse k-means clustering of friendship
edges (Tang and Liu, 2009b). These k features are
fed into an SVM for labels predictions.
Recently, semi-supervised (Thomas and Welling,
2016) and unsupervised approaches (Grover and Le-
skovec, 2016; Perozzi et al., 2014; Yang et al., 2015)
have been proposed to extract latent node represen-
tations in networks data. These models are inspi-
red by the novel approaches for learning latent repre-
sentations of words such as the convolutional neural
networks and the Skip-gram models (Mikolov et al.,
2013) in the domain of natural language processing.
They formulate the network classification problem as
discrete words classification problem by representing
the network as a document and all nodes as a sequence
of words. The Skip-gram can then be used to predict
the most likely labels for each node based on the as-
sumption that similar nodes will have same labels.
In (Krohn-Grimberghe et al., 2012), MR-BPR was
proposed as learning to rank approach for tackling the
multi-label classification problem by extending the
BPR (Rendle et al., 2009) model for multi-relational
settings. This approach expresses the problem as a
multi-relational matrix factorization trained to opti-
mize the AUC measure using BPR loss. Each net-
work relation is represented by a sparse matrix and
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
358

the relation between nodes and labels will be the tar-
get being predicted. Because of the BPR loss, this
model is considered suitable for sparse networks with
implicit feedback relations; however, since all impli-
cit feedback connections are only observed or unob-
served, the MR-BPR fail to realize that some implicit
links are stronger than others in real-life. To solve this
drawback in the original single relation BPR model,
(Lerche and Jannach, 2014) proposed BPR++ an ex-
tended version of the BPR model for user-item rating
prediction. They utilized multiple weighting functi-
ons to approximate the logical weights between users
and items. Those functions relied on the frequency of
interaction and timestamps to weight each edge. In
the training phase, they randomly alternate between
learning to distinguish observed and unobserved re-
lations and learning to rank weighted observed rela-
tions. This learning approach expands the BPR ca-
pacity to differentiate between strong and weak con-
nections.
Finally, our proposed Two-Stage-MR-BPR mo-
del follow a similar intuition to that of BPR++ and
it considers the more general multi-relational set-
tings which allow it to be used for any multi-label
and single-label network classification problems. The
proposed model utilizes the basic transitive node si-
milarity for approximating the weights of implicit re-
lations that have interacting nodes of the same type.
In this work, we also propose MR-BPR++ an ex-
tended version of BPR++ for multi-relational set-
tings. The learning algorithm for Two-stage-MR-
BPR is different from MR-BPR++; it relies on two
consecutive non-overlapping learning stages instead
of random alternation. In the first stage, it allows the
model to sufficiently learns to differentiate between
strong and weak relations and in the second stage, it
allows it to learns to differentiate between observed
and unobserved relations.
3 PROBLEM DEFINITION
The problem can be formulated similarly to (Krohn-
Grimberghe et al., 2012) as a relational learning set-
ting on network data. Let G = (V,E) be a network
where V is a set of heterogeneous nodes, and E is the
set of edges. Each node can be seen as an entity and
each edge represents a relation between two entities.
Let N := {N
1
,N
2
,...,N
|N |
} be a set of node types
and each type has a set of nodes as instances N
i
:=
{n
(1)
i
,n
(2)
i
,...,n
(|N
i
|)
i
}. Let R := {R
1
,R
2
,...,R
|R |
} be a
set of relations and each relation represents interacti-
ons between two specific node types N
1R
and N
2R
such
that R ⊆ N
1R
× N
2R
.
Our primary task in this paper is to predict mis-
sing edges in a primary target relation Y, and all other
relations will be considered auxiliary relations that
can be used to improve the prediction accuracy. In
multi-label network classification, the relation Y re-
presents the relation between a set of nodes and la-
bels Y ⊆ N
Target
× N
Label
, such as the relationship
between multiple interests and users in social net-
works or document-labels and documents in citation
networks. Examples of auxiliary relations are the
friendship relation in social networks or citation links
in citation networks.
The task of predicting missing edges in the tar-
get relation can be formulated as a ranking problem
where we try to drive a ranked list of labels that re-
present the likelihood that a specific node belongs to
each of them.
In case of sparse auxiliary relations with implicit
edges, the current multi-relational matrix factoriza-
tion model with BPR loss (Krohn-Grimberghe et al.,
2012) does not exploit the full potential of the BPR
loss because it only distinguishes between observed
and unobserved edges without considering the edges
weights (Lerche and Jannach, 2014).
Our proposed approach addresses the shortco-
mings of the current multi-relational matrix factori-
zation model by firstly using transitive node simila-
rity for weighting the implicit auxiliary relations and
using a Two-Stage-MR-BPR learning algorithm that
can rank observed edges and distinguish between ob-
served and unobserved edges. The proposed approach
is also suitable for cold-start scenarios where only the
auxiliary relations information are available for the
target nodes.
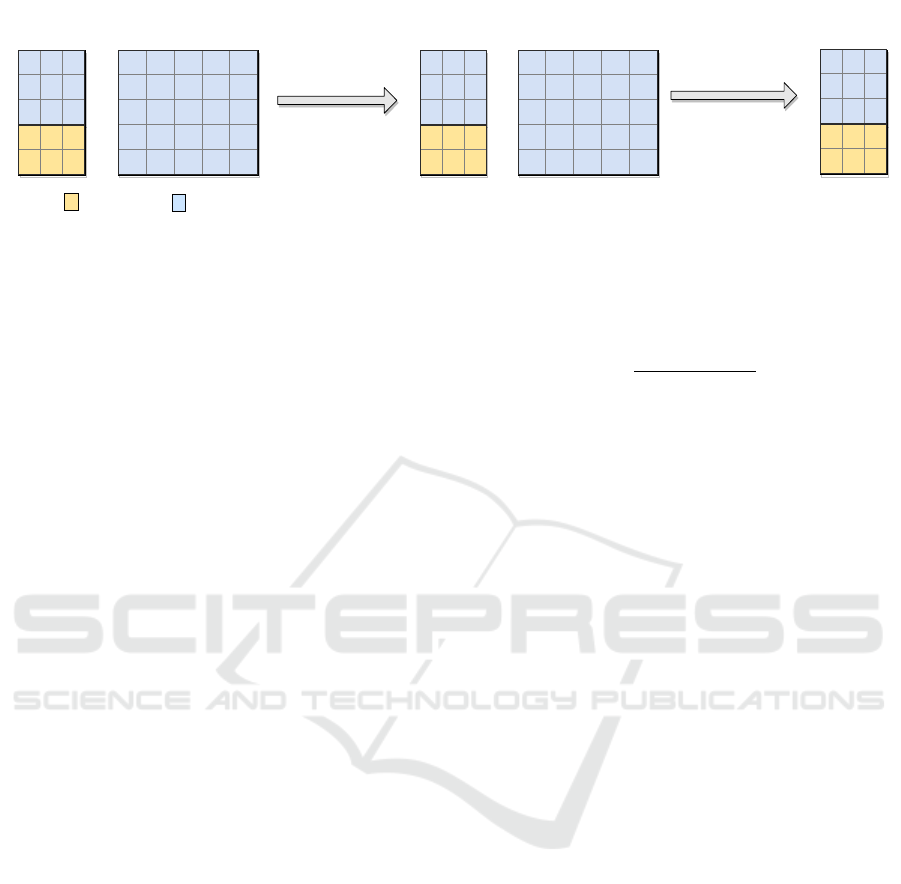
4 PROPOSED MODEL
The proposed model can be formulated as a two-stage
multi-relational matrix factorization using basic tran-
sitive node similarity for weighting implicit relati-
ons. Initially, the transitive node similarity is used to
weight all observed edges in any implicit auxiliary re-
lations that has interacting nodes of the same type. In
the first stage of learning, the model is trained to rank
edges based on their weights. In the second stage, the
model is trained to differentiate between observed and
unobserved edges. Figure 1 illustrates the workflow
of the Two-Stage-MR-BPR model and each step will
be discussed in details in the following subsections.
Multi-Label Network Classification via Weighted Personalized Factorizations
359
1 1
1 1
1
1 1 1
1
1 1 1
1
1 1
TargetRelation
Nodes
Labels
AuxiliaryRelation
Nodes
Nodes
? ? ?
? ? ?
1 1
1 1
1
0.33 0.2 0.25
0.33
0.2 0.33 0.25
0.33
0.25 0.25
TargetRelation
Nodes
Labels
AuxiliaryRelation
Nodes
Nodes
? ? ?
? ? ?
1 1
1 1
1
TargetRelation
Nodes
Labels
5 3 0
0 3 1
TransitiveNodeSimilarity TwoStageMRBPR
TestData TrainData
Figure 1: Two-Stage-MR-BPR workflow. Initially, the transitive node similarity is used to weight all implicit relations with
same type interacting nodes followed by learning a two stage multi-relational matrix factorization on all relations using the
BPR loss to rank all labels with respect to each test node.
4.1 Basic Transitive Node Similarity for
Implicit Feedback Relations
In the relational learning setting, in order to apply
the two-stage MR-BPR learning technique we need
first to convert all possible implicit feedback relati-
ons into weighted relations. To convert implicit re-
lations into weighted relations, one needs a suitable
weighting function that approximate relation weig-
hts by utilizing the available embedded information
in each relation such as frequency or timestamps of
interactions in user-item relations, or similarity mea-
sures in friendship relations. In the most basic case
where there is no available embedded information, an
implicit relation can be considered a relation that was
weighted by a constant weighting function which out-
puts only one value if it encounters an observed edge.
Friendship relations are one of the prominent ty-
pes of implicit relations in networks data. It can
represent any relation between nodes of the same
type such as users friendships in social networks or
web links between web pages or citation links be-
tween documents. For weighting edges in general
friendship relations, the similarity measures such as
Adamic/Adar, common neighbors, Jaccard index and
friend transitive node similarity FriendTNS (Symeo-
nidis et al., 2010) are considered the best candida-
tes to act as weighting functions (Symeonidis et al.,
2010; Liben-Nowell and Kleinberg, 2007). In our
proposed approach we used the FriendTNS function
because it provided superior accuracy over other si-
milarity functions (Symeonidis et al., 2010; Ahmed
et al., 2016) in link prediction tasks and it requires mi-
nimum auxiliary information from the network struc-
ture. FriendTNS was used for weighting all the obser-
ved edges in all available implicit friendship relations
and it was calculated only for observed edges because
it is computationally expensive to calculate weights
for all possible node pairs in very sparse networks.
The FriendTNS similarity between two nodes is cal-
culated using equation (1).
FT NS(n
i
,n
j
) :=
(
1
deg(n
i
)+deg(n
j
)−1
, if (n
i
,n
j
) ∈ R
0, if (n
i
,n
j
) /∈ R
(1)
where deg(n
i
) and deg(n
j
) is the degree of nodes n
i
and n
j
respectively. In case of directed graphs, we
used the summation of the node’s in-degree and out-
degree as the total degree.
4.2 Multi-eelational Matrix
Factorization with Basic Transitive
Node Similarity
To formulate the problem as a multi-relational matrix
factorization, each node type N
i
can be represented by
a matrix E
i
∈ R
|N
i
|×k
where the rows are the latent fe-
ature vectors for all instances in the node type, and k
represents the number of latent factors defined in the
model. Similarly, each implicit relation R can be re-
presented by a matrix R ∈ R
|N
1R
|×|N
2R
|
where N
1R
and
N
2R
are the two types of the interacting nodes inside
relation R. Each entry in the relation matrix is given
by
R(n
(i)
1R
,n
( j)
2R
) :=
Weight(n
(i)
1R
,n
( j)
2R
), if(n
(i)
1R
,n
( j)
2R
) ∈ R
unobserved, if(n
(i)
1R
,n
( j)
2R
) /∈ R
(2)
where Weight(n
(i)
1R
,n
( j)
2R
) is the weighting function
used to approximate the weights of implicit relation
between any two nodes such as similarity functions
in case of friendship relations or frequency of inte-
raction in case of user-item relations. If no available
embedded information can be used to weight relati-
ons, a constant weighting function is assumed.
Finally, each relation R can be approximated by
multiplying the latent matrices of the two relation
node types E
1R
and E
2R
such that R ≈ E
1R
× E
T
2R
. For
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
360

simplicity, we define a set of all the model parameters
Θ := {E
1
,E
2
,...,E
|N |
} which contain the matrices of
all nodes types and our general objective will be to
find the set of matrices Θ that minimize the sum of
losses over all relations.
4.3 Two-stage MR-BPR
The original BPR model (Rendle et al., 2009) assu-
mes that for a given user u, any item i this user in-
teracted with should be ranked higher than any item
j he did not interact with. In order to do so, the BPR
model learns to maximize the difference ˆx
R
u,i, j
between
the predicted rating ˆr(u, i) for an observed item i and
the rating ˆr(u, j) for an unobserved item j.
To follow the same notation in a multi-relational
setting, for any given relation R, the user u will repre-
sent a node of type N
1R
, while i and j will represents
two nodes of type N
2R
. For each relation R the base-
line MR-BPR model samples a set of triples D
R
which
is defined as follows:
D
R
:= {(u, i, j)|(u,i) ∈ R ∧ (u, j) /∈ R}
The sampling is done using bootstrap sampling
with replacement. The model is then trained to max-
imize the difference between the predicted ratings of
the observed edges and unobserved edges for all rela-
tion using equations (2) and (3).
BPR-Opt(R,E
1R
E
2R
T
) =
∑
(u,i, j)∈R
lnσ( ˆx
R
u,i, j
) (3)
MR-BPR(R,Θ) =
∑
R∈R
α
R
BPR-Opt(R,E
1R
E
2R
T
)
+
∑
E∈Θ
λ
E
||E||
2
(4)
where σ is the sigmoid logistic function and α
R
is the
loss weight for relation R. By following this learning
approach, the MR-BPR model learns to distinguish
between observed edges and unobserved edges over
iterations. This approach is not optimal as it fails to
realize the different semantic weights of the implicit
relations. In (Lerche and Jannach, 2014) they pro-
posed a new learning technique for the original BPR
model called BPR++ which extend the BPR to learn
weighted relations. There proposed extension allow
the BPR model to provide better rankings for item
ratings by utilizing the timestamps and frequency of
user interactions to weight user-item edges. BPR++
is randomly alternating between learning to rank ob-
served weighted edges and learning to distinguish be-
tween observed and unobserved edges. Instead of
using such random alternation between the two lear-
ning tasks for multi-relational settings, we propose a
two-stage learning approach that decouple the two le-
arning tasks and learn them sequentially to avoid in-
formation overwrites across iterations. When applied
to multi-relational settings, the proposed two-stage le-
arning protocol and BPR++ will utilize a separate set
of triples D
++
R
beside the original set D
R
. This new
set contains observed weighted edges sampled using
bootstrap sampling with replacement for each availa-
ble weighted relation as follows:
D
++
R
:= {(u, i, j)|Weight(u,i) > Weight(u, j)∧
(u,i) ∈ R ∧ (u, j) ∈ R}
The main difference between the proposed two-
stage learning protocol and BPR++ is that the later
will rely on random alternating sampling from D
R
and
D
++
R
which introduce the risk of having information
loss as some iterations might overwrite the previously
learned information, e.g. if an node was selected first
as an observed item from D
R
and in the next itera-
tion it was selected as the lower weighted item from
D
++
R
, the second iteration will overwrite the informa-
tion gained in the first iteration as it will decrease the
score of the item after it has been increased. On the
other hand, Two-Stage-MR-BPR overcome such pro-
blem by learning to rank all weighted edges first then
it learns to distinguish observed and unobserved ed-
ges afterward with no overlap between the two stages
in each epoch. This means that the second stage will
shift the learned scores of the observed edges away
from the unobserved ones while maintaining the lear-
ned rankings between the weighted observed edges.
In our experiments, we applied both learning pro-
tocols on the MR-BPR model for performance com-
parison and we used the basic FriendTNS similarity
as weighting function for all implicit relations where
the participating nodes have the same type. In each
learning epoch during the training phase, the num-
ber of sampling steps for D
++
R
and D
R
is equal to the
number of observed edges ObsEdges
R
in R, similar to
the original BPR (Rendle et al., 2009) and MR-BPR
(Krohn-Grimberghe et al., 2012) models. The genera-
lized algorithms for training the Two-Stage-MR-BPR
and MR-BPR++ are described in Figures 2 and 3.
In the experiments section, we compared the two
models against each other and the original MR-
BPR model. The results showed that the proposed
two-stage model provides better accuracy for multi-
relational settings where we have multiple sparse rela-
tions without timestamps or frequency of interactions
that can be used to weight relations.
Multi-Label Network Classification via Weighted Personalized Factorizations
361

Table 1: Datasets Statistics.
Type Nodes Labels Edges Features Sparsity
BlogCatalog Undirected 10312 39 667966 - 99.37%
PPI Undirected 3890 50 76584 - 99.49%
Wiki Directed 2405 19 17981 - 99.68%
Cora Directed 2708 7 5429 1433 99.92%
1: procedure TWO-STAGE-MR-BPR(D, R , Θ)
2: Initialize All E ∈ Θ
3: repeat
4: for R ∈ R do
5: // (Stage One)
6: if D
++
R
\D
R
6= φ then
7: for ObsEdges
R
times do
8: draw (u,i,j) from D
++
R
9: Θ ← Θ + µ
∂(MR-BPR(R,Θ))
∂Θ
10: end for
11: end if
12: // (Stage Two)
13: for ObsEdges
R
times do
14: draw (u,i,j) from D
R
15: Θ ← Θ + µ
∂(MR-BPR(R,Θ))
∂Θ
16: end for
17: end for
18: until convergence
19: return Θ
20: end procedure
Figure 2: Two-Stage-MR-BPR algorithm with learning rate
µ and L2 regularization λ
Θ
.
1: procedure MR-BPR++(D, R ,Θ)
2: Initialize All E ∈ Θ
3: repeat
4: for R ∈ R do
5: r = random(0, 1)
6: if r ≤ β ∧ D
++
R
\D
R
6= φ then
7: draw (u,i,j) from D
++
R
8: else
9: draw (u,i,j) from D
R
10: end if
11: Θ ← Θ + µ
∂(MR-BPR(R,Θ))
∂Θ
12: end for
13: until convergence
14: return Θ
15: end procedure
Figure 3: MR-BPR++ algorithm with learning rate µ, pro-
bability threshold β and L2 regularization λ
Θ
.
5 EXPERIMENTS
5.1 Datasets
We applied the Two-Stage MR-BPR and MR-BPR++
on four network classification datasets from four dif-
ferent domains. The first three datasets contain two
relations while the fourth dataset is a citation network
where nodes have an embedded feature vector that
can be considered as third relations.
• BlogCatalog (Zafarani and Liu, 2009) : This da-
taset represents a large social network from the
BlogCatalog website. It has two relations, a tar-
get relation which represents the relation between
groups and users, and an auxiliary relation repre-
senting the friendship between users.
• Wiki (Tu et al., 2016) : This dataset represents a
network of Wikipedia web pages. It also has two
relations, a target relation which represents the ca-
tegories of the web pages, and an auxiliary rela-
tion that represents links between the web pages.
• Protein-Protein Interactions (PPI) (Breitkreutz
et al., 2007) : This dataset is a network of protein-
protein interactions for homo sapiens. It has two
relations, a target one which represents the rela-
tion between protein-labels and proteins, and an
auxiliary relation that represents the interactions
between proteins and other proteins. This dataset
was used to check how well our proposed model
performs in non-web-based domains.
• Cora (Sen et al., 2008) : This dataset represents a
citation network where each document has 1433
binary feature vector representing words occur-
rence. This dataset can be considered as having
three relations, a target relation which represents
the class label of a document, an auxiliary relation
that represents citation links between documents
and a final auxiliary relation that represents a re-
lation between a document and words that exist in
this document.
Table 1 shows the detailed statistics of the datasets.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
362

5.2 Baselines
• MR-BPR (Krohn-Grimberghe et al., 2012) : The
original MR-BPR model that utilizes implicit
auxiliary relations for ranking node labels. This
model does not utilize transitive node similarities.
• DeepWalk (Perozzi et al., 2014) : One of the well-
known models for multi-label network classifica-
tion. This model learns node latent representati-
ons by utilizing uniform random walks in the net-
work.
• Node2Vec (Grover and Leskovec, 2016) : This is
one of the state-of-art models for multi-label net-
work classification and can be seen as a generali-
zed version of DeepWalk with two guiding para-
meters p and q for the random walks.
• GCN (Thomas and Welling, 2016) : This model is
one of the state-of-art models for document clas-
sification in citation networks. It relies on multi-
layered graph convolutional neural network for le-
arning network representation with text features.
• TADW (Yang et al., 2015) :This model is also one
of the state-of-art models for document classifica-
tion in citation networks. It is an extended version
of the original Deep Walk model for learning net-
work representation with text features.
On Cora dataset, our proposed model was compared
only against GCN and TADW because they require
nodes with embedded textual features which is mis-
sing in the first three datasets. On the other hand
DeepWalk and Node2Vec where not used on Cora da-
taset because they can’t represent nodes with embed-
ded features.
5.3 Experimental Protocol and
Evaluation
We followed the same experimental protocol in
(Krohn-Grimberghe et al., 2012; Perozzi et al., 2014;
Grover and Leskovec, 2016). We used 10-fold cross-
validation experiments on each target relation. These
experiments were applied using different percentages
of labeled nodes ranging from 10% to 90%. In each
experiment, we only used the defined percentage of
labeled nodes for training along with all the auxiliary
relations, while the remaining percent of nodes were
used for testing. We used Micro-F1 and Macro-F1
measures for performance evaluation on Blog Cata-
log, PPI and Wiki Dataset, and Accuracy on Cora Da-
taset.
We used the same hyper-parameters that were
used in the original baselines’ papers, and grid-search
was used to find the best hyper-parameters if none
were mentioned for the target dataset.
5.4 Results
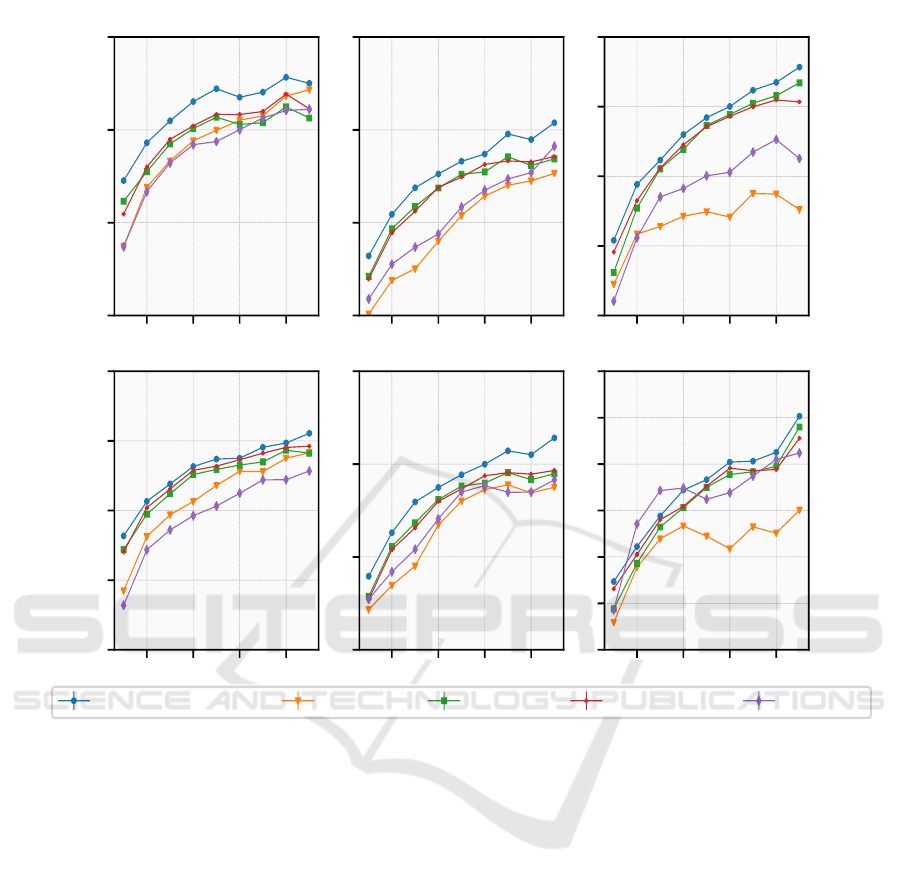
The experimental results on the four datasets are
shown in Tables 2, 3, 4, 5, and Figure 4. The re-
sults shows that Two-Stage-MR-BPR with transitive
node similarity outperformed the original MR-BRP
model in all train-splits. In comparison with other
well-known models for multi-label network classifi-
cation, the Two-Stage-MR-BPR model outperformed
the state-of-art Node2Vec over all trains-splits on Blo-
gCatalog, PPI and Wiki datasets. It is worthy to note
that all improvements over Node2Vec are statistically
significant with a p-value less than 0.01 using pai-
red t-test. Two-Stage-MR-BPR also outperformed
DeepWalk over all trains-splits on BlogCatalog and
PPI, while on Wiki, DeepWalk only achieved bet-
ter Macro-F1 scores on the 20%, 30%, and 40%
trains-splits. The results also show that Two-Stage-
MR-BPR outperformed all other models in terms of
Micro-F1 with 40% less data using the 50% train-split
on the BlogCatalog dataset. On PPI, It outperformed
all other models in terms of Micro-F1 and Macro-
F1 with 30% less data using the 60% train-split. On
the other hand, the document classification results on
the Cora datasets show that Two-Stage-MR-BPR out-
performed the state-of-art models on 10% and 90%
splits, while it achieves comparable results on the
50% train-splits.
In comparison with Two-Stage-MR-BPR, MR-
BRP++ also outperformed MR-BRP on BlogCatalog
over most of the train splits, but it had minimal per-
formance gains in some train-splits on PPI, Wiki and
Cora. These results demonstrate the importance of
using transitive node similarity to weight implicit re-
lations, and they show that using two sequential non-
overlapping stages to train the BPR loss is better than
randomly alternating between ranking observed edges
and distinguishing them from unobserved edges.
5.5 Reproducibility of the Experiments
For each model we used the following hyper-
parameters during in experiments.
• MR-BPR: The hyper-parameters are k = 500, µ =
0.02, λ
user
= 0.0125, λ
item
= 0.0005, 300 ite-
rations and α = 0.5 for BlogCatalog; k = 500,
µ = 0.01, λ
protein
= 0.0125, λ
label
= 0.0005, 400
iterations and α = 0.5 for PPI; k = 600, µ =
0.02, λ
page
= 0.0125, λ
label
= 0.0005, 1000 ite-
rations and α = 0.5 for Wiki; and k = 900, µ =
Multi-Label Network Classification via Weighted Personalized Factorizations
363

Table 2: Mutli-lable classification results on BlogCatalog dataset.
%Lable Nodes 10% 30% 50% 70% 90%
Micro-F1(%) DeepWalk 33.71 38.22 39.37 40.64 41.11
Node2Vec 33.72 38.33 39.98 40.75 42.16
MR-BPR 36.16 39.24 40.68 40.39 40.64
MR-BPR++ 35.47 39.49 40.84 40.99 41.14
Two-Stage-MR-BPR 37.27** 40.49** 42.22** 42.03** 42.51*
Macro-F1(%) DeepWalk 18.19 23.61 25.32 27.20 27.84
Node2Vec 19.24 24.70 26.80 27.80 29.15
MR-BPR 22.21 26.20 27.95 28.49 29.13
MR-BPR++ 22.03 26.55 28.19 29.12 29.62
Two-Stage-MR-BPR 23.18** 26.91** 28.69** 29.54** 30.55*
Significantly outperforms MR-BPR at the: ** 0.01 and * 0.05 levels.
Table 3: Mutli-lable classification results on PPI dataset.
%Lable Nodes 10% 30% 50% 70% 90%
Micro-F1(%) DeepWalk 15.89 18.68 20.85 22.35 24.11
Node2Vec 15.09 17.52 20.38 22.02 22.65
MR-BPR 17.11 20.87 22.61 23.55 23.44
MR-BPR++ 16.97 20.62 22.46 23.33 23.56
Two-Stage-MR-BPR 18.21** 21.88** 23.31** 24.78** 25.38**
Macro-F1(%) DeepWalk 12.73 15.41 18.50 18.49 19.15
Node2Vec 12.17 14.51 18.01 18.89 18.76
MR-BPR 12.88 16.83 18.81 19.54 19.48
MR-BPR++ 12.71 16.58 18.66 19.54 19.66
Two-Stage-MR-BPR 13.96** 17.96** 19.43** 20.72** 21.41**
Significantly outperforms MR-BPR at the: ** 0.01 and * 0.05 levels.
Table 4: Mutli-lable classification results on Wiki dataset.
%Lable Nodes 10% 30% 50% 70% 90%
Micro-F1(%) DeepWalk 56.04 63.52 65.03 66.73 66.27
Node2Vec 57.24 61.40 62.45 63.76 62.61
MR-BPR 58.10 65.54 68.66 70.24 71.71
MR-BPR++ 59.56 65.61 68.56 69.99 70.34
Two-Stage-MR-BPR 60.40** 66.16 69.21 71.18 72.84
Macro-F1(%) DeepWalk 44.33 57.16 56.21 58.71 61.20
Node2Vec 42.95 51.96 52.25 53.25 55.04
MR-BPR 44.41 53.23 57.50 59.17 63.99
MR-BPR++ 46.58 54.01 57.62 59.29 62.79
Two-Stage-MR-BPR 47.35** 54.41* 58.33 60.32 65.16
Significantly outperforms MR-BPR at the: ** 0.01 and * 0.05 levels.
Table 5: Document classification results on Cora dataset.
%Lable Nodes 10% 50% 90%
Accuracy(%) GCN 78.37 86.53 86.39
TADW 75.24 85.99 85.60
MR-BPR 75.03 78.76 81.66
MR-BPR++ 76.24 78.10 81.10
Two-Stage-MR-BPR 79.30** 84.20 86.86
Significantly outperforms GCN at the: ** 0.01 and * 0.05 levels.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
364
0.2 0.4 0.6 0.8
30
35
40
45
Micro F1(%)
BlogCatalog
0.2 0.4 0.6 0.8
15
20
25
30
PPI
0.2 0.4 0.6 0.8
55
60
65
70
75
Wiki
0.2 0.4 0.6 0.8
15
20
25
30
35
Macro F1(%)
0.2 0.4 0.6 0.8
10
15
20
25
Two-Stage-MR-BPR Node2Vec MR-BPR MR-BPR++. DeepWalk.
0.2 0.4 0.6 0.8
40
45
50
55
60
65
70
Figure 4: Evaluation of the Two-Stage-MR-BPR model against other baseline models. The x axis denotes the percent of
labeled nodes used in the training phase, while the y axis denotes the Micro-F1 and Macro-F1 scores.
0.03, λ
document
= 0.005, λ
label
= 0.0001, λ
words
=
0.0001, 1400 iterations and α = 0.33 for Cora.
• MR-BPR++: The hyper-parameters are β = 0.75,
k = 500, µ = 0.02, λ
user
= 0.0125, λ
item
= 0.0005,
300 iterations and α = 0.5 for BlogCatalog; β =
0.75, k = 500, µ = 0.01, λ
protein
= 0.0125, λ
label
=
0.0005, 400 iterations and α = 0.5 for PPI; β =
0.75, k = 600, µ = 0.02, λ
page
= 0.0125, λ
label
=
0.0005, 1000 iterations and α = 0.5 for Wiki; and
k = 900, µ = 0.03, λ
document
= 0.005, λ
label
=
0.0001, λ
words
= 0.0001, 1400 iterations and α =
0.33 for Cora.
• Two-Stage-MR-BPR: We used the same hyper-
parameters of MR-BPR
• DeepWalk: The hyper-parameters are d = 128, r =
10, l = 80 and k = 10 for all datasets.
• Node2Vec: The hyper-parameters are d = 128, r =
10, l = 80, k = 10, p = 0.25 and q = 0.25 for
BlogCatalog; d = 128, r = 10, l = 80, k = 10,
p = 4 and q = 1 for PPI and Wiki.
• GCN: We used the same hyper-parameters from the
original paper. Dropout rate = 0.5, L2 regulariza-
tion = 5.10
−4
and 16 (number of hidden units)
• TADW: We used the same default hyper-
parameters from the original papers which
are k = 80 and λ = 0.2
6 CONCLUSIONS
In this paper, we proposed the similarity based Two-
Stage-MR-BPR model that exploits the full poten-
tial of the Bayesian personalized ranking as a loss
function. Two-Stage-MR-BPR relies on converting
all implicit feedback relations into weighted relations
using basic transitive node similarity to approximate
Multi-Label Network Classification via Weighted Personalized Factorizations
365

the semantic weights of relations in the real world.
This conversion step allows the Two-Stage-MR-BPR
to learn ranking edges based on their weights and to
learn to distinguish observed edges from unobserved
ones. Experiments on four real-world datasets sho-
wed that Two-Stage-MR-BPR outperformed the ori-
ginal MR-BPR and other state-of-art models in the
task of multi-label network classification and docu-
ment classification. In future work, we are planning to
explore and integrate several possible approaches to
further expand the capacity of the BPR models. Two
of those possible approaches for expansion are lear-
ning nonlinear latent representation and using non-
uniform samplers (Rendle and Freudenthaler, 2014).
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the fun-
ding of their work through the
¨
UberDax project
(https://www.ismll.uni-hildesheim.de/projekte/
UberDax.html) which is sponsored by the Bundesmi-
nisterium fr Bildung und Forschung (BMBF) under
the grant agreement no. 01IS17053.
REFERENCES
Ahmed, C., ElKorany, A., and Bahgat, R. (2016). A super-
vised learning approach to link prediction in twitter.
Social Network Analysis and Mining, 6(1):24.
Breitkreutz, B.-J., Stark, C., Reguly, T., Boucher, L.,
Breitkreutz, A., Livstone, M., Oughtred, R., Lackner,
D. H., B
¨
ahler, J., Wood, V., et al. (2007). The bio-
grid interaction database: 2008 update. Nucleic acids
research, 36(suppl 1):D637–D640.
Cai, H., Zheng, V. W., and Chang, K. (2018). A compre-
hensive survey of graph embedding: problems, techni-
ques and applications. IEEE Transactions on Know-
ledge and Data Engineering.
Grover, A. and Leskovec, J. (2016). node2vec: Scalable
feature learning for networks. In Proceedings of the
22nd ACM SIGKDD international conference on Kno-
wledge discovery and data mining, pages 855–864.
ACM.
Jamali, M. and Ester, M. (2010). A matrix factorization
technique with trust propagation for recommendation
in social networks. In Proceedings of the fourth ACM
conference on Recommender systems, pages 135–142.
ACM.
Krohn-Grimberghe, A., Drumond, L., Freudenthaler, C.,
and Schmidt-Thieme, L. (2012). Multi-relational ma-
trix factorization using bayesian personalized ranking
for social network data. In Proceedings of the fifth
ACM international conference on Web search and
data mining, pages 173–182. ACM.
Lerche, L. and Jannach, D. (2014). Using graded implicit
feedback for bayesian personalized ranking. In Pro-
ceedings of the 8th ACM Conference on Recommen-
der systems, pages 353–356. ACM.
Liben-Nowell, D. and Kleinberg, J. (2007). The link-
prediction problem for social networks. journal of the
Association for Information Science and Technology,
58(7):1019–1031.
Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013).
Efficient estimation of word representations in vector
space. arXiv preprint arXiv:1301.3781.
Perozzi, B., Al-Rfou, R., and Skiena, S. (2014). Deepwalk:
Online learning of social representations. In Procee-
dings of the 20th ACM SIGKDD international confe-
rence on Knowledge discovery and data mining, pages
701–710. ACM.
Rendle, S. and Freudenthaler, C. (2014). Improving pair-
wise learning for item recommendation from implicit
feedback. In Proceedings of the 7th ACM internatio-
nal conference on Web search and data mining, pages
273–282. ACM.
Rendle, S., Freudenthaler, C., Gantner, Z., and Schmidt-
Thieme, L. (2009). Bpr: Bayesian personalized ran-
king from implicit feedback. In Proceedings of the
twenty-fifth conference on uncertainty in artificial in-
telligence, pages 452–461. AUAI Press.
Sen, P., Namata, G., Bilgic, M., Getoor, L., Galligher, B.,
and Eliassi-Rad, T. (2008). Collective classification in
network data. AI magazine, 29(3):93.
Singh, A. P. and Gordon, G. J. (2008). Relational learning
via collective matrix factorization. In Proceedings of
the 14th ACM SIGKDD international conference on
Knowledge discovery and data mining, pages 650–
658. ACM.
Symeonidis, P., Tiakas, E., and Manolopoulos, Y. (2010).
Transitive node similarity for link prediction in social
networks with positive and negative links. In Procee-
dings of the fourth ACM conference on Recommender
systems, pages 183–190. ACM.
Tang, J., Qu, M., Wang, M., Zhang, M., Yan, J., and Mei,
Q. (2015). Line: Large-scale information network
embedding. In Proceedings of the 24th International
Conference on World Wide Web, pages 1067–1077.
International World Wide Web Conferences Steering
Committee.
Tang, L. and Liu, H. (2009a). Relational learning via latent
social dimensions. In Proceedings of the 15th ACM
SIGKDD international conference on Knowledge dis-
covery and data mining, pages 817–826. ACM.
Tang, L. and Liu, H. (2009b). Scalable learning of col-
lective behavior based on sparse social dimensions. In
Proceedings of the 18th ACM conference on Informa-
tion and knowledge management, pages 1107–1116.
ACM.
Thomas, N. K. and Welling, M. (2016). Semi-supervised
classification with graph convolutional networks.
arxiv preprint. arXiv preprint arXiv:1609.02907, 103.
Tu, C., Zhang, W., Liu, Z., and Sun, M. (2016). Max-margin
deepwalk: Discriminative learning of network repre-
sentation. In IJCAI, pages 3889–3895.
Yang, C., Liu, Z., Zhao, D., Sun, M., and Chang, E. Y.
(2015). Network representation learning with rich text
information. In IJCAI, pages 2111–2117.
Zafarani, R. and Liu, H. (2009). Social computing data re-
pository at asu.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
366
