
EMFeR: Model Checking for Object Oriented (EMF) Models
Christoph Eickhoff, Martin Lange, Simon-Lennert Raesch and Albert Z
¨
undorf
Kassel University, Germany
Keywords:
Model Checking, Object Models, EMF.
Abstract:
For safety critical systems it is desirable to be able to prove system correctness. If your system is based e.g.
on statecharts or finite automata you may use model checking techniques as provided e.g. by Spin. If your
system uses dynamic object models you may use tools like Alloy or graph based tools like Groove, Henshin, or
SDMLib. Unfortunately, most of theses approaches use proprietary languages for the specification of models
and model transformations. This has the drawback that in order to verify system properties one has to recode
the system and its operations within the specific language of the used verification tool. This is tedious and
error prone. After a successful verification within the specific tool, you still do not know whether your actual
implementation works correct. To overcome these limitations, this paper outlines our new EMFeR (EMF
Engine for Reachability) tool. EMFeR provides complete testing and model checking capabilities for EMF
based models. Unlike most other systems, EMFeR uses directly the code of the system under test. You just
hand your implementation of the employed model operations to EMFeR as lambda expressions. In addition,
you provide some model queries to retrieve model elements to be operated on. Thus, you may implement your
system’s model operation in plain Java, in Kotlin, in Groovy or whatever and than you may use EMFeR to
model check your actual system implementation.
1 INTRODUCTION
Let us assume you have just built a new smart traffic
light. Your smart traffic light has e.g. radar sensors to
detect approaching cars and instead of switching pe-
riodically, it yields green on demand. Thus, when at
rush hour times all the traffic goes in one direction,
this direction gets green all the time. To implement
this smart behavior you have used an EMF based ob-
ject model that keeps track of car positions and traffic
light states. Now, in order to deploy your smart traffic
light in real world you need to get certified and thus
you may need to prove system correctness.
Model Checking is a powerful formal method for
the verification of e.g. liveness and safety features
of parallel systems. There exists a number of pow-
erful model checking tools like e.g. Spin (Holz-
mann, 1997). For dynamic object models one may
use formal tools like Alloy (Jackson, 2002). And the
area of graph transformation tools provide reachabil-
ity graph computation for similar purposes, cf. tools
like Groove (grooveWebSite, 2018), Henshin (Hensh-
inWebSite, 2018), or SDMLib (wwwSDMLib, 2018).
Unfortunately most of these approaches use propri-
etary languages for the specification of models and
model transformations. This has the drawback that in
order to verify system properties, one has to recode
the system and its operations within the specific lan-
guage of the used verification tool. Thus, you basi-
cally specify or implement your smart traffic light, a
second time. This is tedious and error prone. In addi-
tion, you will have to argue, that your implementation
meets your model checking specification.
To overcome these limitations, this paper out-
lines our new EMFeR (EMF Engine for Reachability)
tool (emferWebSite, 2018). EMFeR provides model
checking capabilities for EMF (emf, 2018) based
models and arbitrarily implemented transformations
on such models. Your model transformations may be
implemented as plain Java, Xtend (xtend, 2018), us-
ing ATL (ATL, 2018), or any other approach. The
model transformations are provided to EMFeR as
Java 8 lambda expressions. Ideally, you may pass the
actual method implementations that you want to use
in your productive system to EMFeR in order to do
an exhaustive testing of your system implementation.
EMFeR applies your transformations to (clones of)
a given model and to (clones of) the resulting mod-
els, iteratively. Each time a new model is generated,
EMFeR compares the new model with any previous
model and checks whether a new model has been gen-
erated or whether an old model is reached again. To
Eickhoff, C., Lange, M., Raesch, S. and Zündorf, A.
EMFeR: Model Checking for Object Oriented (EMF) Models.
DOI: 10.5220/0007681605110518
In Proceedings of the 7th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2019), pages 511-518
ISBN: 978-989-758-358-2
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
511

Signal
pass:boolean
Road
Car
travelDirection:Traveldirection
Track
name:String
travelDirection :TravelDirection
RoadMap
1
0..1
track
signal
1
easternSignal
1
westernSignal
0..n
west
0..n
east
1
road
0..n
cars
0..1
track
tracks
0..n
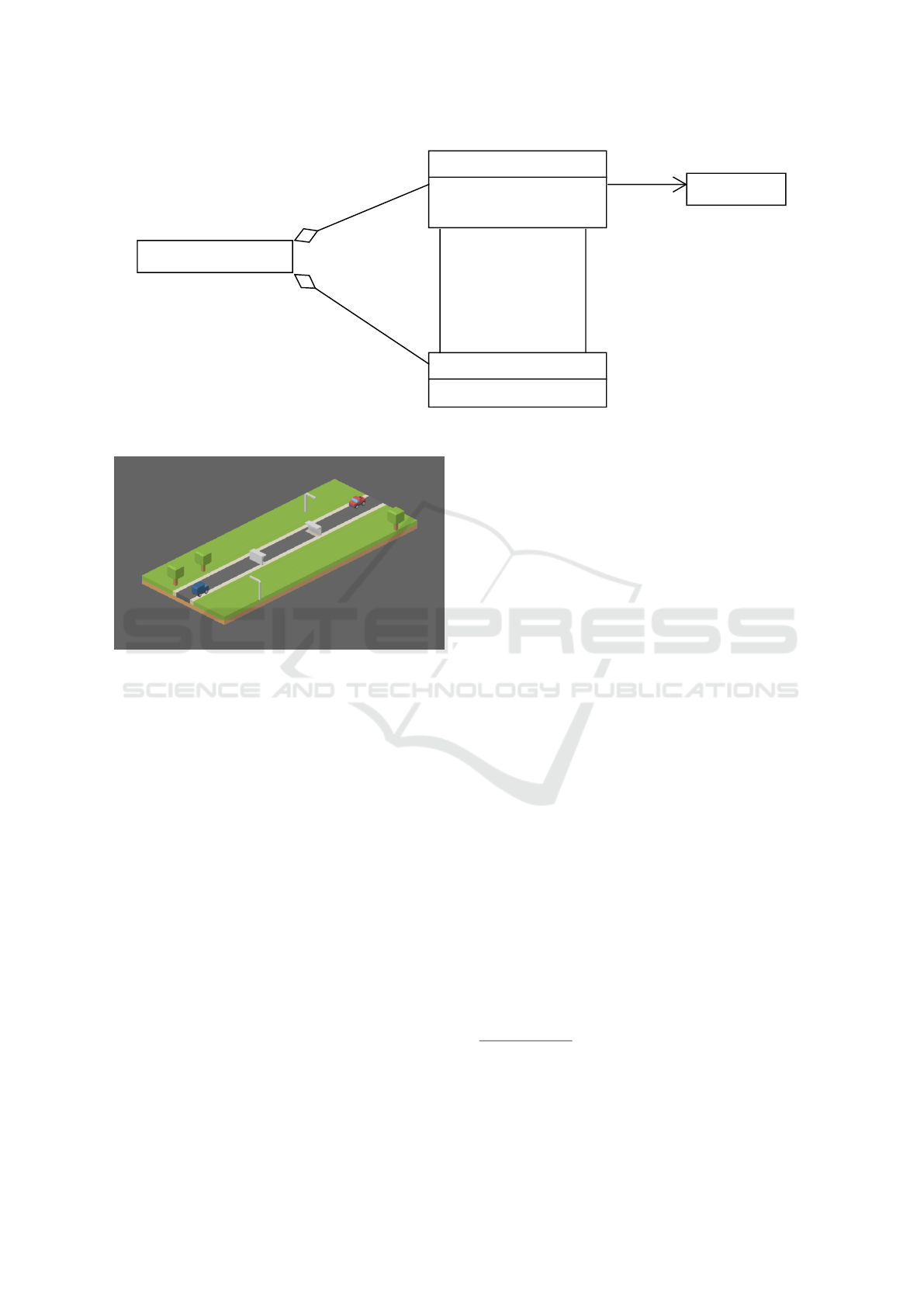
Figure 1: Road Work Class Model.
do this efficiently, EMFeR computes model certifi-
cates, i.e. hash keys, for each model, as proposed by
the Groove system (grooveWebSite, 2018). The pro-
cess terminates when all possible models have been
derived. The set of all generated models with links
corresponding to the applied transformations forms a
Labeled Transition System (LTS). In the context of
graph transformations we call this LTS a reachability
graph. On the resulting reachability graph you may
run CTL (Computational Tree Logic) (Emerson and
Clarke, 1982) queries in order to model check e.g.
safety and liveness features. You may also do any
other model query in your favorite (EMF compatible)
query language e.g. Java or OCL.
2 THE ROADWORK EXAMPLE
As running example for this paper we use a simple
traffic light system for a small one way roadwork area.
This example stems from (Greenyer et al., 2015). Fig-
ure 1 shows the class model of our example. Fig-
ure 2 shows the class model of EMFeR’s reachability
graphs.
Figure 3 shows a 2 1/2 D tile graphic for the
start situation of our road work example. We gen-
erate such tile graphics for the animation of exam-
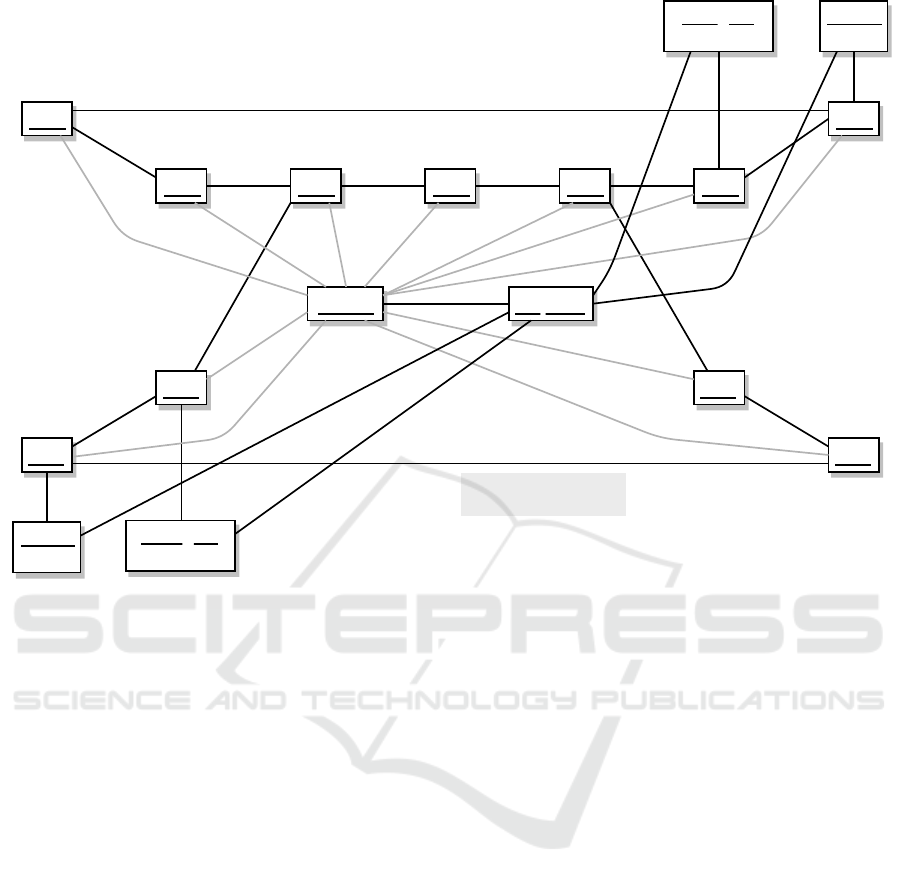
ple scenarios. Figure 4 shows a simplified EMF ob-
ject model for the same start situation. (EMFeR pro-
vides a simple HTML dump for object models based
on Alchemy.js (Alchemy.js, 2018). To allow simplifi-
cations, Figure 4 has been created, manually.) There
are two lanes: the upper (northern) lane goes from
right (east) to left (west) and consists of Track ob-
jects n1 to n7. Above this lane there are two objects
at the upper right corner of Figure 4. From right to
left this is a Car object c1 located at Track object n1.
Car c1 has travelDirection WEST. And next to it
the eastern Signal t2 that is attached to track n2
and currently shows green (pass=true). The mid-
dle row of Figure 4 shows on the left the Road ob-
ject road that contains all tracks and on the right the
RoadMap object map that refers to the road, all Cars
and all Signals. The lower (southern) lane is rep-
resented by only four Track objects named s1, s2
and s6, s7 (numbering from left to right). The three
middle objects of that lane are missing as they are
blocked by road work. Instead, track s2 is connected
to track n5 of the northern lane and track n3 of the
northern lane is continued by track s6. Each track
has a travelDirection which equals to WEST for the
northern tracks and to EAST for the southern tracks
and to UNDEFINED for the tracks in the road work
area. Finally, there are a Car object c2 and a Signal
object t2 in the lower left corner of Figure 4. The
object structure for the initial situation is created us-
ing the standard RoadworkFactory.eINSTANCE gen-
erated by EMF.
Listing 3 shows our swapSignals transformation.
This transformation has been implemented in plain
Java. Basically, swapSignals checks that the road
work area of our street (tracks with undefined travel
direction) is clear of cars (lines 3 to 5). Next, there
shall be a car waiting on red (line 12) and there shall
be no car just in front of a green light (lines 10 to
11). Under these conditions, the red signal becomes
green and the green signal becomes red, lines 13 to
14. Method swapSignals is an example for an oper-
ation that may be used to actually operate our traffic
signals in the final system. Thus the task at hand is, to
prove that swapSignals works save and e.g. fair.
Listing 1 shows how the reachability graph com-
putation is invoked. Line 1 creates an emfer object
and adds the (root of) our start model as first state
to EMFeR. EMFeR accepts simple transformations
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
512
EObject
TrafoApplication
description:String
ReachableState
number:long
metricValue:double
ReachabilityGraph
1
tgt
0..n
resultOf
1
src
0..n
trafoApplications
1
root
0..n
trafoApplications
0..n
states
Figure 2: Road Work Class Model.
Figure 3: Start Situation as Tiles Graphic.
as Java lambda expressions with one (root) parame-
ter. Via this root parameter EMFeR passes the EMF
model that shall be transformed. Line 2 adds our
swapSignals transformation to emfer. The trans-
formation swapSignals operates our traffic lights,
cf. Listing 3. In our example, transformation
swapSignals is the (part of the) system implemen-
tation we want to verify, i.e. to test exhaustively. In
contrast to graph transformations, EMFeR transfor-
mations are deterministic and produce only one new
model state. However, sometimes one wants to apply
a transformation on multiple model objects, alterna-
tively. In our example there exist multiple Car objects
that may move, independently. For such cases, EM-
FeR accepts complex transformations that consist of
a path and a two-parameter transformation. Lines 3
to 4 of Listing 1 add our moveCar transformation to
emfer. Line 4 first adds a lambda expression that
computes the set of cars in the current model. At ex-
ploration time, EMFeR will call the second lambda
expression of line 4 on each of these cars. In addition
to the car that shall be moved, EMFeR also passes
the root of the current model to the transformation in
order to facilitate access to other model elements. Fi-
nally, line 5 starts the reachability graph computation.
Listing 2 shows pseudo code for EMFeR’s reach-
ability graph exploration operation. For each state
(line 2) and each transformation (line 3), EMFeR first
computes the handle objects, on which the trafo
shall be applied (line 4). For complex transforma-
tion, line 4 uses the path lambda provided e.g. in
Listing 1, line 4. For simple transformations, we just
use the root as handle. Now, for each handle (List-
ing 2, line 5) we first clone the current model (line 6)
and then we apply the current transformation to the
cloned model passing the clones of root and handle
as parameters. The transformation may modify the
clone. This may result in a totally new model state.
In this case we add the new model state to our reacha-
bility graph and connect it to the current model via an
TrafoApplication link that carries the name of the
transformation and the used handle as description.
It may also happen, that the new state is isomorphic
1
to an old state, that has been created earlier. In this
case we just add a TrafoApplication link between
the current state and that old state. New states will
also be considered in line 2 of our algorithm, i.e. we
will apply all transformation on all handles of the new
states, again. Thus, EMFeR’s explore operation com-
putes the set of all states that can be created by apply-
ing all trafos on all handles on all states derived from
(and including) the start state, iteratively.
1
We consider two EMF models as isomorphic if there is
a bidirectional mapping between their objects that respects
all attribute values and all references. Although EMF uses
ELists for to-many references, we do NOT consider the
order of references.
EMFeR: Model Checking for Object Oriented (EMF) Models
513
n1:T
n2:Tn3:Tn4:Tn5:Tn6:T
n7:T
road:R map:RM
s2:T s6:T
s1:T s7:T
c1:Car
"west"
c2:Car
"west"
t2: Signal
pass=false
t2:Signal
pass=true
w
wwww
w
w
t
ee
e
e
e
e
e
t
t
t
westernSignal
car
car
easternSignal
Abbreviations:
w = west
e = east
T = Track
R = Road
RM = RoadMap
Figure 4: Start Situation (simplified).
3 REACHABILITY GRAPH
EXPLORATION
EMFeR’s algorithm for the exploration of reachabil-
ity graphs is outlined in Listing 2. However there are
a number of issues to be discussed in more detail.
First, when EMFeR has generated a new model it
uses model certificates, i.e. hash keys, to efficiently
identify possibly isomorphic old models. This fol-
lows the ideas of Arendt Rensink and his Groove sys-
tem (grooveWebSite, 2018). Thus, identifying iso-
morphic old states is reasonably fast. The main effi-
ciency problem of our reachability graphs is the mem-
ory consumption.
In general, the reachability graph exploration
might not terminate or the reachability graph may
become very large. In our road work example the
used transformations (swapSignals and moveCar)
do not create new objects but just change links be-
tween existing objects or change some boolean at-
tributes. Thus, in our road work example there is only
a finite number of reachable states (56 states to be
precise). However, if one employs e.g. a transfor-
mation that creates new cars or that extends the road
or just a counter for the number of car moves done,
the number of possible states would become infinite
or just larger than we can handle. Currently, EM-
FeR holds the whole reachability graph within main
memory (for this work we used a laptop with 8GB
main memory running Windows 10). Our road work
example uses 15 model objects per state (plus EList
objects for to-many references). Depending on the
size of your main memory, EMFeR may handle up to
some million reachable states.
To avoid OutOfMemory exceptions, EMFeR has a
customizable limit for the maximum number of reach-
able states it creates. This limit defaults to 300000.
It may be adapted according to the sizes of the em-
ployed models and according to the memory space
available. When the limit is reached, EMFeR just ter-
minates the exploration and delivers a partial reacha-
bility graph. If you are lucky, the partial reachability
graph already contains the states you are looking for.
In our road work example this might be a dead lock
state, where two cars traveling in opposite directions
on the single road work lane block each other.
Per default, EMFeR does a breadth first explo-
ration of the reachability graph. This means, new
states are managed within a fifo queue for further
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
514

1 EMFeR e mfer = new EMFeR ( ) . w i t h S t a r t ( roadMap )
2 . w i t h T r a f o ( ” swap S i g n a l s ” , r o o t −> s w a p S i g n a l s ( r o o t ) )
3 . w i t h T r a f o ( ”move c a r ” ,
4 r o o t −> ( ( RoadMap ) r o o t ) . g e t C a r s ( ) , ( r o o t , c a r ) −> moveCar ( r o o t , c a r ) ) ;
5 i n t s i z e = emf e r . e x p l o r e ( ) ;
6 R e a c h a b l e S t a t e s t a r t S t a t e = em f e r . g e t R e a c h a b i l i t y G r a p h ( ) . g e t S t a t e s ( ) . g e t ( 0 ) ;
7 A l w a y s G l o b a l l y a l w a y s G l o b a l l y = new Al w a y s G l o b a l l y ( ) ;
8 E x i s t F i n a l l y e x i s t F i n a l l y = new E x i s t F i n a l l y ( ) ;
9 E x i s t G l o b a l l y e x i s t G l o b a l l y = new E x i s t G l o b a l l y ( ) ;
10 bo o l e a n noDeadLock = a l w a y s G l o b a l l y . t e s t ( s t a r t S t a t e , s −>!is Ca r De a d Lo c k ( s ) ) ;
11 bo o l e a n u n f a i r = e x i s t F i n a l l y . t e s t ( s t a r t S t a t e ,
12 s−> e x i s t G l o b a l l y . t e s t ( s , s2−>i s E a s t C a r W a i t s A t R e d ( s2 ) ) ) ;
13 A r r a y L i s t <T r a f o A p p l i c a t i o n > ex a m p l e P a t h = e x i s t G l o b a l l y . g e t E x a m p l e P a t h ( ) ;
14 S yste m . o u t . p r i n t l n ( ex a m p l e P a t h ) ;
Listing 1: Calling Emfer.
1 EMFeR : : e x p l o r e ( ) {
2 f o r e ac h s t a t e {
3 f o r e ac h t r a f o {
4 comp u te h a n d l e s f o r t r a f o
5 f o r e ac h h a n d l e {
6 c l o n e c u r r e n t s t a t e
7 a p p l y t r a f o on c l o n e
8 i f ( new s t a t e )
9 add t r a f o ed g e and
10 new s t a t e t o g r a p h
11 i f ( o l d s t a t e )
12 add t r a f o ed g e t o g r a p h
13 }
14 }
15 }
16 re t u r n number o f s t a t e s
17 }
Listing 2: EMFeR explore.
exploration. In (Eickhoff et al., 2016) we extended
SDMLib’s reachability graph exploration algorithm
with a metric computation provided as Java lambda
expression. EMFeR has adopted this idea. The met-
ric computation computes a metric value for each new
state and then the queue of new states is sorted accord-
ing to this metric value (minimal value first). Thereby,
the metric computation steers the exploration strat-
egy similar to an A* algorithm. This results in a hill
climbing strategy for our reachability graphs where
the most promising states are expanded, first. Ac-
tually, the result is a kind of taboo search as states
that have been considered will not be expanded again.
Thus, our exploration strategy will backtrack out of
local optima (if there is still memory space left).
In the special case of Computational Tree Logic
CTL (Emerson and Clarke, 1982) proof obligations,
the checking of CTL operators and the expansion of
the reachability graph may be inter wined. This would
allow to stop the exploration as soon as a counter ex-
ample (for always operators) or a positive example
(for exist operators) has been found.
The space limitation problem exists also for tra-
ditional model checkers like Spin (Holzmann, 1997):
depending on your formulas and the available mem-
ory space, there is an upper bound for the number of
boolean variables Spin can handle. To deal with the
space limitation problem, traditional model checkers
employ very efficient encodings for states. So far,
EMFeR uses a full copy of the whole EMF model for
each state. This is very space consuming. Usually,
the Groove tool employs full graph copies per state,
too. But to reduce memory consumptions Groove re-
moves e.g. every second state graph and on demand
Groove recreates missing graphs from predecessors
by applying the corresponding transformation again.
(This becomes necessary when a new graph is cre-
ated and an isomorphism test with an old graph is re-
quired. It is also necessary when you run queries on
your whole reachability graph e.g. searching for dead
lock states.) To achieve a more efficient state space
encoding without needing to recreate dropped states,
EMFeR implements a lazy cloning strategy, where
we clone only model elements that are modified and
share unmodified model parts within multiple states.
Technically, EMFeR subscribes a change listener to
all objects of the current model. Then EMFeR just
runs the current transformation on the current model
and records all changes at object and attribute level.
If there are no changes recorded, the transformation
has failed and we go on with the next transforma-
tion. If there are recorded changes, we first undo all
changes to recreate the unchanged model. Then, we
create a new reachable state and a clone of the root
node. Now, we iterate through all recorded changes
and for each change we clone the modified node and
all nodes that refer to the modified node (transitively).
As all model nodes are reachable from the root node,
we will at least clone all nodes on a path from the
root node to the modified node. Of course, if some
node has already been cloned, we reuse that clone.
EMFeR: Model Checking for Object Oriented (EMF) Models
515

1 p r i v a t e v o i d s w a p S i g n a l s ( E O b j e c t r o o t ) {
2 RoadMap roadMap = ( RoadMap ) r o o t ;
3 f o r ( Car c : roadMap . g e t C a r s ( ) ) {
4 i f ( c . g e t T r a c k ( ) . g e t T r a v e l D i r e c t i o n ( ) == UNDEFINED) r e t u r n ;
5 }
6 b oo l e a n c a r I s W a i t i n g = f a l s e ;
7 / / no c a r a b o u t t o e n t e r and one ca r w a i t i n g a t r e d l i g h t
8 S i g n a l w e s t = roadMap . g e t W e s t e r n S i g n a l ( )
9 S i g n a l e a s t = roadMap . g e t E a s t e r n S i g n a l ( ) ;
10 i f ( we s t . i s P a s s ( ) && c a r A t W e st ( r o o t ) r e t u r n ;
11 i f ( e a s t . i s P a s s ( ) && c a r A t E a s t ( r o o t ) ) r e t u r n ;
12 i f ( we s t . i s P a s s ()&& c a r A t E a s t ( r o o t ) | | e a s t . i s P a s s ()&& c ar A t W e s t ( r o o t ) ) {
13 e a s t . s e t P a s s ( ! e a s t . i s P a s s ( ) ) ;
14 we s t . s e t P a s s ( ! w e st . i s P a s s ( ) ) ; } }
Listing 3: Controlling the traffic signals.
Thus, the clone of the currently modified node will be
connected to the clone of the root node via a path of
cloned nodes. Finally, the new state contains a cloned
root node and clones for all nodes that connect this
cloned root node to clones of modified nodes. Nodes
that are neither modified nor refer to modified nodes
are shared with the previous state.
In our road work example the road and its tracks
are not directly modified by our example transforma-
tions. Thus, the road and track objects are shared by
all states and we clone only the root object, modified
cars, and or modified signals. Thus each new state
clones at most 5 model objects and at least 12 model
objects are shared. To enable lazy cloning, our class
model avoids the use of EMF containment associa-
tions and bidirectional associations, cf. Figure 1. The
unidirectional links between cars and tracks and be-
tween signals and tracks, allow the cloning of cars
without cloning their current tracks. Similarly, the
unidirectional association from RoadMap to Road al-
lows to clone the RoadMap root without cloning the
road and the attached tracks. As neither the road ob-
ject nor any track object is ever modified, the bidi-
rectional association between these classes does not
harm.
Overall, for an application of the moveCar trans-
formation our lazy cloning approach clones only the
moved car and the root object, i.e. we share 15 out
of 17 objects and the new reachable state needs only
2 new model objects (plus the object for the reach-
able state and an object for the TrafoApplication).
Similarly, the swapSignals operation clones only the
two modified signals and the root object, i.e. only 3
new model objects for the new state. In our exam-
ple this reduces the number of model objects in the
total reachability graph down to some 15%. In addi-
tion, omitting opposite references safes some mem-
ory space, too. On the down side, our model and our
model transformations must limit the use of bidirec-
tional associations and especially of containment as-
sociations. Unfortunately, in EMF contains associa-
tions are commonly used as part of EMF’s persistence
mechanisms. However, to some extend these are EMF
specific problems and you could go for e.g. SDMLib
based model implementations that avoid these prob-
lems. Generally, we plan to extend EMFeR to apply
for other model implementations.
4 REACHABILITY GRAPH
ANALYSIS
Once a reachability graph has been computed, we
may run all kinds of analysis and query operations
on it. We may e.g. search for all states that contain
a forbidden situation (two cars in the road work area
traveling in opposite direction) or all transformation
edges that connect a valid state with an invalid state.
This gives insight on which model transformations
may need enhanced preconditions in order to avoid
invalid states. You may also search for shortest paths
that lead from the start state to some final state where
you assign e.g. specific costs to each model transfor-
mation. For such queries you may use plain Java or
OCL or graph queries or any other appropriate query
language. After all, our reachability graph is a simple
(EMF) model, again.
For comparability reasons, EMFeR also sup-
ports Computational Tree Logic CTL (Emerson and
Clarke, 1982) to analyze reachability graphs. EM-
FeR provides 8 CTL operators for all combinations
of always and exist quantifiers with finally, globally,
next, and until operators. Listing 1, line 10 shows
the usage of the AlwaysGlobally operator. The op-
erator is parameterized with a predicate to be tested
on all states reachable from the start state. In EM-
FeR, we provide predicates as boolean Java lambda
expressions that may be implemented in plain Java
or e.g. using OCL or some other (your favorite)
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
516

1 [ 2 −−move c a r n1 WEST−> 4 ,
2 4 −−move c a r n2 WEST−> 7 ,
3 7 −−move c a r n3 WEST−> 11 ,
4 11 −−move c a r n4 WEST−> 15 ,
5 15 −−move c a r n5 WEST−> 19 ,
6 19 −−move c a r n6 WEST−> 23 ,
7 23 −−move c a r n7 WEST−> 2 ]
Listing 4: Car traveling east waits at red light, forever.
query language. Listing 1 lines 11 to 12 show how
EMFeR CTL operators may be nested to form more
complex queries. Lines 11 to 12 search for an un-
fair situation, e.g. the east car waits at red light
forever. Unfortunately, lines 11 to 12 detect that
transformation swapSignals from Listing 3 is un-
fair. Thus, the ExistGlobally operator of line 12
succeeds in finding a circle in our reachability graph
where only the car traveling west moves and the other
car waits for ever. On success, the exist operators gen-
erate an example path. (The always operators pro-
duce counterExample paths, on failure.) Listing 1,
Line 14 prints the unfair example path. Listing 4
shows the output for our unfair example. In state 2,
the car traveling east is waiting at its red light. The
other car has not yet moved. From then on, only the
car traveling west moves until it has done a full circle
reaching state 2, again. When the circle is closed, the
car traveling west may just do new circles for ever. In
this case the car traveling east will starve to death at
the red light.
The fairness problem of our current example sys-
tem is easily solved, if the swapSignals transforma-
tion gets executed once the car traveling west leaves
the road work area. Like Groove (grooveWebSite,
2018), EMFeR allows to force a set of transforma-
tions to be executed, if possible, by assigning priori-
ties to them. Doing so, our example system becomes
fair for two cars. If we add a second car on the upper
lane, these two cars might take turns in blocking the
road work area and thus they may block the signals
from swapping, forever. To address this, we need to
enable our signals to show red on both sides, in order
to drain the road work area and then to give yield to
the opposite direction.
Reachability graphs may also be used for con-
troller synthesis. The basic idea for controller syn-
thesis with EMFeR is to provide EMFeR with all the
basic operations. For our Road Map example we may
simply add an operation that switches each signal in-
dependently and without any respect to car move-
ments. Then, we generate all possible situations. The
resulting reachability graph will contain many unde-
sired or forbidden states. Thus, we now use an anal-
ysis function that visits the reachability graph and
marks undesired states and or adds a metric value for
the goodness of states. Now a smart controller for
our signals may just analyze the current traffic situa-
tion, identify the corresponding state within the reach-
ability graph of our system and identify the successor
state we would like to reach and issue the correspond-
ing switch signal operation.
5 CONCLUSION
EMFeR provides reachability graph computation for
(EMF) models based on model transformations pro-
vided as simple Java lambdas. Thus, you can do com-
plete testing and model checking and controller syn-
thesis on your normal EMF model using your favorite
model transformations. Ideally, you may test your
productive code, exhaustively. There is no need to
recode your problem e.g. in Promela or in any other
proprietary language used by current model checkers
or within a graph transformation system as e.g. Hen-
shin.
To cover all possible traffic situations for our traf-
fic light example, we use additional transformations
that create new cars entering the road work area at
both sides and that remove cars that have passed the
crossing. This more dynamic traffic scenario results
4064 different states for our reachability graph. This
results from all possible situations with or without a
car at each track computing to 2
11
possible car distri-
butions. And there are 2
1
different signal states giving
an upper bound of 4096 states.
We have run cases with some ten million states,
i.e. about 2
23
states. If we add more tracks to our
road, each additional track would add a factor of two
to the upper bound of states, thus we could go to
a street with about 20 tracks or a crossing with 10
incoming lanes, roughly double the size of our cur-
rent example. There is hope that EMFeR perfor-
mance can be further enhanced by techniques devel-
oped e.g. in the context of the Spin model checker.
Still the size of manageable object models is quite
limited. For larger problems model abstractions are
necessary. Systematic approaches to model abstrac-
tion like the counter example guided abstraction re-
finement method (Clarke et al., 2000) are future work.
However, EMFeR allows to do full testing and
model checking on dynamic object models using the
actual implementation of your model transformation
that will run in your productive system. This means,
you can guarantee that your actual system is fully
tested and works correct in all possible cases. EM-
FeR enables sharing of common sub-models between
multiple states thus providing a memory efficient en-
coding of large reachability graphs where each state
EMFeR: Model Checking for Object Oriented (EMF) Models
517

is still a usual EMF model. EMFeR basically re-
lies on reflective access to the models as provided by
EMF’s EClass. We need to be able to ask a model
element for its attributes and to read and write those
attributes and to record all attribute changes. Using
java.lang.reflect we could achieve this reflective ac-
cess for general Java objects or at least for Java Bean
objects. Thus, our current work is to generalize EM-
FeR for other modeling frameworks and for POJO
models.
REFERENCES
Alchemy.js (2018). Alchemy.js - A graph visualiza-
tion application for the web. http://graphalchemist.
github.io/Alchemy/.
ATL (2018). ATL Transformation Language. http://www.
eclipse.org/atl/.
Clarke, E., Grumberg, O., Jha, S., Lu, Y., and Veith, H.
(2000). Counterexample-guided abstraction refine-
ment. In International Conference on Computer Aided
Verification, pages 154–169. Springer.
Eickhoff, C., Raesch, L., and Z
¨
undorf, A. (2016). The sdm-
lib solution to the class responsibility assignment case
for ttc2016. In TTC@ STAF, pages 27–32.
Emerson, E. A. and Clarke, E. M. (1982). Using branch-
ing time temporal logic to synthesize synchroniza-
tion skeletons. Science of Computer Programming,
2(3):241–266.
emf (2018). Eclipse Modeling Framework. https://www.
eclipse.org/modeling/emf/.
emferWebSite (2018). EMFeR Github Site. https://
github.com/fujaba/EMFeR.
Greenyer, J., Gritzner, D., Gutjahr, T., Duente, T., Dulle,
S., Deppe, F.-D., Glade, N., Hilbich, M., Koenig,
F., Luennemann, J., et al. (2015). Scenarios@ run.
time-distributed execution of specifications on iot-
connected robots. In MoDELS@ Run. time, pages 71–
80.
grooveWebSite (2018). Groove Web Site. http://groove.
cs.utwente.nl/.
HenshinWebSite (2018). Henshin Web Site. https://www.
eclipse.org/henshin/.
Holzmann, G. J. (1997). The model checker spin. IEEE
Transactions on software engineering, 23(5):279–
295.
Jackson, D. (2002). Alloy: A lightweight object mod-
elling notation. ACM Trans. Softw. Eng. Methodol.,
11(2):256–290.
wwwSDMLib (2018). Story Driven Modeling Library.
http://sdmlib.org/.
xtend (2018). Xtend. https://www.eclipse.org/xtend/.
MODELSWARD 2019 - 7th International Conference on Model-Driven Engineering and Software Development
518
