Performance Prediction of GPU-based Deep Learning Applications

Eugenio Gianniti

, Li Zhang

and Danilo Ardagna

Dip. Elettronica, Informazione e Bioingegneria, Politecnico di Milano, Milan, Italy

IBM Research, Yorktown Heights, N.Y., U.S.A.

Keywords:

Convolutional Neural Networks, Deep Learning, Performance Prediction, General Purpose GPUs.

Abstract:

Recent years saw an increasing success in the application of deep learning methods across various domains

and for tackling different problems, ranging from image recognition and classiﬁcation to text processing and

speech recognition. In this paper we propose, discuss, and validate a black box approach to model the execu-

tion time for training convolutional neural networks (CNNs), with a particular focus on deployments on general

purpose graphics processing units (GPGPUs). We demonstrate that our approach is generally applicable to a

variety of CNN models and different types of GPGPUs with high accuracy. The proposed method can support

with great precision (within 5% average percentage error) the management of production environments.

1 INTRODUCTION

Nowadays, convolutional neural networks (CNNs)

ﬁnd application across industries, most notably for

image recognition and classiﬁcation tasks, which rep-

resented the ﬁrst successful adoption of the tech-

nique (Krizhevsky et al., 2012). Ranging from med-

ical diagnosis to public security, deep learning (DL)

methods are fruitfully exploited in a wide gamut of

products. In addition to the established applications,

there is ongoing work on the technique’s adaptation

for other use cases, like speech recognition (Sainath

et al., 2015) and machine translation (Bahdanau et al.,

2014).

CNNs hail from regular neural networks (NNs),

but improve on them by reducing the connectivity pat-

tern and by introducing novel layers speciﬁcally de-

signed to take advantage of the peculiarities shown by

images (Krizhevsky et al., 2012). The common archi-

tecture for basic NNs is composed of a number of neu-

ron layers organized so that subsequent ones are com-

pletely connected, but without any link among same-

layer neurons or bypassing connections (Srivastava

et al., 2014). This design is well suited for datasets

with a limited set of features that simply become the

input for the ﬁrst neuron layer, but colored images can

easily provide one million of values if their raw pixels

are to be fed as data into the network, even at very low

resolution: NNs at such a scale are computationally

impractical. In order to work around the issue, CNNs

introduce a series of new layer typologies, in partic-

ular the namesake convolutional one (Szegedy et al.,

2015). The general idea is to devise sparser connec-

tivity patterns, so as to reduce the computational com-

plexity and render the problem tractable, but at the

same time to stack several layers, in order to incre-

mentally achieve the same global view of the feature

space offered by ordinary fully connected ones.

Over time, many frameworks have been devel-

oped to provide high level APIs for CNN design,

learning, and deployment. Among the most well

known, we recall Torch, PyTorch, TensorFlow, and

Caffe. Usually DL models are trained by relying on

GPGPU systems (even in clusters for experimental

environments (Wang et al., 2017)), which allow to

achieve from 5 up to 40x time improvement when

compared to CPU deployments (Bahrampour et al.,

2015).

In spite of the widespread adoption of DL sys-

tems, still there are few studies taking a system per-

spective which aim at investigating how, e.g., the

training time changes when running on different

GPGPUs or by varying the number of training itera-

tions or the batch size (Bahrampour et al., 2015; Had-

jis et al., 2016). DL applications are characterized

by a large number of design choices that often do not

apply readily to other domains or hardware conﬁgu-

rations, up to the point that even advanced users with

considerable DL expertise fail at identifying optimal

conﬁguration settings (Hadjis et al., 2016).

The time required to train a new DL model is gen-

erally unknown in advance. Because of this, perfor-

Gianniti, E., Zhang, L. and Ardagna, D.

Performance Prediction of GPU-based Deep Learning Applications.

DOI: 10.5220/0007681802790286

In Proceedings of the 9th International Conference on Cloud Computing and Services Science (CLOSER 2019), pages 279-286

ISBN: 978-989-758-365-0

279

mance analysis is usually done empirically through

experimentation, requiring a costly setup (Bahram-

pour et al., 2015). Performance modeling can help,

e.g., to establish service level agreements with end

users or to predict the budget to train or run produc-

tion DL models in the cloud.

In this paper, we present a method to learn perfor-

mance models for CNNs running on a single GPGPU.

The main metrics under investigation are the forward

time, relevant to quantify the time taken for classiﬁ-

cation when the trained network is deployed, and the

gradient computation time, which on the other hand

is important during the learning phase. In the follow-

ing, we will generally mention forward and backward

passes, referring to the direction in which information

ﬂows through the CNN, with either features incre-

mentally processed for classiﬁcation or partial deriva-

tives that back propagate to reach learnable weights.

Our goal is to lead new users with limited previ-

ous experience from an initial test deployment to real

scale applications. In order to meet the requirements

of both scenarios, i.e., the generality needed in the

preliminary design phase of a project on one side and

the high accuracy expected when running in produc-

tion on the other, we envision two alternative tech-

niques to derive models that boast different trade-offs.

In our previous work (Gianniti et al., 2018), we

proposed a gray box per layer approach where model-

ing is performed layer by layer and the only explana-

tory variable is computational complexity. This tech-

nique allows for great generality, since partial layer

predictions can be easily combined into a full CNN

estimate, even if the speciﬁc network schema has

never been considered as part of the training set. Due

to this, the approach is preeminently interesting dur-

ing the initial design stages, for instance to compare

different alternative CNNs and deployments in terms

of performance. On the other hand, when a deploy-

ment is already available, data coming from the real

system enables a different approach with its focus on

precision rather than ease of generalization.

This second scenario can be tackled with a black

box approach, called end to end modeling, which fo-

cuses on a single CNN and learns the dependency of

execution time on varying batch size and iterations

number. The improved accuracy comes at the expense

of a quite narrower focus centered around a particu-

lar network architecture and deployment, which pre-

vents the application of the model in different situa-

tions. Moreover, this modeling technique requires a

collection of historical data, thus entailing either an

experimental campaign or the proper monitoring of

previous runs in a production environment. However,

as we will demonstrate through our empirical analy-

ses, small scale experiments are enough to extrapolate

to a larger scale range, which mitigates the cost of this

approach.

In our experimental campaign, we considered

three popular DL models, implemented with the Caffe

framework and run on two different GPGPUs. Yet our

methodology is not constrained in any way neither to

a speciﬁc framework, nor GPGPU model. The out-

comes show that we can either obtain per layer mod-

els general enough to yield relative errors below 10%

on average across different CNN architectures and be-

low 23% in the worst case, or more specialized on a

speciﬁc end to end scheme, but accurate within 5% of

measured execution times.

Our contributions in this paper are as follows: 1)

an end to end model capable of predicting both learn-

ing and inference of a convolutional network in a pro-

duction environment, 2) a comparison of the end to

end with the per layer model proposed in (Gianniti

et al., 2018).

This paper is organized as follows. An overview

of other literature proposals is provided in Section 2,

while Section 3 introduces the end to end, black box

performance model. Its accuracy and a discussion of

the key ﬁndings of our experimental analysis are re-

ported in Section 4. Conclusions are ﬁnally drawn in

Section 5.

2 RELATED WORK

DL popularity is steadily increasing thanks to its im-

pact on many application domains (ranging from im-

age and voice recognition to text processing) and

has received a lot of interest from many academic

and industry groups. Advances are boosted by en-

hancements of the deep networks structure and learn-

ing process (e.g., dropout (Srivastava et al., 2014),

network in network (Lin et al., 2013), scale jitter-

ing (Vincent et al., 2010)) and by the availability of

GPUs, which allows to gain up to 40x improvement

over CPU systems (Bahrampour et al., 2015).

Over the last few years, several frameworks have

been developed and are constantly extended to ease

the development of DL models and to optimize dif-

ferent aspects of training and deployment of DL ap-

plications. The work in (Bahrampour et al., 2015)

provides a comparative study of Caffe, Neon, Theano,

and Torch, by analyzing their extensibility and perfor-

mance and considering both CPUs and GPUs. The

paper provides insights on how performance varies

across batch sizes and different convolution algorithm

implementations, but it does not provide means to

generalize performance estimates.

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

280

The authors of (Jia et al., 2012) propose the

Stargazer framework to build performance models

for a simulator running on GPU, so as to correlate

several GPU parameters to the simulator execution

time. Given the daunting size of the design space,

which considers very low level parameters, they ex-

ploit sparse random sampling and iterative model se-

lection, thus creating step by step an accurate lin-

ear regression model. Another approach is proposed

in (Liu et al., 2007), where the authors elaborate a

detailed analytical model of general purpose appli-

cations on GPUs, consisting of three general expres-

sions to estimate the time taken for common opera-

tions, according to their dependencies on data size or

computational capabilities. Similar analytical model-

ing approaches (Baghsorkhi et al., 2010; Zhang and

Owens, 2011; Hong and Kim, 2009; Song et al.,

2013) rely on micro-architecture information to pre-

dict GPU performance. As GPU architectures con-

tinue to evolve, the main issue of analytical models is

that any minor change may require extensive work for

adapting models.

Given the complexity of GPU hardware (many

cores, context switching, memory subsystem, etc.),

recently black box approaches based on machine

learning (ML) are favored over analytical models. In-

deed, black box techniques allow for deriving per-

formance models from data and making predictions

without a priori knowledge about the internals of the

target system. On the other hand, ML models (Dao

et al., 2015; Barnes et al., 2008; Bitirgen et al., 2008;

Kerr et al., 2010; Lu et al., 2017; Gupta et al., 2018)

require to perform an initial proﬁling campaign to

gather training data. An overview and quantitative

comparison among recent analytical and ML-based

model proposals is reported in (Madougou et al.,

2016).

In this research area, the authors of (Venkataraman

et al., 2016) propose Ernest, a black box performance

prediction framework for large scale analytics based

on experiment design to collect the minimum number

of training points. In particular the work allows pre-

dicting the performance of different business analyt-

ics workloads based on Spark MLlib on Amazon EC2

and achieves an average prediction error under 20%.

The authors of (Kerr et al., 2010) proﬁle and build

models for a range of applications, run either on CPUs

or GPUs. Relying on 37 performance metrics, they

exploit principal component analysis and regression

in order to highlight those features that are more likely

to affect performance on heterogeneous processors.

Along the same lines, the authors of (Luk et al., 2009)

describe Qilin, a technique for adaptively mapping

computation onto CPUs or GPUs, depending on ap-

plication as well as system characteristics. With this

approach, they show an improved speedup with re-

spect to manually associating jobs and resources.

Building upon the discussed comparison, the

model proposed in this paper adopts ML with only

high level features, such as batch size and number of

iterations. This allows, on one side, to avoid the issues

posed by analytical approaches when the underlying

hardware architecture changes, on the other it expands

the applicability since, differently from several alter-

natives available in the literature, there is no need to

modify target applications or frameworks in order to

instrument their code.

3 END TO END MODEL

The per layer approach described in (Gianniti et al.,

2018) adopts each CNN layer computational com-

plexity to estimate the layer forward or backward pass

execution times. This technique is quite general in

its applicability, however the prediction errors tend to

increase as more complex networks are considered,

since its generality entails some approximations. In

the case of a working deployment, it is quite natural

to trade off some generality for lower prediction er-

rors, whence the end to end method laid out in the

following.

The basic idea is to extract from historical data,

particularly logs of previous runs or traces collected

by a monitoring platform, the execution time of the

network in its entirety, so as to build a dataset associ-

ating these timings to batch sizes and number of iter-

ations. Then it is possible to apply linear regression

to a sample in order to obtain a model specialized for

the particular CNN and deployment under considera-

tion, but capable of predicting performance with high

accuracy.

Deep learning practice usually involves several al-

ternating phases of CNN training and testing. The

former iteratively feeds the network with labeled im-

age batches, so that its parameters can change fol-

lowing the direction of the back propagated gradient,

whilst the latter evaluates the CNN’s evolving quality

in terms of more human readable metrics, rather than

the loss function used for training, but without con-

tributing to the learning of weights and biases. For

example, generally training is performed minimizing

a loss function that may be SVM-like or based on

cross entropy, but the stopping criterion is likely ex-

pressed in terms of classiﬁcation accuracy or F-score,

for unbalanced datasets. Since training involves back

propagation, but testing does not, it is necessary to

characterize two different models.

Performance Prediction of GPU-based Deep Learning Applications

281

An interesting aspect to consider is the choice of

features for the design matrix. When the use case

is more focused on working with ﬁxed batch size or,

conversely, ﬁxed iteration number, then it is straight-

forward to use only the varying axis as explanatory

variable. In both ways ﬁrst degree polynomials yield

an accurate representation of the dependency of ex-

ecution time on batch size or iterations. The same

does not apply to models learned against a dataset

with both batch size and number of iterations that

vary. However, since the results in the single variable

case corroborate separately afﬁne relations (i.e., in the

form ax + b) of the execution time with either vari-

able, the following Theorem 3.1 guarantees that the

only higher degree term to consider is the quadratic

interaction.

Theorem 3.1. Let F : R

→ R. F is afﬁne in x for all

y ∈ R and, symmetrically, is afﬁne in y for all x ∈ R.

Then, F is a second degree polynomial of the form:

F (x, y) = axy + bx + cy + d.

Proof. Due to afﬁnity, for any x ∈ R we can write:

F (x, y) = f (x)y + g (x) .

Again, afﬁnity guarantees that for all y ∈ R the

pure second order partial derivative with respect to x

is null:

(x, y) = f

(x)y + g

(x) = 0.

By equating the coefﬁcients, it follows that f

= 0

and g

= 0, so f and g are themselves afﬁne in x,

whence the thesis.

Thanks to Theorem 3.1 and knowing that, ﬁxed

every other variable, execution time shows an afﬁne

dependency on either batch size or number of iter-

ations, it follows that the overall dependency when

both quantities vary can be expressed as a quadratic

polynomial where the only second degree term is the

batch-iterations product. This is actually a quite sig-

niﬁcant term, as i · b is the number of processed im-

ages during the training (or prediction) process.

4 EXPERIMENTAL RESULTS

In this section we report numerical results to sup-

port and validate our proposed modeling technique.

In order to provide a reproducible experimental set-

ting, we consider AlexNet (Krizhevsky et al., 2012),

GoogLeNet (Szegedy et al., 2015), and VGG-16 (Si-

monyan and Zisserman, 2015) as CNNs, while the

Table 1: NVIDIA GPUs Speciﬁcations.

Characteristic M6000 P100 Unit

NVIDIA CUDA cores 3072 3584 -

GPU memory 12 16 GB DDR5

Memory bandwidth 317 732 GB/s

Single precision operations 7.0 9.3 TFLOPS

training and validation datasets are the ones released

for ILSVRC2012.

4.1 Experimental Setting

We collected data from two computational nodes with

different GPUs. The ﬁrst has an Intel Xeon E5-

2680 v2 2.80 GHz 10-core processor, an NVIDIA

Quadro M6000 GPU, and runs CentOS 6.8; the sec-

ond sports an Intel Xeon E5-2680 v4 2.40 GHz 14-

core CPU, an NVIDIA Tesla P100-PCIe graphic card,

and CentOS 7.4. Table 1 reports some relevant speci-

ﬁcations of both GPU models. Caffe uses single pre-

cision by default in ﬂoating point arithmetics, hence

the table reports ﬁgures about it. Thanks to the in-

creased speed and more than double memory band-

width, end to end execution times on P100 have im-

provements in the range 40–90%.

Exploiting an ad hoc benchmarking framework in-

ternally developed at IBM Research, we performed

several runs of the three CNNs with varying batch

sizes and iterations numbers. In every conﬁguration

we collected execution logs for the learning proce-

dure. Afterwards we extracted from these logs, via

a custom parser, the time taken to perform both the

training and testing phases of the CNNs, thus con-

structing datasets where these overall times are asso-

ciated with the corresponding batch sizes and itera-

tions.

As accuracy metric we consider signed relative er-

rors:

t − T

, (1)

where T denotes the measured time and

t is the pre-

dicted time, so that negative values highlight too con-

servative predictions, which can be helpful if these

models are to be used to enforce a deadline. Both

the measured times T and the predictions

t refer to

the total time taken for CNN training. As additional

accuracy metric, when we need to summarize the re-

sults, we take absolute values of the relative errors and

compute the average, thus obtaining mean absolute

percentage errors (MAPEs). Our validation dataset

consists of around 500 runs and in the following we

report the most signiﬁcant outcomes.

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

282

4.2 Preliminary Analyses

Table 2 summarizes the most interesting properties

that characterize CNNs’ performance, quantiﬁed with

the formulas that underlie the per layer approach pre-

sented in (Gianniti et al., 2018). For each of the

studied networks, we list its number of layers, over-

all learnable weights, activations, and complexity at

batch size 1. As the batch size increases, activa-

tions and complexity follow a direct proportionality.

These quantities allow for several considerations on

CNNs, for instance it is possible to assess what is

the largest batch size that can ﬁt in a GPU’s mem-

ory based on the number of activations. For example,

VGG-16 has more than twice the number of activa-

tions of GoogLeNet and we observed that its maxi-

mum batch size on a NVIDIA Quadro M6000 is only

half the one for GoogLeNet.

As part of our investigation of CNNs’ perfor-

mance, we initially focused on comparing the break-

down of operation counts and layer execution times.

Table 3 summarizes this analysis on data coming from

our experimental deployment. Both for the forward

and backward pass, convolutional layers account for

more than 98% of the overall computational complex-

ity, yet the time taken for their processing accounts

for a smaller fraction of the total, with GoogLeNet

reaching as low as 70%. This pattern highlights how

GPGPUs are actually a good tool for CNNs, as they

optimize precisely for the most common kind of per-

formed operations. Along the same lines, these break-

downs can be useful in designing special purpose de-

vices, such as the recent NVIDIA Volta V100, which

boasts tensor cores speciﬁcally devised for the matrix

operations that make up most part of convolutional

layers computation.

4.3 End to End Model Validation

This section describes the validation for the end to end

model proposed in Section 3.

Recall that feasible batch sizes are limited by

memory constraints, so in these experiments b varies

with step 8 to achieve a greater sample size: we

ran experiments on the P100 node exploring the

Cartesian product of B = {8, 16, 24, 32, 40, 48, 56, 64}

and I = {100, 120, 150, 170, 200, 230, 250, 300, 350,

400, 500, 700, 800, 950, 1000, 1100, 1400, 1600, 2000,

2300}.

A preliminary investigation consists in learning

end to end models for the three different CNNs over

the full above mentioned data set. Adopting this ap-

proach, it is possible to attain a very high accuracy:

across the 160 data points, the MAPE settles at 2.94%

100

120

140

Predicted [s]

Actual [s]

AlexNet

Figure 1: AlexNet actual vs. predicted.

100

200

300

400

500

Predicted [s]

Actual [s]

GoogleNet

Figure 2: GoogLeNet actual vs. predicted.

for AlexNet, 0.97% for GoogLeNet, and 1.53% for

VGG-16. Vice versa, the per layer models achieved

relative errors below 10% on average and were below

23% in the worst case. See (Gianniti et al., 2018) for

further details. Figures 1, 2 and 3 show the actual vs.

predicted plots for these three models. In line with

the accuracy suggested by the MAPEs, in all the three

plots the blue points lie very close to the black diago-

nal.

In order to assess the quality of execution time

prediction when extrapolating to higher parameter

ranges, for each CNN we split the dataset into train-

ing and test portions. Models were learned on the

subset devoted to the training phase, while the ﬁnal

accuracy metric is the MAPE evaluated on the test set

by comparing overall real execution times with corre-

sponding predictions. By splitting the dataset we can

quantify the predictive capability on conﬁgurations

not available during the learning via linear regression,

particularly in terms of extrapolation towards larger

batch sizes and more overall iterations. This approach

to splitting data is motivated by the economic beneﬁt

Performance Prediction of GPU-based Deep Learning Applications

283

Table 2: CNN Characteristics, Batch Size 1.

Network Layers Weights Activations Complexity

AlexNet 8 6.24E+7 1.41E+6 3.42E+9

GoogLeNet 22 1.34E+7 6.86E+6 4.84E+9

VGG-16 16 1.38E+8 1.52E+7 4.65E+10

Table 3: Operation Count and Layer Time Breakdown.

Network Category c

[%] t

[%] c

[%] t

[%]

AlexNet Conv/FC 99.51 83.11 99.66 80.29

AlexNet Norm 0.21 5.16 0.17 3.95

AlexNet Pool 0.10 5.36 0.05 10.94

AlexNet ReLU/Drop 0.19 6.37 0.12 4.82

GoogLeNet Conv/FC 98.33 69.80 98.94 67.67

GoogLeNet Norm 0.25 2.62 0.20 2.09

GoogLeNet Pool 0.82 16.35 0.46 22.18

GoogLeNet ReLU/Drop 0.60 11.23 0.40 8.07

VGG-16 Conv/FC 99.70 89.23 99.80 88.56

VGG-16 Pool 0.04 2.50 0.02 6.04

VGG-16 ReLU/Drop 0.26 8.27 0.17 5.40

500

1000

1500

2000

2500

Predicted [s]

Actual [s]

VGG-16

Figure 3: VGG-16 actual vs. predicted.

Table 4: End to End Model Validation, NVIDIA Tesla

P100-PCIe.

Network

b ˜ı n

train

test

MAPE [%]

AlexNet 16 150 6 140 3.18

AlexNet 24 170 12 140 6.43

AlexNet 32 200 20 140 3.01

GoogLeNet 16 150 6 140 5.79

GoogLeNet 24 170 12 140 1.09

GoogLeNet 32 200 20 140 2.43

VGG-16 16 150 6 140 3.70

VGG-16 24 170 12 140 2.20

VGG-16 32 200 20 140 3.41

of running only a limited number of small scale exper-

iments, rather than spanning the whole domain where

parameters can attain values.

PSfrag replacements

Iterations

Batch size

Test

Train

Pred.

Execution time [s]

100

120

140

2000

2500

500

1000

1500

AlexNet — n

train

= 6

Figure 4: AlexNet end to end time, n

train

= 6.

Table 4 lists the results obtained with these exper-

iments. The split between training and test set was

performed by setting thresholds on the batch sizes and

numbers of iterations allowed in the former. Every

row corresponds to a model learned on the training

set {(b, i) ∈ B × I : b ≤

b, i ≤ ˜ı}, whose sample size is

train

. For ease of comparison, we used as test set only

the subset of data points that do not appear in any of

the training sets, hence each CNN is associated with

a single test sample size n

test

. All the three CNNs

show good accuracy on the test set, with a worst case

MAPE of 6.43% even when rather small training sets

are used.

Figure 4 reports, as example, a plot depicting the

results obtained with the model learned for AlexNet

using the 6-element training set, which corresponds

to the ﬁrst row in Table 4. Triangles represent the

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

284

100

120

140

Predicted [s]

Actual [s]

AlexNet — n

train

= 6

Figure 5: AlexNet actual vs. predicted, test set, n

train

= 6.

data points in the training set, circles are real measure-

ments in the test set, while crosses are the predictions

given by the linear regression model. The predicted

execution times show a good accordance with the cor-

responding measurements, with a MAPE of 3.18% on

the test set. With this training set, the estimated coef-

ﬁcients are in the order of magnitude of 10

−2

for

and

, while

is in the order of 10

−3

. As the batch

sizes b are typically between 10 and 100 and the num-

ber of iterations i are typically larger than 10000, the

dominant term will be i ·

+ i · b ·

. This outcome

is quite intuitive, since, as discussed previously, the

product i · b quantiﬁes the total number of images fed

into the CNN for processing: the amount of input data

has a major role in determining performance.

In order to provide further intuition on the accu-

racy of the proposed end to end modeling method,

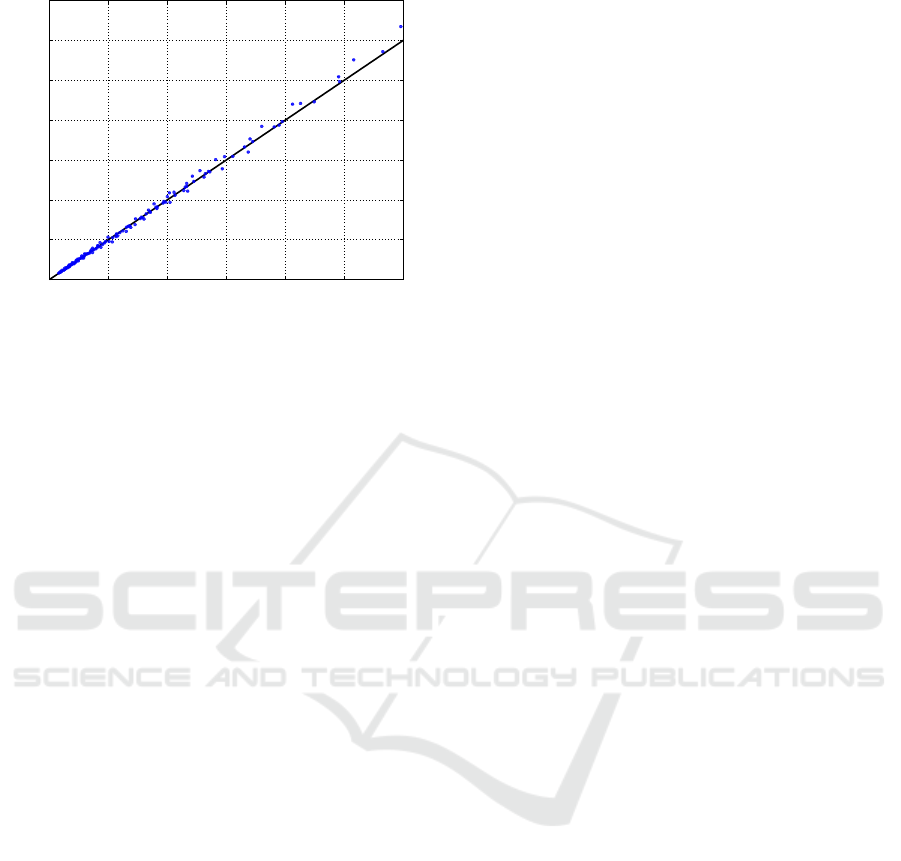
Figure 5 shows the actual vs. predicted plot for test set

data points. The model is again learned for AlexNet

on the training set with n

train

= 6, thus the results

are consistent with Figure 4 and the ﬁrst row of Ta-

ble 4. This ﬁgure allows for visually assessing predic-

tion accuracy, indeed all the blue dots gather closely

around the diagonal, plotted with a solid black line,

proving that prediction errors are small all across the

test set. The behavior in extrapolation remains quite

similar to what observed in Figure 1, where training

could exploit the full data set.

5 CONCLUSION

In this paper we discussed complementary modeling

approaches to predict the performance of DL tech-

niques based on CNNs. When the focus is on gen-

erality, the per layer models devised in our previous

work enable prediction with less than 10% on aver-

age and 23% worst case relative error even when ap-

plied to networks never seen during training, thanks to

their gray box approach. On top of their generaliza-

tion capability, these models also provide insights into

the performance characteristics of CNNs, which we

highlighted in the experimental section. Furthermore,

when users already settled on a speciﬁc network, it is

possible to achieve higher accuracy, with errors as low

as 2%, by switching to end to end models and trading

off generality for improved precision.

ACKNOWLEDGEMENTS

Eugenio Gianniti and Danilo Ardagna’s work has

been partially funded by the ATMOSPHERE project

under the European Horizon 2020 grant agree-

ment 777154.

REFERENCES

Baghsorkhi, S. S., Delahaye, M., Patel, S. J., Gropp, W. D.,

and Hwu, W.-m. W. (2010). An adaptive performance

modeling tool for GPU architectures. In PPoPP, vol-

ume 45, pages 105–114.

Bahdanau, D., Cho, K., and Bengio, Y. (2014). Neural ma-

chine translation by jointly learning to align and trans-

late. CoRR, abs/1409.0473.

Bahrampour, S., Ramakrishnan, N., Schott, L., and Shah,

M. (2015). Comparative study of Caffe, Neon,

Theano, and Torch for deep learning. CoRR,

abs/1511.06435.

Barnes, B. J., Reeves, J., Rountree, B., De Supinski,

B., Lowenthal, D. K., and Schulz, M. (2008). A

regression-based approach to scalability prediction. In

ICS, pages 368–377.

Bitirgen, R., Ipek, E., and Martinez, J. F. (2008). Coordi-

nated management of multiple interacting resources in

chip multiprocessors: A machine learning approach.

In MICRO.

Dao, T. T., Kim, J., Seo, S., Egger, B., and Lee, J.

(2015). A performance model for GPUs with caches.

26(7):1800–1813.

Gianniti, E., Zhang, L., and Ardagna, D. (2018). Perfor-

mance prediction of GPU-based deep learning appli-

cations. In SBAC-PAD.

Gupta, U., Babu, M., Ayoub, R., Kishinevsky, M., Paterna,

F., Gumussoy, S., and Ogras, U. Y. (2018). An on-

line learning methodology for performance modeling

of graphics processors.

Hadjis, S., Zhang, C., Mitliagkas, I., and Ré, C. (2016).

Omnivore: An optimizer for multi-device deep learn-

ing on CPUs and GPUs. CoRR, abs/1606.04487.

Hong, S. and Kim, H. (2009). An analytical model for a

GPU architecture with memory-level and thread-level

parallelism awareness. In ISCA, volume 37, pages

152–163.

Performance Prediction of GPU-based Deep Learning Applications

285

Jia, W., Shaw, K. A., and Martonosi, M. (2012). Stargazer:

Automated regression-based GPU design space explo-

ration. In ISPASS. IEEE.

Kerr, A., Diamos, G., and Yalamanchili, S. (2010). Model-

ing GPU-CPU workloads and systems. In GPGPU-3.

ACM.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

ageNet classiﬁcation with deep convolutional neural

networks. In NIPS.

Lin, M., Chen, Q., and Yan, S. (2013). Network in network.

CoRR, abs/1312.4400.

Liu, W., Muller-Wittig, W., and Schmidt, B. (2007). Perfor-

mance predictions for general-purpose computation

on GPUs. In ICPP. IEEE.

Lu, Z., Rallapalli, S., Chan, K., and La Porta, T. (2017).

Modeling the resource requirements of convolutional

neural networks on mobile devices. In MM. ACM.

Luk, C.-K., Hong, S., and Kim, H. (2009). Qilin: Ex-

ploiting parallelism on heterogeneous multiprocessors

with adaptive mapping. In MICRO. ACM.

Madougou, S., Varbanescu, A., de Laat, C., and van Nieuw-

poort, R. (2016). The landscape of GPGPU perfor-

mance modeling tools. J. Parallel Computing, 56:18–

33.

Sainath, T. N., Kingsbury, B., Saon, G., Soltau, H., Mo-

hamed, A., Dahl, G. E., and Ramabhadran, B. (2015).

Deep convolutional neural networks for large-scale

speech tasks. Neural Networks, 64.

Simonyan, K. and Zisserman, A. (2015). Very deep convo-

lutional networks for large-scale image recognition. In

ICLR.

Song, S., Su, C., Rountree, B., and Cameron, K. W.

(2013). A simpliﬁed and accurate model of power-

performance efﬁciency on emergent GPU architec-

tures. In IPDPS. IEEE.

Srivastava, N., Hinton, G. E., Krizhevsky, A., Sutskever, I.,

and Salakhutdinov, R. (2014). Dropout: A simple way

to prevent neural networks from overﬁtting. JMLR,

15.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (2015). Going deeper with convolutions.

In CVPR. IEEE.

Venkataraman, S., Yang, Z., Franklin, M. J., Recht, B., and

Stoica, I. (2016). Ernest: Efﬁcient performance pre-

diction for large-scale advanced analytics. In NSDI.

Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., and Man-

zagol, P. (2010). Stacked denoising autoencoders:

Learning useful representations in a deep network

with a local denoising criterion. JMLR, 11.

Wang, Y., Zhang, L., Ren, Y., and Zhang, W. (2017). Nexus:

Bringing efﬁcient and scalable training to deep learn-

ing frameworks. In MASCOTS.

Zhang, Y. and Owens, J. D. (2011). A quantitative per-

formance analysis model for GPU architectures. In

HPCA. IEEE.

CLOSER 2019 - 9th International Conference on Cloud Computing and Services Science

286