
Deep Separable Convolution Neural Network for Illumination
Estimation
Minquan Wang
and Zhaowei Shang
College of Computer Science, Chongqing University, No. 174 Shazheng Street, Chongqing, China
Keywords: Illumination Estimation, Deep Convolution Network, Separable Convolution, Global Average Pooling.
Abstract: Illumination estimation has been studied for a long time. The algorithms to solve the problem can be roughly
divided into two categories: statistical-based and learning-based. Statistical-based algorithm has the advantage
of fast computing speed but low accuracy. Learning-based algorithm improve the estimation accuracy to some
extent, but generally have high computational complexity and storage space. In this paper, a new deep
convolution neural network is proposed. We design the network with more layers (11 convolution layers)
than the existing methods, remove the “skip connection” and “Global Average Pooling” is used to replace
“Fully Connection” layer which is commonly used in the existing methods. We use the separable convolution
instead of the standard convolution to reduce the number of parameters. In reprocessed Color Checker Dataset,
compared with the present state-of-the-art the proposed method reduces the average angular error by about
60%. At the same time, using separable convolution and “Global Average Pooling” reduces the number of
parameters by about 86% compared with do not use them.
1 INTRODUCTION
As we all know, image has three main features: color,
texture, and shape. As a global feature, color feature
describes the surface properties of the image or image
region. However, the extraction of color features
needs to be carried out under standard illumination,
so the estimation of illumination (you also can call it
“color constancy”) in the image becomes the top
priority. Although there has been a long history of
research on illumination estimation, it is far from
achieving the goal of "fast and good", and there are
still many problems in practical application.
Currently, illumination estimation algorithms can
be roughly divided into two types: statistical-based
algorithms and learning-based algorithms. Statistical-
based methods estimate parameters based on the
statistical attributes of the image and some
presuppositions, such as Grey-World (Buchsbaum
and Gershon, 1980), Shades-of-Grey (Finlayson et
al., 2004), Grey-Edge (Joost et al., 2007), White-
Patch (Brainard and Wandell, 1986) and so on. The
common advantage of these algorithms is their low
computational complexity. But these methods require
some illumination estimation experience and do not
work well when the scene is complex. Learning-
based methods build model with image features to
estimate illumination. With the development of
machine learning, some techniques have been applied
to build models, such as Gamut mapping (Gijsenij et
al., 2010), Bayesian (Gehler et al., 2008), SVR (Funt
and Xiong, 2006).
They only reduced the error by about 10%
compared with the statistical algorithm, but the
computational complexity was several times or even
tens of times the original.
Figure 1: An example of “illumination estimation”: a color-
casted image I equals a color-corrected image W multiply
the illumination L.
I W L
Ours W and L, err = 0.96
Wang, M. and Shang, Z.
Deep Separable Convolution Neural Network for Illumination Estimation.
DOI: 10.5220/0007684308790886
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 879-886
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
879

State-of-the-art methods are associated with
convolutional neural networks (CNN). Thanks to the
strong fitting ability of CNN, remarkable results have
been achieved. Simone Bianco (Bianco S et al., 2017)
designed a network with a convolution layer 、 a
pooling layer and a full connection layer. At the same
time it use a small patch (32x32) as input to reduce
the amount of computation and use the average of
local results as the global results. It got the best results
of the time, and was very fast. Hu Y (Hu et al., 2017)
fine-tuned the Squeeze Net (Iandola et al., 2016) and
use a big patch (512x512) as input, because the bigger
patch size represents more information and use
squeeze module to reduce the number of parameters.
In general, the research and application of
illumination estimation still face two main problems:
first, whether the accuracy of illumination estimation
can be further improved?
Second, whether the storage space and amount of
calculation of the algorithm can be further reduced?
To address these problems, we propose a new
network with deep separable convolution. First, we
use a deeper network structure which has 11
convolution layers to improve the estimation
accuracy. Then, we use separable convolution
(Chollet, 2017) and “Global Average Pooling” (Lin
M et al., 2013) in the network to reduce the number
of network parameters.
In reprocessed Color Checker Dataset (Shi, 2010),
compared to the state-of-the-art algorithm, the mean
angular error has been reduced by about 60%. And
after using separable convolution and “Global
Average Pooling”, the network parameters are
reduced by about 86%. The storage space of our
method is 0.62MB. So it can be easy used in
equipment of “Internet of things” (IoT) or mobile
device.
2 RELATED WORK
2.1 Illumination Estimation
The goal of “illumination estimation” is to dislodge
the illumination in image. According to Lambertian
reflection (Basri, 2001) theory, the color of the image
is determined by both the pixel value of the image and
the illumination. It can be represented by equation, as
in (1).
I W L=
(1)
I represents the real image we got. And W represents
the white-balanced image and L represents RGB
illumination which is shown in Fig. 1.
( )
( )
( )
R
G
B
R
G
B
MAX
E MAX
MAX
F
E
EF
E
F
==
(2)
“Illumination estimation” is get the image W from
image I. We should build a model f(I)= L. Then we
can get W = I / L. At first, people used statistical-
based algorithm to build models. White-patch
(Brainard and Wandell, 1986) considered that the
maximum pixel value of the three channels of RGB
reflects the illumination color of the image, as in (2).
MAX(F
c
) represents the maximum pixel value of
the channel. The advantage of this method is that it is
easy to calculate, but because of its assumption that
all three channels of RGB should have total reflective
surfaces, it is difficult to satisfy in real life. In general,
the effect of this method is poor.
Gray-World (Buchsbaum and Gershon, 1980) is a
method like White-patch. It considered that the
average pixel value of the three channels of RGB
reflects the illumination color of the image, as in (3).
( )
( )
( )
R
G
B
R
G
B
MEAN
E MEAN
MEAN
F
E
EF
E
F
==
(3)
Compared with White-patch, this method has the
advantage of low computational cost, but the error of
recovery is larger.
In addition to the two methods mentioned above,
there are many similar statistical-based algorithms,
such as Shades-of-Gray (Finlayson et al., 2004),
Gray-Edge (Van De et al., 2007). Because the data set
in the study had a single light intensity and many of
the parameters in these models is built by experience
and reasonable hypothesis, the result of these models
was poor and they have no extensive applicability.
In recent years, learning-based algorithms have
become popular. Gamut mapping (Gijsenij et al.,
2010) calculates a regular gamut of color. For the
image of unknown light source, the mapping between
the gamut of color and the standard gamut of color is
calculated, and the illumination is obtained. Bayesian
(Gehler et al., 2008) and SVR (Funt and Xiong, 2006)
mode the key features such as brightness and
chromaticity distribution of image pixels to estimate
illumination. NIS (Gijsenij and Gevers, 2011) trains
a maximum likelihood classifier to choose method to
estimate illumination. EB (Joze and Drew, 2014)
trains the model by unsupervised learning a model for
each training surface in training images.
These methods are relatively stable and have a
wide range of applications compared to statistical-
based algorithms, and the results are better.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
880

Now, convolution neural network has been used
to solve this problem. CCC (Barron, 2015) extracted
the chromaticity histogram of the image as input and
train the model by a small convolution neural
network. Convolution neural network is introduced to
solve the illumination estimation problem for the first
time, and the results are better than before. However,
because of the simplicity of the network, the effect is
not very good. CNN (Bianco et al., 2017) combined
support vector regression with convolution neural
network. This method solves the problem of multiple
illumination, but because of the simplicity of network
structure, it also does not obtain very good results.
Cheng (Cheng et al., 2014) used principal component
analysis to estimate the illumination in spatial
domain. DS-Net (Shi, 2016) trained a two-branch
structure network and chooses an estimate from
among the hypotheses. Oh (Oh, 2017) transformed
illumination estimation into a classification problem.
Fc4 (Hu, 2017) fine-tuned the Squeeze Net (Iandola,
2016) with confidence-weighted pooling and up to
now got the best result. They all get a good result by
using convolution neural network, but some layers
such as “Fully Connection” in these networks lead to
a waste of storage space.
2.2 Separable Convolution
Convolution layer is the core of convolution neural
network. The traditional way of convolution is well
known, and the study of it has never stopped. AlexNet
(Krizhevsky, 2012) used “group convolution” to
reduce the computation of network. ResNet (He,
2016) used “skip connection” to make it possible for
deep networks to be trained. However, these networks
all use standard convolution which is shown in Fig.
2(a).
We can see that the correlation between the
channel and the space of the feature map is considered
at the same time. There is a question why we consider
them at the same time? So, separable convolution
(Chollet, 2017) which is shown in Fig. 2(b) is
designed to solve it. In Fig. 2, we can see that the
number of parameters are reduced about 50% when
use separable convolution.
In (4), there are feature maps which have size
**H W N
and the kernel is
*KK
and the channel of
output is
M
.
( )
2
22
11
K M HWN
Separable
conv K MHWN M K
+
= = +
(4)
In network, the computation of network can be
reduced about
2
11
MK
+
when use separable convolution.
(a) Standard convolution
(b) Separable convolution
Figure 2: The difference between standard convolution and
separable convolution.
2.3 “Global Average Pooling”
In NIN (Network in Network) (Lin, 2013), authors
came up with a lot of interesting ideas. One of them
is the correlation analysis of replacing “Fully
Connection” with “Global Average Pooling”. In the
classification task, we all know that using the “Fully
Connection” layer can improve the network
performance to some extent, but it has a huge
disadvantage that the number of parameters is too
large. Large amount of parameters will lead to a waste
of time and storage space in training and testing, and
there will be over-fitting problem. “Global Average
Pooling” uses the average of features map to replace
them as output. This not only reduces the number of
parameters, but also gives practical meaning to each
channel. The details about “Fully Connection” and
“Global Average Pooling” are shown in Fig. 3.
Input
Kernel
3x3
Feature
maps
Input
Kernel
3x3
Depthwise
feature
Depthwise conv
Depthwise
feature
Kernel
1x1
Pointwise
feature
Pointwise conv
Deep Separable Convolution Neural Network for Illumination Estimation
881

(a) “Fully Connection”
(b) “Global Average Pooling”
Figure 3: The difference between “Fully Connection” and
“Global Average Pooling”.
3 PROPOSED METHOD
In training, we transform all images into patches and
the size of them is 64x64. The label of them is the
same as the label of image which they belong to. Then
we randomly choose 20,000 of them as training set to
train the model.
In testing, test image is transformed into patched
which have the same as training set. And all of them
are put into the model and get a result to build a local
illumination map. Then we get the median of the map
as the estimated illumination of the image. The
procedure is shown in Fig. 4.
Figure 4: The procedure of proposed method.
Figure 5: The difference between our modules.
3.1 Network Structure
3.1.1 Basic Module
We use basic convolution module as the basic unit of
network structure such as ResNet module (He, 2016),
Xecption module (Chollet, 2017). In designing the
structure of module, we refer to the above two
structures. But compared with them, we use separable
convolution instead of standard convolution and
remove “skip connection” from module. Because
“skip connection” not only transmits useful
information, but also becomes the bridge of noise
transmission. And we've proved through experiments
that with skip connection, the effect is very bad. The
corresponding experimental results are shown in
Table 3. Using separable convolution can reduce
number of parameters. The difference between our
modules is shown in Fig. 5. The corresponding
experimental results are shown in Table 4.
3.1.2 Network
We design a convolution neural network which has
11 convolution layer (contain 4 modules). At the
architectural level, we mainly draw on two important
ideas of VGG [24]. The first is to replace the large
convolution kernel with the small convolution kernel.
The second is to increase the number of feature maps
while reducing the size of feature maps. In tiny
networks, it is important to have enough number of
channels to process the information (Zhang, 2017).
Some details of the network structure are shown in
Table 1 and Fig. 6.
In the network, we get a patch with size (64x64x3)
as input. Then we use two standard convolution layers
followed by four basic modules. At the end of
network, we use a standard convolution layer to
change the channel of output into three. We use GAP
(Global Average Pooling) to replace the Flatten and
“Fully Connection” layer.
This kind of network structure design is a result
that we get the best performance after a lot of
experiments. According to the hardware equipment
and the actual pursuit of the effect can be adjusted
appropriately. The corresponding experimental
results are shown in Fig. 7.
3.1.3 Difference from Other Methods of
using CNN
Compared with the other methods of using CNN
(convolution neural network) to solve the
illumination estimation problem the network
structure we designed has the following difference.
Fully
Connection
Outputs
Feature
maps
Flatten
Average
Outputs
Feature
maps
Images
Patches
Training set
Randomly select 20000
CNN model
Training
Test input
Testing
Patches
One test image
Everyone is used
Local
illumination
map
Output
Global
estimated
illumination
Median
Train Test
SeparableConv
ReLU
SeparableConv
Maxpooling
Conv
Add
Conv
ReLU
Conv
Add
SeparableConv
ReLU
SeparableConv
Maxpooling
ResNet Module
Xecption Module
Proposed Module
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
882
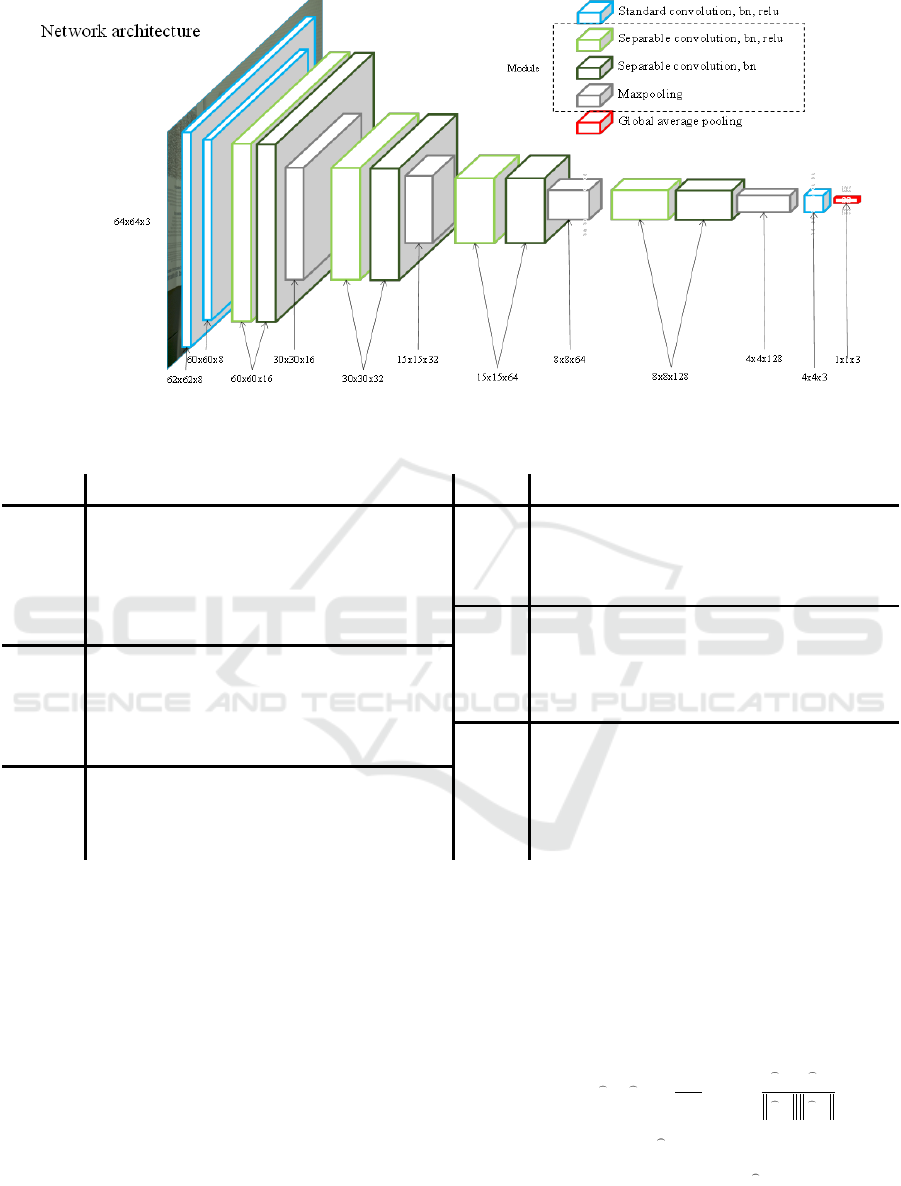
Figure 6: Architecture of our deep separable convolution. We show the different operation by using different color.
Table 1: The details of our network.
Operation
Output
Parameters
Operation
Output
Parameters
Input
-
64x64 , 3
-
3
st
module
3x3 Separable Conv ,
Bn, Relu
15x15 , 64
2,592
Label
-
1x1 , 3
-
3x3 Separable Conv , Bn
15x15 , 64
4,928
1
st
layer
3x3 Conv , Bn, Relu
62x62 , 8
248
Maxpooling
8x8 , 64
-
2
st
layer
3x3 Conv , Bn, Relu
60x60 , 8
608
4
st
module
3x3 Separable Conv ,
Bn, Relu
8x8 , 128
9,280
1
st
module
3x3 Separable
Conv , Bn, Relu
60x60 , 16
264
3x3 Separable Conv , Bn
8x8 , 128
18,048
3x3 Separable
Conv , Bn
60x60 , 16
464
Maxpooling
4x4 , 128
-
Maxpooling
30x30 , 16
-
Last
layer
3x3 Conv
4x4 , 3
3,459
2
st
module
3x3 Separable
Conv , Bn, Relu
30x30 , 32
784
Output
Global average pooling
1x1 , 3
-
3x3 Separable
Conv , Bn
30x30 , 32
1,440
Maxpooling
15x15 , 32
-
Compared with (Barron, 2015) and (Bianco,
2017), a deeper network is designed. Because we
have the experience that more parameters have better
fit ability. And in the same number of parameters, a
“thin and deep” network works well than a “fat and
shallow” network. The reason is a “thin and deep”
network can transform the problem into some small
problems to solve by modules. And we always want
to solve small problems, the network is also.
Compared with (Hu, 2017), the basic module of
network is different and (Hu, 2017) uses transfer
learning to train network. We train the network by
initialization. Of course, another main difference is
the comprehension about building a simple network.
3.2 Loss Function
We train the network by minimizing the loss function
which can be called angular error. The loss function
is shown as in (5). It obtains the angle error between
the real illumination vector and the predicted
illumination vector.
( )
180
, arccos
PP
gp
L
PP
gp
PP
gp
•
=
(5)
In the loss function,
P
g
represents the normalized
result of the real value and
P
p
represents he
normalized result of the output of the network.
Deep Separable Convolution Neural Network for Illumination Estimation
883
Table 2: Compared to the other methods (in degree).
Mean
Med
Tri
Best 25
Worst 25
95% Quant
GW
6.36
6.28
6.28
2.33
10.58
11.30
WP
7.55
5.68
6.35
1.45
16.12
-
SG
4.93
4.01
4.23
1.14
10.23
11.90
GE
5.13
4.44
4.62
2.11
9.26
-
GM
4.22
2.33
2.91
-
-
-
Bayesian
4.82
3.46
3.88
1.26
10.49
-
SVR
7.99
6.67
-
-
-
14.61
NIS
4.19
3.13
3.45
1.02
9.22
11.7
EB
2.77
2.24
-
-
-
5.52
Cheng
3.52
2.14
2.47
0.50
8.74
-
CCC
1.95
1.22
1.38
0.35
4.76
5.85
CNN
2.36
1.98
-
-
-
-
SqueezeNet-FC
4
1.65
1.18
1.27
0.38
3.78
4.73
DS-Net
1.93
1.12
1.33
0.31
4.84
5.99
Oh
2.16
1.47
1.61
0.37
5.12
-
DSCNN
0.67
0.49
0.52
0.16
1.52
1.86
4 EXPERIMENTS AND RESULTS
We have done a lot of experiments to verify the
correctness and effectiveness of our method. In
addition to verifying the effect of the method, we also
verify the setting of some super parameters in the
method through experiments.
4.1 Experimental Setting
We built the whole network through the Keras
framework. To train the network, we use Adam
(Kingma, 2014) to minimize the loss function. All of
the parameters are initialized by “glorot_uniform”
(Glorot, 2010), and to prevent overfitting, we add L2
regularization to all convolution parameters. We train
the network for 200 epochs. In the top 50 epoch, we
use a learning rate of 0.001. In 50 to 150 epoch, we
use a learning rate of 0.0001. In the last 50 epoch, we
use a learning rate of 0.00005.
4.2 Datasets
We use the reprocessed Color Checker Dataset (Shi,
2000) for benchmarking. The dataset has 568 images.
These images were got by using two high quality
DSLR cameras (Canon 5D and Canon1D) with all
settings in auto mode. Using the advice of the authors
of the dataset, each image needs to be subtracted from
the black level in order to solve the color constancy
problem. For the Canon 5D the black level is 129 and
for the Canon 1D it is zero. In all images, there is a
Macbeth Color Checker (MCC) to show the ground
truth illumination color. Because it contains a lot of
color information and our network is learning color
features, we set these pixels of MCC to zero.
We cut the original image to a patch with the size
64x64. We randomly selected 20, 000 patches as the
training set. In training, we selected 2/3 of them for
training and the remaining 1/3 for validation. And the
size of batch is 128.
4.3 Evaluation Criterion
We use it as an evaluation criterion by calculating the
angle between the estimated and real value of the
illumination. The same as Hu Y (Hu et al., 2017), we
get the error matrix of the 568 images and report the
following statistics: mean, median, tri-mean of all the
errors, mean of the lowest 25% of errors, mean of the
highest 25% of errors and 95% Quant. 95% Quant
means 95 percent of the errors is smaller than this
value.
4.4 Experiments
4.4.1 Compared to Other Methods
We selected five statistics-based and ten learning-
based algorithms as benchmark algorithms. The
statistics-based algorithms are: Gray-World (GW),
White-Patch (WP), Shades-of-Gray (SG), Gray-Edge
(GE). The learning-based algorithms are: Gamut
Mapping (GM), Bayesian, SVR, Natural-Image-
Statistics (NIS), Exemplar-Based Color Constancy
(EB), Cheng et al., (2014), CCC, CNN, FC4, DS-Net,
Oh. We show the results in Table 2.
The results show that most of the learning-based
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
884

methods are better than those based on statistics,
which proves that the learning-based method can
better extract the color features of images. Moreover,
the proposed method is superior to the current optimal
algorithm in all evaluation indexes. The average error
is reduced by about 60%. There are two reasons why
we are able to make such a huge advance. First,
compared to most of the CNN-based algorithms, in
our algorithm the depth and width of the network are
guaranteed. This makes the network strong enough to
express feature. Second, compared to the algorithm
which have more parameters like Hu Y (Hu et al.,
2017), the selection of our network structure and the
number of parameters is appropriate. And we do not
use transfer learning to train our model. This avoids
the impact of other types of data.
4.4.2 Whether “Skip Connection” Is Used or
Not
In the design of deep convolution neural network,
“skip connection” is a good technique to ensure the
convergence of the network. However, “skip
connection” is not suitable for all tasks. In
illumination estimation, because of the small amount
of data, if “skip connection” is introduced, it will
propagate noise, which is not good for network
training. In Table 3, we experimented with whether to
add “skip connection” and found that the results were
the same as we had expected.
Table 3: Compare between whether use “skip connection”.
Mean error
YES
0.74
NO
0.67
4.4.3 Effects of Some Super Parameters
It is very important to set some super parameters in
convolutional neural networks. If improper super
parameters are selected, the effect of the whole
network may be very poor or the network is difficult
to converge. Therefore, it is more reliable to
determine some of the parameters by experiment than
to select them directly from experience.
In Fig. 7(a), we can see that when the size of patch
is bigger than 64, there is no significant improvement
in performance. And as we all know, the computation
of neural network is gradual improvement. So, we
choose 64 as our input.
In Fig. 7(b), we can see that when the number of
modules is bigger than 4, there is no significant
improvement in performance. And as we all know,
the computation of neural network is gradual
improvement. So, we choose 4 to build network.
(a) Abscissa axis expresses the size of patch. Vertical axis
expresses the mean angular error and the evaluation time for one
image.
(b) Abscissa axis expresses the number of blocks. Vertical axis
expresses the mean angular error and the evaluation time for one
image. The size of patch is 64. When use five modules, we remove
the pooling layer from the last module.
Figure 7: Results about effects of “size of patch” and
“number of modules”.
4.4.4 Cost of Storage Space
Compared with the current algorithms, we want to get
a better and faster model. So when we design the
network, we change the convolution layer and the
“Fully Connection” layer, which contain a lot of
parameters. We use separable convolution instead of
standard convolution and remove the “Fully
Connection” layer.
Table 4: Cost of storage space.
Mean
error
Conv
layers
Storage
space
SqueezeNet-FC
4
1.65
26
35.2MB
Proposed(standard)
0.47
11
3.56MB
Proposed(separable)
0.67
11
0.62MB
Because we do not use “Fully Connection” and
less convolution layers, the cost of storage space is
reduced by about 90%. At the same time, using
separable convolution replace standard convolution
can reduce storage space by about 86% at the cost of
error increased from 0.47 to 0.67.
5 CONCLUSIONS
In this paper, we propose a new algorithm to solve the
illumination estimation problem. Due to the shallow
network used in the current convolution neural
network methods, we design a deeper convolutional
Deep Separable Convolution Neural Network for Illumination Estimation
885

neural network and obtain good results. The average
angle error on the reprocessed Color Checker Dataset
is reduced by about 60%. In addition, we use the
separable convolution and “Global Average Pooling”
to reduce the computational complexity of the
network and the storage space of the network by
about 86%. Further improvement of estimation
accuracy and estimation of multi-scale illumination
will be the focus of our future work.
REFERENCES
Shi L. Re-processed version of the gehler color constancy
dataset of 568 images[J]. http://www. cs. sfu. ca/~
colour/data/shi_gehler/, 2000.
Buchsbaum, Gershon. "A spatial processor model for object
colour perception." Journal of the Franklin institute
310.1 (1980): 1-26.
Finlayson, Graham D., and Elisabetta Trezzi. "Shades of
gray and colour constancy." Color and Imaging
Conference. Vol. 2004. No. 1. Society for Imaging
Science and Technology, 2004.
Van De Weijer, Joost, Theo Gevers, and Arjan Gijsenij.
"Edge-based color constancy." IEEE Transactions on
image processing 16.9 (2007): 2207-2214.
Brainard D H , Wandell B A . Analysis of the retinex theory
of color vision.[J]. Journal of the Optical Society of
America A-optics Image Science & Vision, 1986,
3(10):1651-1661.
Gijsenij A , Gevers T , Weijer J V . Generalized Gamut
Mapping using Image Derivative Structures for Color
Constancy[J]. International Journal of Computer
Vision, 2010, 86(2-3):127-139.
Gehler P V, Rother C, Blake A, et al. Bayesian color
constancy revisited[C]// IEEE Conference on Computer
Vision & Pattern Recognition. 2008.
Funt B, Xiong W. Estimating Illumination Chromaticity via
Support Vector Regression[C]// Color & Imaging
Conference. 2006.
Bianco S., Cusano C., Schettini R. Single and Multiple
Illuminant Estimation Using Convolutional Neural
Networks[J]. IEEE Transactions on Image Processing,
2017, 26(9):4347-4362.
Hu Y , Wang B , Lin S . FC^4: Fully Convolutional Color
Constancy with Confidence-Weighted Pooling[C]//
IEEE Conference on Computer Vision & Pattern
Recognition. IEEE Computer Society, 2017.
Iandola F N, Han S, Moskewicz M W, et al. SqueezeNet:
AlexNet-level accuracy with 50x fewer parameters and
<0.5MB Model Size[J]. 2016.
Chollet, François. "Xception: Deep learning with depthwise
separable convolutions." arXiv preprint (2017): 1610-
02357.
Lin M , Chen Q , Yan S . Network In Network[J]. Computer
Science, 2013.
Basri, Ronen, and David Jacobs. "Lambertian reflectance
and linear subspaces." Computer Vision, 2001. ICCV
2001. Proceedings. Eighth IEEE International
Conference on. Vol. 2. IEEE, 2001.
Gijsenij A, Gevers T. Color constancy using natural image
statistics and scene semantics[J]. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 2011,
33(4): 687-698.
Joze H R V, Drew M S. Exemplar-based color constancy
and multiple illumination[J]. IEEE transactions on
pattern analysis and machine intelligence, 2014, 36(5):
860-873.
Barron J T. Convolutional color constancy[C]//
Proceedings of the IEEE International Conference on
Computer Vision. 2015: 379-387.
Bianco S, Cusano C, Schettini R. Single and multiple
illuminant estimation using convolutional neural
networks[J]. IEEE Transactions on Image Processing,
2017, 26(9): 4347-4362.
Cheng D, Prasad D K, Brown M S. Illuminant estimation
for color constancy: why spatial-domain methods work
and the role of the color distribution[J]. JOSA A, 2014,
31(5): 1049-1058.
Shi W, Loy C C, Tang X. Deep specialized network for
illuminant estimation[C]// European Conference on
Computer Vision. Springer, Cham, 2016: 371-387.
Oh S W, Kim S J. Approaching the computational color
constancy as a classification problem through deep
learning[J]. Pattern Recognition, 2017, 61: 405-416.
Krizhevsky A, Sutskever I, Hinton G E. Imagenet
classification with deep convolutional neural
networks[C]// Advances in neural information
processing systems. 2012: 1097-1105.
He K, Zhang X, Ren S, et al. Deep residual learning for
image recognition[C]// Proceedings of the IEEE
conference on computer vision and pattern recognition.
2016: 770-778.
Simonyan K, Zisserman A. Very deep convolutional
networks for large-scale image recognition[J]. arXiv
preprint arXiv:1409.1556, 2014.
Kingma D P, Ba J. Adam: A method for stochastic
optimization[J]. arXiv preprint arXiv:1412.6980, 2014.
Glorot X, Bengio Y. Understanding the difficulty of
training deep feedforward neural networks[C]//
Proceedings of the thirteenth international conference
on artificial intelligence and statistics. 2010: 249-256.
Zhang X , Zhou X , Lin M , et al. ShuffleNet: An Extremely
Efficient Convolutional Neural Network for Mobile
Devices[J]. 2017.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
886
