Contextual Action with Multiple Policies Inverse Reinforcement
Learning for Behavior Simulation
Nahum Alvarez and Itsuki Noda
National Institute of Advanced Industrial Science and Technology, Japan
Keywords:
Inverse Reinforcement Learning, Behavioral Agents, Pedestrian Simulation.
Abstract:
Machine learning is a discipline with many simulator-driven applications oriented to learn behavior. However,
behavior simulation it comes with a number of associated difficulties, like the lack of a clear reward function,
actions that depend of the state of the actor and the alternation of different policies. We present a method
for behavior learning called Contextual Action Multiple Policy Inverse Reinforcement Learning (CAMP-IRL)
that tackles those factors. Our method allows to extract multiple reward functions and generates different
behavior profiles from them. We applied our method to a large scale crowd simulator using intelligent agents
to imitate pedestrian behavior, making the virtual pedestrians able to switch between behaviors depending of
the goal they have and navigating efficiently across unknown environments.
1 INTRODUCTION
Simulation applications like traffic simulators or
robotic manipulators, have been benefited from ma-
chine learning techniques since the arrival of the big
data and deep learning. Crowd simulation are another
example, and have been the object of interest because
it can deal with a number of real-life problems in our
society. Pedestrian simulation can help to the design
of evacuation strategies and identifying risky situa-
tions in concrete scenarios like natural disasters or ter-
rorist incidents as it can be seen in (Yamashita et al.,
2009) or (L
¨
ammel et al., 2010).
Crowd simulators have been approached by di-
verse machine learning potential solutions as well,
tackling different problems like trajectory planning,
crowd micro behavior and others. In our case, we are
interested in pedestrian simulation used for predict-
ing business performance and city planning. How-
ever, walking behavior has not been the subject of so
much research, mainly because its inherent character-
istics: like any other living being behavior, it is goal
driven, but its reward function is unknown, humans
usually do not take the most optimal route, and even
congestion can be seen as a positive factor (Crociani
et al., 2016); also it is composed of different patterns
that act at the same time, being able to switch the cur-
rent goal for another.
Inverse Reinforcement Learning techniques help
in solving those issues, as they work by obtaining the
hidden reward function from a set of observed behav-
iors provided by an expert. In our case we developed a
variant of bayesian inverse reinforcement learning for
multiple reward functions and adapted it to work with
contextual actions, as the pedestrians are expected to
show different behaviors depending on their current
goal, and have different available actions depending
on their location, having an exponentially large set of
different actions. We called this method ”Contextual
Action Multiple Policy Inverse Reinforcement Learn-
ing”, or CAMP-IRL. The technique allows to evaluate
different sets of actions depending on the state of the
pedestrian, and also extracts different behavior pat-
terns called profiles.
This work is organized as follows: Section 2 con-
tains a review of previous work on reinforcement
learning used for agent behavior and pedestrian sim-
ulators. Section 3 presents our CAMP-IRL method,
and section 4 describes our pedestrian simulator and
the behavioral model of the agents generated by it.
Section 5 present our preliminary tests and discusses
their results. Finally, section 6 contains the conclu-
sions of our research.
2 RELATED WORK
Apprenticeship learning methods have been widely
used in intelligent agents’ systems to train them to
perform tasks in dynamic environments like (Siebra
Alvarez, N. and Noda, I.
Contextual Action with Multiple Policies Inverse Reinforcement Learning for Behavior Simulation.
DOI: 10.5220/0007684908870894
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 887-894
ISBN: 978-989-758-350-6
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
887

and Neto, 2014) or (Svetlik et al., 2016). We can
observe strategies to emulate predefined driving be-
haviors in (Faccin et al., 2017). There are also works
where agents are given a behavior cognitive model for
pedestrians like in (Luo et al., 2008), (Martinez-Gil
et al., 2017) or (Crociani et al., 2016). However, in
those works the behavior model is predefined by a de-
signer, having a low degree of flexibility, being tied to
its domain, or even escalating badly.
An extra issue in simulating people’s behavior is
that the reward function governing their actions will
be often hidden. We can avoid this problem using in-
verse reinforcement learning (here on after IRL) be-
cause instead a reward function, it only needs a set of
observed expert demonstration behaviors.
IRL works well on domains where the reward
function is hidden, being appropriate to model animal
and human behavior (Ng et al., 2000). IRL techniques
work on domains that can be defined by a Markov
Decision Process (MDP, from here on after) and are
used to learn its hidden reward function. MDPs are
defined by a tuple M = {S,A,T , γ, r}, where S is the
state space of the model, A is the set of actions that
can be performed, T is the transition function, which
returns the probability of transition from one state to
other given a concrete action, and usually is given in
the form of a matrix, r is the reward function that gen-
erates a reward value from reaching a state, and γ is
a discount factor, that applies when calculating accu-
mulated reward through consecutive actions. In IRL,
r is unknown so a set of expert trajectories T is used
to obtain it, each on of the trajectories consisting on a
sequence of states and actions pairs.
We can find many different approaches to IRL,
each one with its own characteristics and issues
(Zhifei and Meng Joo, 2012). For example, we find a
linearly solvable approach in (Kohjima et al., 2017),
with a number of constraints in the MDP defini-
tion, or the Maximum Entropy method contained in
(Ziebart et al., 2008), which works well when we do
not have much information about the solution space.
Other methods have obtained better results under cer-
tain conditions, like (Dvijotham and Todorov, 2010)
which works on a subset of MDPs, but it does not
match well with our domain, or (Levine et al., 2011)
which deals with non-linear reward functions.
Works using IRL to learn agent behavior are
sparse but effective, as it is shown in (Abbeel and Ng,
2004) where driving styles are learned by an agent, or
(Natarajan et al., 2010) where different agents work
together for routing traffic.
In our domain, we have the additional requirement
of obtaining different patterns from the existing data.
The task of obtaining multiple policies from the IRL
process is a desirable characteristic, as the observed
trajectories come from different pedestrians with dif-
ferent goals and creating a combined reward function
for all of them would mix different behaviors that may
not be optimal for a concrete goal or even be antag-
onistic to it. Other works have previously dealt with
this aspect, like (Surana and Srivastava, 2014), show-
ing how to switch between different MDP and obtain
their related policy functions and works well extract-
ing different behaviors. In (Michini and How, 2012)
divides the data in smaller sub-goals in order to ob-
tain simple reward functions, and (Krishnan et al.,
2016) describes a hierarchical method for selecting
MDP partitions with different policies for each sub-
MDP, which can be interesting for domains where the
agent has a number of sequential small sub-goals. Our
CAMP-IRL method is based in (Choi and Kim, 2012)
which works extracting a number of clusters from the
data, obtaining their reward and policy functions, but
we include contextual actions that are different for
each state of the MDP, used to avoid an explosion in
the solution space by cutting redundant actions.
3 THE CAMP-IRL METHOD
IRL techniques work on domains that can be modeled
by a Markov Decision Process (MDP) but have hid-
den reward functions (the reward function dictates the
gain from performing a given action in a given state).
Hence, it is ideal to model human behavior, which
usually is reward driven using unknown reward func-
tions. However human behavior is not only directed
by only one goal but many, with different rewards that
are managed at the same time, IRL has potential to
learn different behavior patterns, but need some adap-
tation as works with single rewards and well defined
actions. We based our method in a non-parametric
Bayesian approach to the problem (Choi and Kim,
2012) extracting a number of clusters from the data,
obtaining different reward and policy functions for
each one of them. Also, we adapted the MDP to be
able to work with this model in our domain includ-
ing contextual actions for the agents, used to avoid an
explosion in the solution space by cutting redundant
actions.
We define Contextual Action Multiple Policy
MDP (CAMP-MDP) as an MDP {S ,A,T ,γ,R } us-
ing the standard definition of S as the set of states,
the transition function T (s, A(s), s’ ) from one state
to another by executing an action, and γ as the dis-
count factor. We also defined the super set A(s) of
actions as a function of an state s, and R (s,π) as a
Reward function where s ∈ S and π is a policy that
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
888

Figure 1: The CAMP-IRL method intuitively depicted. A reward function is trained from the trajectories in the form of a
weight vector, and is used to assign them to groups. Each group learns a policy from their updated reward function that in the
end generates a value vector. In the end, we obtain a set of weight/value vectors couples that will be used later to control an
agent.
contains a list of consecutive pairs of states and ac-
tions in the form s,a where a ∈ A(s). This means that
available actions are dependent of the state (i.e., con-
textual), because each location has a different number
of possible paths to take; when translating the loca-
tions to states and paths to actions, there will be cer-
tain actions only available to certain states. We also
do this in order to avoid a combinatorial explosion in
the solution space, reducing the number of possible
actions for each state. Finally, each state has a set of
features, which influence how the reward function is
calculated.
The CAMP-IRL algorithm uses a Dirichlet pro-
cess (Neal, 2000) to classify the trajectories into dif-
ferent groups we call profiles, and then a reward func-
tion is calculated for each profile using a Bayesian ap-
proach to the IRL method. However, we modified it
to be able to work with the CAMP-MDP considering
that each state will have a different action set. Figure
1 depicts how the CAMP-IRL algorithm works in an
intuitive manner. The algorithm follows the next steps
and formulas:
1. Initialize the profile set C containing K elements
and the reward set {r}
K
k=1
.
(i) The initial clusters (profiles) and their reward
function are randomized. The reward func-
tion consists in a weight vector containing the
weights of all the map features.
(ii) An initial policy is generated randomly from
each reward. This policy consists in a vector
containing the optimal action to perform for
each node, and it is obtained by calculating the
value of performing the most optimal action a
from the available actions in the state s follow-
ing the next function:
V
∗
(s) = max
a∈A(s)
R (s, a) + γ
∑
s
0
∈S
T (s, a, s
0
)V
∗
(s
0
)
2. For each element m in the trajectory set, select
a new profile candidate c
∗
m
using the following
rules:
(i) If the trajectory has no assigned profile, gener-
ate a new one and a reward function for it
(ii) If it has one, obtain the most populated profile
(iii) Assign the trajectory to the new profile with
probability:
P(X
m
|c
∗
m
)
P(X
m
|c
m
)
3. For each class k:
(i) Create a weight vector candidate
r
∗
k
= r
k
+
τ
2
2
∇log(P(X
k
|r
k
)P(r
k
)) + τα
where τ is a scaling factor and α is a random
number sampled from a multinomial distribu-
tion (0,1).
(ii) Update the weight vectors with probability
P(X
k
|r
∗
k
)P(r
∗
k
)g(r
∗
k
,r
k
)
P(X
k
|r
k
)P(r
k
)g(r
k
,r
∗
k
)
being the function g() the gradient from the
Langevin algorithm calculated as follows:
g(x,y) =
exp

−1
2 τ
2



x − y −
τ
2
2
∇log(P(X
k
|x)P(x))




(2πτ
2
)
D/2
where τ is a scaling factor.
4. Repeat the process from (2) until convergence.
Once finished, it is possible to use the obtained
Contextual Action with Multiple Policies Inverse Reinforcement Learning for Behavior Simulation
889

set of optimal policies for each profile to calculate
the value vector as follows:
V
π
(s) = R (s,π) + γ
∑
s
0
∈S
T (s, π, s
0
)V
π
(s
0
)
This value represents the expected reward of exe-
cuting that policy π on a node s.
In order to use this method for pedestrian pre-
diction, we created a CAMP-IRL module that in-
terfaces with a crowd simulator called CrowdWalk
where each pedestrian is represented by an agent.
CrowdWalk can simulate movements of more than
1 million agents in a diverse array of locations, like
multi-storied buildings or large city areas. Maps can
be created by hand or obtained from open source for-
mats, like Open Street Maps
1
, and it is possible to
control agents from external modules.
The model of the map used by CrowdWalk con-
sists in a custom xml that describes the map in the
form of network where nodes represent intersections
and links represent paths, which in our CAMP-MDP
will represent as well as states and actions, respec-
tively. The contextual actions are created using the
number of links each node has, with one action per
link, being semantically different for each node; thus,
the first action in certain state will be different from
the first action in another one, but will have the same
label. Links also have length and width attributes in-
fluencing how long the agents need to walk from a end
to another and how many agents can walk in parallel.
Nodes have features describing what facilities are on
that location, which are represented by the state fea-
tures in the CAMP-MDP.
CrowdWalk has an Agent handler that generates
one agent per pedestrian, using a model with dual
behavior: micro and macro behavior (Torrens et al.,
2012). Micro behavior in in charge of the collision
detection and the agent’s velocity, adjusting itself to
the crowd. The macro behavior deals with the agent’s
route to its goal. Our CAMP-IRL module takes care
of the macro behavior. We called the agents created
by this module CAMP-IRL Agents.
The inputs of the CAMP-IRL method are the
map used by CrowdWalk, which is converted into a
CAMP-MDP, and a file containing the trajectories we
want to train. Once the training process finishes, we
obtain two files: one containing the weights of the
features of each discovered profile, and another con-
taining the value of each map node (as defined in the
step 4 of the algorithm) for each profile. The weight
and value files will be used in the simulation by the
CAMP-IRL agents to decide which path to take, and
to select the behavior profile they should have.
1
https://www.openstreetmap.org
The training method is performed before the sim-
ulation as a pre-processing task, so even if it can take
a long time depending of the complexity of the map
it does not represent a big impact in the simulation
speed as the decision process of the agents once we
have these files is enough fast to use it in real time.
4 THE CAMP-IRL AGENTS
Once the simulation starts, the Agent Controller Mod-
ule generates the CAMP-IRL agents. The agent be-
havior is directed using three input files: the first two
files are the weight and value files from the CAMP-
IRL process we described in the previous section, and
the third one consists in a goal database containing
the locations they will “want” to visit. Those can be
generic features, like “visiting a restaurant”, or con-
crete nodes from the map, like “visiting the node la-
beled as nd00327”. Also, this file contains an evacu-
ation point, where the agent will go after completing
its goals.
The decision making process of the CAMP-IRL
agent is shown in Figure 2. First, the agent selects
the profile that has the highest weight for the features
associated to its goals. As the agent may have mul-
tiple goals and also the weights may be similar, the
agent first selects a set composed of the profiles that
are within a threshold from the one with the highest
weight. From our experiments, we concluded that a
10% of threshold gives the best results. The set of
selected profiles forms the agent’s profile list. Once
completed this step, the agent chooses from its list
the profile with the highest value in its starting node
according to the value file.
Whenever an agent enters in a node, it checks if
that node contains a goal in its list or not. In case it is
not a goal, the agent compares the value of the nodes
connected to the current one and chooses one within
the set of best valued ones. This set is created again
using a threshold range from the highest valued node,
and also a threshold of a 10% laid the best results. The
selection of the best valued nodes ignores the node the
agent is coming from, under the rationale of the agent
coming from a node with an already high value and
having to conform with lower values after that. Once
the best node to go is selected, the agent moves to it.
If the agent is in a node containing a goal, then the
agent enters in a waiting state, simulating the agent
taking time in satisfying its goal. The goal satisfac-
tion time is given by another training process, apart
from the CAMP-IRL process, that consists in a lin-
ear regression method to learn from the waiting times
present in the trajectories, estimating the time from
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
890

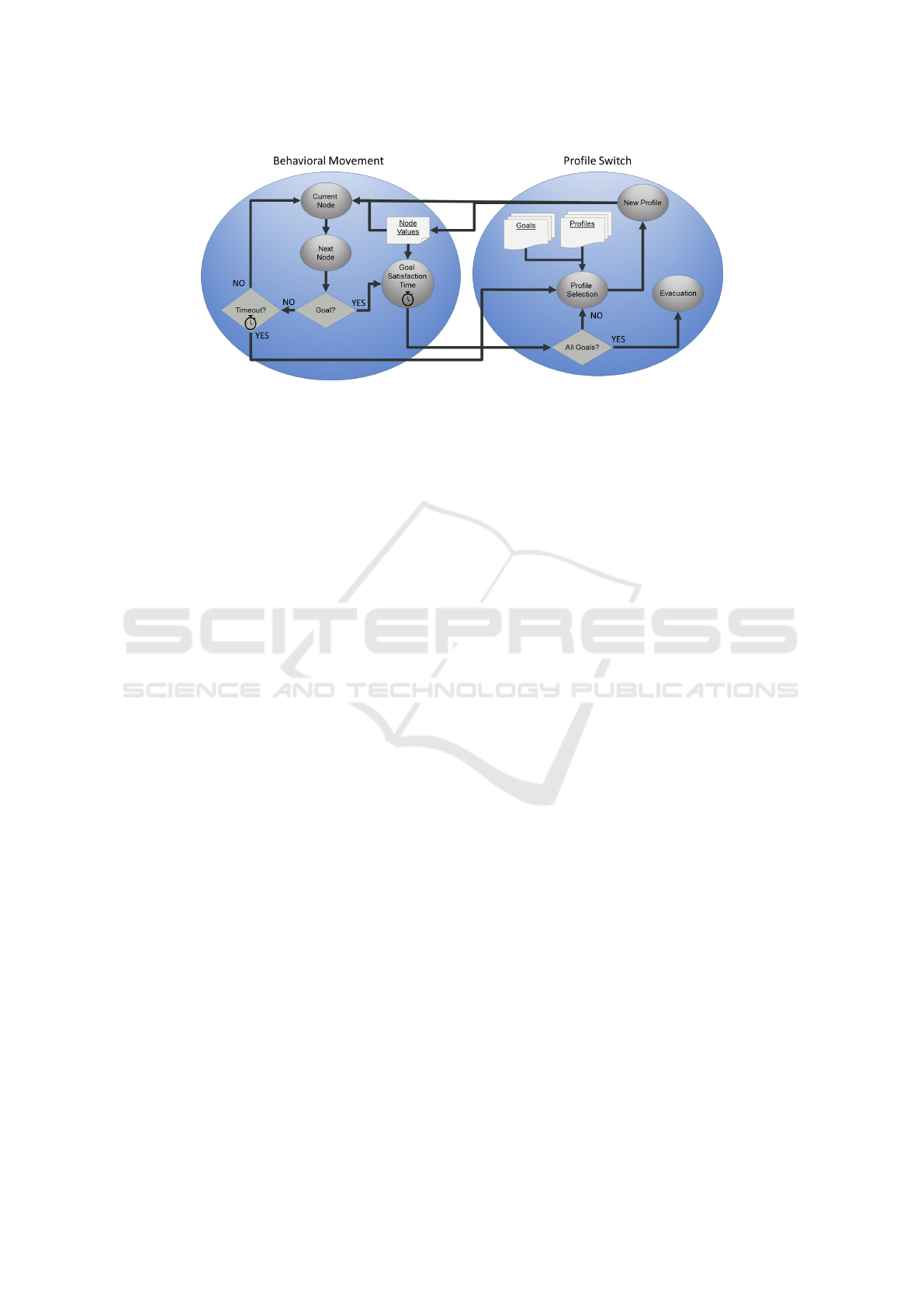
Figure 2: The algorithm followed by the CAMP-IRL agents. Once they reach a map node, they choose their next node by
comparing the values of the available destination nodes. If they satisfy a goal, they change their profile and search for another
goal. Also they calculate the time they should spend in the goal nodes and leave the map when all of them were satisfied.
the node features. Once the goal is satisfied, the agent
verifies if it has remaining goals. If all the goals have
been satisfied, the agent evacuates by going directly
to the evacuation point (this movement is no more be-
havioral, and is performed by calculating the shortest
route to the evacuation node).
If there are still unsatisfied goals, the agent pro-
ceeds to select a new profile. However, before select-
ing one it updates its profile’s list, as it has fewer goals
now and some profiles are not useful anymore. After
deleting those profiles related with already satisfied
goals, the agent chooses the profile in the same way
that it did initially.
Additionally, the agent has a timeout in case it
spends too much time wandering across the map with-
out reaching any goal. If the timeout finishes, the
agent will select a new profile, but this time the
method it uses to do it is different. Instead of select-
ing a profile from its profile’s list, the agent selects
randomly another profile from the whole set, with the
only condition that it has to be different than the pre-
vious one. This represents the agent deciding that its
previous actions where not advancing it to the goal,
and it has to “explore” the map using a different strat-
egy.
5 EXPERIMENTAL RESULTS
We performed a set of tests to compare our method
with others. We wanted to test the efficiency of the
agents in locating goals, so we measured the time the
agents took in satisfying 5 goals belonging to differ-
ent pedestrian profiles whose trajectories were previ-
ously trained using synthetic data. We also wanted
to compare how equivalent were their trajectories to
the trained ones in terms of being “human-like”, so
we also recorded their map coverage and trajectory
information, measuring how many nodes the agents
traversed in their routes.
To contrast the performance of our agents, we
prepared other pedestrian agents using four different
IRL methods; its important to note that all of them
are agents that navigate the map with no informa-
tion of its layout, aside of the data from their learn-
ing technique. Those four agents were: one agent that
chooses randomly its path, called “Random Agent”,
used as a baseline; one agent using a different IRL
method that extracts only a unique policy and reward
function from the whole set of trajectories and does
not use contextual actions (this means it has a fix set
of actions and only one profile) called “NC-Single
IRL Agent”; another agent that uses the same sin-
gle profile IRL technique, but this time modified by
us to include contextual actions into its MDP, called
“Single IRL Agent”; and finally one agent that ex-
tracts multiple profiles but with no contextual actions
called “Multi-IRL Agent”. Both Single IRL Agent
and NC-Single IRL Agent use the maximum entropy
algorithm from (Ziebart et al., 2008), chosen because
it works well when the agents do not have much in-
formation about the layout of the map, and the Multi-
IRL agent uses the method shown in (Choi and Kim,
2012) in which our CAMP-IRL algorithm is based as
well.
We trained all the agents (except Random Agents)
with 150 trajectories that could be divided into five
profiles: “restaurant” for pedestrians that are going
looking for a place to eat; “books” for pedestrians
that are going to buy books, magazines or other paper
ware; “cinema” for pedestrians going to the cinema
or similar entertainment places (theater, games, etc.);
“shopping” for pedestrians that want to buy clothes;
Contextual Action with Multiple Policies Inverse Reinforcement Learning for Behavior Simulation
891

Table 1: Clear times of the agents.
Agents Individual Average Standard Deviation Average Clear Times
CAMP-IRL 3319.99 3006.67 5:57:21
Multi-IRL 5778.09 6141.29 11:22:58
Single IRL 8570.52 7417.15 11:45:35
NC-Single IRL 7326.99 7806.32 14:03:45
Random 32641.40 31610.99 51:05:26
Table 2: Map coverage in visited nodes (total: 140).
Agents Total Coverage Average per Agent Average Trajectory Length
Trained routes 95 31 41
CAMP-IRL 128 26 78
Multi-IRL 133 34 165
Single IRL 140 37 209
NC-Single IRL 140 38 178
Random 140 89 852
and finally “supermarket” that covers pedestrians go-
ing to supermarkets or convenience stores. The tra-
jectories were created by artificial methods due to the
lack of real data in this domain, but they were de-
signed to be as realistic as possible, using real trajec-
tories as inspiration. We also designed the trajectories
to be slightly noisy, with the agents having small de-
tours and wandering a bit while they were going to
their goals in order to contain enough variation and
also to not be always the most optimal. The map
we used was a portion of Tokyo from the Toshima
ward area, containing commercial areas, entertain-
ment spots, a train station, and residential zones. The
map contained a total of 14 different features, and the
trained routes covered around of the 67% of the map
and an 87% of the features.
Once we trained with the trajectories, we obtained
a total of 7 profiles for our CAMP-IRL agents. We
compared the obtained features weights with the in-
formation of the map and we observed that from these
7 profiles, 3 were strongly tied to 3 of the original pro-
files we trained, and the other 4 were combinations of
the 5 original profiles.
Then, we prepared different simulations using
the CAMP-IRL Agents, Random Agents, NC-Single
Agents, Single IRL Agents and Multi-IRL Agents.
The simulator was set under the same conditions for
each type of agent: 150 generated agents, each one
with five goals, one for each one of the original pro-
files. Each simulation was executed five times in or-
der to average the results. We also configured the
agents to not taking any time in satisfying the goals
and keep walking immediately to avoid unwanted
noise in the results; the trained trajectories also were
designed with no goal satisfaction delays.
Table 1 shows the average time in seconds each
type of agent took to satisfy their goals, and also the
average clear times of the five sets of 150 agents in
hours, minutes and seconds. Our agents obtained
clearly better times than the rest. We see small dif-
ferences between Single and NC-Single agents aver-
age times with the NC-Single agents having slightly
better results, albeit having more variance in their re-
sults, causing longer clear times. However, the ad-
vantage of adding contextual actions is more notable
when comparing with Multi-IRL Agents. We also ob-
served high variance values in general, mainly due to
the agents micro behaviors that make them slow their
movements if the paths are too crowded. This effect
was observed in the training routes as well and causes
the first agents to finish very fast, as the streets are
empty, but as soon as they get crowded, the agents
velocity drops until the pedestrian congestion disap-
pears.
Even if Multi-IRL Agents perform way better than
the two single profile agents and obtain a good per-
formance in general, CAMP-IRL Agents take much
less time to finish. We think that the effect of contex-
tual actions increases greatly when the agents have to
choose between different profiles, taking advantage of
its flexibility. Thus, not only CAMP-IRL Agents re-
duced their variance and total clear times like Single
IRL Agents did with respect to their “non-contextual”
versions, but they also improved greatly their aver-
age times, being almost half of the results obtained
by Multi-IRL Agents.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
892

Table 2 shows the average number of different
nodes visited by the whole group of 150 agents, the
average number of different nodes visited per agent
in its trajectory, and the average trajectory length
for each type of agent. As we can see, CAMP-IRL
Agents not only beat the others in the time to clear all
the goals but also they cover less of the map, mean-
ing that their paths are more efficient and they wan-
der less than the others. We noted too that in the
trained routes the coverage per agent was similar to
our CAMP-IRL agents. The trajectories of our agents
were also shorter, being the most similar to the trained
trajectories than the other agents.
We identified one aspect we want to improve in fu-
ture versions of the training system: we observed that
some useful information from the map and the routes
was not being reflected in the learning process: in one
of our experiments, one of the goals was a scarce fea-
ture that only was present in four nodes of the map;
the agents were able to find it, but the wandered ex-
cessively before to do it. The main reason was that the
agents were switching between different profiles after
reaching several times their timeout without finding
any goal. After analyzing why this was happening, we
found that this situation was due to the coincidence of
two factors: scarcity of the goal feature and having
only a few and indirect ways to reach it. In the exam-
ple, in order to reach one of those features, agents had
to cross from one area of the map to another which
could only be entered by three points between them,
but those points were not very remarkable in terms
of value for the selected profiles to reach that feature.
Thus, agents near that feature were conducted by their
profiles to go towards it, but when reaching the men-
tioned area of the map they could not find a crossing
point that was far away. We plan to solve this issue by
improving the learning process by adding enriched in-
formation to the map, establishing semantic relations
between nodes of the map like those crossing points
and the featured nodes.
Also, we want improve our agents to be able to
move across maps that have not been trained, using
training routes from a different one. We will improve
the agents with the capability to estimate the value of
a node using the formula we described in the fourth
step of the CAMP-IRL algorithm in section 3. This
improvement will have a negative impact in the per-
formance of the system (in terms of simulation ve-
locity); however, it also will increase significantly its
usefulness, as only training once would be enough to
simulate the pedestrians, as long as those pedestrians
are from the same distribution (similar background,
same potential profiles, etc.). We want to explore this
potential improvement as even an approximation to
this solution could be beneficial.
6 CONCLUSIONS
This work presents an IRL technique we called Con-
textual Action Multiple Policy Inverse Reinforcement
Learning, or CAMP-IRL, designed to learn pedestrian
behavior. This method has the novel feature of us-
ing different sets of actions for each state combined
with the generation of multiple profiles, reflecting the
different behaviors observed in the training data. We
applied the CAMP-IRL technique to an agent-based
pedestrian simulator using learned profiles to control
pedestrians’ behavior.
Our method converts a city map into a CAMP-
MDP where the states represent locations on the map
and the actions symbolize movements between loca-
tions, being contextual so they have different meaning
on each state. The model is trained using the data
from previously stored pedestrian trajectories, and
produces two data structures: the features weights and
the map nodes value sets. These structures contain
different values for each extracted behavior profiles.
The profiles are used by the agents to traverse the
map, choosing the profile that fits better their goals.
The CAMP-IRL agents are also able to switch profiles
whenever they have to obtain a different goal or when
they consider that their profile is not good enough to
reach the current goal.
We prepared a set of experiments in order to com-
pare the performance of our agents with other exist-
ing methods and check if the obtained profiles are co-
herent with their intended behavior. Our CAMP-IRL
agents performed way better than others trained with
the same data but using single profile IRL methods or
multiple profile methods with no contextual actions
and got the best clear times in the simulator. We no-
ticed also that having multiple profiles and contextual
actions have a positive synergy, yielding better results
when these two improvements are combined than if
we apply them individually and add the performance
gain. The CAMP-IRL agents also have more optimal
routes, having shorter routes than the rest, and having
results similar to the trained ones.
The results of our experiment opened interesting
research paths, and further work is required to give
light to them: as our next step, we plan to improve the
training method by adding a pre-processing stage to
enrich the information of the map. We observed that
under certain conditions it was difficult for the agents
to reach certain goals due to the features weight not
being properly transferred over the distance. We want
our method to be able to automatically modify the fea-
Contextual Action with Multiple Policies Inverse Reinforcement Learning for Behavior Simulation
893

tures of a node or add new ones to it in order to reflect
how influence has the node to the feature globally,
even if such feature is not actually present in it. We
will do it by creating virtual relations between nodes
and influence areas for the features. We also want
to improve our method with the ability to work with
training data from different maps, by calculating an
estimated value of the map nodes in real time.
Finally, we have plans to contrast the behavior of
our agents with real pedestrians data in further exper-
iments. In order to do this and due to legal and logis-
tic issues in tracking crowds effectively, we want to
apply our system to more manageable domains, like
public events (concretely fireworks festivals, which
have been used before to collect data for CrowdWalk)
where it is possible to enact certain degree of control
and surveillance to the crowd, or customer behavior
inside department stores or supermarkets.
REFERENCES
Abbeel, P. and Ng, A. Y. (2004). Apprenticeship learning
via inverse reinforcement learning. In Proceedings of
the twenty-first international conference on Machine
learning, page 1. ACM.
Choi, J. and Kim, K.-E. (2012). Nonparametric bayesian in-
verse reinforcement learning for multiple reward func-
tions. In Advances in Neural Information Processing
Systems, pages 305–313.
Crociani, L., Vizzari, G., Yanagisawa, D., Nishinari, K.,
and Bandini, S. (2016). Route choice in pedestrian
simulation: Design and evaluation of a model based
on empirical observations. Intelligenza Artificiale,
10(2):163–182.
Dvijotham, K. and Todorov, E. (2010). Inverse optimal con-
trol with linearly-solvable mdps. In Proceedings of the
27th International Conference on Machine Learning
(ICML-10), pages 335–342.
Faccin, J., Nunes, I., and Bazzan, A. (2017). Understand-
ing the Behaviour of Learning-Based BDI Agents in
the Braess’ Paradox, pages 187–204. Springer Inter-
national Publishing.
Kohjima, M., Matsubayashi, T., and Sawada, H. (2017).
What-if prediction via inverse reinforcement learning.
In Proceedings of the Thirtieth International Florida
Artificial Intelligence Research Society Conference,
FLAIRS 2017, Marco Island, Florida, USA, May 22-
24, 2017., pages 74–79.
Krishnan, S., Garg, A., Liaw, R., Miller, L., Pokorny, F. T.,
and Goldberg, K. (2016). Hirl: Hierarchical inverse
reinforcement learning for long-horizon tasks with de-
layed rewards. arXiv preprint arXiv:1604.06508.
L
¨
ammel, G., Grether, D., and Nagel, K. (2010). The rep-
resentation and implementation of time-dependent in-
undation in large-scale microscopic evacuation simu-
lations. Transportation Research Part C: Emerging
Technologies, 18(1):84–98.
Levine, S., Popovic, Z., and Koltun, V. (2011). Nonlin-
ear inverse reinforcement learning with gaussian pro-
cesses. In Advances in Neural Information Processing
Systems, pages 19–27.
Luo, L., Zhou, S., Cai, W., Low, M. Y. H., Tian, F., Wang,
Y., Xiao, X., and Chen, D. (2008). Agent-based hu-
man behavior modeling for crowd simulation. Com-
puter Animation and Virtual Worlds, 19(3-4):271–
281.
Martinez-Gil, F., Lozano, M., and Fern
´
andez, F. (2017).
Emergent behaviors and scalability for multi-agent re-
inforcement learning-based pedestrian models. Simu-
lation Modelling Practice and Theory, 74:117–133.
Michini, B. and How, J. P. (2012). Bayesian nonparamet-
ric inverse reinforcement learning. In Joint European
Conference on Machine Learning and Knowledge
Discovery in Databases, pages 148–163. Springer.
Natarajan, S., Kunapuli, G., Judah, K., Tadepalli, P., Ker-
sting, K., and Shavlik, J. (2010). Multi-agent inverse
reinforcement learning. In 2010 Ninth International
Conference on Machine Learning and Applications,
pages 395–400. IEEE.
Neal, R. M. (2000). Markov chain sampling methods for
dirichlet process mixture models. Journal of compu-
tational and graphical statistics, 9(2):249–265.
Ng, A. Y., Russell, S. J., et al. (2000). Algorithms for in-
verse reinforcement learning. In Icml, pages 663–670.
Siebra, C. d. A. and Neto, G. P. B. (2014). Evolving the be-
havior of autonomous agents in strategic combat sce-
narios via sarsa reinforcement learning. In Proceed-
ings of the 2014 Brazilian Symposium on Computer
Games and Digital Entertainment, SBGAMES ’14,
pages 115–122, Washington, DC, USA. IEEE Com-
puter Society.
Surana, A. and Srivastava, K. (2014). Bayesian nonpara-
metric inverse reinforcement learning for switched
markov decision processes. In Machine Learning and
Applications (ICMLA), 2014 13th International Con-
ference on, pages 47–54. IEEE.
Svetlik, M., Leonetti, M., Sinapov, J., Shah, R., Walker,
N., and Stone, P. (2016). Automatic curriculum graph
generation for reinforcement learning agents.
Torrens, P. M., Nara, A., Li, X., Zhu, H., Griffin, W. A., and
Brown, S. B. (2012). An extensible simulation en-
vironment and movement metrics for testing walking
behavior in agent-based models. Computers, Environ-
ment and Urban Systems, 36(1):1–17.
Yamashita, T., Soeda, S., and Noda, I. (2009). Evac-
uation planning assist system with network model-
based pedestrian simulator. In PRIMA, pages 649–
656. Springer.
Zhifei, S. and Meng Joo, E. (2012). A survey of in-
verse reinforcement learning techniques. Interna-
tional Journal of Intelligent Computing and Cybernet-
ics, 5(3):293–311.
Ziebart, B. D., Maas, A. L., Bagnell, J. A., and Dey,
A. K. (2008). Maximum entropy inverse reinforce-
ment learning. In AAAI, volume 8, pages 1433–1438.
Chicago, IL, USA.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
894