Continual Representation Learning for Images

with Variational Continual Auto-Encoder

Ik Hwan Jeon

and Soo Young Shin

Dept. of IT Convergence Engineering, Kumoh National Institute of Technology, Gumi, South Korea

Keywords:

Continual Learning, Generative Models, Representation Learning, Variational Autoencoders.

Abstract:

We propose a novel architecture for the continual representation learning for images, called variational con-

tinual auto-encoder (VCAE). Our approach builds a time-variant parametric model that generates images

close to the observation by using optimized approximate inference over time. When the dataset is sequen-

tially observed, the model efﬁciently learns underlying representations without forgetting previously acquired

knowledge. Through experiments, we evaluate the development of test log-likelihood over time, which shows

resistance to the catastrophic forgetting. The results show that VCAE has stronger immunity against catas-

trophic forgetting in comparison to the benchmark while VCAE requires much less time for training.

1 INTRODUCTION

Artiﬁcial intelligence(AI) should be capable of learn-

ing the knowledge over time-varying domain as bi-

ological agents do in nature (Hassabis et al., 2017).

Continual learning (also called lifelong learning,

incremental learning) is to learn task-independent

knowledge under the environment that contains a

multitude of learning tasks over the agent’s entire life-

time (Thrun and Mitchell, 1995). The main obsta-

cle of continual learning in artiﬁcial intelligence is

so-called catastrophic forgetting (McCloskey and Co-

hen, 1989; French, 1999), which is the phenomenon

that the knowledge of previous tasks that have learned

be degenerated as the model learn new tasks. This

evolves as time goes by with the shift of network pa-

rameters toward new Optima for new tasks while the

covariate and data shift happen. Recent researches

have found evidence on how the biological agents

carry out continual learning tasks (Fagot and Cook,

2006; Cichon and Gan, 2015). Since the connection

between artiﬁcial intelligence and continual learning

is inspiring over the ﬁelds, the solution of catastrophic

forgetting with elegant mathematics has been a chal-

lenge.

Shared representations are helpful to handle multi-

task learning that tasks might arrive over time, or

to apply acquired knowledge to tasks for which few

or no examples are observed but the representation

https://orcid.org/0000-0002-5069-9935

https://orcid.org/0000-0002-2526-2395

of tasks exist. Understanding underlying represen-

tation would make application of machine learning,

ultimately artiﬁcial intelligence, easier to understand

the world. In other words, the key for common sense

in the real world that required for AI would be repre-

sentation learning. Popular type of modern represen-

tation learning is the Auto-Encoders (AEs) (Hinton

and Zemel, 1994). These models explicitly deﬁne a

feature extractor called encoder parametrized closed

form. Encoder tries to ﬁnd latent code or representa-

tion from origin data. Then it deﬁnes another closed

form parametrized function called the decoder, that

maps latent code to origin space. By minimizing re-

construction loss, it ﬁnds the optimal latent represen-

tation of the data. The most popular methods to unsu-

pervised representation learning are Variational Auto-

Encoders (VAEs) (Kingma and Welling, 2013). VAEs

are built on top of standard neural net-based AEs. By

using approximations, it operates efﬁcient inference

and stable learning in directed probabilistic models

for continuous latent variables from intractable poste-

rior distributions and large datasets.

The problem of catastrophic forgetting has been

discussed in different ways entailing each overhead.

The dropout technique (Srivastava et al., 2014) that

regularizes the network parameters shows the ef-

fect of avoiding catastrophic forgetting, including

extra regularization (e.g. L2) helps reduce pertur-

bation during adopting new knowledge (Goodfel-

low et al., 2013). A neuroscience-inspired AI al-

gorithm called Elastic weight consolidation (EWC)

Jeon, I. and Shin, S.

Continual Representation Learning for Images with Variational Continual Auto-Encoder.

DOI: 10.5220/0007687103670373

In Proceedings of the 11th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2019), pages 367-373

ISBN: 978-989-758-350-6

367

slows down learning in a subset of network parame-

ters considered as important to previous knowledge,

thereby anchoring these parameters to the former

conﬁgurations. It allows the networks to be tuned

for multiple tasks without adjusting network capac-

ity (Kirkpatrick et al., 2017). Recent research intro-

duces a method called Learning without Forgetting

(LrF) that only uses new task data to train the network

while preserving the capacity (Li and Hoiem, 2018).

While online Bayesian inference is a natural way

to perform learning by considering prior knowledge

for posterior knowledge (Ghahramani and Attias,

2000), a simple and general framework for contin-

ual learning that exploits variational inference is pro-

posed, which is called variational continual learning

(VCL) (Nguyen et al., 2018). VCL retains a distribu-

tion over model parameters of previous knowledge.

When new data arrives, it reconﬁgures the setting of

parameters with the previous posterior and the likeli-

hood of current data. Through Bayesian inference, it

concocts new posterior while regularizing the sense of

previous knowledge not to be seriously perturbed. For

now, VCL is the closest state of the art technique since

it shows outperforms or be on par with the most recent

techniques such as EWC (Kirkpatrick et al., 2017), SI

(Zenke et al., 2017).

Convolutional neural networks (CNNs) are the

processes inspired by the animal’s visual cortex in that

neuronal connection pattern. Each cortical neurons is

only activated in the related visual ﬁeld known as the

receptive ﬁeld (Hubel and Wiesel, 1968; LeCun et al.,

1998). AI systems using CNN have already shown

competitive capabilities to human’s performances in

tasks that require coping with images (He et al., 2016;

Szegedy et al., 2017). However, VCL does not em-

ploy convolutional networks structure despite it treats

images.

In this paper, we construct a novel framework that

is resistant and stable against catastrophic forgetting

in continual task, which is an essential advantage for

AI. The major contributions of this work can be sum-

marized as follows.

1. This paper proposes a generative model archi-

tecture with convolution that performs continual

learning, which is referred to as Variational Con-

tinual Auto-Encoder (VCAE).

2. It is shown that VCAE outperforms the generative

model of VCL in terms of training time, optimiza-

tion and resistance against catastrophic forgetting

in large gaps.

2 TECHNICAL BACKGROUND

This section provides background knowledge that is

required to develop our method. We adopt the varia-

tional auto-encoder to learn the representation of each

dataset under the framework of the variational contin-

ual learning, which is a general type of online learning

using Bayes’s Rule.

2.1 Variational Auto Encoder

Let x be the observed data, z latent codes, and p(x,z)

be the joint distribution of them. The prior over latent

codes p(z) is assumed to be Gaussian. We want to

approximate posterior inference p(z|x) parameterized

by θ and the marginal likelihood of the data x with

prior. Given a dataset X = x

(1)

,... x

(n)

, we want to

use maximum likelihood to approximate parameters

θ that allows the hidden process to generate artiﬁcial

data alike the real data. But both the marginal likeli-

hood p

(x) =

(z)p

(x|z)dz and the true posterior

(z|x) = p

(x|z)p

(z)/p

(x) are intractable.

A solution is to introduce an amortized inference

model q

(z|x) deﬁned by a neural network, named

encoder, to approximate the posterior p

(z|x). VAEs

jointly train encoder with the probabilistic generative

model, called decoder p

(x|z). Then the marginal

likelihood is composed of a sum over the marginal

likelihoods of each data point:

log p

(1)

,. .. ,x

(i)

) =

∑

i=1

log p

(i)

), (1)

which can be rewritten as:

log p

(i)

) =E

(z|x

(i)

)

[log p

(i)

,z) −logq

(z|x

(i)

)]

+ D

(z|x

(i)

)||p

(z|x

(i)

))

(2)

Since the KL divergence term D

has non-

negative value, the ﬁrst term is called the variational

lower bound on the marginal likelihood of each data

point i. So the loss function of VAE is deﬁned as:

L(θ,φ; x

(i)

) = E

(z|x

(i)

)

[log p

(i)

,z) −logq

(z|x

(i)

)]

= E

(z|x

(i)

)

[log p

(i)

|z) − D

(z|x

(i)

)||p

(z))]

≤ log p

(i)

)

(3)

The loss function, termed as ELBO, comprises of

the expectation of negative reconstruction error and

the KL divergence term as regularization that matches

the posterior q

(z|x) to the prior p(z).

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

368

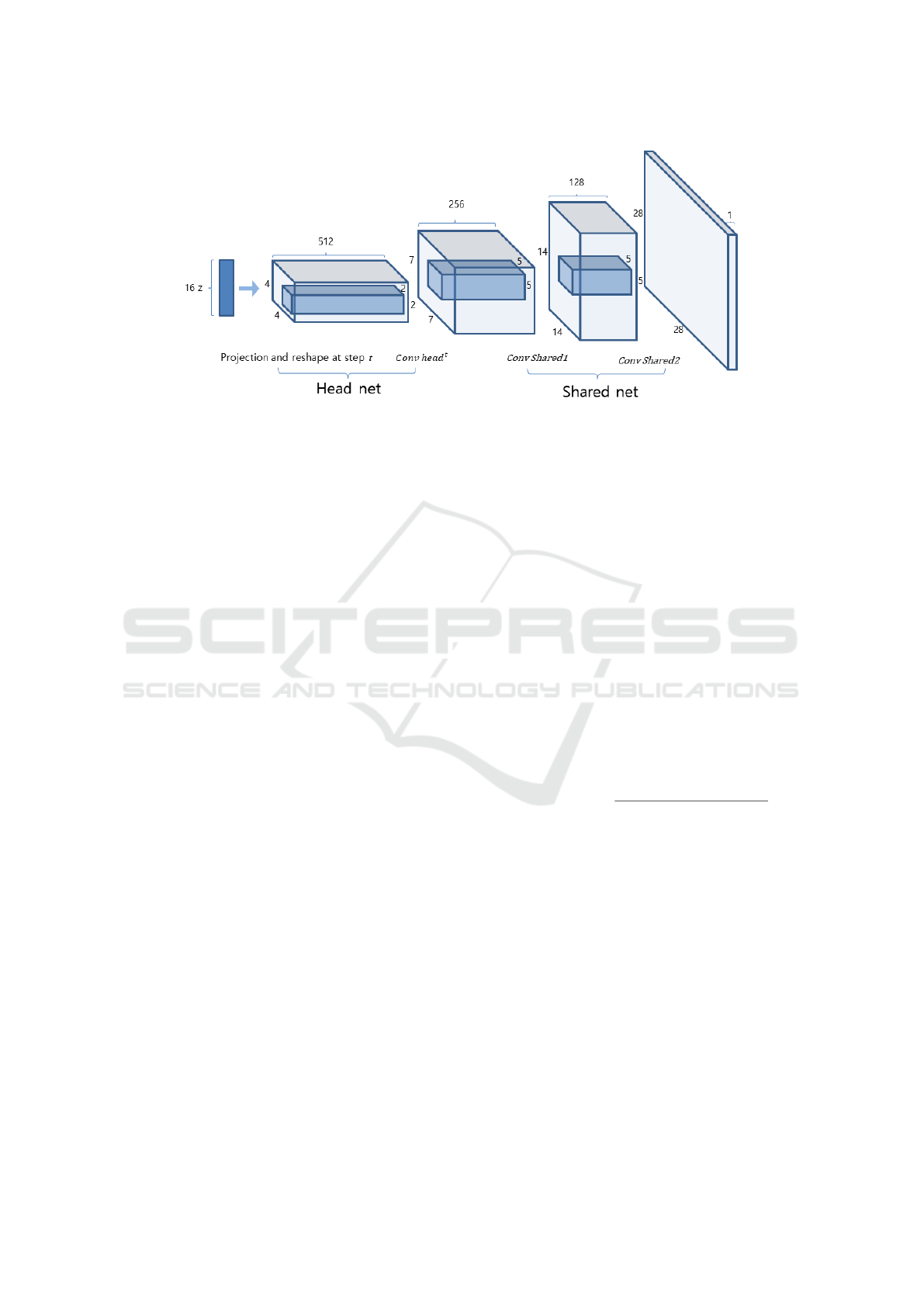
Figure 1: VCAE decoder used for experiments in this paper. For 28x28-sized dataset, 16-dimensional latent variables z is

used as input. As it projected into convolutional decoder, feature maps are employed to sample possible data. The encoder

has same but reverse structure except it does not distinguish head and shared net.

2.2 Variational Continual Learning

From the concept of continual learning, the goal of

VCL is to learn the parameters of the model from se-

quentially arriving datasets X

= {x

(n)

}

n=1

where each

consisting of N

i.i.d. samples and the input domain

might differ over the turns in the sequence of t = 1 : T .

In the perspective of Bayesian, the posterior distribu-

tion is updated by the prior distribution p(θ) after see-

ing T -th datasets:

p(θ|X

1:T

) ∝ p(θ)

∏

t=1

∏

p(x

)

|θ)

=p(θ)

∏

t=1

p(X

|θ) ∝ p(θ|X

1:T −1

)p(X

|θ).

(4)

Thus, the posterior after seeing the (T − 1)-th dataset

and likelihood of T -th dataset are utilized to update

the posterior after seeing T -th dataset. This is a very

general form of online learning emerged naturally

from Bayes’ rule.

2.3 VCL in Deep Generative Models

Let us consider VAEs as a generative model p(x

)

at the step t, where x

is some continuous or dis-

crete variable and z

is an unobserved continuous ran-

dom variable. To overcome catastrophic forgetting,

VCL divides decoder into two subnetworks: the head

net and the shared net. The head net is replaced

with a new head net as task changes. Hence, this

is called multi-head structure. The latent variables

pass through head net ﬁrst then shared net. The

loss function of VAEs is ELBO stated above (2) that a

lower bound of marginal likelihood consisting of re-

construction error and a regularizer. This was because

the second RHS term at (1) is intractable but negli-

gible by the numerical properties. However, in the

continual learning setting, we can render it to return

parameter uncertainty estimates for weighting the old

parameter’s distribution. Thus, the VCL in genera-

tive models approximates full marginal inference of

the variable x.

Loss function of VCL:

VCL

(θ),φ) =E

(θ)

VAE

(θ,φ; X

)]

− D

(θ)||q

t−1

(θ))

(5)

From (3), the loss function of VAE at step t is de-

ﬁned as:

VAE

(θ,φ; X

) =

∑

n=1

VAE

(θ,φ; x

(n)

)

∑

n=1

(n)

)

log p(x

(n)

|,z

(n)

,θ)p(z

(n)

)

(n)

)

(6)

where q

(θ) ≈ p(θ|D

1:t

), after observing the t-th

dataset. The approximate posterior q

is derived from

the complete form of marginal likelihood optimized

with Maximum Likelihood parameterized by θ and φ.

φ is task-speciﬁc parameters of encoder at task t. The

head net’s parameters are used to calculate q

t−1

(θ) as

part of θ but these are re-initialized at every task t.

For a choice of parameters θ, the whole decoder and

encoder are used.

3 VARIATIONAL CONTINUAL

AUTO-ENCODER

CNNs are designed to understand visual scenes by

replicating biological process and have been success-

Continual Representation Learning for Images with Variational Continual Auto-Encoder

369

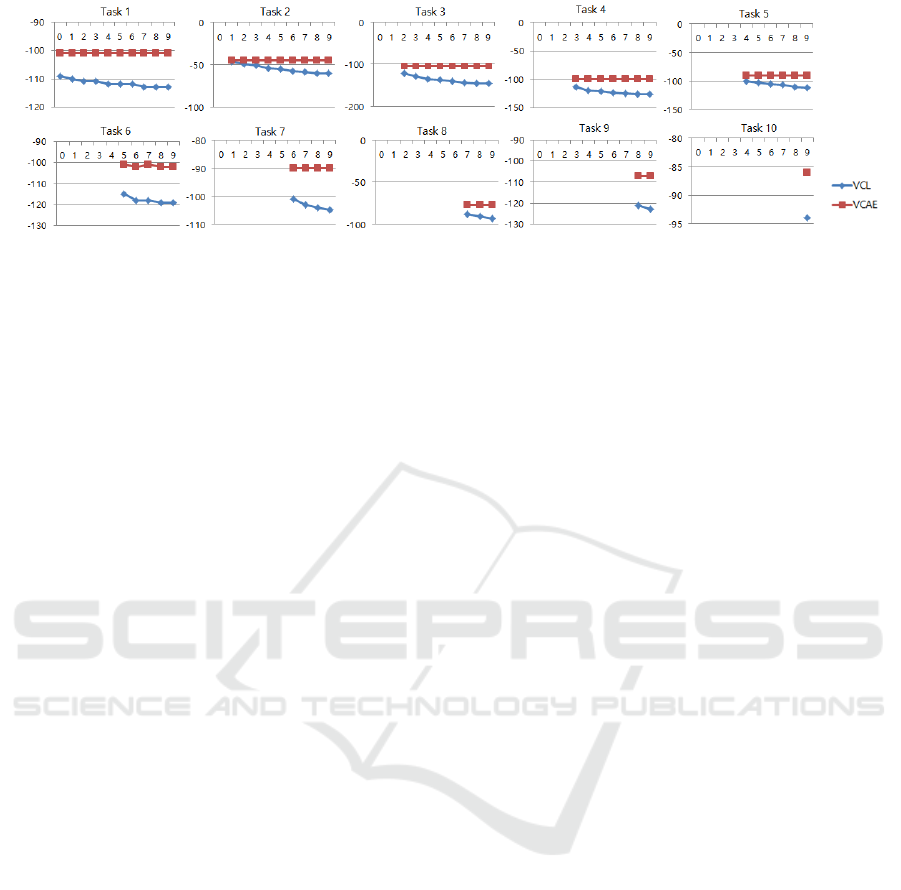
Figure 2: Development of changes of test log-likelihood passing different tasks. The x-axis is task sequence, the y-axis is the

value of the log-likelihood, the higher the better. The generative model of VCL still has resistance for catastrophic forgetting,

but the log-likelihood goes lower as model learn the new task. Meanwhile, VCAE shows almost perfect consistency in overall

tasks.

ful in AI. So, we adopt the convolutional structure

to the VCL and develop a novel framework named

VCAE that memorize sequentially arriving visual

knowledge.

At each stage of learning, convolutional encoder

inference latent variable z concerning visual informa-

tion of the current task. Shared-net in convolutional

decoder stores visual knowledge to generate upcom-

ing task while preserving previously acquired knowl-

edge. And Head-net in convolutional decoder sup-

ports estimating upcoming distribution with respect

to visual information.

After exploration, we found that VCAE shows

better performance in terms of optimization and less

forgetting of the previous task and also stable, faster

training than the generative model of VCL. The struc-

ture is inspired by DCGAN generator (Radford et al.,

2015).

Our approach uses two recent techniques in CNN

architectures. First, global average pooling (GAP)

(Lin et al., 2013) is deployed for the stable training in-

stead of fully connected layers at the end of encoders.

The fully connected layer has two main downsides

than GAP: the larger number of parameter and los-

ing locational information. Hence, it is not necessary

to follow the classic CNN structures that use the FC

layer.

Second, all convolutional net structure (Springen-

berg et al., 2014) replace deterministic spatial pool-

ing (e.g. max pooling) with stridden convolutions.

Max pooling is sufﬁcient when we train classiﬁcation

model because the dominant features learned by max

pooling are enough clues to classify labels. However,

in terms of reconstruction or generation, information

loss incurred by max pooling is disadvantageous. In

addition, since only selected elements would be op-

timized with backpropagation, bias can be incurred

during optimization. By using all convolutional struc-

ture, we can stably keep whole locational information

in maximum.

For the classiﬁcation models, selective linear

functions (e.g. ReLU) are ﬁne to abuse over the whole

structure. But in generative models, the bounded

function can make the training stable since it adjusts

the distribution of output. Consequently, we used the

sigmoid function at the end of the shared network in

the decoder, and Tanh function before the GAP in the

encoder.

4 EXPERIMENTS

These experiments compare VCAE to the genera-

tive model of VCL. For the sake of time efﬁciency,

MNIST dataset is employed as a benchmark. In

VCAE, encoders use Leaky ReLU activation function

except for tanh function before GAP, decoder mainly

utilize ReLU over the head net and the shared net ex-

cluding sigmoid function at the output of shared net.

All the strides are 2. The VCAE decoder is shown

in Figure 1. All the weights of convolutional ﬁlters

in encoder were initialized to the normal distribution

with zero mean and standard deviation of 0.02. VCL

employs linear function at the end of encoders and

sigmoid for the shared part of the decoder. The gen-

erative model in VCL used for comparison consists

of 4 intermediate hidden layers each 500 hidden unit

deployed with the latent variable z of 50 nodes. In de-

coder of VCAE and all VCL weights, mean of the

weights are initialized with Xavier method (Glorot

and Bengio, 2010) and the log standard deviation is

set to 10

−6

. The minibatch size is ﬁxed to 64. Train-

ing epoch and learning rate set to same as 20 itera-

tions for each task with learning rate 0.001, which

was enough to learn generation of MNIST for both

VCL and VCAE. Environmental setup is described in

Appendix A.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

370

Figure 3: The ﬁrst row is samples of VCAE, the second row is from VCL. Development of changes in image generation

passing different tasks (left). 100 generated samples of digit 2 right after the model trained for it as task 3 (middle). 100

generated samples of digit 2 after trained all 10 digit tasks. (right). Middle columns show the samples generated right after it

trained are not different in quality. But as the model learn other tasks, VCL start to make image blurry, while VCAE keeps a

solid memory.

4.1 Evaluation

The generative model of VCL and VCAE are quan-

titatively evaluated using two factors: training time

and sampling estimate of the log-likelihood. Natu-

rally, the likelihood goes less as the model learns new

tasks. If this effect is critical, we call it as the catas-

trophic forgetting.

Figure 2 shows how VCAE is stable over the

growth of knowledge the model learns. Test log-

likelihood refers to estimated log marginal likelihood

after training is ﬁnished. Since VCL and VCAE are

both strong frameworks against catastrophic forget-

ting, they show no critical memory degeneration. But

VCL model still shows degeneration of likelihood

while VCAE constantly retains it. The initial perfor-

mance of VCAE itself is better than VCL model as

well, but also VCAE is far stronger in holding mem-

ory against vaporization of knowledge. Sufﬁce to say,

no catastrophic forgetting is shown.

Generated samples in Figure 3 are consistent with

the numerical result shown in Figure 2. Generated

samples after the stage in learning of task 3, that is

digit 2 in MNIST, show both generative models are

well trained. But after the models are trained with all

10 digits, generated samples from VCL become vague

while ones generated from VCAE are showing equiv-

alent quality. Moreover, the elapsed time for training

has signiﬁcant gaps between VCL and VCAE.

Training time comparison is shown in Figure 4.

While VCL take more and more time as it learns new

tasks, VCAE only requires extremely short time con-

stantly over tasks.

5 CONCLUSIONS

We propose a strategy for continual learning deal-

ing with visual tasks. By using twofold variational

inference and the convolutions, VCAE can perform

continual learning that memorizes image represen-

tation of independent tasks over time. VCL frame-

work is extended to VCAE in which experimental re-

sults show VCAE improves the performances with re-

spect to immunity to catastrophic forgetting and sta-

Continual Representation Learning for Images with Variational Continual Auto-Encoder

371

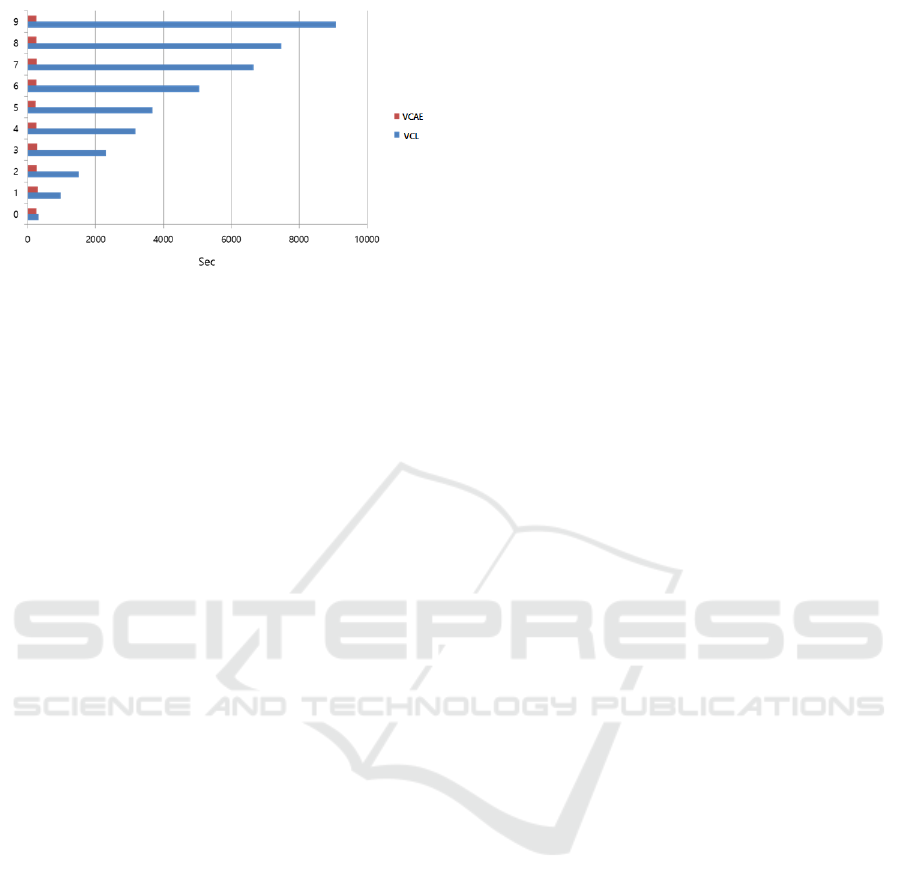
Figure 4: Training time for each task from 0 to 9. Note that

it is not cumulative time. As going for next task, the gener-

ative model of VCL took much more time while VCAE is

only taking less than 300 sec for every task.

ble training. This allows multiple tasks to be learned

without increasing network capacity nor introducing

new parameters to the networks.

Future works should extend this framework for

high dimensional random variables. Also, VCAE can

be adopted to deep reinforcement learning tasks to

support continual learning at large scale so that agents

can learn new knowledge by itself in real-time.

ACKNOWLEDGEMENTS

This research was supported by the MSIT(Ministry

of Science, ICT), Korea, under the ITRC(Information

Technology Research Center) support program(IITP-

2018-2014-1-00639) supervised by the IITP(Institute

for Information & communications Technology Pro-

motion)

REFERENCES

Cichon, J. and Gan, W.-B. (2015). Branch-speciﬁc den-

dritic ca2+ spikes cause persistent synaptic plasticity.

Nature, 520(7546):180–185.

Fagot, J. and Cook, R. G. (2006). Evidence for large long-

term memory capacities in baboons and pigeons and

its implications for learning and the evolution of cog-

nition. Proceedings of the National Academy of Sci-

ences, 103(46):17564–17567.

French, R. M. (1999). Catastrophic forgetting in con-

nectionist networks. Trends in cognitive sciences,

3(4):128–135.

Ghahramani, Z. and Attias, H. (2000). Online variational

bayesian learning. In Slides from talk presented at

NIPS workshop on Online Learning.

Glorot, X. and Bengio, Y. (2010). Understanding the difﬁ-

culty of training deep feedforward neural networks.

In Proceedings of the thirteenth international con-

ference on artiﬁcial intelligence and statistics, pages

249–256.

Goodfellow, I. J., Mirza, M., Xiao, D., Courville, A., and

Bengio, Y. (2013). An empirical investigation of

catastrophic forgetting in gradient-based neural net-

works. arXiv preprint arXiv:1312.6211.

Hassabis, D., Kumaran, D., Summerﬁeld, C., and

Botvinick, M. (2017). Neuroscience-inspired artiﬁcial

intelligence. Neuron, 95(2):245–258.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Hinton, G. E. and Zemel, R. S. (1994). Autoencoders, mini-

mum description length and helmholtz free energy. In

Advances in neural information processing systems,

pages 3–10.

Hubel, D. H. and Wiesel, T. N. (1968). Receptive ﬁelds and

functional architecture of monkey striate cortex. The

Journal of physiology, 195(1):215–243.

Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-

ational bayes. arXiv preprint arXiv:1312.6114.

Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J.,

Desjardins, G., Rusu, A. A., Milan, K., Quan, J.,

Ramalho, T., Grabska-Barwinska, A., et al. (2017).

Overcoming catastrophic forgetting in neural net-

works. Proceedings of the national academy of sci-

ences, page 201611835.

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

Li, Z. and Hoiem, D. (2018). Learning without forgetting.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 40(12):2935–2947.

Lin, M., Chen, Q., and Yan, S. (2013). Network in network.

arXiv preprint arXiv:1312.4400.

McCloskey, M. and Cohen, N. J. (1989). Catastrophic in-

terference in connectionist networks: The sequential

learning problem. In Psychology of learning and mo-

tivation, volume 24, pages 109–165. Elsevier.

Nguyen, C. V., Li, Y., Bui, T. D., and Turner, R. E. (2018).

Variational continual learning. In International Con-

ference on Learning Representations.

Radford, A., Metz, L., and Chintala, S. (2015). Unsu-

pervised representation learning with deep convolu-

tional generative adversarial networks. arXiv preprint

arXiv:1511.06434.

Springenberg, J. T., Dosovitskiy, A., Brox, T., and Ried-

miller, M. (2014). Striving for simplicity: The all con-

volutional net. arXiv preprint arXiv:1412.6806.

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,

and Salakhutdinov, R. (2014). Dropout: a simple way

to prevent neural networks from overﬁtting. The Jour-

nal of Machine Learning Research, 15(1):1929–1958.

Szegedy, C., Ioffe, S., Vanhoucke, V., and Alemi, A. A.

(2017). Inception-v4, inception-resnet and the impact

of residual connections on learning. In AAAI, vol-

ume 4, page 12.

ICAART 2019 - 11th International Conference on Agents and Artiﬁcial Intelligence

372

Thrun, S. and Mitchell, T. M. (1995). Lifelong robot learn-

ing. In The biology and technology of intelligent au-

tonomous agents, pages 165–196. Springer.

Zenke, F., Poole, B., and Ganguli, S. (2017). Continual

learning through synaptic intelligence. arXiv preprint

arXiv:1703.04200.

EXPERIMENTAL ENVIRONMENT

Experiments are progressed with NVIDIA Geforce

GTX 1080 GPU, Intel

 Core i7-3370 CPU @

3.40GHz x8, Ubuntu 18.04.1 LTS, Tensorﬂow-GPU.

Continual Representation Learning for Images with Variational Continual Auto-Encoder

373