An Experimental Evaluation of Design Space Exploration of

Hardware/Software Interfaces

Thomas Rathfux

, Hermann Kaindl

, Ralph Hoch

and Franz Lukasch

Institute of Computer Technology, TU Wien, Vienna, Austria

Robert Bosch AG, G

ollnergasse 15-17, Vienna, Austria

Keywords: Model-driven Engineering, Design Space Exploration, Reuse, Heuristic Search, Hardware/Software Inter-

faces.

Abstract:

We observe ever increasing variability of hardware/software interfaces (HSIs), e.g., in automotive systems.

Hence, there is a need for the reuse of already existing HSIs. In this regard, an important question is whether

automated adaptation of an already existing HSI to one that fulﬁlls the requirements on a new HSI is feasible in

industrial practice. Ideally, the number of adaptation steps should be minimal, so that new hardware production

can be avoided. In this paper, we address the problem of ﬁnding such an optimal solution for a given speciﬁc

HSI and a set of formally speciﬁed requirements on a new HSI. We propose using design space exploration

employing (heuristic) search with optimality guarantees. Hence, a meta-model of such HSIs has been created

together with transformation rules. Based on all that, an experimental evaluation of this approach shows its

feasibility for realistic HSIs.

1 INTRODUCTION

Software has become increasingly important in

cyber-physical systems, which are actually software-

intensive systems in many domains. For instance, in

today’s cars electronic control units (ECUs), i.e., em-

bedded systems are ubiquitous in large numbers.

One important functionality of such ECUs is that

they serve as hardware/software interfaces (HSIs).

Both sensors and actuators are connected to ECUs,

and the HSIs need to make sure that the respective sig-

nals are correctly represented in the software. For ex-

ample, in an automotive system like a car, a pedal po-

sition sensor is connected to the corresponding ECU.

Some pedal position sensors deliver analogue, others

digital signals. Depending on what kind of sensor is

being connected to the ECU, a differently conﬁgured

HSI must be used.

Since there are many variations possible like that,

a variability problem has become important. This

variability can be addressed by reuse. One possibil-

ity is to take already existing HSI speciﬁcations as

reusable assets, and to attempt reusing them by au-

tomated adaptation of an already existing HSI (more

precisely, its speciﬁcation) to one that fulﬁlls the re-

quirements on a new HSI.

For ﬁnding such a new HSI, (heuristic) search

may be employed, see, e.g., (Pearl, 1984). It tries out

different adaptation possibilities and, once it comes

across an HSI that fulﬁls the requirements, it has

found a solution. Of course, the requirements must

be available in a formal representation, which can be

used as goal conditions for the search.

This is reminiscent of search-based software en-

gineering, a notion coined in (Harman and Jones,

2001). Usually, search approaches such as genetic al-

gorithms are employed there for ﬁnding solutions to

very complex problems, but they cannot normally ﬁnd

optimal solutions. Even if they ﬁnd optimal solutions,

they cannot prove that these solutions are indeed op-

timal.

Actually, the search space must be formally rep-

resented as well, in terms of its states and its possible

transformations from one state to the other. Program-

ming such a search space directly, as often done for

puzzles and games, would take unreasonable effort,

however. Model-driven engineering offers the possi-

bility of representing such a search space by deﬁning

meta-models and transformation rules. More speciﬁ-

cally, we use the approach to design space exploration

as exempliﬁed in VIATRA2 (Hegedus et al., 2011).

Since for cost reasons hardware production should

be kept minimal, the number of adaptation steps

should be kept minimal. Hence, we need to em-

Rathfux, T., Kaindl, H., Hoch, R. and Lukasch, F.

An Experimental Evaluation of Design Space Exploration of Hardware/Software Interfaces.

DOI: 10.5220/0007689002890296

In Proceedings of the 14th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2019), pages 289-296

ISBN: 978-989-758-375-9

289

ploy search for optimal solutions, i.e., sequences of

adaptation steps with a guaranteed minimum number

of steps. Unfortunately, such a search typically has

exponential complexity, in our case with an average

branching degree of about one-hundred.

This raises the question of whether this approach

is feasible under realistic conditions such as those in

industrial practice. For answering this question, we

performed an experimental evaluation with a model

realistic for automotive systems, more precisely a

meta-model, for enabling design space exploration.

The remainder of this paper is organized in the fol-

lowing manner. First, we provide some background

and discuss related work, in order to make the paper

self-contained. Then we present our (meta-)modeling

approach for design space exploration of HSIs. Based

on that, we explain our search approach and deﬁne our

heuristic function. After that, we present our experi-

ment using (heuristic) search and its results. Finally,

we conclude and indicate future work.

2 BACKGROUND AND RELATED

WORK

First, we sketch the ECUs that our HSIs are imple-

mented on, and the essence of the HSIs themselves

as far as needed for this paper. Then we refer to the

model-driven tool VIATRA2, which we use for de-

sign space exploration. Since we perform this explo-

ration using heuristic search, we also explain it here

brieﬂy.

2.1 ECUs and HSIs

ECUs are commonly used to provide functionality of

hardware and software components for external sys-

tems that they are embedded in, e.g., in the automo-

tive domain. For this purpose, each ECU provides an

HSI, which enables external hardware components to

interact with internal software functions. This soft-

ware typically runs on a microcontroller and uses var-

ious resources, which are made available through the

pins of the microcontroller.

An ECU may contain different building blocks,

but commonly includes a microcontroller and its in-

ternal resources alongside with its pins, hardware

components for signal processing and ECU pins. In-

ternally, these building blocks are (potentially) con-

nected to others through the wiring of the ECU. For

external connections to other hardware, the ECU pins

are used (and not directly the microcontroller pins).

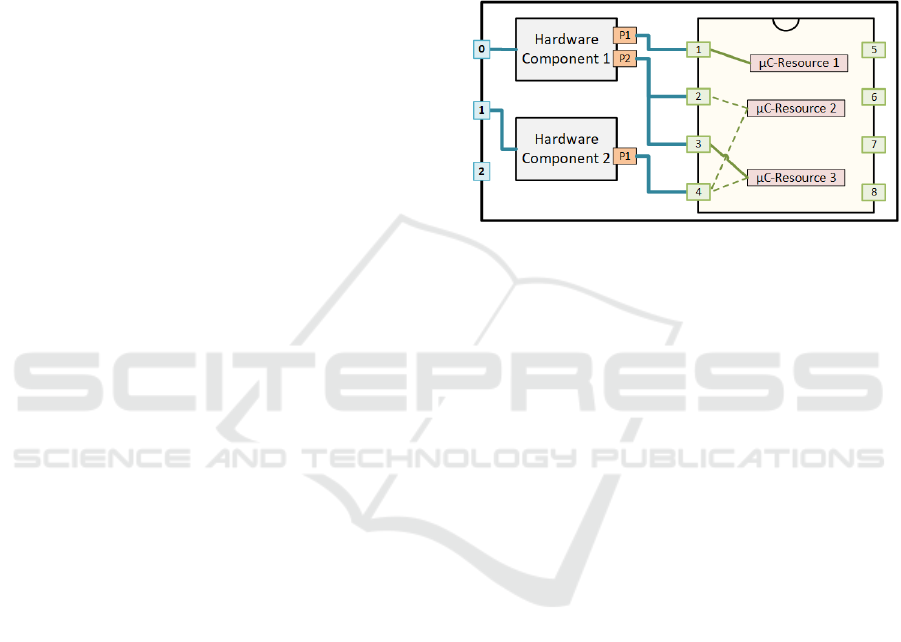
Figure 1 shows the building blocks of a typical

ECU as used in the automotive domain, as well as

their connections. On the right, the microcontroller

is depicted, which contains the possible connections

between its pins and its resources. Note, that this ﬁg-

ure only illustrates the essential structure, while a real

ECU has many more building blocks and connections

between them, and many more resources and their

connections within the microcontroller. Hence, a real

ECU is both larger and more complex, but for the pur-

poses of the explanations in this paper, this schematic

illustration should be sufﬁcient.

Figure 1: Schematic illustration of an ECU and its HSI.

Apart from the microcontroller, which runs the

software, the hardware components represent any

type of hardware that is used to process input or out-

put signals (e.g., power output states, low- or high-

pass ﬁlters). They are both connected to ECU pins

and to one or more microcontroller pins (µC-pins).

The latter connections are through ports (e.g., P1,

P2), and deﬁne the microcontroller resources (e.g.,

µC-Resource 1, µC-Resource 2) that are potentially

available at a port. The microcontroller makes its re-

sources accessible through its µC-pins. One resource

may be connected to several µC-pins, and one µC-pin

to several resources.

It is very important for deﬁning HSIs, that inside

the microcontroller certain of these connections can

be conﬁgured through activating some of the poten-

tial connections, or not. Figure 1 illustrates poten-

tially available connections as dashed lines, and cur-

rently activated connections as bold solid lines. Such

resources can be an analogue digital converter (ADC),

timer input module (TIM), etc. For example, in Fig-

ure 1, µC-Resource 2 is connected to µC-pin 2 and

µC-pin 4.

It is important that the right resources are con-

nected to some hardware component so that it can

provide a certain interface type, such as analogue

measurement of input signals, pulse width modula-

tion measurement, etc. All hardware components to-

gether with their connected resource conﬁgurations

deﬁne an HSI, where the software communicates with

the conﬁgured resources in terms of digital informa-

tion.

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

290

2.2 VIATRA2

VIATRA2 is a model-driven framework for design

space exploration. This framework supports deﬁn-

ing search strategies for traversing the design space,

starting from an initial model by applying rules.

VIATRA2 allows deﬁning rules based on the meta-

model used. They are applied throughout the search

to explore the design space. Goals are deﬁned as con-

ditions that must be satisﬁed for a solution.

VIATRA2 as used in our work presented here, is

actually just one tool of a set of tools developed over

time, where different tools provide different tech-

niques for design space exploration (Bergmann et al.,

2015).

2.3 Heuristic Search for Optimal

Solutions

Many search algorithms have been presented in the

literature, so it would be prohibitive to review all of

them here. Rather, we focus on those we use in the

experiment reported in this paper, a (unidirectional)

search algorithm with certain optimality guarantees

and a special case of it.

The traditional best-ﬁrst search algorithm A*

(Hart et al., 1968) maintains the set OPEN of so-called

open nodes that have been generated but not yet ex-

panded, i.e., the frontier nodes. Much as any best-

ﬁrst search algorithm, it always selects a node from

OPEN with minimum estimated cost, one of those it

considers “best”. This node is expanded and moved

from OPEN to CLOSED. A* speciﬁcally estimates the

cost of some node n with an evaluation function of

the form f (n) = g(n) + h(n), where g(n) is the (sum)

cost of a path found from s to n, and h(n) is a heuris-

tic estimate of the cost of reaching a goal from n, i.e.,

the cost of an optimal path from s to some goal t. If

h(n) never overestimates this cost for all nodes n (it

is said to be admissible) and if a solution exists, then

A* is guaranteed to return an optimal (minimum-cost)

solution (it is also said to be admissible). Under cer-

tain conditions, A* is optimal over admissible unidi-

rectional heuristic search algorithms using the same

information, in the sense that it never expands more

nodes than any of these (Dechter and Pearl, 1985).

Since A* needs an admissible heuristic evaluation

function, which is often not easy to ﬁnd for problems

in industrial practice, let us also mention the special

case of A* without using heuristic knowledge, i.e.,

h(n) ≡ 0, or simply f (n) = g(n). In the special case

of unit costs, i.e., the cost of each step on each path is

exactly 1, this implements breadth-ﬁrst search. Note,

that breadth-ﬁrst search can also be implemented by

the traditional shortest-path algorithm due to (Dijk-

stra, 1959).

3 MODELING APPROACH

First, we present (part of) our meta-model as used by

VIATRA2 for design space exploration. In order to

enable it, we next deﬁne transformation rules based

on this meta-model, and goal conditions as given in

formally speciﬁed requirements for a new HSI. Fi-

nally, we explain how the search approach is im-

plemented in VIATRA2, and deﬁne our admissible

heuristic for guaranteeing optimal solutions.

3.1 Meta-model

Based on the sketch of the application domain above,

we specify here in the meta-model generically what

is needed for design space exploration. This meta-

model covers the structure of an ECU, the possible

variations for activating connections for a conﬁgura-

tion, and the currently selected conﬁguration. Since

the searches for design space exploration must know

when a solution is found, they must be given goal con-

ditions. These are deﬁned in the formally represented

Requirements, which are also generically included in

the meta-model. Technically, we created this meta-

model in Ecore and the Eclipse Modeling Framework

(EMF) (Eclipse, 2017; Steinberg et al., 2009), as this

meta-modeling approach is directly supported by the

VIATRA2 tool.

Figure 2 shows selected parts of the meta-model

that are essential for the purpose of explaining the

design space exploration. The following classes and

their associations deﬁne the application domain: ECU

pins (EcuPin), hardware components (HardwareCom-

ponent, HardwareComponentPort) and the micro-

controller (Microcontroller, McResource, McHwPin,

McPin, McPinConnection). Each instance of a Hard-

wareComponent is connected to a McPin instance

through HardwareComponentPort instances. The

same applies for the McResources of the Micron-

troller and the Ecu. Different interface types on hard-

ware components are expressed via the interfaceType

attribute of the HardwareComponent class.

Each instance of the meta-model represents a spe-

ciﬁc ECU model (and the Requirements on its HSI).

Actually, it also has the HSI conﬁguration deﬁned,

i.e., such an instance represents a speciﬁc state in the

search for design space exploration.

In addition, the meta-model deﬁnes all the possi-

bilities for variation and what is needed for deﬁning

the transformation rules, see below. The variations

An Experimental Evaluation of Design Space Exploration of Hardware/Software Interfaces

291

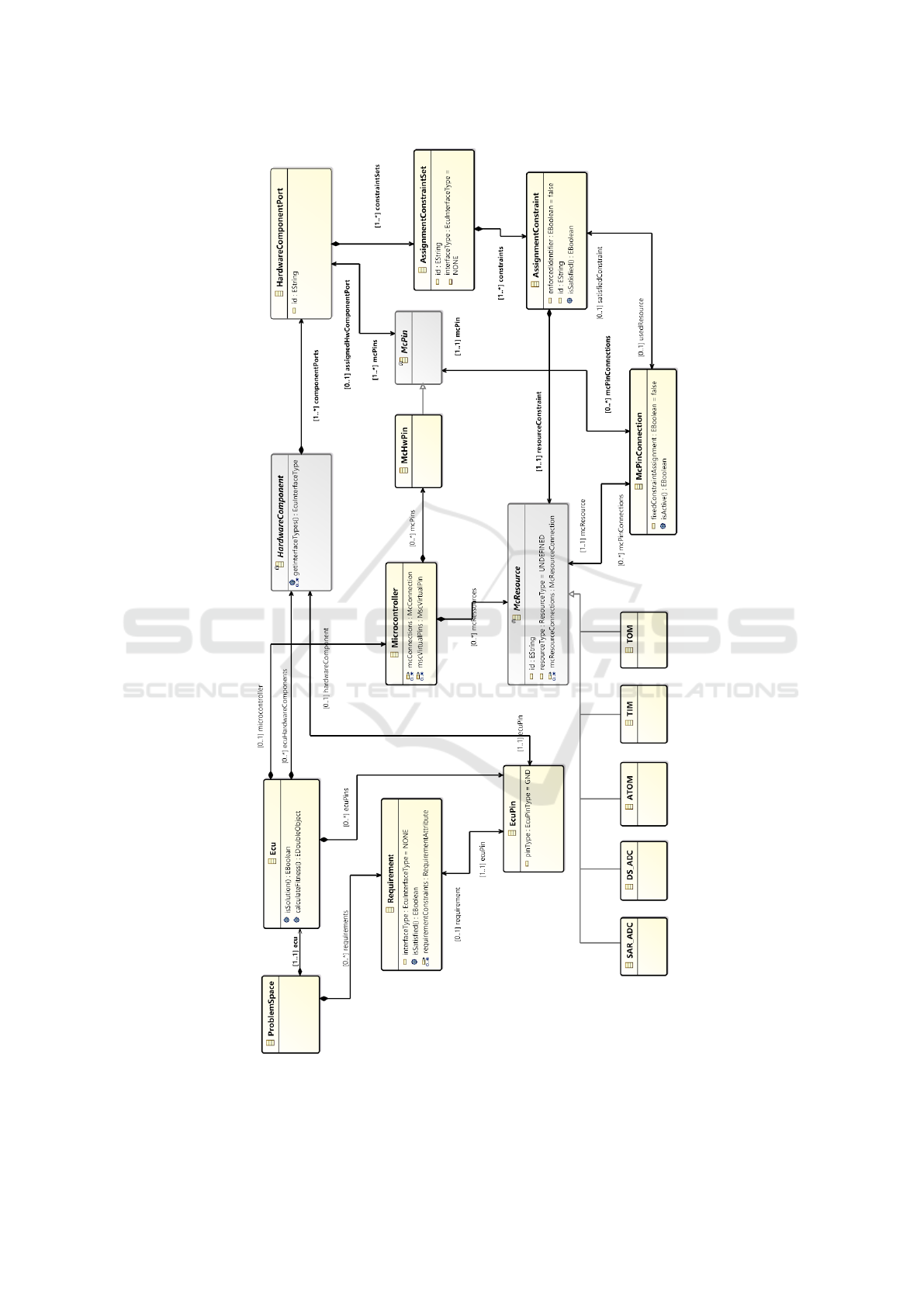
Figure 2: Selected parts of our meta-model.

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

292

are expressed through instances of the McPinConnec-

tion class, which connects instances of McResources

to instances of McPins and, consequently, to Hard-

wareComponentPorts. For deﬁning transformation

rules, it is necessary to specify what kind of resources

are needed by hardware components. In the meta-

model, this is represented by the classes Assignment-

ConstraintSet and AssignmentConstraint. Each Hard-

wareComponentPort may contain several Assign-

mentConstraintSets with AssignmentConstraints and

one speciﬁc AssignmentConstraint speciﬁes which

(type of) McResource is needed. This restricts the

variability of HSIs.

The currently conﬁgured HSI is deﬁned through

the association usedResource, which speciﬁes if a

connection to a resource is activated or not. It links

McResources on McPins through McPinConnections

and AssignmentConstraint(Set)s to HardwareCompo-

nentPorts, and, consequently, to EcuPins. Each value

change on usedResource transforms a state in the

search for design space exploration to another state.

Formally represented Requirements specify the

goal conditions. Each Requirement is associated with

a speciﬁc EcuPin and contains an attribute of type

EcuInterfaceType for specifying what kind of inter-

face is required on this pin.

3.2 Transformation Rules

Based on the variation expressed in the meta-model,

we deﬁned transformation rules in VIATRA2 (using

its query language). Essentially, they model two kinds

of transformations, one for activating a connection in

a conﬁguration, and one for deactivating a connec-

tion.

Figure 3 illustrates both kinds of transformation

rules. The transition from (a) to (b) shows the deacti-

vation of the connection from µ-pin 4 to ADC 2, the

transition from (b) to (c) the activation of the connec-

tion from µ-pin 3 to TIM 1.

Figure 3: Illustration of transformation rules for HSIs.

However, as hardware components have speciﬁc

assignment constraints, not all connections are acti-

vated or deactivated arbitrarily. Each transformation

is only applied in the course of the search if it may

lead to satisfying a goal condition, i.e., fulﬁlling a

given requirement.

Technically, such a transformation rule as deﬁned

in VIATRA2 consists of three parts: pre-condition,

transformation and post-condition. The pre-condition

speciﬁes the applicability of a transformation rule, in

our application in terms of the constraints of Hard-

wareComponentPorts. The transformation speciﬁes

the changes in the model, i.e., the instance of the

meta-model that the transformation rule is applied to.

The post-condition speciﬁes the result of the rule ap-

plication as a condition deﬁned according to the meta-

model.

3.3 Goal Condition

As indicated above, a goal condition for a search is

deﬁned by Requirements (as speciﬁed in our meta-

model). In general, more than one Requirement is

given in this way, and a solution is only found, if

and when all corresponding conditions are satisﬁed.

That is, a goal condition is a conjunction of condi-

tions given by Requirements.

Depending on the EcuInterfaceType attribute of

a given Requirement, the HardwareComponent at

the speciﬁc EcuPin that this Requirement is associ-

ated with needs to ﬁt. Consequently, all constraints

of this HardwareComponent have to be fulﬁlled as

well. This requires the fulﬁllment of Assignment-

ConstraintSets on HardwareComponentPorts as they

also depend on the EcuInterfaceType. One EcuInter-

faceType may be supported by more than one Assign-

mentConstraintSet. In addition, one HardwareCom-

ponent and its HardwareComponentPorts may sup-

port more than one EcuInterfaceType. Thus, spec-

ifying more than one AssignmentConstraintSet per

HardwareComponentPort, each related to a different

EcuInterfaceType, is also possible. If at least one of

these AssignmentConstraintSets is fulﬁlled for a spe-

ciﬁc EcuInterfaceType on all Ports, then also the spe-

ciﬁc Requirement is fulﬁlled and, therefore, the corre-

sponding part of the goal condition. That is, all ports

of a HardwareComponent are connected via conjunc-

tion and all AssignmentConstraintSets of a port are

connected via disjunction.

However, the AssignmentConstraints of a partic-

ular AssignmentConstraintSet have all to be fulﬁlled.

Hence, they are connected via conjunction.

Summarizing, one goal condition of a speciﬁc

EcuInterfaceType is logically expressed in disjunctive

normal form. If one part of the disjunctive normal

form is fulﬁlled, then the interface type may be used.

An Experimental Evaluation of Design Space Exploration of Hardware/Software Interfaces

293

This corresponds to one Requirement only, however.

Hence, such a disjunctive normal form has to be ful-

ﬁlled for each and every Requirement.

4 SEARCH APPROACH

With this modeling approach, a search space is

deﬁned for design space exploration using the

VIATRA2 tool. The transformation rules can be

chained together in sequences. Figure 3 shows an ex-

ample where ﬁrst a deactivation of one connection is

followed by the activation of another one. In this way,

several adaptations of an HSI design can be achieved

in a model. A sequence of transformations that con-

nects a start conﬁguration of an already existing HSI

with another one that satisﬁes a goal condition de-

ﬁned through given Requirements is a solution. For

example, it may be necessary to deactivate a connec-

tion and activate several others in succession. A so-

lution with minimal cost, in our case a minimal num-

ber of transformations is an optimal solution. Since

ﬁnding a solution, in particular an optimal one, is

not straight-forward, in general, alternative transfor-

mations need to be investigated, and this leads to a

search in this space. For this design space exploration,

our search approach is breadth-ﬁrst search (without

heuristic) and A* (with heuristic) as reviewed above.

Such a search for an optimal solution typically has

exponential complexity, in our case with an average

branching degree of about one-hundred. Hence, this

search space is very large for realistic HSIs. Fortu-

nately, it has important properties that need to be uti-

lized for making such searches feasible. Figure 4(a)

illustrates a cycle. It may simply occur after acti-

vating a particular connection in the conﬁguration of

state S1 and subsequently deactivating the very same

connection in the conﬁguration of state S2. This re-

sults in state S5, which is the same as state S1, of

course. Therefore, further search below S5 is not nec-

essary and can be pruned. Figure 4(b) illustrates a

directed acyclic graph (DAG), where the same state

S5/S6 is visited more than once, when reached from

the root S1 via two (or, in general, several) different

paths. This may simply occur after activating a par-

ticular connection c

in the conﬁguration of state S1

and subsequently deactivating another connection c

in the conﬁguration of state S2, where deactivating

in the conﬁguration of state S1 and subsequently

activating c

in the conﬁguration of state S3 leads to

the same conﬁguration, of course. Cycles and DAGs

can be recognized by the VIATRA2 tool, so that the

searches can be effectively pruned for achieving very

strong reductions of the search costs. This makes the

searches much more efﬁcient both in terms of space

and time.

Figure 4: Cycles and DAGs in the search space.

Breadth-ﬁrst search is implemented directly in

VIATRA2, while for best-ﬁrst search an evaluation

function has to be deﬁned. Since we implemented

A*, this evaluation function is f (n) = g(n) + h(n) as

reviewed above. Note, that using f (n) = g(n) leads to

an alternative implementation of breadth-ﬁrst search,

since there are unit costs for all transformations. A*

with a heuristic h usually searches more efﬁciently

than breadth-ﬁrst search.

For A*, admissibility of the heuristic function is

important for guaranteeing the optimality of solutions

found. For evaluating a conﬁguration in such a func-

tion with respect to its goal achievement, the number

of not (yet) fulﬁlled conjunctively related goal condi-

tions is counted. In case of disjunctively related con-

ditions, the minimum is taken. The resulting number

can be used as the heuristic value, since each condi-

tion needs at least one application of a transformation

rule. In fact, these can only be activation rules. De-

activation rules may additionally be necessary, in or-

der to deactivate some connection so that another one

needed can be activated at this particular pin. Con-

sequently, this number is less than or equal to the

number of minimal steps to achieve the goal condi-

tion, i.e., this is an admissible heuristic. This can also

be explained more theoretically based on the meta-

heuristic of problem relaxation, see (Pearl, 1984). A

relaxed problem would only need activation rules for

its solution, i.e., the number calculated by our heuris-

tic function.

5 EXPERIMENT

First, we present our design of the experiment, and

then its results.

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

294

5.1 Experiment Design

The purpose of this experimental evaluation is purely

exploratory, answering the question of feasibility of

this approach under realistic conditions such as those

in industrial practice, more precisely for reusing HSI

designs of automotive ECUs. Hence, we had to make

sure in the experiment design that the given HSI de-

signs and the requirements for new ones are realistic.

Since statistical ﬂuctuation was to be expected for

different instances, we deﬁned several ones and in-

cluded some randomness into their creation. In ad-

dition, we wanted to systematically get data on the

average running times for different (optimal) solution

lengths, in order to evaluate the effect of scaling with

increasing problem difﬁculty.

First, we deﬁned a speciﬁc ECU hardware based

on typical hardware components available on the PCB

of an ECU in our domain. For the microcontroller,

we deﬁned a resource set inspired by a typical 64-pin

ARM microcontroller (STM, 2018; Inﬁnion, 2018).

For creating differently conﬁgured ECUs, ECU-pins

of this ﬁrst ECU were selected and requirements ran-

domly assigned to them. For each of them, a solu-

tion was determined (through searches) and stored as

a base model for the next step of model creation.

Then we created problem instances with differ-

ent solution lengths by generating requirements ran-

domly (again). This resulted in 75 problem instances

for each solution length (up to 20 steps), with dif-

ferent starting conﬁgurations and different target re-

quirements. From this set, ten problem instances each

were selected randomly and used for the searches in

the experiment. Since we experienced some variation

in the runs of VIATRA2 also regarding the ordering

during design space exploration, which inﬂuences the

running time depending on when a solution is found,

we ran each problem instance ﬁve times and calcu-

lated mean values.

We executed the experiment runs on a standard

Windows laptop computer with an Intel Core i7-

8750H Processor (9MB Cache, up to 4.1 GHz, 6

Cores). It has a DDR4-2666MHz memory of 32GB.

The disk does not matter, since all the experimental

data were gathered using the internal memory only.

5.2 Results

On the laptop computer used, we were able to collect

the results of searches with optimal solution lengths

(costs) C* of up to six for breadth-ﬁrst search and of

up to 17 for A*. All the searches found optimal so-

lutions and guaranteed that they are optimal (in terms

of solution length). Figure 5 plots the mean running

times for both kinds of search in seconds (where no

other processes were running on the laptop computer

used). In fact, breadth-ﬁrst search shows up in two

plots, one for running on six cores in parallel and one

on a single core. A* was running on a single core

(only), since VIATRA2 does not support parallel ex-

ecution of searches with cost functions.

In more detail, Table 1 shows the data gathered

from the multi-core runs, including the mean num-

bers of states visited. Table 2 shows the data of the

breadth-ﬁrst searches on a single core, and Table 3 the

detailed results of the A* searches (on a single core).

The number of states visited per second shows mi-

nor ﬂuctuations (presumably due to technical reasons

inside the VIATRA2 engine), but there is no system-

atic deviation due to the running time or the search

depth. The factors of running times (or the numbers of

nodes visited) from level i to i + 1 of C* are an order

of magnitude less than the average branching degree

for breadth-ﬁrst search, and two orders less for A*.

The reasons are the DAGs in the search space, which

can be exploited even much more by best-ﬁrst search,

since it is directed to a goal state and can search much

deeper.

Figure 5: Comparison of running times of breadth-ﬁrst

search vs. A*.

Table 1: Summarized results of breadth-ﬁrst search exe-

cuted on six cores.

C* Running

time

Running

time

factor

No. of

visited

states

No. of

states

per

second

3 0.30 – 1,160 3,890

4 2.73 9.17 12,680 4,640

5 11.54 4.22 32,287 2,800

6 146.89 12.73 301,830 2,050

It is easy to see in Figure 5 that A* is much more

efﬁcient than breadth-ﬁrst search in terms of running

time, even when running on a single core as com-

pared to six cores. Breadth-ﬁrst search running on

six cores can just ﬁnd optimal solutions with a max-

imum length of six, while A* (running on a single

An Experimental Evaluation of Design Space Exploration of Hardware/Software Interfaces

295

Table 2: Summarized results of breadth-ﬁrst search exe-

cuted on a single core.

C* Running

time

Running

time

factor

No. of

visited

states

No. of

states

per

second

3 0.95 – 1,327 1,399

4 16.98 17.91 14,739 868

5 295.29 17.39 214,624 727

Table 3: Summarized results for A*.

C* Running

time

Running

time

factor

No. of

visited

states

No. of

states

per

second

3 0.11 – 133 1,262

4 0.13 1.28 289 2,144

5 0.53 3.96 1,075 2,016

6 1.20 2.26 2,677 2,225

7 3.04 2.52 6,690 2,204

8 12.15 4.00 21,848 1,799

9 76.91 6.33 106,518 1,385

10 213.65 2.78 328,704 1,539

11 396.91 1.86 604,839 1,524

core) can do so nearly twice as deep. Hence, the ad-

missible heuristic serves well its purpose of making

its searches much more directed and, hence, efﬁcient

than breadth-ﬁrst search without any heuristic.

6 CONCLUSION AND FUTURE

WORK

The question is now, whether these search results in-

dicate the feasibility of this approach for reusing re-

alistic HSI designs. We think that breadth-ﬁrst search

does not qualify due to the shallow searches it was

able to perform. It will most likely be insufﬁcient in

practice to ﬁnd optimal solutions of, say, six adapta-

tion steps. However, A* can search much deeper, and

this makes it feasible for such reuse. This shows the

importance of the heuristic knowledge involved.

Of course, the actual applicability for real-world

problems will yet have to be shown in a case study.

Actually, we also plan to address the problem of auto-

matically ﬁnding a previous HSI that is similar to the

new one for which the requirements are given. This

may lead to case-based reasoning where both ﬁnding

a similar previous case and the adaptation of its stored

(previous) solution to the new one is automated.

ACKNOWLEDGEMENTS

The InteReUse project (No. 855399) is funded by

the Austrian Federal Ministry of Transport, Innova-

tion and Technology (BMVIT) under the program

“ICT of the Future” between September 2016 and

August 2019. More information can be found at

https://iktderzukunft.at/en/.

REFERENCES

Bergmann, G., D

avid, I., Heged

us,

A., Horv

ath,

A., R

ath, I.,

Ujhelyi, Z., and Varr

o, D. (2015). Viatra 3: A reactive

model transformation platform. In Kolovos, D. and

Wimmer, M., editors, Theory and Practice of Model

Transformations, pages 101–110, Cham. Springer In-

ternational Publishing.

Dechter, R. and Pearl, J. (1985). Generalized best-

ﬁrst strategies and the optimality of A

∗

. J. ACM,

32(3):505–536.

Dijkstra, E. (1959). A note on two problems in connexion

with graphs. In Numerische Mathematik 1, pages 269–

271.

Eclipse (2017). Package org.eclipse.emf.ecore (emf

javadoc).

Harman, M. and Jones, B. F. (2001). Search-based software

engineering. Information and Software Technology,

43(14):833 – 839.

Hart, P., Nilsson, N., and Raphael, B. (1968). A formal

basis for the heuristic determination of minimum cost

paths. IEEE Transactions on Systems Science and Cy-

bernetics (SSC), SSC-4(2):100–107.

Hegedus, A., Horvath, A., Rath, I., and Varro, D. (2011). A

model-driven framework for guided design space ex-

ploration. In Proceedings of the 2011 26th IEEE/ACM

International Conference on Automated Software En-

gineering, ASE ’11, pages 173–182, Washington, DC,

USA. IEEE Computer Society.

Inﬁnion (2018). STM32 32-bit Arm Cortex product family.

Pearl, J. (1984). Heuristics: Intelligent Search Strate-

gies for Computer Problem Solving. Addison-Wesley,

Reading, MA.

Steinberg, D., Budinsky, F., Paternostro, M., and Merks,

E. (2009). EMF: Eclipse Modeling Framework 2.0.

Addison-Wesley Professional, 2nd edition.

STM (2018). Inﬁneon AURIX

Family TC29xT.

ENASE 2019 - 14th International Conference on Evaluation of Novel Approaches to Software Engineering

296