Cross-provider Platoons for Same-day Delivery

Sînziana-Maria Sebe

1 a

, Philipp Kraus

1 b

, Jörg P. Müller

1 c

and Stephan Westphal

2 d

Institut für Informatik, Technische Universität Clausthal, Julius-Albert Straße 4, Clausthal-Zellerfeld, Germany

Institut für Angewandte Stochastik und Operations Research, Technische Universität Clausthal,

Erzstraße 1, Clausthal-Zellerfeld, Germany

Keywords:

Platoon, Heterogeneous Groups, Route Matching, Group Building.

Abstract:

Platooning – vehicles travelling close together behaving as a unit – aims to improve network throughput both

on highways and in urban trafﬁc. We study the problem of platoon formation in an urban environment us-

ing the scenario of logistic service providers equipped with ﬂeets of autonomously driving pods to carry out

same-day delivery tasks by creating cross-provider platoons. The novelty of our work is that we investigate

the problem of cross-provider platoons, i.e., platoons with members from different self-interested logistic ser-

vice providers. Our aim is to study platoon formation mechanisms and possible beneﬁts of cross-provider

platooning using simulation. We formulate optimal platoon formation as an integer linear optimisation prob-

lem (ILP), aiming to ﬁnd the longest sub-routes to be shared between vehicles by platooning. The proposed

method was implemented and tested on a mesoscopic model to simulate platoon formation and operation, on

real network data with realistic background trafﬁc models. Comparing our method to a simpler route matching

algorithm reveals comparable system level performance; however, our method performs better with respect to

local participant utility, i.e.appears more suited to take vehicle/provider preferences into account.

1 INTRODUCTION

With the growth of e- and m-commerce, same-day de-

livery is emerging as a desirable option for customers.

This new logistics concept has been mostly imple-

mented in hub and spoke architectures so far, where

delivery satellites are connected with hubs (Crainic,

2008), (Crainic and Sgalambro, 2014), and where last

mile delivery is performed from satellite to customer

– usually the most costly part of transport (Gevaers

et al., 2011).

Logistic service providers (LSP) usually plan and

time their deliveries in advance, in order to minimise

the driving distance while maximising the number of

orders honoured. This process is costly in computa-

tional resources and time, thus making it unviable for

same day delivery. Orders that are received should

be handled immediately, making small-sized, possi-

bly automated vehicles with little capacity a better op-

tion not only because of time constraints, but also to

achieve higher ﬂexibility in an urban trafﬁc environ-

https://orcid.org/0000-0002-9435-9879

https://orcid.org/0000-0003-3819-7163

https://orcid.org/0000-0001-7533-3852

https://orcid.org/0000-0002-5893-5533

ment. This creates a huge challenge for LSPs, which

are in need of new and innovative ways to success-

fully complete deliveries in busy urban trafﬁc situa-

tions while limiting their own negative effects on it.

Recently, vehicle platooning in conjunction with

the use of automated (electric) vehicles has been ap-

pearing as a possible technology, enabling more sus-

tainable usage of road space. Starting with early

work on highway platooning (Swaroop and Hedrick,

1999) and work focusing on truck platooning and au-

tonomous vehicles (e.g. SARTRE (Robinson et al.,

2010)), a considerable body of research on platooning

has been recently conducted, including some work

studying urban environments. Yet, so far, research on

urban platooning has focused on control, stability and

operation (see e.g., (Schindler et al., 2018) (Khalifa

et al., 2018) (Ali et al., 2015)). There is also some

work that considers the use of platooning from a traf-

ﬁc management perspective, e.g., by decreasing con-

gestions and emissions at trafﬁc lights (e.g., (Lioris

et al., 2017)).

There is only little research focusing on applying

platooning to city logistics applications (e.g. (Scherr

et al., 2018)), and to our knowledge; no work that

studies methods for platoon formation and operation

involving vehicles operated / owned by different ser-

106

Sebe, S., Kraus, P., Müller, J. and Westphal, S.

Cross-provider Platoons for Same-day Delivery.

DOI: 10.5220/0007689601060116

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 106-116

ISBN: 978-989-758-374-2

vice providers, including possible beneﬁts and disad-

vantages of these methods. For a more detailed ac-

count of the state of the art, we refer to Section 2.

Our research aims at closing this gap, and the

work described in this paper establishes a ﬁrst step

to investigate beneﬁts and trade-offs of urban cross-

provider platooning for same-day delivery. For the

scope of this paper, we assume that LSPs operate lo-

cal ﬂeets of smaller-sized automated delivery vehicles

(Pods) which are dispatched into urban trafﬁc. We

further assume that platooning is encouraged by traf-

ﬁc management by offering them easier / faster pas-

sage through the network. We study methods for pla-

toon formation and operation in this context.

In order to increase the usage (and hence achiev-

able beneﬁt) of platooning in the urban network, we

propose cross-provider platoons; that is platoons with

vehicles belonging to different LSPs. This leads to

heterogeneous groups not only as far as the destina-

tions are concerned, but also – due to the fact that

LSPs are self-interested – with respect to constraints,

preferences and valuation functions. Platoons are as-

sumed to form spontaneously in the network, and a

pod will only join a platoon if its local utility when

joining is lower than when traveling alone. Said util-

ity is hereby named costs but measured in terms of

time-savings based on trafﬁc density.

In Section 2, we analyse the state of the art and

formulate the research gap. In Section 3, we formu-

late optimal platoon formation as an integer linear op-

timisation (ILP) problem, aiming to ﬁnd the longest

possible routes to be shared between vehicles. In Sec-

tion 4, we describe a simulation system implement-

ing the proposed method, and its evaluation against

real network data with synthetic but realistic back-

ground trafﬁc models. Preliminary results reported

in Section 5 are encouraging and show that overall

(system-level) performance of our method is com-

parable to that of state-of-the-art methods, but may

lead to higher acceptance by LSPs because it achieves

higher average local utility values. We end with a con-

clusion and outlook in Section 6.

2 STATE OF THE ART

2.1 Platoons

Platooning – multiple vehicles travelling together as

one logical unit– has been getting plenty of atten-

tion as of late, since it shows great promise for large

freight transport on a highway system (Bengtsson

et al., 2015), (Amoozadeh et al., 2015), (Biswas et al.,

2006) as far as resource usage is concerned. Platoons

take up less road space since they travel closer to-

gether than individual vehicles do, thus positively af-

fecting ﬂow within the network and fuel consumption.

The latter is due again, to the smaller gap between ve-

hicles, which in turn reduces wind drag, leading to a

lower consumption. This is particularly effective on

highways due to the straight roads and high speeds.

Trafﬁc management beneﬁts of platooning have

been investigated e.g., by (Lioris et al., 2017), who

showed that platoons can increase network through-

put at urban intersections and that adapting trafﬁc sig-

nalling to allow for the faster passing of platoons can

potentially improve overall city trafﬁc.

With regards to urban platooning, related work fo-

cuses on models describing ways of control, ensur-

ing stability within the platoon and ways of operation

(how vehicles form, travel within and split from the

platoon). Ali et al. (Ali et al., 2015) have shown that

in order to account for curved roads, as well as vary-

ing speeds which tend to occur in an urban network

more so than in highway trafﬁc, longitudinal control

must be decoupled from the lateral one. They pro-

pose three different models, one for each movement

type (longitudinal, lateral and platoon). Khalifa et

al. (Khalifa et al., 2018) propose a new consensus-

based longitudinal control model which is capable of

ensuring string stability even in the case of commu-

nication breakdown. Schindler et al (Schindler et al.,

2018) investigate stable and ﬂexible platooning on ur-

ban roads. The authors propose the use of state ma-

chines, one for each aspect of the platooning logic

(platooning, forming, message, distance).

All previous papers do not address the issue of

platoon grouping, which is how the vehicles decide

whether to platoon or not and who platoons with

whom. Even when discussing joining (Schindler

et al., 2018), only the actions leading to forming

or joining the platoon are discussed, but not the

characteristics which would indicate whether join-

ing/forming makes sense.

Using platooning in the context of logistic same-

day delivery is a rather new area of study, where the

subject of network design was broached (Scherr et al.,

2018). This paper presents how a service network for

such a process could be modelled, considering mixed

autonomous platoons. The authors consider that fully

automated platoons could only be viable on certain

parts of the network, and would rely on a human

driver to navigate through the others. All vehicles,

both human-driven and autonomous belong to a sin-

gle LSP and focus on minimising the cost of delivery.

Even with this study, the subject of grouping vehicles

into platoons is not touched upon, mainly due to the

homogeneity of the vehicles, and the fact that such

Cross-provider Platoons for Same-day Delivery

107

platoons would be grouped and planned to maximise

utility in the ﬁrst place.

2.2 Group Formation

When looking at group building algorithms we have

different approaches based on the ﬁeld in which they

are applied. More general and largely applied meth-

ods are described in (Amir and Lindenbaum, 1998)

with algorithms solely based on recognising impor-

tant information and sorting by a particular criterion

(Havaldar et al., 1994); Wertheimers laws of group-

ing (Gordon, 2004); grouping by maximising a con-

sistency function between group assignment and data;

hierarchical grouping (Mojena, 1977); Walds SPRT

Algorithm (Wald and Wolfowitz, 1948) or simply by

maximum likelihood.

When focusing on vehicle or trips grouping there

are again multiple facets, each belonging to a spe-

ciﬁc domain. To form, maintain and dissolve a group,

communication is required; so a clear ﬁrst grouping

strategy would be based on vehicles maintaining com-

munication. (Taleb et al., 2007) state in their paper

that a group can be made only by vehicles being able

to maintain a communication link and for that they

must be grouped by velocity headings. The vehicles

must all head in the same direction as well as main-

tain a constant speed within the group to avoid link

breakages due to distance. They assume a very basic

set of criteria which is not sufﬁcient for our problem.

Kagaya et al. (Kagaya et al., 1994) present ways

to group vehicles with drivers and passengers (some

of which with special needs) while also taking into ac-

count routing and scheduling. They deﬁne their prob-

lem as a many-to-many advanced reservation travel

problem. They identiﬁed different characteristics

upon which a group could be built, namely: close-

ness of desired departure times, the location of ori-

gins and destinations, the direction of the trips, the

passenger type and trip purpose, number and capac-

ity of available vehicles. Routing and scheduling al-

gorithms often focus on the operating companies by

minimising their cost, the length of distance travelled

and the empty vehicle travel time/distance. They tend

to neglect preferences of the passengers/customers,

which should be given more importance. The algo-

rithm proposed by Kagaya works with a fuzzy rela-

tion to deﬁne similarity of trips. While not exactly the

same, a parallel can be drawn between our delivery

problem and that of Kagaya. We are less concerned

with the human factor, since our vehicles are fully au-

tomated, and we have no need to combine trips, since

pods cannot exchange packages between them.

Dennisen and Müller (Dennisen and Müller, 2016)

propose preference-based group formation through it-

erative committee elections. Passengers visiting sev-

eral points of interest need to be grouped in a ride-

sharing autonomous vehicle. They express their pref-

erences on their desired destinations and by iteratively

removing the most dissatisﬁed passenger using the

Minisum or Minimax approval committee rules and

recounting votes, a suitable grouping is found. In our

work, while the goal of ﬁnding the best common route

is the same, we consider packages instead of passen-

gers. Hence, the voting approach appears less obvi-

ously suited to our problem.

3 A METHOD FOR CROSS-LSP

PLATOON FORMATION

Coming back to our problem of heterogenous group

building, we need to identify the important charac-

teristics and limitations that will inﬂuence our algo-

rithm. Considering all actors in the trafﬁc scenario,

especially logistic trafﬁc, we get different preferences

making the problem of heterogeneity more and more

complex. We have the clients with the preference of

delivery time (delivery window), the pods themselves

which have a preferred speed, and an energy budget

they must not overdraft (length of route). Then the

different providers would want to keep the costs un-

der a certain margin, cooperate with some but not all

other competing companies, and also fulﬁl a certain

number of orders per time unit.

A simple implementation of a grouping algorithm

to solve our problem of heterogenous group build-

ing is to treat it as an optimisation problem based

on preferences. All the preferences mentioned above

are modelled as constraints in the optimisation prob-

lem with the objective of minimising the route costs

(thus positively affecting the time and the length of

road travelled). The algorithm proposed, presented at

length in subsection 3.4, is deterministic and provides

one or more "best" solutions.

Employing the previously presented fuzzy the-

ory approach would not be a good ﬁt to the prob-

lem simply because the weights given to the criteria

are not constant over the different logistics service

providers. For some it might be more important to

have as many orders fulﬁlled as possible, thus disre-

garding platooning as long as it is not immediately

available; whereas other might prefer to wait for a

platoon instead of travelling alone. So while the set

of preferences might contain the same values for all

pods (mentioned above), their weight in the decision

making process might differ.

In the case where the optimisation problem offers

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

108

more than one similar solution (for example in a Man-

hattan grid scenario), a voting procedure, like the one

presented before, could be employed to determine the

route and the grouping of pods. This would ensure

that route selection is not left up to one entity, but

all potential platooning pods contribute to the selec-

tion. Such an approach would be a secondary decision

mechanism, a fail-safe method to determine a singular

solution.

3.1 Input

The cities network is transformed into a structure

which allows routing; a graph where streets are rep-

resented by edges and connecting points by vertices.

Trafﬁc demand (Q(x,t))is modelled as a collection of

routes given by origin and destination pairs in the

network. This represents background trafﬁc, more

speciﬁcally how many vehicles travel on a speciﬁc

edge(∆N) on average in an hour(∆t). (1) (Treiber and

Kesting, 2013).

Q(x, t) =

∆N

∆t

(1)

This is then transformed into trafﬁc density (ρ(x, t)),

by dividing the number of vehicles per hour(∆N)

through the length of the edge(Σ

), and added on

as that speciﬁc edge’s weight (2) (Treiber and Kest-

ing, 2013).

ρ(x, t) =

∆N

(2)

This will act as our cost to minimise, thus being trans-

lated into time-savings; for the more free an edge is,

the faster would a vehicle transverse it. Since the pods

are electric, the longer they travel and are away from

an energy source, the higher the costs of recharging

will be in order to dispatch them again.

In the above described environment we add pods

and run the optimisation algorithm to determine their

routes. The pods have a given destination as well as a

set of preferences.

3.2 Assumptions

We assume the pods to be functioning independently

while also attempting to form a platoon. A platoon

can be formed by two or more pods. It can only form

at intersections in the network. Platoons form spon-

taneously. Pods must not only be at the same place

in order to platoon but also in the same time space.

A pod only joins a platoon if the expected platooning

cost is lower than that of travelling alone and all its

restrictions respected. After formation, pods travel in

a platoon with a uniform speed.

Short range communication must be present. The

pods communicate with a local agent which performs

the optimisation algorithm. Lastly, it communicates

the groups, common route, length and expected costs

back to the pods.

Platooning is encouraged by trafﬁc management,

through treating platoons as one entity, exactly like

a vehicle would be. Thus, the members of a platoon

all contribute to the cost of a route. We assume the

cost of the route to be the sum of the trafﬁc density

on all edges taken. When travelling in a platoon, all

participants contribute equally with the same amount.

This naturally reduces the cost of the whole route for

all participating pods and encourages the formation of

larger platoons.

3.3 Deﬁnitions

In Table 1 we introduce the basic symbols used in the

formalisation of the optimisation problem, and their

meaning:

Table 1: Symbols and meaning.

Symbol Deﬁnitions

G=(V, E) graph

n ∈ V vertices

e ∈ E edges, e ≡ (i, j)

d(e) trafﬁc density of edge e

l(e) length of edge e

dest destination vertex of a pod, ﬁxed

c(e) cost of a pod to transverse edge e

∗

costs of alone travel for pod v

Ω

maximum delivery time for pod v

maximum length of route for pod v

p(e)

price pod v pays for edge e

NP the number of pods in the platoon

3.4 Optimisation Problem

The goal of the optimisation problem is to have the

longest overlapping route for all pods, all the while

taking into account their particular preferences. This

can be written as an adapted shortest path problem.

min

∑

(i, j)∈E

x(i, j) ∗ c(i, j)

x(i, j) ∈ 0, 1∀edge (i, j)

∑

x(i, j)−

∑

x( j, i) =











1 ⇐⇒ i = Origin

−1 ⇐⇒ i = Destination

0 otherwise.

The variable x indicates whether the edge denoted

by the vertices i and j is used in the shortest path

Cross-provider Platoons for Same-day Delivery

109

(value of one) or not (value of zero). The three cases

represent the ﬂow constrain which ensures that the

route ﬂows through intermediary vertices. Then the

objective function reduces the costs to a minimum.

In the case of platooning, we have to add in a new

variable to cover all routes for all pods, namely y.

Much like x it will have the value of one if it is in-

cluded in the route of any pod, or zero if it is not. This

is the variable that replaces x in the objective function.

The ﬂow constraint remains the same, and we add one

more to ensure that y takes the value of one only when

one or more x for that speciﬁc edge has the value of

one.

This leads us to the formulation of the platooning

optimisation problem:

Given a group of pods Pods, being at the same

vertex O in the graph at the same time; let the routes

for all the pods be given by y(i, j), and the individual

pod routes by x(i, j)

where

min

∑

(i, j)∈E

y(i, j) ∗ d(i, j)

y(i, j), x(i, j) ∈ {0, 1}, ∀edge (i, j)

x(i, j)

≤ y(i, j)∀edge (i, j), ∀pod v

∑

x(i, j)

−

∑

x( j, i)











1 ⇐⇒ i = O

−1 ⇐⇒ i = dest

0 otherwise.

∀v ∈ Pods, ∀(i, j) ∈ E

Preferences are modelled as restrictions in the op-

timisation problem, so in addition to the base problem

presented previously, one could add

∑

(i, j):x(i, j)

c(i, j)

≤ K

∗

, ∀ pod v, cost restric-

tions

∑

x(i, j)

l(i, j) ≤ Λ

∀pod v, length of route re-

strictions

∑

x(i, j)

l(i, j)

≤ Ω

∀pod v, time restrictions

(delivery-window)

and so on.

To incentivise the pods to form a platoon we

grant vehicles a reduction in costs; the more pod in

a platoon, the lower the cost of the edge is. In this

paper’s case, it is equal across all pods forming the

platoon. Therefore we get

p(i, j)

c(e)

∀pod v

p(i, j)

≥ 0 ∀vehicle v and edge (i, j)

and the previous cost restriction becomes

∑

(i, j):x(i, j)

p(i, j)

≤ K

∗

, ∀ pod v.

4 SIMULATION

4.1 Overall Architecture

The simulation kicks off with loading the environ-

ment and starting the internal clock. Then the pods

would be generated, either at speciﬁc locations (de-

livery satellites) or random ones, given a destination

and a set of characteristics and preferences. The pods

follow the best route toward their destination while

also attempting to build platoons. If pods/ pods and

a platoon/ platoons, meet at the same vertex, they

communicate their destination and preferences to a

centralised agent situated at that vertex, which runs

the aforementioned optimisation algorithm. Alterna-

tively, a pod may choose to wait to form or join a

platoon, and communicates the necessary information

upon arrival at the vertex. The algorithm provides

the groups, common route and expected costs for all

pods.

After the pods are grouped in a platoon, they fol-

low the common route until its end, then disband and

continue toward their destination. To accommodate

the ﬁckle nature of urban trafﬁc, the platoon may be

re-routed at each intermediary vertex. The simulation

ends when all pods have successfully reached their

destination.

4.2 Implementation

To execute and run the program, a simulation was

built using Java. For each of the components of

the simulation an appropriate framework was found

and used. For the environment we used Jung

(O’Madadhain et al., 2018) a powerful and ﬂexible

library to model data into a network or a graph. It

comes with routing and analysis algorithms, as well

as additional libraries for visualisation purposes. To

help with visualisation of the routes, we use a heat

map. This is built using colour maps, kindly provided

by (Kraus, 2018). A JXMapViewer2 (Steiger, 2012)

painter was deﬁned, based on existing examples, to

draw the routes.

The optimisation method is executed using the

commercial solver Gurobi (Gurobi, 2018), chosen

since it can be easily introduced in a Java program

as a Jar ﬁle. The process of deﬁning the problem goes

as follows; at ﬁrst, the optimisation environment and

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

110

model are deﬁned. Based on the number of pods in

our theoretical platoon, several x’s as well as one y

are deﬁned as binary variables for each of the edges

in the graph. When creating the y variables, the ob-

jective function is also deﬁned. The next step is to

add the constraints; ﬁrst is the ﬂow constraint, which

is deﬁned for each of the pods; then the x ≤ y con-

straint, and lastly, whichever preference constraints

the user deems as necessary. In the infancy stages of

the project we just used the length constraint, forcing

pods to not take detours longer than a given coefﬁ-

cient × their ideal shortest path. The model is then

optimised, the results saved into another data struc-

ture and the model then made redundant. The results

can be displayed anytime by calling the display func-

tion.

In order to be able to compare our optimisation

approach with a state-of-the-art alternative, we con-

ceived a baseline algorithm, which creates an overlap

of all the pods’ best routes. Assuming the current po-

sition of the pods as the origin point, the best (fastest)

route is identiﬁed with a normal routing algorithm.

After a route has been found for all pods, they are ag-

gregated, and the number of times an edge appear in

a route, counted. This gives the number of pods per

edge, giving a crude approximation of where a pla-

toon could form and who could be a part of it. This

approach is fairly straightforward and easy to calcu-

late, but does not take into account all the possible

restrictions and preferences that may arise.

4.3 Simulation Settings and Input Data

The data acting as the environment for our sim-

ulation can be found at https://github.com/bstabler/

TransportationNetworks (Stabler et al., 2018). We fo-

cused on the Berlin neighbourhoods since they were

the most ﬁnely granular example provided. The net-

work was transformed into a Json ﬁle respecting a

Json schema deﬁned for this speciﬁc purpose.

Trafﬁc demand was not given along with the net-

works but had to be generated based on trips between

given zones. The vertices were divided into zones

which were provided in the trips ﬁle. To simulate the

trips given, random vertices were pulled from each

zone and then the best route between them calculated.

For example, if there were 14 trips from zone 1 to

zone 8, the process would be as follows: pull a ran-

dom vertex from zone 1, pull a random vertex from

zone 8, route, save the edges taken. Repeat this pro-

cess for another 13 times. All the resulting routes

were aggregated and divided by the edges’ length giv-

ing us the trafﬁc density which is then added in the

form of edge weights to the environment. The results

from this process are not constant, but they are similar

enough to be consistent throughout the runs.

4.4 Simulation Output

A simulation run delivers two types of outputs. The

ﬁrst is a visualisation of the network, with edges

painted to represent how many pods travel on them,

in the form of a heat map. The colour range cho-

sen to display the heat map was the Inferno palette

since the spectrum (yellow for hot to dark purple for

cold) is uniformly perceived and understood by the

human eye. (Thyng et al., 2016) Thus, a light yellow

coloured edge would indicate that all pods would use

that edge, whereas a dark purple edge would mean

that it is a part of only one pods’ route. An edge with

no colour means that it is not used in any of the routes.

Figure 1: Heat scale.

Figure 2: Route for a ten pod platoon, on real Berlin net-

work. For legend see Figure 1.

The second output is a log ﬁle consisting of six

parts:

1. the origin and destination vertices. These are

given to help with the understanding and interpre-

tation of results.

2. the routes of individual pods. Since the individual

route is also given by the optimisation function;

the list of xs with the value one is displayed for

each of the pods/destinations.

Cross-provider Platoons for Same-day Delivery

111

3. the route of the ﬂeet. The ys with the value of one

are also displayed, thus rendering the route of the

whole ﬂeet.

4. the number of pods per edge. For each of the

edges displayed in step three, we get the number

of pods which would travel it.

5. the cost savings. For each of the destinations,

the original costs (travelling alone) are displayed

along with the new costs if the pods were to pla-

toon how the optimiser suggests.

6. the system optimal solution costs, i.e. the sum of

the weights of all edges mentioned in step three.

The baseline algorithm follows the same structure,

creating ﬁrst a heat map visualisation of the network

and then presenting written results following the same

6 step pattern as before.

5 RESULTS

Experiments were run on a set of real and syn-

thetic environments using both realistic and gener-

alised background trafﬁc density. For the real envi-

ronments we used the Berlin networks mentioned in

Chapter 4 coupled with realistic trafﬁc density data.

For the synthetic environments a simple ﬁve by ﬁve

vertex Manhattan grid was created with higher trafﬁc

density on the outside edges and lower in the center

of the network. The algorithm was run both with and

without restrictions (preferences), in our experiments

case length of route and cost restrictions, performing

well. All common routes could be determined and the

number of pods in the platoon speciﬁed.

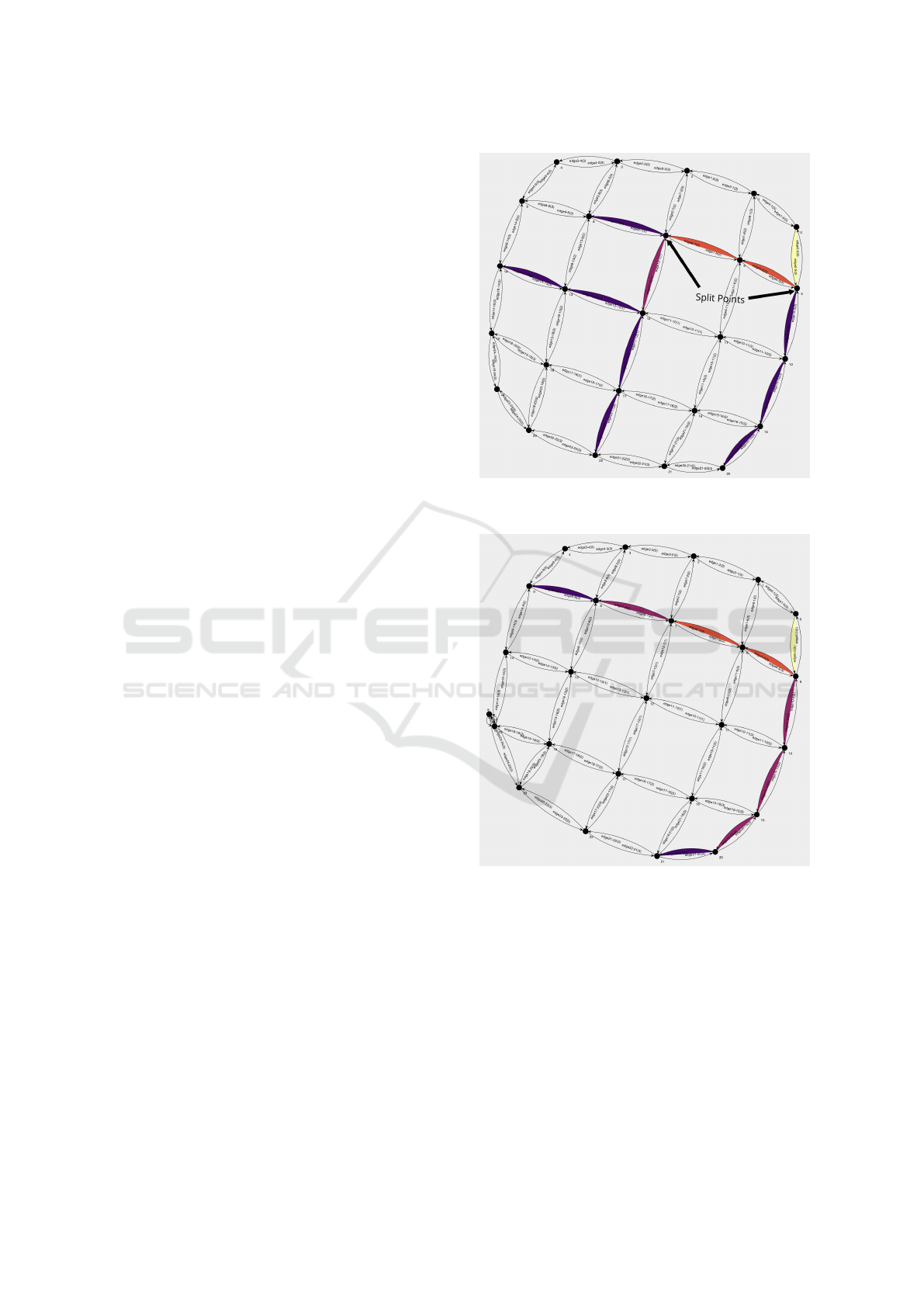
When studying the resulting heat maps, one can

easily identify potential split and also join points in

the routes. Whenever the colour changes to colder

it means pods would leave the platoon and whenever

it would get warmer, pods would potentially join the

platoon. For ease of visualisation and understand-

ing, the remaining ﬁgures exemplifying results will be

shown on a smaller synthetic environment with lower

edge weights in the center and higher on the outside.

To identify join points, we must assume that two

groups of pods are platooning from different origins

and spontaneously meet at a different vertex in the

network. If their routes have a common set of edges,

they may choose to form an even larger platoon. To

illustrate we have the following example presented in

ﬁgures 4, 5 and 6. Each of the problems has a sepa-

rate instance of the optimisation algorithm set as their

route, and upon meeting, would run another one to

determine the combined platoon.

Figure 3: Route for ﬁve pods, synthetic network, featuring

split points. For legend see Figure 1.

Figure 4: Route for ﬁve pods, synthetic network, starting

vertex 0. For legend see Figure 1.

We can see that the two problems (Figures 4 and

5), have edges 7-8 and 8-9 in common, so vertex 7

could act as a join point. Here a four pod platoon

could be created, with two pods pertaining to the pla-

toon starting from vertex 0 and two other from the

platoon starting from vertex 2 (Figure 6).

5.1 Comparison to Baseline Algorithm

To illustrate this we go back to our real-life example

of the Berlin Tiergarten neighbourhood. To mimic

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

112

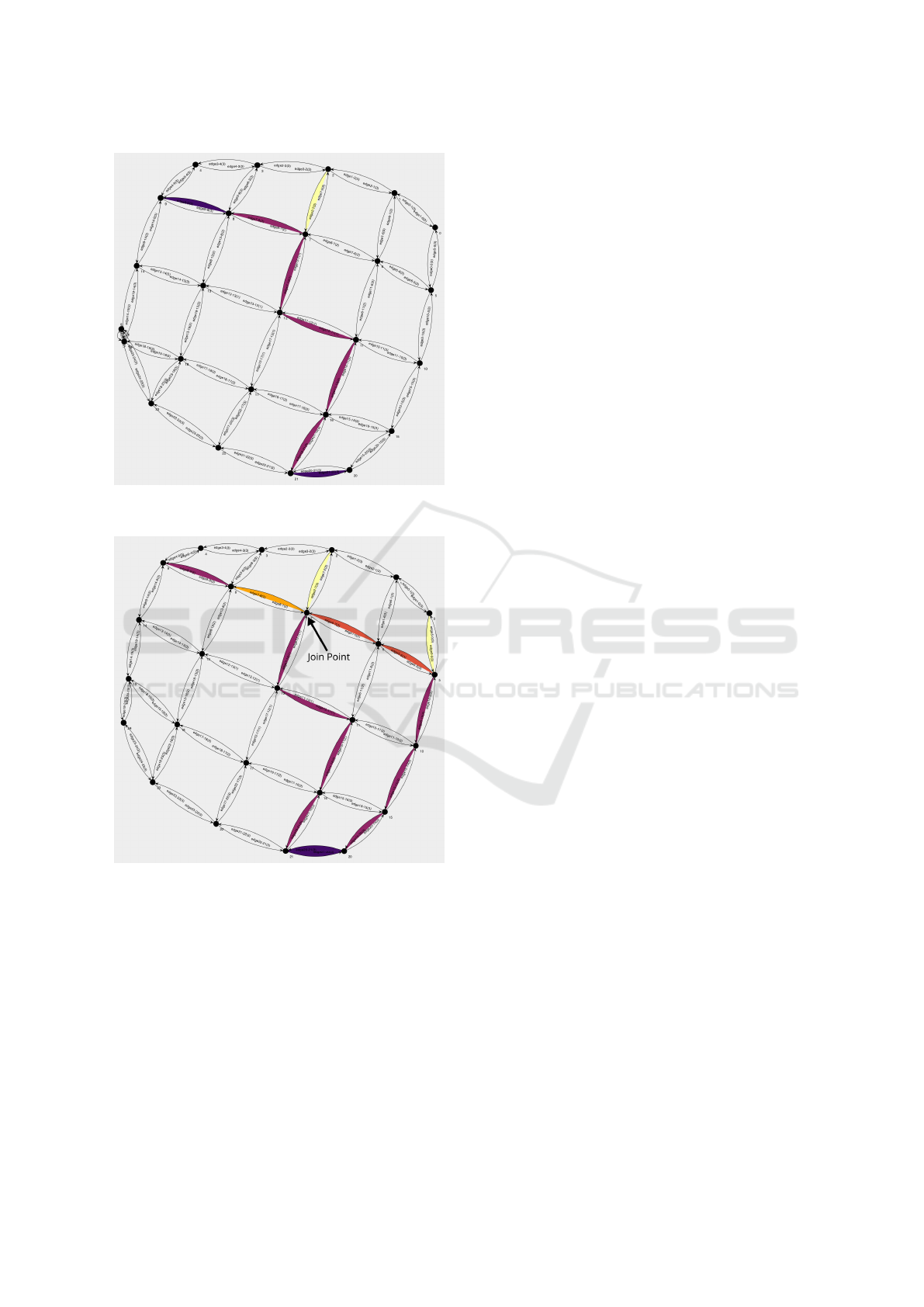
Figure 5: Route for ﬁve pods, synthetic network, starting

vertex 2. For legend see Figure 1.

Figure 6: Route for ten pods, synthetic network, two start-

ing vertices, featuring join point. For legend see Figure 1.

real trafﬁc, we assumed the pods would meet at the

most popular intersection (where most trafﬁc takes

place) and considered that our origin point. For the

destinations, we selected the vertices where the sub-

traction of entering and exiting vehicles was the low-

est. With these origin-destination pairs we performed

both algorithms and studied their results as far as costs

are concerned. In Table 2 the results are presented; the

ﬁrst column denotes how many pods meet and could

platoon, the second and third column present the over-

all costs for the overlapping and optimiser algorithms

respectively. The fourth column presents the pods,

and the last four columns show their costs; if they

were to travel alone, platooning by the overlapping

solution, platooning by the optimiser solution, and ﬁ-

nally the cost of the tour with the optimiser solution

without the platooning incentives.

In some cases, especially for smaller platoons, the

algorithms deliver the same solution, like the case

presented with six pods. With eight or ten pods we

see how the optimisation algorithm produces a bet-

ter solution than the simplistic algorithm. This is

due to the fact that the resulting route from the op-

timiser presents the system optimal solution; provid-

ing the longest, but most cost-efﬁcient common route

of the pods. When looking into the simple overlap-

ping example, we get the pod speciﬁc optimal solu-

tion, which is to be expected.

We can also see, in the case of pod v8 for both

of the last cases, that in our optimiser approach it is

included in a platoon, whereas for the overlapping one

it travels alone.

Although one can see that the overlapping solu-

tion provides more cost savings for individual pods,

its simplistic method would not be suitable as a com-

plete solution, since the preferences cannot be mod-

elled in. The optimiser approach treats preferences as

restrictions on the system and would provide a more

complete solution to the platooning problem.

5.2 Runtime Performance Analysis

As far as performance of the algorithm is concerned,

the runtime increases exponentially with the number

of pods as expected, but due to the nature of our sce-

nario this bears little importance. In a trafﬁc scenario

where the pods must be close in both space and time,

we do not foresee more than twenty individual pods

forming a platoon. In the case where more platoons

would join forming a larger one, they still act as in-

dividual pods, thus keeping the optimisation problem

small. Even though the optimisation approach is sub-

stantially slower, it still performs within an acceptable

margin of 23 seconds for ﬁfty pods. For a more realis-

tic scenario of ﬁve or ten pods, it performs in 2.8 and

3.7 seconds respectively.

In Figure 7 both algorithms’ performance is por-

trayed, with each point representing the runtime of

one instance of the optimisation problem / overlap-

ping algorithm respectively for the number of vehicles

speciﬁed.

Cross-provider Platoons for Same-day Delivery

113

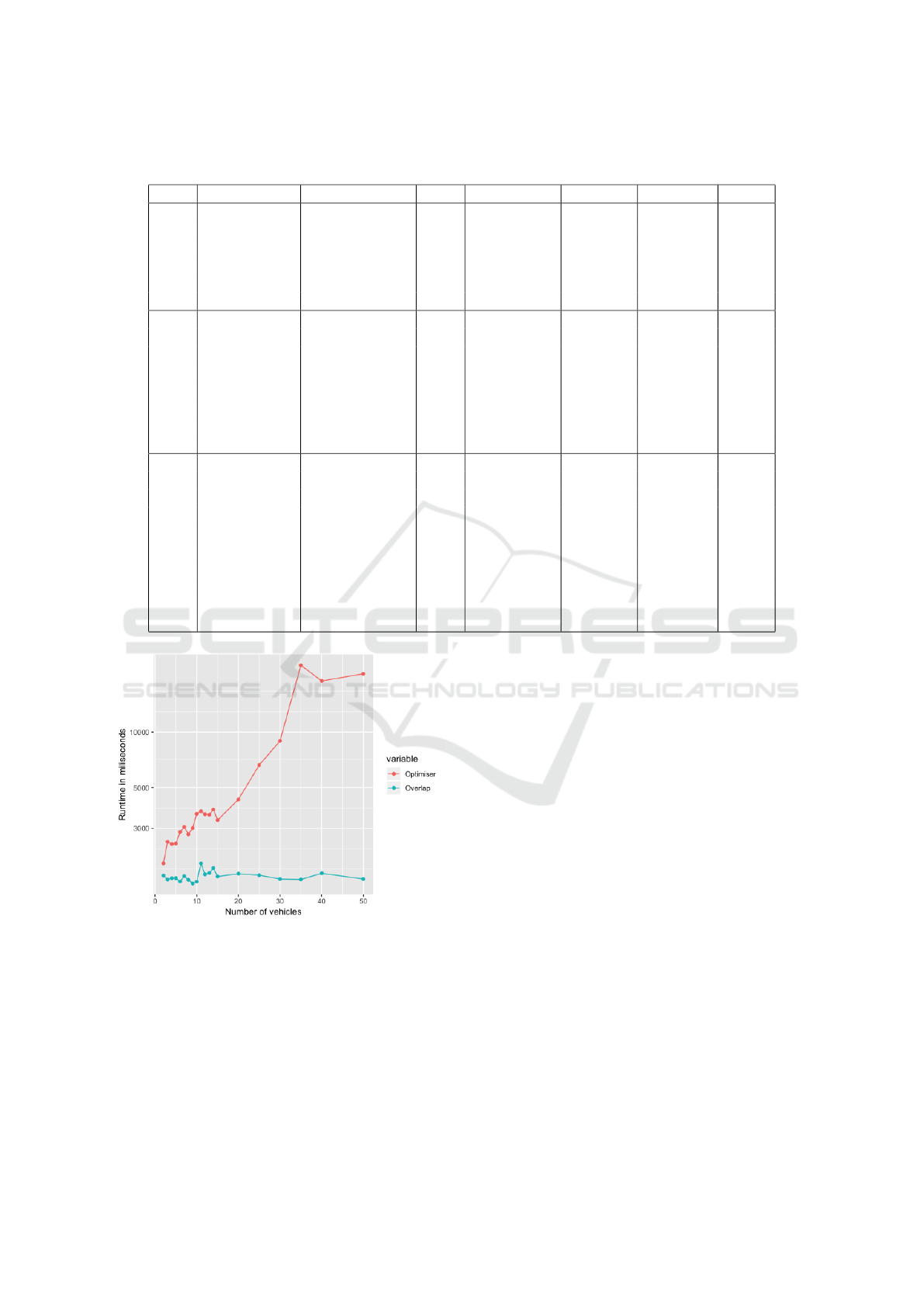
Table 2: Resulting costs comparison of the two algorithms. Costs represented in trafﬁc density, measured in number of

vehicles per length unit of the edge.

Pods Total Overlap Total Optimiser Pods Alone-travel Overlap Optimiser Tour

6 51954 51954 v1 3510 1010.58 1010.58 3510

v2 4818 2318.58 2318.58 4818

v3 5765 3508.58 3508.58 5765

v4 16578 16329.5 16329.5 16578

v5 30702 28538.25 25538.25 30702

v6 497 248.5 248.5 497

8 75103 73161 v1 3510 773.75 880.3 3510

v2 4818 2033.25 3265.5 6868

v3 5765 3352.75 3378.3 5765

v4 16578 16329.5 16329.5 16578

v5 30702 28394 28408 30702

v6 497 248.5 248.5 497

v7 16330 13545.25 13700.3 16330

v8 10426 10426 6950.5 10553

10 119682 98455 v1 3510 677.58 880.3 3510

v2 4818 1937.08 3265.5 6868

v3 5765 3256.58 3378.3 5765

v4 16578 16274.3 5484 16578

v5 30702 24762.83 28408 30702

v6 497 193.3 124.25 497

v7 16330 13449.08 13700.3 16330

v8 10426 10426 6950.5 10553

v9 25113 24892 11066.38 27742

v10 29752 23812.83 25186.58 41862

Figure 7: Comparing the two performances.

5.3 Discussion

Overall the algorithm performs well and gives a vi-

able route and a possible grouping for the pods to

platoon. It provides the system optimal route, which

may not guarantee the best individual cost savings for

the pods, but a substantial cost saving nevertheless.

When dealing with a heterogenous group, an individ-

ual optimal solution would most likely mean that the

pod is not part of the group, and since costs are equal

across all pods, the system optimum is the individual

optimum as well. The optimisation method is simple,

easy to understand and to use, however it may prove

to be slow when comparing to other more novel ap-

proaches. It makes up for it though, by being a very

straight forward and precise way of including prefer-

ences into the routing and grouping algorithm.

The next steps of this research, are to complete

this program creating a fully functioning simulation,

including discreet time and moveable pods in the en-

vironment. With the inclusion of time, more restric-

tions can be added (such as delivery windows and

speed) thus adding another degree of realism to the

results. To further improve on the accuracy of the sim-

ulation, we plan on using more real cities with exact

visualisation by means of Graphhopper (Karich et al.,

2018)and Open Street Map (OpenStreetMap, 2018).

This information is readily available and easy to im-

plement but trafﬁc density data is scarce and hard to

ﬁnd.

This application will then be further developed

into a fully ﬂedged agent-based simulation of urban

logistic trafﬁc, which is immensely useful in the fur-

ther research on urban platooning.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

114

6 CONCLUSION

Using self driving electric vehicles to carry out pack-

age deliveries in cities is a logical next step for lo-

gistic companies. Not only do they cut costs on em-

ploying human drivers, but they also cut down on

harmful emissions in an already polluted environ-

ment. Given that these vehicles are small for the time

being, they can only carry one or very few packages

in one trip. Having many such vehicles swarming an

already overcrowded network would be chaotic and

confusing, so for their sake as well as the general traf-

ﬁc, they could form platoons and travel in a convoy.

To ensure that groups are formed, all pods are vi-

able for platooning, but can impose certain limita-

tions, whether they are characteristics (such as speed),

restrictions (must arrive at their destination by a spe-

ciﬁc time) or preferences (would platoon with some

but not all other pods).

This paper presents a simple and ﬂexible algo-

rithm in order to create cross-provider platoons of au-

tonomous electric pods used for same day delivery.

Routing and grouping are handled by an optimisation

problem, treating features and preferences as restric-

tions. The objective function is minimising the pla-

toons cost, which is modelled as trafﬁc density for

each edge transversed. The aforementioned charac-

teristics and limitations are represented by linear con-

straints. This offers more freedom to add or limit the

system without much difﬁculty, all the while main-

taining a clear and optimal result.

The program performs well and is accurate even

with a large number of vehicles, giving not only the

route of the platoon, but each individual pods route as

well.

ACKNOWLEDGMENTS

This work has been funded by the Deutsche

Forschungsgemeinschaft (DFG, German Research

Foundation) under Grant 227198829 / GRK1931.

The focus of the SocialCars Research Training Group

is on signiﬁcantly improving the city‘s future road

trafﬁc, through cooperative approaches. The ﬁrst au-

thor gratefully acknowledges helpful discussions with

Prof. Dirk Mattfeld, and the help of Nelly Nyeck

Mbialeu Nicaise in the data transposing process.

REFERENCES

Ali, A., Garcia, G., and Martinet, P. (2015). Urban pla-

tooning using a ﬂatbed tow truck model. In Intelligent

Vehicles Symposium (IV), 2015 IEEE, pages 374–379.

IEEE.

Amir, A. and Lindenbaum, M. (1998). A generic grouping

algorithm and its quantitative analysis. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

20(2):168–185.

Amoozadeh, M., Deng, H., Chuah, C.-N., Zhang, H. M.,

and Ghosal, D. (2015). Platoon management with co-

operative adaptive cruise control enabled by vanet. Ve-

hicular communications, 2(2):110–123.

Bengtsson, H. H., Chen, L., Voronov, A., and Englund,

C. (2015). Interaction protocol for highway platoon

merge. In Intelligent Transportation Systems (ITSC),

2015 IEEE 18th International Conference on, pages

1971–1976. IEEE.

Biswas, S., Tatchikou, R., and Dion, F. (2006). Vehicle-

to-vehicle wireless communication protocols for en-

hancing highway trafﬁc safety. IEEE communications

magazine, 44(1):74–82.

Crainic, T. G. (2008). City logistics. In State-of-the-Art

Decision-Making Tools in the Information-Intensive

Age, pages 181–212. INFORMS.

Crainic, T. G. and Sgalambro, A. (2014). Service network

design models for two-tier city logistics. Optimization

Letters, 8(4):1375–1387.

Dennisen, S. L. and Müller, J. P. (2016). Iterative commit-

tee elections for collective decision-making in a ride-

sharing application. In ATT@ IJCAI.

Gevaers, R., Van de Voorde, E., and Vanelslander, T.

(2011). Characteristics and typology of last-mile lo-

gistics from an innovation perspective in an urban

context. City Distribution and Urban Freight Trans-

port: Multiple Perspectives, Edward Elgar Publish-

ing, pages 56–71.

Gordon, I. E. (2004). Theories of visual perception. Psy-

chology Press.

Gurobi (2018). Gurobi optimization.

Havaldar, P., Medioni, G., and Stein, F. (1994). Extraction

of groups for recognition. In European Conference on

Computer Vision, pages 251–261. Springer.

Kagaya, S., Kikuchi, S., and Donnelly, R. A. (1994). Use

of a fuzzy theory technique for grouping of trips in

the vehicle routing and scheduling problem. European

Journal of Operational Research, 76(1):143–154.

Karich, P., Schröder, S., and Zilske, M. (2018). Graphhop-

per.

Khalifa, A., Kermorgant, O., Dominguez, S., and Mar-

tinet, P. (2018). Vehicles platooning in urban envi-

ronment: Consensus-based longitudinal control with

limited communications capabilities. In International

Conference on Control, Automation, Robotics and Vi-

sion.

Kraus, P. (2018). Colormap.

Lioris, J., Pedarsani, R., Tascikaraoglu, F. Y., and Varaiya,

P. (2017). Platoons of connected vehicles can double

throughput in urban roads. Transportation Research

Part C: Emerging Technologies, 77:292–305.

Mojena, R. (1977). Hierarchical grouping methods and

stopping rules: An evaluation. The Computer Jour-

nal, 20(4):359–363.

Cross-provider Platoons for Same-day Delivery

115

O’Madadhain, J., Fisher, D., and Nelson, T. (2018). Jung,

java universal network/graph framework.

OpenStreetMap (2018). Open street map.

Robinson, T., Chan, E., and Coelingh, E. (2010). Operating

platoons on public motorways: An introduction to the

sartre platooning programme. In 17th world congress

on intelligent transport systems, volume 1, page 12.

Scherr, Y. O., Neumann-Saavedra, B. A., Hewitt, M., and

Mattfeld, D. C. (2018). Service network design for

same day delivery with mixed autonomous ﬂeets.

Transportation research procedia, 30:23–32.

Schindler, J., Dariani, R., Rondinone, M., and Walter, T.

(2018). Dynamic and ﬂexible platooning in urban ar-

eas. In AAET Automatisiertes und vernetztes Fahren

conference 2018.

Stabler, B., Bar-Gera, H., and Sall, E. (2018). Transporta-

tion networks for research.

Steiger, M. (2012). jxmapviewer2 github.

Swaroop, D. and Hedrick, J. K. (1999). Constant spacing

strategies for platooning in automated highway sys-

tems. Journal of dynamic systems, measurement, and

control, 121(3):462–470.

Taleb, T., Sakhaee, E., Jamalipour, A., Hashimoto, K.,

Kato, N., and Nemoto, Y. (2007). A stable routing pro-

tocol to support its services in vanet networks. IEEE

Transactions on Vehicular technology, 56(6):3337–

3347.

Thyng, K. M., Greene, C. A., Hetland, R. D., Zimmerle,

H. M., and DiMarco, S. F. (2016). True colors of

oceanography: Guidelines for effective and accurate

colormap selection. Oceanography, 29(3):9–13.

Treiber, M. and Kesting, A. (2013). Trajectory and ﬂoating-

car data. In Trafﬁc Flow Dynamics, pages 15–18.

Springer.

Wald, A. and Wolfowitz, J. (1948). Optimum character of

the sequential probability ratio test. The Annals of

Mathematical Statistics, pages 326–339.

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

116