
Gaussian Model Trees for Traffic Imputation
Sebastian Buschj
¨
ager, Thomas Liebig and Katharina Morik
Artificial Intelligence Unit, TU Dortmund University, Germany
Keywords:
Gaussian Processes, Ensemble, Product of Experts, Parallel.
Abstract:
Traffic congestion is one of the most pressing issues for smart cities. Information on traffic flow can be used
to reduce congestion by predicting vehicle counts at unmonitored locations so that counter-measures can be
applied before congestion appears. To do so pricy sensors must be distributed sparsely in the city and at
important roads in the city center to collect road and vehicle information throughout the city in real-time.
Then, Machine Learning models can be applied to predict vehicle counts at unmonitored locations. To be
fault-tolerant and increase coverage of the traffic predictions to the suburbs, rural regions, or even neighboring
villages, these Machine Learning models should not operate at a central traffic control room but rather be
distributed across the city.
Gaussian Processes (GP) work well in the context of traffic count prediction, but cannot capitalize on the vast
amount of data available in an entire city. Furthermore, Gaussian Processes are a global and centralized model,
which requires all measurements to be available at a central computation node.
Product of Expert (PoE) models have been proposed as a scalable alternative to Gaussian Processes. A PoE
model trains multiple, independent GPs on different subsets of the data and weight individual predictions based
on each experts uncertainty. These methods work well, but they assume that experts are independent even
though they may share data points. Furthermore, PoE models require exhaustive communication bandwidth
between the individual experts to form the final prediction. In this paper we propose a hierarchical Product of
Expert model, which consist of multiple layers of small, independent and local GP experts. We view Gaussian
Process induction as regularized optimization procedure and utilize this view to derive an efficient algorithm
which selects independent regions of the data. Then, we train local expert models on these regions, so that
each expert is responsible for a given region. The resulting algorithm scales well for large amounts of data and
outperforms flat PoE models in terms of communication cost, model size and predictive performance. Last,
we discuss how to deploy these local expert models onto small devices.
1 INTRODUCTION
With increasing integration of ubiquitous comput-
ing in urban areas, smart cities became more and
more a reality (Bowerman et al., 2000). One of the
most pressing issues in todays cities is traffic conges-
tion (Artikis et al., 2014). Data collection can help
to reduce traffic congestion by providing information
on vehicle counts at monitored locations in real-time
throughout the entire city. Furthermore, Machine
Learning models can use this data to impute vehicle
counts at unmonitored locations and to predict vehi-
cle counts in the future. This way, countermeasures
to congestion can be applied by a smart city before it
even occurs.
So far, sensors have been deployed in different
cities across the world to measure traffic counts, e.g.,
the city of Dublin (Artikis et al., 2014). Few works
exist which capitalizes on the vast amount of data
available in these cities (Schnitzler et al., 2014; Rieke
et al., 2018). To enable real-time predictions of traffic
counts in the entire city, a forecasting system should
have the following properties: (1) Sensing devices
should be as small and as energy efficient as possible
to minimize running costs (2) Sensing devices should
be low-priced to minimize initial investment costs (3)
Data should not be processed globally to minimize
communication overhead and maximize privacy (4)
Prediction models should be small, but sufficiently
accurate to be executed on the sensing devices (5)
The system should report possible locations for sen-
sor placement with respect to its forecasting accuracy.
To make things a little more concrete, consider for
example the ESP8266 microchip
1
. The ESP8266 con-
tains a 32− bit CPU running at 80 Mhz with 32 KiB
1
https://tinyurl.com/yd8jhqe2
Buschjäger, S., Liebig, T. and Morik, K.
Gaussian Model Trees for Traffic Imputation.
DOI: 10.5220/0007690502430254
In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 243-254
ISBN: 978-989-758-351-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
243

instruction RAM and 80 KiB user RAM. It supports
IEEE 802.1 b/g/n Wi-Fi and is optimized for low-
power scenarios, in which the chip needs to preserve
energy over longer periods of time. It is cheaply avail-
able for around 5$. Due to its low price and inbuilt
networking capabilities, such a device is ideal to be
distributed around the city. However, its scarce mem-
ory resources require small models. Furthermore,
communication should be limited to preserve energy.
Gaussian Processes (GP) have shown great suc-
cess in the context of traffic count imputation (Liebig
et al., 2013; Liebig et al., 2017). However, GPs are
a centralized and computationally expensive model,
which cannot run on small, sensing devices. Product
of Expert (PoE) models have been proposed as a scal-
able alternative to Gaussian Processes, which can be
viewed as a Bayesian ensemble approach. Instead of
training one large GP, PoE models train many small
GPs on different subsets of data and combine the pre-
dictions of each individual GP by a weighted vote.
PoE models scale well with large amounts of data
while requiring few computation resources for each
individual expert. However, to form the final predic-
tion, all expert models need to exchange their predic-
tions. Thus, if we distribute the individual experts
across the city we still require extensive communica-
tion bandwidth to communicate the final prediction.
Furthermore, we note that PoE models assume that
individual experts are independent of each other. This
assumption is violated, if two experts in the model
share the same data point during training, which re-
quires the careful construction of individual experts.
In this paper, we propose a hierarchical PoE
model, which explicitly constructs independent ex-
pert models. To do so, we view Gaussian Processes as
the solution to a regularized optimization problem and
use this view to derive an efficient algorithm which
splits the data into independent regions. Then, we
train individual experts on each region, so that every
expert in the resulting PoE model is responsible for
exactly one region. This way, our approach splits the
city into increasingly smaller regions and we can use
the regions to distribute the sensors across the city.
Since each expert is responsible for its own region, no
further communication is required. Our contributions
are:
• We establish a connection between PoE models
and the full Gaussian Process by using the under-
laying optimization problem.
• We use this connection to derive an efficient algo-
rithm to construct a hierarchical PoE model which
promotes the independence of the local experts.
• The resulting algorithm improves the perfor-
mance of PoE models while having comparable
runtime.
• The resulting algorithm does not require commu-
nication and minimizes the workload on the sens-
ing devices during application.
The paper is organized as the following. The next
chapter introduces Gaussian Processes and our nota-
tion. Then we discuss Product of Expert models. In
section 4 we give a detailed derivation of our algo-
rithm along with a runtime analysis and considera-
tions the deployment of the model. Section 5 cover
the related work and in section 6 we present experi-
ments on three different data-sets for traffic imputa-
tion and from the context of smart cities in general.
We conclude this paper in section 7.
2 GAUSSIAN PROCESSES
We quickly review the Gaussian Process frame-
work and introduce our notation. A comprehensive
overview of Gaussian Processes can be found in (Ras-
mussen and Williams, 2006).
We consider a regression problem y = f (x) + ε with
noise ε ∼ N (0,σ
2
) and x ∈ R
d
. Our goal is to es-
timate f based on a training set D = (X,y), where
X = [x
1
,. ..,x
n
] ∈ R
n×d
denotes the matrix of all ob-
servations andy = (y
1
,. ..,y
n
) ∈ R
n
denotes the vector
of all targets.
The Gaussian Process framework models f by assum-
ing an infinite dimensional Gaussian distribution over
the target y. Since every marginal distribution of a
Gaussian distribution is also normal distributed, the
target vectory is normal distributed with mean vector
m and covariance Σ. We model m by using a suit-
able mean-function m(·), e.g. m(·) = 0. The covari-
ance matrix Σ can be modeled by introducing a kernel
function k(x
i
,x
j
) that measures the similarity between
x
i
and x
j
. In short, we write K(D) = Σ + σ
2
· I =
[k(x
i
,x
j
)]
i, j
+ σ
2
· I , where I denotes the n × n iden-
tity matrix. Given a new, yet unseen observationx, we
wish to predict the corresponding target y. Since all
marginals of a Gaussian distribution are also Gaussian
distributed, it is possible to compute the distribution
N( f (x), σ(x)) to which a new, unseen observation x
belongs:
f (x) = m(x) + K(x,D)K(D)
−1
· (y − m) (1)
σ(x) = k(x,x) + σ
2
− K(x, D)K(D)
−1
K(D,x) (2)
Here K(D) denotes the kernel matrix between all ob-
servations in D and K(x,D) denotes the kernel (col-
umn) vector betweenx and all observations in D. Re-
spectively, K(D,x) denotes the row vector between x
and all observations in D.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
244

The maximum likelihood prediction for a Gaus-
sian distribution is its mean, hence y = f (x) is a suit-
able prediction, in which σ(x) provides some sense
of reliability. If σ(x) is relatively small, the true y
will not deviate much from f (x) and thus y = f (x) is
a good prediction, whereas larger σ(x) tells, that the
true y might deviate quite a lot from the prediction
f (x). Note that, because GPs are a Bayesian model,
it offers the possibility for hyperparameter optimiza-
tion (e.g. kernel weights) based on maximizing the
marginal log-likelihood of the data (cf. (Rasmussen
and Williams, 2006)).
3 PRODUCT OF EXPERTS
Gaussian Processes do not scale well with larger data
sets, because K(D) needs to be inverted which gener-
ally requires O(n
3
) runtime. Product of Expert mod-
els have been introduced as an ensemble technique for
GPs (Deisenroth and Ng, 2015). A PoE model consist
of m small independent GP models. More formally,
let D
k
⊆ D denote a subset of the training, then the
generalized PoE model factorizes the marginal like-
lihood of the full GP into a product of m individual
likelihoods:
p(y|D) ≈
m
∏
k=1
β
k
p
k
(y|D
k
) (3)
where β
k
denotes the weight of the kth expert and
p
k
denotes its probability distribution. Deisenroth
and Ng show (Deisenroth and Ng, 2015), that many
well-known approximation schemes for Gaussian
Processes can be understood in this framework of
generalized PoE models, where different weighting-
schemes are the result of different prior assumptions.
In its most general form equation 3 gives rise to the
following prediction rule (Deisenroth and Ng, 2015)
f
PoE
(x) =
σ
PoE
(x)
2
m
∑
k=1
β
k
σ
−2
k
(x) f
k
(x) (4)
σ
PoE
(x) =
m
∑
k=1
β
k
σ
−2
k
(x) (5)
Here f
k
(x) and σ
k
(x) denote the predictive mean and
variance of the kth experts using the subset of data
D
k
. Note, that each individual expert is based on
D
k
instead of D, which only requires the inversion
of K(D
k
) instead of K(D). Additionally, the train-
ing of this model can easily be performed in paral-
lel. In this sense, PoE models are similar to bag-
ging (Breiman, 1996), in which we train classifiers
on different subsets of features and/or data to perform
a majority vote . However PoE models also incorpo-
rate each experts uncertainty (the predictive variance)
to weight it individually instead of performing a sim-
ple majority vote. Additionally, we note, that a PoE
model retains this uncertainty information by also of-
fering a predictive variance and retains the possibility
to perform hyperparameter optimization by the means
of log-likelihood maximization (Deisenroth and Ng,
2015).
4 GAUSSIAN MODEL TREES
PoE models offer a scalable alternative to the full GP
model, but rely on the critical assumption that indi-
vidual experts are independent of each other. Current
literature suggests using random subsets of data to
train the experts (see e.g. (Deisenroth and Ng, 2015)),
which violates the independence assumption if sam-
pling is not done with care. Furthermore, we see
that in order to compute the overall prediction com-
municate between all experts is necessary, which can
quickly lead to a communication bottleneck.
In this section, we derive an efficient algorithm
to train hierarchical PoE models which respect the
independence assumption. To do so, we utilize the
optimization-based view of Gaussian Processes to se-
lect representative data points. Each representative
defines an independent region, which can either be
used to train a local expert model or which can be split
further to create a more refined splitting. We show
that the resulting model can be seen as a generalized
PoE model, in which each expert is responsible for
exactly one region.
To keep the derivation short, we will assume
m(·) = 0 in the following. Note, that this is not a real
restriction, because we can scaley to have zero mean.
We start our derivation by noting that equation 1 can
be derived as the solution for the following optimiza-
tion problem (Rasmussen and Williams, 2006):
arg min
f ∈H
1
2
|| f ||
2
H
+
1
2σ
2
n
∑
(x,y)∈D
(y
i
− f (x))
2
(6)
Here H denotes a reproducing kernel Hilbert space
with kernel function k. For a positive definite ker-
nel we note that || f ||
2
H
=
∑
N
i=1
∑
N
j=1
α
i
α
j
k(x
i
,x
j
) ≥ 0.
Let A ⊆ D denote a set of c inducing points for a
GP, and B = D \ A the set of remaining points. Fur-
thermore, let f
A
denote a function based on A with
|| f
A
||
2
H
=
∑
(x
i
,y
i
)∈A
∑
(x
j
,y
j
)∈A
α
i
α
j
k(x
i
,x
j
). Similar,
let f
B
denote a function based on B with || f
B
||
2
H
=
∑
x
i
∈B
∑
x
j
∈B
β
i
β
j
k(x
i
,x
j
). Now, if we find two sets
A and B with k(x
i
,x
j
) ≈ 0 for x
i
∈ A and x
j
∈ B,
the optimization problem 6 decomposes into two dis-
joint problems which can both be solved indepen-
dently from each other by using equation 1:
Gaussian Model Trees for Traffic Imputation
245

arg min
f
A
∈H , f
B
∈H
1
2
|| f
A
||
2
H
+
1
2σ
2
n
∑
(x,y)∈A
(y − f
A
(x))
2
+
1
2
|| f
B
||
2
H
+
1
2σ
2
n
∑
(x,y)∈B
(y − f
B
(x))
2
(7)
We note, that this formulation resembles the in-
dependence assumption in equation 3 from an
optimization-based point of view. In general, we can
split problem 6 into m small, non-related subproblems
D
i
which can be dealt with in parallel:
arg min
A
i
⊆D
i
m
∑
i=1
1
2σ
2
n
∑
(x,y)∈D
i
f
D
i
(x) −y
2
+
1
2
|| f
D
i
||
2
H
!
s.t. |A
i
| ≤ c
and k(x
i
,x
j
) ≈ 0 ∀(x
i
,y
i
) ∈ D
i
,(x
j
,y
j
) ∈ D
j
for
m
[
i=1
D
i
= D,D
i
∩ D
j
=
/
0 ∀i 6= j
(8)
To solve optimization problem 8, we need to eval-
uate every possible combination of subsets D
i
, which
can be difficult for large D. For isotropic kernels
k(x
i
,x
j
) which depend on the distance between x
i
and x
j
we can represent each region D
k
by its cen-
ter. Then, we essentially need to find a set of centers
A ⊂ D with |A| = c, so that the similarity between
centers k(x
i
,x
j
) ≈ 0 forx
i
,x
j
∈ A. More formally, we
wish to select those points, so that the values on the
off-diagonal of K(A) are close to zero. Interestingly,
the log-determinant of K(A) precisely captures this
intuition (Buschjaeger et al., 2017), which gives rise
to the following optimization problem:
arg max
A⊂D,|A|=c
1
2
logdet(I + aK(A)) (9)
where a > 0 is a scaling-parameter and I is the c × c
identity matrix.
For intuition, consider the two extreme cases: As-
sume that we select the same point x with k(x,x) =
1 exactly c-times. Then we can lower-bound
logdet(I + aK(A)) ≥ 1 + ac (Buschjaeger et al.,
2017). Similarly, suppose we select c completely dif-
ferent data points, so that k(x
i
,x
j
) = 0 for all i, j. In
this case we have logdet(I + aK(A)) = c.
Problem 9 has already been discussed in liter-
ature in the context of the Informative Vector Ma-
chine (IVM) (Lawrence et al., 2003). The IVM is a
GP deviate which selects a subset of data points in
a greedy manner and keeps track of the GPs poste-
rior distribution. Based on a diversity argument, the
authors propose to iteratively select that point, which
covers the training data best, that is maximizing the
prior GP entropy
1
2
log|K(A)|. In (Seeger, 2004)
the authors note, that the function logdet(K(A)) is
sub-modular. Intuitively, a sub-modular function ful-
fills the property of diminishing returns: Selecting
the first representative will greatly increase the func-
tion value of logdet(K(A)), whereas selecting the last
point will increase the function value to a lesser ex-
tent. Nemhauser has shown in (Nemhauser et al.,
1978), that the simple greedy algorithm depicted in
algorithm 1, has a guaranteed performance of at least
(1 − (1/e)) ≈ 63%.
Algorithm 1 : Simple greedy algorithm for sub-modular
function maximization.
1: function SIMPLEGREEDY(A, f ,c)
2: S ←
/
0
3: for 1,... ,c do
4: e = argmax{ f
S∪{e}
(x) − f
S
(x)|x ∈ A}
5: S ← S ∪ {e}
6: end for
7: end function
Algorithm 1 proceeds in a simple greedy fashion:
Given a set of objects A and a sub-modular function
f , it iteratively picks that element from A which max-
imises the function value f the most. As shown by
Lawrence etal. in (Lawrence et al., 2003), the max-
imum gain ∆(e|S) = f
S∪{e}
(x) − f
S
(x) of the entropy
of a GP is given by the maximum predictive variance,
that is ∆(x|S) = σ
S
(x).
It follows that we can solve problem 9 with a guar-
anteed performance in linear time by rating each point
x ∈ D
i
in the current region using the predictive vari-
ance σ
A
(x) given the current set of inducing points
A.
Before presenting our final algorithm, we quickly
summarize the overall approach: Our goal is to solve
problem 8. As argued above, we can solve the in-
dependent sub-problems
1
2σ
2
n
∑
(x,y)∈D
i
f
D
i
(x) −y
2
+
1
2
|| f
D
i
||
2
H
by using eq. 1. Thus, the question remains
how to construct the regions D
i
. To do so, we use
the simple greedy algorithm presented above to com-
pute the set of c most informative points. Then, we
view each selected point as a representative for a re-
gion and split the training data into c independent re-
gions D
i
. After that, we either continue to split these
regions into even smaller regions by solving problem
9 on those regions or we train the full Gaussian Pro-
cess using eq. 1 and the data D
i
for a given region.
Algorithm 2 depicts the resulting algorithm: Start-
ing with the complete dataset D, we first compute a
small ‘summary’ subset A in a greedy, manner. Note,
that for A =
/
0 we cannot invert K(A) since it is empty.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
246

By convention, we use a random point from D as a
reference to start our the summary selection. Once a
summary is computed, we view each element of the
summary as reference point for one region. Then we
check whether a region contains sufficient data-points
(e.g. at least τ = 500). If not we train the full GP
on the remaining points using eq. 1. This way, we
guarantee that every local expert contains at most τ
reference points. Otherwise, we continue to split re-
gions with enough data points. This approach results
in a hierarchy of increasingly more refined GP experts
based on the selection of the most informative points
according to the GPs predictive variance.
For prediction, we traverse the resulting tree:
Given an observation x, we compute the relevant re-
gion using the kernel similarly of x to all regions
based. Once the relevant region is computed, we
check whether there are more sub-regions (local ex-
perts) available in that region. If so, we recursively
continue to calculate the relevant region until we find
the most relevant local expert. Consequently, our
method implements a generalized PoE model, where
exactly one expert receives weight β
k
(x) = 1 based
on kernel similarities of the input x. In this sense, our
model generalizes gPoE models by introducing data-
dependent weights β
k
(x). Note, that for deployment
we only need to distribute the leaf-nodes of the tree,
so that each leaf performs predictions for its region.
4.1 Runtime Analysis
Before presenting the experiments in detail, we
briefly discuss some details of an efficient implemen-
tation. Lets first consider the termination condition.
If |D| < τ we train the full GP on at-most τ elements
(line 22), which has a complexity of O(τ
3
).
If |D| ≥ τ we first create a summary. The com-
putation of σ
A
(x) in line 6 of the algorithm, requires
K(A)
−1
, which takes cubic runtime O(|A|
3
). Note,
that we can reduce this computation by a constant fac-
tor to O(
1
2
|A|
3
) by storing the Cholesky decomposi-
tion L
A
of K(A).
When adding a new element to A one needs to
add a new row/column to K(A) and L
A
, respectively.
This update of the Cholesky decomposition can be
performed in O(|A|
2
) steps. Once the updated ver-
sion of the Cholesky decomposition is obtained, we
can compute the actual inverse of K(A) by Gaussian
elimination which requires O(
1
2
|A|
3
) (Cormen et al.,
2001) steps due to the triangular form of the Cholesky
decomposition.
The computation of σ
A
(x) requires a vector-
matrix-vector computation which takes O(|A|
2
). In
total, lines 4−8 require O(n ·c
2
+c
3
) = O(n ·c
2
) con-
Algorithm 2: Gaussian Model Tree (GMT) algorithm.
1: function TRAINGMT(D, c,τ)
2: if |D| ≥ τ then
3: Compute A according to algorithm 1
4: e = rand(D)
5: A = {e}
6: for i = 2, .. .,c do
7: e = argmax{σ
A
(x)|x ∈ D \ A}
8: A = A ∪ {e}
9: end for
10:
11: Assign points to region
12: for (x,y) ∈ D do
13: r = argmax{k(x,e)|e ∈ A}
14: D
r
= D
r
∪ {x}
15: end for
16:
17: Train GPs on subsets
18: for i = 1, .. .,c do
19: trainGMT(D
i
,c, τ)
20: end for
21: else
22: Train GP on D using eq. 1
23: trainFullGP(D)
24: end if
25: end function
sidering n >> c.
The for-loop (line 11 − 14) computes the corre-
sponding region for each data point. Excluding the
computation of the kernel function which is problem
dependent this can be performed in O(n · c).
Line 17 − 19 train a new expert GP on each re-
gions, involving the recursive call to trainGMT. In the
worst case, all but one region contain exactly one el-
ement. Consequently, the largest of these regions has
n−c+1 elements. Thus, the algorithm involves O(
n
c
)
recursive calls and constructs a tree with n leaf-nodes,
which all contain 1 except of one. Combining these,
we get a total runtime of O(
n
c
(O(n ·c
2
)+n ·c
2
)+(n −
1) · 1 +τ
3
) = O(n
2
· c + τ
3
) for n >> c.
In practice, however, we expect that the training
data is more equally distributed among all regions,
leading to O(log
c
(n)) recursive calls. This in turn
gives O(c
log
c
(n)
) = O(n) leaf-nodes which leads to a
total expected runtime of O(log
c
(n) · n ·c
2
+ n · τ
3
).
The training of the individual GPs in line 18 can
be parallelized easily without any locking. Note,
however, that this parallelization has to be imple-
mented with caution. First, simply spawning new
threads for each recursive call leads to up to c new
threads per local GP, quickly leading to an uncon-
trollable amount of threads competing for CPUs and
degrading performance. Second, individual branches
Gaussian Model Trees for Traffic Imputation
247

of the tree can become quite large and thus recursive
function calls may need a large amount of stack mem-
ory
2
.
To overcome these problems, we used a thread-
pool with a fixed number of threads during experi-
ments. Instead of training a local GP directly, we
schedule its training using a job queue. The parent
GP thus can finish execution immediately and free
its stack memory directly after all local experts have
been submitted into this queue. Once one thread in-
side the pool finished execution, it will fetch the next
GP job in the job queue and begin its execution, uti-
lizing the system as much as possible without over-
loading it
3
.
4.2 Deployment
Our goal is to deploy the small, local expert models
onto a small devices such as an ESP8266. These de-
vices usually come with restricted memory capacity
and often do not include floating point units. In or-
der to execute a trained GP model on these devices
we employ the following method: Given a subset of τ
data points A, it is enough to communicate and exe-
cute α = K(A)
−1
· (y − m) to the sensors. For predic-
tion we use equation 1:
f (x) = m(x) +K(x,A)
α
The runtime is linear in α and thus feasible if A is
comparably small. To avoid the need for floating
point units, we can a pre-compute a look-up table
of K(·,A) with fixed-point arithmetic and perform all
operations using a fixed precision. If we store K(·,A)
and α with precision ε << 1 we can upper-bound the
error (compared to floating-point) of the inner product
K(x,A)
α with τε
2
. Here, ε depends on the specific
kernel and specific device used, but should generally
as small as possible. On the other hand, τ is a user
parameter, which should be chosen as small as pos-
sible while the model still offers sufficient predictive
performance.
5 RELATED WORK
As already mentioned, Gaussian Processes do not
scale well with larger data sets, because K(D) needs
to be inverted. Therefore, sparse approximations of
GPs have been proposed in the literature. An exten-
sive review of these methods is presented in (Ras-
mussen and Williams, 2006; Hoang et al., 2015), so
2
Most Linux distributions limit the stack to 8 MB.
3
In the current implementation we use openmp with the
schedule(dynamic, 1) directive.
that we focus on the most related literature to our ap-
proach, here.
In (Abbasnejad et al., 2013), the authors develop
a more general framework for sparsification of GPs
in the context of preference learning. The proposed
framework incorporates the loss function directly into
selecting the active set so that the most valuable items
are selected with respect to that loss. Unfortunately,
the proposed Valuable Vector Machine does not in-
clude regression problems.
In (Shen et al., 2006) the authors propose parti-
tioning of the training sets using a KD-tree to train
an ensemble of local GP models. KD-trees partition
the input space into rectangular boxes using the Eu-
clidean distance between examples. This approach
requires the pre-processing of the data into a KD-tree
which takes additional time and lacks variance pre-
diction. Furthermore, there is no theoretical connec-
tion between the partition of the training data and the
predictive performance, since both use different simi-
larity measures.
Building on (Shen et al., 2006) the authors of (Ng
and Deisenroth, 2014) also partition the training data
into increasingly smaller subsets using a KD-tree. Af-
ter the KD-tree has been computed, the authors use
a PoE model formulation similar to (Deisenroth and
Ng, 2015) to recover the variance prediction. Note,
that the hierarchical PoE architecture, i.e., the depth
of the tree and number of local experts of this mixture
model, must be specified before training. Addition-
ally, there is still a link missing between the predic-
tive performance of the resulting model, as well as
the partition scheme of the KD-Tree.
Traffic volume estimation is a fundamental task
in macroscopic street-based traffic analysis systems
and has important applications, e.g., quality-of-
service evaluation, location evaluation or risk anal-
ysis. Nowadays, intelligent transportation systems
rely on stationary sensors, which provide traffic vol-
ume measurements at predefined locations. However,
imputation of the unobserved traffic flow values and
short-term predictions are highly important research
topics.
Existing literature distinguishes between aver-
age daily traffic (ADT) estimation and average an-
nual daily traffic flow (AADT or AADF) estimation.
Whereas AADF focuses on estimation of a traffic vol-
ume depending on the day of the year, ADT esti-
mation provides an average for a particular day. In
contrast to the ADT and AADF problem that we fo-
cus on in this paper, also short-term traffic progno-
sis problems exist. We concentrate on more extended
temporal resolutions, where microscopic influences,
e.g., signals have no impact on the traffic flow. For
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
248

short-term prediction problems, we point the inter-
ested reader on these related works, e.g., Cellular Au-
tomaton (Nagel and Schreckenberg, 1992), Poisson
Dependency Networks (Habel et al., 2016), or Con-
volutional Neural Networks (Ma et al., 2017).
Naive approach for AADF estimation is utiliza-
tion of ordinary linear regression (OLR) (Zhao and
Park, 2004). Street segment attributes (e.g. the num-
ber of lanes or function classes) are multiplied by
weights which are subject for least squares regres-
sion. Improvements of this technique were achieved
by respecting the geographical space by usage of ge-
ographically weighted regression (GWR) (Zhao and
Park, 2004) and by application of k-nearest neighbor
approaches (kNN) (Gong and Wang, 2002). In (Lam
et al., 2006) the AADF prediction of kNN for a partic-
ular location is improved by weighting measurements
by their temporal distance to the prediction time. This
approach showed better results than the application of
Gaussian maximum likelihood (GML) approaches for
weighting of the historical data points.
Being a spatial regression problem, usage of the
Kriging method seems to be a natural choice to tackle
the AADF problem. This was successfully carried on
at University of Texas (Selby, 2011; Selby and Kock-
elman, 2011). To machine learning persons the Krig-
ing method is better known as Gaussian Process Re-
gression, which allows a better understanding of the
underlying spatial correlation model by reformulation
with a kernel matrix (compare Section 2). Applica-
tion of Gaussian Process Regression is an appealing
state-of-the-art method that outperforms recent meth-
ods (Liebig et al., 2013). The method bases on a co-
variance matrix that denotes the correlations among
the traffic flux values at various locations. The work
in (Liebig et al., 2013) tested various covariance ma-
trices among them some that incorporate spatial lay-
out of the sensor locations or even the topology of
the street network. However, the performance did
not change much for these different correlation mod-
els. However, due to the computational complexity of
Gaussian Process Regression, application to urban ar-
eas was restricted either to small sites or a sample of
locations (Artikis et al., 2014).
6 EXPERIMENTS
In this section, we analyze the presented method ex-
perimentally on three different datasets in the con-
text of traffic imputation and smart cities. We com-
pare our method with a full GP (FGP) based on a
randomly sampled subset of data points (Rasmussen
and Williams, 2006), the Informative Vector Machine
Table 1: Grid-search parameters for the experiments.
Parameter Parameter-Range
Kernel {0.5, 1,2, 5}
FGP c {500,1000, 2000,2800(3000)}
IVM c {50,100, 200,300}
DGP c {500,1000, 2000,2800(3000)}
DGP m {50,100, 200}
GMT c {500,1000, 2000,2800(3000)}
GMT τ {50,100, 200,300}
(IVM) (Seeger, 2004) and the generalized PoE model
where every model receives the same weight β
k
= 1
(Deisenroth and Ng, 2015). Due to its fully dis-
tributed training we call this method distributed GP
(DGP). In all experiments, we use the squared expo-
nential kernel
k(x
i
,x
j
) = exp
−
d
∑
j=1
(x
i, j
−x
i, j
)
2
l
2
j
!
in which every dimension receives an individual
weighting l
j
. As already mentioned, all methods sup-
port hyper-parameter optimization by means of log-
likelihood maximization. However, we noticed that
for small dimensions a simple grid search yields faster
results. Table 1 summarizes the parameter for the
grid-search. We test 576 configurations per data set
which leads to 1728 experiments in total.
In all experiments we report the average standard-
ized mean squared (SMSE) error over a 5−fold cross-
validation. The SMSE is defined as
SMSE =
1
var (D
Test
)|D
Test
|
∑
(x,y)∈D
Test
( f (x) − y)
2
(10)
where var (D
Test
) denotes the label variance of the
test-data D
Test
. We report the SMSE here, because
it is independent of the scale of labels. For example,
consider the mean m =
1
|D|
∑
y∈D
y as a simple base-
line model, then we expect this model to roughly have
a SMSE of 1.
Note, that the first data-set contains 3523 data
points. Thus, with a 5− fold cross-validation we
use 3523/5 = 704 points for testing in each cross-
validation run which leaves 3523 −704 = 2819 points
for training. Therefore, we set c to be at most 2800 for
this experiment, whereas the other experiments use
c = 3000. For space reasons we report and discuss
the 5 best configurations per algorithm.
Furthermore, we add the size of the resulting
model concerning the (average) number of inducing
points to our discussion, because we ultimately want
to distribute these model across the sensing nodes.
We do not include training times here for two rea-
Gaussian Model Trees for Traffic Imputation
249
sons: First, our primary focus is the model applica-
tion on small devices, but not training it. Second, the
training time for all algorithms was neglectable across
all configurations (milliseconds to seconds). Interest-
ingly, test-time was the main limiting factor during
experiments: The DGP models combine the predic-
tive variance of m learners, where each learner uses c
inducing points. In order to compute the variance (c.f.
formula 2) one has to compute a vector-matrix-vector
product in O(c
2
+ c) which leads to a total runtime of
O(m · (c
2
+ c)). Thus, for small c the cost of a single-
point prediction with the DGP model lies in the same
range as the cost of training the complete model.
Our implementation is written in C++ and avail-
able at https://bitbucket.org/sbuschjaeger/ensembles/
src. All experiments are performed on an Intel Core
i7-6700 CPU machine with 3.40GHz and 32 GB
RAM running Linux Mint 18.3.
6.1 Luxembourg Traffic Imputation
In our first experiment, we use an open simulation
scenario of the city of Luxembourg (Codeca et al.,
2015) (LuST) for the Sumo simulator (Krajzewicz
et al., 2012). The simulation enables reproduction
of 24 hours of mobility in this city. For our ex-
periments, we simulate the most congested morning
hours from 7:45 till 11:00 and monitor the average
density, speed, waiting time and occupancy per street
segment. The resulting data set contains 131357 data
points from 3523 simulated sensors and is available
with our implementation. The data-set is compara-
bly small, which enables us to compute the full Gaus-
sian Process model as comparison basis (c = 2800).
Our goal is to predict the average vehicle density per
sensors given its location (x/y coordinate) in the sim-
ulation grid. We normalize the input features to the
interval [0,1].
Table 2 depicts the performance of the discussed
methods on the Luxembourg data set. First, we note
that all methods achieve an SMSE from 0.58 − 0.87,
which is significantly better than the baseline learner.
The presented GMT method is the best algorithm
with an SMSE around 0.58, followed by DGP with
0.73 to 0.74. Third places the full Gaussian Process
with 0.76−0.79, whereas the IVM shows the weakest
performance in this experiment with an SMSE from
0.86 − 0.87. It is interesting to note, that all meth-
ods favor different kernel parameter. For example, the
IVM and GMT seems to favor the x-coordinate more,
whereas DGP uses the same kernel parameter in all
dimensions in all experiments. It is also worth noting,
that the full GP does not rank among the best models,
but c = 1000 seems to be the best choice.
Table 2: Results of the Luxembourg experiments. Smaller
SMSE and smaller size is better.
Method and Parameters Kernel SMSE Avg. Size
FGP, c = 1000 0.5/0.5 0.767 1000
FGP, c = 2000 0.5/0.5 0.784 2000
FGP, c = 1000 1.0/0.5 0.786 1000
FGP, c = 1000 0.5/1.0 0.791 1000
FGP, c = 1000 2.0/0.5 0.798 1000
IVM, c = 500 2.0/2.0 0.866 500
IVM, c = 500 2.0/5.0 0.871 500
IVM, c = 500 1.0/5.0 0.871 500
IVM, c = 500 1.0/2.0 0.872 500
IVM, c = 200 1.0/5.0 0.875 200
DGP, c = 2800,m = 50 0.5/0.5 0.733 2800
DGP, c = 2800,m = 200 0.5/0.5 0.738 2800
DGP, c = 2000,m = 100 0.5/0.5 0.739 2000
DGP, c = 2000,m = 50 0.5/0.5 0.741 2000
DGP, c = 1000,m = 50 0.5/0.5 0.741 1000
GMT, c = 50,τ = 1000 1.0/2.0 0.583 56.80
GMT, c = 200,τ = 2000 2.0/5.0 0.584 15.48
GMT, c = 200,τ = 2800 5.0/5.0 0.586 15.43
GMT, c = 200,τ = 500 5.0/5.0 0.587 15.56
GMT, c = 200,τ = 1000 2.0/5.0 0.588 15.56
The IVM, DGP and FGP guarantee to use exactly
c data points, whereas GMT guarantees to use at-most
c points. Looking at table 2 we see that GMT only
uses 15 to 56 inducing points on average per region
while achieving the lowest error. Next, the IVM uses
only 500 data points, which explains the worse SMSE
compared to the FPG and DGP. Third, FGP use c =
1000 inducing points and thus is twice as large the
as the IVM and 17 times larger than GMT models.
Last, DGP uses the most reference points with c =
2800, which is roughly 50 times larger than the GMT
models.
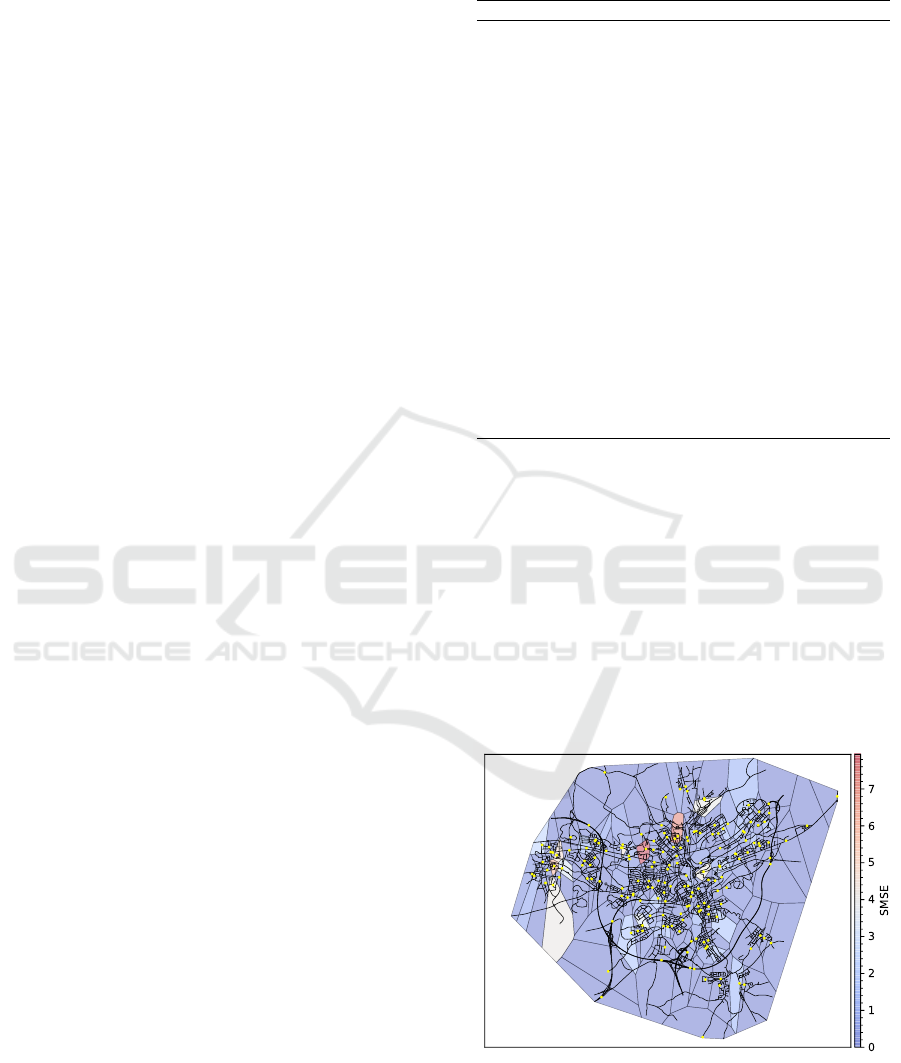
Figure 1: The street network of Luxembourg SUMO sim-
ulation including the selected reference points of the best
GMT model.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
250

We are interested in distributing sensors across the
city to monitor the traffic. By construction, GMT
trains small, local models which are responsible for
a given region. Figure 1 visualizes the road-network
of the city of Luxembourg and includes the region se-
lected by the best GMT model. Here, yellow points
represent the reference point which was selected by
the model, whereas colored areas mark the perfor-
mance in their respective region. We note two impor-
tant things: Expectantly, the model selects more refer-
ence points in regions where we find more roads. For
example, consider the inner city which contains vastly
more reference points than for example in the outer
regions highways. Similarly, the outer congregations
such as Bartringen in the west include more reference
points than the smaller, less inhabited regions such
as Gasperich in the south. Second, we note that the
model behaves differently depending on the region. In
most regions, the model performs very well, but there
are some areas - e.g., in the north - where the model
suffers performance. If we cross-reference these re-
gions with an actual map of Luxembourg, we notice,
that there is a Hospital in the north-west of Luxem-
bourg. A hospital naturally comes with an increased
volume of (fast driving) ambulances, which leads to
a vastly different traffic behavior in this region. Our
model does not fully capture this difference at the mo-
ment, but enables the user to pinpoint these abnormal
locations. Once these regions are found, we can fo-
cus on improving in this region specifically, e.g. by
changing the kernel parameters of the respective GP
expert.
6.2 UK Traffic Imputation
In the previous experiment, we verified the perfor-
mance of our method on comparably small and sim-
ulated data. In this experiment, we explore the per-
formance of our method using real-world data. To do
so, we combine the estimated annual average daily
flows (AADF) on minor and major roads (without di-
rection) in Great Britain
4
from the year 2017. In to-
tal, the data-set contains 18149 WGS84 coordinates
of traffic measuring units along with other informa-
tion such as street names and detailed counts for each
vehicle type. Our aim is to predict the AADF of all
motor vehicles (‘FdAll MV’) given the coordinate of
the location (‘S Ref E’ and ‘S Ref N’). Again, we
normalize the input features to the interval [0,1].
Table 3 depicts the results of the AADF-prediction
experiment. In this experiment we see mixed results.
All models seem to favor different combinations of
kernel parameters and there does not seem to be a
4
Available at https://tinyurl.com/y9mnt9qb
Table 3: Results of the AADF-prediction experiments in
UK. Smaller SMSE and smaller size is better.
Method and Parameters Kernel SMSE Avg. Size
FGP, c = 500 0.5/2.0 0.967 500
FGP, c = 500 1.0/1.0 0.972 500
FGP, c = 1000 0.5/5.0 0.973 1000
FGP, c = 1000 1.0/2.0 0.974 1000
FGP, c = 1000 5.0/0.5 0.975 1000
IVM, c = 300 2.0/5.0 0.972 300
IVM, c = 200 0.5/5.0 0.976 200
IVM, c = 200 5.0/5.0 0.98 200
IVM, c = 300 2.0/2.0 0.981 300
IVM, c = 300 5.0/5.0 0.981 300
DGP, c = 1000,m = 100 0.5/0.5 0.951 1000
DGP, c = 1000,m = 50 0.5/0.5 0.953 1000
DGP, c = 1000,m = 75 0.5/0.5 0.953 1000
DGP, c = 1000,m = 75 1.0/0.5 0.955 1000
DGP, c = 3000,m = 100 0.5/1.0 0.956 3000
GMT, c = 300,τ = 500 2.0/5.0 0.865 49.69
GMT, c = 300,τ = 1000 2.0/5.0 0.868 49.89
GMT, c = 300,τ = 1000 1.0/5.0 0.869 49.93
GMT, c = 300,τ = 2000 2.0/5.0 0.874 247.11
GMT, c = 300,τ = 500 2.0/5.0 0.874 49.86
clear best choice. Again, GMT offers by far the best
performance with an SMSE around 0.86. After that,
we find DGP next with an SMSE around 0.95, closely
followed by FGP and the IVM with an SMSE of 0.96
and 0.97 respectively. It is worth noting, that, against
common intuition, smaller GPs with c = 500 seem
to work better in this scenario, whereas the ensem-
ble methods GMT and DGP seem to favor larger GPs
with c ≥ 1000.
Table 3 also depicts the average model sizes.
Again, GMT offers the smallest models with roughly
50 inducing points per node. There is one notable
exception which selects approximately 250 inducing
points, which is around the same size of the IVM and
FGP. The DGP again favors the largest models with
c = 1000 and c = 3000. We conclude, that our model
is on average 10 to 50 times smaller than the other
methods.
In a similar fashion to the previous experiment
we may look at the predictive regions in Figure
2 of the best GMT model to derive some insights
about the data. First, we note that GMT selects
the most reference points in densely populated ar-
eas such as London in the south-east or Liver-
pool/Manchester/Sheffield/Leeds in the middle of the
UK. Furthermore, we note, that in the south-west one
of the eastern-islands has been selected. However, we
again find a few regions where our model fails, for
example Birmingham in the middle of the UK. This
region mostly belongs to the Cotswolds area, an Area
of Outstanding Natural Beauty (AONB). AONBs are
protected landscapes, which aim to preserve their nat-
Gaussian Model Trees for Traffic Imputation
251
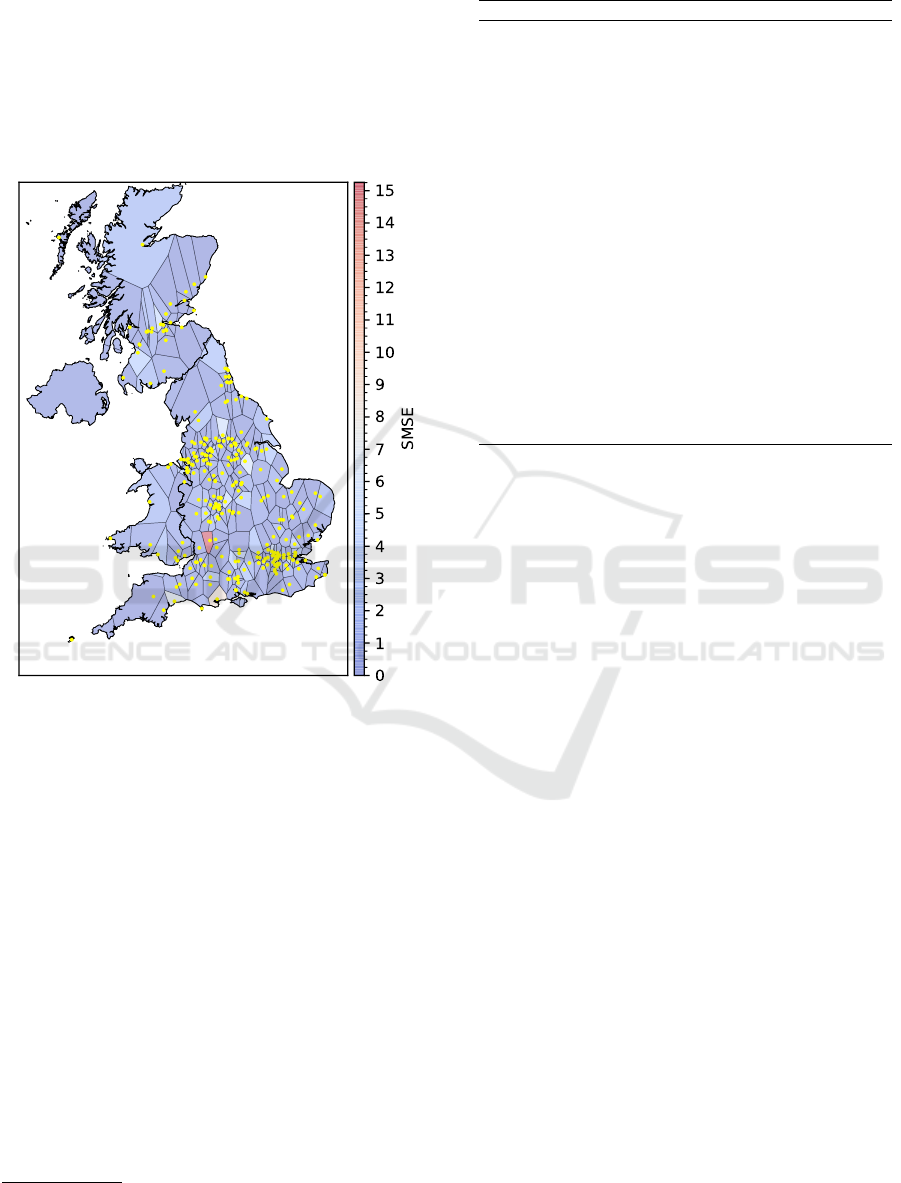
ural state and to reduce human interference, which
may explain why the GMT model fails in this area.
Again we argue that we can focus on these areas once
they have been identified and deploy specialized local
experts, e.g. by changing kernel parameters for that
region. Please note, that for technical reasons Wales
is colored in this plot, but there is no reference point.
The training data only contains AADF counts from
the UK, not including Wales.
Figure 2: The coastline of the UK including the selected
reference points of the best GMT model.
6.3 UK Apartment Prices
So far, we have evaluated our method in the context
of traffic imputation. In the broader context of smart
cities it might also be of interest, how the housing sit-
uation changes across the city, the district, and even
the exact location. To study this problem, we evalu-
ate our method with a data set containing the house
and apartment prices paid in the UK and Wales in
2012
5
.Since the raw-data does not contain numeri-
cal locations, but the property addresses, we cross-
referenced these addresses with an OpenStreet map
database to generate numeric coordinates of the prop-
erties. The resulting dataset contains 462484 lati-
tude/longitude pairs and their corresponding property
prices. For experiments, we filtered the data set for
apartments resulting in 64431 examples in total. We
5
https://tinyurl.com/y96yufkg
Table 4: Results of the apartment-price prediction experi-
ments in the UK. Smaller SMSE and smaller size is better.
Method and Parameters Kernel SMSE Avg. Size
FGP, c = 500 1.0/0.5 0.934 500
FGP, c = 500 2.0/0.5 0.937 500
FGP, c = 1000 0.5/2.0 0.938 1000
FGP, c = 1000 2.0/0.5 0.938 1000
FGP, c = 1000 0.5/1.0 0.939 1000
IVM, c = 300 0.5/2.0 0.947 300
IVM, c = 100 5.0/0.5 0.952 100
IVM, c = 200 2.0/0.5 0.954 200
IVM, c = 300 1.0/2.0 0.955 300
IVM, c = 100 0.5/1.0 0.956 100
DGP, c = 500,m = 200 1.0/0.5 0.92 500
DGP, c = 500,m = 50 0.5/0.5 0.922 500
DGP, c = 500,m = 100 1.0/0.5 0.923 500
DGP, c = 1000,m = 100 1.0/0.5 0.925 1000
DGP, c = 1000,m = 200 0.5/1.0 0.926 1000
GMT, c = 100,τ = 500 0.5/1.0 0.553 177.317
GMT, c = 50,τ = 500 0.5/2.0 0.602 110.827
GMT, c = 50,τ = 500 0.5/1.0 0.607 113.25
GMT, c = 50,τ = 500 0.5/0.5 0.615 114.512
GMT, c = 100,τ = 500 1.0/0.5 0.622 134.559
normalize the input dimensions to the interval [0,1]
and aim to predict the apartment prices.
Table 4 depicts the results of the housing-price
experiment. In general, the results follow the previ-
ous results for traffic imputation. Again, all models
seem to favor different combinations of kernel pa-
rameters, and there does not seem to be a clear best
choice. GMT offers by far the best performance with
an SMSE around 0.55 to 0.6. After that, we find DGP
next with an SMSE around 0.92, closely followed by
FGP and the IVM with an SMSE of 0.93 and 0.95
respectively. Again we find that smaller GPs with
c = 500 seem to work better, however now across all
experiments.
Looking at the model size we see a similar picture
as before. The IVM uses the fewest data points with
c = 100 − 300, closely followed by GMT which use
around 110 − 170 points. Next, the full GP uses 500
and 1000 data points which is similar to DGP. Again
we see that the presented is among the smallest mod-
els while offering the best performance.
Again we want to quickly discuss the results
of this experiments regarding the selected reference
points. First, we see that the GMT model chooses
more reference points compared to the previous ex-
periment. Second, we see a similar but different dis-
tribution of reference points: Densely populated ar-
eas such as London again receives the most attention
of the algorithm, but now reference points are more
equally distributed across the coastline compared to
the previous experiment. Especially in the center and
the far north of the UK find fewer reference points. It
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
252
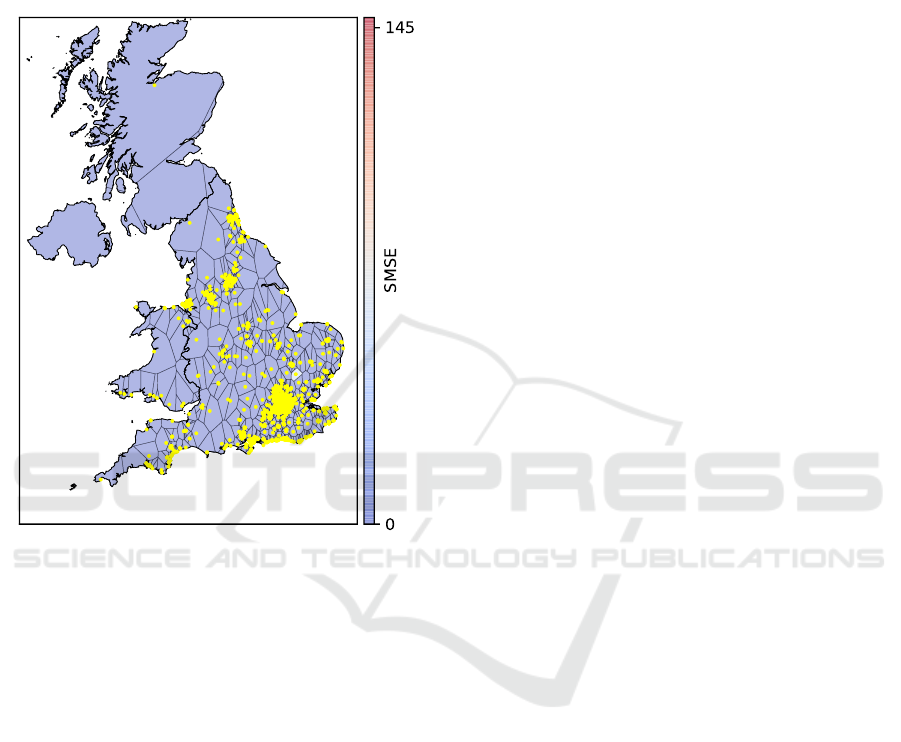
is worth noting that there are notable outliers regard-
ing the SMSE, which can be attributed to the few fea-
tures we are using here. We the apartment-price using
predict the latitude/longitude coordinates of the apart-
ment and to not attribute for the size of the apartment
or other features.
Figure 3: The coastline of the UK including the selected
reference points of the best GMT model in the apartment-
price experiment.
7 CONCLUSION
In this paper, we tackled the issue of traffic conges-
tion in modern cities. Data on traffic flow can help
to reduce congestion by predicting vehicle counts at
unmonitored locations. With these future prediction
counts, one is able to pursue countermeasures to pre-
vent congestion before it happens. Gaussian Pro-
cesses have shown to work well in the context of
traffic imputation, but are a large, centralized model,
which cannot utilize large amounts of data. Product
of Expert models have been presented as a scalable al-
ternative, but require ongoing communication to form
the final prediction. In this paper, we have proposed a
hierarchical Product of Expert model, which assigns
independent regions to local experts. Every local ex-
pert performs predictions for its region, so that no fur-
ther communication is required while maintaining the
benefits of PoE models. To do so, we viewed Gaus-
sian Processes as a regularized optimization problem
and connected it to the Bayesian formulation of PoE
models. We used this new optimization problem to
derive an efficient algorithm, which offers theoreti-
cal guarantees for its performance. We discussed the
runtime of our algorithm in detail and showed how to
parallelize its implementation. Furthermore, we dis-
cussed the deployment of the model on small devices.
In a total of 1728 experiments on three data-sets,
we showed that our method outperforms the conven-
tional approaches of a full Gaussian Process, the In-
formative Vector Machine and ‘flat’ PoE models by
a factor around two on some data-sets. Furthermore,
we showed that our model is up to 50 times smaller
compared to the other methods which makes perfectly
suitable to be executed on small sensor devices.
Last we note, that our method also offers the in-
sight in which regions it specifically fails. In the fu-
ture we want to use this information to further refine
the overall model, by e.g. tuning hyper-parameters
such as the kernel function individually for each re-
gion.
ACKNOWLEDGEMENTS
Part of the work on this paper has been sup-
ported by Deutsche Forschungsgemeinschaft (DFG)
within the Collaborative Research Center SFB 876
(http://sfb876.tu-dortmund.de) ”Providing Informa-
tion by Resource-Constrained Analysis”, project
A1 and B4. The work received also funding
from the European Union Horizon 2020 Programme
(Horizon2020/2014-2020), under grant agreement
number 688380, “Variety, Veracity, VaLue: Handling
the Multiplicity of Urban Sensors”.
REFERENCES
Abbasnejad, M. E., Bonilla, E. V., and Sanner, S. (2013).
Decision-theoretic sparsification for gaussian process
preference learning. In ECML-PKDD.
Artikis, A., Weidlich, M., Schnitzler, F., Boutsis, I., Liebig,
T., Piatkowski, N., Bockermann, C., Morik, K.,
Kalogeraki, V., Marecek, J., Gal, A., Mannor, S.,
Gunopulos, D., and Kinane, D. (2014). Heteroge-
neous stream processing and crowdsourcing for urban
traffic management. In Proc. 17th International Con-
ference on Extending Database Technology (EDBT),
Athens, Greece, March 24-28, 2014, pages 712–723.
OpenProceedings.org.
Bowerman, B., Braverman, J., Taylor, J., Todosow, H., and
Von Wimmersperg, U. (2000). The vision of a smart
city. In 2nd International Life Extension Technology
Workshop, Paris.
Gaussian Model Trees for Traffic Imputation
253

Breiman, L. (1996). Bagging predictors. Machine learning,
24(2):123–140.
Buschjaeger, S., Morik, K., and Schmidt, M. (2017). Sum-
mary extraction on data streams in embedded sys-
tems. In ECML Conference Workshop IoT Large Scale
Learning from Data Streams.
Codeca, L., Frank, R., and Engel, T. (2015). Luxembourg
sumo traffic (lust) scenario: 24 hours of mobility for
vehicular networking research. In IEEE VNC, pages
1–8.
Cormen, T. H., Stein, C., Rivest, R. L., and Leiserson, C. E.
(2001). Introduction to Algorithms. McGraw-Hill
Higher Education, 2nd edition.
Deisenroth, M. P. and Ng, J. W. (2015). Distributed gaus-
sian processes. In International Conference on Ma-
chine Learning (ICML 2015).
Gong, X. and Wang, F. (2002). Three improvements
on knn-npr for traffic flow forecasting. In Intelli-
gent Transportation Systems, 2002. Proceedings. The
IEEE 5th International Conference on, pages 736–
740. IEEE.
Habel, L., Molina, A., Zaksek, T., Kersting, K., and
Schreckenberg, M. (2016). Traffic simulations with
empirical data: How to replace missing traffic flows?
In Traffic and Granular Flow’15, pages 491–498.
Springer.
Hoang, T., Hoang, Q., and Low, B. (2015). A unifying
framework of anytime sparse gaussian process regres-
sion models with stochastic variational inference for
big data. In ICML, pages 569–578.
Krajzewicz, D., Erdmann, J., Behrisch, M., and Bieker,
L. (2012). Recent development and applications of
SUMO - Simulation of Urban MObility. International
Journal On Advances in Systems and Measurements,
5(3&4):128–138.
Lam, W. H., Tang, Y., and Tam, M.-L. (2006). Compar-
ison of two non-parametric models for daily traffic
forecasting in hong kong. Journal of Forecasting,
25(3):173–192.
Lawrence, N., Seeger, M., Herbrich, R., et al. (2003). Fast
sparse gaussian process methods: The informative
vector machine. NIPS.
Liebig, T., Piatkowski, N., Bockermann, C., and Morik, K.
(2017). Dynamic route planning with real-time traffic
predictions. Information Systems, 64:258–265.
Liebig, T., Xu, Z., and May, M. (2013). Incorporating mo-
bility patterns in pedestrian quantity estimation and
sensor placement. In Citizen in Sensor Networks,
pages 67–80.
Ma, X., Dai, Z., He, Z., Ma, J., Wang, Y., and Wang, Y.
(2017). Learning traffic as images: a deep convo-
lutional neural network for large-scale transportation
network speed prediction. Sensors, 17(4):818.
Nagel, K. and Schreckenberg, M. (1992). A cellular
automaton model for freeway traffic. Journal de
physique I, 2(12):2221–2229.
Nemhauser, G. L., Wolsey, L. A., and Fisher, M. L. (1978).
An analysis of approximations for maximizing sub-
modular set functions—i. Mathematical Program-
ming, 14(1):265–294.
Ng, J. W. and Deisenroth, M. P. (2014). Hierarchi-
cal mixture-of-experts model for large-scale gaussian
process regression. arXiv preprint arXiv:1412.3078.
Rasmussen, C. and Williams, C. (2006). Gaussian pro-
cesses for machine learning. The MIT Press.
Rieke, M., Bigagli, L., Herle, S., Jirka, S., Kotsev, A.,
Liebig, T., Malewski, C., Paschke, T., and Stasch,
C. (2018). Geospatial iot – the need for event-
driven architectures in contemporary spatial data in-
frastructures. ISPRS International Journal of Geo-
Information, 7(10).
Schnitzler, F., Liebig, T., Mannor, S., Souto, G., Bothe, S.,
and Stange, H. (2014). Heterogeneous stream pro-
cessing for disaster detection and alarming. In IEEE
International Conference on Big Data, pages 914–
923. IEEE Press.
Seeger, M. (2004). Greedy forward selection in the infor-
mative vector machine. Technical report, Technical
report, University of California at Berkeley.
Selby, B. and Kockelman, K. (2011). Spatial prediction
of aadt in unmeasured locations by universal kriging.
Technical report.
Selby, B. F. (2011). Spatial prediction of AADT in unmea-
sured locations by universal kriging and microsimu-
lation of vehicle holdings and car-market pricing dy-
namics. PhD thesis, University of Texas, Austin.
Shen, Y., Ng, A., and Seeger, M. (2006). Fast gaussian
process regression using kd-trees. NIPS.
Zhao, F. and Park, N. (2004). Using geographi-
cally weighted regression models to estimate an-
nual average daily traffic. Transportation Research
Record: Journal of the Transportation Research
Board, (1879):99–107.
ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods
254
