
Modelling the Semantic Change Dynamics using Diachronic Word
Embedding
Mohamed Amine Boukhaled, Benjamin Fagard and Thierry Poibeau
Laboratoire Langues, Textes, Traitements Informatique, Cognition, LATTICE, CNRS, ENS & Université Paris 3,
PSL & USPC, Paris, France
Keywords: Semantic Change, Diachronic Word Embedding, Recurrent Neural Networks, Distributional Semantics,
Computational Modelling.
Abstract: In this contribution, we propose a computational model to predict the semantic evolution of words over
time. Though semantic change is very complex and not well suited to analytical manipulation, we believe
that computational modelling is a crucial tool to study such phenomenon. Our aim is to capture the systemic
change of word’s meanings in an empirical model that can also predict this type of change, making it
falsifiable. The model that we propose is based on the long short-term memory units architecture of
recurrent neural networks trained on diachronic word embeddings. In order to illustrate the significance of
this kind of empirical model, we then conducted an experimental evaluation using the Google Books N-
Gram corpus. The results show that the model is effective in capturing the semantic change and can achieve
a high degree of accuracy on predicting words’ distributional semantics.
1 INTRODUCTION
The availability of very large textual corpora
spanning several centuries has recently made it
possible to observe empirically the evolution of
language over time. This observation can be targeted
toward a few isolated words or a specific linguistic
phenomenon, but it can also be interesting to
combine these specific studies with the search for
more general laws of language evolution. In this
contribution, we propose a computational model that
aims to predict the semantic evolution of words over
time. Computational modelling of language change
is a relatively new discipline, which includes early
works that aimed at characterizing the evolution
through statistical and mathematical modelling
(Bailey, 1973; Kroch, 1989) and more recent and
advanced works involving artificial intelligence,
robotics and large-scale computer simulations
(Steels, 2011).
Semantic change, on which we shall focus in this
paper, includes all changes affecting the meaning of
lexical items over time. For example, the word awful
has drastically changed in meaning, moving away
from a rather positive connotation, as an equivalent
of impressive or majestic, at the beginning of the
nineteenth century, and toward a negative one, as an
equivalent of disgusting and messy nowadays
(Oxford Dictionary, 1989). It has been established
that there are some systemic regularities that direct
the semantic shifts of words meanings. Not all words
exhibit the same degree and speed of semantic
change. Some words (or word categories) might be
more resistant than others to the phenomenon of
semantic change, as proposed by (Dubossarsky et
al., 2015). Various hypotheses have been proposed
in the literature to explain such regularities in
semantic change from a linguistic point of view
(Traugott and Dasher, 2001).
In this work, we address the question of semantic
change from a computational point of view. Our aim
is to capture the systemic change of a word’s
meanings in an empirical model that can also predict
such changes, making it falsifiable. The proposed
model makes use of two techniques:
1. Diachronic word embeddings to represent the
meanings of words over time as the data
component of the model
2. A recurrent neural network to learn and predict
the temporal evolution patterns of these data
The idea is to train a Long Short Term Memory
units (LSTMs) recurrent neural network (RNN) on
944
Boukhaled, M., Fagard, B. and Poibeau, T.
Modelling the Semantic Change Dynamics using Diachronic Word Embedding.
DOI: 10.5220/0007698109440951
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 944-951
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

word embeddings corresponding to given time-
periods (measured in decades) and try to predict the
word embeddings of the following decade. We then
evaluate the model using a large scale diachronic
corpus, namely the English Google Books N-Gram
corpus.
The rest of the paper is organized as follows:
Section 2 presents a brief review of related works
concerned with the computational study of semantic
change and regularities. Section 3 discusses the
vector word representation using diachronic word
embedding and describes our approach based on
LSTMs recurrent neural networks for predicting the
semantic change. Finally, the proposed model is
experimentally evaluated and discussed on the
Google Books N-Gram corpus in Section 4.
2 RELATED WORKS ON
COMPUTATIONAL ANALYSIS
OF SEMANTIC CHANGE
One of the main challenges facing researchers
studying the phenomenon of semantic change is its
formidable complexity. It seems impossible to grasp
all details and factors involved in such change, its
abstract nature making it analytically intractable.
However, computational models have no difficulties
in handling complexity, and can therefore be used as
means to make the study of semantic changes more
accessible.
The computational study of text temporality in
general, and semantic change in particular, has
become an active research topic, especially with the
emergence of new and more effective methods of
numerical word representations. The interest of
taking into account the temporal dimension and the
diachronic nature of meaning change as a research
direction has been effectively demonstrated in
several studies. It makes it possible to analyse
trajectories of meaning change for an entire lexicon
(Kim et al., 2014), to model temporal word analogy
or relatedness (Rosin et al., 2017) (Szymanski,
2017), to capture the dynamics of semantic relations
(Kutuzov et al., 2017), and even to spell out specific
laws of semantic change, among which:
• The Law of Conformity, according to which
frequency is negatively correlated with semantic
change (Hamilton et al., 2016b).
• The Law of Innovation, according to which
polysemy is positively correlated with semantic
change (Hamilton et al., 2016b).
• The Law of Prototypicality, according to which
prototypicality is negatively correlated with
semantic change (Dubossarsky et al., 2015).
However, these works, despite the fact that they are
highly useful for our purposes, are mostly based on
descriptive formalisms and they do not attempt to
explore predictive approaches (Bollack, 1903).
In this work, our aim is to model the semantic
change based on a predictive approach. These
predictions can then be examined through empirical
observation and experimentation.
3 PROPOSED METHODOLOGY
In this attempt to capture semantic change, our goal
is to define a model capable of learning how the
meanings of words have changed over time, and
then use this model to predict how these meanings
may evolve. This can then be checked against the
actual meaning change which can be assessed with
the same corpus. We propose a model that consists
of two steps. The first step is to represent the
evolution of word meanings over time using
diachronic word embedding. The second consists in
learning the temporal pattern behind this evolution
using a recurrent neural network. The next two
subsections describe more thoroughly these two
steps.
3.1 Modelling Semantic Change with
Diachronic Word Embedding
To represent computationally the meaning of words
over time-periods, it is necessary first to extract the
embedded projections of these words in a continuous
vector space according to their contextual
relationships (Turney and Pantel, 2010). Various
methods can be used to obtain such vectors, such as
Latent Semantic Analysis (Deerwester et al., 1990)
and Latent Direchlet Allocation (Blei et al., 2003).
However, more recent and advanced techniques such
as word2vec (Mikolov et al., 2013) and GloVe
(Pennington et al., 2014), known commonly as word
embedding techniques, seem capable of better
representing the semantic properties and the
contextual meaning of words compared to traditional
methods. Indeed, word embedding techniques have
established themselves as an important step in the
processing pipeline of natural languages.
The word2vec algorithm is one of the most
frequently used techniques to construct word
embeddings with a huge impact in the field. It
Modelling the Semantic Change Dynamics using Diachronic Word Embedding
945
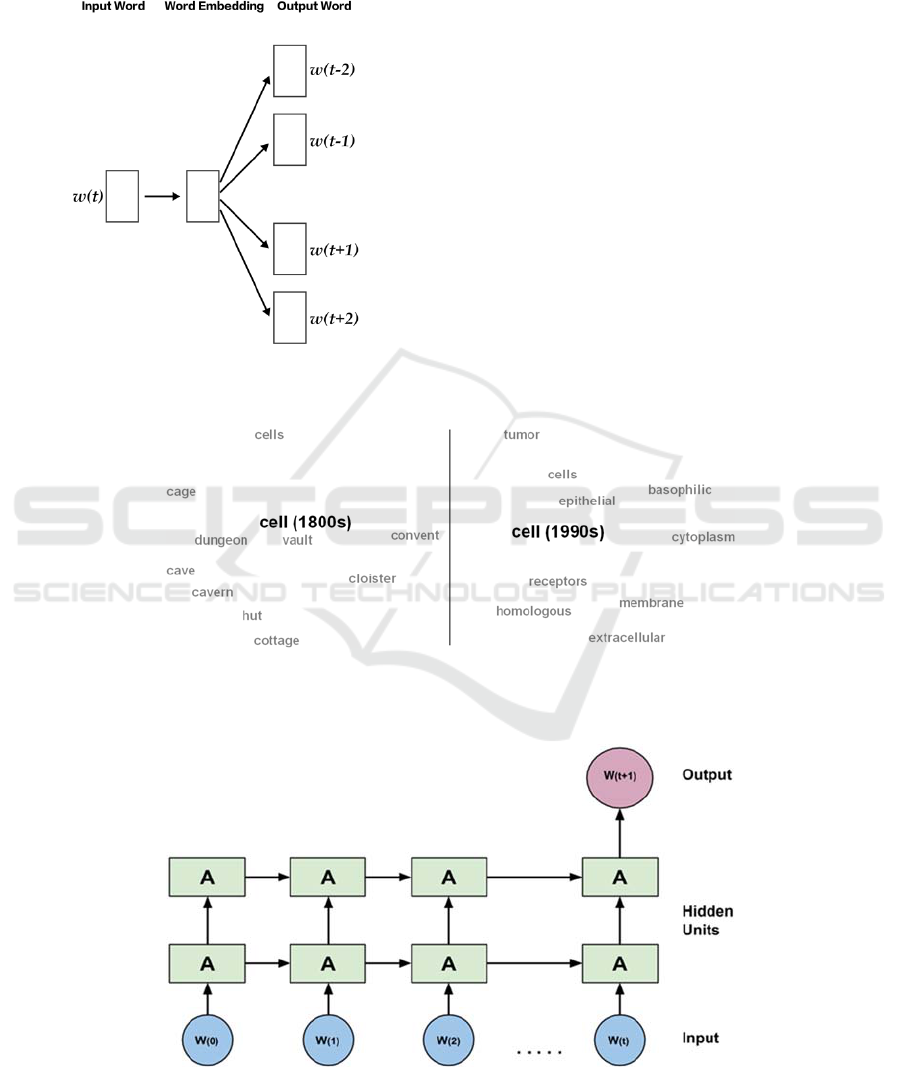
consists in training a simple neural network with a
single hidden layer to perform a certain task (see
Figure 1). Training is achieved through stochastic
gradient descent and back-propagation.
Figure 1: Architecture of the Skip-gram Model (Mikolov
et al., 2013).
In the case of the skip-gram with negative
sampling (SGNS) variant of the algorithm (Mikolov
et al., 2013), the learning task is as follows: Given a
specific word in the middle of a sentence, the model
uses this current word to predict the surrounding
window of context words. The words are in fact
projected from a discrete space of dimensions
(where is the vocabulary size) onto a lower
dimensional vector space using the neural network.
The goal is not to use the network afterward.
Instead, it is just to learn the weights of the hidden
layer. These weights constitute actually the word
embedding vectors. Despite its simplicity, the
word2vec algorithm, given an appropriate amount of
training text, is highly effective in capturing the
contextual semantics of words.
Such word embedding techniques can be
extended to work in a diachronic perspective. The
method consists first in training and constructing
embeddings for each time-period, then in aligning
them temporally, so as to finally use them as means
to track semantic change over time (see Figure 2).
Figure 2: Two-dimensional visualization of the semantic change in the English word cell using diachronic word embedding.
In the early 19th century cell referred to cage or dungeon, in the late 20th century its meaning shifted toward a scientific
usage.
Figure 3: The many-to-one LSTMs architecture used in our work to predict word embedding vectors. For each word in the
vocabulary, the network is trained on diachronic word embedding vectors of time-periods 1,…, as input and tries to
predict the embedding vector for time 1 as output.
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
946

In our case, the pre-trained diachronic word
embeddings were constructed on the basis of time-
periods measured by decades from 1800 to 1990
(Hamilton et al., 2016b). The training text used to
produce these word embeddings is derived from the
Google Books N-gram datasets (Lin et al., 2012)
which contain large amounts of historical texts in
many languages (N-Grams from approximately 8
million books, roughly 6% of all books published at
that time). Each word in the corpus appearing from
1800 to 1999 is represented by a set of twenty
continuous 300- dimensional vectors; one vector
for each decade.
3.2 Predicting Semantic Change with
Recurrent Neural Networks
As we are interested in predicting a continuous
vector of dimensions representing a word’s
contextual meaning in a given decade, this task is
considered to be a regression problem (by opposition
to a classification problem, where the task is to
predict a discrete class).
Many algorithms have been proposed in the
literature to deal with this kind of temporal pattern
recognition problem, such as Hidden Markov
Models (Bengio, 1999) and Conditional Random
Fields (Lafferty et al., 2001).
In this work, we propose to use a recurrent neural
network with a many-to-one LSTMs architecture to
address this problem.
RNNs are a powerful class of artificial neural
networks designed to recognise dynamic temporal
behaviour in sequences of data such as textual data
(Medsker and Jain, 2001). RNNs are distinguished
from feed-forward networks by the feedback loop
connected to their past states. In this feedback loop,
the hidden state
at time step is a function of
the input at the same time step
modified by a
weight matrix, added to the hidden state of the
previous time step
multiplied by its own
transition matrix as in equation (1):
h
ϜWx
Uh
‐
(1)
More specifically, we used a LSTMs architecture
(Hochreiter and Schmidhuber, 1997) (see Figure 3)
which is a variety of RNNs designed to deal
effectively with the problem of vanishing gradient
that RNNs suffer from while training (Pascanu et al.,
2013).
3.3 Problem Formulation
Let us consider a vocabulary
consisting in the
top- most frequent words of the corpus and
∗
to be the matrix of word embeddings at time
step.
The LSTMs network is trained on word
embeddings over time-period
1, … ,
as input and
asked to predict word embeddings
1 of
time 1as output. The predicted embedding
1 is then compared to the ground truth
word embedding 1 in order to assess the
prediction accuracy. Predicting a continuous 300-
dimensional vector representing a word’s contextual
meaning is thus, as indicated above, formulated as a
regression problem. Traditionally, researchers use
mean-squared-error or mean absolute-error cost
functions to assess the performance of regression
algorithms. However, in our case, such cost
functions would not be adapted, as they provide us
with an overview (i.e., numerical value) of how the
model is performing but little detail on its prediction
accuracy. To have a more precise assessment of the
prediction accuracy, we need to be able to say
whether the prediction, for each word taken
individually, is correct or not. Overall prediction
accuracy is then computed. To do so, we proceed as
follows:
Given the vocabulary
constituted from the
top-most frequent words and the matrix of
word embeddings at decade , let us consider a word
and
1 its predicted word-embedding
at decade 1. Though it is impossible to predict
exactly the same ground truth vector
1
for
this decade, as we are working on a continuous 300-
dimensional space, one can assess the accuracy of
the predicted vector
1 by extracting the
words that are closest semantically based on cosine-
similarity measure. If the word
is actually the
nearest semantic neighbour to the predicted vector
1 then it is considered to be a correct
prediction. Otherwise, it is considered to be a false
prediction.
4 EXPERIMENTAL
EVALUATION
In our experiment, we used word embeddings of all
decades from 1800 to 1990 as input for the network,
and we trained it to predict the embeddings of the
1990-1999 decade as output. We then conducted two
types of evaluations. The first one consisted in
Modelling the Semantic Change Dynamics using Diachronic Word Embedding
947

reconstructing the overall large-scale evolution of
the prediction accuracy on most frequents words
from the corpus. The second consisted in evaluating
the prediction accuracy for a handful of word forms
that have known considerable semantic shifts in the
past two centuries. The next two subsections
describe the experimental protocol and results for
both evaluations.
4.1 Overall Evaluation
In this first part of the evaluation, we experimented
with different vocabulary sizes (top-1,000, 5,000,
10,000 and 20,000 words respectively, consisting of
the most frequent words as computed from their
average frequency over the entire historical time-
periods). The experimental settings can help us
evaluate the effect of a word’s frequency on the
degree of semantic change, and hence on prediction
accuracy. For each experiment, and in order to get a
reasonable estimate of the expected prediction
performance, we used a 10-fold cross-validation
method. Each time, we used 90% of the words for
training the model, and the remaining 10% for
testing its prediction accuracy. The training and
testing process was repeated 10 times. The overall
prediction accuracy is taken as the average
performance over these 10 runs.
The results of measuring the prediction accuracy
in our experimental evaluation are summarised in
Table 1.
Table 1: Results of prediction accuracy measured for
different vocabulary sizes.
Vocabulary Size Acc.
1,000 91.7%
5,000 86.1%
10,000 71.4%
20,000 52.2%
The results show that the model can be highly
effective in capturing semantic change and can
achieve a high accuracy when predicting words’
distributional semantics. For example, the model
was able to achieve 71% accuracy trained and tested
exclusively on embeddings coming from the 10,000
most frequent words of the corpus. The results also
show a better performance when using a smaller
vocabulary size, containing only the most frequent
words. This is due to the fact that frequent words are
repeated a sufficient number of times for the
embedding algorithm to represent them accurately,
and therefore to have a better distinction of the
semantic change pattern which those embeddings
may contain, which in turn can lead the RNN model
to better capture this semantic change pattern and
yield a more accurate prediction. Indeed, having a
large corpus is essential to enable the models to
learn a better word representation. These results are
also in line with previous works claiming that
frequency plays an important role in the semantic
change process. For instance, Hamilton et al.,
(2016b) have shown that frequent words tend to be
more resistant to semantic change (statistical Law of
Conformity).
4.2 Case Studies
We further examined the prediction accuracy on a
handful of words. We automatically extracted, as
explained below, from the Google Books N-Gram
Corpus the top-100 words that have known
considerable semantic shifts in the past two
centuries. We noticed that these words correspond
mostly to cases that have undergone some important
cultural shifts, which makes them a harder challenge
for the prediction model compared to datasets used
earlier in the overall evaluation. Table 2 presents
sample words that gained new meanings due to their
evolution towards uses in scientific and
technological contexts.
From a technical point of view, one can
computationally examine the degree of semantic
change using two different measures.
The first one, known as the global measure,
simply consists in computing the cosine distance
between a given word’s vectors from two
consecutive decades and 1. The bigger the
distance, the higher the semantic change (Kim et al.,
2014).
The second measure, which we chose to use in
our work, is known as the local neighbourhood
measure, recommended by Hamilton et al., (2016a).
It consists of evaluating the semantic change of a
word based on how much its corresponding semantic
neighbours have changed between two consecutive
decades.
To do so, we first extract for each word
, with
its corresponding embedding vector
, the set of
most nearest neighbours, denoted by
,
according to cosine-similarity for both consecutive
decades and 1. Then, to measure the change
which took place between these two decades, we
compute a second-order similarity vector for
from these neighbour sets. This second-order vector,
denoted by
, contains the cosine similarity of
and the vectors of all
’s nearest semantic neigh-
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
948
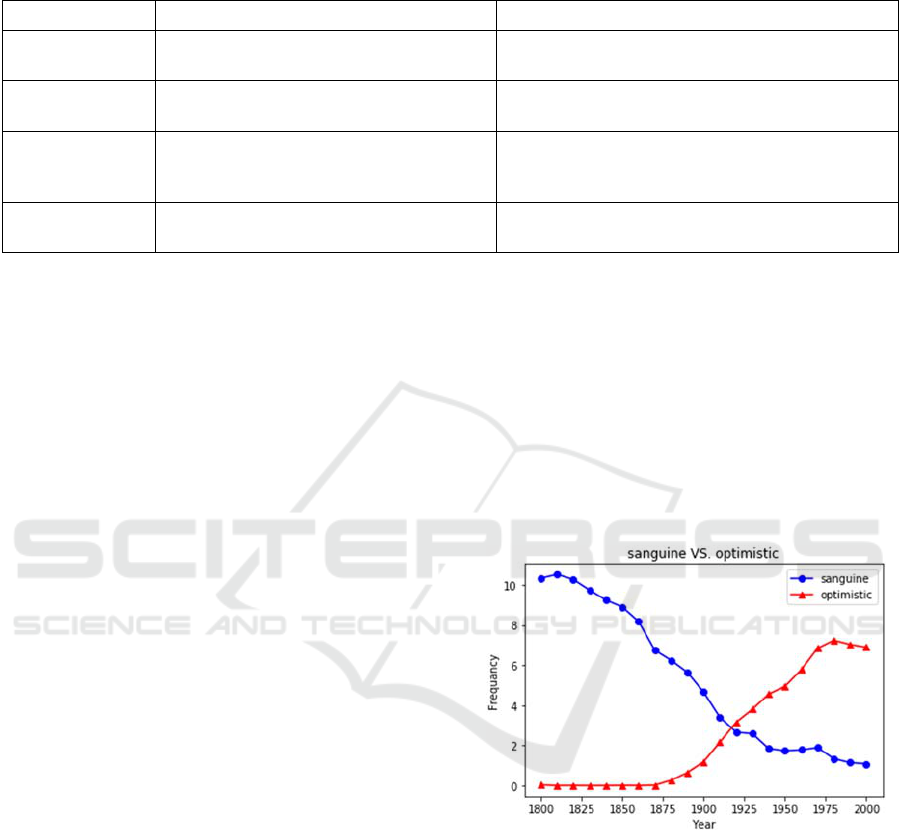
Table 2: Neighbouring words according to cosine similarity for sample words that have known considerable semantic shifts
in the past two centuries.
Word Neighbours in 1800s Neighbours in 1990s
mail
waistcoat, boots, shirt, gloves, breeches,
velvet, pistols, shoe, helmet, spurs
mailing, email, send, internet, telephone, sending,
fax, messages, mails, postage
circuit
habitable, district, lanes, range, area, outer,
globe, traverse
circuits, appeals, amplifier, voltage, transitor,
capacitor, appellate, court, resistor, district
signal
commodore, hoisted, victory, tack, admiral,
commemoration, victories, chace, flag,
announce
signals, modulated, amplitude, input, noise,
modulation, transmitter, analog, waveform,
transduction
array
banners, spears, shields, ensigns, ranged,
pikes, trumpets, banner, standards
arrays, variety, range, integers, integer, byte, wide,
pointer, formats, pointers
bours in the time-periods and 1,with entries
defined as:
,
∀
⋃
(2)
An analogous vector for
is similarly
computed as well.
Finally, we compute the local neighbourhood
distance that measures the extent to which
’s
similarity with its nearest neighbours has changed
as:
,
,
(3)
Hamilton et al., (2016a) have found that the local
neighbourhood measure is more effective in
capturing specific cultural and semantic shifts than
the global measure, while being less sensitive to
other types of change such as grammaticalization.
The model was able to correctly predict the
semantic evolution of 41% of the studied cases,
including words that have known an important and
attested semantic change in the last two centuries
such as the word cell. Moreover, a large portion of
the false predictions corresponds to borderline cases
for which the model has a tendency to predict
vectors that are closer to much more frequent words,
occurring in the same semantic context in the
corpus, such as predicting a vector closer to the
(emerging but more frequent) word optimistic for the
(declining) word sanguine. The word sanguine
comes from Old French sanguin (itself from Latin
sanguineus, on sanguis ‘blood’). It originally means
‘blood-red’ (14
th
c., Merriam-Webster’s), and by
extension ‘hopeful, optimistic’ (15
th
c., ibid.). In our
corpus examples from the early 18
th
c., it is already
used with the meaning ‘optimistic’, as in “My lords,
I am sanguine enough to believe that this country
has in a great measure got over its difficulties”
(Speech of the Earl of Liverpool, 1820: 31) and “she
is sanguine enough to expect that her various
Novelties will meet the approbation of all Ladies of
taste” (La belle assemblee, vol. XV, April 1
st
, 1817).
But Figure 4 shows that its frequency in the 19
th
and
20
th
c. has dropped steadily, while optimistic has
seen its frequency rise sharply. Thus, the pair
sanguine / optimistic seems to be a good example of
lexical replacement, which explains our model’s
prediction.
Figure 4: Frequency profiles of sanguine and optimistic in
Google Books N-Gram Corpus measured in millions.
Thus, among other benefits for historical
linguists, our method makes it possible to identify
the semantic replacement of one word by another in
a specific context.
4.3 Discussion
Despite being effective in predicting the semantic
evolution of words, some difficulties remain
regarding our method. For instance, our model
works best for the most frequent words, i.e.,
Modelling the Semantic Change Dynamics using Diachronic Word Embedding
949

according to the Law of Conformity, those with the
least semantic evolution. One could thus wonder
whether the words for which the model correctly
predicts the semantic are not simply those which
display little or no semantic change. The examples
given in section 4.2 show that this is at least not
always the case, but a more systematic investigation
of individual cases is in order to get a clear picture.
Another way to answer this question would be to
explore more finely the effect that both polysemy
and word frequency may have on our results,
especially on the word representation part of our
model. These two factors have been shown to play
an important role in the semantic change, and their
effects need to be studied and formalized more
explicitly. Exploring more advanced and semantic-
oriented word embedding techniques, referred to as
sense embeddings, such as S
ENSEMBED (Iacobacci
et al., 2015), could help make the model less
sensitive to those factors.
5 CONCLUSIONS
In conclusion, we describe in this paper a method
that accurately models the evolution of language and
that can to some extent predict future evolution,
based on past observations. Although our
experiment is still in its preliminary stages, we
believe it can provide linguists with a refreshing
look on linguistic evolution. Our method makes it
possible to observe large-scale evolution in general
and semantic change in particular. It thus nicely
complements existing methods and reinforces a
falsifiability approach to linguistics. Based on the
current study, we have identified several future
research directions from a technical point of view.
The RNN model that we propose to use is rather
standard and simplistic compared to the complexity
of semantic change. We therefore intend to explore
deeper networks and to put more time and effort in
the fine tuning process of its hyper-parameters.
ACKNOWLEDGEMENTS
This work is supported by the project 2016-147
ANR OPLADYN TAP-DD2016. Our Thanks go to
the anonymous reviewers for their constructive
comments.
REFERENCES
Bailey, C.-J. N. (1973) ‘Variation and linguistic theory.’
ERIC.
Bengio, Y. (1999) ‘Markovian models for sequential data’,
Neural computing surveys, 2(199), pp. 129–162.
Blei, D. M., Ng, A. Y. and Jordan, M. I. (2003) ‘Latent
dirichlet allocation’, Journal of machine Learning
research, 3(Jan), pp. 993–1022.
Bollack, L. (1903) La langue franc
̜
aise en l’an 2003...
Bureau de La Revue.
Deerwester, S. et al. (1990) ‘Indexing by latent semantic
analysis’, Journal of the American society for
information science. Wiley Online Library, 41(6), pp.
391–407.
Dictionary, O. E. (1989) ‘Oxford english dictionary’,
Simpson, JA & Weiner, ESC.
Dubossarsky, H. et al. (2015) ‘A bottom up approach to
category mapping and meaning change.’, in
NetWordS, pp. 66–70.
Hamilton, W. L., Leskovec, J. and Jurafsky, D. (2016a)
‘Cultural shift or linguistic drift? comparing two
computational measures of semantic change’, in
Proceedings of the Conference on Empirical Methods
in Natural Language Processing. Conference on
Empirical Methods in Natural Language Processing,
p. 2116.
Hamilton, W. L., Leskovec, J. and Jurafsky, D. (2016b)
‘Diachronic word embeddings reveal statistical laws of
semantic change’, in Proceedings of the 54th Annual
Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers), pp. 1489-1501.
Hochreiter, S. and Schmidhuber, J. (1997) ‘Long short-
term memory’, Neural computation. MIT Press, 9(8),
pp. 1735–1780.
Iacobacci, I., Pilehvar, M. T. and Navigli, R. (2015)
‘Sensembed: Learning sense embeddings for word and
relational similarity’, in Proceedings of the 53rd
Annual Meeting of the Association for Computational
Linguistics and the 7th International Joint Conference
on Natural Language Processing (Volume 1: Long
Papers), pp. 95–105.
Kim, Y. et al. (2014) ‘Temporal analysis of language
through neural language models’, in Proceedings of
the ACL 2014 Workshop on Language Technologies
and Computational Social Science, pp. 61-65.
Kroch, A. S. (1989) ‘Reflexes of grammar in patterns of
language change’, Language variation and change.
Cambridge University Press, 1(3), pp. 199–244.
Kutuzov, A., Velldal, E. and Øvrelid, L. (2017) ‘Temporal
dynamics of semantic relations in word embeddings:
an application to predicting armed conflict
participants’, in Proceedings of the 2017 Conference
on Empirical Methods in Natural Language
Processing, pp. 1824-1829. 2017.
Lafferty, J., McCallum, A. and Pereira, F. C. N. (2001)
‘Conditional random fields: Probabilistic models for
segmenting and labeling sequence data’.
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
950

Lin, Y. et al. (2012) ‘Syntactic annotations for the google
books ngram corpus’, in Proceedings of the ACL 2012
system demonstrations, pp. 169–174.
Medsker, L. R. and Jain, L. C. (2001) ‘Recurrent neural
networks’, Design and Applications. Citeseer, 5.
Mikolov, T. et al. (2013) ‘Efficient estimation of word
representations in vector space’, arXiv preprint
arXiv:1301.3781.
Pascanu, R., Mikolov, T. and Bengio, Y. (2013) ‘On the
difficulty of training recurrent neural networks’, in
International Conference on Machine Learning, pp.
1310–1318.
Pennington, J., Socher, R. and Manning, C. (2014) ‘Glove:
Global vectors for word representation’, in
Proceedings of the 2014 conference on empirical
methods in natural language processing (EMNLP),
pp. 1532–1543.
Rosin, G. D., Radinsky, K. and Adar, E. (2017) ‘Learning
Word Relatedness over Time’, in Proceedings of the
2017 Conference on Empirical Methods in Natural
Language Processing, pp. 1168-1178.
Steels, L. (2011) ‘Modeling the cultural evolution of
language’, Physics of Life Reviews. Elsevier, 8(4), pp.
339–356.
Szymanski, T. (2017) ‘Temporal Word Analogies:
Identifying Lexical Replacement with Diachronic
Word Embeddings’, in Proceedings of the 55th
Annual Meeting of the Association for Computational
Linguistics (Volume 2: Short Papers), pp. 448–453.
Traugott, E. C. and Dasher, R. B. (2001) Regularity in
semantic change. Cambridge University Press.
Turney, P. D. and Pantel, P. (2010) ‘From frequency to
meaning: Vector space models of semantics’, Journal
of artificial intelligence research, 37, pp. 141–188.
Modelling the Semantic Change Dynamics using Diachronic Word Embedding
951
