
Prior Probabilities of Allen Interval Relations over Finite Orders
Tim Fernando and Carl Vogel
ADAPT Centre, Computer Science Department, Trinity College Dublin, Ireland
Keywords:
Allen Interval Relations, Probabilities, Events.
Abstract:
The probability that intervals are related by a particular Allen relation is calculated relative to sample spaces
Ω
n
given by the number n of, in one case, points, and, in another, interval names. In both cases, worlds in
the sample space are assumed equiprobable, and Allen relations are classified as short, medium and long,
according to the number of shared borders.
1 INTRODUCTION
A useful basis for relating intervals are the 13 rela-
tions described in (Allen, 1983) and widely applied
to temporal relations in text and beyond (Liu et al.,
2018; Verhagen et al., 2009; Allen and Ferguson,
1994; Kamp and Reyle, 1993, among many others).
The present work proceeds from the following ques-
tion.
(Q) Given an Allen relation R, what is the probability
that R relates intervals a and a
0
, aRa
0
?
Let us understand (Q) as saying nothing about a and
a
0
, not even that they are distinct (equality being an
Allen relation). As there are 13 Allen relations,
1
13
is
a plausible answer to (Q), under the principle of in-
difference (commonly ascribed to Laplace). But are
Allen relations a matter of indifference when, for ex-
ample, some Allen relations occur more often than
others in the transitivity table of (Allen, 1983)? That
table is a central tool in interval networks formed
from nodes representing intervals, and arcs labelled
by Allen relations that may hold between the inter-
vals. We will return to the transitivity table below.
For now, suffice it to observe that some care is in or-
der when proposing a sample space of equiprobable
outcomes (hereafter, worlds) against which to answer
(Q).
It is natural to interpret (Q) as presupposing a lin-
ear order relative to which a and a
0
are intervals. To
accommodate all Allen relations, let us assume there
are at least 4 points in that linear order, and for sim-
plicity, let us suppose it is finite — say, the usual order
on the set
[n] := {i ∈ Z | 1 ≤ i ≤ n}
of integers between 1 and n (inclusive). A pair (l,r)
from the linear order
<
n
:= {(l,r) ∈ [n] × [n] | l < r}
on [n] defines the <
n
-interval
(l,r] := {i ∈ [n] | l < i ≤ r}
(with left border l and right border r, allowing = with
r but not l). Now, over the linear order <
n
, the proba-
bility that aRa
0
becomes the probability that
(l,r] R (l
0
,r
0
]
for (l, r) and (l
0
,r
0
) drawn from <
n
. Note that 1 is
excluded from (l,r] for all l,r ∈ [n]. To lift this re-
striction, it suffices to work with copies in <
n+1
given
by mapping i ∈ [n] to i+1 ∈ [n + 1]. Similarly, the re-
quirement that a <
n
-interval be strictly bounded to the
right can be imposed by passing to <
n−1
with i > 1
mapped to i − 1. Without loss of generality, we iden-
tify <
n
-intervals with (l,r] for l <
n
r.
1
Over a sample space Ω
n
given by a linear or-
der on n points, probabilities for each Allen relation
R are calculated in section 2, under the assumption
that worlds in Ω
n
are equiprobable. The probabili-
ties queried by (Q) vary with n and depend on the
extent to which the intervals share borders, given R.
As n approaches infinity, 7 of the 13 Allen relations
have vanishing probabilities, leaving each of the other
6 probability
1
6
.
But should Allen probabilities be assessed around
the number n of points in the linear order? The guid-
ing perspective behind (Allen, 1983) (and many other
1
As for why an interval should be half open and half
closed, some motivation from Leibniz’s law is presented in
section 4 below.
952
Fernando, T. and Vogel, C.
Prior Probabilities of Allen Interval Relations over Finite Orders.
DOI: 10.5220/0007699609520961
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 952-961
ISBN: 978-989-758-350-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
works such as (Hamblin, 1971)) is that intervals, not
points, are basic, suggesting that n pertain to inter-
vals, not points. We take up this suggestion in section
3, working with interval names (also known as events
under, for example, the Russell-Wiener construction
of temporal instants described in (Kamp and Reyle,
1993, page 667)). Calculating probabilities becomes
more complex without, as far as we can tell, straying
from the asymptotic behavior determined in section
2: at the limit n → ∞, 7 of the 13 Allen relations have
probability 0, while 6 have
1
6
each.
So what? The main thrust of this work is not so
much to calculate numbers but to uncover structure
lurking behind Allen relations. Concrete examples of
structure in natural language semantics are described
in the passage below from (Kamp, 2013, page 11)
when we interpret a piece of discourse — or
a single sentence in the context in which it
is being used — we build something like a
model of the episode or situation described;
and an important part of that model are its
event structure, and the time structure that can
be derived from that event structure by means
of Russell’s construction.
The event structure Kamp has in mind is “made up
by those comparatively few events that figure in this
discourse” (page 9). The aforementioned Russell con-
struction turns the finitely many events mentioned in a
(finite) discourse into a finite linear order of temporal
instants (each instant being a certain set of events).
This contrasts sharply with the continuum R with
which “real” time is commonly identified (Kamp and
Reyle, 1993, for example) or, for that matter, any un-
bounded linear order for the time periods of (Allen
and Ferguson, 1994). Indeed, if an event is equipped
with its past and future — or, in the terminology of
(Freksa, 1992), an interval is represented by its semi-
intervals — then the resulting time structure amounts
to ordering the left and right borders l and r of events
(Fernando, 2016, page 3635). The case of two events
yields the Allen relations, which can be formulated
naturally in terms of strings (Durand and Schwer,
2008). That formulation is recounted in Table 1 in
section 2 below.
The appeal to left and right borders runs counter
to the use of the transitivity table in (Allen, 1983),
where borders are buried out of sight. That said, both
sections 2 and 3 end with links to the transitivity table.
A more serious issue is the assumption of equiprob-
able worlds, which we reconsider in section 4, after
the nature of the sample spaces becomes clearer. That
space is formed in section 3 out of strings that go well
beyond pictures of Allen relations between two inter-
vals. Throughout this paper, however, our focus is on
answering the question (Q) against a finite temporal
structure (given by a finite discourse).
2 PROBABILITIES OVER n
ORDERED POINTS
Let AR be the set of 13 names
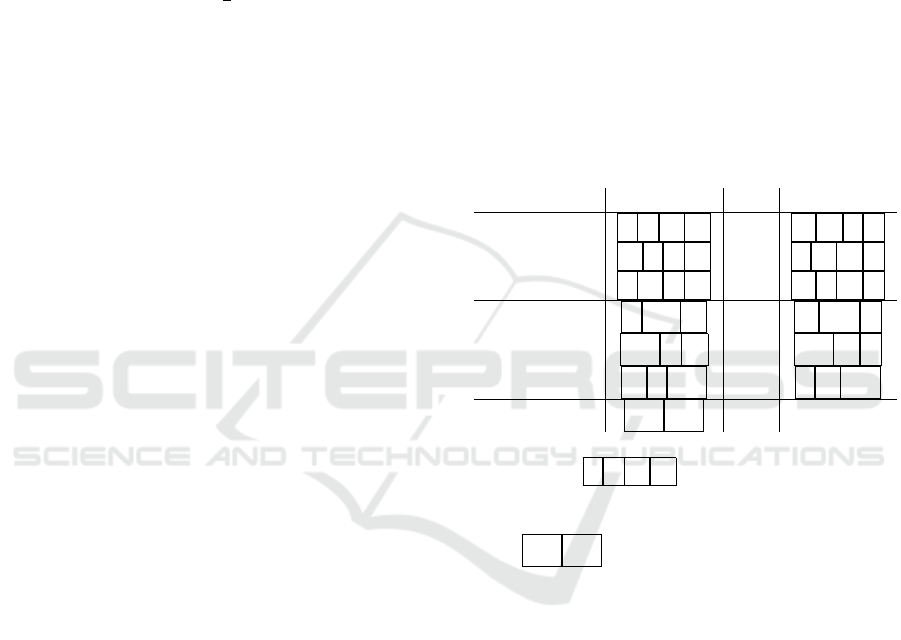
b, bi, d, di, o, oi, m, mi, s, si, f, fi, e
of Allen relations. For each R ∈ AR , Table 1 pictures
(l,r] R (l
0
,r
0
] as a string s
R
of boxes arranged from left
to right so that all borders in the same box are equal
and are < borders in boxes to the right (Durand and
Schwer, 2008).
Table 1: Allen relations in strings, following Figure 4 of
(Durand and Schwer, 2008).
(l,r] R (l
0
,r
0
] s
R
R
−1
s
R
−1
(l,r] b (l
0
,r
0
] l r l
0
r
0
bi l
0
r
0
l r
(l,r] d (l
0
,r
0
] l
0
l r r
0
di l l
0
r
0
r
(l,r] o (l
0
,r
0
] l l
0
r r
0
oi l
0
l r
0
r
(l,r] m (l
0
,r
0
] l r,l
0
r
0
mi l
0
r
0
,l r
(l,r] s (l
0
,r
0
] l,l
0
r r
0
si l,l
0
r
0
r
(l,r] f (l
0
,r
0
] l
0
l r,r
0
fi l l
0
r, r
0
(l,r] e (l
0
,r
0
] l,l
0
r, r
0
e
For example, l r l
0
r
0
depicts the ordering
l < r < l
0
< r
0
characteristic of (l,r] b (l
0
,r
0
]
while l, l
0
r, r
0
depicts the ordering
l = l
0
< r = r
0
characteristic of (l,r] e (l
0
,r
0
].
Each R ∈ AR can be classified as either long
{R ∈ A R | length(s
R
) = 4} = {b,d,o,bi,di,oi}
or medium
{R ∈ AR | length(s
R
) = 3} = {m,s,f,mi,si,fi}
or short
{R ∈ AR | length(s
R
) = 2} = {e}
according to the length of s
R
, which also happens
to be the cardinality of the set {l,l
0
,r, r
0
} when
(l,r] R (l
0
,r
0
]. The probabilities assigned in this paper
to each R ∈ AR will turn out to depend on whether R
is long, medium or short.
More precisely, given an integer n ≥ 4, let us agree
an n-world is a function
f : {x,y,x
0
,y
0
} → [n]
Prior Probabilities of Allen Interval Relations over Finite Orders
953

assigning four distinct variables x,y, x
0
,y
0
integers in
[n] such that
f (x) < f (y) and f (x
0
) < f (y
0
).
For each R ∈ AR , we say an n-world f satisfies R if
( f (x), f (y)] R ( f (x
0
), f (y
0
)].
Now comes a key observation.
Lemma 1. Given an integer n ≥ 4,
(i) the number of n-worlds satisfying e (equal) is
n
2
=
n(n −1)
2
(ii) for each medium R ∈ AR , the number of n-worlds
satisfying R is
n
3
=
n
2
n −2
3
(iii) for each long R ∈ A R , the number of n-worlds
satisfying R is
n
4
=
n
3
n −3
4
.
Proof. Let im be the map from an n-world f to its
image
im( f ) = { f (x), f (y), f (x
0
), f (y
0
)} ⊆ [n].
For each R ∈ AR , let im
R
be the restriction of im to
n-worlds satisfying R. It suffices to observe that im
R
is a bijection to subsets of [n] of cardinality
4 if R is long
3 if R is medium
2 if R is e.
Let Ω
n
be the set of n-worlds, and for each R ∈
AR , let p
n
(R) be the fraction of Ω
n
satisfying R
p
n
(R) =
cardinality({ f ∈ Ω
n
| f satisfies R})
cardinality(Ω
n
)
.
Representing the medium relations by meet, m, and
long relations by before, b, we have from Lemma 1,
p
n
(m)
p
n
(e)
=
n −2
3
and
p
n
(b)
p
n
(m)
=
n −3
4
which with
1 =
∑
R∈AR
p
n
(R) = p
n
(e) +6p
n
(m) +6p
n
(b)
allows us to solve for p
n
(e). A simpler alternative sug-
gested by a referee is to use
cardinality(Ω
n
) =
n
2
·
n
2
(as Ω
n
consists of all choices of pairs l,r and l
0
,r
0
from [n]). Either way, we obtain
Theorem 2. For n ≥ 4 and R,R
0
∈ A R ,
p
n
(R) = p
n
(R
0
) if length(s
R
) = length(s
R
0
)
where the short relation e (equal) has probability
p
n
(e) =
2
n(n −1)
while medium relations have probabilities
p
n
(m) =
2(n −2)
3n(n −1)
and long relations have probabilities
p
n
(b) =
(n −3)(n −2)
6n(n −1)
.
Corollary 3. For R ∈ AR ,
lim
n→∞
p
n
(R) =
0 if R is short or medium
1
6
otherwise.
To put Corollary 3 in context, the probabilities at the
start are strikingly different, with e the most probable
at n = 4, m catching up at n = 5, and b at n = 6 (and
the most probable from n ≥ 8).
Table 2: Some probabilities from Theorem 2.
n p
n
(e) p
n
(m) p
n
(b)
4 1/6 1/9 1/36
5 1/10 1/10 1/20
6 1/15 4/45 1/15
8 1/28 1/14 5/56
Recall from the Introduction that 1 should be added to
or subtracted from n to lift or impose bounds. At any
rate, there is an arbitrariness in any choice of n that
calls out for attention. Letting n approach +∞ (as in
Corollary 3) is an admittedly crude way to attend to
this. A more sophisticated approach would build on a
probability distribution on the lengths n — a direction
not pursued below.
What is pursued is the short-medium-long classi-
fication of Allen relations, which we pause now to
note is implicit in the transitivity table at the center
of (Allen, 1983). That table maps a pair (R
1
,R
2
) of
Allen relations to the set t(R
1
,R
2
) of Allen relations
R such that there are intervals i, j and k for which
iR
1
j and jR
2
k and iRk.
Let us define the t-number of an Allen relation R to
be the sum
#(R) :=
∑
R
0
∈AR
cardinality(t(R,R
0
))
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
954

of the numbers of entries in the row for R, including
the Allen relation of equality, e, omitted from the tran-
sitivity table in (Allen, 1983), which we incorporate
into t as expected
t(R,e) = t(e,R) = {R} for each R ∈ AR .
Proposition 4. For R ∈ AR ,
#(R) =
41 if R is long
25 if R is medium
13 if R is e.
Proposition 4 characterizes short, medium and long
Allen relations in terms of a notion #(R) that does not
explicitly mention interval borders. The same sum
#(R) arises down the column of the transitivity table
#(R) =
∑
R
0
∈AR
cardinality(t(R
0
,R))
and is the cardinality of the set
{(R
0
,R
00
) ∈ AR × AR | R
00
∈ t(R,R
0
)}.
In the next section, t-numbers #(R) are built into the
probabilites assigned to Allen relations R when three
or more intervals are considered.
3 PROBABILITIES OVER n
INTERVAL NAMES
The sample space Ω
n
in section 2 fixes the number
n of linearly ordered points. An alternative is to let
n ≥ 2 be the number of intervals under consideration,
construing each element i of [n] not as a point but as an
interval. Following (Allen, 1983), we might redefine
an n-world to be a function
ω : ([n] × [n]) → AR
that labels every pair (i, j) from [n]×[n] with an Allen
relation ω(i, j) ∈ AR in a consistent manner.
2
Con-
sistency of ω here can be understood as the existence
of functions
α : [n] → [2n]
and
β : [n] → [2n]
such that for all i ∈ [n],
α(i) < β(i) (1)
2
Subsets of AR assigned to edges between intervals in
(Allen, 1983) are reduced to singletons to keep worlds dis-
joint, and avoid double counting when basing probabilities
on world counts.
and for all j ∈ [n],
ω(i, j) is the Allen relation R such that
(α(i),β(i)] R (α( j),β( j)]. (2)
Together, (1) and (2) turn i, j ∈ [n] into <
2n
-intervals
(α(i),β(i)] and (α( j),β( j)] that satisfy the specifica-
tion encoded by ω. The functions α and β above need
not be unique, as [2n] may offer plenty of room to
satisfy (1) and (2). An extreme example is where all
intervals in [n] are equal
ω(i, j) = e for all i, j ∈ [n] (3)
in which case there are
2n
2
pairs
α,β : [n] → [2n]
that work. At the other extreme, exactly one such pair
satisfies ω if each interval i < n is before i + 1
ω(i,i +1) = b for i ∈ [n − 1]. (4)
These two extreme examples make clear that n is the
number of interval names, as opposed to intervals. In
the former case, (3), there is just one interval; in the
latter, (4), there are un-named intervals between those
named in [n]. Should we not insist that n count in-
tervals and not just some names? But what, in the
finite case, are intervals other than pairs of endpoints?
Counting these pairs would lead us back to section 2,
with
k
2
many intervals from k points (give or take 1,
for bounds explained in the Introduction). Moreover,
it bears noting that interval names are events, which
are important ingredients in not only philosophical
reconstructions of time but also natural language se-
mantics (Kamp and Reyle, 1993; Kamp, 2013).
For a handle on consistent labellings ω : [n] ×
[n] → AR , we turn to strings of sets. Recall from
Table 1, the strings s
R
for Allen relations R, such as
the string
s
m
= l r,l
0
r
0
of length 3, the middle symbol of which is the set with
r and l
0
as its elements. It will be crucial below not to
conflate the notions l,l
0
,r, r
0
even when, as with r and
l
0
in the middle box of s
m
, they name the same point.
Reconstrual of l, l
0
,r, r
0
in Table 1. The letters l, l
0
,r
and r
0
appearing in the strings s
R
in Table 1 are un-
interpreted terms (e.g., variables), each distinct from
the other (whether or not they co-occur in a box of a
string).
We draw boxes instead of curly braces {·} so as not
to confuse string symbols with sets such as
{s
R
| R ∈ AR }
Prior Probabilities of Allen Interval Relations over Finite Orders
955

which we can form from l r and l
0
r
0
through a
certain ternary relation & on strings s of sets
&( l r , l
0
r
0
, s) ⇐⇒ s ∈ {s
R
| R ∈ AR }. (5)
(5) is a consequence of defining & by induction ac-
cording to
(i0)
&(ε,ε,ε)
(i1)
&(s,s
0
,s
00
)
&(sa,s
0
a
0
,s
00
(a ∪a
0
))
(i2)
&(s,s
0
,s
00
)
&(sa,s
0
,s
00
a)
(i3)
&(s,s
0
,s
00
)
&(s,s
0
a
0
,s
00
a
0
)
where ε is the empty string, and a,a
0
are sets, qua
string symbols (Fernando, 2018).
3
The base case (i0)
puts (ε,ε,ε) into &, which is closed under rules (i1)
for superposition, and (i2), (i3) for shuffling. For ex-
ample,
&( l r , l
0
r
0
, s
m
)
follows from (i0), (i2), (i1) and (i3)
(i0)
(ε,ε,ε)
(i2)
( l , ε, l )
(i1)
( l r , l
0
, l r,l
0
)
(i3)
( l r , l
0
r
0
, l r,l
0
r
0
).
Collecting strings into sets (i.e., languages), we
can express & as a binary operation on languages
L,L
0
, defining
L&L
0
:= {s
00
| (∃s ∈ L)(∃s
0
∈ L
0
) &(s, s
0
,s
00
)} .
We apply & repeateadly to form languages L
n
encod-
ing consistent labellings ω : [n] × [n] → AR . Let
L
1
:= 1 1
(following the custom of conflating a string s with the
singleton language {s}) and
L
n+1
:= L
n
& n +1 n +1 for n ≥ 1.
To see how L
n
encodes consistent labellings, a few
definitions are in order. Given a set X and a string
s = a
1
···a
k
of sets,
(i) the X -reduct ρ
X
(s) of s is its componentwise in-
tersection with X
ρ
X
(a
1
···a
k
) := (a
1
∩ X)···(a
k
∩ X)
(ii) the X-projection π
X
(s) of s is the result of deleting
all occurrences of the empty box in ρ
X
(s)
3
A special case, mix, of the join operation in (Durand
and Schwer, 2008) suffices for an unmarked version of (5).
The calculation of probabilities below is, however, based on
(i0)–(i3).
(Durand and Schwer, 2008). For example,
ρ
{2,3}
( 1,2,4 1 2,3 3 4 ) = 2 2,3 3
π
{2,3}
( 1,2,4 1 2,3 3 4 ) = 2 2,3 3
and for any string s, 3 occurs exactly twice in s if
π
{3}
(s) = 3 3 . Clearly, L
n
is the set
{s ∈ (2
[n]
− {})
+
| (∀i ∈ [n]) π
{i}
(s) = i i }
of strings of non-empty subsets of [n] where each i ∈
[n] occurs exactly twice. Next, for distinct i, j ∈ [n]
and R ∈ AR , we let s
R/i, j
be the string s
R
(from Table
1) with l,r replaced by i, and l
0
,r
0
replaced by j. For
example,
s
m/2,3
= 2 2,3 3 and s
e/1,2
= 1,2 1,2
and
L
2
= {s
R/1,2
| R ∈ AR }.
For i 6= j, we can always invert s
R
7→ s
R/i, j
because
i and j each occur exactly twice in s
R/i, j
. If s =
a
1
···a
k
∈ L
n
, and i, j ∈ [n], then
π
{i, j}
(s) = s
R/i, j
⇐⇒ (l,r] R (l
0
,r
0
]
where l,r are positions in s marked by i
l := (least p ∈ [k]) i ∈ a
p
r := (greatest p ∈ [k]) i ∈ a
p
and similarly for l
0
,r
0
and j
l
0
:= (least p ∈ [k]) j ∈ a
p
r
0
:= (greatest p ∈ [k]) j ∈ a
p
.
Accordingly, let us agree s satisfies iR j if its {i, j}-
projection is s
R/i, j
s |= iR j ⇐⇒ π
{i, j}
(s) = s
R/i, j
.
Proposition 5. Let n ≥ 2.
(i) For all s ∈ L
n
and (i, j) ∈ [n]×[n], there is a unique
R ∈ AR such that s |= iR j.
(ii) For all s ∈ L
n
, let ω
s
: [n]×[n] → AR be the func-
tion that sends (i, j) to the unique R ∈ AR such
that s |= iR j (given by part (i)). The map s 7→ ω
s
is a bijection from L
n
onto the set of consistent
labellings from [n] × [n] to AR .
Proposition 5 follows by induction on n. Henceforth,
we adopt L
n
as our official sample space, equating the
probability of R (for each R ∈ AR ) with the propor-
tion of L
n
in which interval 1 is R-related to interval
2
p
n
(R) :=
cardinality(L
n
(R))
cardinality(L
n
)
(6)
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
956

where L
n
(R) is the subset
L
n
(R) := {s ∈ L
n
| s |= 1R2}
of L
n
satisfying R. The languages L
n
(R) vary with
R ∈ AR , but have a common part (in a sense to be
made precise presently), the language L
3:n
, defined as
follows
L
3:2
:= ε
L
3:n+1
:= L
3:n
& n +1 n +1 for n ≥ 2.
Note that ε is the identity of the binary operation &,
which is associative and commutative.
Proposition 6. For n ≥ 2, and R ∈ AR ,
L
n
(R) = s
R/1,2
& L
3:n
.
Behind Proposition 6 is a relationship between & and
π
X
that can be explained with a couple more defini-
tions. An X-component of a string s of sets is a string
s
0
of subsets of X such that
&(s
0
,s
00
,s) for some string s
00
of
subsets disjoint from X.
We say s is an S-word (Durand and Schwer, 2008) if
does not occur as a symbol in s — i.e.,
s = π
voc(s)
(s)
where the vocabulary voc(s) of s is the least set X
such that s ∈ (2
X
)
∗
voc(a
1
···a
n
) =
n
[
i=1
a
i
.
Lemma 7. For all strings s of sets, and disjoint sets
X and Y ,
&(π
X
(s),π
Y
(s),π
X∪Y
(s)) (when X ∩Y =
/
0)
and if s is an S-word, then π
X
(s) is the unique S-word
that is an X-component of s.
X-components of S-words need not be S-words (e.g.,
1 is a {1}-component of 1 2 ) but they are
unique after deleting .
Proposition 8. Let n ≥ 2 and s be a string of length
k > 1 with n 6∈ voc(s). The set
s& n n
consists of strings of length k, k + 1, and k + 2, of
which there are exactly
d
0
(k) :=
k(k − 1)
2
strings of length k,
d
1
(k) := k(k + 1) strings of length k + 1, and
d
2
(k) :=
(k + 1)(k + 2)
2
strings of length k + 2.
A string in s& n n of length k chooses 2 positions
from s in which to put n, whence
d
0
(k) =
k
2
while length k + 1 chooses a position from s and one
of k + 1 positions not in s
d
1
(k) = k(k +1)
and length k + 2 chooses 2 positions outside s, which
may be different or the same
d
2
(k) =
k + 1
2
+ k +1 =
(k + 1)(k + 2)
2
.
Returning now to the probabilities defined by line (6)
above, let c
n
(R) be the number
c
n
(R) := cardinality(L
n
(R))
of strings in L
n
satisfying R. It is instructive to ob-
serve that c
3
(R) is just the t-number #(R) defined at
the end of section 2 as the sum of the transitivity table
row for R
c
3
(R) =
∑
R
0
∈AR
cardinality(t(R,R
0
)).
For all n ≥ 2, we can calculate the quantities c
n
(R) in
terms of
c
n
(R;k) := cardinality({s ∈ L
n
(R) | length(s) = k})
for which we have the recurrence
c
2
(R;k) =
1 if length(s
R
) = k
0 otherwise
(7)
c
n+1
(R;k) = c
n
(R;k)d
0
(k) + c
n
(R;k − 1)d
1
(k − 1)
+ c
n
(R;k − 2)d
2
(k − 2)
= d
0
(k)(c
n
(R;k) + 2c
n
(R;k − 1)
+ c
n
(R;k − 2)) (8)
from Proposition 8, with Lemma 7 ruling out the pos-
sibility that (8) double counts. Propositions 6 and 8
reduce the variation in p
n
(R) to the length of s
R
c
n
(R) = c
n
(R
0
) if length(s
R
) = length(s
R
0
)
for all R,R
0
∈ A R and n ≥ 2. For the record,
Prior Probabilities of Allen Interval Relations over Finite Orders
957

Table 3: Some probabilities of e, m, b.
n p
n
(e) p
n
(m) p
n
(b) γ
n
γ
0
n
1 −6p
n
(b)
2
1
13
1
13
1
13
1 1
7
13
≈ 0.538461538
3 0.031784841 0.061124694 0.100244499 2 2 0.398533007
10 0.002527761 0.021841026 0.144404347 9 7 0.133573915
100 0.000023782 0.002283051 0.164379652 96 72 0.013722086
500 0.000000959 0.000460405 0.166206102 480 361 0.002763387
1000 0.000000240 0.000230840 0.166435786 961 721 0.001385281
1500 0.000000107 0.000153893 0.166512755 1442 1082 0.000923468
Theorem 9. For n ≥ 2 and R ∈ AR , the probabili-
ties p
n
(R) = c
n
(R)/c
n
can be calculated as follows
c
n
(e) =
2n−2
∑
k=2
c
n
(e;k) (9)
c
n
(R) =
2n−1
∑
k=3
c
n
(R;k) for medium R
c
n
(R) =
2n
∑
k=4
c
n
(R;k) for long R
where c
n
(R;k) is given by lines (7) and (8) above, and
c
n
= c
n
(e) +6(c
n
(m) +c
n
(b)) (10)
(representing medium relations by meet, m, and long
relations by before, b).
The summation index k in Theorem 9 ranges over
the possible lengths of strings in L
n
(R), according to
whether R is short, medium or long. One can map the
language L
n
to L
n+1
(e) by a bijection that renames
interval i to i + 1 and inserts 1e2, establishing
c
n
= c
n+1
(e).
Hence, as an alternative to (9), we can specify c
n
(e)
by the recurrence
c
2
(e) = 1 (= c
2
(m) = c
2
(b))
c
n+1
(e) = c
n
(e) +6(c
n
(m) +c
n
(b)) for n ≥ 2.
It is (9) and c
n
(e;k), however, that appear in Sloane’s
On-line Encyclopedia of Integer Sequences for the
“number of different relations between n intervals on
a line”
a(n) =
2n
∑
i=2
λ(i,n) where λ(i,n) = c
n
(e;i)
(according to (7), (8) above)
in https://oeis.org/A055203.
4
4
It is conjectured there that a(n) = 1 mod 12, which is
equivalent to the claim that c
n
(m) + c
n
(b) is even, by (10)
in Theorem 9.
Some values of p
n
(R) are listed in Table 3, along-
side integers γ
n
and γ
0
n
that compare p
n
(m) to p
n
(e)
γ
n
:=
p
n
(m)
p
n
(e)
=
c
n
(m)
c
n
(e)
and p
n
(b) to p
n
(m),
γ
0
n
:=
p
n
(b)
p
n
(m)
=
c
n
(b)
c
n
(m)
respectively. The inequalities
c
n
(m)
c
n
(e)
<
c
n+1
(m)
c
n+1
(e)
and
c
n
(b)
c
n
(m)
<
c
n+1
(b)
c
n+1
(m)
have been verified computationally for 2 ≤ n ≤ 1500,
providing evidence but not a proof that the asymp-
totic probabilities described in Corollary 3 carry over
to L
n
. The case n = 2 reproduces our first answer to
the question (Q) in the Introduction above
p
2
(R) =
1
13
while the transitivity table numbers #(R) are the basis
for n = 3
p
3
(R) =
#(R)
∑
R
0
∈AR
#(R
0
)
which varies according to whether R is short, medium
or long.
4 DISCUSSION
The study of probabilities above has led us to partition
Allen relations between the short, medium and long,
which is far less common than that between overlap
=
_
{d,di,o,oi,s,si,f,fi,e},
precedence
≺ =
_
{m,b},
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
958

and its converse
=
_
{mi,bi}
(Kamp and Reyle, 1993; Durand and Schwer, 2008,
among others). Using section 2, the asymptotic prob-
abilities
p() = lim
n→∞
p
n
(d) + p
n
(di) + p
n
(o) + p
n
(oi)+
p
n
(s) + p
n
(si) + p
n
(f) + p
n
(fi) + p
n
(e)
=
2
3
p(≺) = lim
n→∞
p
n
(m) + p
n
(b) =
1
6
p() = lim
n→∞
p
n
(mi) + p
n
(bi) =
1
6
do not differ vastly from the numbers
9/13, 2/13, 2/13
obtained by replacing the probabilities p
n
(R) of an
Allen relation R uniformly with 1/13, the probability
p
2
(R) where section 3 starts (at n = 2). While varia-
tions in n are of limited consequence for , ≺ and ,
it is a another matter once , ≺ and are refined to
Allen relations. But why invite such complications?
An important reason to be interested in n is granu-
larity, which takes on particular significance when it is
varied. One way to see this is through Leibniz’s law,
indiscernibility as identity. The requirement that any
difference x 6= y is discernible via some property P can
be expressed in monadic second-order logic (Libkin,
2010, for example) as
x 6= y ⊃ (∃P)¬(P(x) ≡ P(y)). (LL)
If we replace 6= by adjacency S and restrict P to be
given by some finite set X, (LL) becomes “time steps
S
require change
X
”
xSy ⊃ x 6≡
X
y (LL
S,X
)
where x 6≡
X
y means: x and y differ over some predi-
cate from X
x 6≡
X
y :=
_
i∈X
¬(P
i
(x) ≡ P
i
(y)).
For each i ∈ X , let us mark P
i
’s left and right borders
with subscripts l(i) and r(i) for predicates P
l(i)
saying:
P
i
is false but S-after true
P
l(i)
(x) ≡ ¬P
i
(x) ∧(∃y)(xSy ∧ P
i
(y)) (11)
and P
r(i)
saying: P
i
is true but not S-after
P
r(i)
(x) ≡ P
i
(x) ∧¬(∃y)(xSy ∧ P
i
(y)). (12)
Formulating x 6≡
X
y as
_
i∈X
((¬P
i
(x) ∧P
i
(y)) ∨(P
i
(x) ∧¬P
i
(y))
brings us, under xSy, to
W
i∈X
(P
l(i)
(x) ∨P
r(i)
(x)))
xSy ⊃ (x 6≡
X
y ≡
_
i∈X
(P
l(i)
(x) ∨P
r(i)
(x)))
assuming (11), (12) and S is deterministic
(∀z)(xSy ∧ xSz ⊃ y = z). (13)
That is, under (11)–(13), (LL
S,X
) says:
(∃y)(xSy) ⊃
_
i∈X
(P
l(i)
(x) ∨P
r(i)
(x)). (14)
To enforce (14), we let X
•
be the set
X
•
:= {l(i) | i ∈ X} ∪ {r(i) | i ∈ X}
of borders in X, and define a translation
β : (2
X
)
∗
→ (2
X
•
)
∗
with for example,
β( i, i
0
i
0
) = l(i),l(i
0
) r(i) r(i
0
)
mapping, in general, a string a
1
···a
k
of subsets of X
to the string b
1
···b
k
of subsets of X
•
according to (11)
and (12)
b
x
:= {l(i) | i ∈ a
x+1
− a
x
} ∪
{r(i) | i ∈ a
x
− a
x+1
} for x < k (15)
b
k
:= {r(i) | i ∈ a
k
}
(Fernando, 2018). While (13) is built into every
string, (14) is not. For a non-final position x, (15)
says
b
x
6= ⇐⇒ (a
x+1
− a
x
) ∪(a
x
− a
x+1
) 6=
⇐⇒ a
x+1
6= a
x
.
That is, for b
1
···b
k
= β(a
1
···a
k
),
b
1
···b
k−1
is an S-word ⇐⇒ a
1
···a
k
has no stutter
where a stutter of a
1
···a
k
is a non-final position x ∈
[k − 1] such that
a
x
= a
x+1
.
An S-word β(s) satisfies (14) and a bit more
(∀x)
_
i∈X
(P
l(i)
(x) ∨P
r(i)
(x))
without the precondition
(∃y)(xSy)
that x is not S-final.
For each Allen relation R, we can picture 1R2 not
only as the S-word s
R/1,2
from Table 1, but also as a
stutterless string s
◦
R
in Table 4 (Fernando, 2016, page
3635), stepping outside S-words for
s
◦
b
= 1 2
and
s
◦
bi
= 2 1 .
Prior Probabilities of Allen Interval Relations over Finite Orders
959
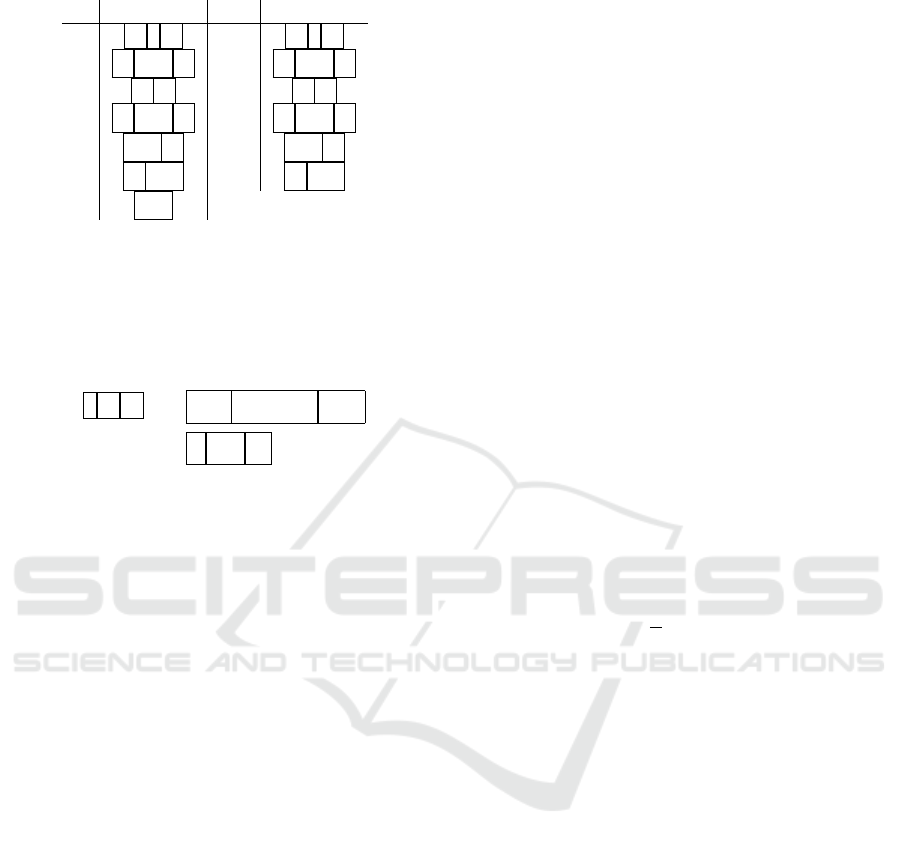
Table 4: Allen relations via stutterless strings.
R s
◦
R
R
−1
s
◦
R
−1
b 1 2 bi 2 1
o 1 1, 2 2 oi 2 1,2 1
m 1 2 mi 2 1
d 2 1, 2 2 di 1 1,2 1
s 1, 2 2 si 1,2 1
f 2 1,2 fi 1 1,2
e 1,2
From Table 4, Table 1 is a small step away
s
R
≈ β(s
◦
R
) for l ≈ l(1), r ≈ r(1),
l
0
≈ l(2), r
0
≈ r(2).
For example, R = m gives
β( 1 2 ) = l(1) r(1),l(2) r(2)
≈ l r,l
0
r
0
.
Stutterless strings arise from de-stuttering
saas
0
sas
0
(16)
just as S-words arise from -removal
ss
0
ss
0
. (17)
(17) implements the Aristotelian slogan
no time without change
under the assumption that
(†) all predicates in a string symbol a express change.
By contrast, (16) reflects the assumption that strings
are built from cumulative predicates, where by defini-
tion, a predicate P on intervals is cumulative if when-
ever an interval i meets an interval i
0
for the combined
interval i t i
0
,
P(i) and P(i
0
) =⇒ P(i t i
0
).
The converse
P(i ti
0
) =⇒ P(i) and P(i
0
)
(for i meets i
0
) is what it means for P to be divisive. P
is cumulative and divisive precisely if it satisfies the
condition (H) for homogeneity
(H) for all intervals i and i
0
whose union i ∪ i
0
is an
interval,
P(i ∪i
0
) ⇐⇒ P(i) and P(i
0
).
A bias towards stutterless strings (as opposed to S-
words) is in line with the well-known aspect hypoth-
esis from (Dowty, 1979) claiming
the different aspectual properties of the vari-
ous kinds of verbs can be explained by pos-
tulating a single homogeneous class of predi-
cates — stative predicates — plus three or four
sentential operators or connectives. (page 71)
That said, it is no accident that non-stative borders are
strung together in Table 1 for use in both sections 2
and 3, whereas their stative interiors are relegated (for
present purposes) to Table 4. Our analysis of Allen
relations above focuses not on the static condition of
interiors (described by (H)), but on the change marked
by borders (in accordance with (†)).
There are reasons to shift the aforementioned fo-
cus towards a more even balance in future work.
Statives and non-statives are boxed together in dis-
course representation structures (Kamp and Reyle,
1993), which can be put one after another in strings
to describe regularities (such as the preconditions and
effects of actions) beyond chance. Chance is as-
sessed above relative to sample spaces Ω
n
consist-
ing of worlds linked to model-theoretic interpreta-
tions of discourse representation structures. These
model-theoretic interpretations can be recast in ordi-
nary predicate logic, on which probabilities can be
defined. An equation assigning probabilities p(x) to
worlds x that has received considerable attention in
recent years is
p(x) =
1
Z
exp(
∑
i∈I
w
i
n
i
(x)) (18)
(Domingos and Lowd, 2009) given some finite set I
of first-order formulas i and weights w
i
∈ R that shape
the probability of x according to the number n
i
(x) of
groundings in x that satisfy i. (18) is applied to in-
terval networks for event recognition in (Morariu and
Davis, 2011), one of a number of works with data-
driven assignments of probabilities to Allen relations
(Zhang et al., 2013; Liu et al., 2018, among others).
The contribution of I to (18) is neutralized if every
weight w
i
is 0 (or equivalently, I =
/
0), resulting in
equiprobable worlds (with Z in (18) equal to the num-
ber of such worlds). It is this null, data-free case on
which we focus when raising in the Introduction the
question (Q) of the probability of aRa
0
, for arbitrary
intervals a, a
0
. Our answers, Theorem 2 in section 2
and Theorem 9 in section 3, are based on finite sam-
ple spaces Ω
n
of temporal entities that divide Allen
relations into the short, medium and long. No previ-
ous attention has, as far as we know, been paid to this
division. Does the division fade into insignificance
once an account of actions is introduced through a
non-empty set I of formulas and non-zero weights in
(18)? That would depend on I, which we have put
aside in answering (Q).
NLPinAI 2019 - Special Session on Natural Language Processing in Artificial Intelligence
960

5 CONCLUSION
The probability an Allen relation holds between two
arbitrary intervals is specified in Theorems 2 and 9
under the assumption that intervals are drawn from
a finite model by a fair method (in accordance with
the principle of indifference). The finite model as-
sumed depends on the particular application at hand.
(For example, the passage above from (Kamp, 2013)
describes a range of applications where that model
is based on the events mentioned in a discourse.)
Whether or not the notion of a fair coin can or should
extend to the choice of intervals from any such model
is a natural question that, in our view, merits study.
ACKNOWLEDGEMENTS
We are grateful to three anonymous referees for their
helpful comments.
This research is supported by Science Foun-
dation Ireland (SFI) through the CNGL Pro-
gramme (Grant 12/CE/I2267) in the ADAPT Cen-
tre (https://www.adaptcentre.ie) at Trinity College
Dublin. The ADAPT Centre for Digital Content
Technology is funded under the SFI Research Centres
Programme (Grant 13/RC/2106) and is co-funded un-
der the European Regional Development Fund.
REFERENCES
Allen, J. (1983). Maintaining knowledge about temporal
intervals. Communications of the ACM, 26(11):832–
843.
Allen, J. and Ferguson, G. (1994). Actions and events in
interval temporal logic. Journal of Logic and Compu-
tation, 4(5):531–579.
Domingos, P. and Lowd, D. (2009). Markov Logic: An
Interface Layer for Artificial Intelligence. Morgan and
Claypool Publishers.
Dowty, D. (1979). Word Meaning and Montague Grammar.
Reidel, Dordrecht.
Durand, I. and Schwer, S. (2008). A tool for reasoning
about qualitative temporal information: the theory of
S-languages with a Lisp implementation. Journal of
Universal Computer Science, 14(20):3282–3306.
Fernando, T. (2016). Prior and temporal sequences for nat-
ural language. Synthese, 193(11):3625–3637.
Fernando, T. (2018). Intervals and events with and without
points. In Proceedings of the Symposium on Logic and
Algorithms in Computational Linguistics 2018, pages
34–46. Stockholm University DiVA Portal for digital
publications.
Freksa, C. (1992). Temporal reasoning based on semi-
intervals. Artificial Intelligence, 54:199–227.
Hamblin, C. (1971). Instants and intervals. Studium gen-
erale, 24:127–134.
Kamp, H. (2013). The time of my life. https://lucian.
uchicago.edu/blogs/elucidations/files/2013/
08/Kamp
TheTimeOfMyLife.pdf.
Kamp, H. and Reyle, U. (1993). From Discourse to Logic.
Kluwer.
Libkin, L. (2010). Elements of Finite Model Theory.
Springer.
Liu, L., Wang, S., Hu, B., Qiong, Q., Wen, J., and Rosen-
blum, D. (2018). Learning structures of interval-
based Bayesian networks in probabilistic generative
model for human complex activity recognition. Pat-
tern Recognition, 81:545–561.
Morariu, V. and Davis, L. (2011). Multi-agent event recog-
nition in structured scenarios. Proc.IEEE Conf. Com-
puter Vision and Pattern Recognition, pages 3289–
3296.
Schwer, S. (Last modified Dec 2018). Sequence A055203
in The On-Line Encyclopedia of Integer Sequences.
https://oeis.org/A055203.
Verhagen, M., Gaizauskas, R., Schilder, F., Hepple,
M., Moszkowicz, J., and Pustejovsky, J. (2009).
The TempEval Challenge: Identifying temporal rela-
tions in text. Language Resources and Evaluation,
43(2):161–179.
Zhang, Y., Zhang, Y., Swears, E., Larios, N., Wang, Z., and
Ji, Q. (2013). Modeling temporal interactions with in-
terval temporal Bayesian networks for complex activ-
ity recognition. IEEE Transactions on Pattern Analy-
sis and Machine Intelligence, 35(10):24682483.
Prior Probabilities of Allen Interval Relations over Finite Orders
961
