
Smart General Variable Neighborhood Search with Local Search based
on Mathematical Programming for Solving the Unrelated Parallel
Machine Scheduling Problem
Marcelo Ferreira Rego
1,2
and Marcone Jamilson Freitas Souza
1
1
Universidade Federal de Ouro Preto (UFOP), Programa de P
´
os-Graduac¸
˜
ao em Ci
ˆ
encia da Computac¸
˜
ao,
35.400-000, Ouro Preto, Minas Gerais, Brazil
2
Universidade Federal dos Vales do Jequitinhonha e Mucuri (UFVJM),
Keywords:
Unrelated Parallel Machine Scheduling, Makespan, VNS, Metaheuristic, Mathematical Programming.
Abstract:
This work addresses the Unrelated Parallel Machine Scheduling Problem in which machine and job sequence-
dependent setup time are considered. The objective is to minimize the makespan. For solving it, a Smart
General Variable Neighborhood Search algorithm is proposed. It explores the solution space through five
strategies: swap of jobs in the same machine, insertion of job in the same machine, swap of jobs between
machines, insertion of jobs to different machines and an application of a Mixed Integer Linear Programming
formulation to obtain optimum scheduling on each machine. The first four strategies are used as shaking mech-
anism, while the last three are applied as local search through the Variable Neighborhood Descent method.
The proposed algorithm was tested in a set of 810 instances available in the literature and compared to three
state-of-the-art algorithms. Although the SGVNS algorithm did not statistically outperform them in these
instances, it was able to outperform them in 79 instances.
1 INTRODUCTION
The Unrelated Parallel Machine Scheduling Problem
with Setup Times (UPMSP-ST) consists of
scheduling a set N of n independent jobs on a
set M of m unrelated parallel machines. Each job
j ∈ N must be processed for exactly one of the
machines, and requires a processing time p
i j
to be
processed in machine i ∈ M. Each machine can
process only one job at a time. In addition, job
execution requires a setup time S
i jk
, which depends
on the machine i and the sequence in which job j and
k will be processed. In this work the objective is to
minimize the makespan.
The study of the UPMSP-ST is relevant due to
its theoretical and practical importance. From a
theoretical point of view, it attracts the interest of
researchers because it is NP-hard. In practical, it
is found in a large number of industries, such as
the textile industry (Lopes and de Carvalho, 2007).
According to (Avalos-Rosales et al., 2013), in a lot
of situations where there are different production
capacities, the setup time of machine depends on
the previous job to be processed (Lee and Pinedo,
1997). This situation is also found in manufacture
of chemical products, where the reactors must be
cleaned between handling of two mixture; however,
the time required for cleaning depends on the jobs that
were previously completed (Tran et al., 2016).
In this work a hybrid algorithm, based on the
General Variable Neighborhood Search – GVNS
(Mladenovi
´
c et al., 2008) is proposed. It explores the
solution space through five strategies: swap of jobs
in the same machine, insertion of job in the same
machine, swap of jobs between machines, insertion
of jobs to different machines and an application
of a Mixed Integer Linear Programming (MILP)
formulation to obtain optimum scheduling on each
machine. The first four strategies are used as
shaking mechanism, while the last three are applied
as local search through the Variable Neighborhood
Descent. This algorithm was able to outperform three
state-of-art algorithms in 79 among 810 instances
used for testing.
The remainder of this paper is organized as
follows. Section 2 gives a brief review of the
literature. In Section 3 a mathematical programming
formulation for the problem is presented. In Section 4
Rego, M. and Souza, M.
Smart General Variable Neighborhood Search with Local Search based on Mathematical Programming for Solving the Unrelated Parallel Machine Scheduling Problem.
DOI: 10.5220/0007703302870295
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 287-295
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
287

the proposed algorithm is detailed. The results are
presented in Section 5, while in Section 6 the work is
concluded.
2 RELATED WORK
(Arnaout et al., 2014) proposed a two-stage
Ant Colony Optimization algorithm (ACOII) for
minimizing the makespan in the UPMSP-ST. This
algorithm is an enhancement of the ACOI algorithm
that was introduced in (Arnaout et al., 2010). An
extensive set of experiments was performed to verify
the quality of the method. The results proved the
superiority of the ACOII in relation to the other
algorithms with which it was compared.
(Tran et al., 2016) addressed the UPMSP-ST
having as objective the minimization of the makespan.
The authors introduced a new mathematical
formulation, which provides better dual bounds
that are more efficient to find the optimum solution.
The computational experiments showed that it is
possible to solve larger instances than it was possible
to solve with other previously existing formulations.
A variant of the Large Neighborhood Search
metaheuristic, using Learning Automata to adapt the
probabilities of using removal and insertion heuristics
and methods, named LA-ALNS, is presented in (Cota
et al., 2017). The algorithm was used to solve
instances of up to 150 jobs and 10 machines. The
LA-ALNS was compared with three other algorithms
and the results show that the developed method
performs best in 88% of the instances. In addition,
statistical tests indicated that LA-ALNS is better than
the other algorithms found in the literature.
The UPMSP-ST was dealt in (Fanjul-Peyro and
Ruiz, 2010), where the objective was to minimize
the makespan. Seven algorithms were proposed: IG,
NSP, VIR, IG+, NSP+, VIR+ and NVST-IG+. The
first three are the base algorithms. The following
three are improved versions of these latest algorithms.
Finally, the last algorithm is a combination of the
best ideas from previous algorithms. These methods
are mainly composed of a solution initialization,
a Variable Neighborhood Descent – VND method
(Mladenovi
´
c et al., 2008) and a solution modification
procedure. Tests were performed with 1400 instances
and it was showed that the results were statistically
better than the algorithms previously considered
state-of-the-art, that is, (Mokotoff and Jimeno, 2002)
and (Ghirardi and Potts, 2005).
A Genetic Algorithm was proposed by (Vallada
and Ruiz, 2011) to solve the UPMSP-ST. The
algorithm includes a fast local search and a new
crossover operator. Furthermore, the work also
provides a mixed integer linear programming model
for the problem. After several statistical analyzes, the
authors concluded that their method provides better
results for small instances and, especially, for large
instances, when compared with other methods of the
literature at the time (Kurz and Askin, 2001; Rabadi
et al., 2006).
3 MATHEMATICAL MODEL
This Section provides a Mixed Integer Linear
Programming (MILP) model for the problem from
(Tran et al., 2016). Assume the following parameters:
• p
jk
: processing time of job j on machine i.
• S
i jk
: setup time required for processing job k ∈ N
immediately after job j ∈ N on machine i ∈ M.
• V : a very large real number.
For describing the model, consider the following
decision variables:
X
i jk
=
1, if job j immediately precedes job k
on machine i
0, otherwise
C
j
= Completion time of job j
O
i
= Completion time of machine i.
C
max
= Maximum completion time
The objective function is given by Equation (1):
min C
max
, (1)
and the constraints are given by Equations (2)-(10):
∑
i∈M
∑
j∈N∪{0},
j6=k
X
i jk
= 1, ∀k ∈ N, (2)
∑
i∈M
∑
k∈N∪{0},
j6=k
X
i jk
= 1, ∀ j ∈ N, (3)
∑
k∈N∪{0},
k6= j
X
i jk
=
∑
h∈N∪{0},
h6= j
X
ih j
,∀ j ∈ N, ∀i ∈ M, (4)
C
k
> C
j
+ S
i jk
+ p
ik
−V (1 − x
i jk
),
∀ j ∈ N ∪ {0},∀k ∈ N, j 6= k,∀i ∈ M, (5)
∑
j∈N
X
i0 j
6 1, ∀i ∈ M, (6)
C
0
= 0 (7)
∑
j∈N∪{0},
j6=k
∑
k∈N
(S
i jk
+ p
ik
)X
i jk
= O
i
, ∀i ∈ M, (8)
O
i
6 C
max
, ∀i ∈ M, (9)
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
288

X
i jk
∈ {0,1},∀ j ∈ N ∪ {0},∀k ∈ N, j 6= k,∀i ∈ M,
(10)
Equation (1) defines the objective function of
the problem, which is to minimize the maximum
completion time or makespan. Equations (2) – (10)
define the constraints of the model. The constraint
set (2) ensures that each job is assigned to exactly
one machine and has exactly one predecessor job.
Constraints (3) define that every job has exactly one
successor job. Each constraint (4) establishes that if a
job j is scheduled on a machine i, then a predecessor
job h and a successor job k must exist in the same
machine. Constraints (5) ensure a right processing
order. Basically, if a job k is assigned to a machine
i immediately after job j, that is, if X
i jk
= 1, the
completion time C
k
of this job k) must be greater
than or equal to the completion time C
j
of job j,
added to setup time between jobs j and k and the
processing time p
ik
of k on machine i. If X
i jk
= 0,
then a sufficiently high value V makes this constraint
redundant. With constraint set (6) we define at most
one job is scheduled as the first job on each machine.
Constraints (7) establish that the completion time of
the dummy job is zero. Constraints (8) compute, for
each machine, the time it finishes processing its last
job. Constraints (9) define the maximum completion
time.
4 PROPOSED ALGORITHM
4.1 Initial Solution
The initial solution is generated by a constructive
heuristic defined by the Algorithm 1.
Algorithm 1: Initial Solution.
input : M, N
1 foreach k ∈ N do
2 Find the machine i and the position j for the
job k that produces the lowest cost for the
objective function;
3 Insert job k in position j on machine i;
4 end
Algorithm 1 receives the sets M and N of machines
and jobs as parameters, respectively. At each
iteration, a position j on a machine i that provides the
smallest increase in the objective function according
to Eq. (1) is chosen to insert the job k. This process is
repeated for all jobs. The method ends when all jobs
are allocated on some machine.
4.2 Smart GVNS
The proposed algorithm, so-called Smart GVNS, is
based on the General Variable Neighborhood Search
metaheuristic – GVNS (Mladenovi
´
c et al., 2008).
GVNS explores the solution space of the problem
through systematic neighborhood exchanges and has
the Variable Neighborhood Descent method – VND
(Mladenovi
´
c and Hansen, 1997) as the local search
method.
In Smart GVNS, the decision for increasing the
perturbation level occurs only after a certain number
of VND applications without improvement in the
quality of the current solution. Smart GVNS was
implemented according to the Algorithm 2:
Algorithm 2: Smart GVNS.
input : stopping criterion, Max, N
1 s
0
← Initial Solution();
2 ItSameNeigh ← 1;
3 p ← 2;
4 s ← VND(s
0
,N );
5 while (stopping criterion was not satisfied) do
6 s
0
← Shaking(s, p);
7 s
00
← VND(s
0
,N );
8 if ( f (s
00
) < f (s)) then
9 s ← s
00
;
10 p ← 2;
11 ItSamePerturb ← 1;
12 end
13 else
14 ItSamePerturb ← ItSamePerturb +1;
15 if (ItSamePerturb > Max) then
16 p ← p + 1;
17 ItSamePerturb ← 1;
18 end
19 end
20 end
21 return s ;
Algorithm 2 receives as input: 1) the stopping
criterion, which in this case was the CPU time t, given
by t = n × 5 seconds, where n is the number of jobs;
2) Max, the maximum number of iterations without
improvement in f (s) with the same perturbation
level; 3) the set N of neighborhoods. In line 1 the
solution s is initialized from the solution obtained
by the procedure defined in Section 4.1. In line 6, a
random neighbor s
0
is generated from a perturbation
performed according to the procedure defined in
Section 4.2.1. The loop from lines 5-20 is repeated
while the stopping criterion is not satisfied. In line 7,
Smart General Variable Neighborhood Search with Local Search based on Mathematical Programming for Solving the Unrelated Parallel
Machine Scheduling Problem
289

Algorithm 3: VND.
input : s, N
1 k ← 1;
2 while (k ≤ 3) do
3 s
00
← BestNeighbor(s,N
k
);
4 if ( f (s
00
) < f (s)) then
5 s ← s
00
;
6 k ← 1;
7 end
8 else
9 k ← k + 1 ;
10 end
11 end
12 return s ;
a local search on s
0
using the neighborhood structures
described in Section 4.2.2 is performed. It stops
when it finds the first solution that is better than s
or when the whole neighborhood has been explored.
The solution returned by this local search is attributed
to s
00
if its value is better than the current solution.
Otherwise, a new neighborhood structure is explored.
4.2.1 Shaking
An important step of a VNS-based algorithm is the
shaking procedure of a solution. This step is applied
so that the algorithm does not get stuck in a same
region of the solution space of the problem and to
explore other regions. For this reason, the algorithm
progressively increases the level of perturbation in a
solution when it is stuck in a local optimum.
In this work, the shaking procedure consists of
applying to the current solution p = 2 moves chosen
among the following: 1) change of execution order of
two jobs of the same machine; 2) change of execution
order of two jobs belonging to different machines; 3)
insertion of a job from a machine into another position
of the same machine and 4) insertion of a job from one
machine into a position of another machine.
It works as follows: p independent moves are
applied consecutively on the current solution s,
generating an intermediate solution s
0
. This solution
s
0
is, then, refined by the VND local search method
(line 7 of the Algorithm 2). The level of perturbation
p increases after a certain number of attempts to
explore the neighborhood without improvement in
the current solution. This limit is controlled by the
variable Max. When p increases, then p random
moves (chosen from those mentioned above) are
applied to the current solution. Whenever there is an
improvement in the current solution, the perturbation
returns to its lowest level, that is, p = 2.
The operation of each type of perturbation is
detailed below:
Swap in the Same Machine: The process of
perturbation by swap of jobs on the same
machine consists in randomly choosing two jobs
j
1
and j
2
that are, respectively, in the positions
x and y of a machine i, and allocate j
1
in the
position y and j
2
in the position x of the same
machine i.
Swap between Different Machines: This
perturbation consists in randomly choosing
a job j
1
that is in the position x in a machine i
1
and another job j
2
that is in the position y of
the machine i
2
. Then, job j
1
is allocated to
machine i
2
in position y, and job j
2
is allocated to
machine i
1
in position x.
Insertion in the Same Machine: The process of the
insertion in the same machine starts with the
random choice of a job j
1
that is initially in the
position x of the machine i. Then, a random
choice of another position y of the same machine
is made. Finally, job j
1
is removed from position
x and inserted into position y of machine i.
Insertion between Different Machines: This
perturbation consists of initially choosing a
random job j
1
that is in the position x in a
machine i
1
and a random position y of the
machine i
2
. After the choice, job j
1
is removed
from machine i
1
and inserted into position y of
machine i
2
.
4.2.2 Local Search
The exploration of the solution space of the problem
uses three different neighborhood structures: the first
one based on job insertion between machines; the
second one in swap of jobs between machines and
the third one in a mathematical heuristic. These
neighborhood structures are described below.
N
1
: Insertion Neighborhood Between Machines:
Given a scheduling π = {π
1
,π
2
,..., π
n
} in a
machine i
1
and a sequencing σ = {σ
1
,σ
2
,..., σ
n
}
in a machine i
2
, the insertion neighborhood
between machines generates neighboring
solutions as follows. Each job π
x
is removed from
machine i
1
and added to machine i
2
at position y.
The set of insertion moves of every the jobs of a
machine i
1
in every possible positions of another
machine i
2
defines the neighborhood N
1
(π,σ),
which is composed by |π| × (|σ| + 1) possible
solutions.
Figure 1 illustrates an insertion move of a job π
x
of a machine i
1
in the position y of the machine i
2
,
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
290
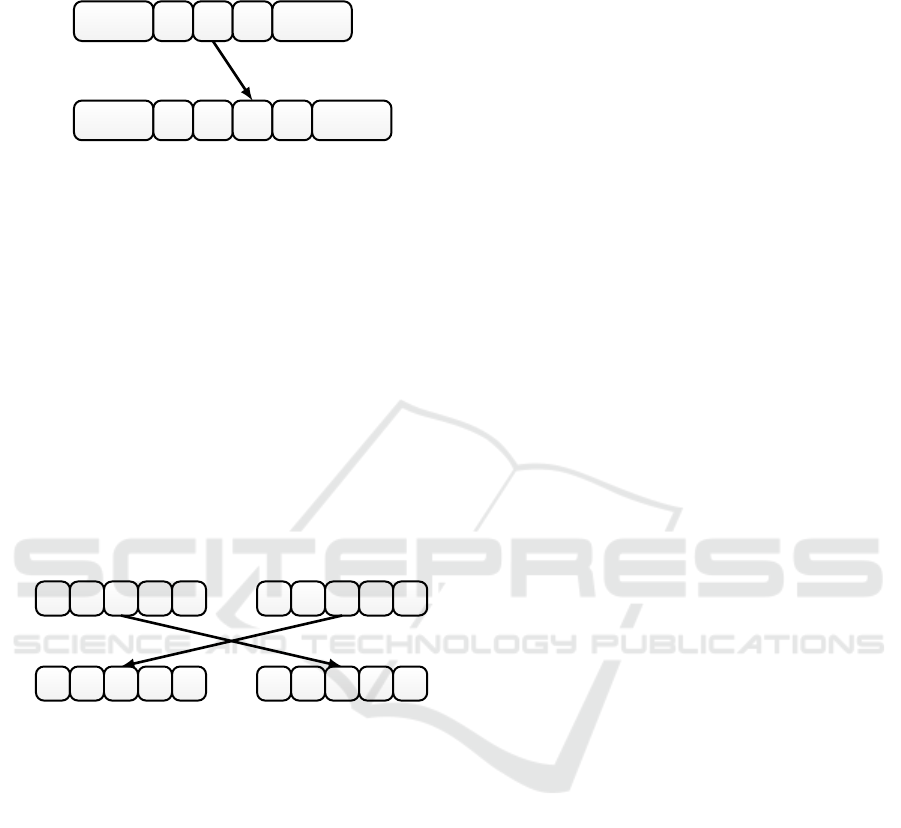
considering a value of x less than y .
i
1
π
x-1
π
x
π
x+1
i
2
σ
y-1
σ
y
π
x
σ
y+1
Figure 1: Insertion Move Between Machines i
1
and i
2
.
N
2
: Swap Move between Machines: Given a
scheduling π = {π
1
,π
2
,..., π
n
} in a machine
i
1
and a scheduling σ = {σ
1
,σ
2
,..., σ
n
} in a
machine i
2
, the swap move between machines
performed with two jobs π
x
and σ
y
moves the
job π
x
to the position y of the machine i
2
and the
job σ
y
to the position x on the machine i
1
. The
set of swap moves between two machines i
1
and
i
2
defines the neighborhood N
2
(π,σ), formed by
|π| ×|σ| solutions.
Figure 2 illustrates the swap between two jobs π
x
and σ
y
, which are initially allocated to machines
i
1
and i
2
, respectively. After the swap move, the
job σ
y
is allocated to machine i
0
1
and job π
x
to
machine i
0
2
.
i
1
π
x-1
π
x
π
x+1
i
2
σ
y-1
σ
y
σ
y+1
i
0
1
π
x-1
σ
y
π
x+1
i
0
2
σ
y-1
π
x
σ
y+1
Figure 2: Swap Move Between Machine i
1
and i
2
s.
N
3
: Scheduling by Mathematical Programming:
In this local search, the objective is to determine
the best scheduling of the jobs in each machine
by the application of a MILP formulation. This
single machine version that is solved by a MILP
is basically a Traveling Salesman Problem due to
the sequence-dependent setup times.
So, a MILP formulation is solved for the
sequencing problem in each of the machines at
a time. If there is improvement in the current
solution, it returns to the first neighborhood (N
1
).
If there is no improvement in one machine,
then the model will be applied to the next
machine. If there is no improvement by applying
this formulation to all m machines, then the
exploration is ended to neighborhood N
3
and also
to the local search. In this case, the local search
returns a local optimum in relation to all three
neighborhoods N
1
, N
2
and N
3
.
The mathematical formulation given by
Equations (11)–(16) was applied to the jobs
N
i
⊆ N of each machine i. The decision variables
are:
Y
jk
=
1, if job k is processed directly after job j
0, otherwise
C
i
max
= Maximum completion time on machine i
min C
i
max
, (11)
∑
j∈N
i
∪{0},
j6=k
Y
jk
= 1, ∀k ∈ N
i
, (12)
∑
k∈N
i
∪{0},
j6=k
Y
jk
= 1, ∀ j ∈ N
i
, (13)
∑
j∈N
i
∪{0}
j6=k
∑
k∈N
i
(S
i jk
+ p
ik
)Y
jk
= C
i
max
, (14)
Y
jk
∈ {0,1}, (15)
∑
j∈δ
∑
k /∈δ
Y
jk
≥ 1 ∀δ ⊂ N
i
,δ 6=
/
0 (16)
Equation (11) defines the objective function,
which is to minimize the completion time of the
machine i.
Equations (12)–(16) define the constraints for the
sub-model. Constraints (12) ensure that every
job k has exactly one predecessor job, and the
predecessor job of the first job is the dummy
job 0. Constraints (3) ensure that each job k
has a successor job, and the successor of the
last job is the dummy job 0. Constraints (14)
compute the completion time on the machine i.
Constraints (15) define the domain of the decision
variables. Constraints (16) ensure that there is no
sub-sequencing, therefore, any subset of jobs δ
contained in N
i
must have at least one link with
another subset complementary to δ. This strategy
is similar to the subtour elimination constraints
for the traveling salesman problem, proposed by
(Bigras et al., 2008).
The mathematical model has a constraint for
each subset of jobs. Thus, in cases where the
scheduling problem has many subsets of jobs, the
model will present a high computational cost. For
this reason, the set of constraints (16) was initially
disregarded from the model. However, the relaxed
model can produce an invalid solution, that is, a
solution containing one or more cyclic sequences.
If this happens, a new set of constraints for each
Smart General Variable Neighborhood Search with Local Search based on Mathematical Programming for Solving the Unrelated Parallel
Machine Scheduling Problem
291

cyclic sequencing is added to the mathematical
model to be solved again. In this new set of
constraints (16), the set δ is formed by the group
of jobs belonging to the cyclic sequencing. This
process is repeated until a valid solution is found.
For illustrating this situation, consider the matrix
below that represents the values of the decision
variables for a problem of a machine with 5 jobs.
Table 1: Example of an invalid solution.
Y 0 1 2 3 4 5
0 0 0 0 0 0 1
1 0 0 1 0 0 0
2 0 1 0 0 0 0
3 1 0 0 0 0 0
4 0 0 0 1 0 0
5 0 0 0 0 1 0
Consider that if Y
jk
= 1 then job j immediately
precedes job k, and that the first job of the
sequence is preceded by the dummy job 0. Then
we have the following sequencing: δ
1
= {5,4,3}
and δ
2
= {1,2}. In this example, δ
2
is a cyclic
sequencing. This solution is invalid since there
should be a single sequencing and not two as
can be observed. It is possible to observe that
δ
2
represents a cyclic sequencing, since job 1
precedes job 2 and this, in turn, precedes job 1.
Thus, a new constraint must be added for any
solution that presents a cyclic sequencing, since
this situation does not meet the Equation (16).
4.3 Parameter Tunning
The implementation of the Smart GVNS algorithm
requires the calibration of two parameters: Max,
which is defined in Algorithm 2, and the time t as
stopping criterion. The maximum execution time
t of the algorithm for each instance was calculated
according to Equation (17):
t = F ×n (17)
where n is the number of jobs of the instance.
In order for tunning the values of these
parameters, the Irace package (L
´
opez-Ib
´
a
˜
nez
et al., 2016) was used. Irace is an algorithm
implemented in R that implements an iterative
procedure having as main objective to find the
most appropriate configurations for an optimization
algorithm, considering a set of instances of the
problem.
We tested the following values for these
parameters: Max ∈ {4, 5, 6, 7, 8, 9, 10} and
F ∈ {4, 5, 6, 7, 8}. The best configuration returned
by Irace was Max = 9 and F = 7. However, as will be
shown later, only the Max parameter was used, since
the criterion of stopping by processing time was fixed
for a more just comparison with other algorithms of
the literature.
5 RESULTS
The Smart GVNS algorithm was coded in C++
language and the tests were performed on a
microcomputer with the following configurations:
Intel (R) Core (TM) i7 processor with clock frequency
2.4 GHz, 8 GB of RAM and with a 64-bit
Ubuntu operating system installed. The mathematical
heuristic, used as local search, was implemented
using the Gurobi API (Gurobi Optimization, 2018)
for the C++ language.
The proposed algorithm was tested in three sets of
instances available in (Rabadi et al., 2006): Balanced,
Process Domain and Setup Domain. Each set is
formed by 18 groups of instances, and each group
contains 15 instances. In the first set, the processing
time and the setup time are balanced. In the second,
the processing time is dominant in relation to the
setup time and in the third, the setup time is dominant
in relation to the processing time.
Tables 2, 3 and 4 present the results of
the proposed Smart GVNS algorithm (denoted by
SGVNS, for simplicity) in these three set of instances.
These tables compare the results of SGVNS with
those of ACOII reported in (Arnaout et al., 2014)
and AIRP and LA-ALNS reported in (Cota et al.,
2017), considering the value of the Relative Percent
Deviation (RPD), which is given by:
RPD
l
=
f
alg
l
− f
?
l
f
?
l
× 100 (18)
where f
alg
l
is the value of the objective function for
the algorithm alg in relation to the instance l, while
f
?
l
represents the best value for the objective function
obtained in the l-th instance by the ACOI algorithm
as reported in (Arnaout et al., 2014).
As stopping criterion of the Smart GVNS
algorithm and for a fair comparison, the average
execution time of ACOII in (Arnaout et al., 2014) was
used. Their time was divided by 2.37 because our
computer is approximately 2.37 times faster than the
computer used in (Arnaout et al., 2014) according to
(PassMark, 2018). (Cota et al., 2017) also used the
same stopping criterion to present the results of AIRP
and LA-ALNS algorithms.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
292

In these tables, the first and second columns
represent the number of machines and jobs,
respectively. In the subsequent columns is the average
RPD for the ACOI, ACO-II, AIRP, LA-ALNS and
SGVNS algorithms, respectively. The average RPD
presented considers a group of 15 instances.
Table 2: Average RPD in Balanced instances.
m n ACOII AIRP LA-ALNS SGVNS
2
80 -0.349 0.440 0.191 -0.103
100 -0.306 0.560 0.123 -0.057
120 -0.420 0.440 0.015 -0.181
4
80 0.747 0.840 0.243 1.287
100 0.739 0.910 0.171 1.395
120 0.428 0.810 0.183 1.137
6
80 1.682 0.910 0.296 1.855
100 1.481 1.120 0.206 2.146
120 1.028 1.130 0.262 2.309
8
80 0.012 0.595
100 0.000 0.474
120 0.020 1.002
10
80 1.739 1.060 0.462 2.790
100 2.854 1.280 0.371 3.073
120 2.270 1.390 0.287 3.282
12
80 0.017 1.665
100 -0.028 1.335
120 0.036 1.372
Table 3: Average RPD in the Process Domain instances.
m n ACOII AIRP LA-ALNS SGVNS
2
80 -0,224 0,250 0,119 -0,114
100 0,773 0,370 0,082 -0,076
120 0,619 0,340 0,062 -0,111
4
80 0,499 0,490 0,160 0,782
100 0,469 0,550 0,106 0,658
120 0,388 0,340 0,129 0,484
6
80 0,508 0,440 0,364 1,071
100 1,223 0,840 0,185 1,499
120 0,759 0,510 0,160 0,876
8
80 -0,018 0,333
100 -0,006 0,172
120 0,010 0,238
10
80 0,894 0,420 0,261 1,900
100 1,849 0,840 0,248 1,910
120 1,487 0,530 0,157 1,460
12
80 0,026 1,021
100 0,020 0,686
120 -0,004 0,385
According to Tables 2, 3 and 4, the LA-ALNS
algorithm was superior in 27 groups of instances,
while the ACOII algorithm was superior in 21 groups
of instances and the Smart GVNS algorithm was
superior in 5 groups of instances. Considering
the presented results, it is possible to affirm that
the LA-ALNS algorithm obtained the best average
results, even though it was not applied to all the
instances made available in (Rabadi et al., 2006).
Table 4: Average RPD in the Setup Domain instances.
m n ACOII AIRP LA-ALNS SGVNS
2
80 -0,163 0,220 0,120 -0,102
100 0,597 0,340 0,070 -0,091
120 0,588 0,320 0,067 -0,076
4
80 0,639 0,440 0,118 0,788
100 0,452 0,580 0,135 0,643
120 0,351 0,490 0,072 0,542
6
80 0,786 0,590 0,346 1,131
100 1,273 0,820 0,175 1,870
120 0,576 0,510 0,173 1,094
8
80 -0,025 -0,053
100 -0,006 0,164
120 0,000 0,325
10
80 0,953 0,650 0,209 2,003
100 1,759 0,790 0,212 1,969
120 1,204 0,580 0,167 1,510
12
80 0,000 1,285
100 0,012 1,055
120 -0,014 0,906
The proposed algorithm presented a value for
RPD less than 0 in instances with two machines.
If we consider instances with 4 machines, the RPD
was always less than 2, while for instances with up
to 8 machines, the RPD was always less than 3.
For the other instances, the RPD was always less
than 4. These results indicate that the proposed
method obtained a better performance in instances
with fewer machines, in which the solution space
is smaller. In other cases, the method has lower
performance, given the high computational cost of the
mathematical heuristic, which is used as one of the
local search operators.
A hypothesis test was performed to verify if
the differences between the results presented by the
algorithms are statistically significant. Therefore, the
following hypothesis test was used:
(
H
0
: µ
1
= µ
2
= µ
3
H
1
: ∃i, j | µ
i
6= µ
j
in which µ
1
, µ
2
and µ
3
are the average RPDs for
ACOII, LA-ALNS and Smart GVNS, respectively.
As it was not possible to establish that the samples
do not originate from a population with a normal
distribution, it was decided to use the Kruskal-Wallis
test. It is a nonparametric test used to compare three
or more populations. It tests the null hypothesis that
all populations have the same distribution functions
versus the alternative hypothesis that at least two of
the populations have different distribution functions.
The paired Kruskal-Wallis test for the samples of
the average results of the ICOII, LA-ALNS and Smart
GVNS algorithms returned p-value = 9.866e-05.
Considering that this p-value is much lower than
Smart General Variable Neighborhood Search with Local Search based on Mathematical Programming for Solving the Unrelated Parallel
Machine Scheduling Problem
293

0.05, then the null hypothesis of equality between the
means is rejected and it is concluded that there is
evidence that at least two populations have different
distribution functions.
In order to identify which samples have RPDs
with statistically significant differences, the Nemenyi
test (Nemenyi, 1963) was adopted. Table 5 shows the
results with pairwise comparisons. It is a post-hoc
test, that is, a multiple comparison test that is applied
after a test with three or more factors.
Table 5: Results of the Nemenyi test.
ACOII LA-ALNS
LA-ALNS 0.242 –
SGVNS 0.012 9.8e-05
According to Table 5 there is statistically
significant difference between our algorithm and
the ACOII and LA-ALNS algorithms. Although
the LA-ALNS algorithm outperformed the ACOII
algorithm in all sets of instances in which they were
compared, except in sets with two machines, there
was no statistical evidence of its superiority.
6 CONCLUSIONS
This work addressed the Unrelated Parallel Machine
Scheduling Problem in which machine and job
sequence-dependent setup time are considered. The
objective is to minimize the makespan.
In order to solve it, a GVNS-based algorithm,
named SGVNS, is proposed. It explores the solution
space of the problem by means of insertion and
exchange moves of jobs in the same machine and in
different machines, as well as by the application of
a mathematical programming formulation to obtain
optimum scheduling on each machine.
The proposed algorithm was tested in 810
instances of the literature and compared to three other
literature methods (ACOII, AIRP and LA-ALNS).
SGVNS behaved better in instances with a small
number of machines, even though the number of jobs
was high.
From a hypothesis test it was possible to obtain
statistical evidence that the result presented by
LA-ALNS and ACOII are significantly better than the
Smart GVNS algorithm. Despite this, SGVNS was
superior in 5 groups of instances and able to find best
results in 79 of the 810 instances.
In the future we intend to increase the efficiency
of our algorithm to make it more competitive. An
alternative is to test other mathematical programming
formulations to perform the local search. Another
alternative is to apply the local search based on
mathematical programming only periodically, since it
consumes a high computational time.
ACKNOWLEDGEMENTS
The authors thank Coordenac¸
˜
ao de Aperfeic¸oamento
de Pessoal de N
´
ıvel Superior (CAPES) - Finance
Code 001, Fundac¸
˜
ao de Amparo
`
a Pesquisa
do Estado de Minas Gerais (FAPEMIG, grant
PPM/CEX/FAPEMIG/676-17), Conselho Nacional
de Desenvolvimento Cient
´
ıfico e Tecnol
´
ogico (CNPq,
grant 307915/2016-6), Universidade Federal de Ouro
Preto (UFOP) and Universidade Federal dos Vales
do Jequitinhonha e Mucuri (UFVJM) for supporting
this research. The authors also thank the anonymous
reviewers for their valuable comments.
REFERENCES
Arnaout, J.-P., Musa, R., and Rabadi, G. (2014). A two-
stage ant colony optimization algorithm to minimize
the makespan on unrelated parallel machines – part
ii: enhancements and experimentations. Journal of
Intelligent Manufacturing, 25(1):43–53.
Arnaout, J.-P., Rabadi, G., and Musa, R. (2010). A two-
stage ant colony optimization algorithm to minimize
the makespan on unrelated parallel machines with
sequence-dependent setup times. Journal of Intelli-
gent Manufacturing, 21(6):693–701.
Avalos-Rosales, O., Alvarez, A. M., and Angel-Bello, F.
(2013). A reformulation for the problem of scheduling
unrelated parallel machines with sequence and ma-
chine dependent setup times. In Proc. of the 23th In-
ternational Conference on Automated Planning and
Scheduling – ICAPS, pages 278–283, Rome, Italy.
Bigras, L.-P., Gamache, M., and Savard, G. (2008). The
time-dependent traveling salesman problem and sin-
gle machine scheduling problems with sequence de-
pendent setup times. Discrete Optimization, 5(4):685–
699.
Cota, L. P., Guimar
˜
aes, F. G., de Oliveira, F. B., and Souza,
M. J. F. (2017). An adaptive large neighborhood
search with learning automata for the unrelated par-
allel machine scheduling problem. In Evolutionary
Computation (CEC), 2017 IEEE Congress on, pages
185–192. IEEE.
Fanjul-Peyro, L. and Ruiz, R. (2010). Iterated greedy
local search methods for unrelated parallel machine
scheduling. European Journal of Operational Re-
search, 207(1):55–69.
Ghirardi, M. and Potts, C. N. (2005). Makespan minimiza-
tion for scheduling unrelated parallel machines: A re-
covering beam search approach. European Journal of
Operational Research, 165(2):457–467.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
294

Gurobi Optimization, L. (2018). Gurobi optimizer refer-
ence manual. Available at http://www.gurobi.com.
Kurz, M. and Askin, R. (2001). Heuristic scheduling
of parallel machines with sequence-dependent set-up
times. International Journal of Production Research,
39(16):3747–3769.
Lee, Y. H. and Pinedo, M. (1997). Scheduling jobs
on parallel machines with sequence-dependent setup
times. European Journal of Operational Research,
100(3):464–474.
Lopes, M. J. P. and de Carvalho, J. V. (2007). A branch-and-
price algorithm for scheduling parallel machines with
sequence dependent setup times. European journal of
operational research, 176(3):1508–1527.
L
´
opez-Ib
´
a
˜
nez, M., Dubois-Lacoste, J., P
´
erez C
´
aceres, L.,
St
¨
utzle, T., and Birattari, M. (2016). The irace pack-
age: Iterated racing for automatic algorithm configu-
ration. Operations Research Perspectives, 3:43–58.
Mladenovi
´
c, N., Dra
ˇ
zi
´
c, M., Kova
ˇ
cevic-Vuj
ˇ
ci
´
c, V., and
ˇ
Cangalovi
´
c, M. (2008). General variable neighbor-
hood search for the continuous optimization. Euro-
pean Journal of Operational Research, 191(3):753–
770.
Mladenovi
´
c, N. and Hansen, P. (1997). Variable neigh-
borhood search. Computers & Operations Research,
24(11):1097–1100.
Mokotoff, E. and Jimeno, J. (2002). Heuristics based on
partial enumeration for the unrelated parallel proces-
sor scheduling problem. Annals of Operations Re-
search, 117(1):133–150.
Nemenyi, P. (1963). Distribution-free Mul-
tiple Comparisons. Available at
https://books.google.com.br/books?id=nhDMtgAACAAJ.
PassMark (2018). Cpu benchmarks. Available at
https://www.cpubenchmark.net/. Acessed on Febru-
ary 12, 2018.
Rabadi, G., Moraga, R. J., and Al-Salem, A. (2006). Heuris-
tics for the unrelated parallel machine scheduling
problem with setup times. Journal of Intelligent Man-
ufacturing, 17(1):85–97.
Tran, T. T., Araujo, A., and Beck, J. C. (2016). Decom-
position methods for the parallel machine scheduling
problem with setups. INFORMS Journal on Comput-
ing, 28(1):83–95.
Vallada, E. and Ruiz, R. (2011). A genetic algorithm for the
unrelated parallel machine scheduling problem with
sequence dependent setup times. European Journal of
Operational Research, 211(3):612–622.
Smart General Variable Neighborhood Search with Local Search based on Mathematical Programming for Solving the Unrelated Parallel
Machine Scheduling Problem
295
