Analytical Modelling of Cyber-physical Systems

Paul Tavolato

and Christina Tavolato-Wötzl

Institute of IT Security Research, UAS St. Pölten, Matthias-Corvinus-Straße 15, A-3100 St. Pölten, Austria

MeteoServe, Wagramer Straße 19, A-1220 Vienna, Austria

Keywords: Cyber-physical System, Anomaly Detection, Security, Analytical Modelling, Kinetic Theory.

Abstract: In connection with anomaly detection in cyber-physical systems, we suggest in this paper a new way of

modelling large systems consisting of a huge number of sensors, actuators and controllers. We base the

approach on analytical methods usually used in kinetic gas theory, where one tries to describe the overall

behaviour of a gas without looking at each molecule separately. We model the system as a multi-agent

network and derive predictions on the behaviour of the network as a whole. These predictions can then be

used to monitor the operation of the system. If the deviation between the predictions and the measured

attributes of the operational cyber-physical system is sufficiently large, the monitoring system can raise an

alarm. This way of modelling the normal behaviour of a cyber-physical system has the advantage over

machine learning methods mainly used for this purpose, that it is not based on the effective operation of the

system during a training phase, but rather on the specification of the system and its intended use. It will detect

anomalies in the system’s operation independent of its source – may it be an attack, a malfunction or a faulty

implementation.

1 INTRODUCTION

Cyber-physical systems (CPS) are integrations of

physical processes with networks and computation

(Adepu et al., 2015). Embedded computing devices

sense, monitor, and control the physical processes

through networks, usually with feedback loops in

which physical processes affect computations and

vice versa (Lee, 2008). Cyber-physical systems are

used in various areas including industrial and

production systems, public infrastructure (Stouffer et

al., 2015) such as for electricity (Sridhar et al., 2012),

water, purification and transportation (Zhao et al.,

2013), as well as health care (Haque et al., 2014).

These systems often represent critical infrastructures,

which play an essential and critical role in our

interdependent society and economy.

Dependencies on cyber infrastructure in industrial

systems and open communication make them more

vulnerable to cyber-attacks and hence represent a

considerable amount of risk for our society. Most

CPSs in use today were developed to meet

availability and reliability requirements but not

security requirements, as security was not considered

an important aspect in a secluded IT infrastructure

strictly separated from other systems. This has

changed dramatically in the last years: the

introduction of IP-based technology and standard

computing devices into operational environments

made an end to this separation and opened points of

exposure and increased the attack surface of CPSs in

a way that cannot be neglected any more. Moreover,

the complexity of the systems is increasing rapidly as

they become smarter and use advanced technologies

as well as the number of devices incorporated in such

systems is growing rapidly. This is reflected by the

concerns about attacks on industrial control systems

that were recognized at the latest with the detection of

incidents such as Stuxnet (Falliere et al., 2011),

Dragonfly (Symantec, 2017), or the BlackEnergy-

borne power outage in 2015 (Lee et al., 2016). The

possibility of such advanced attacks on industrial

systems show the urgent need for counter-measures.

Traditional intrusion defense strategies for

common IT systems are often not applicable in smart

CPS environments. To ensure the protection of these

environments, certain security controls that monitor

the systems communications and operation in real-

time, or at least close-to-real-time, are needed. One

possibility for such defense systems is the

implementation of an anomaly detection system.

Tavolato, P. and Tavolato-Wötzl, C.

Analytical Modelling of Cyber-physical Systems.

DOI: 10.5220/0007704706850689

In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 685-689

ISBN: 978-989-758-359-9

685

Anomaly detection systems consist of a formal model

of normal system behavior and a monitoring system

that compares in real time the actual behavior of the

system with this model. Too large deviations of the

system’s behavior from the model are distinguished

as anomalies and will raise an alarm. As of today the

formal systems used in connection with anomaly

detection systems are mostly of statistical nature:

outlier detection, cluster analysis, hidden Markov

models; few are of structural nature: neural networks,

association rules, syntactic pattern matching

(Chandola et al., 2009).

This paper suggests a new method for describing

the behavior model of a CPS. The idea is to model a

CPS in a way known from physics and similar to

equations used in kinetic theory. The macroscopic

behavior of a gas (or a liquid) is derived from the

behavior – the interactions – of the molecules it

consists of. For reason of the vast number of

molecules, it is not feasible to look at each molecule

individually. Kinetic theory overcomes that difficulty

by analytically deriving the macroscopic behavior of

the gas or liquid. The analogy used here is the fact

that a large CPS consists of a huge number of sensors,

actuators and PLCs, and can be modelled as a multi-

agent system. The components interact by

exchanging data over the network. An interaction is

the exchange of data between two agents. We want to

model the behavior of such multi-agent systems

without looking at each component individually.

In the area of information processing the idea of

modeling multi-agent systems analytically by

drawing analogies to physics has so far mainly been

used to study opinion dynamics in social networks

(Monica and Bergenti, 2018; Monica and Bergenti,

2016). Only for very specific problems in mobile

wireless networks, analytical models have been used

so far as in (Keung et al., 2010). The main difference

to applications in physics is contained in the rules that

guide the interactions of the components: while

molecules behave according to the laws of physics,

the interactions of components of a CPS are mainly

driven by the program logic of the PLC software. An

overview of kinetic theory can be found e.g. in

(Pareschi and Toscani, 2013), more advanced topics

are covered in (Bellouquid and Delitala, 2006).

2 MODELLING OUTLINE

We assume that every component of the CPS is an

agent in a multi-agent system. There is a set of

attributes (a vector) associated with each agent

representing its current state. Usually statements

about multi-agent systems are calculated by means of

simulations. In this paper, however, we introduce an

analytic point of view. This has the advantage that it

is independent of the simulation setup and will lead

to a more general model – provided that the

hypotheses used to derive them are valid.

We have:

 A set of components (agents) C

 Each component is associated with a state

vector q that changes dynamically.

 Components interact by exchanging

messages.

 Interactions are determined by interaction

protocols that define the reactions on input

(either as a message from another component

or as an input from the outside).

 Interactions occur when a component receives

a message from another component or from an

external source (input).

As we have three main different kinds of components,

we group them statically into three disjoint classes

C = S  A  PLC:

 The class of sensors S

 The class of actuators A

 The class of programmed logic controllers

PLC

The interaction between the components can only

occur according to the topology of the network

interconnecting the components. This network is

modelled by a directed graph NW = (C,E); the

vertexes of the graph are the components and we

define the set of edges E between a sender vertex c

and a receiver vertex c

if c

can send a message to c

Usually the receiver changes its state upon receiving

a message. External inputs may induce state changes,

too. As a rule, the components of class S receive

external inputs and send messages to components of

class PLC; components of class PLC receive

messages from components of classes S and PLC and

send messages to components of class A and class

PLC; components of class A receive messages from

components of class PLC and may send messages to

external devices (like e.g. motors, or human

interfaces).

Furthermore, we assume that the system is large

(consists of many components), so it is not feasible to

look at the state of each component individually, but

the analysis of the system as a whole is interesting.

The goal is the study of the dynamics of specific

features of the system that characterize its normal

behaviour. The first step towards this goal is

ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering

686

formulate functions that will predict the behaviour of

the system. This means to find a function that would

relate the state of a component of a class to its

changing over time. Time being a continuous variable

we have to define a density function of a class x:

(q,t)d’q (1)

Representing the number of agents of class x whose

states are in (q, q+dq) at time t >= 0.

The density function of the CPS as a whole can be

computed as:

f(q,t)d’q =  f

(q,t)d’q (2)

for each of the three classes x.

The average state of the components of class x at

time t >= 0 can then be computed as

(t) =







 



(3)

where n

is the number of elements of class x and Q

is the set of all states. Moreover, we could compute a

weighted standard deviation.

The next step would be to define a balance

equation for the system. Such an equation must define

a collisional operator I

that accounts for all possible

interactions between the components of class x with

components of any other class s.



=  Q

s,x

, f

] =





, t) (4)

by summing over all classes s. The term Q

s,x

, f

]

depends on the interaction rules.

The definition of Q

s,x

, f

] is the most

complicated part of the modelling. We assume that an

interaction consists of a component c

sending a

message to another component c

containing the

current state of c

and component c

replying with

another message (and may or may not send other

messages to other components). Both components

may update their state in the course of an interaction.

The interaction rules must account for external inputs

by containing flow terms that influence the

interaction. Interactions change the states of the two

neighbouring components that interact; more

precisely, they link pre-interaction states with post-

interaction states.

The interaction of components from classes S and

A are rather simple and do not need special attention.

Interactions from components of class S to

components of class PLC just change one (or more)

values in the state vector of the receiver. Interactions

from components of class PLC to components of

class A change a value in the state vector of the

receiver and may induce an external output.

Interactions of the components of class PLC are more

complex as they represent the computational logic of

the CPS, which is realised by the software running at

the component.

To define the interactions of the components from

class PLC, we must look at the pre- and post-

interaction states of these components; these

relationships define the interactions. We assume that

PLC software for CPS is developed in a rigorous way,

which means that the functions of the program are

language (such as SysML or other UML derivatives)

or even a formal language (like TLA+ or PROMELA

or Uppaal) that allow for the definition of pre- and

post-conditions. These definitions can then be used to

define the interaction matrix Q

s,x

, f

]. The pre- and

post-conditions define logical expressions on the state

attributes of the PLC-component. There are two

different kinds of conditions or constraints: those that

are given by the logic of the program (and are defined

by the afore-mentioned pre- and post-conditions) and

those given by the physical constraints on the external

inputs. The latter ones may define for example

restrictions on the development in time of the

function describing the external input (changes in

temperature for example cannot happen at arbitrary

speed).

Having defined the model, we can use it to predict

the normal behaviour of the CPS during operation and

compare the current state of the CPS with this

prediction. Deviations of the current state of the

system from the prediction are hints to anomalous

operations. Anomalous operation of the CPS can have

various reasons: wrong programming logic,

malfunction, erroneous user input, or cyber-attacks.

A classification of the reasons based on the

differences between predictions and actual behaviour

of the system, is difficult and not in the scope of this

paper.

3 APPLICATION TO CPS

We will present a very simple and (too) small

example to show the main idea of this modelling

approach: a conveyor belt where work pieces are

transported by the conveyor to and from a heating

chamber where they are heated to a predefined

temperature. The system consists of four optical

sensors, one temperature sensor, two actuators (one

for starting and stopping the belt, one for turning on

and off the heating chamber), and a PLC controlling

Analytical Modelling of Cyber-physical Systems

687

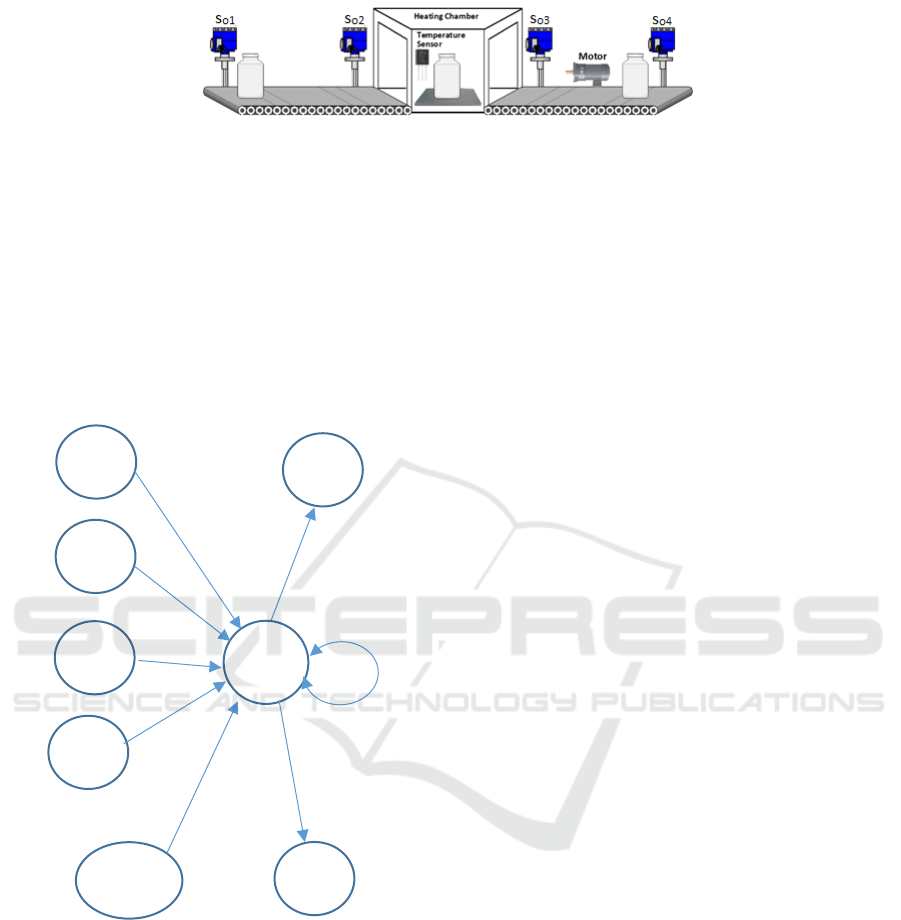
Figure 1: Experimental setup.

the setup. A more detailed description of the setup can

be found in (Eigner et al., 2018).

We have:

S = {s

, s

temp

} is the set of sensors,

A = {a

, a

} is the set of actuators, and

PLC = {plc} is the PLC controlling the system.

The connections between these components are

shown in the interaction graph in figure 2.

Figure 2: Interaction graph.

The respective states are: for each optical sensor s

is a binary value {0,1}, for the temperature sensor

temp

it is the last measured temperature value (a

positive decimal number within a predefined range).

For both actuators it is a binary value {0,1} meaning

on/off. For the plc it is a vector with the last received

measurements of the sensors and the states of the two

actuators together with an additional value referring

to the current state of the plc (idle, sending, receiving,

calculating).

An example of an interaction rule is:

Interaction: s

temp

is sending a measured temperature

value x to the plc

Pre-condition: the state of s

temp

is x

Post-conditions: the temperature attribute in the

state of the plc is x

if x is greater or equal than a fixed

threshold, the heating attribute is

0 (off)

if x is less than a fixed threshold

and s

is 1 (a work piece is in the

heating chamber) the heating

attribute is 1 (on)

Other constraints concerning the input values can be

defined, too. For example, the temperature changes in

time cannot happen at an arbitrary speed. This is

captured by defining the maximum (and maybe

minimum) gradient of the temperature curve. By

applying the analytical model to this situation, we get

a description of the progression in time of the state of

the CPS as a whole.

4 DISCUSSION

The ideas described in this paper are still in a very

preliminary state and need further elaboration and

application to real large cyber-physical systems. This

is more a position paper that is supposed to present

some interesting ideas and to foster further

discussion.

So far, models of normal behaviour of a system

have been created by methods of machine learning:

Data is collected during assumed normal operation

and a machine-learning algorithm selects features and

“learns” the valid range of these features. The

advantage of our model over machine-learning

models is that it does not depend on a training phase

that might not cover all possible situations and were

one cannot really guarantee that the software works

properly in all situations or that there is no attack (or

effects of an attack) present during the training phase.

The analytical model, on the other side, starts with the

specification of the CPS and therefore encompasses

all situations defined by the software. This model

could even detect implementation errors.

temp

plc

ForSE 2019 - 3rd International Workshop on FORmal methods for Security Engineering

688

The main difficulty of the modelling process itself

lies within the construction of the interaction matrix.

In this paper, we assume that a rigorous specification

of the control programs containing pre- and post-

conditions is available (which in practice will not

always be the case). However, if such specifications

do exist in a formal notation, even an automatic or at

least semi-automatic generation of the interaction

matrix is possible. One can conclude this from the

code generation features present in specification and

design tools for software, which take the pre- and

post-conditions as input and transforms them into

another formal description (code). The maintenance

of the model, which is necessary if changes in the

configuration or the control programs occur, depends

on the formal specifications of the changes, too.

As mentioned above a lot of work is still to be

done to transfer the model to real practical

applications with a large number of components.

REFERENCES

Adepu, S., Mathur, A., Gunda, J., and Djokic, S. 2015.

Algorithms and Architectures for Parallel Processing.

In Proceedings of the 15th International Conference,

ICA3PP 2015, Zhangjiajie, China, Part III. Springer

International Publishing, pp. 785–798.

Lee, E. 2008. Cyber Physical Systems: Design Challenges.

Technical Report UCB/EECS-2008-8. EECS

Department, UC California, Berkeley.

http://www.eecs.berkeley.edu/Pubs/TechRpts/2008/EE

CS-2008-8.html [online; Dec 20

2018].

Stouffer, K., Pillitteri, V. and Lightman, S. 2015. Guide to

industrial control systems (ICS) security. Special

Publication (NIST SP) - 800-82 Rev 2.

Sridhar, S., Hahn, A. and Govindarasu, M. 2012. Cyber–

Physical System Security for the Electric Power Grid.

In Proceedings of IEEE 100(1), pp 210-224.

Zhao, M., Walker, J. and Wang, C. 2013. Challenges and

Opportunities for Securing Intelligent Transportation

System. IEEE Journal on Emerging and Selected

Topics in Circuits and Systems 3(1), pp 96–105.

Haque, S., Aziz, S. and Rahman, M. 2014. Review of

Cyber-Physical System in Healthcare, International

Journal of Distributed Sensor Networks 10(4).

Falliere, N., Murchu, L. and Chien, E. 2011. W32. stuxnet

dossier, White paper, Symantec Corp., Security

Response 5.

https://www.symantec.com/content/dam/symantec/doc

s/security-center/white-papers/security-response-w32-

stuxnet-dossier-11-en.pdf [online: Dec 20

2018].

Symantec 2014. Dragonfly: Cyberespionage Attacks

against Energy Suppliers.

https://www.symantec.com/content/dam/symantec/doc

s/security-center/white-papers/dragonfly-

cyberespionage-attacks-14-en.pdf 2014 [online: Apr 6

2017].

Lee, R., Assante, M. and Conway, T. 2016. Analysis of the

cyber attack on the Ukrainian power grid. Electricity

Information Sharing and Analysis Center SANS-ISC

and E-ISAC.

Chandola, V., Banerjee, A. and Kuma, V. 2009. Anomaly

detection: A survey, ACM Computing Surveys Volume

41(3).

Monica, S, and Bergenti, F. 2018. Outline of a

Generalization of Kinetic Theory to Study Opinion

Dynamics, International Symposium on Distributed

Computing and Artificial Intelligence.

Monica, S, and Bergenti, F. 2016. An analytic study of

opinion dynamics in multi-agent systems, Computers &

Mathematics with Applications,

10.1016/j.camwa.2017.03.008.

Keung, Y., Li, B. and Zhang, Q. 2010. The intrusion

detection in mobile sensor network, in Proceedings of

the eleventh ACM international symposium on Mobile

ad hoc networking and computing (MobiHoc '10).

ACM, New York, 2010, 11-20.

Pareschi, L. and Toscani, G. 2013. Interacting Multiagent

Systems: Kinetic Equations and Montecarlo Methods,

Oxford University Press, Oxford.

Bellouquid, A. and Delitala, M. 2006. Mathematical

Modelling of Complex Biological Systems, Birkhäuser,

Boston.

Eigner, O., Kreimel P. and Tavolato, P. 2018. Attacks on

Industrial Control Systems – Modelling and Anomaly

Detection. In ICISSP 2018 - 4th International

Conference on Information Systems Security and

Privacy, 2nd International Workshop on FORmal

methods for Security Engineering – ForSE.

SCITEPRESS.

Analytical Modelling of Cyber-physical Systems

689