
Adapting Linear Hashing for Flash Memory Resource-constrained
Embedded Devices
Andrew Feltham, Spencer MacBeth, Scott Fazackerley and Ramon Lawrence
University of British Columbia, Kelowna, Canada
Keywords: Linear Hash, Index, Embedded, Query, Database, Arduino.
Abstract:
Linear hashing provides constant time operations for data indexing and has been widely implemented for
database systems. Embedded devices, often with limited memory and CPU resources, are increasingly col-
lecting and processing more data and benefit from fast index structures. Implementing linear hashing for
flash-based embedded devices is challenging both due to the limited resources and the unique properties of
flash memory. In this work, an implementation of linear hashing optimized for embedded devices is presented
and evaluated. Experimental results demonstrate that the implementation has constant time performance on
embedded devices, even with as little as 8 KB of memory, and offers benefits for several use cases.
1 INTRODUCTION
There is a renewed focus on data processing on de-
vices with limited capabilities as applications such as
sensor-based monitoring grow in deployments. The
Internet of Things (Lin et al., 2017) relies on these de-
vices for data collection and filtering, and it is widely
known that there are performance and energy benefits
to processing data on the edge (where it is collected)
rather than sending it over the network for later pro-
cessing. Manipulating data on these edge devices rep-
resents similar challenges to the early days of comput-
ing with limited resources and supporting software.
There have been several efforts to construct
database libraries and software tools for these em-
bedded devices starting with the sensor-database net-
works such as TinyDB (Madden et al., 2005) and
COUGAR (Bonnet et al., 2001) to database software
installed and executing on the device such as Ante-
lope (Tsiftes and Dunkels, 2011), PicoDBMS (An-
ciaux et al., 2003), LittleD (Douglas and Lawrence,
2014), and IonDB (Fazackerley et al., 2015). There
have also been data structures and algorithms specifi-
cally developed for flash-memory including (Gal and
Toledo, 2005; Lin et al., 2006). No prior work devel-
oped a linear hash implementation and explored its
potential benefits for this domain.
Linear hashing dates back to work done by Litwin
(Litwin, 1980) and later expanded by Larson (Larson,
1982; Larson, 1985). Linear hashing is an expand-
able hash table on storage that provides constant time
operations. Although B+-trees are generally favored
for database workloads as they also provide ordered
access, linear hashing is implemented in many rela-
tional database systems and has benefits for certain
use cases. In the embedded domain, linear hashing
is interesting as it may allow for even better perfor-
mance and less resource usage than B+-trees.
In this work, linear hashing is adapted and opti-
mized for flash-based, memory-constrained embed-
ded devices and shown to work for devices with as
little as 8 KB of memory. Optimizations include im-
plementing the linked list of overflow buckets in a
backwards chaining fashion to avoid writes, trading
off writes for reads due to asymmetric performance
of flash memory, and minimizing the memory con-
sumed so that most operations require only one mem-
ory buffer and at most two memory buffers are re-
quired for a split during insert.
The next section discusses the background of lin-
ear hashing and embedded device data management.
Section 3 describes the linear hash implementation,
and Section 4 provides experimental results. The pa-
per closes with future work and conclusions.
2 BACKGROUND
First introduced by Litwin in 1980 (Litwin, 1980), the
linear hash data structure is a dynamically-resizable
hash table which maintains constant-time complexity
176
Feltham, A., MacBeth, S., Fazackerley, S. and Lawrence, R.
Adapting Linear Hashing for Flash Memory Resource-constrained Embedded Devices.
DOI: 10.5220/0007709301760181
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 176-181
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

for hash table operations. A search generally takes
about one access, and the space utilization may be up
to 90%. This performance is superior to B+-trees for
key-based lookup operations. Linear hashing does not
require an index to lookup bucket locations on storage
if the buckets are allocated continuously on storage or
allocated in fixed size regions. Computing the address
of a record is done by using the output of the hash
function computed on the key to identify the appropri-
ate region (if multiple) and bucket within the region.
Thus, the memory consumed is minimal and consists
of information on the current number of buckets and
next bucket to split.
Collisions are handled using overflow buckets that
are chained to the primary (or home) bucket. The hash
file is dynamically resized when the storage utiliza-
tion (load factor) increases beyond a set amount. At
that point, a new bucket is added to the end of the
hash file and records are divided between the new
bucket and the current bucket to split in the table. It is
this predefined, ordered splitting of buckets that is the
main contribution of linear hashing.
Linear hashing was extended and generalized by
Larson (Larson, 1982) using partial expansions. It
was shown that performance can be increased if dou-
bling of the file size is done in a series of partial ex-
pansions with two generally being a good number.
Search performance is increased at the slight trade-
off of additional algorithm complexity and the need
for buffering and splitting k + 1 buckets in memory
where k is the number of partial expansions. Further
work (Larson, 1985) allowed for the primary buckets
and overflow buckets to use the same storage file by
reserving pre-defined overflow pages at regular inter-
vals in the data file. This work also added the ability
to have multiple overflow chains from a single pri-
mary bucket by utilizing several hash functions to de-
termine the correct overflow chain. Popular database
management systems such as PostgreSQL use imple-
mentations of linear hashing.
Variations of linear hashing optimized for flash
memory use the idea of log buffering to increase
performance. The Self-Adaptive Linear Hash (Yang
et al., 2016) buffers logs of successive operations be-
fore flushing the result to storage. This often de-
creases the total number of read and write operations
and allows for some random writes to be performed
sequentially. Self-Adaptive Linear Hash also adds
higher levels of organization to achieve more coarse-
grained writes to improve the bandwidth. Unfortu-
nately, the extra memory consumed is impractical for
embedded devices.
Embedded systems come in a wide variety of con-
figurations and are often developed and deployed for
particular use cases, which results in software that
is often customized both to the hardware and to the
problem. Arduinos (Severance, 2014) have increased
in usage as their designs are open source and a builder
community has emerged with resources to help de-
velopers. The Arduino Mega 2560, one of the most
popular Arduino boards, has 8 KB of SRAM and a
clock speed of 16 MHz. It also has a microSD card in-
terface for non-volatile, flash-memory storage. With
such limited capabilities, many applications cannot
run on an Arduino without adapting them to the more
resource-constrained environment.
Data structures include special indexed structures
for flash memory (Gal and Toledo, 2005; Lin et al.,
2006). Devices such as smart cards and sensor nodes
cannot afford the code space (often less than 128
KB), memory (between 2KB and 64KB), and en-
ergy requirements for typical database query pro-
cessing. Databases designed for local data storage
and querying on embedded devices, such as Ante-
lope (Tsiftes and Dunkels, 2011), PicoDBMS (Anci-
aux et al., 2003), and LittleD (Douglas and Lawrence,
2014), simplify the queries that are executable and the
data structures and algorithms used. Systems such as
TinyDB (Madden et al., 2005) and COUGAR (Bon-
net et al., 2001) are distributed data systems intended
to manage information over many networked sen-
sors. There has not been an experimental evaluation
of the performance and implementation requirements
for linear hash on embedded devices.
3 IMPLEMENTATION
The implementation of linear hashing requires several
key decisions that are heavily influenced by the lim-
ited resources, flash memory properties, and embed-
ded use cases:
• Bucket Structure - Are buckets stored as a linked
list or in sequential addresses on storage?
• Overflow Buckets - Are overflow buckets in a sep-
arate file or in the data file?
• Deletions - How are deletions handled? How is
free space reclaimed?
• Caching and Memory Usage - How much of the
data structure is memory-resident? Is memory-
usage tuneable for devices with more memory?
The implementation was optimized for the spe-
cific properties of embedded use cases. The goal is to
minimize RAM consumed, favor reads over writes on
flash, and optimize for sequential writing of records.
Many embedded systems perform logging applica-
tions where the device is collecting sensed data over
Adapting Linear Hashing for Flash Memory Resource-constrained Embedded Devices
177

time. Thus, optimizing inserts is the most important
with some emphasis on data retrieval. Update and
delete operations are relatively rare.
The first key decision is how buckets are repre-
sented on storage, either as a linked list or by sequen-
tial addresses. The advantage of using a sequential
address space is that no memory-resident bucket in-
dex structure is required as the location of a bucket on
storage can be directly calculated based on an offset
using its bucket index. The advantage of the linked
list approach is that buckets can move locations, and
there is flexibility on where they are allocated. The
negative is that a separate bucket index structure is re-
quired to determine the physical bucket location, and
the linked list structure is expensive to maintain in
flash. The trade-off chosen was to use an in-memory
bucket index lookup structure that contained offsets
into the storage file of where the bucket was located.
Although this consumed some memory and limits the
maximum size of the hash table, it allows flexibility
on bucket allocation and faster inserts. This index can
also be maintained on flash if it grows too large.
Overflow buckets are conceptually explained as a
linked list from the main bucket index, but there are
decisions in how this is implemented. Implementing
the overflow buckets in separate files per main bucket
was determined to be too expensive in terms of mem-
ory and created lots of open files. This is especially
a concern if the embedded device does not have a file
system and the developer is responsible for managing
raw storage. The decision was to implement the over-
flow buckets in the same file as the data buckets and
virtually link them as a linked list. To avoid expensive
linked list updates, when an overflow bucket is added,
it is added to the start of the list and then points to the
previous head of the list.
For embedded devices such as Arduinos, the block
size matches the size of the block on the SD card
(512 bytes). Each block has a header containing
the file block index (logical starting at 0), the num-
ber of records it contains and the block index of the
next overflow bucket. Overflow buckets are linked to-
gether as a linked list using a property in the bucket
header. When a new overflow bucket is added it is
added to the top of the linked list to prevent extra
block reads and writes that would be required to up-
date the bottom bucket link. The bucket map is an
array mapping the table index to the file block index
for the top level bucket. Two 512 byte buffers are al-
located when the linear hash table is initialized. Two
is the minimum number required in order to perform
the split functionality. Most other functions require
only one buffer. All reads and writes are at the block
level through the SD library, and changes are made to
a block buffered in memory before writing it to flash.
In Table 1 is a summary of the components of
the linear hash implementation. For determining a
bucket index given a key value, the hash functions
h0 and h1 are implemented as: h0 : hash&(size − 1)
and h1 : hash&((2 ∗ size)− 1), where hash is the hash
value produced by the hash function and & is a bit-
wise AND operator. A bucket index is h0(hash) if the
calculated value is less than nextSplit otherwise it is
h1(hash).
The insert algorithm is in Figure 1. The algo-
rithm reads the top level bucket, and either adds to
that bucket or creates and writes a new bucket. A
split is triggered after writing the block if the load
((100 ∗ numRecords)/(size ∗ recordsPerBucket)) has
increased passed the threshold. An insert operation
(without a split) always performs exactly one block
read and one block write. Note for faster insert per-
formance the algorithm only inserts into the top level
block even if there may be space in another block in
the bucket. This is to maximize insert performance
and recognizes that deletes are relatively rare.
Hash key and map to a bucket index
Get top level block index from bucketMap
Read that block into a memory buffer (buffer1)
If block->records == recordsPerBucket:
Initialize an empty block at nextBlock
Increment totalBuckets
Add record to block
Increment block->records
Write to file
Else:
Add record to the next record position
Increment block->records
Write to file
Increment the total table numRecords
Figure 1: Insert Algorithm Pseudocode.
The get algorithm is in Figure 2. In the worst
case, the item does not exist, and the method reads
all blocks in the bucket, which is typically around 2
for a well-balanced hash function. Note that buckets
are not always completely full (due to deletes), which
has a minor negative impact on performance.
Hash key and map to a bucket index
blockIndex = block index from bucketMap
Do:
Read blockIndex into buffer1
For each record in block:
Compare keys, if equal return the value
blockIndex = block->overflowBlockIndex
While (block has overflow)
Figure 2: Get Algorithm Pseudo-code.
The delete algorithm is in Figure 3. At a high level
the delete function reads each block, iterates through
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
178

Table 1: Summary of Linear Hash Components.
Name Description
size The number of buckets when the linear hash table was last doubled
nextSplit The bucket index which will be split next
splitThreshold The integer percent when to split the linear hash table
currentSize The number of top level buckets
totalBuckets The total number of buckets in the linear hash table including overflow buckets
numRecords The total number of records stored in the hash table
recordsPerBucket The total number of records that can be stored in a bucket
nextBlock The next available file block index to be used
recordTotalSize Convenience value for the size of a record in bytes. Key size + value size.
buffer1 Byte buffer with 512 bytes
buffer2 Byte buffer with 512 bytes
bucketMap Array list mapping bucket indexes to the top block index
every record, deletes matching records and shifts the
non-deleted records up to ensure an unbroken array
of records in each block. Only changed blocks are
written out. Note that we do not remove empty blocks
from the chain as that requires additional block reads
and writes. This method will read all blocks in the
bucket chain and write anywhere from 0 to all blocks
in the bucket chain.
Do:
Read the blockIndex into the buffer
readPtr, writePtr = first record position
For record in block:
If key == searchKey:
Clear the read key data
Mark the buffer as dirty
Decrement numRecords
Decrement bucketRecords
Else:
If readPtr != writePtr:
copy record at readPtr to writePtr
Increment writePtr
Increment readPtr
If block is dirty:
Write block
blockIndex = block->overflow
While (block has overflow)
Figure 3: Delete Algorithm Pseudocode.
The update algorithm is in Figure 4. The algo-
rithm performs exactly n reads and 0 to n writes where
n is the number of blocks in the bucket.
The split algorithm is in Figure 5. A new bucket
index is created and records in the bucket to split are
re-indexed and moved to the new bucket as required.
Empty slots in the splitting bucket are shuffled up to
create a continuous block of records. As with delete,
blocks in the splitting bucket may end up with space
at the end of the blocks and potentially empty blocks.
It would cost more reads and writes in order to remove
empty blocks or swap records to fill blocks. The algo-
Do:
Read the blockIndex into the buffer
For record in bucket:
If key == searchKey:
Update the value with the new value
Mark the buffer as dirty
If block is dirty:
Write block
blockIndex = block->overflow
While (bucket has overflow)
Figure 4: Update Algorithm Pseudocode.
rithm reads and writes every block in the bucket split.
Functions trade-off having more space and buck-
ets for less writes and potentially more reads. Empty
buckets are not removed which will cause additional
reads in get, delete and split function. However, since
reads are less costly then writes both in terms of time
and SD card wear, this is a reasonable trade-off.
4 EXPERIMENTAL RESULTS
The experimental device was an Arduino Mega2560
with SD card and Ethernet shield with 8 KB RAM and
256 KB of code space. It has a 16 MHz 8-bit AVR
processor. An 8 GB Micro SD card class 6 was used
for storage. Although the experiments were run on an
Arduino, the implementation will work on other em-
bedded devices. The record size was 4 bytes. Record
keys were random integers. All experimental results
are the average of 5 runs.
The raw I/O speed of the SD card was measured
by reading and writing 1000 blocks (512 bytes each)
in a file. The average block read time was 2.5 ms
with a standard deviation of 0.0008 ms. The average
block write time was 3.4 ms with a standard deviation
of 0.017 ms. These results show that read and write
times are consistent with minimal variance, and the
Adapting Linear Hashing for Flash Memory Resource-constrained Embedded Devices
179
Get blockIndex for split bucket from bucketMap
Create a new bucket in buffer2 using index from
currentSize at the next block index
Add the new bucket to the bucket map
Increment currentSize
newInsertPtr = first record loc in new bucket
Do:
read the splitBlock into buffer1
readPtr, writePtr = first record in buffer1
For record in splitBlock:
If (h0(record->key) != h1(record->key):
Copy record from split bucket to
the new bucket at newInsertPtr
Increment newBucket record count
Decrement splitBucket record count
Increment newInsertPtr
If newBucket is full:
Write out to the file block
Create a new bucket
Reset newInsertPtr
Else:
If (readPtr != writePtr):
copy record at readPtr to writePtr
Increment writePtr
Increment readPtr
splitBlock = splitBlock->overflow
While (splitBlock has an overflow)
If currentSize = 2 * size:
size = currentSize
nextSplit = 0
Else:
nextSplit++
Figure 5: Split Pseudocode.
average write time is about 35% slower than reading.
For benchmarking the insert operation, each run
started with an empty hash table and the time to insert
a given number of records was recorded. Statistics
recorded include the overall time, average time per
insert, and average number of block reads and writes
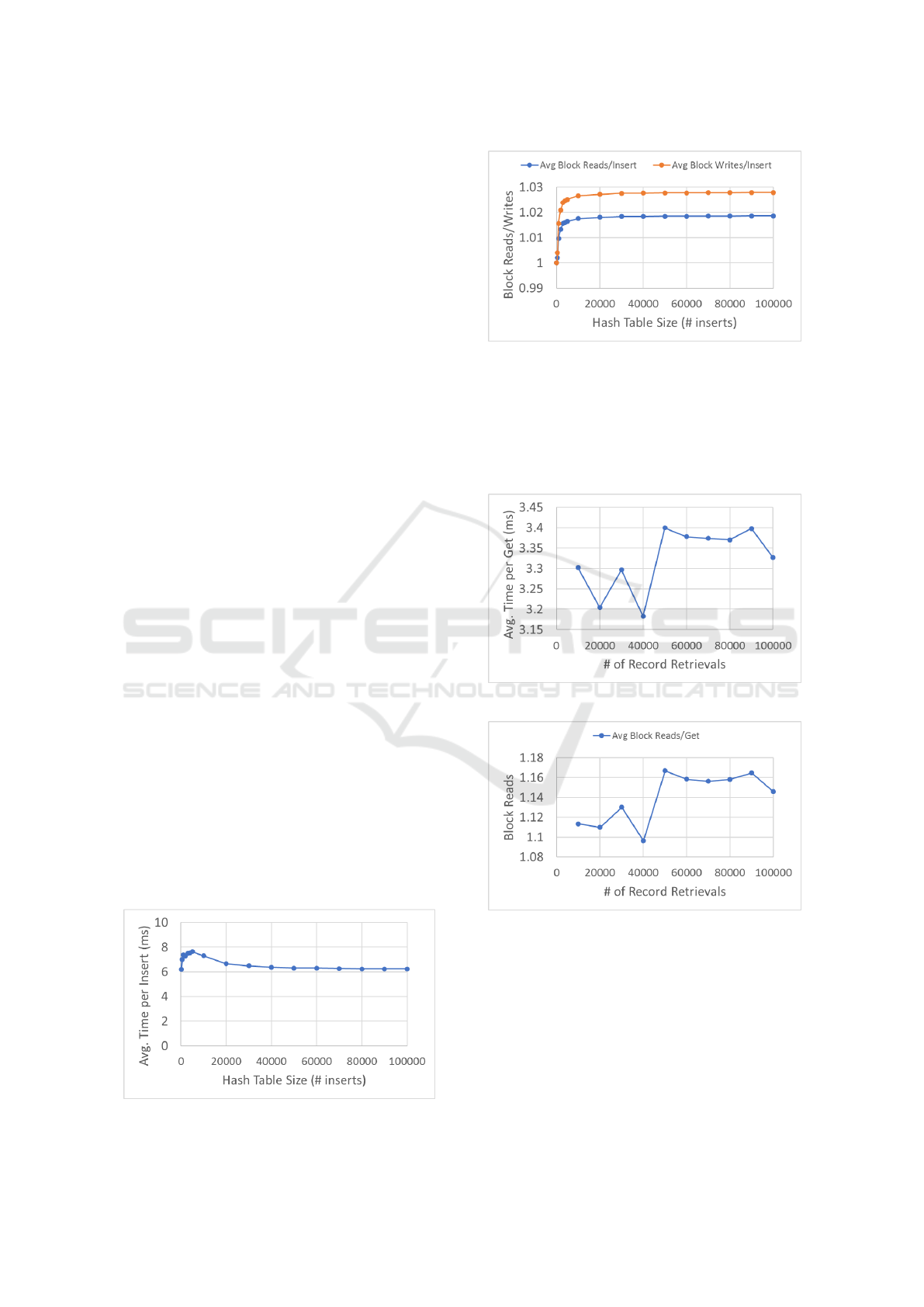
per insert. Figure 6 shows the average time per insert
is linear as the hash table grows and mostly represents
the time to read and write one block (approx. 6 ms).
Figure 7 shows that the average number of blocks read
and written is just over one, which is expected as an
insert without an overflow performs 1 block write.
Figure 6: Average Insert Time per Hash Table Size.
Figure 7: Average Block Reads/Writes per Insert.
For evaluating record get, a hash table of 100,000
records was created and an increasing number of
records were retrieved. The average time per record
retrieval was consistent (Figure 8) as was the average
number of blocks read (Figure 9).
Figure 8: Average Get Time.
Figure 9: Average Block Reads/Writes per Get.
For evaluating record deletion, a hash table of
100,000 records was created and an increasing num-
ber of records were deleted from the hash table. The
average time per record deleted decreased slightly as
more records were deleted as the hash table was get-
ting smaller (Figure 10). The number of block I/Os
also decreased (Figure 11). Another experiment was
run involving deleting 50% of the records of hash ta-
ble of various sizes, and the deletion time and I/Os
were similar.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
180
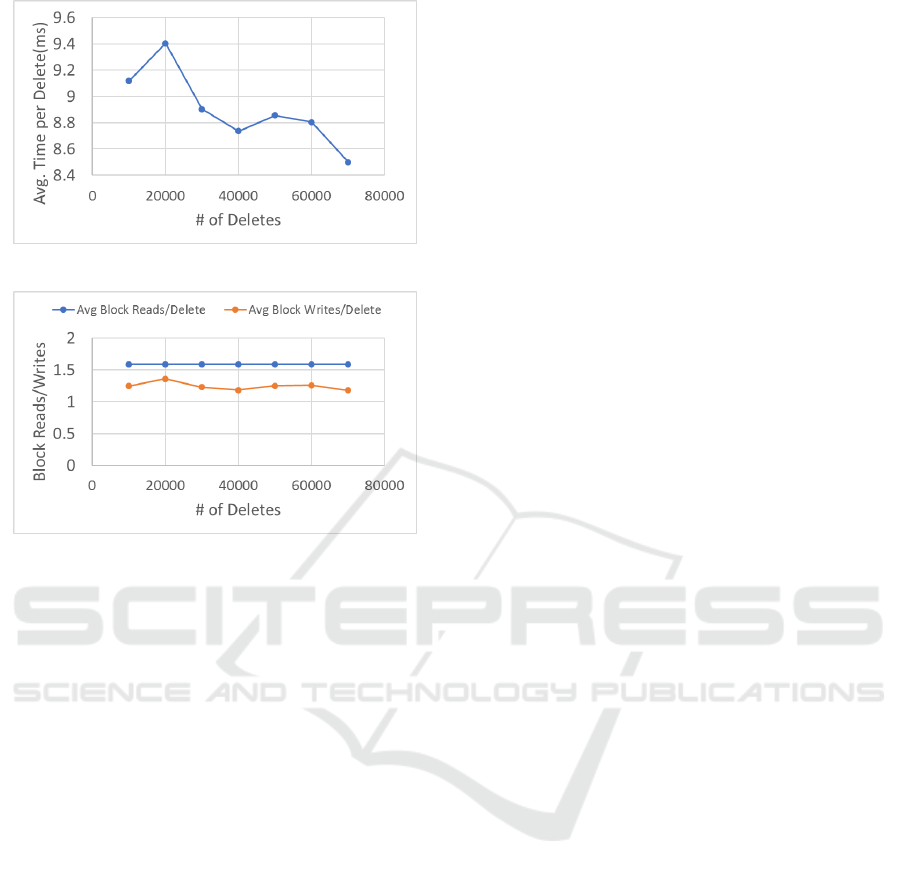
Figure 10: Average Delete Time.
Figure 11: Average Block Reads/Writes per Delete.
Overall, the results demonstrate an optimized lin-
ear hashing implementation for small memory em-
bedded devices that has superior and linear perfor-
mance for all operations, but especially strong per-
formance for insert and get. For insert, the average
insert time of about 6.3 ms is only about 6% higher
than the average time to read and write a block of 5.9
ms. The algorithm is CPU efficient. A limitation is
that the bucket map consumes memory and limits the
size of the hash table unless it is stored in flash.
5 CONCLUSIONS
Linear hashing is an interesting index structure for
small embedded devices as this work has shown that it
can be implemented efficiently while retaining linear
performance. The performance for inserts has very
minor overhead and is effective for common environ-
mental and sensor logging applications.
Future work will involve further experimental
testing and optimization for particular SD cards and
embedded system platforms and a performance com-
parison with B+-trees.
REFERENCES
Anciaux, N., Bouganim, L., and Pucheral, P. (2003). Mem-
ory Requirements for Query Execution in Highly Con-
strained Devices. VLDB ’03, pages 694–705. VLDB
Endowment.
Bonnet, P., Gehrke, J., and Seshadri, P. (2001). Towards
Sensor Database Systems. MDM ’01, pages 3–14,
London, UK, UK. Springer-Verlag.
Douglas, G. and Lawrence, R. (2014). LittleD: A SQL
Database for Sensor Nodes and Embedded Applica-
tions. In Proceedings of the 29th Annual ACM Sym-
posium on Applied Computing, SAC ’14, pages 827–
832, New York, NY, USA. ACM.
Fazackerley, S., Huang, E., Douglas, G., Kudlac, R., and
Lawrence, R. (2015). Key-value store implemen-
tations for arduino microcontrollers. In IEEE 28th
Canadian Conference on Electrical and Computer
Engineering, pages 158–164.
Gal, E. and Toledo, S. (2005). Algorithms and Data
Sructures for Flash Memories. ACM Comput. Surv.,
37(2):138–163.
Larson, P. (1985). Linear hashing with overflow-handling
by linear probing. ACM Trans. Database Syst.,
10(1):75–89.
Larson, P.-A. (1982). Performance analysis of linear hash-
ing with partial expansions. ACM Trans. Database
Syst., 7(4):566–587.
Lin, J., Yu, W., Zhang, N., Yang, X., Zhang, H., and Zhao,
W. (2017). A survey on internet of things: Archi-
tecture, enabling technologies, security and privacy,
and applications. IEEE Internet of Things Journal,
4(5):1125–1142.
Lin, S., Zeinalipour-Yazti, D., Kalogeraki, V., Gunopulos,
D., and Najjar, W. A. (2006). Efficient Indexing Data
Structures for Flash-Based Sensor Devices. Trans.
Storage, 2(4):468–503.
Litwin, W. (1980). Linear hashing: A new tool for file and
table addressing. In 6th International Conference on
Very Large Data Bases, pages 212–223. IEEE Com-
puter Society.
Madden, S. R., Franklin, M. J., Hellerstein, J. M., and
Hong, W. (2005). TinyDB: An Acquisitional Query
Processing System for Sensor Networks. ACM Trans.
Database Syst., 30(1):122–173.
Severance, C. (2014). Massimo Banzi: Building Arduino.
Computer, 47(1):11–12.
Tsiftes, N. and Dunkels, A. (2011). A Database in Every
Sensor. SenSys ’11, pages 316–332, New York, NY,
USA. ACM.
Yang, C., Jin, P., Yue, L., and Zhang, D. (2016). Self-
adaptive linear hashing for solid state drives. In ICDE,
pages 433–444.
Adapting Linear Hashing for Flash Memory Resource-constrained Embedded Devices
181
