Reaction-diffusion Model Describing the Morphogenesis of Urban
Systems in the US
John Friesen, Ruben Tessmann and Peter F. Pelz
Chair of Fluid Systems, Technische Universit
¨
at Darmstadt, Otto-Berndt-Str. 2, Darmstadt, Germany
Keywords:
Urbanization, Reaction-diffusion Models, Urban Development, US.
Abstract:
Urbanization is currently one of the greatest challenges facing mankind. In order to be able to anticipate
the rapid changes in urban structures, models are in need, mapping the morphological development of these
structures. In this paper we present an urban development model that is based on reaction diffusion equations
and can be interpreted sociologically. We apply this model to the urban development of US-American cities
and show that this very simple model can already map basic characteristics of urban development.
1 INTRODUCTION
More than every second person on earth lives in a
city. According to UN estimates, this share will rise
to almost two thirds by 2050 (United Nations, 2016).
These rapid changes lead to major challenges for the
infrastructure systems (energy, water, wastewater) of
urban areas (Kraas et al., 2016). In order to develop
adequat solution stragetegies to face this problem it
is necessary to anticipate the development of cities.
Therefore, for many years efforts have been made to
understand, model and simulate the development of
urban structures. Very common are statistically, cel-
lular automata and agent based models. A compre-
hensive summary of these different approaches can be
found in (Benenson and Torrens, 2004). The question
is, what the central mechanisms of this structure for-
mation are and how they can be simulated.
While in earlier studies it was repeatedly assumed
that urban systems behave scale free, more recent
studies have shown that urban systems do indeed con-
tain typical variables, as shown for example in the
work of (Gonz
´
alez-Val et al., 2015) for cities within
countries, or of (Friesen et al., 2018) for slums within
cities. Assuming that urban systems are free of scales,
simulation models are also developed that lead to
scale free systems. This can be seen for example in
the development of models for fractal morphogenesis
(Frankhauser, 1998). However, if urban systems have
typical scales, it is advantageous to use models that
take this circumstance into account.
Therefore, in this paper we use an analogy from
another scientific discipline to model urban change.
Structural changes can not only be identified in ur-
ban structures, but are also observed in other systems,
for example in biology. These processes of morpho-
genesis were fundamentally described in a mathemat-
ical way in 1952 by Alan Turing, who was able to
show how processes of pattern formation in biolog-
ical systems can be described using relatively sim-
ple reaction-diffusion equations (Turing, 1952). He
showed, that when certain conditions are satisfied,
diffusion can lead to instability of the system.
In this paper we use a framework based on the
work of Turing for describing the structural devel-
opment of cities with a system of reaction-diffusion
(RD) equations. Although RD equations have already
been used to describe urban processes (Schweitzer
and Steinbink, 2002), no stability analyses of the
equations have been performed. An exeption is a re-
cent paper of (Pelz et al., 2019) using instability ef-
fects to explain the formation of slums, a specific ur-
ban class. Also worth mentioning in this context is the
work of Paul Krugman, who also relates the spatial
distribution of industry to the work of Turing (Krug-
man, 1996). However, the equations presented in the
last mentioned paper describe economic and not soci-
ological aspects.
We take up this idea and ask the research ques-
tion whether and to what extend it is possible to pre-
dict the structural development of cities with reaction-
diffusion equations. For this purpose, we use Census
data from cities in the USA from the years 2000 and
2010, showing particularly strong economic growth.
After first recapitulating a stability analysis of the
equations from literature, we interpret the equations
88
Friesen, J., Tessmann, R. and Pelz, P.
Reaction-diffusion Model Describing the Morphogenesis of Urban Systems in the US.
DOI: 10.5220/0007711300880096
In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 88-96
ISBN: 978-989-758-371-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sociologically and examine their suitability for de-
scribing structural changes in the cities. To do this,
we conduct a simulation study varying four different
parameters on two cities to find the parameter com-
binitation describing the structural change within the
cities the best. We then simulate the structal change in
a thrid city by using the best parameters found before
and analyse the results.
In this paper we first describe the reaction-
diffusion model, the sociological processes it de-
scribes, the data used and then our approach (sec. 2).
We then present our results (sec. 3), discuss them
(sec. 4) and finally summarize the work (sec. 5).
2 METHODS AND DATA
Our approach is as follows: First, we briefly present
the mathematical principles of the RD equations.
Building on this, we explain the sociological pro-
cesses that can be mapped with these equations and
discuss the assumptions we made within our setup.
2.1 Reaction-diffusion Model
The Reaction-Diffusion Model which shall be used
for this simulation study is presented by Gray and
Scott first in (Gray and Scott, 1983; Gray and Scott,
1984), which is why we shall refer to it as the
“Reaction-Diffusion Model by Gray/Scott” or short
the “Gray/Scott-model”. The basic model as de-
scribed in (Gray and Scott, 1983) can be expressed
as follows:
∂v
∂t
= D
v
∆v + R[uv
2
−(F +k)v]
∂u
∂t
= D
u
∆u + R[−uv
2
+ F(1 −u)]
(1)
v and u are (dimensionless) concentrations of two
chemicals V and U. Here V is the autocatalytic
activator, whereas U represents the substrate in the
activator-depleted substrate scheme. D
v
and D
u
are
the diffusion constants of V and U. F and k are two
more constants, which have an outstanding effect on
the emergence of the outcoming patterns. We added
the reaction rate R, which is set to one in the original
papers, but is needed for proper dimensional analysis.
As a first step Eq. 1 shall be transformed to a non-
dimensional representation. Therefore we introduce
the dimensonsless parameters
d :=
D
u
D
v
;γ :=
RL
2
D
v
;t
∗
:=
D
v
t
L
2
;x
∗
:=
x
L
(2)
with the time t and the typical length L and of
the system. The non-dimensional reaction-diffusion
equations are then:
∂v
∂t
∗
= ∆v + γ[uv
2
−(F +k)v]
∂u
∂t
∗
= d∆u + γ[−uv
2
+ F(1 −u)]
(3)
We use the common zero-flux boundary conditions
((n · ∇)). For the stability analysis we follow the
structure of the derivations by (Gray and Scott, 1984).
When investigating the steady state (i.e. ∂/(∂t
∗
) = 0),
one can find three steady states. The first is the
trivial solution and shall be called “red state” (in-
dex R) in accordance with (Gray and Scott, 1984):
(v
R
,u
R
) = (0,1). Furthermore, one can derive the
”blue state” (index ”B”)
(v
B
,u
B
) = (
F
2(F + k)
(1 +
√
p),
1
2
(1 −
√
p)) (4)
and the “intermediate state” (index “I”)
(v
I
,u
I
) = (
F
2(F + k)
(1 −
√
p),
1
2
(1 +
√
p)) (5)
when the discriminator p is:
p := 1 −
4(F + k)
2
F
> 0. (6)
A further analysis of the steady states shows, that the
red state is always stable, the intermediate state is al-
ways unstable and the blue state can be stable, but
does not have to be. Thus the blue state is the only
steady state which can lead to diffusion driven insta-
bility, the so called Turing instability. The necessary
and sufficient condition for Turing instability can be
derived to:
2
p
d detA
B
< a
11
d + a
22
(7)
with the Jacobian
A
B
=

a
11
a
12
a
21
a
22

(8)
Eq. 7 and Eq. 8 deliver the stability map (Fig. 1) of
the Gray/Scott-model for different values of d. Every
(F,k)-combination to the right of the Saddle-Node-
Bifurcation curve leads to a system which only leads
towards the red state. Every (F,k)-combiantion that
is located between the Saddle-Node-Bifurcation and
the respective instability curve for a given value of d
leads towards Turing patterns, whereas every (F,k)-
combination to the left of the instability curve can ei-
ther lead to a stable blue state or a red state solution,
depending on the initial conditions.
Further examination of the stability of the steady
states leads to the implicit formula that is the neces-
sary and sufficient condition for Turing instability in
the Gray-Scott-model:
Reaction-diffusion Model Describing the Morphogenesis of Urban Systems in the US
89

Figure 1: Stability Map of the Gray/Scott-model for differ-
ent values of d. The region right to the curve is the red state
(R). The grey regions are the Intermediate states according
to the different diffusion numbers (I). The region left to the
intermediate regions is the blue state (B).
2
v
u
u
u
u
u
u
u
t
d
"

(F + k)

F
2(F + k)
(1 +
√
p)

2
+ F

−

F
2(F + k)
(1 +
√
p)

2
(−2(F + k))

#
< (F + k)d −

F
2(F + k)
(1 +
√
p)

2
+ F

(9)
2.2 Methodology
A simulation study is chosen to test the capability of
reaction diffusion equations to predict human move-
ment patterns within cities. To reach the highest data
availability, the USA was chosen to provide city data.
One can get data down to the level of so called “Cen-
sus Blocks”, which vary in size but typically cover an
area of about 10 000 m
2
. At this level of resolution,
the accessible data is limited to:
• Population count,
• Age and sex,
• Marital status and
• Ethnicity.
This paper connects the natural science in form of
reaction-diffusion-model by Gray-Scott with certain
sociological phenomena (Figure 2). A broad litera-
ture analysis led to two phenomena that were regu-
larly stated as typical for (fast) growing cities. These
are segregation (S. Fowler, 2016; Farrell, 2016; Alba
and Logan, 1993; England et al., 1988; Koch, 2011;
Schulz et al., 2006) and gentrification (Timberlake
and Johns-Wolfe, 2017; Hwang and Sampson, 2014;
Janoschka et al., 2014; Lees, 2012; Smith, 2002;
Smith, 2005). Segregation in this context means a
separation of people and groups with similar social
(religious, ethnical, class-specific, a.o.) backgrounds
from groups with other social backgrounds to avoid
reciprocal contact. The Gray/Scott-model shows sim-
ilar behavior in being able to produce stripe and bub-
ble patterns out of a simulated “mixed fluid bowl”.
Figure 2: Sociological interpretation of the Gray/Scott
Model.
The gentrification in contrast to the segregation
means that a wealthier population is slowly squeezing
the former – poorer – population out of their neigh-
borhood or district. This squeeze-out is happening
due to a valorization of these neighborhoods by ren-
ovations and redevelopment of houses, as well as a
different business structure being attracted by a more
solvent clientele, up to a point where the former pop-
ulation cannot or does not want to afford to live there
anymore. Looking at the Gray/Scott-model, this can
be incorporated if you see the richer population as
the activator (V ) and the poorer population as the in-
hibitor (U). The Gray/Scott-model contains the di-
minisher term −(F +k)v and the refill term F(1 −u).
Given above made assumption, the rich population is
diminished more likely in areas where there is already
a high concentration of rich people v ≈ 1). At the
same time some of the poorer population has to move
out of their neighborhoods into close-by districts (in-
dicated by the higher diffusion of the inhibitor [d > 1])
or further away (indicated by the refill term). This
shows that wealth would be an excellent morphogene
for the Gray/Scott-model. Unfortunately – as stated
above – at the highest resolution, no wealth data is
available. Therefore ethnicity data was chosen, as it
shows the highest correlation to wealth of the accessi-
ble data (Shapiro et al., 2013; Tessmann and Friesen,
2017).
For the simulation study different cities have to
be chosen. As megacities in developing countries are
particularly interesting in their fast growth and fast
changes in both population and infrastructure, cities
were chosen that behave similarly to those megacities
of developing countries. Four criteria can be identi-
fied, that characterize such cities: An already large
number of inhabitants, a fast growth of population, a
high inequality and strong economic growth.
Especially strong economic growth is seen to be
a key factor in attracting rural population to migrate
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
90

Table 1: Variation of non-dimensional parameters in the simulation study.
Parameters Values
d d
−
= 2 d
0
= 6 d
+
= 10 d
++
= 100
F F
min
= 0 F
max
= 0.25
k k
min
= 0 k
max
= 0.65
γ γ
−
=
(
(588.31 +
1961.7
d
)L
2
for 2 ≤d ≤ 10
280.82L
2
for d = 100
γ
+
=
(
(58831 +
196170
d
)L
2
for 2 ≤d ≤ 10
28082L
2
for d = 100
towards those mega cities. Economic growth also has
the potential to change city layouts when e.g. resi-
dential areas are replacing industrial zones due to the
influx of inhabitants. Therefore, the US sample set
was chosen based on economic growth, i.e. the GDP
growth between the census years 2000 and 2010 of all
Metropolitan Statistical Areas (MSA). The cities with
the highest GDP growth rates were:
1. Midland/Odessa, TX
2. Victoria, TX
3. Bismarck, ND.
For these cities/metropolitan areas all available shape-
files and available population data was gathered from
the respective sources at the highest available res-
olution. As simulation software a combination of
FlexPDE for the calculation of the reaction-diffusion-
equations and MATLAB for the preparation and eval-
uation of FlexPDE results was used. For the simula-
tion various pre-assessments had to be performed to
define the variation of the non-dimensional parame-
ters. L is defined to be the square root of the city
area in m
2
and the other parameters were defined like
shown in Table 1.
While d and γ are simulated as stated in Table 1, F
and d are simulated with a higher resolution. In total
11 F steps of 0.025 between F
min
and F
max
and 14 k
steps of 0.005 between k
min
and k
max
are simulated.
This results in 4
d
∗11
F
∗14
k
∗2
γ
= 1232 simulations
per city.
The values u and v are calculated by determining
the number of inhabitants N per block. u := N
u
/N at
a given location then corresponds to the percentage of
all non-white inhabitants N
u
relative to the total num-
ber of inhabitants N in that block. Accordingly, v is
then defined as v := N
v
/N, where N
v
is the number of
white residents.
Defining the nondimensional simulation time
t∗
max
is crucial to the simulation experiment as it
needs to be equivalent to the 10 years of change that
the census data represent. As it is – per definition
– not independent of γ, two nondimensional simu-
lation times – one per γ simulated – were defined
based on pre-simulations to: t
∗
max,Simγ−
= 5 ∗10
−6
and
t
∗
max,Simγ+
= 5 ∗10
−8
. Furthermore a quality measure
QF =
B
max
∑
i=1
|AC
2010,i
−AC
Sim,i
| (10)
has to be defined to evaluate the results of the sim-
ulation experiments, with AC
2010,i
the activator con-
centration at point i in 2010. B
max
is the number of
discrete simulation points used for the respective sim-
ulated city. The smaller the QF value is, the better is
the result of the simulation. In the experiment Mid-
land/Odessa, TX and Bismarck, ND shall be simu-
lated to find the best factor combination and identify
main and interdependency effects of the individual
factors. Then, to test a linear dependency, Victoria,
TX, the city with the 2nd fastest GDP growth is tested
with the interpolated factor combination also.
2.3 Assumptions
For the simulations, some further general, simplify-
ing assumptions are made in order to obtain a simpli-
fied city model, which can then provide insights into
the suitability of the reaction-diffusion equations for
predictions of city morphology by means of the sim-
ulation. First, it should be assumed that the cities to
be simulated represent homogeneous levels, i.e. the
entire urban area can in principle be developed within
its boundaries. So undevelopable geographies (e.g.
rivers or steep mountains) are neglected as well as de-
liberately undeveloped areas such as roads, parking
lots, parks and other means of transport (e.g. trams,
etc.). Besides that, only ”concentrations” of people
are considered. This means that ultimately no con-
crete statements can be made about the total number
of people living in a block, but only the proportion
of a certain ethnic group (or, if a lower resolution was
chosen, the proportion of rich/poor population). How-
ever, since the core of the model is an interplay be-
tween two social groups, this should be regarded as a
reasonable simplification.
3 RESULTS
In this section we present the results of our study.
First, we present the two cities we trained on (Mid-
Reaction-diffusion Model Describing the Morphogenesis of Urban Systems in the US
91

land/Odessa, TX and Bismarck, ND). We show the
effects, the different parameters have on the qual-
ity function and interpret the outcoming simulations
qualitivly. Then we present the result for the city (Vic-
toria, TX) we gained using the best parameters from
the two cities simulated before.
3.1 Midland
The minimal QF value is 105,881 at a combination of
(γ,d,F, k) = (−,10, 0.075,0.005). The maximal QF
value is 188,349 is the result of (-, 2, 0.25, 0.065).
Furthermore, the main and interdependency effects
(derived from a regression model) on the QF value
are shown in Table 2. Here γ,d ,F and k are normed,
so that γ
∗
,d
∗
,F
∗
,k
∗
∈ [−1, 1]. The regression model
based on Table 2, can be used to estimate the effects
of the parameters γ,d,F and k on the QF value.
If minimized within the set boundaries, the regres-
sion model leads to an optimized factor combination
of (γ
∗
,d
∗
,F
∗
,k
∗
) = (−, +,−,−), which means that
small γ,F and k and large d values seem to lead to
better results for Midland/Odessa, TX. The graphical
results of the simulation based on the factor combina-
tions is shown in Figure 3.
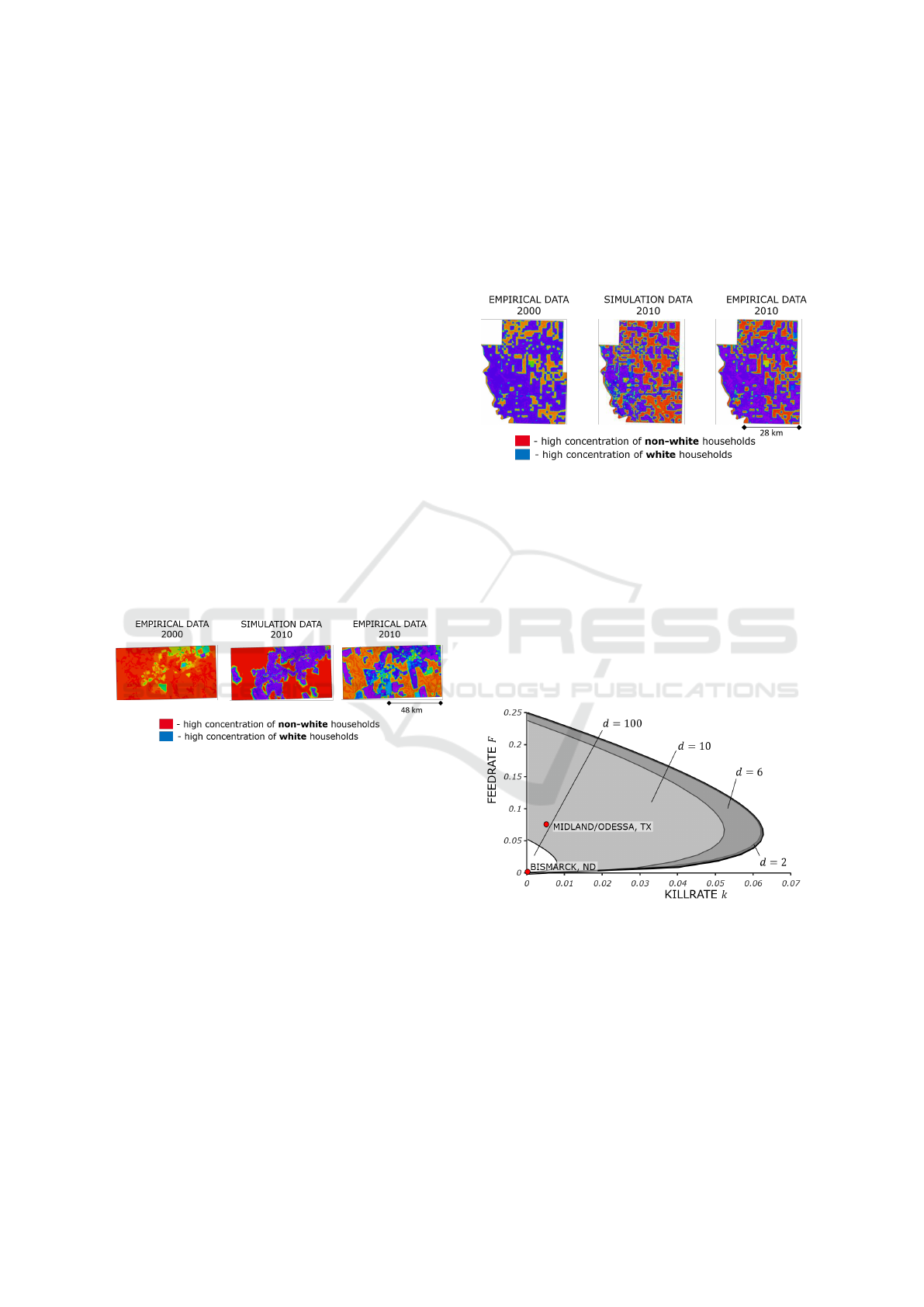
Figure 3: Representation of the empirical and simulation
data for Midland/Odessa. The simulation was conducted
with (γ,d, F, k) = (−,10,0.007, 0.005).
Looking at Midland/Odessa’s graphical results, it
can be seen that there have been significant demo-
graphic changes between 2000 and 2010. In the west
and southeast of the simulation area completely new
structures were created. These fundamental structural
changes could be mapped by the simulation model,
even if larger deviations can still be detected.
3.2 Bismarck
The minimal QF value is 154,584 at a combination of
(γ,d,F, k) = (+,100, 0,0). The maximal QF value is
287,979 is the result of (-, 2, 0, 0.05). Furthermore,
the main and interdependency effects (derived from a
regression model) on the QF value are as presented in
Table 2. Once again γ,d,F and k are normed, so that
γ
∗
,d
∗
,F
∗
,k
∗
∈ [−1,1]. The regression model based
Table 2, can be used to estimate the effects of the pa-
rameters γ,d,F and k on the QF value.
If minimized within the set boundaries, the regres-
sion model leads to an optimized factor combination
of (γ
∗
,d
∗
,F
∗
,k
∗
) = (+, +,−,−), which means that
small F and k and large γ and d values seem to lead to
better results for Bismarck, ND.
Figure 4: Representation of the empirical and simulation
data for Bismarck. The simulation was conducted with
(γ,d, F, k) = (+,100,0, 0).
The so far presented results lead to the various ef-
fects on the QF factor for the two simulated cities pre-
sented in Table 2.
If the results just described are summarized, the
best combinations found can be entered in the stabil-
ity map (Figure 1). This Figure 5 shows that the best
results are obtained with small values of k and F, as
well as large values for d. The only difference is γ.
Figure 5: Stability Map of the Gray/Scott-model with the
best factor combination for both cities investigated (Mid-
land/Odessa, TX and Bismarck, ND).
3.3 Victoria
As described above, to test the linear dependency of
the factor effects, Victoria, TX, which had the 2nd
strongest GDP growth of all US cities, shall be tested
with an altered simulation scenario. On the one hand,
the “regular” test plan described in the methodology
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
92

Table 2: Effects.
Midland/Odessa
Main effect γ
∗
d
∗
F
∗
k
∗
-8726 -6680 21317 13909
Interdependency effect 1st O. γ
∗
d
∗
γ
∗
F
∗
γ
∗
k
∗
D
∗
F
∗
D
∗
k
∗
F
∗
k
∗
5853 -6729 -7823 -3600 -4554 732
Inter-dependency effect 2nd & 3rd O. γ
∗
d
∗
F
∗
γ
∗
d
∗
k
∗
γ
∗
F
∗
k
∗
d
∗
F
∗
k
∗
γ
∗
d
∗
F
∗
k
∗
-2318 455 1336 392 343
Bismarck
Main effect γ
∗
d
∗
F
∗
k
∗
-35605 -24505 8684 19681
Interdependency effect 1st O. γ
∗
d
∗
γ
∗
F
∗
γ
∗
k
∗
D
∗
F
∗
D
∗
k
∗
F
∗
k
∗
8377 5952 -6703 2056 -4127 3903
Inter-dependency effect 2nd & 3rd O. γ
∗
d
∗
F
∗
γ
∗
d
∗
k
∗
γ
∗
F
∗
k
∗
d
∗
F
∗
k
∗
γ
∗
d
∗
F
∗
k
∗
-2362 -1393 -4388 -2107 1983
Table 3: Overview to factor combinations, that promise low QF values for Midland/Odessa, TX and Bismarck, ND. The “best
factor combination” is the one that delivered the lowest QF for the respective city. The factor combinations in the last column
are based on a GRG (generalized reduced gradient method) minimization of the respective regression model when respecting
all constraints.
Best factor combination Main Effects with interdependency effects
γ
∗
d
∗
F
∗
k
∗
γ
∗
d
∗
F
∗
k
∗
γ
∗
d
∗
F
∗
k
∗
Midland/ Odessa - + - - + + - - - + - -
Bismarck + + - - + + 0 - + + - -
and used for Midland/Odessa, TX and Bismarck, ND,
was simplified to test less combinations of F and k.
These were now only varied in three steps each. On
the other hand, an additional factor combination was
tested, that lies – with regards to the factor combina-
tion – in the middle of the optimized solutions found
for Midland/Odessa, TX and Bismarck, ND, which
are displayed in the table above.
Figure 6: Simulation for Victoria, TX with γ
0
= 10 ∗γ
−
for
variations of the factor d. F and k are changed equally from
small (−) to medium (0) to large (+). (−) is F = k = 0,
(0) is F = 0.125 and k = 0.03 and (+) is F = 0.25 and
k = 0.065.
As the results for the two cities are consistent
for d,F and k, but not for γ,γ
0
= 10γ
−
was de-
fined as the middle between γ
−
and γ
+
. Con-
sequently, if the factor effects were linear depen-
dent across the tested cities, one would expect the
best factor combination for Victoria, TX to be at
(γ
∗
,d
∗
,F
∗
,k
∗
) = (0,+,−,−). The results for the Vic-
toria, TX simulation can be seen in Figure 6.
Figure 7: Representation of the empirical and simulation
data for Victoria. The simulation was conducted with
(γ,d, F, k) = (10γ
−
,100,0, 0).
The best QF value for Victoria, TX was found
with the factor combination that was indicated by the
linearity test, i.e. with small values for F and k, a
large value for d and the middle value of γ, γ
0
.
It is interesting to note that both the formation of
a kind of coridor, in the east of the area under con-
Reaction-diffusion Model Describing the Morphogenesis of Urban Systems in the US
93

sideration, and the splitting off of a small ”island”
with a high concentration of non-white population at
the northern edge of the area was represented by the
model in the simulation and can also be seen in the
empirical data (Figure 7).
4 DISCUSSION
An analysis of the above results shows that small val-
ues for F and k lead to the best quality values.
For F, a slight tendency towards small values can
be observed, which in terms of the reaction-diffusion
equations means that the inhibitor or substrate U - i.e.
in the sociological analogy the non-white population
- is ”filled up” at a low rate. This means that few
non-white population ”react” into the system, which
can be interpreted in such a way that there is little in-
flux of non-white population groups from outside the
system boundaries under consideration. The factor k
stands for the difference between the filling rate for
the inhibitor/substrate and the reduction of the activa-
tor. If k is zero, the activator in the system decreases
at the same rate as the inhibitor/substrate is replen-
ished. The factor d, which represents the ratio of
the diffusion coefficient of the inhibitor or substrate
U to that of the activator V , gives a similar picture
to the factor γ. For most of the cities investigated, it
seems advantageous to use a large value for d for the
simulation of urban morphology development. This
means that the diffusion coefficient of the inhibitor
or substrate - i.e. in the sociological analogy used
here the diffusion coefficient of the non-white pop-
ulation - is significantly higher than the coefficient of
the white population. This means that in relation to
the real cities, the non-white population must have a
higher migration rate in order to better reflect real de-
velopments. This means that non-white households,
i.e. households that tend to be poorer, have to move
more often. In principle, this is very much in line
with the sociological phenomena of segregation and
gentrification, since poorer households are displaced
from their previous residential locations by gentrifica-
tion and segregation and therefore have to move more
frequently.
This interpretation is to be understood qualita-
tively and should be investigated in further studies
with extended data material.
The simulations carried out depict a total of 10
years of urban development, as the best data avail-
ability in the USA is available for the census years
2000 and 2010. The population data from the year
2000 serve as starting values for the simulations. The
boundary conditions correspond to the usual zero flux
conditions for the Gray-Scott model, i.e. there is
no flow across system boundaries. In later investi-
gations it is therefore necessary to check more pre-
cisely whether the selected boundary conditions have
a significant influence on the quality of the results and
to what extent a different simulation time can have
a positive or negative influence on the results. The
evaluation of the result quality of a simulation was
carried out using a so-called quality function, which
forms the absolute difference between the reference
solutions from the census data of 2010 and the simu-
lation result at each simulation grid point. These sim-
ulation grid points depend on the individual geome-
try of the city under investigation, but always have
a distance of 0.001. The results of the simulation
study suggest that the investigated factor combina-
tions are only applicable to a very limited extent for
the prediction of urban structures. Thus, the initial
values in for out of six cities are a better prediction
for the reference solution than the result of the simu-
lation with the best factor combination in each case.
On the other hand, in two cases, for Midland/Odessa,
TX and Victoria, TX, the simulation result of the best
factor combination is a much better estimate of the
reference solution than the corresponding initial val-
ues. It is noticeable that the changes from 2000 to
2010 in Midland/Odessa, TX are particularly large
compared to the other cities investigated. This may
suggest that the reaction-diffusion equations are bet-
ter suited to approximate large changes than to depict
the smallest change in detail. This in turn would mean
that a lower data resolution than that available in the
USA would suffice. A more detailed mapping of city
structures may be possible with the reaction-diffusion
equations, but then a local optimization of the factors
is very likely necessary. At present, however, it re-
mains questionable whether the Gray/Scott equations
can be used to map the patterns.
Other quality values should also be examined in
further investigations, since the quality measure pre-
sented here is only an integral quantity and does not
say anything about which areas in the area under con-
sideration the deviations between simulation and em-
piricism are large and which they are small.
Finally, it remains to be seen that good factor com-
binations can actually be derived to a limited extent
from other, similar cities. This was investigated for
two cities. To what extent future developments can
be estimated by a historical determination of the best
factor combination has to be examined in further in-
vestigations.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
94

5 CONCLUSIONS
In this paper we have investigated a Gray/Scott
reaction-diffusion equation model to simulate the de-
velopment of economically strong cities in the USA.
We transferred the model known from chemistry and
biology to the development of urban systems. We
show that reaction-diffusion equations can be inter-
preted sociologically and we describe fundamental
structural changes in a third city by training the equa-
tions on two cities.
A more detailed mapping of urban structures may
be possible with the reaction-diffusion equations, but
then a local optimization of the factors will be nec-
essary. At the moment, however, it remains ques-
tionable whether the patterns can be mapped with the
Gray-Scott equations investigated here. Finally, it re-
mains to be seen that good factor combinations can
actually be derived to a limited extent from other, sim-
ilar cities. This was investigated for two cities. To
what extent future developments can be estimated by
a historical determination of the best factor combina-
tion is to be examined in further investigations.
Finally, it should be noted that the approach pre-
sented here is not intended to show that simple math-
ematical equations can fully describe complex phe-
nomena such as urbanisation. Rather, it addresses
the question of whether (i) there are fundamental pro-
cesses that dominate urbanization, while other pro-
cesses may be neglected. On the other hand, (ii) it
is examined whether these processes can be mapped
with simple equations.
ACKNOWLEDGEMENTS
We would like to thank the KSB Foundation for pro-
viding funds for the research.
REFERENCES
Alba, R. D. and Logan, J. R. (1993). Minority proximity to
whites in suburbs: An individual-level analysis of seg-
regation. American journal of sociology, 98(6):1388–
1427.
Benenson, I. and Torrens, P. M. (2004). Geosimulation:
automata-based modelling of urban phenomena. John
Wiley & Sons, Hoboken, NJ.
England, P., Farkas, G., Kilbourne, B. S., and Dou, T.
(1988). Explaining occupational sex segregation and
wages: Findings from a model with fixed effects.
American Sociological Review, pages 544–558.
Farrell, C. R. (2016). Immigrant suburbanisation and the
shifting geographic structure of metropolitan segrega-
tion in the united states. Urban Studies, 53(1):57–76.
Frankhauser, P. (1998). Fractal geometry of urban patterns
and their morphogenesis. Discrete Dynamics in Na-
ture and Society, 2(2):127–145.
Friesen, J., Taubenb
¨
ock, H., Wurm, M., and Pelz, P. F.
(2018). The similar size of slums. Habitat Interna-
tional, 73:79–88.
Gonz
´
alez-Val, R., Ramos, A., Sanz-Gracia, F., and Vera-
Cabello, M. (2015). Size distributions for all cities:
Which one is best? Papers in Regional Science,
94(1):177–196.
Gray, P. and Scott, S. (1983). Autocatalytic reactions in the
isothermal, continuous stirred tank reactor: isolas and
other forms of multistability. Chemical Engineering
Science, 38(1):29–43.
Gray, P. and Scott, S. (1984). Autocatalytic reactions in the
isothermal, continuous stirred tank reactor: Oscilla-
tions and instabilities in the system a+ 2b→ 3b; b→
c. Chemical Engineering Science, 39(6):1087–1097.
Hwang, J. and Sampson, R. J. (2014). Divergent pathways
of gentrification: Racial inequality and the social or-
der of renewal in chicago neighborhoods. American
Sociological Review, 79(4):726–751.
Janoschka, M., Sequera, J., and Salinas, L. (2014). Gen-
trification in s pain and l atin a merica—a critical di-
alogue. International journal of urban and regional
research, 38(4):1234–1265.
Koch, A. (2011). Soziale segregation aus der
modellierungs-und simulationsperspektive. I
¨
OR
Schriften, page 25.
Kraas, F., Leggewie, C., Lemke, P., Matthies, E., Messner,
D., Nakicenovic, N., Schellnhuber, H. J., Schlacke, S.,
Schneidewind, U., and Brandi, C. (2016). Humanity
on the move: Unlocking the transformative power of
cities. WBGU-German Advisory Council on Global
Change.
Krugman, P. R. (1996). The self-organizing economy, vol-
ume 122. Blackwell Oxford.
Lees, L. (2012). The geography of gentrification: Thinking
through comparative urbanism. Progress in Human
Geography, 36(2):155–171.
Pelz, P. F., Friesen, J., and Hartig, J. (2019). Similar size
of slums caused by a turing-instability of migration
behaviour. Physical Review E.
S. Fowler, C. (2016). Segregation as a multiscalar phe-
nomenon and its implications for neighborhood-scale
research: the case of south seattle 1990–2010. Urban
geography, 37(1):1–25.
Schulz, A. J., Gravlee, C. C., Williams, D. R., Israel, B. A.,
Mentz, G., and Rowe, Z. (2006). Discrimination,
symptoms of depression, and self-rated health among
african american women in detroit: results from a lon-
gitudinal analysis. American journal of public health,
96(7):1265–1270.
Schweitzer, F. and Steinbink, J. (2002). Analysis and
Computer Simulation of Urban Cluster Distributions.
In Fundamental Principles of Urban Growth, pages
142–157. M
¨
uller + Busmann, Wuppertal.
Shapiro, T., Meschede, T., and Osoro, S. (2013). The
roots of the widening racial wealth gap: Explaining
the black-white economic divide. Research and pol-
icy brief.
Reaction-diffusion Model Describing the Morphogenesis of Urban Systems in the US
95

Smith, N. (2002). New globalism, new urbanism: gentrifi-
cation as global urban strategy. Antipode, 34(3):427–
450.
Smith, N. (2005). The new urban frontier: Gentrification
and the revanchist city. Routledge.
Tessmann, R. and Friesen, J. (2017). Study of Reaction-
Diffusion Equations as structural forming mecha-
nisms in urban morphologies in the USA. Research
Project, TU Darmstadt.
Timberlake, J. M. and Johns-Wolfe, E. (2017). Neigh-
borhood ethnoracial composition and gentrification in
chicago and new york, 1980 to 2010. Urban Affairs
Review, 53(2):236–272.
Turing, A. M. (1952). The Chemical Basis of Morphogene-
sis. Philosophical Transactions of the Royal Society of
London. Series B, Biological Sciences, 237(641):37–
72.
United Nations (2016). Urbanization and development:
emerging futures. World cities report. United Nations
Publicatio, New York. OCLC: 953977423.
GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management
96