Skeleton Line Extraction Method in the Areas with Dense Junctions

Considering Stroke Features

Pengda Wu, Yong Yin and Chengming Li

Chinese Academy of Surveying and Mapping, Lianhuachi West Road, Beijing, China

Keywords: Areas with Dense Junctions, Skeleton Line, Stroke Features, Long-edge Adaptive Node Densification and

Type III Triangles Aggregation.

Abstract: Polygon skeleton line extraction is a key and difficult problem in map generalization. Aiming at the problem

that the traditional method is difficult to maintain the main structure and extension characteristics when

dealing with areas with dense junctions, a method for extracting skeleton lines in areas with dense junctions

considering stroke features is proposed in this study. Firstly, a long-edge adaptive node densification

algorithm is put forward to construct boundary-constrained Delaunay triangulation for extracting the initial

skeleton line. Then, Type III triangles are automatically identified as the basic unit. According to the local

width feature, Type III triangles aggregation is achieved to obtain the areas with dense junctions. Finally, we

define the connecting arc and evaluate their importance. The stroke is iteratively constructed according to the

importance of the arc, and the good continuity feature of the stroke is used to optimize the skeleton line. The

actual water system data of Jiangsu Province are used to verify the results. The experimental results show that

the proposed method can better identify the areas with dense junctions, and the extracted skeleton line is

naturally smooth and well connected, which accurately reflects the main structure of the area.

1 INTRODUCTION

Ai (2002) believe that the extraction of skeleton lines

is a key step to realize the comprehensive operation of

maps such as polygon dimensionality reduction and

split melting. The extraction of skeleton lines takes into

account the shape features of polygons and

summarizes the main body structure and extension

characteristics of polygons. It shall meet the human

visual cognition while conforming to the drawing

specifications. Therefore, how to accurately and

reasonably determine the skeleton line has always been

a difficult point of research (Ai, 2010). There are three

common methods for extracting skeleton lines: round

skeleton line (LEE, 1982), straight skeleton line (Das

et al, 2010) and skeleton line based on Delaunay

triangulation (Cao et al.2015; Sintunata et al., 2016).

Delaunay triangulation with “circular rule” or

“maximum/minimum angle rule” has become a

method of skeleton line extraction widely used by

researchers (Ware, 1997), and the research in this paper

also falls within this scope.

DeLucia et al. (1987) first proposed a skeleton line

extraction method based on boundary constrained

Delaunay triangulation (CDT) ; Zou et al. (2001) used

this method to construct a polygonal skeleton and

proved the effectiveness of this method . Li et al.

(2006) attempted to apply this method to extract the

main skeleton line of the polygon and achieved good

results. However, in the course of research, some

scholars have also found some problems, e.g.,

Penninga et al. (2005) pointed out that the skeleton line

extracted based on Delaunay triangulation has at least

the following three aspects: (1) at the branch

connection point, skeleton lines present “saw tooth”;

(2) tiny bumps on the boundary result in the formation

of redundant “spike” skeleton lines; (3) fewer

boundary nodes cause the end split line to be elongated

and offset. Accordingly, Jones et al. (1995), Uitermark

et al. (1999) and Penninga et al. (2005) proposed to use

the branch skeleton line direction, boundary

simplification, densification boundary nodes and other

methods to modify the proposed skeleton line, which

have better solved the above problem. However, these

methods are only applicable to simple polygons with

regular shapes and flattened boundaries. Haunert et al.

(2008) have studied a large number of road data and

found that when dealing with polygons with irregular

shapes or complex branching convergence features,

existing methods are difficult to maintain the main

Wu, P., Yin, Y. and Li, C.

Skeleton Line Extraction Method in the Areas with Dense Junctions Considering Stroke Features.

DOI: 10.5220/0007712601930200

In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2019), pages 193-200

ISBN: 978-989-758-371-1

193

structure and extension characteristics at this place. Li

et al. (2018) made a preliminary exploration of the

skeleton line extraction in the areas with many

junctions, but the method relies on the skeleton line

direction and the branch gathering distance

characteristics, so that it is still unable to handle

complex area with dense junctions.

On this bases, according to the existing research, a

method of extracting the skeleton line of the areas with

dense junctions considering the stroke features is

proposed to optimize the extraction effect of the

skeleton line of the complex branch convergence.

2 RELATED WORKS

2.1 Existing Extraction Method of

Skeleton Line

Li et al. (2018) proposed a method for extracting

skeleton lines from narrow long map-spot branch

convergence area. The basic idea is to introduce a

constrained Delaunay triangulation, identify the branch

convergence area based on the degree of node

correlation, and eliminate the jitter on the skeleton line

of the branch convergence area under the direction and

distance constraints. The specific steps are shown as

below:

Step 1: Construct a constrained Delaunay

triangulation to divide the narrow long map-spot.

According to the number of adjacent triangles in the

inner triangle of the polygon, the triangles in the

Delaunay triangulation can be subdivided into three

categories:

Type I triangle: There is one and only one adjacent

triangle. As shown by ΔABC in Figure 1(a), the vertex

A is the end point of the skeleton line.

Type II triangle: There are two adjacent triangles.

As shown by ΔABC in Figure 1(b), the advancement

direction of the skeleton line in the Type II triangle is

unique.

Type III triangle: There are three adjacent triangles.

As shown by ΔABC in Figure 1(c), the three extension

directions occur at point O.

Step 2: Extract the central axis from the three types

of triangles as follows for connection to form a

skeleton line, wherein the common edges of two

adjacent triangles are called adjacent edges:

Type I triangle: Connect the midpoint of the unique

adjacent edge with its corresponding vertex, as shown

by segment AD in Figure 1 (a);

Type II triangle: Connect the midpoints of two

adjacent edges, as shown by segment DF in Figure

1(b);

Type III triangle: Connect the center of gravity

and the midpoint of the three sides, as shown by

segments OD, OF, OH in Figure 1 (c).

(a) (b) (c)

Figure 1: Triangle classification. (a) Type I triangle, (b)

Type II triangle, (c) Type III triangle.

Step 3: Since the area where the Type III triangle

is located is a branch convergence area, the branch

aggregation area can be identified by the location of

Type III triangle;

Step 4: Calculate the direction of the three related

skeleton line branches in the branch convergence

area. If there is a branch skeleton line with the same

direction, it is preferentially connected as a straight

line, and the remaining branch skeleton lines extend

to the straight line in their respective directions; If

there is no arbitrary two skeleton lines in the same

direction, the Euclidean distance between the nodes

is used as a measure of similarity, the branch nodes

are aggregated to the geometric centre of the range,

and the branch skeleton lines are connected to the

aggregation nodes in respective directions.

2.2 Defects in the Existing Method of

Extracting Skeleton Lines

In the existing method, each trigeminal region is used

as a processing unit, and by setting a direction

threshold and a branch node distance threshold, the

skeleton line of simple junctions aggregation area can

be obtained well. However, when the junctions is

complicatedly converged, the existing method is

difficult to precisely strip single branch convergence

area, leading to no accurate extracted skeleton line. In

addition, the shape of the skeleton line in the

junctions is complicated, and each branch

convergence area is used as a unit for processing,

unable to consider the overall characteristics of the

area formed by the mutual association between the

branches, resulting in the destruction of the overall

structure of the area.

3 METHODOLOGY

In this paper, a method for extracting skeleton line in

the areas with dense junctions considering stroke

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

194

features is proposed, including three key steps as

follows. (1) Long-edge adaptive node densification:

Create Delaunay triangulation with polygon

boundary constraints for long-edge adaptive

densification; (2) Areas with dense junctions

identification: Identify the branch structure and

aggregate the qualified branches; (3) The skeleton

line extraction in the Areas with dense junctions:

According to the good continuity characteristics of

the stroke, the skeleton line is optimized, leading to

more in line with humans cognitive law.

3.1 Long-edge Adaptive Node

Densification

Boundary densification is one of the key steps in

establishing a boundary-constrained Delaunay

triangulation. In the dense area of the bifurcation,

there will be a large number of complex areas with

one side branch dense while no branch on the other

side. If not densified, the constrained Delaunay

extraction directly extracts the skeleton line, which

will cause a large deviation in the identification of the

branch convergence area. If the traditional overall

densification method is used, it will lead to invalid

branches in the normal end. Therefore, the long-edge

adaptive densification is proposed to perform node

densification on such complex areas in this paper. The

specific steps are shown as below:

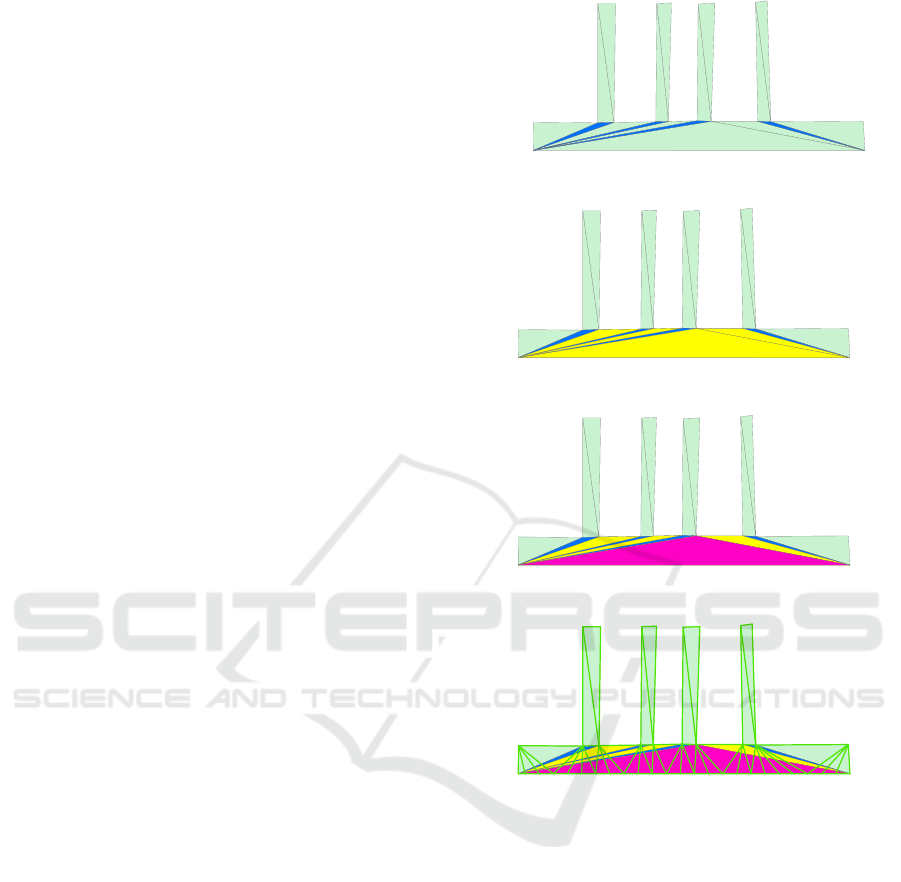
Step 1: Identify the obtuse triangle in the Type III

triangle and set the minimum angle threshold Amin.

If the minimum angle in an obtuse triangle is smaller

than Amin, it is marked and put it into the triangle set

S, as shown by the blue triangle in Figure 2 (a );

Step 2: Identify the longest edges of all the

triangles in the set S, and find the Type II triangles

adjacent to the longest edges with one edge as the

boundary, as shown by the yellow triangle in Figure

2(b);

Step 3: Identify the longest edge of the above-

mentioned Type II triangle and determine whether it

is a boundary edge. If it is a boundary edge, it is

marked as the local long edge to be densified, and the

Type II triangle is marked as the triangle to be

densified. The purple triangle is shown in Figurer

2(c);

Step 4: Set the densified step size to the smallest

and shortest edge of Type III triangle set associated

with Type II triangle to be densified;

Step 5: Densify by the densified step size, as

shown in Figure 2(d).

(a)

(b)

(c)

(d)

Figure 2: Long-edge adaptive densification. (a) Elongated

Type III triangle, (b) Type II triangle with one edge as the

boundary, (c) Local long edge to be densified, (d) Densify

by densified step size.

3.2 Identification of Areas with Dense

Junctions

3.2.1 Trident Identification

The first step in the identification of the areas with

dense junctions is to identify the trident area in the

polygon. The identification method is shown as

follows. (1) After long-edge adaptive densification,

construct a polygonal boundary constraint Delaunay

triangulation and extract the initial skeleton line; (2)

Construct a point and line topology for the initial

skeleton line, and for any node of the skeleton line

Skeleton Line Extraction Method in the Areas with Dense Junctions Considering Stroke Features

195

topologies, the number of arcs associated with the

node is ArcNum(Node); (3) When ArcNum(Node)=3

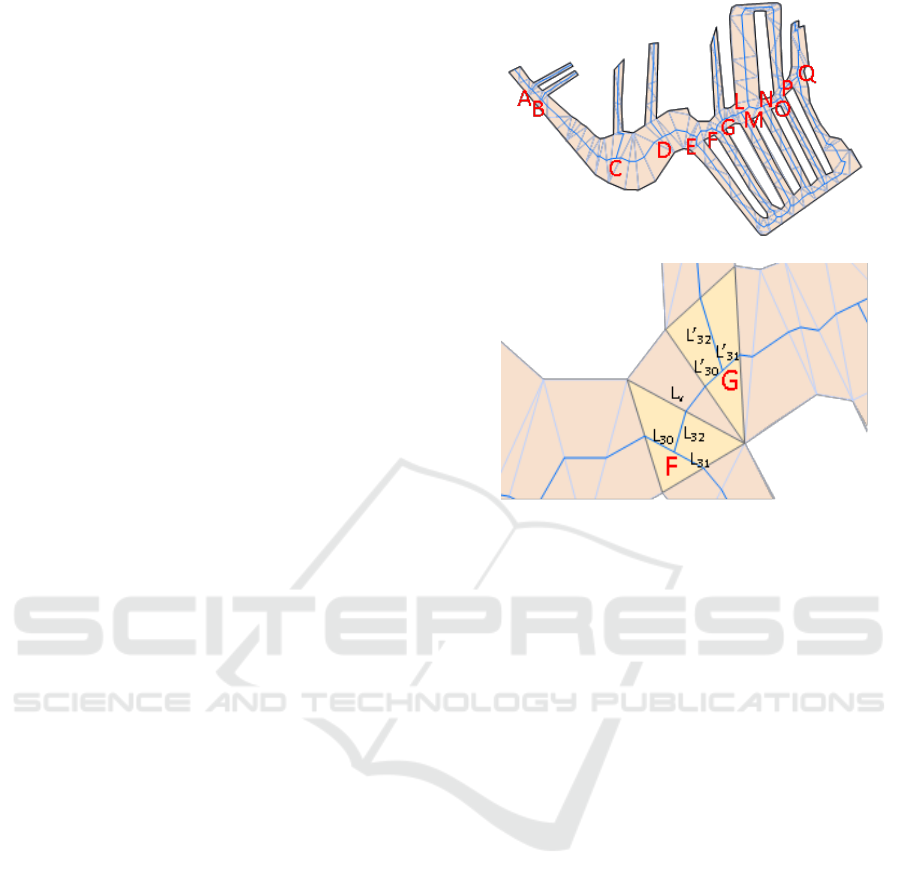
of a node, the node is a trident node, and the area is

the trident area, as shown by the nodes A-P in Figure

3(a). It can be found that these trident nodes are the

center points of Type III triangles.

3.2.2 Trident Association

Whether the identified tridents can be aggregated

needs to be judged by the connecting arc between

the tridents, wherein the connecting arc segment is

defined as below. If the first and end points of an arc

segment are trident nodes, then the arc segment is a

trident connecting arc. The specific steps for

determining the associated relationship are shown as

follows:

Step 1: Calculate the local approximate width

NODE

of the area where the trident is located: record

twice the maximum value among the three edges of

Type III triangle corresponding to the trident as the

local approximate width W

NODE

of the area where

the trident is located, i.e.,

NODE

=Max(L

)×2;

Step 2: Calculate the local approximate width

ARC

of the area where the connecting arc is located:

calculate the local approximate widths W

and W

of the area where the first node N

and the end node

of the connecting arc are located, and use the

large value as the local approximate width W

ARC

the area where the connecting arc is located, i.e.,

ARC

=Max(W

);

Step 3: Calculate the effective length L

of the

connecting arc segment: record the part of the

connecting arc between the first and end nodes of

the connecting arc segment with the internal length

of Type III triangle as the effective length L

of the

connecting arc segment, as shown in Figure 3(b),

and the effective length of the connecting arc

between the first node F and the end node G is

-L

-L’

;

Step 4: If the effective length L

of the connecting

arc between the two trident nodes is smaller than the

local approximate width W

ARC

of the area where the

connecting arc is located, i.e., ArcNum(N

)=3,

ArcNum(N

)=3 and L

ARC

are satisfied

simultaneously, then the two tridents are associated

with each other, and the connecting arc between them

is marked Arc

link

(a)

(b)

Figure 3: Trident association judgement. (a) Trident node,

(b) Effective length Lv of connecting arc.

3.2.3 Trident Aggregation

Calculate the associated arc Arc

link

for all trident nodes

of the polygon to be placed in the set S (Arc

link

). Select

an Arc

link

and use its first node N

and end node N

tracking nodes to detect whether Arc

link

also exists in

the first node N

and end node N

(except Arc

link

itself)

and record to the neighboring association Arc

link

set

NeighborArc

link

(Arc

link

). After each Arc

link

is detected,

it is clustered and expanded to obtain the junctions

aggregation result.

3.3 Skeleton Line Extraction in Areas

with Dense Junctions

For any trident aggregation area, this paper takes into

account the stroke feature to extract its internal

skeleton line.

Accordingly, a stroke is first constructed with the

connecting arc as a unit in this paper, and then the

skeleton line of the trident region is extracted, leading

to natural extension according to the stroke feature

and obtain a skeleton line more in line with human

cognition.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

196

Table 1: The meaning and calculation method of connecting arc parameters.

Parameter

name

Meaning

Calculation method

Length

Length of connecting arc

L=Distance(Ns,Ne)

Approximate

width

Local approximate width of connecting arc

NODE

=Max(L

)×2

Connectivity

The number of other connecting arcs that

intersect this connecting arc

( ) ( , )

i i k

D v r v v





Where,

( , )

r v v

indicates the connectivity

between nodes.

Proximity

The minimum number of connections from the

connecting arc to all other connecting arcs, reflecting

the possibility that other connecting arcs will be

aggregated in this connecting arc

()

( , )

d v v









Where,

( , )

d v v

indicates the shortest

distance between two nodes.

Betweenness

Measure the extent of this connecting arc

between other connecting arcs and whether the

connecting arc acts as a “bridge”

. ; ;

()

( 1)( 2)

jk i

j k n j k k i

n n m

  







Where,

indicates the number of the

shortest distance between two nodes;

()

jk i

indicates the number of the shortest

distance between two nodes passing the node

3.3.1 Arc Importance Evaluation

The basic idea to determine the importance of

connecting arcs in this paper is to use the length,

connectivity, proximity and mediation of connecting

arcs, weighted by CRITIC (Criteria Importance

Though Intercrieria Correlation) method (Diakoulaki

et al., 1995) to obtain the importance of connecting

arcs. The meanings of the parameters of connecting

arc segments are shown in Table 1.

3.3.2 Construct a Stroke Connection

Based on the importance of each connecting arc

segment, the stroke connection of the areas with

dense junctions is iteratively calculated, and the main

steps are shown as follows:

Step 1: Identify the trident node with only the

associated arc on one side, and select one as the stroke

connection to track the starting node. Then, the

connecting arc is taken as the tracking arc to get the

node on the other side of the arc, which is used as a

tracking node;

Step 2: The connecting arc of the tracking node

is taken as the stroke connection candidate set R to

calculate the importance of each connecting arc

segment;

Step 3: Preferentially connect the arc segment of

larger importance with the previous arc segment to

form a stroke;

Step 4: According to the ideas of Steps 2 and 3,

continue to track the calculation of the stroke

connection until there is no connection arc of the

tracking node, then the single stroke connection ends;

Step 5: Explore the branch connecting arc of the

existing stroke connection until all the connecting

arcs of intersecting dense areas have been calculated,

then the stroke connection calculation ends, as shown

by the thick blue line in Figure 4.

Figure 4: Junctions aggregation result.

3.3.3 Skeleton Line Adjustment

The connecting arc Arc

link

as the basic unit of stroke

connection in areas with dense junctions, consists of

two trident nodes. For any of the trident nodes, the

two arcs with the stroke connection are used as the

reference arc. The midpoint of the two-point line on

the edge of Type III triangle is used as the adjustment

position of the trident node, and the three arc

segments associated with the trident node are

connected with the midpoint to complete the skeleton

line adjustment of each trident region. As shown in

Skeleton Line Extraction Method in the Areas with Dense Junctions Considering Stroke Features

197

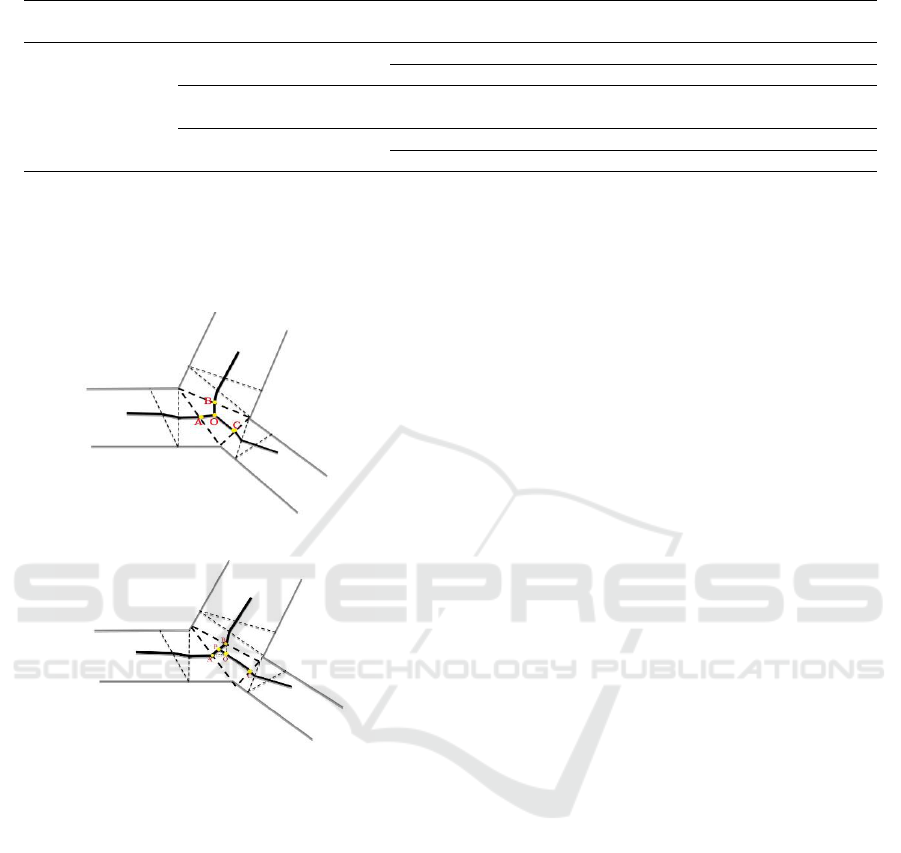
Table 2: Overall situation statistics of experimental surface element processing results.

Trident number

Number of areas with

dense junctions

The case of areas with dense junctions containing connecting

arc segments

2286

124

Max

Min

Average

Total

307

15.6

1939

stroke connection number

in the dense area

Stroke containing connecting arc

385

Max

Min

Average

Total

3.1

1939

Figure 5, assuming that the arcs of OA and OB belong

to the same stroke at the trident node O, the

intermediate point P of AB is taken to connect AP,

BP and OP to form a new skeleton line.

(a)

(b)

Figure 5: Skeleton line adjustment in trident area. (a) Before

adjustment, (b) After adjustment.

4 EXPERIMENT AND ANALYSIS

4.1 Experimental Data and

Environment

Relying on the WJ-III map workstation developed by

China Institute of Surveying and Mapping, the

method of extracting the skeleton line of the areas

with dense junctions considering of stroke features

proposed in this paper is embedded, and a complex

water topographic map in Jiangsu with a scale of

1:10000 is taken as a case for reliability and

superiority verification. The experimental data space

range is 2.7×2.7 km2, the software system running

environment is Windows 7 64-bit operating system,

the CPU is Intel Core I7-3770, the main frequency is

3.2GHz, the memory is 16GB, and the solid state hard

disk is 1024GB.

4.2 Reliability and Superiority Analysis

In order to verify the reliability and superiority of

the proposed method, the method of this paper is

compared with the skeleton line extraction method of

Li et al. (2018). The overall situation of the

processing area using the method of this paper is

shown in Table 2.It can be seen from Table 2 that the

junctions is densely distributed, and about 85% of the

tridents meet the aggregation conditions.

4.2.1 Visual Cognition Analysis

The densely distributed areas of typical junctions in

the experimental area are as shown in Figure 6.

It can be seen from Figure 6 that for complex areas

with dense junctions, the method of Li et al. (2018) is

subject to severe interference of the complex

boundary and arrangement structure of the branch,

unable to process the skeleton line jitter of this area,

and the extracted skeleton line has a large degree of

distortion, thus losing the overall structure of this

region. In contrast, the method of this paper can better

extract the main structure of this region and more

accurately describe the skeleton line of the main

structure. For the backbone area with larger

connectivity within the rectangle A, the skeleton line

extracted in this method can also summarize its

extension characteristics well.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

198

(a)

(b)

(c)

Figure 6: Comparison in extraction results of skeleton lines

in complex areas with dense junctions. (a) Original skeleton

line, (b) Extraction results of Li (2018), (c) Extraction

results of this paper.

4.2.2 Network Function Analysis

The global efficiency commonly used in complex

network theory is used to evaluate the network function

of the results in this paper. The concept of dual graphs

is introduced, where the nodes represent the connecting

arcs between trident nodes, and the edges represent the

relationship between the connecting arc segments and

other connecting arc segments. It is formalized as

( , )G G V E

, where V is the set of nodes and E is

the set of edges. Then the “global efficiency” of the

network G is calculated as below:

)1(

ji,ji











，

)1(

ji,ji









G，

Where N is the total number of nodes,



is the

efficiency between node i and node j, and

is the

minimum number of steps required by connecting node

i and node j, i.e., the path length. The global efficiency

range is [0, 1]. Meanwhile, the number of stroke

connections formed by the arcs of the experimental

area is counted, as shown in Table 3.

It can be found from Table 3 that in terms of

global efficiency, the overall efficiency of the result in

this paper is improved by 0.023 compared with the

traditional method, which indicates that the method in

this paper improves the smoothness of information

dissemination in the network. Meanwhile, in the case

of same number of arcs, the number of strokes

constructed by the method in this paper is reduced by

72 compared with the traditional method, indicating

that the network stroke access is better.

5 CONCLUSIONS

Aiming at the problem that the traditional method

cannot accurately maintain the main structure and

extension characteristics of the areas with dense

junctions, a method of extracting the skeleton line of

the areas with dense junctions considering the stroke

feature is proposed in this paper. After verifying the

topographic map of the actual water system in a certain

area of Jiangsu, the main conclusions are shown as fol-

lows:

(1) Applicability: The method in this paper can

better distinguish the areas with dense junctions and

the areas with sparse junctions. For the identified 124

areas with dense junctions, the traditional method can

only process 58% of the tridents, but this method can

process all tridents.

Skeleton Line Extraction Method in the Areas with Dense Junctions Considering Stroke Features

199

Table 3: Comparison in global efficiency and number of stroke connections.

Method

Number of arc

segment

Stroke number

Global efficiency

Method of Li et al. (2018)

3617

1330

0.096

Method in this paper

3617

1258

0.119

(2) Superiority: Visual cognition analysis shows

that for the complex areas with dense junctions, the

skeleton line extracted by this method can better

display the regional main structure and extension

characteristics. The analysis of network function

indicates that the skeleton line extracted by this method

has better accessibility.

The stroke generation strategy has an important

influence on the accuracy of the skeleton line

extraction results by the method in this paper. The next

research focus is to further refine the arc importance

evaluation system and establish a more reasonable

stroke generation strategy, so as to make the skeleton

line extraction result more refined.

ACKNOWLEDGEMENTS

This research was funded by National Natural Science

Foundation of China under grant number 41871375.

REFERENCES

Ai T., Liu Y., 2002. Aggregation and Amalgamation in Land-

use Data Generalization. Geomatics and Information

Science of Wuhan University, 27(5): 486-492. (in

Chinese)

Ai T., Yang F., Li J.,2010. Land-use Data Generalization for

the Database Construction of the Second Land

Resource Survey. Geomatics and Information Science

of Wuhan University, (8): 887-891. (in Chinese)

Lee D. T., 1982. Medial Axis Transformation of a Planar

Shape. IEEE Transactions on pattern analysis and

machine intelligence, (4): 363-369.

Das, G.K., et al., 2010. Computing the straight skeleton of a

monotone polygon in O(nlogn) time. Proceedings of the

22nd Annual Canadian Conference on Computational

Geometry, Winnipeg, Manitoba, Canada; pp. 207–210.

Sintunata, V., and Aoki, T., 2016. Skeleton extraction in

cluttered image based on delaunay triangulation.

multimedia (ISM). 2016 IEEE International Symposium

on. IEEE, California, USA; pp.365–366.

Cao, T., Edelsbrunner, H., and Tan, T., 2015. Proof of

correctness of the digital Delaunay triangulation

algorithm. Computational Geometry: Theory and

Applications, 48.

Ware J. M., Jones C. B., Bundy G. L., 1997. A Triangulated

Spatial Model for Cartographic Generalization of Areal

Objects. In: Kraak M J, Molenaar M eds. Advance in

GIS Research II(the 7th Int. Symposium on Spatial Data

Handling). London: Taylor & Francis, 173-192.

Delucai A. A., Black R. T., 1987. A Comprehensice

Approach to Automatic Feature Generalization.

International Cartographic Conference.

Zou J. J., and Yan H., 2001. Skeletonization of ribbon-like

shapes based on regularity and singularity analyses.

IEEE Transactions on Systems, Man, and Cybernetics,

Part B (Cybernetics), 31(3), 401–407.

Li Z., 2006. Algorithmic foundation of multi-scale spatial

representation. Boca Raton, FA: CRC Press.

Penninga F., Verbree E., Quak W., et al., 2005. Construction

of the Planar Partition Postal Code Map Based on

Cadastral Registration. GeoInformatica, 9(2): 181-204.

Jones C. B., Bunday G. L., Ware M. J., 1995. Map

Generalization with a Triangulated Data Structure.

Cartography and Geographic Information Systems,

22(4): 317-331.

Uitermark H., Vogels A., Van Oosterom P., 1999. Semantic

and Geometric Aspects of Integrating Road Networks.

Interoperating Geographic Information Systems.

Springer, Berlin, Heidelberg, 177-188.

Haunert J. H., Sester M., 2008. Area Collapse and Road

Centerlines Based on Straight Skeletons.

GeoInformatica, 12(2): 169-191.

Li, C.; Yin, Y.; Wu, P.; Liu, X.; Guo, P., 2018. Improved

Jitter Elimination and Topology Correction Method for

the Split Line of Narrow and Long Patches. ISPRS Int. J.

Geo-Inf., 7, 402.

Diakoulaki D, Mavrotas G, Papayannakis L. 1995.

Determining objective weights in multiple criteria

problems: The critic method. Computers & Operations

Research, 22(7): 763-770.

GISTAM 2019 - 5th International Conference on Geographical Information Systems Theory, Applications and Management

200