
Manipulating Triadic Concept Analysis Contexts through Binary
Decision Diagrams
Kaio H. A. Ananias, Julio C. V. Neves, Pedro H. B. Ruas, Luis E. Z
´
arate and Mark A. J. Song
Pontifical Catholic University of Minas Gerais (PUC Minas),
Keywords:
Formal Concept Analisys,Triadic Concept Analisys, Binary Decision Diagram, TRIAS Algorithm.
Abstract:
Formal Concept Analysis (FCA) is an approach based on the mathematization and hierarchy of formal con-
cepts. Nowadays, with the increasing of social network for personal and professional usage, more and more
applications of data analysis on environments with high dimensionality (Big Data) have been discussed in
the literature. Through the Formal Concept Analysis and Triadic Concept Analysis, it is possible to extract
database knowledge in a hierarchical and systematized representation. It is common that the data set trans-
forms the extraction of this knowledge into a problem of high computational cost. Therefore, this paper has an
objective to evaluate the behavior of the algorithm for extraction triadic concepts using TRIAS in high dimen-
sional contexts. It was used a synthetic generator known as SCGaz (Synthetic Context Generator a-z). After
the analysis, it was proposed a representation of triadic contexts using a structure known as Binary Decision
Diagram (BDD).
1 INTRODUCTION
The discovery of valid, tacit, understandable and use-
ful information is the goal of several areas of knowl-
edge in Computer Science. The difficulty in reach-
ing this goal is aggravated as these bases become ever
larger. One of the challenges is the problem of find-
ing relationships and rules that describe the behavior
of the elements. For example, the growing popular-
ization of social networks and the volume of data pro-
duced by their users. This is an application that cre-
ates a demand for new techniques to extract knowl-
edge in order to make explicit the interactions be-
tween users and to define patterns that represent the
behavior of the network.
A possible solution to the problem is the use of
Formal Concept Analysis (FCA), which is a technique
based on the mathematization of the notion of con-
cepts and the structuring of concepts into a concep-
tual hierarchy. With the use of FCA it is possible to
analyze the data through associations and dependen-
cies of objects and attributes formally described from
a real or synthetic dataset (Wille, 1982) (Bernhard and
Rudolf, 1999). The representation of the knowledge
contained in the base is done through a description of
the objects, attributes and the relations of incidence
between them, known as a formal context. In this tra-
ditional approach, called dyadic, information is rep-
resented by a triple (G, M, I), where G is the set of
objects, M is the set of attributes and the binary inci-
dence relation between G and M.
However, in several situations it is necessary to
describe the condition that establishes the relation be-
tween the different objects and their attributes. An ex-
tension of the classical (dyadic) FCA, called Triadic
Concept Analysis (TCA) was proposed with the goal
of dealing with this problem (Lehmann and Wille,
1995). Although it is from the FCA, the triadic ap-
proach is more complex because it deals with three-
dimensional data. TCA is based on the triadic re-
lationship between objects, attributes and conditions
defined by the quadruple (K
1
, K
2
, K
3
, Y) where K
1
, K
2
and K
3
are respectively the sets of objects, attributes,
and conditions, and Y the ternary relation between
them.
As with the FCA, the triadic approach has to deal
with problems in which databases are of high dimen-
sionality. Although several algorithms have been pro-
posed in the literature in order to extract information
from triadic concepts, neither one directly attacks the
high dimensionality problem (Jaschke et al., 2006)
(Cerf et al., 2009) (Trabelsi et al., 2012).
Regarding this scenario, the main goals of this pa-
per is:
182
Ananias, K., Neves, J., Ruas, P., Zárate, L. and Song, M.
Manipulating Triadic Concept Analysis Contexts through Binary Decision Diagrams.
DOI: 10.5220/0007716101820189
In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 182-189
ISBN: 978-989-758-372-8
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

• Evaluate the behavior of the algorithm in a high
dimensional triadic bases (specifically TRIAS
(Jaschke et al., 2006));
• Propose modifications in the synthetic dyadic
contexts generator called SCGaz (Rimsa et al.,
2013) to be used in order to generate triadic con-
texts;
• Generate synthetic contexts that allow the analy-
sis of TRIAS algorithm behavior to extract triadic
concepts (main point is to understand the behav-
ior of this algorithm when processing high dimen-
sional databases);
• Represent triadic contexts using BDDs (Binary
Decision Diagram) in order to store and manipu-
late high-dimensional contexts efficiently (Akers,
1978). In this case, a set of boolean operations
was implemented to be able to retrieve objects, at-
tributes and conditions.
This paper is divided as following: the Section 2
presents the theoretical basis; Section 3 has the re-
lated works; Section 4 the proposed approach, tests
and analyzes are showed; and finally, in Section 5,
conclusions and future works.
2 BACKGROUND
2.1 Formal Concepts Analysis (FCA)
Developed by Rudolf Wille in the 1980s, Formal
Analysis of Concepts (FCA) is a branch of applied
mathematics based on concept mathematics and the
conceptual hierarchy (Wille, 1982) (Bernhard and
Rudolf, 1999). The formalization of the concepts
should be transparent and simple, but also compre-
hensive, so that the main aspects of a concept can
have their explicit references in the formal model
(Lehmann and Wille, 1995).
The dyadic approach is based on the primitive no-
tion of a formal context which is a triple (G, M, I),
where G is the set of objects, M the set of attributes
and i is the binary incidence relation between G and
M, indicating that a G object has a certain m attribute
of G of M. The Table 1 represents a dyadic context.
Formal concepts and rules of implication can be de-
fined from dyadic contexts.
Table 1: Dyadic context represented by a cross-table.
G/M m
1
m
2
m
3
g
1
× ×
g
2
× ×
g
3
×
A formal concept of a formal context (G, M, I) is
defined by a pair (A, B) which A ⊆ G, B ⊆ M. The pair
(A, B) that defines the concept follows the conditions
A = B’ and B = A’, defined by the derivation operator
(
0
): A’ = {g ∈ G | gIm ∀ m ∈ B} and B’ = {m ∈ M |
gIm ∀ g ∈ G} - the extent A contains each object of G
which has all the attributes of B, and the intent B con-
tains all attributes of M which belongs to all objects
of A.
Implications are dependencies between elements
of a set obtained from a formal context. For example,
given the context (G, M, I) the implication rules are
of the form B → C, if and only if, B, C ⊆ M and B’
⊆ C’. An implication rule B → C is considered valid
if and only if, every object that has the attributes of B
also have the attributes of C.
2.2 Triadic Concept Analysis (TCA)
The TCA was introduced by Lehmann and Wille
(Lehmann and Wille, 1995), extends the classic FCA,
but a new dimension was added. The primitive notion
of a triadic formal context is defined by a quadruple
(K
1
, K
2
, K
3
, Y) where K
1
, K
2
and K
3
are sets and Y
the ternary relation between K
1
, K
2
and K
3
. The el-
ements of K
1
, K
2
and K
3
are known as objects, at-
tributes and conditions respectively and (o
1
, a
2
, c
3
) ∈
Y is interpreted as the object o
1
that has the attribute
a
2
under the condition c
3
(Lehmann and Wille, 1995)
(Wille, 1995). The Table 2 presents a triadic context
where the incidences are represented through the rela-
tion between the objects o
i
, attributes a
i
and concepts
c
i
of the context, assigned or not, marked by a ×.
Table 2: Triadic context represented by a cross-table.
K
1
/K
2
-K
3
c
1
c
2
c
3
a
1
a
2
a
3
a
1
a
2
a
3
a
1
a
2
a
3
o
1
× × × ×
o
2
× × × ×
o
3
× × ×
Although it comes from the FCA, the triadic ap-
proach has concept definitions, implication rules and
derivation much more complex than the dyadic ap-
proach. It’s due to the third dimension that was added,
which includes, for example, quality metrics (trust
and support) to the formally defined implication rules.
A formal triadic concept is defined by a triple
(A, B, C), where A ⊆ K
1
, B ⊆ K
2
and C ⊆ K
3
and
A × B × C ⊆ Y. The set A, B, C are called objects, at-
tributes and mode respectively (Lehmann and Wille,
1995). The set of all the concepts of a partially or-
dered triadic context form a complete lattice called
conceptual lattice (Missaoui and Kwuida, 2011).
Manipulating Triadic Concept Analysis Contexts through Binary Decision Diagrams
183
2.3 Synthetic Generator SCGaz
Using a synthetic database for generating formal con-
texts becomes interesting due to the complexity of
the databases obtained from real scenarios. Real
databases usually require preprocessing, a task that
can, if not done correctly, directly interfere in the re-
sults. Considering that, using tools for database sim-
ulation becomes interesting and extremely useful in
comparative analyzes between algorithms, as realized
in (de Moraes et al., 2016) (Santos et al., 2018).
The SCGaz tool proposed in (Rimsa et al., 2013)
is a random synthetic generator of dyadic formal con-
texts with density control. Through SCGaz it is pos-
sible to specify the amount of objects and attributes
desired in a formal context, as well as density, to gen-
erate irreducible contexts. Density values for a given
context vary according to their dimensions and/or can
be specified in advance. The generated context is ir-
reducible, that is, there are no attributes that are not
shared by at least one object or attributes that are
shared by all objects. The same occurs with objects
that do not have any attributes or objects that share
all the attributes of the context. Objects that share the
same attributes, in FCA, are considered redundant and
therefore are not inserted into the context.
2.4 TRIAS Algorithm
The authors in (Jaschke et al., 2006) define the prob-
lem of mining all the most frequent triadic concepts
of a formal context and proposes a solution called
TRIAS, based on dyadic projections to resolve the
problem. The authors adapt the dyadic notion of min-
ing all item sets of a formal dyadic context, defined in
(Pei et al., 2000) for a triadic approach.
Given K = (U, T, R, Y) a triadic context, the prob-
lem of extracting all the common triadic concepts
from a context is to determine all triples (A, B, C)
of the context K such as
|
A
|
|
U
|
≥ u-minsup,
|
B
|
|
T
|
≥
t-minsup and
|
C
|
|
R
|
≥ r-minsup. TRIAS algorithm first
constructs a dyadic context L = (U, T × R, Y
1
) where
its columns correspond to pairs of elements that be-
longs to T and R and via projection, it extracts all the
formal concepts. The second step consists of, for each
formal concept, check if they are closed in relation to
U. The main feature of the algorithm is to explore the
subsets of newly computed triadic concepts to see if
these are new concepts.
2.5 Binary Decision Diagram
Introduced by (Akers, 1978) and further developed by
(Bryant, 1986), binary decision diagrams (BDD) pro-
vide a canonical representation for much more com-
pact boolean formulas than normal conjunctive and
disjunctive forms. Additional to that, it is more effi-
cient to handling data.
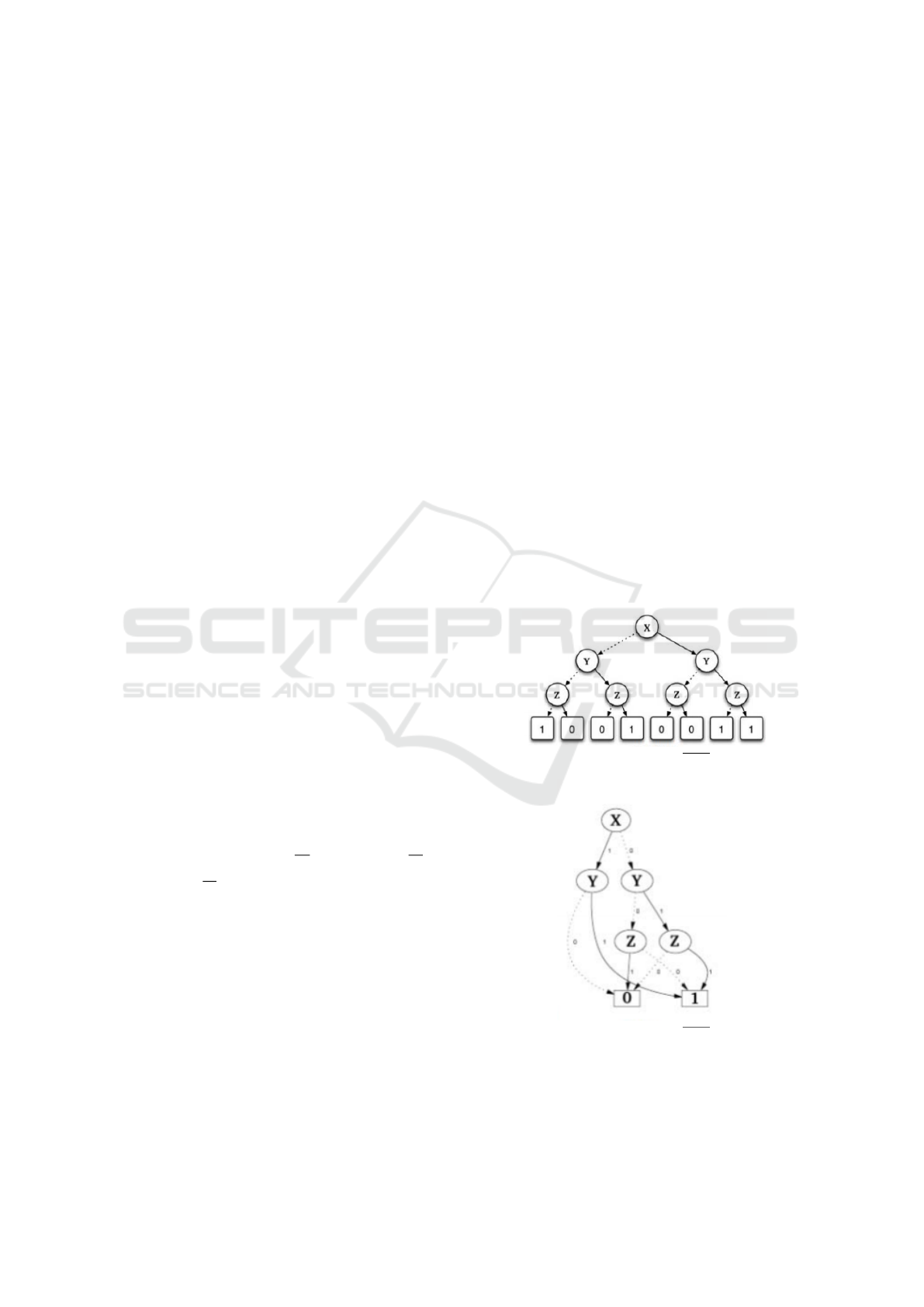
It is possible to get a BDD from a binary deci-
sion tree (Figure 1) which the dotted strokes represent
zero transitions. In other words, the value 1 and the
solid strokes represent positive transitions with value
1. The main idea of decision binary diagrams is to
merge sub-trees of the binary decision tree and elimi-
nate identical (redundant) nodes resulting in a canon-
ical representation. The result of the optimizations
gives us an acyclic directed graph, as represented in
Figure 2, where the dotted transitions represent a null
transition. Note that the node affected by the edge has
a null value and the nodes bound by edges in bold
have a positive value.
A BDD is a directed acyclic graph with two types
of nodes: terminals and non-terminals. Non-terminal
nodes represent the variables of the boolean formula
and the only two terminal nodes represent the values
0 or 1 when the function assumes true or false value.
Even as in the representation of the decision tree, the
dotted and continuous transitions represent false and
positive transitions, respectively.
Figure 1: F(X, Y, Z) = XY + Y Z + XY Z represented by a
decision tree.
Figure 2: F(X, Y, Z) = XY + Y Z + XY Z represented by a
binary decision diagram.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
184

3 RELATED WORK
Several papers used BDDs with different goals. In
(Salleb et al., 2002) the BDDs were used to store
transaction logs as a truth table and to find common
patterns in large transactional data sets. The use of
BDDs allowed authors to load all transactions into the
main memory, avoiding database processing on disk.
In (Neto et al., 2018) the authors used the bi-
nary decision diagram to deal with high dimensional
dyadic contexts in order to extract formal dyadic con-
cepts. The authors proposed modifications in the
NextClosure algorithm and In-Close2 through BDD
to manipulate objects in a dyadic context.
For the tests, they used the NextClosure algorithm
and dyadic contexts with 50,000 objects and 25 at-
tributes, generated through the SCGaz tool. They ob-
tained significant gains using BDD, taken results up to
4 times better than the original implementation. In ad-
dition, the use of diagrams allowed authors to explore
contexts with greater dimensionality, such as 50,000
objects, 20 attributes and 70% density.
The authors also explored the In-Close2 algorithm
with BDD. Once again, the approach proved to be ef-
ficient in many cases. They obtained speedup of up to
2 in contexts with 500,000 objects and maximum den-
sity. In several situations the approach with BDD was
able to generate concepts while the original algorithm
stopped the execution due to memory overflow.
In (Santos et al., 2018) the authors proposed mod-
ifications in the algorithm of extraction of dyadic im-
plications PropIm, using BDDs as the data structure
in order to manipulate and extract proper rules from
dyadic contexts. The ImplicPBDD algorithm pre-
sented significantly better run time. The tests varied
the number of objects, attributes and their density.
The results showed that the version using BDD
has a better performance − up to 80% faster − than
its original algorithm, regardless of the number of at-
tributes, objects and densities. The authors were also
able to explore contexts with higher dimensionality
than the original algorithm was able to process, ex-
panding the horizon of applications.
4 THE APPROACH, TESTS AND
ANALYZES
This paper aimed to analyze the behavior of the
TRIAS algorithm in high dimensional triadic contexts
that was generated from a synthetic tool (SCGaz). It
was also proposed a representation of triadic contexts
using BDDs. This approach can be used in future
work as the main structure of the triadic algorithms
such as TRIAS, as explained in previous sections.
Modifications in the dyadic synthetic contexts
generator SCGaz were performed in order to gener-
ate triadic contexts by adding a third dimension, not
computed by the tool. The rules of reducibility de-
fined in (Rimsa et al., 2013) were maintained for the
triadic contexts. A third dimension chosen by the user
is added and the objects of the dyadic context are then
replicated to the triadic context subject to the previ-
ously defined conditions.
From the previous modifications, evaluations on
the behavior of the TRIAS algorithm were per-
formed using the contexts previously generated by the
SCGaz. Average execution time, number of concepts
found, dimensions and density were evaluated in the
initial tests of this paper in order to find the limits of
the algorithm. Through projections of the triadic con-
text in dyadic, boolean functions are generated from
the context and then the BDD was built.
4.1 Triadic Contexts using SCGaz
The synthetic generator SCGaz proposed in (Rimsa
et al., 2013) provides a dyadic approach to generating
random contexts. However, the triadic TCA approach
has a third dimension commonly called conditions.
This dimension provides a greater characterization of
the objects, since they are now related to a given at-
tribute under a condition.
In this paper, the tool SCGaz was extended by
adding dimension of conditions in the generated con-
texts. The amount of conditions is set by the user.
Given an irreducible formal context (G, M, I), gen-
erated through of the SCGaz, a dyadic incidence is
defined by gIm ⊆ I, where g ∈ G and m ∈ M. A tri-
adic context (K
1
, K
2
, K
3
, Y) is generated in K
1
= G
and each attribute a
i
∈ K
2
is defined by the Equation
(1). Therefore, the attributes of the new context are
given by the modular relation between the attributes
of the dyadic context and the size of the third dimen-
sion defined by the user.
a
i
= m
i
mod |K
3
| (1)
Given an incidence gIm ∈ I, where g ∈ G and m ∈ M,
from a irreducible formal context (G, M, I), obtained
from the SCGaz, a triadic context (K
1
, K
2
, K
3
, Y) is
generated, and the rule that adds the incidence gIm
linked to the condition c
i
is defined by the ratio of
the original context attribute and the size of the third
dimension that was defined by the user. The Equation
(2) represents the obtaining of the conditions of the
triadic context.
c
i
=
m
i
|K
3
|
(2)
Manipulating Triadic Concept Analysis Contexts through Binary Decision Diagrams
185

4.2 TRIAS Algorithm Evaluation
From the random synthetic generator SCGaz, several
contexts were generated in order to evaluate the be-
havior of the TRIAS triadic concept extraction algo-
rithm. Synthetic triadic contexts with arbitrary num-
ber of dimensions and density were generated in order
to understand the behavior of the algorithm.
Initially, the number of attributes and conditions
were fixed, maximizing the number of objects in order
to obtain a greater number of incidents. Contexts with
500, 1.500, 3.000, 5.000 and 10.000 objects were gen-
erated with 15 attributes and 5 conditions. The den-
sity was set at 30 % for all contexts because the main
objective was to understand the boundary dimensions
for the TRIAS algorithm (the amount of attributes,
objects and conditions supported).
The tests were run on an Intel Core i7-4790
3.60GHz with 4 cores, 8 threads, 32Gb RAM and an
Ubuntu 14.04 LTS operating system. Table 3 presents
the results initially considering contexts with reduced
dimensions according to (Old and Priss, 2006). It is
possible to notice that even with a reduced number of
objects, attributes and conditions, the algorithm took
approximately 40 minutes to compute all the concepts
of the first synthetic context. Note that the test with
10,000 objects, 15 attributes and 5 conditions required
a time greater than 7 days and was not properly com-
puted.
Table 3: TRIAS Algorithm Results for Minor Contexts.
Context
(Objects X Attributes X Conditions
Incidences
TRIAS
(Minutes)
500 x 15 x 5 13,500 42.68
1,500 x 15 x 5 33,750 212.4
3,000 x 15 x 5 67,500 376.2
5,000 x 15 x 5 112,500 768.8
10,000 x 15 x 5 225,000 -
It is interesting note that the high dimensionality
characteristics in triadic applications may differ from
the same dyadic ones investigated. In 2006, the In-
ternational Conference on Formal Concept Analysis
(ICFCA) at Desdren (Old and Priss, 2006) discussed
the main challenges of formal analysis, including the
need to deal with dense and high dimensional formal
contexts, 120,000 objects and 70,000 attributes, these
are considerably larger than the tests observed here.
New tests were performed, with contexts char-
acterized by high dimensionality. Table 4 presents
the results obtained with contexts of 120,000 objects,
varying attributes and conditions respectively. It is
possible to note that in none of the cases of high di-
mensionality was possible to reach the end of the ex-
ecution of the algorithm, keeping it running for more
than 7 days and no conclusion was taken.
The results obtained in the implementation of
TRIAS showed the high computational cost of the
extraction of knowledge from triadic contexts. The
impossibility of using TCA with high-dimensional
databases is notorious. This fact certainly demands
more investigation and new proposals to make feasi-
ble the use of TCA algorithms in this context.
Table 4: TRIAS Algorithm Results for High-dimensional
Contexts.
Context
(Objects X Attributes X Conditions
Incidences
TRIAS
(Days)
120,000 x 15 x 5 2,999,984 >7
120,000 x 10 x 5 1,776,769 >7
120,000 x 5 x 10 1,776,769 >7
4.3 TRIAS Algorithm Results for Real
Datasets Contexts
The use of synthetic databases is a great help in test-
ing algorithms and knowledge extraction tools. How-
ever, understand the behavior of the algorithm in real
scenarios is extremely important to understand its ef-
ficiency.
Considering that, we applied the algorithm to an
extensive database of movie ratings called Movie-
Lens
1
. The database consists of ratings of more
than 6,000 anonymous users in approximately 4,000
movies. In the more than 1 million records, users
rate movies with 1 to 5 ratings. This base is con-
sidered sparse, meaning despite the huge number of
ratings, there is no guarantee that users rated the same
movies, consequently generating sparse triadic con-
texts regarding the number of incidents.
The contexts generated from the database have as
a set of objects the users who have made classifica-
tions, the attributes of the context are the classified
movies and the conditions are the notes received. So,
our triadic context can be defined as K = (U, T, R, Y)
where U are the set of users in the dataset, T are set
of movies, R the set of evaluations given by users and
Y are the relation between users and movies and their
respective evaluations.
Figure 3 represents one example of a triadic con-
cept extract from the dataset movie. Note that in first
concept users 646, 1015 rated the same movie with
the same note.
Table 5 shows the results of the algorithm applied
to contexts generated from the real dataset Movie-
Lens. It was decided to fix the number of objects
1
https://grouplens.org
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
186

Figure 3: Example of triconcepts from MovieLens Dataset.
(users), using the maximum number of objects avail-
able in the dataset, and vary the amount of attributes
(movies) of the context.
Table 5: TRIAS Algorithm results for MovieLens dataset.
Context
(Objects X Attributes X Conditions
Incidences
TRIAS
(Days)
6,000 x 100 x 5 105,986 >7
6,000 x 150 x 5 158,029 >7
6,000 x 200 x 5 203,898 >7
As opposed to synthetic contexts, where we have
control of the dimensions and density of the context,
as shown in Section 4.1, in real databases we can not
guarantee that. In the context generated, it can not
be determined that a movie has been classified by all
users of the context, making it extremely sparse. In
order to increase the number of incidents, we vary the
number of attributes so that even in sparse contexts,
these can express the behavior of the algorithm.
As said before, the dataset contains 4,000 movies
that was classified by the 6,000 users. In number of
incidences, this dataset has high dimensional and a
fully context generated from that will have 1 million
of incidences.
In tests performed with synthetic data presented in
Table 4, TRIAS algorithms showed to be inefficient
for contexts with this number of incidences. Even for
a reduced set of the original data, like as shown in
Table 5, the algorithm showed to be inefficient and
time prohibitive for use in large real scenarios.
Notice that in each test for the Table 5 the al-
gorithm did not finish the computation of all formal
concepts, running for more than seven days with-
out conclusion. The biggest formal context generate
from MovieLens (6.000x200x5) has approximately
only 20% of the full database, reinforcing that the tri-
adic approach using the algorithm TRIAS is not effi-
cient, even in small subsets of real data.
4.4 Triadic Contexts using BDD
Some FCA applications use BDD as main struc-
tures for efficient storage and manipulation of objects
(Salleb et al., 2002) (Neto et al., 2018) (Santos et al.,
2018). However, there are few triadic approaches that
use the efficiency provided by binary decision dia-
grams. Therefore, this paper proposed a triadic rep-
resentation of contexts using BDDs, through dyadic
projections.
Given a formal triadic context (K
1
, K
2
, K
3
, Y)
where K
1
, K
2
and K
3
are called objects, attributes and
condition respectively and Y the ternary relation be-
tween K
1
, K
2
and K
3
, a projection can be performed
in the triadic context (Table 6) resulting in a dyadic
context (K
1
, K
2
× K
3
, Y) (Table 7).
Table 6: Triadic Context (K
1
, K
2
, K
3
, Y).
K
1
/K
2
-K
3
c
1
c
2
c
3
a
1
a
2
a
1
a
2
a
1
a
2
o
1
× × ×
o
1
× × ×
o
3
× × × ×
The projection results from the combination of at-
tributes and conditions where each attribute is re-
named according to the condition to which it belongs.
The retrieval and manipulation of attributes and con-
ditions can be done from the label assigned to each
attribute. In the context represented by Table 7 the
dyadic incidence given by the tuple (o1, a1c1) is
equivalent to the triadic incidence given by the triple
(o1, a1, c1) of the context presented in Table 6.
Table 7: Dyadic Context Projection (K
1
, K
2
× K
3
, Y).
K
1
/K
2
×K
3
a
1
c
1
a
2
c
1
a
1
c
2
a
2
c
2
a
1
c
3
a
2
c
3
o
1
× × ×
o
2
× × ×
o
3
× × × ×
Once projected, the triadic context, now described by
a dyadic context, can be represented by a binary deci-
sion diagram converting the context to a boolean for-
mula used to generate the corresponding BDD. Table
7 describes the triadic context projected in a dyadic
context and Equation 3 represents it through conjunc-
tive and disjunctive operations between objects and
attributes. The symbols accented by a slash represent
the negation of the attribute.
f (a
1
c
1
, a
2
c
1
, a
1
c
2
, a
2
c
2
, a
1
c
3
, a
2
c
3
) = (a
1
c
1
· ¯a
2
c
1
· ¯a
1
c
2
· a
2
c
2
· a
1
c
3
·)
( ¯a
2
c
3
+ a
1
c
1
· ¯a
2
c
1
· ¯a
1
c
2
· a
2
c
2
· a
1
c
3
· ¯a
2
c
3
) + (a
1
c
1
· ¯a
2
c
1
· ¯a
1
c
2
· a
2
c
2
· a
1
c
3
· ¯a
2
c
3
)
(3)
Manipulating Triadic Concept Analysis Contexts through Binary Decision Diagrams
187
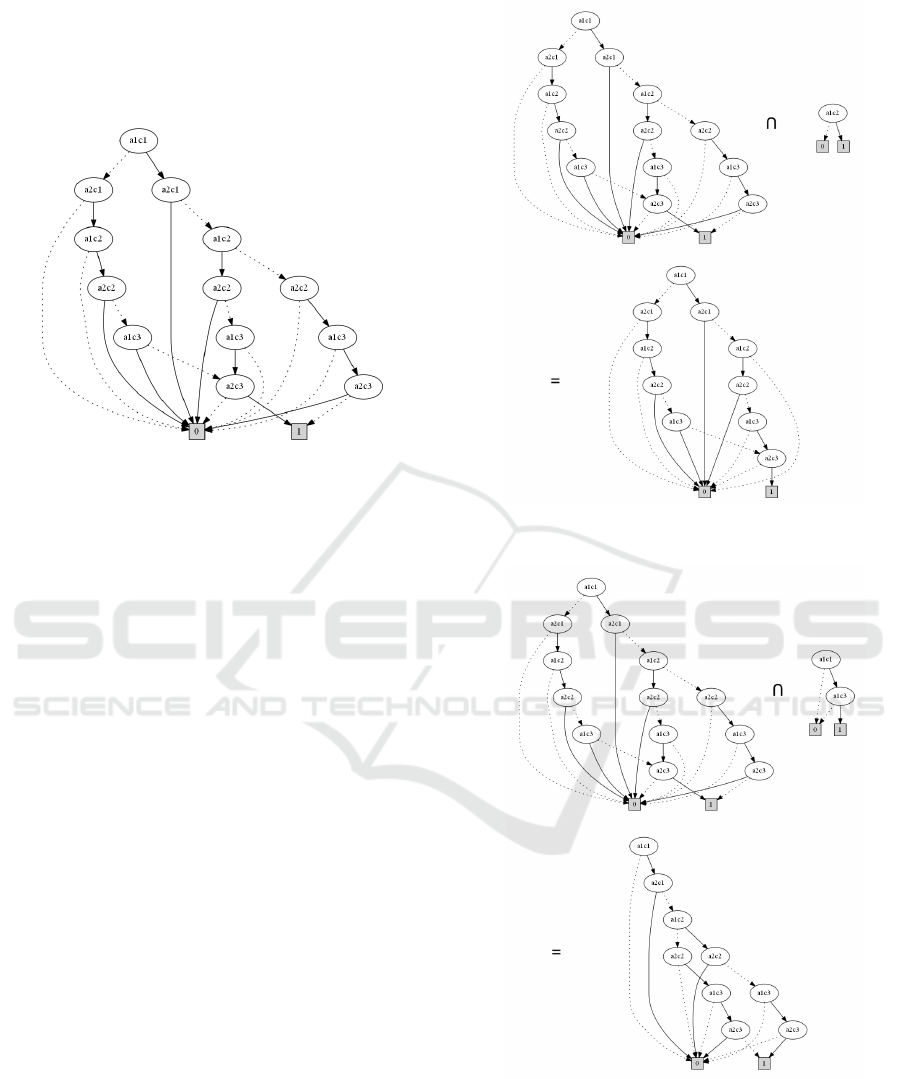
Figure 4 represents the dyadic projection of the tri-
adic context defined above. This approach allows ma-
nipulating triadic contexts using a BDD, providing ef-
ficient manipulation and storage.
Figure 4: Context (K
1
, K
2
× K
3
, Y) represented by a BDD.
Given a triadic context projected and represented
by a BDD, it is interesting to provide techniques for
recovering objects, attributes and conditions, since
any application that uses this representation will need
features that allow the recovery and efficient alter-
ation of these elements.
Consider the context presented in the Table 6, re-
trieval of objects can be done, for example, from log-
ical operations AND or OR under Equation 3 of the
context. If it is necessary to obtain all the objects of
the context represented in Table 7 that have the at-
tribute a
1
c
2
, it can create a BDD object that represents
such an attribute and apply a logical operation AND
between the BDDs. Figure 5 represents such an oper-
ation, returning in a new BDD with the objects o
2
and
o
3
since both share the attribute a
1
c
2
.
In some situations, if it is necessary to retrieve all
the objects they have, for example, the attributes a
1
c
1
and a
1
c
3
of the context presented in Table 7, a BDD
with both attributes must be created and the logical
AND operation between this new BDD with the con-
text BDD must be performed. This returns only the
objects that is required. Figure 6 illustrates such an
operation.
5 CONCLUSION AND FUTURE
WORKS
The task of extracting triadic concepts from a triadic
context is more complex than in the classic approach
of FCA. The representation of the data in three di-
Figure 5: Logical operation between the attribute a
1
c
2
and
the BDD Context.
Figure 6: Logical operation between the attribute a
1
c
1
and
a
1
c
3
and the BDD Context.
mensions leads to the greater dimensionality of the
databases. Considering that and with the growth of
the contexts, techniques like the TRIAS algorithm be-
come inefficient to extract information, as presented
in this paper.
ICEIS 2019 - 21st International Conference on Enterprise Information Systems
188

In order to improve the performance of these algo-
rithms, the representation of contexts through struc-
tures such as BDD has showed to be an interesting
and efficient alternative in information retrieval.
The paper presented a number of challenges, such
as generating triadic contexts through a synthetic gen-
erator of dyadic contexts. In addition, contexts must
respect the formal triadic definition that all conditions
have the same amount of attributes.
Through this study, it is noticed that the problem
of high dimensionality in triadic contexts already hap-
pens with a reduced number of objects, attributes (and
conditions) when compared to the dyadic approach.
The tests performed showed that the TRIAS algo-
rithm, for example, can not handle dimensions char-
acterized as dyadic high dimensionality and showed
to be inefficient when used with larger context for the
triadic approach.
The retrieval of objects, attributes and conditions
showed to be efficient since operations are performed
under contexts and variables represented as BDDs.
Unlike conventional structures such as lists, queues,
and stacks, where computational complexity is re-
quired, BDDs provide attribute extraction through
unique logical operations that reduce the retrieval
time of elements in a context.
As a future work, we intend to implement a BDD
version of the TRIAS algorithm. The objective is to
reduce the time of the queries performed in order to
classify the subset of newly discovered concepts and
consequently increase the extractive power of more
frequent triadic concepts in a triadic context. It is
also expected to reduce execution time since the re-
sults presented in Table 4 proved to be infeasible.
REFERENCES
Akers, S. B. (1978). Binary decision diagrams. IEEE
Transactions on Computers, C-27(6):509–516.
Bernhard, G. and Rudolf, W. (1999). Formal concept anal-
ysis: mathematical foundations.
Bryant, R. E. (1986). Graph-based algorithms for boolean
function manipulation. Computers, IEEE Transac-
tions on, 100(8):677–691.
Cerf, L., Besson, J., Robardet, C., and Boulicaut, J.-F.
(2009). Closed patterns meet n-ary relations. ACM
Transactions on Knowledge Discovery from Data
(TKDD), 3(1):3.
de Moraes, N. R., Dias, S. M., Freitas, H. C., and Zarate,
L. E. (2016). Parallelization of the next closure algo-
rithm for generating the minimum set of implication
rules. Artificial Intelligence Research, 5(2):40.
Jaschke, R., Hotho, A., Schmitz, C., Ganter, B., and
Stumme, G. (2006). Trias–an algorithm for mining
iceberg tri-lattices. In Data Mining, 2006. ICDM’06.
Sixth International Conference on, pages 907–911.
IEEE.
Lehmann, F. and Wille, R. (1995). A triadic approach to
formal concept analysis. Conceptual structures: ap-
plications, implementation and theory, pages 32–43.
Missaoui, R. and Kwuida, L. (2011). Mining triadic asso-
ciation rules from ternary relations. Formal Concept
Analysis, pages 204–218.
Neto, S. M., Z
´
arate, L. E., and Song, M. A. (2018). Han-
dling high dimensionality contexts in formal concept
analysis via binary decision diagrams. Information
Sciences, 429:361–376.
Old, J. and Priss, U. (2006). Some open problems in formal
concept analysis. problems presented at international
conference on formal concept analysis (icfca).
Pei, J., Han, J., Mao, R., et al. (2000). Closet: An effi-
cient algorithm for mining frequent closed itemsets. In
ACM SIGMOD workshop on research issues in data
mining and knowledge discovery, volume 4, pages
21–30.
Rimsa, A., Song, M. A., and Z
´
arate, L. E. (2013). Scgaz-a
synthetic formal context generator with density con-
trol for test and evaluation of fca algorithms. In Sys-
tems, Man, and Cybernetics (SMC), 2013 IEEE Inter-
national Conference on, pages 3464–3470. IEEE.
Salleb, A., Maazouzi, Z., and Vrain, C. (2002). Mining
maximal frequent itemsets by a boolean based ap-
proach. In European Conf. on Artificial Intelligence,
Lyon France (July 2002), pages 285–289.
Santos, P., Ruas, P. H., Neves, J., Silva, P., Dias, S. M.,
Z
´
arate, L., and Song, M. (2018). ImplicPBDD: A New
Approach to Extract Proper Implications Set from
High-Dimension Formal Contexts Using a Binary De-
cision Diagram. Journal of Information, 9(11).
Trabelsi, C., Jelassi, N., and Yahia, S. B. (2012). Scalable
mining of frequent tri-concepts from folksonomies.
In Pacific-Asia Conference on Knowledge Discovery
and Data Mining, pages 231–242. Springer.
Wille, R. (1982). Restructuring lattice theory: an approach
based on hierarchies of concepts. In Ordered sets,
pages 445–470. Springer.
Wille, R. (1995). The basic theorem of triadic concept anal-
ysis. Order, 12(2):149–158.
Manipulating Triadic Concept Analysis Contexts through Binary Decision Diagrams
189
