Training and Validation Methodology for Range Estimation Algorithms

Patrick Petersen

, Adam Thor Thorgeirsson

2,3

, Stefan Scheubner

, Stefan Otten

, Frank Gauterin

and Eric Sax

FZI Research Center for Information Technology, Haid-und-Neu-Straße 10-14, 76131 Karlsruhe, Germany

Dr. Ing. h.c. F. Porsche AG, Porschestraße 911, 71287 Weissach, Germany

Institute of Vehicle System Technology, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany

Keywords:

Automotive Systems Engineering, Veriﬁcation and Validation, Testing, Range Estimation, Battery Electric

Vehicles.

Abstract:

Estimating the range of battery electric vehicles is one of the most challenging topics for the current trend

in the automotive industry, the electriﬁcation of vehicles. Range anxiety still limits the adoption of battery

electric vehicles. Since the range estimation is dependent on different inﬂuencing factors, complex algorithms

to accurately estimate the vehicles consumption are required. To evaluate the accuracy of data-driven machine

learning algorithms, an exhaustive training and validation procedure is mandatory. In this paper, we propose

a novel methodology for the development and validation of range estimation algorithms based on machine

learning validation approaches. The proposed methodology considers the evaluation of driver-speciﬁc and

driver-unspeciﬁc performance. In addition, an error measure is introduced to assess the performance of range

estimation algorithms. This approach is demonstrated and evaluated on a set of recorded real-world driving

data. It is shown that our approach helps to analyze the performance of the range estimation algorithm and the

inﬂuences of different parameter sets.

1 INTRODUCTION

Range prediction for battery electric vehicles (BEVs)

has, in recent years, been intensively researched. As

range is one of the key factors of customer satis-

faction. The route-based range is principally depen-

dent on the energy stored in the battery and the en-

ergy required to reach a destination following a given

route. Predicting the energy required for a certain

route is not trivial. The driving range is dependent

on different factors, some of which can be easily

modeled with physical relations. Other factors, such

as the inﬂuences of driver and trafﬁc behavior, are

non-deterministic. Both of these heavily inﬂuence

the driving speed, which is one of the most impor-

tant inﬂuencing factors on the vehicle’s consumption

(Wu et al., 2015; Wager et al., 2016). By apply-

ing machine learning (ML) algorithms, these non-

deterministic factors can be included in the range es-

timation.

A lot of the research about range estimation mod-

els focuses on including as many input parameters as

possible, such as the inﬂuences of trafﬁc (Grubwin-

kler et al., 2014), route (Yu et al., 2012), weather

(Fetene et al., 2017), driving style (Bingham et al.,

2012a), auxiliary consumers (Horrein et al., 2017)

and vehicle characteristics (Tannahill et al., 2016). To

validate and verify the model and evaluate its accu-

racy, the feature space should be covered sufﬁciently.

With most ML algorithms, the size of the training

data set correlates with the number of features, i.e.

if the feature space is large, a large training data set is

needed (Lewis, 1992). For non-ML models, the vali-

dation is still of great importance and having a realis-

tic and representative test set is required. Additionally

a suitable error measure needs to be chosen or formu-

lated.

As a result, the validation becomes complex and

time-consuming, especially when performed with real

test drives. In this paper, a virtual framework for val-

idation and performance evaluation is presented. The

approach is based on real-world driving data to ensure

coverage and realism. This allows a scalable approach

without highly-sophisticated simulation models.

This paper is structured as follows: in Section 2,

the state of the art in Automotive Systems Engineer-

ing (ASE) and validation approaches for ML algo-

rithms are presented. In addition, open challenges

434

Petersen, P., Thorgeirsson, A., Scheubner, S., Otten, S., Gauterin, F. and Sax, E.

Training and Validation Methodology for Range Estimation Algorithms.

DOI: 10.5220/0007717004340443

In Proceedings of the 5th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2019), pages 434-443

ISBN: 978-989-758-374-2

for the validation of range estimation algorithms are

identiﬁed. In Section 3, our proposed validation con-

cept for range estimation algorithms is described and

its prototypical implementation will be discussed. In

Section 4, the approach is demonstrated based on a

small test campaign. Section 5 concludes this paper

and discusses future work based on the results of this

paper.

2 STATE OF THE ART

Due to the increasing complexity of Advanced Driver

Assistant Systems (ADAS), the need for exhaus-

tive test coverage increases (Mazzega et al., 2016).

ISO29119-1 postulates that dynamic testing is essen-

tial for the validation of correct functional behavior

(ISO, 2013). Boehm described a software program as

a mapping from a space of inputs into a space of out-

puts (Boehm, 1976) meaning that covering the com-

plete input space ensures the quality of a system. For

complex and non-deterministic systems like range es-

timation algorithms, covering the complete parameter

space is not feasible for automated test case genera-

tion. Therefore, another approach is to use real-world

data for the evaluation of such systems e.g. in the

domain of computer vision, recorded video data is

a common method to solve this issue (Cordts et al.,

2016).

In the automotive ﬁeld, features are primarily

tested in the real-world with the help of prototype

vehicles. This ensures the highest possible realism

for testing features in the veriﬁcation and validation

(V&V) process but fails to scale, since these few se-

lected test drives are primarily tailored for manual in-

depth debugging (Sax, 2008).

(Bach et al., 2017b) and (Langner et al., 2017)

propose a data-driven development approach that sug-

gests utilizing the steadily growing pool of recorded

real-world driving data for the development of fea-

tures and executing them in a Software-in-the-loop

(SiL) environment. (Bach et al., 2015) introduces the

Reactive-Replay approach, which enables the execu-

tion of a closed-loop feature on system level by uti-

lizing recorded real-world driving data. Thus, feature

maturity can be ensured in early development stages.

Previous recorded data can now be reused for devel-

opment and enables continuous tracking of software

maturity without the need for running new test drives

(Bach et al., 2017a). Reducing redundancy and sim-

ulation time can be achieved by carefully selecting

test cases without loosing test coverage (Bach et al.,

2017c).

For testing range estimation algorithms, real-

world test drives are primarily used for validation

(Rolim et al., 2012), (Tannahill et al., 2016). Statis-

tically signiﬁcant evaluation is achieved by collecting

thousands of kilometers of real-world test drives. Var-

ious situations and scenarios need to be considered,

such as different trafﬁc situations or weather condi-

tions, to achieve a sufﬁcient test coverage. This ap-

proach lacks scalability due to the fact that for each

new soft- ware version new data must be recorded.

However, using simulations can be executed as often

as needed (Yi and Bauer, 2017), (Enthaler and Gau-

terin, 2016). For creating realistic simulations, non-

deterministic factors, such as environmental, trafﬁc

and driver behavior, need to be considered, requiring

complex models (Helmer et al., 2015). Due to the fact

that a lot of effort needs to be invested to create such

models, a hybrid of simulation and real-world data is

preferred. This hybrid allows the beneﬁts of the real-

ism of real-world data to be reused for the simulation

based execution of future software versions.

Although selecting the best data for the validation

of range estimation algorithms is still a challenge, the

methodology for an accurate training and validation

process is a major challenge as well.

It is necessary that data-driven range estimation

algorithms adapt to driving characteristics of an indi-

vidual or changing drivers to further improve the es-

timation of the energy consumption and range (Bing-

ham et al., 2012b). Therefore, for the validation of

such algorithms it is important to assess the driver-

speciﬁc and driver-unspeciﬁc performance. A driver-

speciﬁc performance indicates whether the algorithm

adapts and optimizes its energy consumption estima-

tions of one consistent driver. A driver-unspeciﬁc per-

formance indicates whether the algorithm is capable

of adapting to different drivers in an appropriate pe-

riod of time. To validate ML algorithms, data samples

must be split into a set of training data D and a set of

test data T . The classiﬁers are then trained on D and

the accuracy measured by testing on T . By testing on

unseen data, an assessment of how the algorithm will

perform in practice is achieved. In (Mitchell, 2012),

several methods are suggested:

• Resubstitution

• Holdout

• Leave-one-out

• K-Fold Cross-Validation

Resubstitution uses the whole data set for both train-

ing and testing and will result in an optimistic biased

accuracy estimation. Holdout uses half of the data for

training and the other half for testing. The estima-

tion will be pessimistic biased. Leave-one-out uses

all but one data samples for training the classiﬁer and

Training and Validation Methodology for Range Estimation Algorithms

435

the last data sample for the test. The estimate is unbi-

ased but with large variance. K-fold cross validation

is the middle road between holdout and leave-one-out

as the number of splits is somewhere between 1 and

N with N being the number of samples.

(Bolovinou et al., 2014) uses a 10-fold cross-

validation to evaluate the performance of the initial

range prediction (in km) using support vector regres-

sion (SVR), linear regression (LR) and a conven-

tional, history-based range estimation. Mean absolute

error (MAE) is used as an error measure.

(Fukushima et al., 2018) uses two validation meth-

ods, a leave-one-out cross-validation, where the test

set consists of different BEV trips on the same route,

and a two-fold cross-validation, where BEV trips on

one route are used for training and trips on another

route are used for testing, and vice versa. With these

methods, the performance of ordinary least squares

(OLS) and an own method in predicting energy con-

sumption is measured, and the relative test error is

used as an error measure. (Gebhardt et al., 2015) uses

a leave-one-out cross-validation to test two range es-

timation approaches, where each test set represents a

trip with a BEV. The relative error in the prediction

of each trip’s energy consumption is used as an error

measure.

(Cauwer et al., 2017) splits selected data sets into

80% for training and 20% for testing of a model

that combines a neural network (NN) and a multi-

ple linear regression (MLR), which predict the en-

ergy consumption. The metrics root-mean-squared

error (RMSE) and MAE are used to measure the per-

formance of the initial prediction, and the prediction

for each route segment. (Qi et al., 2018) splits a data

set with real BEV data into 70% for training and 30%

for testing of regression models for the estimation of

the energy consumption, and the symmetric mean ab-

solute percentage error (SMAPE) is used as an error

measure. (Wang et al., 2017) tests only the goodness

of ﬁt of LR models estimating the energy consump-

tion of BEVs. The goodness of ﬁt is measured with

and the Akaike information criterion (AIC). From

the article, it can not be determined if the data was

split in training and test sets or whether the goodness

of ﬁt is measured in-sample.

(Thibault et al., 2018) validates a physical model

for the energy consumption with 35 real BEV trips

and SMAPE is used as an error measure. (Wang

et al., 2015) validates a physical model for the en-

ergy consumption with real BEV trips. However, no

error measure for the performance is calculated, but it

is shown that the measured energy consumption lies

within the maximum and minimum values of the pre-

diction. (Genikomsakis and Mitrentsis, 2017) vali-

dates a physical model for the energy consumption us-

ing simulated data. Driving cycles are used to specify

the velocity proﬁle. MAE, mean squared error (MSE)

and mean absolute percentage error (MAPE) are used

as error measures.

Only a few validation approaches describe a

driver-speciﬁc validation of range estimation algo-

rithms. (Ondr

ska and Posner, 2014) uses a data set

with 50 different drivers. A separate model is trained

for each driver, in order to predict the energy con-

sumption of a trip. The models are validated with

different sizes of training sets, but always tested on

the whole data set for each driver, i.e. a variable com-

bination of in- and out-of-sample testing. The relative

error is used to measure the performance of the mod-

els.

(Tseng and Chau, 2017) uses randomly selected

80% of collected BEV data to train a regression

model, and the rest is used to test the performance of

the predicted energy consumption. Since the selection

is done randomly, the validation is not driver-speciﬁc.

RMSE and the accumulative error over a whole trip

are used as error measures.

Up to now, there is no general methodology for

data selection and validation of range estimation algo-

rithms for driver-speciﬁc and driver-unspeciﬁc evalu-

ation. Only one or the other is used for the evaluation

of such algorithms. Even though it is important to

evaluate the performance of a range estimation algo-

rithm in the two different use-cases. There is also a

need for a standardized and non-biased error measure

for the evaluation. In addition, the process of split-

ting data samples into a set of training data and a set

of validation data is done randomly, which could lead

to a possible bad distribution of training and valida-

tion data e.g. training on drives with low velocities

and validation on drives with high velocities. Thus,

a data selection method is needed to ensure balanced

training and validation data sets.

In the following, we present a methodology for

the validation process. Covering the data selection

and the standardized training and validation concept

of data-driven learning range estimation algorithms.

Additionally, a universal error measure is introduced

to assess the performance of such algorithms.

3 CONCEPT FOR TESTING

RANGE ESTIMATION

ALGORITHMS

In the context of evaluating the performance of range

estimation algorithms, considerable attention needs to

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

436

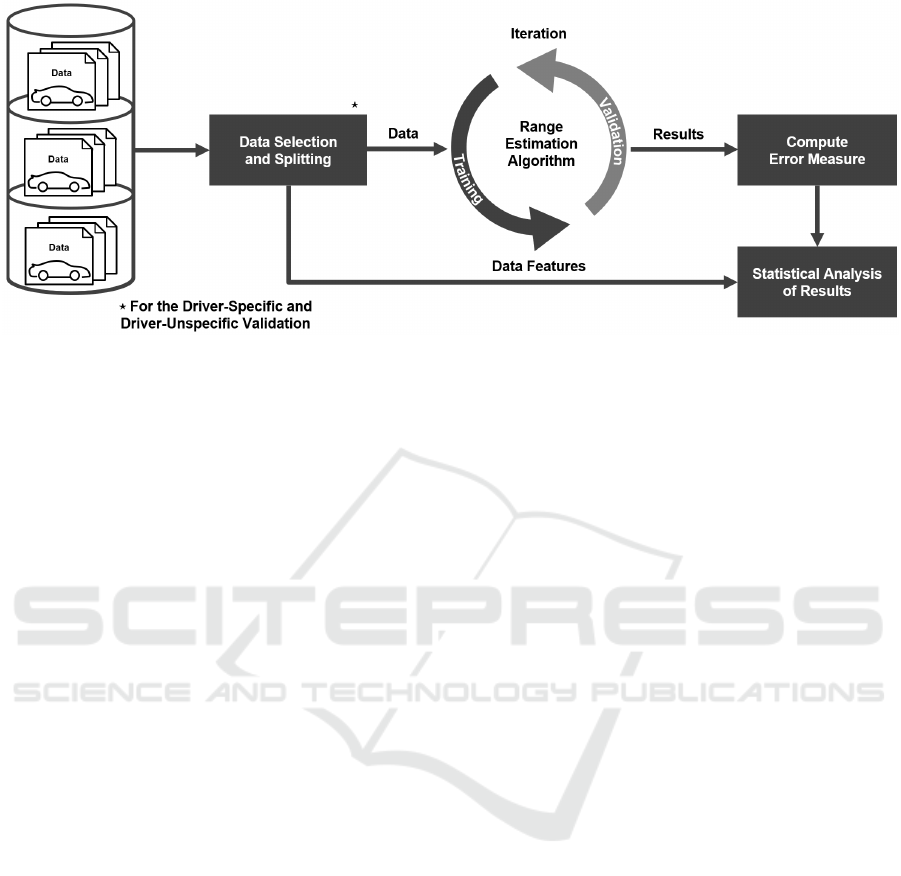
Figure 1: Overview of the training and validation methodology for range estimation algorithms.

be paid to the training and validation phase. Thus,

our goal was to create a methodology which enables

the assessment of driver-speciﬁc and driver-unspeciﬁc

performance. Figure 1 shows an overview of our pro-

posed methodology covering the data selection, split-

ting the data into training and validation sets for the

driver-speciﬁc and driver-unspeciﬁc validation and

the statistical analysis of the results based on our in-

troduced error measure. In the following, the indi-

vidual methodology steps shown in the Figure will be

described.

To ensure the highest possible realism for train-

ing and validation, we suggest the usage of recorded

real-world data from different drivers. Since driv-

ing style has a signiﬁcant impact on a vehicles en-

ergy consumption, its inclusion in the validation will

improve the evaluation of the range estimation. On

that account, the accuracy of the range estimation

with consistent driving style can be measured, as well

as its robustness during changes in driving behavior,

such as driver changes. For the driver-speciﬁc eval-

uation, we suggest a k-fold cross-validation where

the data set includes only a single driver. For the

general, driver-unspeciﬁc evaluation, we suggest a

leave-one-out cross-validation with a data set includ-

ing more than one driver. Both approaches test the

out-of-sample performance, which is always the case

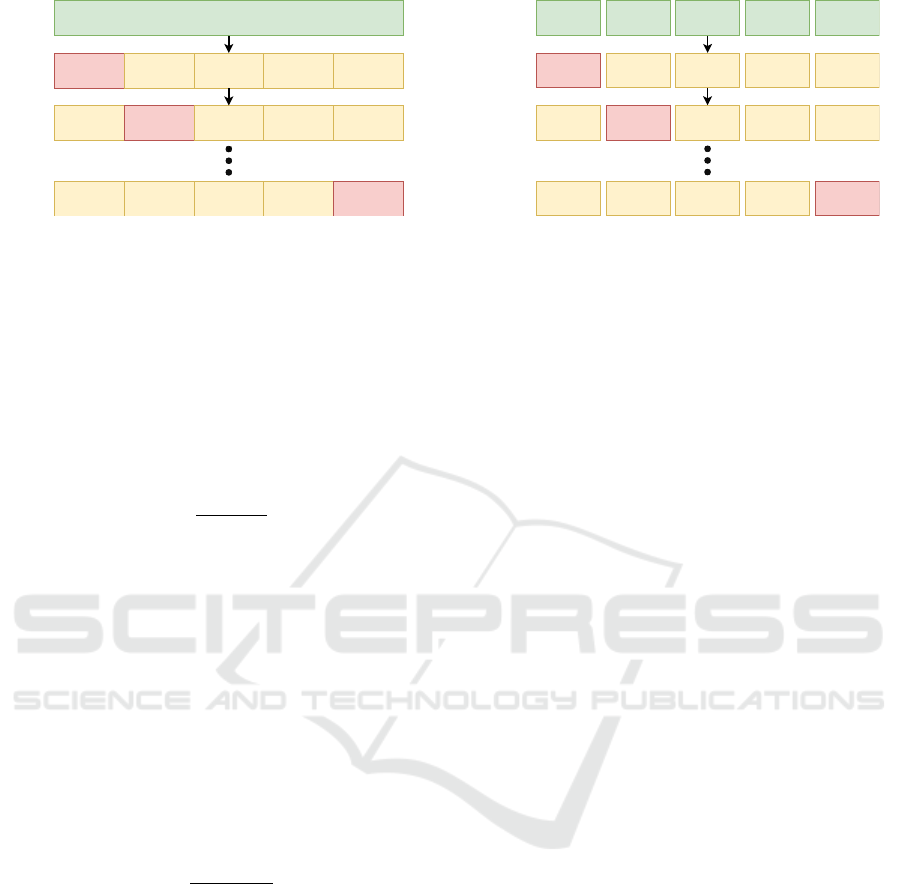
in real applications. Figure 2 shows the concept for

the driver-speciﬁc and driver-unspeciﬁc evaluation.

3.1 Driver-speciﬁc Validation

To evaluate driver-speciﬁc performance of a range es-

timation algorithm, it must be ensured that data from

the same driver is used. Due to the protection of pri-

vacy, the driver for certain trips is usually not known.

Also, the driving behavior of a driver could vary be-

tween trips, which could lead to the false assumption

that this data comes from a different driver. There-

fore, we split each recorded real-world drive into seg-

ments for the k-fold cross-validation to ensure that the

same driver is used for training and validation. Fig-

ure 2a shows the procedure exemplary for one trip.

In this scenario, the data is split into k = 5 segments

and for each iteration, one segment will be used for

the validation and the rest for training. This enables

the assessment of the driver-speciﬁc performance of

the used range estimation algorithm on different seg-

ments.

3.2 Driver-unspeciﬁc Validation

To evaluate the performance of a range estimation al-

gorithm for the more general case of inconsistent driv-

ing behavior, the validation technique needs to be dif-

ferent from the driver-speciﬁc evaluation. To repre-

sent a changing driver or another driving behavior, the

training and validation is done on different trips. To

this end, one complete trip is left out for the valida-

tion, and other trips from the data basis are used for

training. In Figure 2b, an example of the procedure

for ﬁve trips is shown. In each iteration, one trip will

be selected for the validation and the rest for train-

ing, leading to ﬁve results. The order of trips used for

training is randomized.

3.3 Error Measure

For the evaluation of the performance of the range es-

timation algorithm, a suitable error measure needs to

be chosen or formulated. Since the actual measured

energy consumption could be close to zero for some

segments, because of the ability of BEVs to recuper-

ate energy, the percentage error is not an appropriate

Training and Validation Methodology for Range Estimation Algorithms

437

Trip A

Test

Train Train Train Train

It. 1

It. 2

It. 5

(a) K-fold cross-validation for driver-speciﬁc training and

validation.

Test

Train Train Train Train

Trip A Trip B Trip C Trip D Trip E

It. 1

It. 2

It. 5

(b) Leave-one-out cross-validation for driver-unspeciﬁc

training and validation.

Figure 2: Exemplary visualization for the k-fold cross-validation and leave-one-out cross-validation for splitting the data into

a training and validation set.

error measure, as the error is divided by the actual

value. The RMSE is not as convenient to interpret as

the MAE, and could over-penalize large errors. Thus,

we introduce our non-biased error measure: The ab-

solute error of the prediction of energy consumption

ε is shown in Equation 1.

ε =

− E

(1)

This is calculated by the absolute difference between

the initial energy consumption prediction E

of a

range estimation algorithm A and the actual measured

energy consumption E normalized by the length of

the validation segment s. The initial prediction for

the energy consumption was chosen due to its impor-

tance for the charge planning at the beginning of each

trip. In addition, the initial prediction is the most chal-

lenging, as it has the longest prediction horizon and

therefore the highest amount of uncertainties. For n

training and validation iterations, the weighted sum

of the absolute error of the prediction of energy con-

sumption is then calculated. This is shown in Equa-

tion 2.

ε =

∑

i=1

∗ s

∑

j=1

(2)

The weighted mean absolute error (wMAE) is calcu-

lated for the driver-speciﬁc (

) and driver-unspeciﬁc

(

) validation iterations, which describe the perfor-

mance of A in each situation. Through weighting

with the length of the validation segment, the error

measure takes longer trips more into account, which

is reasonable due to the higher difﬁculty for an ac-

curate initial prediction. Since the driving behavior

inﬂuences the learned parameters used for the estima-

tion, only those validation segments should be eval-

uated which require those parameters for the estima-

tion. This prevents validation of the initial parame-

ters, which were not trained during the training phase.

As with all recursive algorithms learning with lots of

data, newer data points have more signiﬁcance than

older ones. Thus, to deal with this characteristic be-

havior, it may be reasonable to validate with all pos-

sible permutations of the training data.

In summary our methodology addresses the chal-

lenges identiﬁed in state of the art evaluation of range

estimation algorithms: a non-biased validation for the

driver-speciﬁc and driver-unspeciﬁc performance of

range estimation algorithms with a given error mea-

sure, which evaluates the most challenging predic-

tion for such algorithms, the initial prediction. Dif-

ferent trip lengths are also taken into account for a

signiﬁcant evaluation. In addition, our methodol-

ogy covers the process of selecting suitable (out-of-

sample) algorithms data for the validation phase for

the driver-speciﬁc and driver-unspeciﬁc performance

evaluation.

4 EVALUATION

To demonstrate the practicability of our validation

methodology, we implemented a framework for the

evaluation of a range estimation algorithm. Our data

basis consists of 21 recorded real-world test drives

from different drivers. The accumulated length of

the data basis is approximately 2088.03 km. Each

recorded data contains logged signals from the Con-

troller Area Network (CAN). Table 1 gives an infor-

mation overview of the used data.

The data basis was also enriched by external

sources for historic trafﬁc information, which was

used for the range estimation algorithm described in

(Sautermeister et al., 2017). For the k-fold cross-

validation of the driver-speciﬁc performance a drive

was splitted into k = 3 segments. In Figure 3, a box

plot shows the calculated absolute error for the driver-

speciﬁc, driver-unspeciﬁc evaluation and its variance.

The ﬁgure shows that for the driver-speciﬁc evalua-

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

438

Table 1: Overview of the used data for the training and val-

idation evaluation

Number of trips 21

Total length 2088.03 km

Shortest trip 13.87 km

Longest trip 219.93 km

Average length 99.42 km

Average trip length on highway 60.82 km

Average positive slope 0.64

◦

Average negative slope 1.06

◦

Average absolute curvature 1.62 rad

Average velocity 67.65 km/h

Figure 3: Box plot showing the absolute error for driver-

speciﬁc (ε

) and driver-unspeciﬁc (ε

) estimation of energy

consumption.

tion, the absolute error for each iteration of the k-

fold cross-validation has a greater variance than the

error for the driver-unspeciﬁc leave-one-out evalua-

tion. Less training data for the driver-speciﬁc evalu-

ation may be the cause of this result due to splitting

one trip into a training and validation segment. The

mean training length for the driver-speciﬁc evaluation

was 66.29 km compared to 2042.21 km for the driver-

unspeciﬁc evaluation.

To further utilize the methodology, we examined

7 different parameter sets such as different learning

rates for the range estimation algorithm. For each

parameter set, we obtained an error measure pair,

and

. In Figure 4, each pair was plotted in a scatter

plot to visualize the performance of each parameter

set. The blue line represents the Pareto frontier,

which highlights feasible choices for parameter sets

of the used range estimation algorithm. Therefore,

the best parameter set can be chosen based on

different criteria e.g. the best parameter set for the

driver-speciﬁc or driver-unspeciﬁc performance. Its

up to the developer to choose the parameter set,

which has the desired performance.

Figure 4: Scatter plot showing the weighted mean abso-

lute errors

and

for the given parameter set evaluation.

Showing the Pareto frontier for the parameter sets with the

lowest error measure.

To further investigate the performance of spe-

ciﬁc parameter sets during the driver-speciﬁc and

driver-unspeciﬁc evaluation, certain features were

factorial analyzed. For the factorial analysis in-

dependent driving patterns where chosen, which

describe a certain dimension of the driving pattern

in regards to the energy consumption during the

trip. (Ericsson, 2001) worked out 16 driving pattern

factors with signiﬁcant effect on emissions and

fuel-use for internal combustion engine vehicles.

(Braun and Rid, 2018) further investigated the driving

patterns which inﬂuence the energy use of BEVs.

Furthermore (Hu et al., 2017) explored the inﬂuence

of driving behavior, personal driving style, trafﬁc

conditions and infrastructure design on the energy

consumption of BEV. Therefore we analyzed 15

features which cover personal driving style, route and

trafﬁc characteristics of the training and validation

data during each iteration. Table 2 shows the chosen

features. Then we analyzed the correlation between

the error measure and absolute difference between

the training and validation data of the features

(∆F = |F

− F

|) in each iteration. This was done for

the driver-speciﬁc and drive-unspeciﬁc validation. In

Table 3 the Pearson correlation is calculated to show

the relationship between each feature and the error

measure.

Due to the limited number of data most of the

Pearson correlation coefﬁcients are not signiﬁcant at

the signiﬁcance level of 0.05. However, the fea-

tures describing the driving style correlate differently

which substantiates our approach to separately eval-

uate the driver-speciﬁc and driver-unspeciﬁc perfor-

mance of the range estimation algorithm. In gen-

eral, changes in the route and trafﬁc characteristics

Training and Validation Methodology for Range Estimation Algorithms

439

Table 2: The chosen features for the driving style, route and trafﬁc characteristics that were calculated for each training and

validation data set during each iteration.

Feature Denotation

driving style

Relative positive acceleration RPA

Relative negative deceleration RNA

Percentage of time when speed < 2 km/h PC ST OPP

Percentage of time when va is 3 − 6 m

PC va3 6

Percentage of time when acceleration exceeds 2.5 m/s

PC a25

route

Relative positive slope RPS

Relative negative slope RNS

Relative absolute curvature RAC

Percentage of highway PC H

Average speed limit AV G S PL

Standard derivation speed limit AV G S PL

trafﬁc

Average ratio of v

online

lim

AV G vOL

Standard derivation ratio of v

online

lim

ST D vOL

Percentage of travel distance where v

online

lim

< 0.5 during the trip PC vOL 50

Percentage of travel distance where v

online

lim

> 0.9 during the trip PC vOL 90

online

describes the measured average velocity of each segment of a route. v

lim

describes the

speed limit of each segment of a route.

Table 3: Pearson correlation coefﬁcient and p-value between features and the error measure for the driver-speciﬁc and driver-

unspeciﬁc validation.

Feature

Pearson correlation coefﬁcient (r) Pearson correlation p-values

driver-speciﬁc driver-unspeciﬁc driver-speciﬁc driver-unspeciﬁc

driving style

RPA 0.05 0.02 0.73 0.93

RNA 0.06 −0.03 0.64 0.91

PC ST OPP −0.12 0.28 0.34 0.21

PC va3 6 −0.05 −0.34 0.71 0.10

PC a25 0.13 0.29 0.32 0.21

route

RPS 0.18 0.34 0.16 0.13

RNS 0.02 −0.10 0.88 0.66

RAC 0.25 0.28 0.05 0.21

PC H −0.04 0.35 0.76 0.12

AV G S PL −0.27 0.31 0.03 0.17

ST D SPL −0.15 0.49 0.23 0.02

trafﬁc

AV G vOL −0.24 0.47 0.06 0.03

ST D vOL −0.26 0.41 0.04 0.06

PC vOL 50 0.05 0.02 0.72 0.93

PC vOL 90 −0.08 0.13 0.53 0.58

between training and validation tend to be stronger

correlated with the estimation error. Signiﬁcant re-

sults for AV G SPL and ST D SPL have a weak op-

positely correlation for the driver-speciﬁc and driver-

unspeciﬁc evaluation. The same phenomena can be

observed for the signiﬁcant correlation for AV G vOL

and ST D vOL. Trafﬁc has a signiﬁcant inﬂuence on

the velocity prediction of such algorithms, hence also

on the estimated energy consumption. This is reason-

able for learning algorithms which tend to perform

worse in unknown situations and are therefore sensi-

tive for differences in training and validation data.

5 CONCLUSION AND FUTURE

WORK

We introduced this contribution with an analysis of

the current challenge of range prediction for bat-

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

440

tery electric vehicles. Depending on different

factors, range estimation requires novel algorithms to

cope with the complexity. Improving the accuracy of

these algorithms is essential to address range anxiety,

which, in turn, is necessary to increase acceptance

of battery electric vehicles. Thus, being able to

measure the accuracy of range estimation algorithms

is of great importance. We analyzed the current

approaches for the training and validation of ML and

non-ML range estimation algorithms. We identiﬁed

the demand for a standardized methodology for

the training and validation process to evaluate the

driver-speciﬁc and driver-unspeciﬁc performance.

We then introduced our data-driven training and

validation methodology of range estimation algo-

rithms, which allows the evaluation of driver-speciﬁc

and driver-unspeciﬁc performance. Furthermore, an

error measure for such algorithms was introduced,

which is, in contrast to some publications, non-biased

and can handle segments with zero consumption.

Also the focus of the error measure was put on the

most crucial estimation for such algorithms: the ini-

tial prediction. Through weighting with trip length,

shorter and easier estimations carry less weight than

longer and tougher estimation challenges, which al-

lows a more signiﬁcant evaluation. We presented our

methodology by analyzing a small set of recorded

real-world data. Reusing already recorded data al-

lows easier and faster evaluation of range estimation

algorithms under development. Additionally, we an-

alyzed the correlation between the error measure and

the feature differences in the training and validation

data sets. These features covered the driving style,

route and trafﬁc characteristics. The results can be

utilized to improve the developed range estimation

algorithm in regards to factors which inﬂuence the

energy consumption of BEVs. Different results for

the driver-speciﬁc and driver-unspeciﬁc correlation

such as for the trafﬁc features have shown that our

methodology to evaluate both the driver-speciﬁc and

the driver-unspeciﬁc performance of a range estima-

tion algorithm is reasonable.

Future work will focus on to further investigate

inﬂuences on estimation errors for range estima-

tion algorithms. In addition, the impact of differ-

ent lengths of the training and validation segments

will be evaluated. The steadily increasing database

of recorded real-world data requires exhaustive eval-

uation. Therefore, concepts for coping with the eval-

uation of a larger data basis need to be addressed. The

recent trend of fog computing, especially in the auto-

motive industry, might offer a scalable and more cen-

tralized computing architecture for computing com-

plex algorithms or their evaluations in the cloud (Xiao

and Zhu, 2017). Further analysis of the data regarding

test coverage is reasonable, due to planning future test

drives to collect novel data. Thus, features to describe

and categorize these data sets need to be developed.

Data-driven approaches can be used to select drives

for a minimal test set for the validation of range es-

timation algorithms. Execution time for computing

evaluations can be reduced by using these minimal

test sets instead of running evaluations on the whole

data basis. They can also be used in automated pa-

rameter optimization, to further increase the accuracy

of range estimation algorithms.

REFERENCES

(2013). ISO/IEC/IEEE International Standard - Soft-

ware and systems engineering –Software testing –Part

1:Concepts and deﬁnitions. ISO/IEC/IEEE 29119-

1:2013(E), 2013:1–64.

Bach, J., Bauer, K.-l., Holz

apfel, M., Hillenbrand, M., and

Sax, E. (2015). Control based driving assistant func-

tions’ test using recorded in ﬁeld data. Proc. 7. Tagung

Fahrerassistenzsysteme.

Bach, J., Holz

apfel, M., Otten, S., Sax, E., Holz

apfel, M.,

Sax, E., Otten, S., and Sax, E. (2017a). Reactive-

Replay Approach for Veriﬁcation and Validation of

Closed-Loop Control Systems in Early Development.

SAE Technical Paper 2017-01-1671, (May).

Bach, J., Langner, J., Otten, S., Holzapfel, M., and Sax, E.

(2017b). Data-driven development, a complementing

approach for automotive systems engineering. 2017

IEEE International Symposium on Systems Engineer-

ing, ISSE 2017 - Proceedings.

Bach, J., Langner, J., Otten, S., Sax, E., and Holzapfel, M.

(2017c). Test scenario selection for system-level veri-

ﬁcation and validation of geolocation-dependent au-

tomotive control systems. 2017 International Con-

ference on Engineering, Technology and Innovation

(ICE/ITMC), (June):203–210.

Bingham, C., Walsh, C., and Carroll, S. (2012a). Impact of

driving characteristics on electric vehicle energy con-

sumption and range. IET Intelligent Transport Sys-

tems, 6(1):29–35.

Bingham, C., Walsh, C., and Carroll, S. (2012b). Impact of

driving characteristics on electric vehicle energy con-

sumption and range. IET Intelligent Transport Sys-

tems, 6(1):29.

Boehm, B. W. (1976). Software Engineering. IEEE Trans-

actions on Computers, 25(12):1226–1241.

Bolovinou, A., Bakas, I., Amditis, A., Mastrandrea, F., and

Vinciotti, W. (2014). Online prediction of an electric

vehicle remaining range based on regression analysis.

In 2014 IEEE International Electric Vehicle Confer-

ence (IEVC). IEEE.

Braun, A. and Rid, W. (2018). Assessing driving pattern

factors for the speciﬁc energy use of electric vehicles:

A factor analysis approach from case study data of the

Training and Validation Methodology for Range Estimation Algorithms

441

Mitsubishi i–MiEV minicar. Transportation Research

Part D: Transport and Environment, 58(2018):225–

238.

Cauwer, C. D., Verbeke, W., Coosemans, T., Faid, S., and

Mierlo, J. V. (2017). A data-driven method for energy

consumption prediction and energy-efﬁcient routing

of electric vehicles in real-world conditions. Energies,

10(5):608.

Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler,

M., Benenson, R., Franke, U., Roth, S., and Schiele,

B. (2016). The Cityscapes Dataset for Semantic Urban

Scene Understanding. Proc. of the IEEE Conference

on Computer Vision and Pattern Recognition (CVPR).

Enthaler, A. and Gauterin, F. (2016). Method for reduc-

ing uncertainties of predictive range estimation algo-

rithms in electric vehicles. 2015 IEEE 82nd Vehicular

Technology Conference, VTC Fall 2015 - Proceedings.

Ericsson, E. (2001). Independent driving pattern factors and

their inﬂuence on fuel-use and exhaust emission fac-

tors. Transportation Research Part D: Transport and

Environment, 6(5):325–345.

Fetene, G. M., Kaplan, S., Mabit, S. L., Jensen, A. F., and

Prato, C. G. (2017). Harnessing big data for estimat-

ing the energy consumption and driving range of elec-

tric vehicles. Transportation Research Part D: Trans-

port and Environment, 54:1–11.

Fukushima, A., Yano, T., Imahara, S., Aisu, H.,

Shimokawa, Y., and Shibata, Y. (2018). Prediction of

energy consumption for new electric vehicle models

by machine learning. IET Intelligent Transport Sys-

tems, 12(9):1174–1180.

Gebhardt, K., Schau, V., and Rossak, W. R. (2015). Ap-

plying stochastic methods for range prediction in e-

mobility. In 2015 15th International Conference on

Innovations for Community Services (I4CS). IEEE.

Genikomsakis, K. N. and Mitrentsis, G. (2017). A computa-

tionally efﬁcient simulation model for estimating en-

ergy consumption of electric vehicles in the context of

route planning applications. Transportation Research

Part D: Transport and Environment, 50:98–118.

Grubwinkler, S., Hirschvogel, M., and Lienkamp, M.

(2014). Driver- and situation-speciﬁc impact factors

for the energy prediction of EVs based on crowd-

sourced speed proﬁles. IEEE Intelligent Vehicles Sym-

posium, Proceedings, (Iv):1069–1076.

Helmer, T., Wang, L., Kompass, K., and Kates, R. (2015).

Safety Performance Assessment of Assisted and Au-

tomated Driving by Virtual Experiments: Stochastic

Microscopic Trafﬁc Simulation as Knowledge Syn-

thesis. In Intelligent Transportation Systems (ITSC),

2015 IEEE 18th International Conference on, volume

2015-Octob, pages 2019–2023. IEEE.

Horrein, L., Bouscayrol, A., Lhomme, W., and D

epature,

C. (2017). Impact of heating system on the range of

an electric vehicle. IEEE Transactions on Vehicular

Technology, 66(6):4668–4677.

Hu, K., Wu, J., and Schwanen, T. (2017). Differences

in energy consumption in electric vehicles: An ex-

ploratory real-world study in Beijing. Journal of Ad-

vanced Transportation, 2017:1–17.

Langner, J., Bach, J., Otten, S., Sax, E., Esselborn, C., Holz,

M., and Eckert, M. (2017). Framework for using real

driving data in automotive feature development and

validation.

Lewis, D. D. (1992). Representation and Learning in In-

formation Retrieval. PhD thesis, Amherst, MA, USA.

UMI Order No. GAX92-19460.

Mazzega, J., K

oster, F., Lemmer, K., and Form, T. (2016).

Testing of Highly Automated Driving Functions. ATZ

worldwide, 118(10):44–48.

Mitchell, H. B. (2012). Data Fusion: Concepts and Ideas.

Springer Berlin Heidelberg, Berlin, Heidelberg, 2nd

ed. 2012 edition.

Ondr

ska, P. and Posner, I. (2014). The route not taken:

Driver-centric estimation of electric vehicle range.

In Proceedings of the Twenty-Fourth International

Conferenc on International Conference on Automated

Planning and Scheduling, ICAPS’14, pages 413–420.

AAAI Press.

Qi, X., Wu, G., Boriboonsomsin, K., and Barth, M. J.

(2018). Data-driven decomposition analysis and esti-

mation of link-level electric vehicle energy consump-

tion under real-world trafﬁc conditions. Transporta-

tion Research Part D: Transport and Environment,

64:36–52.

Rolim, C. C., Gonc¸alves, G. N., Farias, T. L., and Ro-

drigues,

O. (2012). Impacts of Electric Vehicle Adop-

tion on Driver Behavior and Environmental Perfor-

mance. Procedia - Social and Behavioral Sciences,

54:706–715.

Sautermeister, S., Ott, F., Vaillant, M., and Gauterin, F.

(2017). Reducing Range Estimation Uncertainty with

a Hybrid Powertrain Model and Online Parameter Es-

timation. 2017 IEEE 20th International Conference

on Intelligent Transportation Systems (ITSC), pages

910–915.

Sax, E. (2008). Automatisiertes Testen Eingebetteter

Systeme in der Automobilindustrie. Hanser, Carl,

unchen.

Tannahill, V. R., Muttaqi, K. M., and Sutanto, D. (2016).

Driver alerting system using range estimation of elec-

tric vehicles in real time under dynamically varying

environmental conditions. IET Electrical Systems in

Transportation, 6(2):107–116.

Thibault, L., Nunzio, G. D., and Sciarretta, A. (2018). A

uniﬁed approach for electric vehicles range maximiza-

tion via eco-routing, eco-driving, and energy con-

sumption prediction. IEEE Transactions on Intelligent

Vehicles, pages 1–1.

Tseng, C.-M. and Chau, C.-K. (2017). Personalized pre-

diction of vehicle energy consumption based on par-

ticipatory sensing. IEEE Transactions on Intelligent

Transportation Systems, 18(11):3103–3113.

Wager, G., Whale, J., and Braunl, T. (2016). Driving elec-

tric vehicles at highway speeds: The effect of higher

driving speeds on energy consumption and driving

range for electric vehicles in australia. Renewable and

Sustainable Energy Reviews, 63:158–165.

Wang, J., Besselink, I., and Nijmeijer, H. (2015). Electric

vehicle energy consumption modelling and prediction

VEHITS 2019 - 5th International Conference on Vehicle Technology and Intelligent Transport Systems

442

based on road information. World Electric Vehicle

Journal, 7(3):447–458.

Wang, J., Liu, K., Yamamoto, T., and Morikawa, T. (2017).

Improving estimation accuracy for electric vehicle en-

ergy consumption considering the effects of ambient

temperature. Energy Procedia, 105:2904–2909.

Wu, X., Freese, D., Cabrera, A., and Kitch, W. A. (2015).

Electric vehicles’ energy consumption measurement

and estimation. Transportation Research Part D:

Transport and Environment, 34:52–67.

Xiao, Y. and Zhu, C. (2017). Vehicular fog computing: Vi-

sion and challenges. 2017 IEEE International Con-

ference on Pervasive Computing and Communications

Workshops, PerCom Workshops 2017, pages 6–9.

Yi, Z. and Bauer, P. H. (2017). Adaptive Multiresolu-

tion Energy Consumption Prediction for Electric Ve-

hicles. IEEE Transactions on Vehicular Technology,

66(11):10515–10525.

Yu, H., Tseng, F., and McGee, R. (2012). Driving pattern

identiﬁcation for ev range estimation. In 2012 IEEE

International Electric Vehicle Conference, pages 1–7.

Training and Validation Methodology for Range Estimation Algorithms

443