
Technical Validation of the RLS Smart Grid Approach to Increase Power
Grid Capacity without Physical Grid Expansion
Ram
´
on Christen
1
, Vincent Layec
2
, Gwendolin Wilke
1
and Holger Wache
2
1
Department of Computer Science, University of Applied Science Lucerne, Rotkreuz, Switzerland
2
Institute of Information Systems, University of Applied Science and Arts of Northwestern Switzerland, Olten, Switzerland
Keywords: Smart Grid, Power Grid, Grid Capacity, Grid Reinforcement, Load Prediction, Load Management.
Abstract:
The electrification of the global energy system and the shift towards distributed power production from sus-
tainable sources triggers an increased network capacity demand at times of high production or consumption.
Existing energy management solutions can help mitigate resulting high costs of large-scale physical grid rein-
forcement, but often interfere in customer processes or restrict free access to the energy market. In a preceding
paper, we proposed the RLS regional load shaping approach as a novel business model and load management
solution in middle voltage grid to resolve this dilemma: market-based incentives for all stakeholders are pro-
vided to allow for flexible loads that are non-critical in customer processes to be allocated to the unused grid
capacity traditionally reserved for N-1 security of supply. We provide a validation of the technical aspects of
the approach, with an evaluation of the day-ahead load forecasting method for industry customers and a load
optimization heuristics. The latter is tested by a simulation run on a scenario of network branch with provoked
capacity bottlenecks. The method handles all provoked critical network capacity situations as expected.
1 INTRODUCTION
With the ongoing change away from fossil resources
toward electric power, an increase in electric power
demand and in production and consumption concur-
rency can be foreseen. As a result, higher grid capac-
ities are required to avoid grid congestion. To help
mitigate the high costs of assumed future large scale
physical grid expansions, IT-based energy manage-
ment solutions in the ”Smart Grid” have been pro-
posed for a more efficient use of existing capacities
(Atzeni, 2014). Yet, most of these grid-optimizing ap-
proaches interfere with customer processes and do not
rely on market-based principles. In contrast, market-
based energy management approaches usually disre-
gard the perspective of grid optimization.
In (Bagemihl et al., 2018), a business model has
been proposed that provides market-based incentives
to all stakeholders on the medium voltage grid lev-
els to utilize so-called ”conditional” flexible loads for
grid capacity optimization. The business model is as-
sociated with a load management approach for ”Re-
gional Load Shaping” (RLS) with a day-ahead opti-
mization heuristics that considers both, customer-side
energy prizes and grid capacity constraints of network
branches, at the same time. In order to allow for grid
capacity increase without necessitating physical grid
expansion, the RLS approach proposes to allocate
for so-called ”conditional loads” the currently unused
grid capacity dedicated to ensuring the (n-1) security
of supply. That capacity is reserved for the case of
rare grid disturbance where one branch takes over the
loads of another branch. I.e., conditional loads com-
prise flexibilities that may be temporarily shedded in
the event of grid disturbance. They contrast with ”un-
conditional loads”, which require security of supply
all-time, such as, loads required for industrial produc-
tion processes.
In the present paper, we test and validate the tech-
nical aspects of the RLS approach, namely the RLS
optimization heuristics and the underlying day-ahead
load forecasting method. For testing and validation
we simulate network congestions by extrapolating
a real world scenario of our pilot customers to fu-
ture scenarios with increased power demand and sup-
ply. We show that the proposed load scheduling so-
lution with its prize optimization heuristics handles
the critical network capacity situations as expected.
For the evaluation of the day-ahead load forecasting
method, we evaluate the Mean Absolute Percentage
Error (MAPE) as a measure of accuracy and show
that the results achieved with our pilot customers’
Christen, R., Layec, V., Wilke, G. and Wache, H.
Technical Validation of the RLS Smart Grid Approach to Increase Power Grid Capacity without Physical Grid Expansion.
DOI: 10.5220/0007717101230130
In Proceedings of the 8th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2019), pages 123-130
ISBN: 978-989-758-373-5
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
123

data sets are comparable with results in the literature.
Additionally, we evaluate the prediction reliability as
a means for the Distribution System Operator (DSO)
and end customer to assess the prediction quality from
a pragmatic perspective.
2 STATE OF THE ART
2.1 Load Scheduling Approaches
Shifting the electrical consumption to another time is
a Demand Response (DR) case, a change in electric
usage by prosumer (household or industrial customer)
from its normal demand pattern in reaction to an in-
centive payment. The review of (Shariatzadeh et al.,
2015) distinguished dispatchable programs where the
prosumers let the DSO control their systems from
non-dispatchable programs where the prosumers de-
centrally set their load schedule. The latter category
spans from simple Time-Of-Use (TOU) with constant
day and night prices to Real-Time Pricing (RTP), a
tariff changing at each time step. In (Doostizadeh and
Ghasemi, 2012), the information about the price is
communicated one day in advance so prosumers do
not need to predict prices. But automatic schedulers
participating with the same information will plan their
load in the same cheapest timestep and unfortunately
create new peaks (Zhao et al., 2013). The formula-
tion of the schedulers (mathematical programming,
metaheuristics or other controllers) depends on the
type of tariff system, but also on the type of elec-
trical loads, their operating constraints, the number
of timesteps, the type of variables (without integer or
not), as classified in (Shaikh et al., 2014). The case of
photovoltaic in combination with several battery types
is addressed in (Thirugnanam et al., 2018). The is-
sue of synchronisation is tackled in (Mohsenian-Rad
and Leon-Garcia, 2010) with tariff of Inclining Block
Rates (IBR) where high consumption levels are dis-
suasively expensive. (Hunziker et al., 2018) showed
that the total load of a community of prosumers can be
well shaped with tariffs combining RTP with IBR. So
far, no tariff system targets the paradox that in grids
half of the transmission capacity is reserved as a re-
dundancy for the rare case of failure and remains an
expensive unused resource.
2.2 Prediction Methods for Day-ahead
Forecasting for Industry Customers
A growing importance of efficient energy usage and
an even more decentralized sustainable power pro-
duction increases the focus in research on prediction
of time series for power demand. In that field, James
W. Taylor has done several works in time series pre-
diction such as (Taylor et al., 2006; Taylor et al., 2007;
Taylor, 2010). A major differentiation in research is
done in the aggregation level of the predicted power
demand. Commonly it is said, the higher the level the
less the prediction accuracy. This behavior is shown
in several papers (Zufferey et al., 2016; Arora and
Taylor, 2016; Mirowski et al., 2014). A comparison
of the aggregation level versus the prediction accu-
racy in (Mirowski et al., 2014) confirms this depen-
dency. A similar behaviour is also shown by Kong et.
al that predicted individual residential power demand
with a Long Short-Term Memory (LSTM) network
and a precision of a MAPE of approx. 44% com-
pared to an aggregate forecast with a MAPE of ap-
prox. 8% (Kong et al., 2017). The strength of a LSTM
network for an electrical load forecast compared to
other common methods such as Support Vector Re-
gression (SVR) are shown in (Zheng et al., 2017) with
an achieved MAPE of less than 6%.
Further, for a prediction also the usage of power
is differentiated, i.e. whether the time series is of a
residential or an industrial consumption. In (Kong
et al., 2017) it is mentioned that industrial electric-
ity consumption patterns would be more regular than
residential ones such that Ryu et al. achieved in (Ryu
et al., 2016) a prediction accuracy for industrial loads
with a MAPE of about 8.85%. Less accurate predic-
tions were obtained in (Ghofrani et al., 2011) for res-
idential loads by means of a Kalman filter estimator.
Mocanu et. al presented in (Mocanu et al., 2016) dif-
ferent deep learning approaches whereas the imple-
mentation of a Factored Conditional Restricted Bolz-
man Machine (FCRBM) outperformed several Ma-
chine Learning (ML) algorithms.Comparable results
were achieved by Marino et. al by using a LSTM net-
work (Marino et al., 2016) and Shi for household load
forecasting (Shi et al., 2018).
3 THE RLS APPROACH
3.1 Increasing Grid Capacity
In most grids system availability must be guaranteed
in case of failure of a single network component such
as, e.g., a power line or transformer unit. As a result a
percentage of the grid capacity is not used in normal
operation, but reserved for this so-called (N-1) secu-
rity of supply. However, the large majority of days go
without grid failure.
The RLS approach proposes to allocate the nor-
mally unused grid capacity reserved for (N-1) secu-
SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems
124

rity of supply to conditional loads. Here, conditional
loads are loads for which (1) (N-1) security of supply
is not essential, (2) that are highly price-sensitive, and
(3) that are flexible and may thus be used for price
optimization purposes via load management. Condi-
tional loads comprise, e.g., the charging of stationary
batteries for internal consumption or power heat cou-
pling for fuel substitution. Unconditional loads are
all other loads.
Since security of supply is by definition not es-
sential for conditional loads this unused grid capac-
ity may be dedicated to them without compromising
the important security of supply level for conventional
household and industrial loads: in case of a branch
failure, conditional loads are shedded to provide se-
curity for unconditional loads.
Figure 1 illustrates a simplified version of the used
and unused grid capacity. Here, the component’s
maximal capacity is split exemplarily in two capac-
ity bands of 50% each. The lower band shown in
blue is the capacity used in normal operation, while
the upper band shown in grey represents the unused
capacity reserved for security. We call this band the
N-1 band because it ensures N-1 security to another
branch. Notice that the width of the N-1 band of a
network branch is determined by the component with
smallest capacity. The day-ahead prediction of un-
conditional loads (dark blue) and the scheduling of
conditional loads (green) is the subject of the rest of
this paper.
Figure 1: Example of a load schedule split in unconditional
loads (blue) and conditional loads (green).
In the RLS approach, the market-based incentive
for customers to register some of their flexibilities as
conditional loads is (1.) a load schedule management
for energy price optimization and (2.) a significantly
lower grid fee compared to unconditional loads. In-
centives for distribution system operators (DSO) to
implement the RLS approach comprise (1.) the pos-
sibility to postpone or avoid large scale physical grid
expansion, (2.) achieving a small increase in income
by additionally charged grid costs for the N-1 band,
and (3.) higher transparency within the grid due to
customer side load measurement and DSO-registered
load schedules.
3.2 Scheduling Conditional Loads
The goal of the day-ahead scheduling of conditional
loads is to minimize energy prizes for all customers
connected to the network branch under consideration.
The minimization is subject to (1.) the customers’
chosen prizing models, (2.) to their operating con-
straints (dependent on the flexible loads in use), and
(3.) to given grid constraints. Since regulations re-
quire that grid control and provision of energy supply
must be operated by separate legal entities, the man-
agement software is split in two independent subsys-
tems: the Grid Manager (GM) is operated by the DSO
and monitors grid constraints; the Energy Manager
(EM) implements the customer perspective and col-
lects the individually price-optimized load schedules
of all connected customers and aggregates them. An
iterative optimization heuristics implements the inter-
action of GM and EM in order to ensure grid and cus-
tomer constraints. Each iteration comprises two steps:
1. Local optimization: The EM calculates a price-
optimized conditional load schedule for a partici-
pating customer, which (if given) respects the grid
constraints prescribed by step 2. It submits the
schedule to the GM.
2. Global optimization: The GM aggregates the ac-
cumulated loads from different customers and
checks grid capacity constraints. In case the N-1
band capacity is exceeded, the GM curtails each
customer’s schedule according to their chosen
prizing model and submits to the EM an adapted
schedule based on load optimization on the aggre-
gated level; they then can optimise theri schedule
again (step 1).
The process is reiterated until a predefined time-based
deadline is reached and final schedules of the next day
are sent to the controllers of each customer’s devices.
In step one, each customer initially submits his
desired schedule of conditional loads for the next day
to the GM, i.e. a time series of the power of each ag-
gregate a for each timestep t. It is computed by solv-
ing a minimization of the daily energy costs subject
to operations constraints of conditional loads, such as
the energy balance for battery. Costs of substituted
fossil fuels and costs of electricity - via the actual
power and the actual electricity price - are considered.
The actual power is the net power supplied by the
grid, so the sum of unconditional resp. conditional
loads, corrected by the own photovoltaic (PV) pro-
duction. The electricity price is made of a spot price
timeserie predicted for year 2035 plus other fees OF
(grid, taxes and duties). For unconditional loads in
the so-called Standard Tariff (STT), OF is assumed
to grow up to 10 ct. / kWh until 2035. We introduce
Technical Validation of the RLS Smart Grid Approach to Increase Power Grid Capacity without Physical Grid Expansion
125

a so-called Power Alliance Tariff (PAT) with reduced
OF of only 4.8 ct / kWh in order to give a financial
incentive to use conditional loads. OF is 0 ct / kWh
when the power is fed back to the grid, so that the use
of own overproduction of PV remains the cheapest
option to schedule conditional loads, whereas import-
ing power at PA Tariff during timesteps of low spot
price becomes the second cheapest option.
In step two, initially submitted schedules are ag-
gregated, controlled and adjusted by the GM. On the
time steps with synchronized original loads exceed-
ing the grid limit, a centralized algorithm computes
an allocation respecting them with consideration of
the load asked by each customer c and their finan-
cial participation of this system of conditional loads.
Once completed, a decentralized algorithm allocates
loads at customer level for each of the aggregates.
3.3 Day-ahead Load Forecasting
The second technical aspect of the RLS approach
evaluated in the paper is the day-ahead prediction
of the unconditional loads of industry customers. It
serves two purposes: (1.) to provide customers with
higher transparency and thus better control of their
energy usage - it thereby serves as an additional in-
centive to participate in the program; (2.) to allow for
optimized usage of the currently unused grid capacity
in future scenarios.
For the day-ahead load forecasting of customer
load profiles, a model selection approach (MSA) has
been chosen. Thereby, a set of different time series
forecasting models are trained, fitted and evaluated
based on historical load profile data that comprises
14, 28, 42, 56 and 70 days for every individual cus-
tomer. The best model and training data length is cho-
sen separately for each customer based on the MAPE
performance evaluation metric. The MSA is executed
in regular time intervals (e.g. every month) in order
to allow for continuous adaptations to changes in the
customer load profile characteristics.
16 different prediction models where included:
As a benchmark model, the load profile of the pre-
vious workday / non-working day was used as fore-
cast for the following day, respectively. The simi-
lar days model was included in three variants: SD1
uses the median of a set of historical days of the same
weekday (e.g., the five previous Mondays) as a fore-
cast, SD2 uses the median of a set of previous work-
days or non-working days, respectively, and SDEns
takes the median of the forecasts of SD1 and SD2.
The classical time series prediction models Expo-
nential Smoothing (ES), Random Walk Drift (RWD),
Hold Winters (HW), Auto-Regressive Integrated Mov-
ing Average (ARIMA) and Generalized Autoregressive
Conditional Heteroskedasticity (GARCH) each where
applied both directly to the original load profile and
to the residual of the load profile after decomposition.
The latter version is referred to with the add on Dec
after the model name: ES Dec, RWD Dec, HW Dec,
ARIMA Dec, and GARCH Dec. Finally, a support vec-
tor machine with a radial bias kernel was applied in
both variants, SVR and SVR Dec.
4 SCHEDULING VERIFICATION
In order to test the scheduling approach for condi-
tional loads, we provoke a grid congestion in a sce-
nario based on real data of three pilot customers A, B
and C and one ad-hoc customer X.
4.1 Settings of the Experiment
Present energy usage of customers A, B and C are
classified in Table 1 in thermal or non thermal usage.
Photovoltaic panels will be installed on their roofs.
A new customer X, representative for several new
customers like freight shipping companies with new
Power-To-Gas units up to 7 MW but without signifi-
cant own compulsory loads nor PV, is added to simu-
late a congestion of the band of conditional loads. No
other grid related carrier (district heating) or off grid
(heating oil, pellets, etc.) is considered here. New
units of Table 2 are assumed to be added. ”Other”
aggregates of C (a food industry) are hereby cooling
machines using the frozen food as thermal storage and
substituting electricity of a cooling machine of a later
timestep of the same day.
Table 1: Energy carrier and usage (kW peak) of customers.
usage electric cooling electric process process with gas heat from gas
A 700 1000 - 500
B - 300 - 200
C 2000 1700 1000 1000
Table 2: Assumed new conditional loads and PV (kW).
P-to-Heat P-to-Gas Battery other PV
A 500 - - - 1500
B - 300 100 - 900
C - - - 2x250 1900
X - 7000 - - -
A fictive grid configuration with all customers A,
B, C and X in the same branch is assumed to evaluate
our method. Each power line (asset) has here a capac-
ity of 12 MW and is not used over 6 MW to provide
reserve capacity. In the first asset of the branch, com-
pulsory loads reaches today 5.4 MW (no bottleneck).
SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems
126

With the new loads, the sum grows to 13.8 MW (bot-
tleneck). Moreover, simultaneous conditional loads
can reach 8.4 MW and thus exceed the capacity of 6
MW of the N-1 band.
4.2 Initially Submitted Schedules
Figure 2 with power on left y-axis against time on x-
axis shows the initial solution (i.e. before control of
grid limits) of the load scheduling problem for cus-
tomers A (top row), B (middle row) and X (bottom
row) for the cloudy winter day of January, 11th. Con-
sumption respectively production are displayed sepa-
rately on the left resp. right graph. Grey bands repre-
sent the split in Standard Tariff for compulsory loads
in the lower part of positive power and Power Alliance
Tariff in the upper part with conditional load. Nega-
tive power is fed back to the grid. In customer A,
the PV unit (yellow) substitutes part of electricity im-
port from grid (black), and is used to run the power-
to-heat unit (blue) to substitute natural gas. The P-t-
H unit will also run with the cheap electricity price
of PAT (black, brindled) during afternoon hours with
the lowest spot price of the day. The Power-to-Gas
units of Customer X, as well as the Power-to-Gas
unit (blue) and the charging (red) of battery of Cus-
tomer B will run at the same afternoon hours as cus-
tomer A due to the spot price. Discharging (green)
happens here in morning hours, before charging, ei-
ther for substituting import from grid (black) or for
feed back to grid (purple), with a sufficient battery
capacity assumed in this model. The cooling units of
Customer C (not displayed) are modelled like a bat-
tery but with the hygiene constraint that charging can
only precede discharging, as the storage medium is
the frozen food. Therefore they run in the morning at
a different timestep than A and B.
4.3 Curtailment in Case of Excess Load
On Grid Level: GM controls the cumulative load of
all customers, displayed in Figure 3 with compulsory
resp. conditional loads in the lower resp. upper part.
When the lowest electricity spot price is attained be-
tween 2 p.m. and 6 p.m., conditional loads from A,
B and X get aggregated with 7.9 MW (left graph).
The conditional loads exceed the grid capacity limit
of 6 MW of the N-1 band and should be reduced by
1.9 MW. The loads are re-allocated for all customers
A, B and X according to a rationing scheme of Table
3. The curtailment is done proportionally to the num-
ber of points (allowances) of each customer without
exceeding their initially submitted schedule. In case
a customer asked less than its allowance (here C), the
remaining non-allocated capacity is redistributed iter-
atively among the other customers to avoid waste of
capacity.
Table 3: Curtailment on grid level.
points submitted (kW) final (kW)
A 500 500 379.7
B 400 400 303.8
C 500 0 0
X 7000 7000 5316.5
sum 8400 7900 6000
On Aggregate Level: After each customer reads
the amount of its curtailment for each timestep, it
computes the local curtailment on the level of each
aggregate. Aggregates are modelled here with an inte-
ger number of stages between a minimal (here 0) and
maximal power. The allocation with least wasted ca-
pacity is solved as a subsum problem. Table 4 shows
the local curtailment of timestep 53 of customer B.
Both units are cut in order to reach 303 kW, the max-
imal value not exceeding the allowance of 303.8 kW
from Table 3. The cases of Customer A (with only one
unit of P-to-H) and of Customer X (with four units of
P-to-G) are treated in a similar way. The schedule
of ”discharging” is finally adjusted on customers with
battery like B to respect the daily energy balance.
Table 4: Curtailment on aggregate level for customer B.
max levels original (kW) final (kW)
P-to-G 300 100 300 204
charging 100 100 100 99
sum 400 - 400 303
4.4 Discussion
With new loads, two issues were expected: (1.) In
the absence of the concept of conditional loads, a grid
reinforcement would have been needed in the first as-
set (even with only the new loads of customers A, B
and C). (2.) in presence of customer X and due to load
synchronization at the cheapest timestep, the 6 MW of
N-1 band were overbooked in the initial schedules and
a reinforcement would have been needed in absence
of curtailment. The RLS approach with use of N-1
band and with curtailments solves both problems and
enables finding schedules valid for both sides. The
schedule curtailed by GM fulfills the grid limit with-
out wasting of capacity in the N-1 band. EM reduces
schedules on aggregate level accordingly without nei-
ther wasting capacity nor disturbing the energy bal-
ance of batteries. In the aggregated schedule in Figure
3, the effective use of the N-1 band drops from 26.7 %
(left) to only 22.0 % (right, after curtailment) but the
system is safe for all stakeholders to be operated.
Technical Validation of the RLS Smart Grid Approach to Increase Power Grid Capacity without Physical Grid Expansion
127
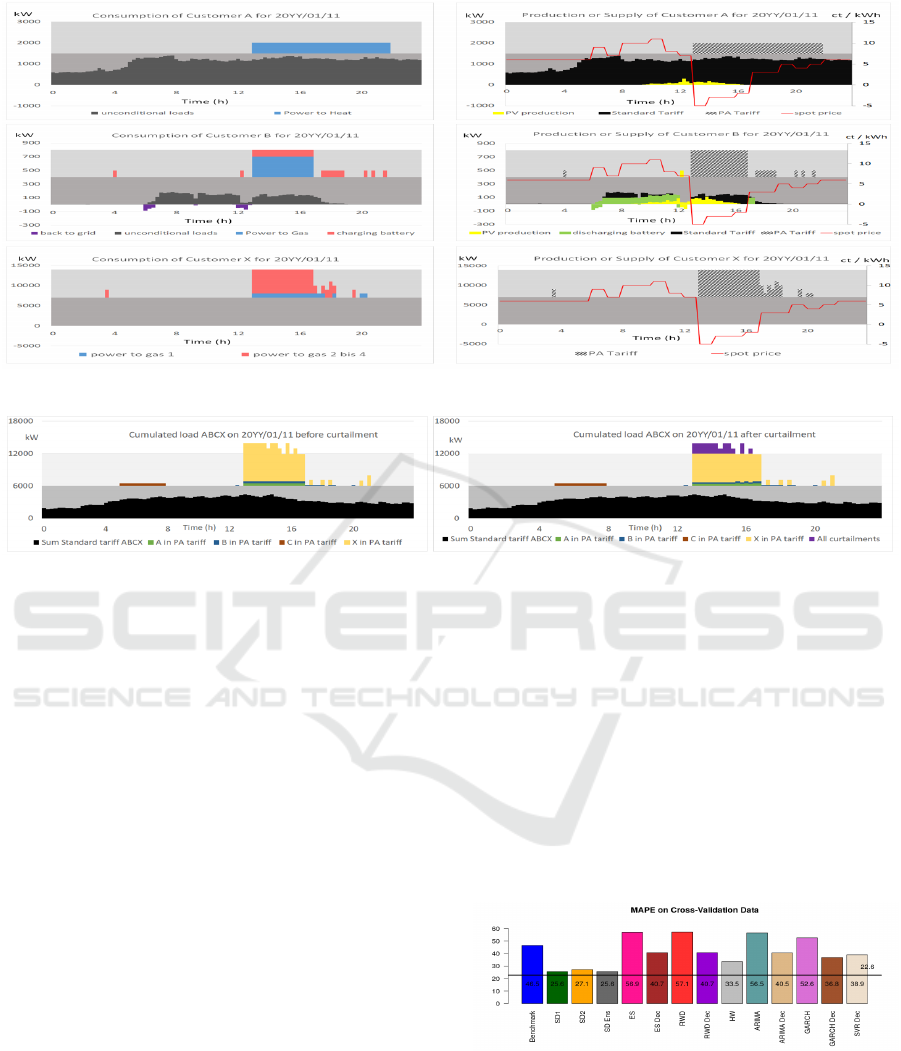
Figure 2: Initial solution of schedule for customers A (top), B (middle) and X (bottom).
Figure 3: Cumulated load of Customers A, B, C and X in the first asset of the grid branch: initial (left) and curtailed (right).
5 LOAD FORECASTING
5.1 Underlying Data Set
Our test data set comprises 34 end node load profiles
of 31 customer including three pilot customers. All
of them have a minimum yearly power demand of
200kW. Time series that were available for multiple
years have been split into separate fictitious end nodes
such that finally time series of 40 end nodes were
available for one full year. Applied pre-processing
steps as down- and up-sampling, replacement of miss-
ing data points, time shifts to match summer and win-
ter time as well as leap years ensure the comparability
between all time series.
5.2 Evaluation of Prediction Accuracy
We use the MAPE as a metric for evaluating the pre-
diction accuracy of our test data set. Figure 4 summa-
rizes the results. Here, the employed models are indi-
cated on the horizontal axes and ordered by increas-
ing complexity, on the y-axes the average MAPE is
shown when a model is applied in a one-fits-all man-
ner to all end-nodes. The black horizontal line in-
dicates the average MAPE of the MSA with 22.6%
(averaged over all end-nodes). This result is compet-
itive with results in literature in comparable settings
(Marino et al., 2016; Shi et al., 2018). A single model
yields a considerable higher average MAPE than the
MSA. Yet, when compared to the SD1 model with an
average MAPE of 25.6%, the MSA does not achieve
considerably higher prediction accuracy on average.
This result suggests that the much higher computa-
tional effort of employing the MSA does not justify
the relatively small gain in prediction accuracy when
employing the very simple SD1 model.
Figure 4: Overview of prediction accuracy of all integrated
algorithms in the Model Selection Approach (MSA).
In order to analyze this result in more detail, we
compared the prediction accuracy of the MSA with
the prediction accuracy of the SD1 model for each
single end-node. The distribution of the differences
MAPE(SD1) − MAPE(MSA) shows that no accuracy
gain is provided by the MSA for 10 of the 40 end
SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems
128

nodes. In other words, for 25% of the end-nodes,
the best performing model selected by the MSA is
the SD1 model itself. Yet, it also showed that the
MSA achieves a MAPE increase of more than 25.6%
for 14 of the 40 end-nodes. This amounts to an ac-
curacy improvement of more than 100% when com-
pared to SD1. Particularly, for two end-nodes, the
MSA achieves a MAPE increase of about 140% and
200%, respectively. That means while the MSA does
not provide considerable improvement of prediction
accuracy on average, it does improve the prediction
accuracy for some single end-nodes dramatically.
Furthermore, figure 4 shows that for our test data
on average simpler models tend to achieve better re-
sults than more complex ones. This result is consis-
tent with the experience of our partner DSOs.
5.3 Evaluation of Prediction Reliability
The MAPE as a measure of prediction accuracy does
not provide end-customers and DSOs with a measure
of prediction reliability (i.e., accuracy and precision).
Yet, a reliable day-ahead prediction of load demands
is pivotal since it increases their ability to plan and
decreases financial risk considerably. Prediction in-
tervals as measures of prediction reliability rely on the
assumption of normally distributed errors, an assump-
tion that is violated for most of our test data. While it
is usually possible to find suitable transformations for
single load profiles manually, automating this process
as a part of the RLS software is not a straight forward
task. Hence, we assessed the ”true” reliability of pre-
diction intervals based on historic data.
Figure 5: Historic prediction reliability per end node.
The lower part of figure 5 shows the historic pre-
diction reliability for our test data: for each of the 40
end nodes the percentage of observations falling in the
80%, 95%, 99% and 99.73% prediction interval (PI)
is shown in the figure as a blue, green, yellow and
grey line plot, respectively. It can be seen that the his-
toric reliability of the 99% and 99.73% PI is greater
than 95% for all end nodes. The upper part shows
the inverse percentage (i.e., the percentage of obser-
vations exceeding the upper limits of the respective
PIs), together with error bars indicating the PI.
5.4 Discussion
Two main findings are discussed. (1.) While the MSA
only achieves a negligible increase of 3% in MAPE
on average compared to the simplistic SD1 model,
it allows an accuracy increase of more than 25% for
35% of the end nodes and a dramatic increase of over
100% in MAPE for two end nodes. The result justi-
fies the drastically higher computational effort in em-
ploying an MSA compared to SD1. In operation, ex-
cluding never chosen models from the MSA will in-
crease the computational efficiency. Yet, to accom-
modate possible changes in the data sources, they are
included in every n-th model training/fitting iteration
step. To further improve prediction accuracy, LSTM
neural networks are tested for selected customers with
additional customer-specific information. (2.) With
a true reliability of 95%, tests on the prediction re-
liability - measured by the true percentage of obser-
vations falling in the 99% prediction interval - have
been satisfactory, and serve to assess the usefulness
of predictions as a day-ahead load schedule for un-
conditional loads within the RLS context. Here, the
upper band of the prediction interval determines the
margin of unused grid capacity that may be used to
further optimize the scheduling of conditional loads.
6 CONCLUSIONS
We tested and validated the technical aspects of the
RLS approach currently deployed at the pilot cus-
tomers with live data and comprising (1.) grid-aware
load scheduling with heuristic price optimization, and
(2.) day-ahead prediction of individual unconditional
customer loads. Thanks to the control of grid lim-
its by the DSO and subsequent curtailment, the load
scheduling method is safe for use even if the amount
of initially submitted conditional loads exceeds the
N-1 band. The functionality of the system is veri-
fied. Planned improvements include an analysis of
the fairness, efficiency and performance of the cur-
tailment mechanisms with the goal to further decrease
energy costs. The evaluation of the model selection
approach for predicting unconditional loads w.r.t. ac-
curacy and reliability showed competitive results with
the literature. Future work include an extension of the
load scheduling approach with the goal to use the full
range of unused grid capacity for future congestion
scenarios. To this end the band used for load shifting
will be extended from the fixed-width N-1 band to the
Technical Validation of the RLS Smart Grid Approach to Increase Power Grid Capacity without Physical Grid Expansion
129

variable-width CL-band (cf. figure 1). It is bounded
by the upper limit of the PI of the day-ahead predic-
tion of uncond. loads used as day-ahead schedule.
REFERENCES
Arora, S. and Taylor, J. W. (2016). Forecasting electricity
smart meter data using conditional kernel density es-
timation. Omega, 59:47–59.
Atzeni, I. (2014). Distributed demand-side optimization in
the smart grid. PhD thesis.
Bagemihl, J., Boesner, F., Riesinger, J., K
¨
unzli, M., Wilke,
G., Binder, G., Wache, H., Laager, D., Breit, J.,
Wurzinger, M., Zapata, J., Ulli-Beer, S., Layec, V.,
Stadler, T., and Stabauer, F. (2018). A market-based
smart grid approach to increasing power grid capacity
without physical grid expansion. Computer Science -
Research and Development, 33(1-2):177–183.
Doostizadeh, M. and Ghasemi, H. (2012). A day-ahead
electricity pricing model based on smart metering and
demand-side management. Energy, 46:221–230.
Ghofrani, M., Hassanzadeh, M., Etezadi-Amoli, M., and
Fadali, M. S. (2011). Smart meter based short-term
load forecasting for residential customers. In 2011
North American Power Symposium, pages 1–5.
Hunziker, C., Schulz, N., and Wache, H. (2018). Shap-
ing aggregated load profiles based on optimized local
scheduling of home appliances. Computer Science -
Research and Development, 33:61–70.
Kong, W., Dong, Z. Y., Jia, Y., Hill, D. J., Xu, Y., and
Zhang, Y. (2017). Short-term residential load fore-
casting based on lstm recurrent neural network. IEEE
Transactions on Smart Grid.
Marino, D. L., Amarasinghe, K., and Manic, M. (2016).
Building energy load forecasting using deep neural
networks. In Industrial Electronics Society, IECON
2016-42nd Annual Conference of the IEEE, pages
7046–7051. IEEE.
Mirowski, P., Chen, S., Ho, T. K., and Yu, C.-N. (2014). De-
mand forecasting in smart grids. Bell Labs technical
journal, 18(4):135–158.
Mocanu, E., Nguyen, P. H., Gibescu, M., and Kling, W. L.
(2016). Deep learning for estimating building energy
consumption. Sustainable Energy, Grids and Net-
works, 6:91–99.
Mohsenian-Rad, A.-H. and Leon-Garcia, A. (2010). Op-
timal residential load control with price prediction
in real-time electricity pricing environments. IEEE
Transactions on Smart Grid, 1:120–133.
Ryu, S., Noh, J., and Kim, H. (2016). Deep neural network
based demand side short term load forecasting. Ener-
gies, 10(1):3.
Shaikh, P. H., Bin Mohd Nor, N., Nallagownden, P., Elam-
vazuthi, I., and Ibrahim, T. (2014). A review on op-
timized control systems for building energy and com-
fort management of smart sustainable buildings. Re-
newable and Sustainable Energy Reviews, 34:409–
429.
Shariatzadeh, F., Mandal, P., and Srivastava, A. K. (2015).
Demand response for sustainable energy systems: A
review, application and implementation strategy. Re-
newable and Sustainable Energy Reviews, 45:343–
350.
Shi, H., Xu, M., and Li, R. (2018). Deep learning for
household load forecasting—a novel pooling deep
rnn. IEEE Transactions on Smart Grid, 9(5):5271–
5280.
Taylor, J. W. (2010). Triple seasonal methods for short-term
electricity demand forecasting. European Journal of
Operational Research, 204(1):139–152.
Taylor, J. W., De Menezes, L. M., and McSharry, P. E.
(2006). A comparison of univariate methods for fore-
casting electricity demand up to a day ahead. Interna-
tional Journal of Forecasting, 22(1):1–16.
Taylor, J. W., McSharry, P. E., et al. (2007). Short-term
load forecasting methods: An evaluation based on eu-
ropean data. IEEE Transactions on Power Systems,
22(4):2213–2219.
Thirugnanam, K., Kerk, S. K., Yuen, C., Liu, N., and Zhang,
M. (2018). Energy management for renewable micro-
grid in reducing diesel generators usage with multiple
types of battery. IEEE TRANSACTIONS ON INDUS-
TRIAL ELECTRONICS, 65:6772–6786.
Zhao, Z., Lee, W., Shin, Y., and Song, K. (2013). An opti-
mal power scheduling method for demand response in
home energy management system. IEEE Transactions
on Smart Grid, 4:1391–1400.
Zheng, J., Xu, C., Zhang, Z., and Li, X. (2017). Electric
load forecasting in smart grids using long-short-term-
memory based recurrent neural network. In Informa-
tion Sciences and Systems (CISS), 2017 51st Annual
Conference on, pages 1–6. IEEE.
Zufferey, T., Ulbig, A., Koch, S., and Hug, G. (2016). Fore-
casting of smart meter time series based on neural net-
works. In International Workshop on Data Analyt-
ics for Renewable Energy Integration, pages 10–21.
Springer.
SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems
130
