Efﬁcient Routing for Overlay Networks in a Smart Grid Context

Lasse Orda

, Tue Vissing Jensen

, Oliver Gehrke

and Henrik W. Bindner

Department of Electrical Engineering, Technical University of Denmark, Kongens Lyngby, Denmark

Keywords:

Smart Grid, Overlay Network, Peer-to-Peer (P2P), Distributed Hash Table (DHT), Routing Table, Location-

aware Routing.

Abstract:

In the modern smart grid, prosumers and communities, organized in energy collectives, are showing an in-

creased desire to trade energy directly using different forms of decentralized market models. To support local

autonomy and distributed services, decentralized networking, using peer-to-peer (P2P) networks, can be used

to facilitate dynamic discovery and establish communication between peers. When using a modern overlay

network based on a Distributed Hash Table (DHT), the performance of the overlay network can be improved

by using the physical properties found in the smart grid context. This paper presents an improved network

routing model that takes advantage of these properties, to add a location-aware heuristic to the search algo-

rithms of a standard overlay network. Concepts from complex networks are utilized to improve the average

search path and provide a more efﬁcient design over previous solutions. A proof of concept shows that the

design results in a more efﬁcient routing model, when used in a smart grid context, compared to a standard

uniformly distributed network model.

1 INTRODUCTION

Peer-to-peer networks provides decentralized and dis-

tributed communication that can facilitate the dy-

namic network conﬁguration of distributed energy re-

sources (DER) in a distributed network. Large net-

works such as consumer broadband and the internet

is slow to adapt to changes (Nygren et al., 2010) and

do not provide all of the features to support decentral-

ized communication. Overlay networks are developed

to provide these features, can be rolled out with a fast

cadence, and provides features such as predictable la-

tency (Andersen et al., 2001), scalability, improved

robustness and resilience.

The desire from prosumers and energy collectives

(Moret and Pinson, 2018) to engage in dynamically

changing contract relationships, building micro-grids

and operate fully decentralized, requires a communi-

cation layer that can handle decentralization and the

continuous changes in network topology.An overlay

network can provide the solution and facilitate the

growth of new services and markets (Greer et al.,

2014).

https://orcid.org/0000-0002-1787-3559

https://orcid.org/0000-0002-6594-5094

https://orcid.org/0000-0001-8184-6435

https://orcid.org/0000-0003-1545-6994

In a smart grid, DERs connected to the grid, have a

location property. The location can be static as in the

case of stationary DERs or it can be dynamic in the

case of electric vehicles (EV). An overlay network is

generally based on a uniform distribution of nodes in

the network, which ensures robustness and resilience.

However the additional properties introduced by the

smart grid add both requirements (Budka et al., 2014)

to the overlay network as well as the possibility to

optimize the distribution of nodes.

The topic of location aware overlay networks and

multi-dimensional identiﬁers has been touched upon

by related research, however these works have fo-

cused on their speciﬁc goals and interests, e.g. the

work of (Gross et al., 2013) on searching for peers in

a speciﬁc geographical location. This paper presents a

design of an overlay network that, in a smart grid con-

text, supports using multiple attributes for routing and

improves performance over previous solutions. The

location property of the smart grid, makes it possible

to add location aware routing to the overlay network

and use a location-based heuristic to calculate the dis-

tance between nodes. To support multi-dimensional

routing, concepts from complex network theory is

used to structure a routing table that improves rout-

ing efﬁciency.

The overlay network presented in this paper builds

Orda, L., Jensen, T., Gehrke, O. and Bindner, H.

Efﬁcient Routing for Overlay Networks in a Smart Grid Context.

DOI: 10.5220/0007717702510258

In Proceedings of the 8th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2019), pages 251-258

ISBN: 978-989-758-373-5

251

upon the related work presented in section 2, with the

design of an efﬁcient multi-dimensional routing table

presented in section 3. A proof of concept is described

and tested in section 4 and the results are presented

and evaluated in section 5.

2 RELATED WORK

Modern overlay networks are based on a distributed

hash table (DHT) (Stoica et al., 2001) which contains

nodes with a unique identiﬁer using a uniform dis-

tribution of nodes in the network. The identiﬁer is

used to calculate the distance between nodes, which

is used in the search algorithms. Making overlay net-

works location-aware has seen several suggestions.

One way is to map the multi-dimensional space onto

the one-dimensional space of the identiﬁer (Lopes and

Baquero, 2007), (Nam and Sussman, 2006), (Zahn

et al., 2006), e.g. using space ﬁlling curves (Kova

et al., 2007), (Chawathe et al., 2005a), (Knoll and

Weis, 2006), but it has been shown that it is difﬁ-

cult to do this optimally and it is hard to preserve

the original location (Chawathe et al., 2005b). Other

designs are based on tree structures that are parti-

tioned into a two dimensional space that maps the

two dimensions of a location (Harwood and Tanin,

2003), (Ara

ujo and Rodrigues, 2003), (Asaduzzaman

and von Bochmann, 2009), (Heutelbeck and Hemmje,

2006), (Picone et al., 2010). In (Harwood and Tanin,

2003) super-peers are used to control a region and

handle load balancing, but these approaches are sus-

ceptible to dynamic changes in the network. Another

approach is to partition the space into grids (Kantere

et al., 2009), but this suffers from poor performance

during high churn as well as load balancing issues

(Chawathe et al., 2005b).

Kademlia (Maymounkov and Mazieres, 2002) is a

well-known overlay network based on a DHT. The ba-

sic Kademlia routing table is an unbalanced tree with

leafs (known as k-buckets) covering a 160 bit address

space. Each k-bucket covers a part of the range of

the 160 bit space and together all the k-buckets covers

the entire address space in the network. This rout-

ing table provides a segmentation of the network and

fast lookup. However, encoding multiple dimensions

into the 160 bit identiﬁer is not easy without losing

the data needed to calculate the distance metric. Re-

placing the original XOR metric with one based on,

e.g., the Haversine distance (Korn, 2000) presents a

problem as the address space of the identiﬁer is un-

known in a dynamic system. This makes it difﬁcult to

efﬁciently create a k-bucket range, or would require

continuously restructuring of the k-bucket space, re-

sulting in poor performance.

Geodemlia (Gross et al., 2013) proposes a solution

to this by creating a small range of buckets which ﬁrst

sorts nodes into buckets depending on their bearing

and then into a number of distance-buckets with expo-

nentially increasing distance. However, the width of

the address space in the k-buckets used in Geodem-

lia is statically deﬁned, which makes it susceptible

to having unbalanced buckets e.g. in the case of

heavily clustered nodes within a small area, resulting

in a longer search path. Geodemlia add new nodes

with a probability inverse proportional to the distance,

meaning that it contains more nodes nearby than far

away. This fulﬁlls the long-range property (Aberer

et al., 2005), but leaves room to optimize the average

path length.

Applying small-world network and scale-free net-

work models can improve network performance

(Amaral et al., 2000), while the average path length

can be reduced by organizing the nodes in a network

using the concepts in a small-world network. Watts-

Strogatz (Watts and Strogatz, 1998) were some of the

ﬁrst to study small-world networks and describes a

model to produce graphs with small-world properties.

The Barabasi-Albert model describes an algorithm to

generate scale-free network with preferential attach-

ment, which can be used to generate small-world net-

works (Albert and Barab

asi, 2002). The Barabasi-

Albert model is interesting because it generates net-

works without the need for a ﬁxed address space. This

makes it especially useful for use in a dynamic net-

work growth scenario.

A smart grid can be a highly dynamic system e.g.

in the case where EV’s move around, resulting in new

locations, while properties of the nodes change de-

pending on the applications and services they provide

and participate in. The overlay network can be im-

proved over previous solutions by using a heuristic

that enables a directed search in the network. Routing

efﬁciency and load balancing can be improved by ap-

plying concepts from scale-free and small-world net-

works, most importantly local clustering, long-range

property and random hubs, resulting in an overall

shorter average path.

3 ROUTING IN A SMART GRID

The overlay network presented in this section builds

on the Kademlia overlay network and uses its proto-

cols and search algorithms. The routing table in the

underlying network has been replaced to support lo-

cation aware routing and search, but can support any

number of dimensions. The new routing table is de-

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

252

(a) A search using uni-

form node distribution rip-

ples out from the starting

position.

(b) Using a location based

heuristic results in directed

search and a shorter average

path.

Figure 1: Using a heuristic to optimize the search path.

signed to support a multi-dimensional metric and dis-

tance calculation.

A standard DHT based overlay network uses a

uniform distribution of nodes that provides global re-

silience, load-balancing, good support for churn and

many other features. When location is introduced,

the distribution becomes clustered around the nodes

physical location, this improves local resilience, per-

formance and efﬁciency, but at the cost of global ro-

bustness. To improve global performance, the model

and properties of small-world networks is used to im-

prove both local and global performance.

As the underlying routing and iterative search al-

gorithm is based on uniformly distributed nodes, the

result is that the search will spread out in all directions

as shown on ﬁgure 1a. With the additional properties

in the smart grid, the search performance is improved

by using the location in the heuristic for the distance

calculation. The heuristic is based on the geograph-

ical distance between the nodes and by directing the

search towards the target node, shown on ﬁgure 1b,

the search path length is reduced.

3.1 Improved Routing Table

In a small-world network most of the nodes are not

neighbors, but there likely exists a connection be-

tween the neighbour of a given node and other nodes.

A property of small-world networks is that most

nodes can be reached with a small number of steps.

Another property of small-world network is robust-

ness as the shortest paths between nodes ﬂow through

hubs, and if a peripheral node is deleted it is unlikely

to interfere with connection between other periph-

eral nodes. As the amount of peripheral nodes in a

small world network is much larger than the amount

of hubs, the probability of deleting an important hub

node is low.

These properties of the small-world network pro-

vides good average performance both when querying

(a) Local neighbors. (b) Random neighbors.

Figure 2: Network model concepts used to improve routing

efﬁciency.

local clustered nodes as well as nodes in remote clus-

ters. In a standard overlay network, the identiﬁer as-

signed to each node is a simple hash value. To provide

support for multiple dimensions, a complex identiﬁer

is required to contain multiple dimensions, such as

a unique id, and coordinates. Because the identiﬁer

of the node consist of multiple dimensions, the un-

derlying DHT design with k-buckets cannot be used.

Instead the design must handle multiple dimensions

and do it in a dynamic way, such that the grouping of

nodes does not causes hot-spots. Previous solutions

uses ﬁxed ranges for the buckets or require continuous

recalculation. Preferably the design should adapt to

changes in the network by adjusting the bucket ranges

over time and in a way that does not require recalcu-

lation.

The local nodes in ﬁgure 2a ensures detailed

knowledge of nearby nodes. This is the most ba-

sic bucket of nodes, but needs a dynamic approach

that adapts the probability of nodes being added so

that it can adjust to different networks automatically.

The random neighbors in ﬁgure 2b provides the long-

range property, which compliments the local nodes by

providing access to random remote nodes. The in-

clusion of random nodes results in a shorter path on

average. The random hubs in ﬁgure 2c is an addi-

tional improvement, where hubs in the network fur-

ther cut down the average path. A hub is known by

many nodes and know many nodes, which compared

to random nodes results in fewer network hops. The

routing table uses dynamic ranges, such that as the

network grows, the routing table dynamically adapts.

Efﬁcient Routing for Overlay Networks in a Smart Grid Context

253

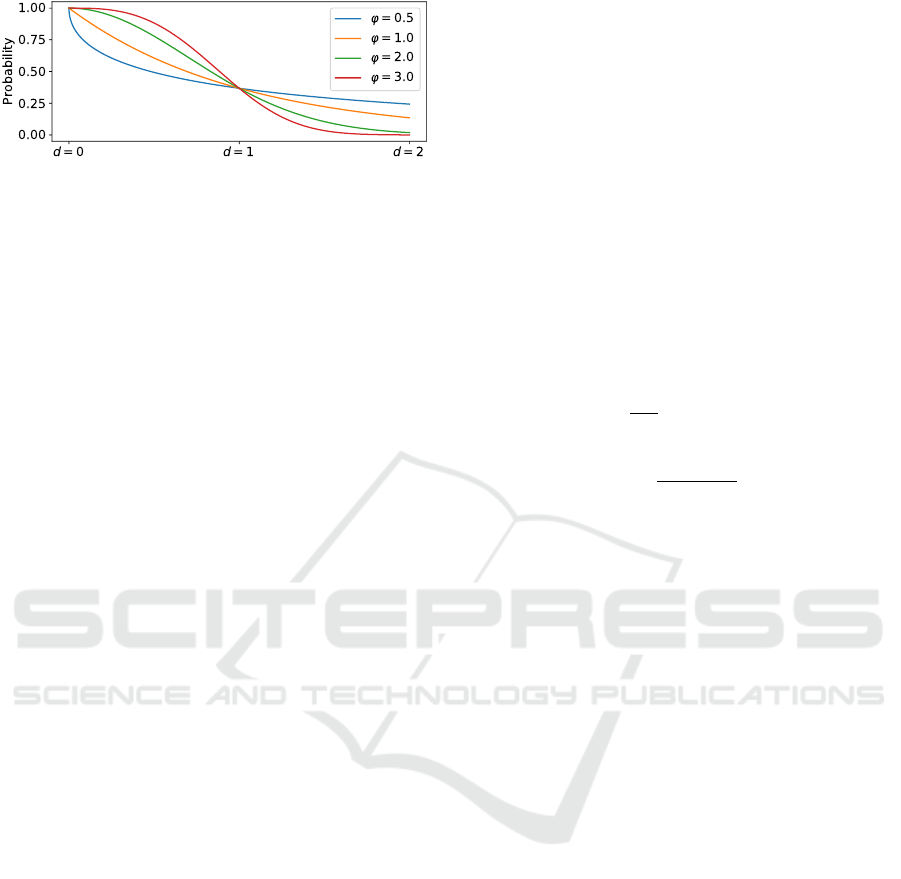
Figure 3: Probability curves for d

avg

= 1. ϕ affects the prob-

ability of nodes being added to A, such that more remote

nodes can be allowed or disallowed into A.

The design of the routing table consists of three

classes of buckets: A, a dynamic range based bucket

of local nodes; B, a bucket containing random nodes;

and C, a bucket of network hubs.

The local nodes bucket A, holds the local neigh-

bor nodes and creates a cluster with neighboring

nodes such that local nodes have good connectivity.

This provides very fast local communication and fast

lookup when queried by a remote node.

(d) = e

−(d/d

avg

)

(1)

A has a max size A

max

of suitable proportions such

as 1.000. Nodes are added to A with a probability P

shown in equation 1, such that the chance of nodes

being added to routing table A decreases exponen-

tially as the distance grows. d denotes the distance

to the node, d

avg

is the average distance of the nodes

currently in A and ϕ describes the slope of the curve,

whether it should include more nodes with long dis-

tance or with a short distance.

Figure 3 shows the characteristics of probability

with changes to ϕ. The probability curve is dynami-

cally updated as d

avg

changes with time, as the net-

work grows and the overlay network learns about

other nodes. When there are many nearby nodes,

the curve will prefer nodes that are even closer and

nodes far away have less probability for being added.

When there are less nearby neighbors, the algorithm

allows for nodes further away to be added. This is an

improvement over previous solutions that uses ﬁxed

sizes for sub-buckets, which can lead to unbalanced

buckets.

Removal of nodes, happens using a FIFO queue,

though with a preference for nodes which are inac-

tive, described in equation 2 and 3. When a node

becomes inactive e.g. because it is unresponsive or

returns bad results, it is placed in a passive queue. As

nodes are removed from a bucket, the passive nodes

are removed ﬁrst, and then active nodes are removed,

both in FIFO order.

n =

(

[0] if L

∩ Q =

∩ Q)[0] otherwise

(2)

(L,Q) =

(

(L \ {n}, Q{n}) if n ∈ Q

(L \ {n}, Q) otherwise

(3)

L denotes the node bucket to remove a node n

from, i.e A, B or C, and Q is the queue of passive

node.

The random neighbor bucket B, contains nodes

which exhibit the long-range property of small-world

networks and the distribution is completely random.

Nodes with any distance can be added, as statistically,

the larger portion of nodes in the network are further

away from a given node, than its nearby neighbors

and as such, there is no need to cut-off nodes with a

short distance. The long-range property is important

to provide connectivity to nodes far away and thereby

reduce the path length for non-local queries.

rate = r ·

last

+ (1 − r) · prev rate (4)



rate

target rate



−1

(5)

Nodes are added to and removed randomly from

B, operating on a passive modus. I.e. whenever other

nodes makes contact, they are added to B. The ran-

dom property of B is important to keep the robust-

ness of the network, but to avoid excessive rotation

of nodes and mitigate abuse or bad behavior, the in-

clusion of nodes is rate limited. The rate, in equation

4, continually adjusts to reach a target rate. The tar-

get rate can be some constant e.g. add max 10 nodes

per second or it can be dynamically updated based on

network performance or user preference. The rate is

based on the previous rate and to help dampen ﬂuctu-

ations, a smoothing factor r is added to the rate. P

then calculated based on the rate and the target rate, in

equation 5, to provide a probability for adding a new

node to the bucket.

The random hubs bucket C, consists of nodes that

are estimated to be hubs. As the network grows, some

nodes becomes known to many nodes and as such,

over time, they become a hub in the network. A node

is acquired on an active modus, by actively querying

random known nodes for a single random node. This

action is scheduled to happen periodically, e.g. on the

underlying maintenance loop. New nodes are simply

added with no restrictions, as the discovery of new

nodes happens in a controlled loop.

When a search is initiated or a query is received

from the network, the standard procedure is to com-

pute and return k nodes from the routing table by

calculating the distance with a given identiﬁer. In

Kademlia the standard speciﬁes that k is 20. Here,

using A, B and C a mix of nodes from each is returned

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

254

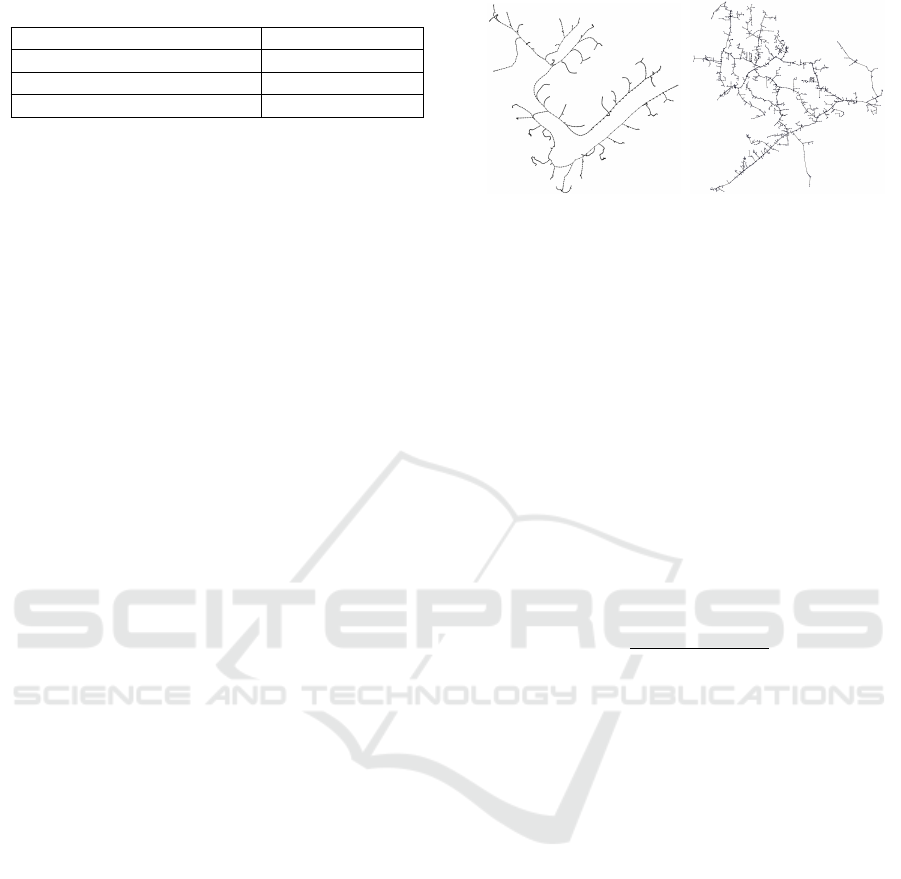
Table 1: Nodes in test networks.

Test network Number of nodes

European test feeder 900

8500 entity test feeder 2.500

NetworkX geometric network 2.000

to fulﬁll the properties of a small-world network to

form the search set S:

S = A{m} ∪ B{n} ∪C{n},k = m + n + n, (6)

where the notation A{m} indicates that m random

nodes are selected from A.

A smaller range from B and C e.g. n = 5 is re-

turned and a larger range from A e.g. m = 10 is re-

turned. A larger portion of nodes from A is used to in-

crease the probability of returning a local node which

may be relevant for the request and to support the un-

derlying algorithm, which has several functions that

requires the nearest neighbours of a node. S in equa-

tion 6, is sorted according to the distance to the given

target node deﬁned in the query and returned to the

network query or to the underlying routing algorithm.

4 PROOF OF CONCEPT

To evaluate the efﬁciency of the routing table, it was

tested in 3 different scenarios. The scenarios consists

of networks based on the IEEE European Low Volt-

age Test Feeder, the IEEE 8500 Entity Test Feeder

(Dugan et al., 2009) and a generated geometric scale

free network created with the Python library Net-

workX (Hagberg et al., 2008).

The routing table design has been implemented

in a prototype overlay network along with an imple-

mentation of the default Kademlia speciﬁcation. The

two implementations utilizes the same underlying al-

gorithms described by Kademlia.

The IEEE Test Feeder networks, shown in ﬁgure

4, provides realistic test cases for testing the location

aspect of the heuristic and routing. The test feeders

are used both to provide the location data as well as

the initialization of the DHT state of the communica-

tion links between the nodes in the overlay network.

Using the test feeder as a model for a computer net-

work, where every node is more or less chain-linked

to only one or two other nodes, results in an unnatural

state on initialization for the overlay network. It does

however provide a good initialization state for com-

paring how efﬁcient the routing is able to ﬁnd its way

through the network and to analyze how the routing

table is built as it interacts with the network.

Tests are performed using multiple iterations, each

with a randomized start point and end points in the

(a) 900 node test feeder lay-

out.

(b) 2.500 node test feeder

layout.

Figure 4: IEEE Test Feeders.

network. Each iteration has multiple sub-iterations

using the same starting node for the iteration, but with

randomized end nodes. This ensures that the network

is subjected to queries across more than 90% of the

network.

As each search in the network results in a path

that has a different length and because the nodes are

randomly chosen, the results cannot be directly com-

pared and needs to be normalized with the shortest

path. The shortest path is obtained by utilizing Di-

jkstra’s shortest path algorithm on the full network

model, which is used to initialize the network. The

resulting efﬁciency factor ω can be used to compare

the tests:

ω =

query path length

shortest path

, (7)

where the query path length is the total path tra-

versed in the query including the path count of the

sub-queries sent as parallel queries in the algorithm.

Note, that ω may be less than 1, as the query path may

be shorter than the initial path length after routing ta-

ble updates.

To simulate an active network, where every node

is alive, each node should randomly do some work to

exercise its routing table, this will help build the con-

nections between the nodes. To achieve this, a random

amount of nodes performs a search in the network for

each sub-iteration of the reference node.

4.1 Test Conﬁguration

The test feeder networks are tested with the standard

bucket size k = 20 and k = 10 for the default overlay

network and with a range of sizes, noted in table 2,

for the multi-dimensional routing table. The purpose

is to explore the impact of various bucket sizes. Since

a bucket size of 3.000 would equate to a DHT that can

contain every node in the European test feeder and

about half of the nodes in the 8500 entity test feeder

network, it is necessary to test the network using a

smaller bucket size to simulate a network where the

Efﬁcient Routing for Overlay Networks in a Smart Grid Context

255

DHT can only know a portion of the total nodes. This

will make the efﬁciency of the routing table have an

effect as the nodes learns about the network.

Table 2: DHT bucket sizes used for testing.

Overlay network Bucket sizes (k)

Kademlia 3.200 (k = 20)

1.600 (k = 10)

Multi-Dimensional 3.000

300

150

The size of each bucket: A, B and C in the multi-

dimensional routing table is 1/3 of the number in table

2, which means that e.g. A has a size of 1.000.

The NetworkX generated network uses a geomet-

ric network model with small-world network proper-

ties, to provide an initialization that is similar to a

real computer network. This provides a more real-

istic starting point for testing albeit less realistic with

regards to the location aspect.

5 RESULTS

5.1 Efﬁciency of Routing Tables

The ﬁgures 5a, 5b and 5c show the results of running

the test on the three different network models. On

ﬁgure 5 and 6, md references the multi-dimensional

routing table and kd references the standard Kadem-

lia routing table. The dotted lines are the results of

the default overlay routing based on Kademlia with

standard bucket size and also k = 10. The other lines

shows the multi-dimensional routing table using the

four different bucket sizes. The curve is very steep in

the ﬁrst few iterations, as the overlay networks learn

about the nodes in the network. Because the nodes are

initialized with a very simple state, the ﬁrst queries in

the network will ﬁll up the routing tables quickly. The

results on ﬁgure 6 show the average bucket size across

the entire network for each iteration. The connection

between the efﬁciency on ﬁgure 5 and the bucket size

shows that, as the buckets are ﬁlled, the efﬁciency im-

proves. Generally the standard routing table is ﬁlled

faster than the multi-dimensional routing table, this

is partly because the standard routing table performs

more queries in the network and partly because of the

conﬁguration of the probability curves for the multi-

dimensional routing table. A continuous increase in

performance on ﬁgure 5 can be seen from the graphs

as the properties from small-world networks begins to

have an effect. The Kademlia curve reaches a plateau,

where it doesn’t really improve any further with the

given network. But the multi-dimensional routing ta-

ble continually improves its efﬁciency as it is able to

bring down the average path length by taking advan-

tage of the long-range and random hub properties.

The difference in efﬁciency, using different bucket

sizes becomes visible in two different ways: ﬁrst the

initial learning curve lands on different levels, where

the size of the bucket dictates the efﬁciency level, a

larger bucket can hold more nodes giving a larger

knowledge space. The second way is less obvious,

in the test feeder networks, the smaller buckets actu-

ally converges to about the same efﬁciency, but still

with an improving trend. However, using too small a

bucket size hinders increase in efﬁciency as the bucket

will start forgetting nodes. The overall efﬁciency in-

crease across all three networks is about a factor 10.

A good solution has both a small ω and a small bucket

size. The less space used, the more optimal the solu-

tion is.

5.2 Discussion

In the presented routing table, an issue arises, when

the algorithm has to move in a direction that goes

against the heuristic. Since the heuristic prefers to

move towards the target node location, it tends to ex-

amine the nodes in that direction ﬁrst, but if the only

connection to the node is through a node that lies fur-

ther away than the given start node, it will prefer to

not take that route. This is where the random neighbor

and random hubs are important, as they allow the al-

gorithm to try a search starting from a different point

in the network. This not only allows the search to

succeed, it also improves the average path length.

To improve network stability and to provide

some protection against attacks like denial of service

(Douceur, 2002), additional properties may be tied to

the nodes to affect whether a node should be kept in

the routing table or removed. These properties could

range from long-lived nodes, query round-trip time,

bandwidth, load-balancing indicator etc. Adding a la-

tency property to the routing would enable the algo-

rithm to ﬁnd the path with the lowest congestion.

Churn, i.e. nodes entering and leaving the over-

lay network, is an inherent and signiﬁcant property

of overlay networks (Stutzbach and Rejaie, 2006). In

our work, it was not necessary to test churn, as the

focus was on location based heuristics and establish-

ing an efﬁcient routing table. The simulated systems

were based on power grids, where the unit state, based

on location, updates rarely. Applying the small-world

network model is something that can improve routing

during churn, e.g. if a node leaving has blocked the

path to a target node, the small-world network is able

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

256

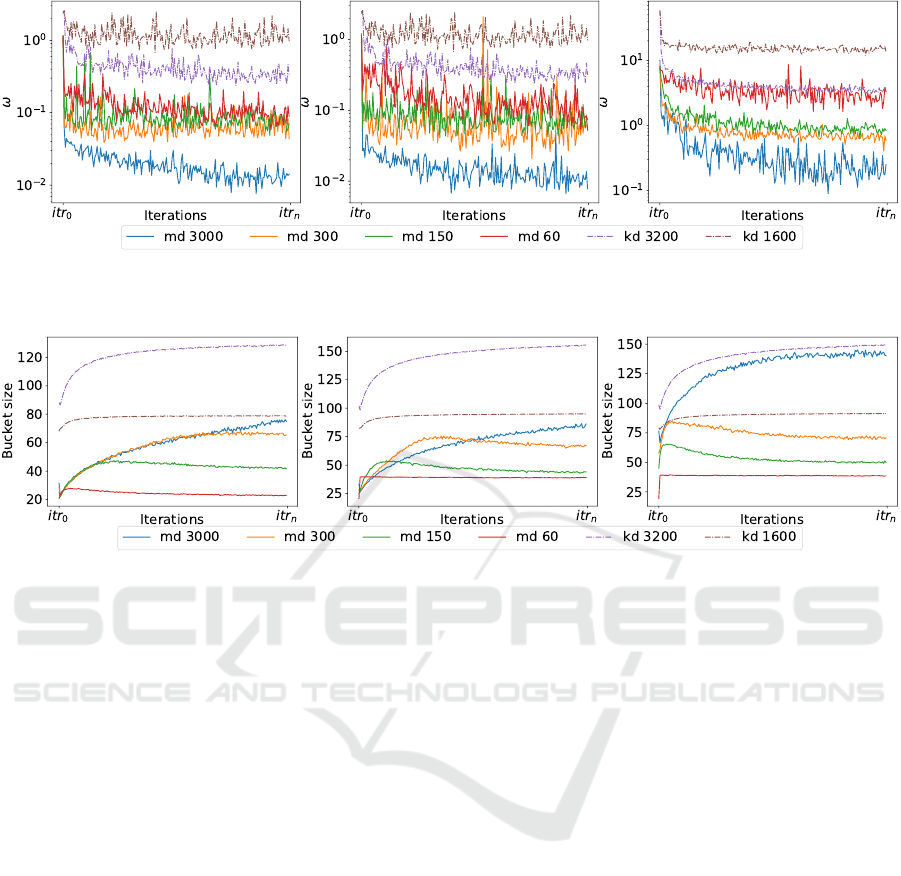
(a) ω: 900 node test feeder. (b) ω: 2.500 node test feeder. (c) ω: NetworkX geometric generated

network.

Figure 5: Routing efﬁciency results for IEEE test feeders and NetworkX generated network.

(a) Bucket size: 900 node test feeder. (b) Bucket size: 2.500 node test feeder. (c) Bucket size: NetworkX geometric

generated network.

Figure 6: Average bucket size calculated from every node in the network on each iteration.

to ﬁnd a new route with a shorter search path on aver-

age, than the underlying routing, which may have to

start a search that fans out in every direction again.

Using a complex identiﬁer comes with a cost.

Most importantly the computing cost goes up as more

properties are added to the identiﬁer. The distance

calculation is performed multiple times for each node

in the routing algorithm. When another property is

added, that increases the cost and more so if the cal-

culation is complex. The cost of the distance calcu-

lation for the Pythagorean location is very small and

the increased efﬁciency of the heuristic far outweighs

the cost in the scenarios tested here.

6 CONCLUSIONS

With the desire of prosumers and energy collectives

to trade energy directly and increasing autonomy at

the local level, overlay networks can provide the

required decentralized communication. The multi-

dimensional overlay network presented in this pa-

per was shown to utilize the properties in the smart

grid to provide a heuristic based on location that im-

proved routing efﬁciency and using the concepts from

complex networks both averted the inherent problems

with robustness in a clustered node distribution and

improved the average path length when searching in

the network. The results showed a increase in perfor-

mance over the standard Kademlia overlay network in

the context of a smart grid.

In future work, churn is going to an interest-

ing parameter to test when the unit state is based

on system dynamics that changes rapidly. The de-

fault storage algorithm causes hot-spots with clus-

tered nodes and load-balancing needs to handled and

measured. Both the small-world properties and the

location based heuristic improved efﬁciency, however

testing the small-world properties with the heuristic

enabled and disabled would provide additional valu-

able insight.

REFERENCES

Aberer, K., Alima, L. O., Ghodsi, A., Girdzijauskas, S.,

Haridi, S., and Hauswirth, M. (2005). The essence of

p2p: a reference architecture for overlay networks. In

Fifth IEEE International Conference on Peer-to-Peer

Computing (P2P’05), pages 11–20.

Albert, R. and Barab

asi, A.-L. (2002). Statistical mechanics

of complex networks. Rev. Mod. Phys., 74:47–97.

Amaral, L. A. N., Scala, A., Barthelemy, M., and Stan-

Efﬁcient Routing for Overlay Networks in a Smart Grid Context

257

ley, H. E. (2000). Classes of small-world networks.

Proceedings of the national academy of sciences,

97(21):11149–11152.

Andersen, D., Balakrishnan, H., Kaashoek, F., and Mor-

ris, R. (2001). Resilient overlay networks, volume 35.

ACM.

Ara

ujo, F. and Rodrigues, L. (2003). Geopeer: A location-

aware peer-to-peer system. FC-DI - Technical Re-

ports.

Asaduzzaman, S. and von Bochmann, G. (2009).

Geop2p: An adaptive peer-to-peer overlay for efﬁ-

cient search and update of spatial information. CoRR,

abs/0903.3759.

Budka, K. C., Deshpande, J. G., and Thottan, M. (2014).

Smart Grid Applications, pages 111–147. Springer

London, London.

Chawathe, Y., Ramabhadran, S., Ratnasamy, S., LaMarca,

A., Shenker, S., and Hellerstein, J. (2005a). A case

study in building layered dht applications. ACM SIG-

COMM Computer Communication Review, 35(4):97–

108.

Chawathe, Y., Ramabhadran, S., Ratnasamy, S., LaMarca,

A., Shenker, S., and Hellerstein, J. (2005b). A case

study in building layered dht applications. SIGCOMM

Comput. Commun. Rev., 35(4):97–108.

Douceur, J. R. (2002). The sybil attack. In International

workshop on peer-to-peer systems, pages 251–260.

Springer.

Dugan, R. C., Kersting, W. H., Carneiro, S., Arritt, R. F.,

and McDermott, T. E. (2009). Roadmap for the ieee

pes test feeders. In 2009 IEEE/PES Power Systems

Conference and Exposition, pages 1–4.

Greer, C., Wollman, D. A., Prochaska, D. E., Boynton,

P. A., Mazer, J. A., Nguyen, C. T., FitzPatrick, G. J.,

Nelson, T. L., Koepke, G. H., Hefner Jr, A. R., et al.

(2014). Nist framework and roadmap for smart grid

interoperability standards, release 3.0. National Insti-

tute of Standards and Technology.

Gross, C., Richerzhagen, B., Stingl, D., M

unker, C.,

Hausheer, D., and Steinmetz, R. (2013). Geodemlia:

Persistent storage and reliable search for peer-to-peer

location-based services. In IEEE P2P 2013 Proceed-

ings, pages 1–2. IEEE.

Hagberg, A., Swart, P., and S Chult, D. (2008). Explor-

ing network structure, dynamics, and function using

networkx. Technical report, Los Alamos National

Lab.(LANL), Los Alamos, NM (United States).

Harwood, A. and Tanin, E. (2003). Hashing spatial content

over peer-to-peer networks. In In Australian Telecom-

munications, Networks, and Applications Conference-

ATNAC, pages 1–5.

Heutelbeck, D. and Hemmje, M. (2006). A peer-to-peer

data structure for dynamic location data. In Fourth

Annual IEEE International Conference on Perva-

sive Computing and Communications (PERCOM’06),

pages 5–pp. IEEE.

Kantere, V., Skiadopoulos, S., and Sellis, T. (2009). Stor-

ing and indexing spatial data in p2p systems. IEEE

Transactions on Knowledge and Data Engineering,

21(2):287–300.

Knoll, M. and Weis, T. (2006). Optimizing locality for self-

organizing context-based systems. In Self-Organizing

Systems, pages 62–73. Springer.

Korn, Grandino Arthur; Korn, T. M. (2000). Mathemat-

ical handbook for scientists and engineers: Deﬁni-

tions, theorems, and formulas for reference and re-

view, chapter Appendix B: B9. Plane and Spherical

Trigonometry: Formulas Expressed in Terms of the

Haversine Function, pages 892–893. Dover Publica-

tions, Inc, 3 edition.

Kova, A., Liebau, N., Steinmetz, R., et al. (2007).

Globase.kom - a p2p overlay for fully retrievable

location-based search. In Seventh IEEE International

Conference on Peer-to-Peer Computing (P2P 2007),

pages 87–96.

Lopes, N. and Baquero, C. (2007). Implementing range

queries with a decentralized balanced tree over dis-

tributed hash tables. In International Conference on

Network-based Information Systems. Springer.

Maymounkov, P. and Mazieres, D. (2002). Kademlia: A

peer-to-peer information system based on the xor met-

ric. In International Workshop on Peer-to-Peer Sys-

tems, pages 53–65. Springer.

Moret, F. and Pinson, P. (2018). Energy collectives: a com-

munity and fairness based approach to future electric-

ity markets. IEEE Transactions on Power Systems.

Nam, B. and Sussman, A. (2006). Dist: fully decentral-

ized indexing for querying distributed multidimen-

sional datasets. In Parallel and Distributed Processing

Symposium, 2006. IPDPS 2006. 20th International,

pages 10–pp. IEEE.

Nygren, E., Sitaraman, R. K., and Sun, J. (2010). The aka-

mai network: a platform for high-performance inter-

net applications. ACM SIGOPS Operating Systems

Review, 44(3):2–19.

Picone, M., Amoretti, M., and Zanichelli, F. (2010).

Geokad: A p2p distributed localization protocol.

In Pervasive Computing and Communications Work-

shops (PERCOM Workshops), 2010 8th IEEE Inter-

national Conference on, pages 800–803. IEEE.

Stoica, I., Morris, R., Karger, D., Kaashoek, M. F., and Bal-

akrishnan, H. (2001). Chord: A scalable peer-to-peer

lookup service for internet applications. SIGCOMM

Comput. Commun. Rev., 31(4):149–160.

Stutzbach, D. and Rejaie, R. (2006). Understanding churn

in peer-to-peer networks. In Proceedings of the 6th

ACM SIGCOMM Conference on Internet Measure-

ment, IMC ’06, pages 189–202, New York, NY, USA.

ACM.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ‘small-world’networks. nature, 393(6684):440.

Zahn, T., Wittenburg, G., and Schiller, J. (2006). Towards

efﬁcient range queries in mobile ad hoc networks us-

ing dhts. In Proceedings of the 1st international

workshop on Decentralized resource sharing in mo-

bile computing and networking, pages 72–74. ACM.

SMARTGREENS 2019 - 8th International Conference on Smart Cities and Green ICT Systems

258