Some Reﬂections on the Discovery of Hyponyms between Ontologies

Ignacio Huitzil

, Fernando Bobillo

1,2

, Eduardo Mena

1,2

, Carlos Bobed

1,3

and Jes

us Berm

udez

University of Zaragoza, Zaragoza, Spain

Aragon Institute of Engineering Research (I3A), Zaragoza, Spain

everis / NTT Data, Zaragoza, Spain

University of the Basque Country (UPV/EHU), Donostia-San Sebasti

an, Spain

Keywords: Ontology Alignment, Hyponymy Relationships, Semantic Web.

Abstract:

Using intelligent techniques to automatically compute semantic relationships across ontologies is a challeng-

ing task that is necessary in many real-world applications requiring the integration of semantic information

coming from different sources. However, most of the work in the ﬁeld is restricted to the discovery of syn-

onymy relationships. Hyponymy relationships, although in the real world they are more frequent than syn-

onymy, have not received similar attention. In this paper, we evaluate a technique based on shared properties

used in the discovery of hyponymy relationships and identify some limitations of ontology sets commonly

used as benchmarks. We also argue that new lexical similarity measures are needed and discuss a preliminary

proposal.

1 INTRODUCTION

In recent years, ontologies have become a standard for

knowledge representation. An ontology is an explicit

and formal speciﬁcation of the concepts, individuals,

and relationships that exist in some area of interest,

created by deﬁning axioms that describe the proper-

ties of these entities (Baader et al., 2017; Staab and

Studer, 2009). They have been successfully used in

many applications, making knowledge maintenance,

addition of semantics to data, information integration,

and reuse of components easier.

As each ontology expresses the point of view of a

certain group of people about a given knowledge ﬁeld,

it is not uncommon that different ontologies have re-

lated semantic terms. Ontology alignment consists in

using intelligent techniques to ﬁnd semantic relation-

ships between elements belonging to different ontolo-

gies (Ehrig, 2006; Euzenat and Shvaiko, 2013), so

that the integration of the original ontologies becomes

easier. For example, it is common to look for syn-

onymy, hyponymy, or disjointness relations between

a concept from a source ontology and a concept from

a target ontology.

Ontology alignment is widely recognized as a

very important problem for data integration from dif-

ferent sources, and we ﬁnd it particularly interesting

in semantic mobile distributed systems. For exam-

ple, semantic apps using semantic reasoners on mo-

bile devices (Bobed et al., 2017; Bobed et al., 2015)

typically needs to integrate the user context (usually

represented using an ontology) with more general do-

main ontologies or, in multiagent scenarios, with on-

tological knowledge from other users that co-operate

to solve complex tasks. This is the case, for exam-

ple, of the SHERLOCK system (Yus et al., 2014),

where users exchange information among themselves

related to existing Location-Based Services in the

area.

Although there has been a considerable amount

of work in the ﬁeld of ontology alignment, most of

the approaches restrict themselves to the problem of

ﬁnding synonymy relationships (i.e., ﬁnding pairs of

elements from different ontologies such that are se-

mantically equivalent). In this paper, we will focus

on the the less studied problem of ﬁnding hyponymy

relationships (i.e., ﬁnding pairs of elements from dif-

ferent ontologies such that one of them is more gen-

eral than the other). Indeed, synonymy is a very de-

manding relationship that implies that the two aligned

entities have exactly the same meaning: two equiva-

lent concepts must have exactly the same individuals

in all possible interpretations. On the contrary, in real

world domains it is more common to ﬁnd terms that

are quite similar but not exactly the same, as it hap-

pens with hyponymy, where two related concepts rep-

130

Huitzil, I., Bobillo, F., Mena, E., Bobed, C. and Bermúdez, J.

Some Reﬂections on the Discovery of Hyponyms between Ontologies.

DOI: 10.5220/0007720201300140

In Proceedings of the 21st International Conference on Enterprise Information Systems (ICEIS 2019), pages 130-140

ISBN: 978-989-758-372-8

resent similar semantics but one subsumes the other.

As an example of the smaller attention that the

community has paid so far to the discovery of

hyponymy relationships, we can mention the fact

that the Ontology Alignment Evaluation Initiative

(OAEI)

has been organizing (annually since 2004)

a benchmark of ontology alignment systems, mainly

focused on synonymy relationships, and only two of

these editions (2009

and 2011

) included an “ori-

ented matching” track dedicated to subclass relation-

ships.

This paper provides the following contributions:

• We evaluate the impact of the shared properties in

the discovery of hyponyms. Based on our experi-

ments, we conjecture that existing benchmarks are

not appropriate enough and that new datasets are

needed.

• We claim that new lexical measures between on-

tology entity names are needed, and show the re-

sults of an evaluation of a simple heuristic.

The rest of this paper is organized as follows.

Firstly, Section 2 recalls the notion of hyponymy in

ontologies and some salient properties. Next, Sec-

tion 3 evaluates empirically the impact of shared

properties in hyponymy relationships. Then, Sec-

tion 4 proposes and evaluates a novel lexical measure

on entity names. Finally, Section 5 overviews some

related work and Section 6 sets out some conclusions

and ideas for future work.

2 HYPONYMYS IN ONTOLOGIES

As in natural language, two synonyms in an ontology

have the same meaning. Clearly, synonymy is a re-

ﬂexive, symmetric and transitive relation.

A common deﬁnition of hyponym in natural lan-

guage is that of a word with a more speciﬁc meaning

than a general or superordinate term called hypernym.

We can see how this almost directly maps to the no-

tion of subsumption between two ontological terms

and E

, which might belong to the same ontol-

ogy O or two different ontologies. Note that if two

terms have a hyponymy relationship, they cannot be

synonyms.

Hyponymy is irreﬂexive and asymmetric relation:

a term is never a hyponym of itself, and if E

is a hy-

ponym of E

, E

is not a hyponym of E

. Hyponymy

is also a subproperty of subsumption. If E

is an hy-

ponym of E

then E

is a subclass of E

. Indeed,

http://oaei.ontologymatching.org

http://oaei.ontologymatching.org/2009/oriented

http://oaei.ontologymatching.org/2011/oriented

in any interpretation model I we have that E

⊆ E

The converse of the previous property does not hold in

general because subsumption is not asymmetric: it is

possible to have two classes such that each of them is

a subclass of the other one. Note that the approaches

in (Bobillo et al., 2017; Yus et al., 2015) sometimes

use the term subsumption relationships when they ac-

tually mean hyponymy relationships.

Deﬁnition 1. E

is a direct hyponym of the term E

is a hyponym of the term E

and there is not a term

T such that E

is a hyponym of T and T is a hyponym

of E

In the following, we will restrict to direct hy-

ponymy relationships. From a linguistic point of

view, one could also be interested in computing the

transitive closure of this relation to obtain indirect hy-

ponymy relationships, but we will not address this

case further. Thus, from now on, we will write hy-

ponyms to mean direct hyponyms.

As in Description Logic languages or OWL lan-

guage there is not usually syntactic sugar to deﬁne

strict subclasses (C

@ C

), in practice it is usual to

encode hyponymy relationships as subclass relation-

ships (Bobillo et al., 2017; Yus et al., 2015). However,

when doing so, one is implicitly excluding that the

two classes are synonyms because otherwise a syn-

onymy relationship would be encoded by stating that

the two classes are equivalent (C

≡ C

). Thus, to be

precise, we should also add the axiom

> v ∃U.(C

u ¬C

) , (1)

where U denotes a universal role

(owl:topObjectProperty). This axiom states

that the set of individuals that belong to the hypernym

and do not belong to the hyponym is not empty, i.e.,

there should be examples that justify specializing

concept C

Equation 1 is not necessary if the ontology already

contains instances of C

u ¬C

, i.e., if O |= i : C

and

O |= i : ¬C

holds. Note also that Equation 1 can-

not be expressed in some inexpressive languages such

as RDF-S or OWL 2 EL. A similar situation raises

when trying to encode hyponymy relationships be-

tween properties. In this case, however, Equation 1

cannot be expressed in OWL 2 DL.

3 ON SHARED PROPERTIES IN

HYPONYMY DISCOVERY

In this section we discuss how to use the set of shared

properties in hyponymy discovery. Clearly, a hy-

ponym concept should include all the properties of its

Some Reﬂections on the Discovery of Hyponyms between Ontologies

131

hypernym concept, but we argue that in most of the

cases it should also have some additional properties

of its own. That is, when an ontology designer de-

cides to specialize a concept by deﬁning a more spe-

ciﬁc one, his/her decision will be based very often on

the existence of some attribute that characterizes such

concept. Thus, the existence of new properties in-

creases our conﬁdence in the existence of a hyponymy

relationship. Unfortunately, these new properties are

sometimes not included explicitly due to modeling

decisions, as we will see.

Deﬁnition 2. Let O be an ontology, C ∈ O a

concept name, R ∈ O a (data or object) property,

and dom(O, R) =



D is a concept name ∈ O | O |=

{∃R.> v D}



. Now:

• C deﬁnes R if C is one of the direct domains of

R, i.e., C ∈ dom(O, R) and 6 ∃D ∈ dom(O, R) such

that O |= {D v C} and O 6|= {D ≡ C}.

• C has R if a concept name D ∈ O deﬁnes R and

D v C.

We can see that C has a property R if C deﬁnes R or if

it inherits it from an ancestor in the concept hierarchy

that deﬁnes it.

Example 1. Let O be the Wine ontology (to be dis-

cussed later). dom(O, hasWineDescriptor) includes

Wine and their superclasses, such as Consum-

ableThing, because O |= {∃hasWineDescriptor.> v

Wine} and O |= {∃hasWineDescriptor.> v

ConsumableThing} hold. Thus, Wine deﬁnes

(and has) hasWineDescriptor. Any subclass of

Wine, such as SweetWine, has (but does not deﬁne)

hasWineDescriptor. 

To be precise, the semantics of Description Logic-

based ontologies states that if, for example, the do-

main of hasWineDescriptor is Wine, then anything

with a wine descriptor must be a wine. Instead, we

assume that hasWineDescriptor is a characteristic fea-

ture of the class Wine, as common in frames or object

orientation design.

The properties that a concept has/deﬁnes must be

computed by a semantic reasoner, as they could not

be implicitly represented in the ontology. Please note

that range restrictions must be taken into account at

this point. For example, if the range of an object

property R is C, then C deﬁnes the inverse of R, even

if the inverse property is not explicitly represented in

the ontology.

Our claims regarding the set of shared properties

is based on some intuitive ideas such as the duck test,

the opposite duck test, and the weak duck test (Yus

et al., 2015):

• Duck test: if it looks like a duck, swims like a

duck, and quacks like a duck, then it probably is

a duck. In our setting, this implies for example

that the hyponymy degree is proportional to the

percentage of shared properties.

• Opposite duck test: if it does not look like a duck,

does not swim like a duck, and does not quack

like a duck, then it probably is not a duck. For

example, if there are no shared properties, the

hyponymy degree is inversely proportional to the

number of properties.

• Weak duck test: if it looks like a duck and quacks

like a duck, then it is probably a kind of duck,

although we are not sure that it swims like a

duck. In this case, shared properties should have a

higher impact in the hyponymy degree than non-

shared properties.

In the rest of this section, we will discuss an evalua-

tion of the previous claims on several datasets.

Datasets. Firstly, we have considered OAEI 2009

and OAEI 2011 oriented track benchmarks. They pro-

vide reference alignments (or ofﬁcial results) between

ontology pairs formed by a ﬁxed source ontology and

several target ones. The results include equivalence

and subclass relationships. As discussed in Section 2,

we assume that such subclass relationships actually

denote hyponymy relationships. Furthermore, we will

restrict to those direct relationships explicitly repre-

sented in the ontology (recall that one could also con-

sider the transitive closure). Let us now discuss these

datasets in detail.

The OAEI 2009 dataset includes 30 pairs of on-

tologies describing bibliographic references. On-

tologies are part of the regular benchmark used in

OAEI 2006, but the alignments are different and, in

particular, include hyponymy relationships between

concepts. Each ontology pair is formed by a ﬁxed

ontology (called 101) and a variable ontology (names

from 102 to 304

). Unfortunately, 8 pairs of ontolo-

gies (27%) of the OAEI 2009 had to be discarded be-

cause the ontology reasoner that we used (described

later) could not support them.

The OAEI 2011 dataset includes 12 pairs of on-

tologies that can be classiﬁed in two categories:

Academia and Course catalogs. Academia involves

bibliographic references and includes 6 ontology

pairs obtained after some modiﬁcations of 4 ontolo-

gies in the OAEI 2006 dataset (from 301 to 304).

Course catalogs involves description of courses in the

universities of Cornell and Washington and also in-

cludes 6 ontology pairs obtained by modifying 4 real

Not each number in the interval corresponds to an on-

tology, there are only 30 pairs.

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

132

ontologies. For each pair of ontologies, reference

alignments include subsumption mappings between

concepts. In this case, 3 pairs (25 %) could not be pro-

cessed successfully by the semantic reasoner. Since

some of the ontologies in the OAEI 2011 dataset do

not include any property, we have identiﬁed a frag-

ment, denoted OAEI 2011*, restricted to ontologies

with some (object or data) property.

More recently, A. Vennesland developed a very

small dataset to evaluate his work in (Vennesland,

2017).

The dataset contains 3 pairs of ontologies; 4

ontologies from the Conference track of OAEI 2016,

another one from the Benchmark track of OAEI 2016,

and the well-known Bibo ontology.

We will call it

OAEI 2016 dataset.

So far, the number of ontologies was small and

there were some limitations (for example, there

were no subproperty relationships in the reference

alignments). Thus, we additionally considered the

ORE 2015

ontology set, with 1920 ontologies al-

though not oriented to ontology alignment (Parsia

et al., 2016). To this dataset we have added the well-

known Wine

ontology. Wine is a general ontology

only used for didactic purposes, but it will be useful

for us to show very illustrative examples of our met-

rics. In this case, we consider intra-ontology subclass

relationships between entities of one ontology (and,

again, we will assume that they denote hyponymy re-

lationships), so we do not consider ontology pairs.

During our experiments, we set a timeout of 15

minutes for each ontology to complete our experi-

ments (it only had an effect on ORE 2015 dataset).

Because of that, we discarded 848 ontologies (44%)

that reached the timeout, 47 ontologies (2.4%) that

were found to be inconsistent and 12 ontologies

(0.6%) that were not supported by the reasoner.

Research Questions. Our ﬁrst experiment aims

at answering the following questions:

a) What is the proportion of hyponymy relationships

where the hyponym has all the properties of its

hypernym?

b) What is the proportion of hyponymy relationships

such that the hyponym deﬁnes some property that

its hypernym does not have?

c) What is the proportion of hyponymy relationships

such that the hyponym deﬁnes no properties or de-

ﬁnes some properties that its hypernym also has?

http://github.com/audunve/

COMPOSE-ReferenceAlignments

http://bibliontology.com

http://mowlrepo.cs.manchester.ac.uk/datasets/

ore-2015-reasoner-competition-dataset

http://www.w3.org/TR/owl-guide/wine.rdf

d) How many different pairs of concepts C, D are

there such that C has all the properties of D plus

some new deﬁned properties, and C is not a hy-

ponym of D?

To do so, we will compute the precision (percentage

of positive examples) and the number of false posi-

tives or counter-examples.

One would expect a) and b) to be as high as pos-

sible, whereas the other cases should be as small as

possible. Note also that in cases b) and d) we are in-

terested in properties that are actually deﬁned by the

hyponym, excluding properties deﬁned by a different

ancestor, which could happen in multiple inheritance

scenarios.

When considering intra-ontology relationships, a

semantic reasoner is used to decide if two proper-

ties are equivalent and correspond to the same en-

tity. In the case of inter-ontology relationships, we

would need a reference alignment or an alignment

software deﬁning synonymy relationships. Because

existing benchmarks do not provide such information

(they only provide alignments between concepts, but

not between properties), in this paper we needed to

assume that two properties from different ontologies

denote the same entity if and only if they have the

same name (fragment) and they are of the same type

(object and data properties).

Technical Details. All experiments were per-

formed on a desktop computer with Intel Core i5-

2320 3.0 GHz, 16 GB RAM (12 GB were allocated

for the JVM in the experiments) under Windows 7

64-bits. We used Java 1.8, OWL API (Horridge and

Bechhofer, 2011) to manage the ontologies, and the

ontology reasoner HermiT 1.3.8 (Glimm et al., 2014)

to retrieve implicit axioms. We selected HermiT be-

cause it provides a simple method to retrieve directly

the direct domain and range of object and data prop-

erties, even if they are not explicitly represented in

the ontology.

To best of our knowledge, a similar

method is not available in other reasoners such as Pel-

let (Sirin et al., 2007) or Konclude (Steigmiller et al.,

2014). We also use the reasoner when dealing with

the range of an object property P to check if the in-

verse property of P exists;

otherwise we create a

new inverse property called P@inverse. All the meth-

ods above that we use belong to the Reasoner class

(org.semanticweb.HermiT.Reasoner).

Example 2. Let us illustrate the measures that we are

computing by providing some examples, taken from

http://www.hermit-reasoner.com

Methods getObjectPropertyDomains and getObject-

PropertyRanges, respectively.

Method getInverseObjectProperties.

Some Reﬂections on the Discovery of Hyponyms between Ontologies

133

Table 1: Statistics of the datasets.

Dataset TOT OK C sub C pairs C OOP OP ODP DP sub OP

pairs

sub DP

pairs

OAEI 2009 30 22 77 49 1432 22 52 22 89 0 0 0 0

OAEI 2011 12 9 154 109 5982 3 17 3 14 0 0 0 0

OAEI 2011* 6 3 56 27 588 3 52 3 43 0 0 0 0

OAEI 2016 3 3 101 11 2619 3 73 3 51 0 0 0 0

ORE 2015 1920 1013 792 857 1834180 925 44 375 9 25 6600 3 1373

the Wine ontology, that appeared in our experiments.

An example of case b) are the pair of classes

WineGrape and Grape which have a hyponymy re-

lationship. Both of them have the same proper-

ties (producesWine, hasMaker, locatedIn, madeFrom-

Fruit, and the inverse of madeFromFruit). WineGrape

is an hyponym of Grape and deﬁnes a new property

called madeIntoWine that Grape does not have.

As an example of case c), AmericanWine class

is a hyponym of Wine. Both of them have the

same properties (producesWine, hasSugar, hasColor,

hasMaker, locatedIn, hasFlavor, hasWineDescrip-

tor, madeFromGrape, madeFromFruit, and hasBody).

However, AmericanWine deﬁnes itself no new prop-

ertys.

An example of case d) are Vintage and Winery,

two classes without a hyponymy relationship. Vin-

tage has all the properties of Winery (namely, pro-

ducesWine, hasMaker, and locatedIn) but also a new

one ( hasVintageYear). 

Results. In this section, we summarize the results

of our experiments. The detailed results can be found

online.

Firstly, Table 1 shows some statistical data

of each dataset considered in our experiments: TOTal

number of examples in the dataset (TOT), examples

correctly processed within a timeout (OK), average

number of Classes (C), average number of subClasses

(sub C), average number of pairs of Classes (pairs C),

number of ontologies with Object Properties (OOP),

average number of Object Properties (OP), number of

ontologies with Data Properties (ODP), average num-

ber of Data Properties (DP), average number of sub-

ObjectProperties (sub OP), average number of sub-

DataProperties (sub DP), average number of pairs of

Object Properties (pairs OP), and average number of

pairs of Data Properties (pairs DP). In ORE 2015,

OK is the number of ontologies; in OAEI 2009 and

OAEI 2011 it is the number of ontology pairs. Com-

pared to OAEI 2009, OAEI 2011 has a smaller num-

ber of ontologies with a smaller average number of

properties but a higher average number of classes.

Table 2 shows the result of the measures related

http://webdiis.unizar.es/

∼

ihvdis/Hyponyms\ Results.

htm

to shared properties, from a) to d). For each dataset,

we show the total number of examples found (Sum),

the total number of ontologies with at least one exam-

ple (#Onts), and the average percentage of examples

(Mean%). These values are always shown for classes

(C). Note that the denominator of Mean% is not the

same in the three criteria e.g., it is the total number of

hyponym pairs in cases a)–c), and the total number of

(possibly non-hyponym) pairs in case d).

Because sometimes one of these metrics can be-

have well in some ontologies and bad in others, the

last four columns compare case b) versus c), and b)

versus d). For each of these comparisons, #b> de-

notes the number of ontologies with more positive

examples than negative ones, whereas Dif denotes

the difference between the number of ontologies with

more positive examples than negative ones and vice

versa (the number of ontologies with more negative

examples). Thus, a positive value indicates that there

are more ontologies with more positive examples than

the other way around.

Discussion. Firstly, note that in all cases we ob-

tain the same values in Sum and #Ont for OAEI 2011

and OAEI 2011* (the percentages are different be-

cause the dataset sizes are different).

Regarding case a), as expected, we obtained a

100 % in the case of intra-ontology relationships

(ORE 2015). For inter-ontology relationships, much

smaller values are obtained. In OAEI 2011 we ob-

tained a surprising result of 0 %. In this case, only

3 ontology pairs involved properties, and none of the

properties of an hyponym matched a property of the

hypernym. This clearly shows that there is a lot of

missing information in the ontologies.

Case b) only produces reasonably good results in

OAEI 2009 and OAEI 2016 (48% and 36%, respec-

tively); in other datasets the percentage are 0.3% or

2%. Note that the absolute number of positive ex-

amples is quite signiﬁcant in ORE 2015 (17273), but

the high total number of subclass axioms produces a

small percentage. Again, the small value obtained

in OAEI 2011 can be partially explained by the low

number of ontology pairs with properties.

The numbers of counter-examples c) and d) are

higher than b) if we consider total numbers, except

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

134

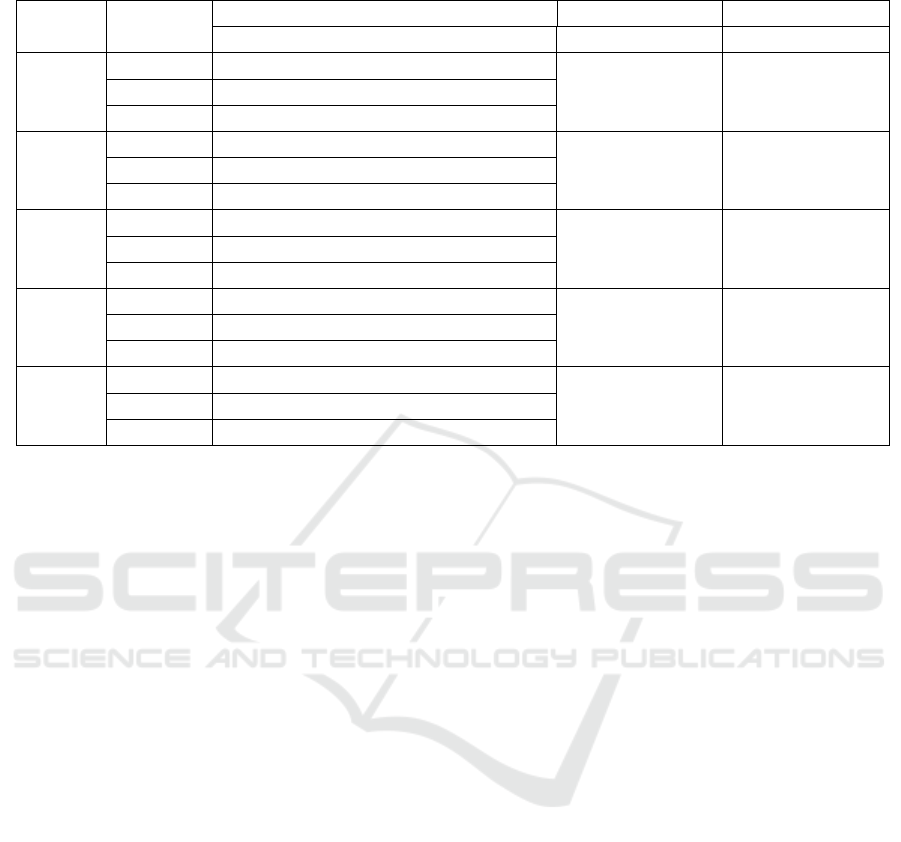
Table 2: Metrics for shared properties on each dataset.

Dataset Item

Criteria b vs. c b vs. d

a b c d #b> Dif #b> Dif

OAEI

2009

(C)

Sum 346 509 559 2188

#Onts 8 22 22 8 15 8 14 6

Mean % 32 48 52 7

OAEI

2011

(C)

Sum 0 3 77 0

#Onts 0 2 3 0 0 -3 2 2

Mean % 0 0.3 7.8 0

OAEI

2011*

(C)

Sum 0 3 77 0

#Onts 0 2 3 0 0 -3 2 2

Mean % 0 4 96 0

OAEI

2016

(C)

Sum 0 12 21 0

#Onts 0 3 3 0 1 -1 3 3

Mean % 0 36 64 0

ORE

2015

(C)

Sum 867810 17273 850537 1327113

#Onts 1013 504 938 454 123 -706 85 -352

Mean % 100 2 98 0.1

in the cases of d) for OAEI 2011, OAEI 2011*, and

OAEI 2016, where there are no examples of d). How-

ever, there is usually a (small) class of ontologies

where the value is greater than the number of counter-

examples. In OAEI 2011 and OAEI 2011*, the num-

ber of cases with more positive cases b) than nega-

tive cases c) or d) ranges between 14 and 123. In

OAEI 2016, 33% and in 100% of the ontology pairs

have more positive cases b) than c) or d), respectively.

Nevertheless, one should not be too optimistic to ap-

ply this idea to every ontology. In general, there are

more ontologies with negative cases c) than positive

cases b), except in OAEI 2009 dataset, and in some

datasets (ORE 2015) there are more ontologies with

negative cases d) than positive cases b). This sug-

gests that further work is needed to identify that class

of ontologies where our claim about shared properties

provides good results.

Since we strongly think that our claim about

shared properties is reasonable, the somehow disap-

pointing results make us question the benchmark it-

self, and we think that the datasets are incomplete

(small number of properties and subproperty align-

ments) and contain an unnatural modeling.

In ontology modeling it is common to pay much

more attention to classes than properties. Historically,

ontology languages have indeed supported more ex-

pressivity for concepts than for properties. Because

the ontologies in the datasets include much more con-

cepts than properties (a big quantity of the ontologies

do not have any properties at all), heuristics based

on properties are penalized. Indeed, in OAEI 2009,

OAEI 2011, and OAEI 2016 there were no exam-

ples of property hyponymy. Furthermore, ORE 2015

dataset is more useful for object property hyponymy

than for data property hyponymy. Although the aver-

age number of subproperty axioms is 25, 47.2 % of

the ontologies do not have any subproperty axiom.

Example 3. WineFlavor, WineSugar, and WineBody

are candidates to be subproperties of WineDescriptor,

although this is not represented in the Wine ontology.

Regarding the unnatural modeling, there is often a

rather different representation of the reality in the two

ontology pairs: sometimes one of them uses an ob-

ject property and the other one a data property, some-

times properties are assigned to concepts with differ-

ent granularity levels, etc.

Example 4. Class Entry in ontology 301 is a hyponym

of class Resource in ontology 302. One of the data

properties of Entry is has author, but Resource does

not have a similar data property. Instead, Publication

is a subclass of Resource in the same ontology 302

with two object properties Resource author and Re-

source ﬁrst author. Thus, there are notable differences

in the modeling. 

We claim that in many cases the fact that a hy-

ponym does not specialize the hypernym with a new

property is a modeling error, as the hyponym needs

to have some feature that justiﬁes the existence of a

subclass. For example, a database developer does not

create a new table if there are not any additional at-

tributes. In the case of ontologies, it makes sense to

Some Reﬂections on the Discovery of Hyponyms between Ontologies

135

create a subclass without adding a new property: for

example, one can restrict the range of possible val-

ues, or increase the minimal cardinality. However, in

several cases, we think that a new property should be

added.

Example 5. RedWine could deﬁne a tannin level (al-

though all wines have tannins, they have a stronger

impact in red wines) or SweetWine could deﬁne a fer-

mentation procedure (as it is different in a naturally

sweet wine and in a natural sweet wine or vin doux

naturel).

We also observed that too many properties do not

have a domain and/or a range axioms, so we infer that

they are the Thing class. Enriching ontologies with

those axioms will make it possible to identify proper-

ties that a class has or deﬁnes, and thus to improve the

applicability of our heuristic for shared properties.

Another ﬁnding is that some properties might have

a different interpretation in different concepts (the

evaluated datasets do not provide enough formal or

informal information about the semantics of the terms

to be completely sure). Of course, such polysemic

properties make discovering hyponyms harder.

Example 6. In the Wine ontology, producesWine

property is related to WineGrape and Winery classes,

but with different semantics (a winery produces a spe-

ciﬁc wine brand, whereas a grape is used to produce

a general wine type).

4 ON ENTITY NAMES IN

HYPONYMY DISCOVERY

In this section we study a lexical measure that seems

particularly useful in the discovery of hyponyms.

For our purpose, the name of an entity is only

the fragment identiﬁer of its URI, e.g., hasEnd-

Time is the name of <http://sweet.jpl.nasa.gov/

2.0/time.owl#hasEndTime>.

In ontology alignment, it is usual to consider sim-

ilarity between the names of a pair of entities as a

heuristics to identify relationships between the en-

tities. There are many well-known string similar-

ity metrics (the interested reader can ﬁnd a good

overview in (Cheatham and Hitzler, 2013)), but we

argue that they are mostly appropriate when looking

for synonymy relationships. Because we ﬁnd it rea-

sonable to assume that the conﬁdences on two enti-

ties having a synonymy or a hyponymy relationship

are somehow contradictory, we think that hyponym

and hypernym usually have a similar name but not an

equivalent one. If two entities have a similar name,

our conﬁdence in the existence of a hyponymy rela-

tionship usually increases except if the name is ex-

actly the same one: in this case our conﬁdence in

the existence of a synonymy relationship increases.

Thus, we are interested in metrics that penalize a per-

fect similarity.

In particular, we observed that the name of the hy-

ponym is sometimes a speciﬁcation of the name of its

hypernym, which is an afﬁx substring. Clearly, this is

just a heuristic that does not need to hold in general.

Deﬁnition 3. Given a reference ontology O and a

pair of entities (two concepts or two properties) e

and e

, we say that e

is an afﬁx substring of e

if the name of e

, denoted name(e

), has either a

preﬁx or a sufﬁx relationship with the name of e

That is, name(e

) has one of the following forms:

name(e

) ◦S or S ◦ name(e

), where S is a non-empty

string and ◦ denotes string concatenation. If e

is an

afﬁx substring of e

, e

is an afﬁx superstring of e

That is, e

is an afﬁx substring of e

if e

contains

the name of e

as a preﬁx (i.e., at the beginning of

the string) or as a sufﬁx (i.e., at the end of the string),

and the name of e

is different from the name of e

Note that we do not look for arbitrary substrings but

we look for indications of compound names. For ex-

ample, Student is an afﬁx substring of its hyponym

PhDStudent.

Research Questions. Now we are interested in

computing (using the same datasets):

e) What is the proportion of hyponymy relationships

that involve a hypernym with a name being an af-

ﬁx substring of the hyponym?

f) What is the proportion of hyponymy relationships

that involve a hypernym with the same name as

the hyponym?

g) How many different pairs of concepts/properties

are there such that one of them has a name being

an afﬁx substring of the other one, but they do not

have a hyponymy relationship?

One would expect e) to be as high as possible,

whereas the other cases should be as small as pos-

sible. One could also think that the case f) does not

make sense if we are using a single ontology. Ap-

parently, two different entities cannot have the same

name if they have different URIs, but it is possible if

we only consider the fragment, as shown in Exam-

ple 4.

Both e), f), and g) can be measured not only for

concepts but also for properties (both object an data

properties). This will be interesting for the ORE 2015

dataset, as the other datasets do not contain subprop-

erty alignments.

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

136

Example 7. Let us now illustrate our metrics regard-

ing entity names.

Examples of case e) are pairs with a hyponymy

relationship where the hyponym is an afﬁx super-

string of the hypernym, such as the object properties

hasEndTime and hasEnd, the data properties (from

the 204 ontology) number or volume and volume, and

the classes SweetWine and Wine.

Examples of case f) are pairs with a hy-

ponymy relationship and the same name.

This happens with the object properties

<http://sweet.jpl.nasa.gov/2.0/time.owl#hasBegin-

ning> and <http://www.w3.org/2006/time#hasBe-

ginning>, the data properties <http://www.fao.org/

aims/aos/ﬁ/eez#hasMeta> and <http://www.fao.

org/aims/aos/ﬁ/water#hasMeta>, and the classes

<http://purl.org/olia/emille.owl#Noun> and

<http://purl.org/olia/olia.owl#Noun>.

Examples of g) are pairs where an entity is an afﬁx

substring of the other one but it is not its hypernym.

This happens in the object properties hasTimeRefer-

ence and hasTime, and in the data properties has-

NameEN and hasName. 

Results and Discussion. Table 3 shows the result

of our measures from e) to g) for pairs of Object Prop-

erties (OP), Data Properties (DP) and Concept Names

(C). Sum, #Onts, Mean%, #e>, and Dif have the same

meaning as in Table 2.

The percentage of e) was very low for proper-

ties, smaller than 1 % in ORE 2015 (the only dataset

where there are computed). Percentages are higher

for classes, ranging from 4% to 48%, and the highest

value happens in OAEI 2011, where it is applied in all

(3) pairs of ontologies. Note that the absolute num-

ber of positive examples is signiﬁcant in ORE 2015,

34863.

Values of f) are surprisingly high. For properties,

the number of hypernyms with the same name than

the hyponym is even higher than the number of hy-

pernyms with an afﬁx substring.

The total number of cases g) is higher than the

number of e). Nevertheless, in OAEI 2011 and

ORE 2015 there is a (small) class of ontologies where

the value of e) is greater than the number of counter-

examples g), with 3 and 124 ontologies, respectively.

As in the case of shared properties, further studies to

identify those ontologies are needed, as in all datasets

there are more ontologies where our heuristics gives

more false positives than positives than the other way

around, as the Dif column shows.

We expected a small number of positives (we are

just proposing a simple heuristic), but not such a high

number of counter-examples. We think that cases f)

are modeling mistakes: the same name should not

designate two different things. Let us now discuss

some reasons of the small number of positives.

• Some of the entity names in the datasets are inten-

tionally unreadable, so that ontology alignments

approaches cannot take advantage of lexical mea-

sures. Any lexical measure, and not only ours,

performs poorly on these scenarios. This happens

for example in 7 ontologies of OAEI 2009.

• Another example where our measure fails are

pairs of ontologies with entity names written in

different languages. As it is well known, cross-

lingual ontology alignment requires speciﬁc tech-

niques (Gracia and Asooja, 2013). This happens

for example in 3 ontology pairs of OAEI 2009.

• It can be the case that it is the hypernym the

one specializing the name of the hyponym, as it

happens in aggregated concepts. This shows that

more sophisticated techniques are needed.

• Sometimes, what an afﬁx substring implies is a

meronymy (part-whole) relationship.

Example 8. Let us illustrate the above reasons for the

small number of cases e):

• Concept Chapter (in ontology 101) is an hyper-

nym of sqdsopq (in 101).

• Ontology 210 is written in French.

• SemillonOrSauvignonBlanc is an hypernym of

Semillon.

• Concept BookPart (in ontology 222) is a meronym

of Book but not a hyponym. 

5 RELATED WORK

This section recaps some related work on the discov-

ery of subsumption relationships in ontologies. Most

of the work in ontology alignment is focused on the

discovery of synonymy relationships, and only a few

works consider the discovery of subsumption rela-

tionships. Among them, some authors have addressed

the discovery of subsumption intra-ontology relation-

ships (see e.g., (Lambrix et al., 2015)), but we will

focus here on the discovery inter-ontology subsump-

tion relationships

Some of the previous works are based on the ex-

traction of subsumption relationships on shared in-

stances, but do not take schema information into ac-

count (Chua and Kim, 2012; Kang et al., 2005; Tour-

naire et al., 2011; Zong et al., 2015). Some of these

works also assume that ontology instances are anno-

tated with phrases of text (Chua and Kim, 2012).

Some Reﬂections on the Discovery of Hyponyms between Ontologies

137

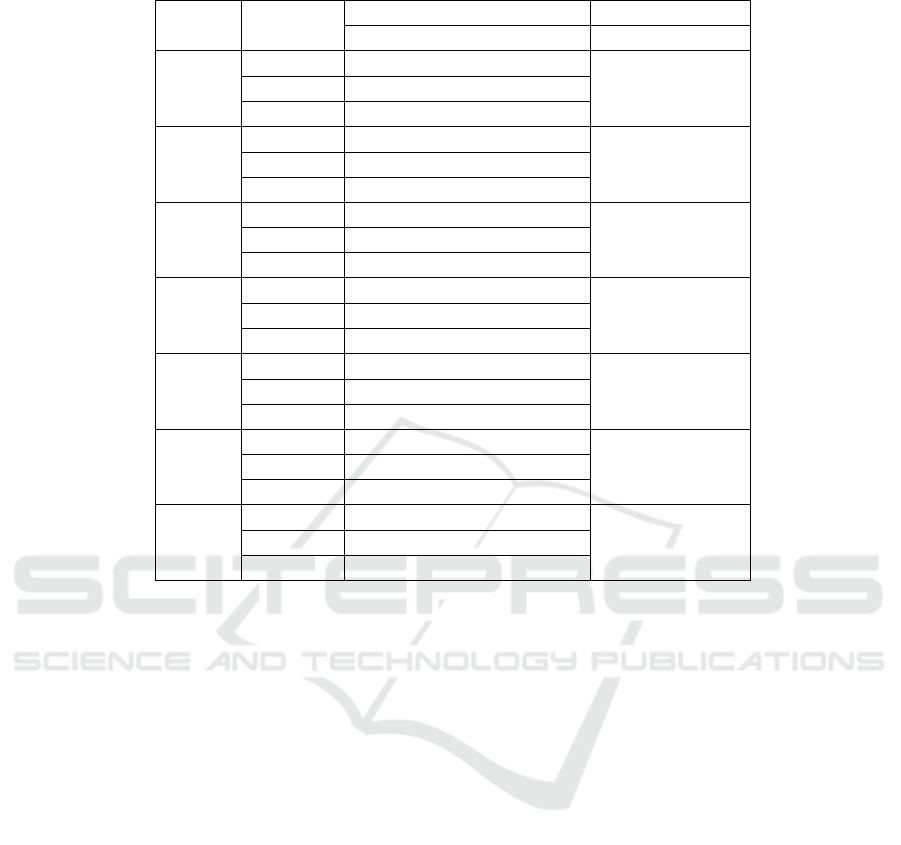
Table 3: Metrics for string afﬁxes on each dataset.

Dataset Item

Criteria e vs. g

e f g #e> Dif

OAEI

2009

(C)

Sum 47 2 185

#Onts 15 2 22 0 -22

Mean % 5 0.2 1

OAEI

2011

(C)

Sum 125 106 138

#Onts 8 9 9 3 -3

Mean % 13 11 0.3

OAEI

2011*

(C)

Sum 6 19 15

#Onts 2 3 3 0 -3

Mean % 8 24 1

OAEI

2016

(C)

Sum 16 0 68

#Onts 3 0 3 0 -3

Mean % 48 0 0.87

ORE

2015

(C)

Sum 34863 403 186357

#Onts 486 43 667 124 -410

Mean % 4 0.05 0.01

ORE

2015

(OP)

Sum 29 119 4851

#Onts 28 42 491 0 -491

Mean % 0.1 0.46 0.07

ORE

2015

(DP)

Sum 1 11 1118

#Onts 1 3 178 0 -178

Mean % 0.03 0.37 0.01

Previous approaches extracting relationships at

the schema level include the systems MOMIS (Ben-

eventano et al., 2000), SCARLET (Sabou et al.,

2008), RepOSE (Lambrix and Liu, 2013; Lambrix

and Ivanova, 2013) and Classiﬁcation-based learn-

ing of Subsumption Relations (CSR) (Spiliopoulos

et al., 2008). The alignments that MOMIS and

SCARLET can ﬁnd must already exist in third-party

sources (Wordnet and other ontologies, respectively),

whereas RepOSE ﬁnds missing is-a relationships that

are derivable from a set of an ontology network (a

set of ontologies). CSR uses machine learning tech-

niques so it requires a previous training step. The au-

thors of CSR recognize that not all the ontologies are

suitable for the training step.

Another relevant work applies machine learning

techniques in order to learn a structure (what they call

a lightweight ontology) in a list of terms (Movshovitz-

Attias et al., 2015). However, they do not consider on-

tology alignment, but only relationships between two

low-level terms.

STROMA system uses a two-step ap-

proach (Arnold and Rahm, 2014), using any

matching system to retrieve a list of mappings

between ontology terms, and a second step using

some heuristics to determine the type of relationships

(i.e., synonymy or hyponymy).

More generally, (Vennesland, 2017) supports hav-

ing several matchers (e.g., a structural one and a lexi-

cal one), and studies how to choose them and how to

combine their results.

We must also cite our previous work in (Yus et al.,

2015). The present paper studies and evaluates some

of the techniques used in that system.

6 CONCLUSIONS AND FUTURE

WORK

This paper has discussed several issues related to

the automatic discovery of hyponymy relationships

across ontology elements. We hope that this will con-

tribute to an increase in the interest in such a kind of

relationships, which have received much less atten-

tion than synonymy relationships.

Firstly, we discussed the impact on shared prop-

erties on the discovery of hyponymy relationships. A

hyponym concept should include all the properties of

its hypernym concept, and we also argue that it is

very likely to specialize it with some additional prop-

erties. An empirical evaluation over 4 datasets (the

only three existing sets considering inter-ontology re-

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

138

lationships and an additional one considering intra-

ontology relationships) shows that there is a signif-

icant amount of examples conﬁrming our claim but

there are also a notable number of exceptions. In par-

ticular, there is usually a class of ontologies where

the number of examples is greater than the number of

counter-examples.

The number of counter-examples made us ques-

tion the benchmark itself, and we conclude that the

datasets are incomplete and contain often an unnatu-

ral modeling. On the one hand, existing benchmarks

are restricted to hyponymy relationships between con-

cepts and exclude the case of properties. Moreover,

they have strong limitations in terms of size and num-

ber of properties and axioms (in particular, subprop-

erty, domain, and range axioms). This penalizes very

much heuristics based on properties as ours. On the

other hand, we were able to identify several reasons

to explain cases where our measures did not perform

well and illustrated them by providing concrete exam-

ples.

Finally, we claimed that new lexical measures be-

tween ontology entities are needed. Indeed, we ar-

gue that if two entities have the same name, our con-

ﬁdence in a possible hyponymy relationship should

decrease, as they are more likely to be synonyms. As

a ﬁrst step towards lexical measures that penalize a

perfect similarity, we studied a simple heuristic based

on the fact that the name of the hyponym is sometimes

a specialization of the name of its hypernym, which is

an afﬁx substring. An empirical evaluation shows that

this heuristic is much more useful for classes than for

properties, and the existence of ontologies where this

idea leads to more positive examples than counter-

examples. We also analyzed some cases where our

measure fails and provided some justiﬁcations and

concrete examples, such as the existence of ontolo-

gies with unreadable or multilingual names.

Future Work. There are many directions for

our future research. Our main priority is to develop

a more general system computing at the same time

both synonymy and hyponymy relationships (but also

other semantic relationships). The key idea is that

our conﬁdence in a synonymy relationship should

decrease our conﬁdence in a hyponymy relationship

and vice versa. This idea, and the fact that our al-

gorithm to compute hyponymy relationship assumes

some synonymy relationships could create a chicken-

egg problem that needs to be properly addressed. An

interesting alternative to evaluate such approach is us-

ing external RDF triple stores to measure the con-

ﬁdence in the discovered axioms (Tettamanzi et al.,

2017).

As we have already mentioned, further research

is needed to identify the class of ontologies where

our measures provide good results. Lexical measures

across entity names also require more sophisticated

techniques than those presented here. For instance,

to compare entity names one can use word stem-

ming and services providing semantic relationships

between some common terms. Furthermore, we will

not only assume that hyponyms can add a property

but also that they can restrict the values of a property

inherited from its hypernym.

Furthermore, the identiﬁed limitations of existing

datasets lead us to consider developing a new bench-

mark. Needless to say, it is important to develop a

benchmark which is not biased to beneﬁt our speciﬁc

heuristics, so the contributions of the community will

be extremely important.

ACKNOWLEDGMENTS

We have been partially supported by the projects

TIN2016-78011-C4-3-R (AEI/ FEDER, UE), JIUZ-

2018-TEC-02 (Fundaci

on Ibercaja y Universidad de

Zaragoza), and DGA/FEDER. I. Huitzil was partially

funded by Universidad de Zaragoza - Santander Uni-

versidades (Ayudas de Movilidad para Latinoameri-

canos - Estudios de Doctorado).

REFERENCES

Arnold, P. and Rahm, E. (2014). Enriching ontology map-

pings with semantic relations. Data & Knowledge En-

gineering, 93:1–18.

Baader, F., Horrocks, I., Lutz, C., and Sattler, U. (2017). An

Introduction to Description Logic. Cambridge Uni-

versity Press.

Beneventano, D., Bergamaschi, S., Castano, S., Corni,

A., Guidetti, R., Malvezzi, G., Melchiori, M., and

Vincini, M. (2000). Information integration: The

MOMIS project demonstration. In Proceedings of

the 26th International Conference on Very Large Data

Bases (VLDB 2000), pages 611–614.

Bobed, C., Bobillo, F., Mena, E., and Pan, J. Z. (2017).

On serializable incremental semantic reasoners. In

Proceedings of the 9th International Conference on

Knowledge Capture (K-CAP 2017), pages 187–190.

ACM.

Bobed, C., Yus, R., Bobillo, F., and Mena, E. (2015). Se-

mantic reasoning on mobile devices: Do androids

dream of efﬁcient reasoners? Journal of Web Seman-

tics, 35(4):167–183.

Bobillo, F., Bobed, C., and Mena, E. (2017). On the

generalization of the discovery of subsumption rela-

tionships to the fuzzy case. In Proceedings of the

26th IEEE International Conference on Fuzzy Systems

(FUZZ-IEEE 2017), pages 1–6. IEEE Press.

Some Reﬂections on the Discovery of Hyponyms between Ontologies

139

Cheatham, M. and Hitzler, P. (2013). String similarity met-

rics for ontology alignment. In Proceedings of the

12th International Semantic Web Conference (ISWC

2013), Part II, volume 8219 of Lecture Notes in Com-

puter Science, pages 294–309. Springer.

Chua, W. W. K. and Kim, J.-J. (2012). Discovering cross-

ontology subsumption relationships by using ontolog-

ical annotations on biomedical literature. In Proceed-

ings of the 3rd International Conference on Biomed-

ical Ontology (ICBO 2012), volume 897 of CEUR

Workshop Proceedings.

Ehrig, M. (2006). Ontology Alignment: Bridging the Se-

mantic Gap. Springer.

Euzenat, J. and Shvaiko, P. (2013). Ontology Matching, 2nd

Edition. Springer.

Glimm, B., Horrocks, I., Motik, B., Stoilos, G., and Wang,

Z. (2014). HermiT: An OWL 2 reasoner. Journal of

Automated Reasoning, 53(3):245–269.

Gracia, J. and Asooja, K. (2013). Monolingual and cross-

lingual ontology matching with CIDER-CL: evalua-

tion report for OAEI 2013. In Proceedings of the 8th

International Workshop on Ontology Matching (OM

2013), volume 1111 of CEUR Workshop Proceedings,

pages 109–116.

Horridge, M. and Bechhofer, S. (2011). The OWL API: A

Java API for OWL ontologies. Semantic Web Journal,

2(1):11–21.

Kang, D., Lu, J., Xu, B., Wang, P., and Li, Y. (2005).

A framework of checking subsumption relations be-

tween composite concepts in different ontologies. In

Proceedings of the 9th International Conference on

Knowledge-Based Intelligent Information and Engi-

neering Systems (KES 2005), Part I, volume 3681 of

Lecture Notes in Computer Science, pages 953–959.

Springer.

Lambrix, P. and Ivanova, V. (2013). A uniﬁed approach for

debugging is-a structure and mappings in networked

taxonomies. Journal of Biomedical Semantics, 4:10.

Lambrix, P. and Liu, Q. (2013). Debugging the missing is-a

structure within taxonomies networked by partial ref-

erence alignments. Data & Knowledge Engineering,

86:179–205.

Lambrix, P., Wei-Kleiner, F., and Dragisic, Z. (2015). Com-

pleting the is-a structure in light-weight ontologies.

Journal of Biomedical Semantics, 6:12.

Movshovitz-Attias, D., Whang, S. E., Noy, N., and Halevy,

A. (2015). Discovering Subsumption Relationships

for Web-Based Ontologies. Proceedings of the

18th International Workshop on Web and Databases

(WebDB 2015), pages 62–69.

Parsia, B., Matentzoglu, N., Gonc¸alves, R. S., Glimm, B.,

and Steigmiller, A. (2016). The OWL reasoner evalua-

tion (ORE) 2015 resources. In Proceedings of the 15th

International Semantic Web Conference ISWC 2016),

Part II, volume 9982 of Lecture Notes in Computer

Science, pages 159–167. Springer.

Sabou, M., d’Aquin, M., and Motta, E. (2008). SCARLET:

semantic relation discovery by harvesting online on-

tologies. In Proceedings of the 5th European Seman-

tic Web Conference (ESWC 2008), volume 5021 of

Lecture Notes in Computer Science, pages 854–858.

Springer.

Sirin, E., Parsia, B., Cuenca-Grau, B., Kalyanpur, A., and

Katz, Y. (2007). Pellet: A practical OWL-DL rea-

soner. Journal of Web Semantics, 5(2):51–53.

Spiliopoulos, V., Valarakos, A. G., and Vouros, G. A.

(2008). CSR: discovering subsumption relations for

the alignment of ontologies. In Proceedings of the 5th

European Semantic Web Conference (ESWC 2008),

volume 5021 of Lecture Notes in Computer Science,

pages 418–431. Springer.

Staab, S. and Studer, R., editors (2009). Handbook on On-

tologies, 2nd edition. International Handbooks on In-

formation Systems. Springer.

Steigmiller, A., Liebig, T., and Glimm, B. (2014). Kon-

clude: System description. Journal of Web Semantics,

27–28:78–85.

Tettamanzi, A. G. B., Faron-Zucker, C., and Gandon, F.

(2017). Possibilistic testing of OWL axioms against

RDF data. International Journal of Approximate Rea-

soning, 91:114–130.

Tournaire, R., Petit, J., Rousset, M., and Termier, A.

(2011). Discovery of probabilistic mappings between

taxonomies: Principles and experiments. Journal on

Data Semantics, 15:66–101.

Vennesland, A. (2017). Matcher composition for identiﬁ-

cation of subsumption relations in ontology matching.

In Proceedings of the 2017 International Conference

on Web Intelligence (WI 2017), pages 154–161. ACM.

Yus, R., Mena, E., Ilarri, S., and Illarramendi, A.

(2014). SHERLOCK: semantic management of

location-based services in wireless environments. Per-

vasive and Mobile Computing, 15:87–99.

Yus, R., Mena, E., and Solano-Bes, E. (2015). Generic

rules for the discovery of subsumption relationships

based on ontological contexts. In Proceedings of the

2015 IEEE/WIC/ACM International Joint Conference

on Web Intelligence and Intelligent Agent Technology

(WI-IAT 2015), Volume I, pages 309–312. IEEE.

Zong, N., Nam, S., Eom, J.-H., Ahn, J., Joe, H., and Kim,

H.-G. (2015). Aligning ontologies with subsumption

and equivalence relations in linked data. Knowledge-

Based Systems, 76:30–41.

ICEIS 2019 - 21st International Conference on Enterprise Information Systems

140